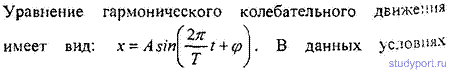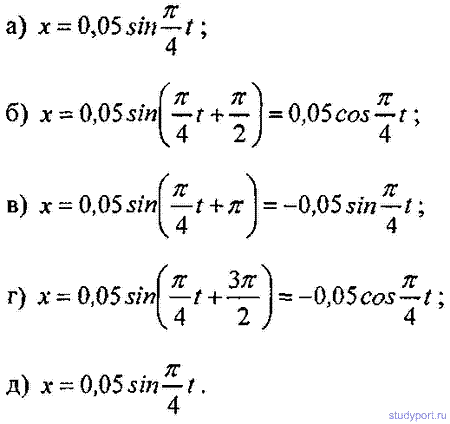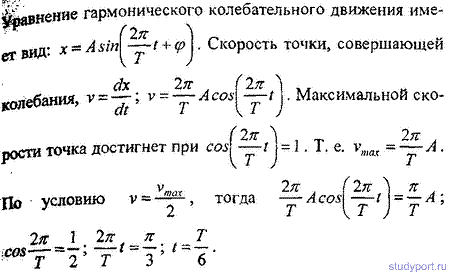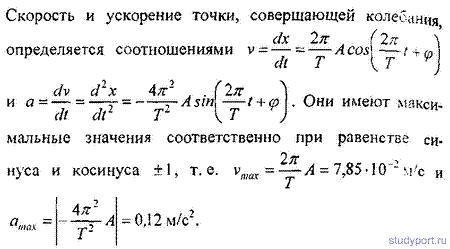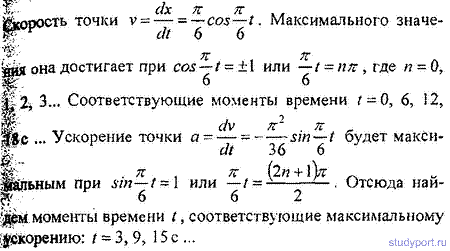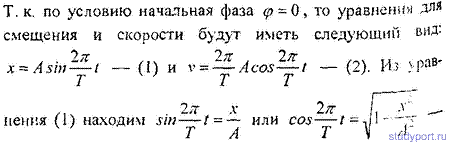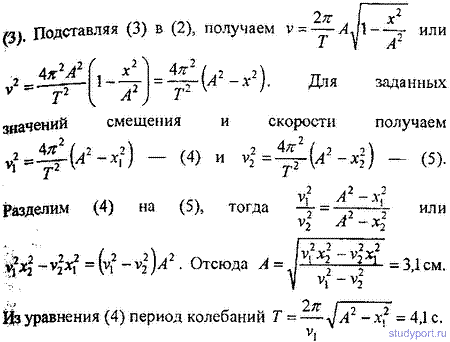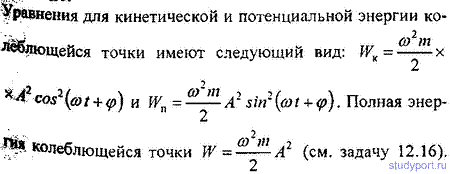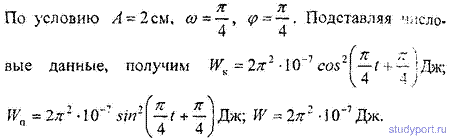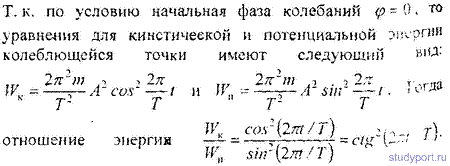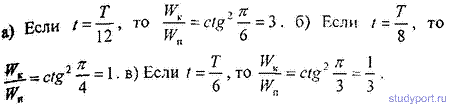Как найти максимальную силу fmax

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Страница 1 из 4

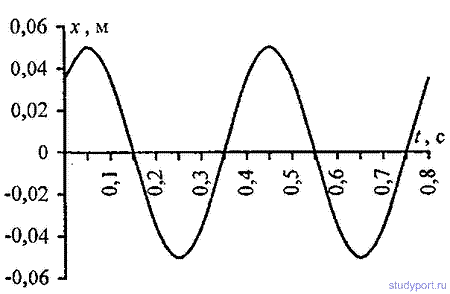
12.1. Написать уравнение гармонического колебательного движения с амплитудой A = 5см, если за время t = 1мин совершается 150 колебаний и начальная фаза колебаний φ = P/4. Начертить график этого движения.

12.2. Написать уравнение гармонического колебательного движения с амплитудой A = 0,1M, периодом T = 4с и начальной фазой φ = 0.

12.3. Написать уравнение гармонического колебательного движения с амплитудой A = 50мм, периодом T = 4с и начальной фазой φ = P/4 . Найти смещение х колеблющейся точки от положения равновесия при t = 0 и t= 1,5 с. Начертить график этого движения.

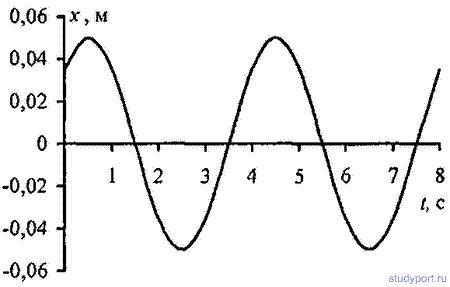
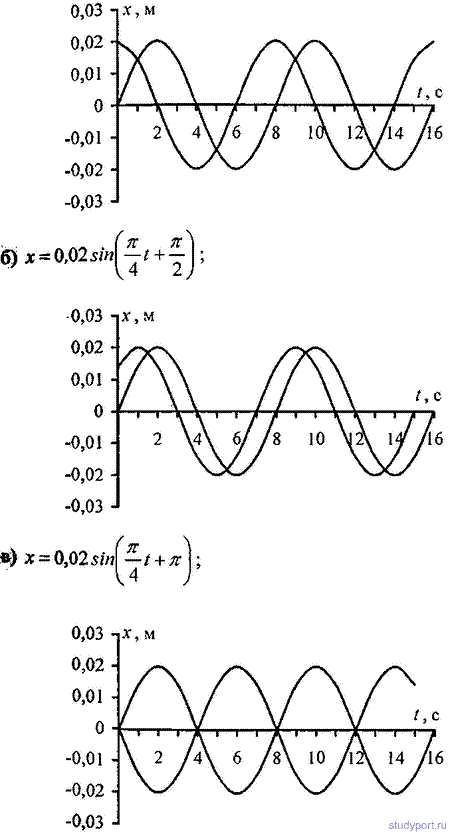
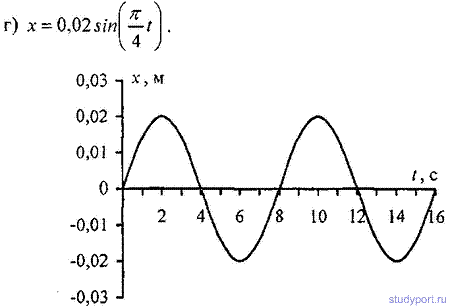
12.4. Написать уравнение гармонического колебательного движения с амплитудой А = 5 см и периодом Т = 8 с, если начальная фаза φколебаний равна: а) 0; б) P/2; ^в) P ^г) 3P/2 д) 2P. Начертить график этого движения во всех случаях.

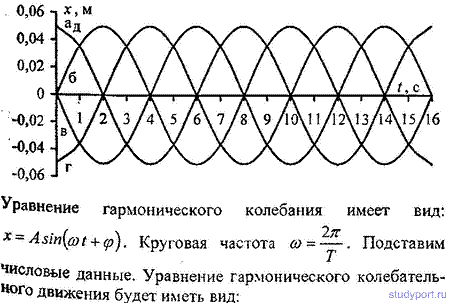
12.5. Начертить на одном графике два гармонических колебания с одинаковыми амплитудами A₁ = А₂ = 2 см и одинаковыми периодами T₁ = Т₂ = 8 с, но имеющие разность фаз φ₂–φ₁,

равную: а) P/4; о) P/2; в) P; г) 2P.

12.6. Через какое время от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний Т = 24 с, начальная фаза φ = 0.

12.7. Начальная фаза гармонического колебания φ= 0. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?

12.8. Через какое время от начала движения точка, совершающая колебательное движение по уравнению х = 7 sinP/2*t, проходит путь от положения равновесия до максимального смещения?

12.9. Амплитуда гармонического колебания /4 = 5 см, период Г = 4с. Найти максимальную скорость v_mat колеблющейся _Точ кн и ее максимальное ускорение a_тах.

12.10. Уравнение движения точки дано в виде х = 2si>i^( ^{+ СМ}‘ ^^{аити пе}Р^П0‘^а колебаний Г, максимальную скорость >_тах и максимальное ускорение a_та точки.

t2.ll. Уравнение движения точки дано в виде x = sin—t. > 6

ahftm моменты времени /, в которые достигаются максималь-

^шГскорость и максимальное ускорение.

12.12. Точка совершает гармоническое колебание. Период колебаний Т = 2 с, амплитуда А = 50 мм, начальная фаза <р = 0. .$айти скорость v точки в момент времени, когда смешение точ-^;виот положения равновесия х = 25 мм.

12.13. Написать уравнение гармонического колебательного ^юкения, если максимальное ускорение точки a_тах =49,3 см/с²,

период колебаний T = 2с и смещение точки от положения равновесия в начальный момент времени х₀ = 25 мм.

12.14. Начальная фаза гармонического колебания φ= 0 . При смещении точки от положения равновесия х₁ = 2,4 см скорость точки v₁ = 3 см/с, а при смещении x₂ = 2,8 см ее скорость v₂ = 2 см/с. Найти амплитуду А и период Т этого колебания.

12.15. Уравнение колебания материальной точки массой

m=16г имеет вид х = 0,1 sin(P/8*t+P/4)- Построить график

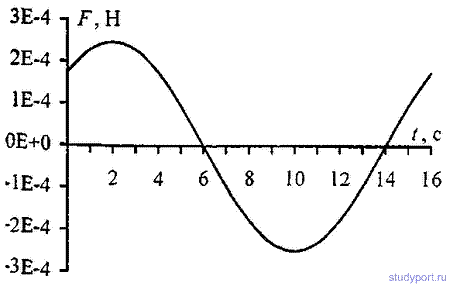
зависимости от времени t ( в пределах одного периода) силы F, действующей на точку. Найти максимальную силу F_max.

12.16. Уравнение колебаний материальной точки массой

m=10г имеет вид x=5sin(P/5*t+P/4) см. Найти максимальную силу F_mix, действующую на точку, и полную энергию Wколеблющейся точки.

12.17. Уравнение колебания материальной точки массой

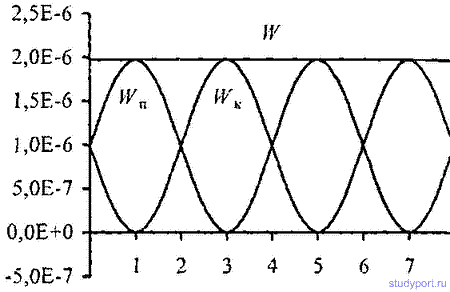
m=16г имеет вид х = 2sin(P/4*t+P/4) см. Построить график зависимости от времени t ( в пределах одного периода) кинетической W_K, потенциальной W„ и полной W энергии ТОЧКИ.

12.18. Найти отношение кинетической W_K энергии точки, совершающей гармоническое колебание, к ее потенциальной энергии W_n для моментов времени: a) t = T/12; б) t=T/8 в) t= T/6 . Начальная фаза колебаний φ= 0.

12.19. Найти отношение кинетической энергии W_K точки, совершающей гармоническое колебание, к ее потенциальной энергии W_a для моментов, когда смещение точки от положения равновесия составляет: а) х = A/4; б) х = A/2 ; в) х = А , где А — амплитуда колебаний.

12.20. Полная энергия тела, совершающего гармоническое колебательное движение, W=30 мкДж; максимальная сила, действующая на тело, F_mm. = 1,5 мН. Написать уравнение движения этого тела, если период колебаний Т = 2с и начальная фаза φ=P/3

Решение: :  Рассмотрим уравнение координаты:

x = X_m∙соs(ω∙t + φ₀),

где: х – координата тела, Х_m – амплитуда, ω – угловая скорость, φ₀ – начальная координата.
Для нахождения скорости возьмем первую производную по времени от х:

υ = – ω∙Х_m∙sin(ω∙t+ φ₀), υ = – 0,4∙π∙sin(4πt+π/4).

Для нахождения ускорения возьмем вторую производную по времени от х:

а = – ω²∙Х_m∙соs(ω∙t+ φ₀), а = -0,16∙π∙соs(4πt+π/4).

а_max = 0,5 м/с², F_max = m∙a, F_max = 0,5 м/с²∙10∙10^-3 кг, = 5∙10^-3 Н.

[ {{E}_{Kmax }}=frac{mcdot upsilon _{max }^{2}}{2},  ]

υ_max = 1,256 м/с, Е_Кmax = 7,9∙10^-3 Дж.    Ответ: 5∙10^-3 Н, 7,9∙10^-3 Дж.