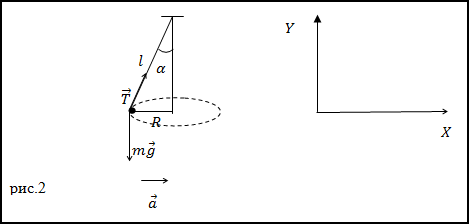Сила натяжения нити — формулировка
Определение
Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.
Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:
- создание строительного отвеса;
- установка растяжек для фиксации радиоантенн;
- поведение арматуры внутри напряженного бетона;
- устройство корабельного такелажа.
Как определить силу, формулы
Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
С неподвижно закрепленным верхним концом
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:
(F=F_{тяж}=m*g)
где m – это масса тела, а g представляет собой ускорение свободного падения.
Если нить под углом
В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.
(F_n=m*g*cos(a))
где а равен углу отклонения.
Формула с учетом ускорения и массы
В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:
(F=F_{тяж}+m*a)
Сила натяжения во вращающейся системе
Описание
Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:
- приближение к земле приводит к увеличению силы;
- во время удаления от земли сила слабеет.
Формула расчета
Рассчитать силу натяжения в условиях вращающейся системы можно так:
(F=frac{mtimes nu ^{2}}{r})
Обозначение, единица измерения
Существуют определенные стандарты для написания формулы силы натяжения. Как и другие физические силы, натяжение обозначается F. В качестве единицы измерения используют Ньютон (H)
(H=frac{kgtimes m}{c^{2}})
Примеры решения задач
Задание 1
На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.
Решение
Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.
(bar{T}+mbar{g}=mbar{a})
(bar{T}) является силой натяжения нити.
Проекция уравнения будет иметь следующий вид:
(T – mg = ma)
Данное выражение позволяет рассчитать ускорение:
(a=frac{T-mg}{m})
Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления
(a=frac{4400-4*9,8}{400})
Ответ: a = 1.2 (м/с^2)
Задание 2
На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.
Решение
Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:
(bar{T}+mbar{g}=mbar{a})
Проекции данной формулы по осям определяются следующим образом:
X: (T sin α = ma = mω2R)
Y: (-mg + T cos α = 0)
Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:
(T=frac{mg}{cos alpha })
Анализ рисунка позволяет вывести следующее уравнение:
(sin alpha = frac{R}{l}rightarrow cos alpha = sqrt{1-left(frac{R}{l} right)^{2}})
Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:
(T=frac{mg}{sqrt{1-left(frac{R}{l} right)^{2}}}= frac{mgl}{sqrt{l^{2}-R^{2}}})
Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:
(T=frac{0,1*9,8*5}{sqrt{5^{2}-3^{2}}}=1,225left(H right))
Ответ: Т=1,225 H
Определите, в каких пределах меняется сила натяжения нити математического маятника, амплитуда колебаний которого х0 много меньше длины нити l, если масса маятника m.
Спрятать решение
Решение.
Наименьшая сила натяжения нити в крайних положениях маятника и равна
при этом
где по свойству малых величин при
Таким образом, минимальное значение силы натяжения равно
Наибольшее значение сила натяжения будет иметь при вертикальном расположении нити. По второму закону Ньютона в проекции на вертикальную ось при этом
По закону сохранения энергии для крайнего положения маятника и положения равновесия откуда
при этом
Из уравнений находим, что максимальная сила натяжения нити
Учитывая из изложенного вышел, что находим максимальное значение силы натяжения нити
Таким образом, сила натяжения нити находится в пределах
Ответ:
Источник: Савченко О. Я. Задачи по физике, М.: «Наука», 1988 (№ 3.1.16)
Как определить силу натяжения нити между двумя телами
Содержание:
- Сила натяжения нити — основные понятия, обозначение, единица измерения
-
Как определить для разных условий, формулы для расчета
- Определение силы натяжения на одной нити
- Нахождение силы натяжения на нескольких нитях
- Примеры решения задач
Сила натяжения нити — основные понятия, обозначение, единица измерения
Сила натяжения — сила, которую прикладывают к концам объекта, она создает внутри объекта упругую деформацию.
Длина тела, к которому прилагают силу, обычно во много раз больше, чем толщина этого тела. Такими телами могут быть обыденные вещи — канат, веревка, трос, проволока, леска и т. д.
Приведем примеры силы натяжения нити в быту:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- применение отвеса для строительства;
- установка растяжек для того, чтобы зафиксировать радиоантенны;
- характер арматуры внутри напряженного бетона;
- устройство такелажа корабля.
Фото такелажа:
Сила натяжения нити является суммой сил, которые действуют на нить, а также противоположна по своему направлению.
F=-F
Здесь F — сила натяжения. Также встречаются обозначения силы натяжения нити с помощью букв «T» и «N». За единицу измерения у силы натяжения нити принимают Ньютон (сокращенно — H).
Как определить для разных условий, формулы для расчета
Существует множество разных вариантов определения силы напряжения нити. Рассмотрим некоторые из них.
Определение силы натяжения на одной нити
Определение силы натяжения на одной нити происходит в несколько этапов.
Первый этап — нужно определить силы на обоих концах нити. Сила натяжения этой нити или веревки считается результатом сил, которые натягивают веревку с каждого из концов.
Напомним, что сила будет равна произведению массы m на ускорение a.
Предположим, что веревка туго натянута. Каждое изменение массы или ускорения объекта, который подвешен на веревке, приведет к тому, что силы на самой веревке изменятся. Не стоит забывать также о постоянном ускорении силы тяжести. Учитывать его нужно даже тогда, когда система остается в покое, а составляющие системы являются объектами воздействия силы тяжести.
Формула 1
Можно сделать предположение, что сила натяжение этой веревки будет рассчитываться по следующей формуле: (T=(mtimes{g})+(mtimes{a})). В данной формуле (g) будет ускорением силы тяжести тела, которое поддерживается веревкой, а показатель «a» будет любым иным ускорением, которое действует на тело.
Примечание 1
Для решения большей части физических задач предполагается, что веревка идеальна. То есть, она идеально тонкая, у нее нет массы, она не способна рваться и растягиваться.
Пример 1
Рассмотрим пример, в котором груз подвешивается к деревянной балке при помощи одной веревки. Ни веревка, и груз не передвигаются — система в абсолютном покое. Чтобы груз находился в полном равновесии, сила натяжения обязана равняться силе тяжести: (F_{т}=F_{g}=mtimes{g}). Если у груза масса 10 кг, то сила натяжения будет равна (98 Н (10times9,8)).
Второй этап — нужно учитывать ускорение. Сила тяжести является не единственной силой, которая может повлиять на силу натяжения нити. Ровно такое же действие совершает каждая сила, которую прикладывают к объекту на нити с ускорением.
Пример 2
Если объект, который подвешен на кабеле или веревке, ускоряется под воздействием силы, то к силе натяжения будет добавляться сила ускорения. Представим, что на веревку подвешивают груз с массой в 10 кг, потом тянут вверх с ускорением, которое равно 1 м/с². В данном случае нужно учитывать ускорение груза вместе с ускорением силы тяжести:
(F=F+(mtimes{a}))
(F=98+(10times{1}))
(F=108 Н.)
Третий этап — нужно учитывать угловое ускорение. Тело находится на веревке, которая вращается вокруг определенной точки, ее считают условным центром (по типу маятника). Оно оказывает натяжение на нить при помощи центробежной силы.
Центробежная сила — побочная сила натяжения, вызванная веревкой. Возникает при толчке внутрь веревки таким образом, чтобы груз сохранял свое движение по дуге, а не по прямой. Центробежная сила тем больше, чем быстрее движется объект: (F=mfrac{v^{2}}{r}.)
В этой формуле m является массой, v — скоростью, r — радиусом окружности, по которой происходит движение груза.
Так как значение и направление центробежной силы изменяются в зависимости от того, как тело передвигается и изменяет собственную скорость, полное натяжение нити становится параллельным нити в центральной точке.
Важно запомнить, что сила притяжения всегда воздействует на тело, тянет его вниз. Если объект совершает амплитудное действие вертикально, полное натяжение сильнее всего будет в нижней точке дуги (точка равновесия для маятника) — когда тело достигает самой большой скорости, а слабее всего — в верхней точке дуги, когда тело начинает замедляться.
Пример 3
Приведем пример: объект не ускоряется вверх, а раскачивается как маятник. Допустим, что нить будет иметь длину 1,5 м, а груз передвигается со скоростью 2 м/с (в случае прохождения через нижнюю точку размаха). Если необходимо рассчитать силу натяжения в нижней точке дуги (в момент, когда она самая большая), то нужно найти сначала, какое давление силы тяжести ощущает на себе груз в данной точке (в состоянии покоя — 98 Н). Для нахождения центробежной силы нужно применить следующие формулы:
(F=mfrac{v^{2}}{r})
(F=10frac{2^{2}}{1,5})
(F=10times2,67=26,7 Н.)
Так полное натяжение нити будет (98+26,7=124,7 Н.)
Еще одна формула — сила натяжения способна изменяться по мере того, как проходит груз по дуге. Величина и направление центробежной силы изменяются по мере того, как тело качается. Даже если сила тяжести постоянная, результирующая сила натяжения изменяется. В тот момент, когда качающееся тело располагается не в нижней точке дуги, сила тяжести тащит тело вниз, однако сила натяжения тянет тело вверх под углом. По данной причине сила натяжения обязана находиться в противодействии лишь части силы тяжести, а не всей.
Деление силы гравитации на два вектора может помочь визуально показать данное состояние. В каждой точке дуги объекта, который раскачивается вертикально, нить создает угол (ominus) с линией, проходящей через точку равновесия, центр вращения. После того как маятник раскачивается, сила гравитации разделяется на два вектора:
- (mgsinominus), воздействует по касательной к дуге по направлению к точке равновесия;
- (mgcosominus), воздействует параллельно силе натяжения, однако в ином направлении.
Натяжение имеет возможность противостоять (mgcosominus)— только такой силе, которая направлена против нее, а не полноценной силе тяготения (кроме точки равновесия).
Пример 4
Представим пример: маятник имеет отклонение в 15° от вертикали, движение происходит со скоростью 1,5 м/с. Можно найти силу натяжения следующим образом:
- Найдем отношение силы натяжения к силе тяготения: (Т=98cos15=98(0,96)=94,08 Н).
- Найдем центробежную силу: (F=10timesfrac{1,5^{2}}{1,5}=10times1,5=15).
- Полное натяжение будет следующим: (T + F = 94,08 + 15 = 109,08 Н).
Еще одна формула — с учетом расчета трения. Каждый объект, который тянут нитью по поверхности, чувствует на себе силу замедления из-за трения, и передает данное воздействие натяжению в нити.
Сила трения между двумя телами рассчитывается, как и в другой любой ситуации, в соответствии со следующим уравнением: (F=(mu)N). В данной формуле (mu) является коэффициентом силы трения между телами, N является силой взаимодействия двух объектовсила, с которой они воздействуют друг на друга.
Примечание 2
Трение покоя — трение, возникающее в итоге попыток привести тело, находящееся в состоянии покоя, в движение.
Трение движения — трение, которое возникает в итоге попыток заставить движущееся тело продолжать это движение.
Приведем пример: представим, что груз в 10 кг не раскачивается, его тянут по горизонтальной плоскости при помощи нитиверевки. Коэффициент трения по земле будет равен 0,5. Груз передвигается со скоростью, которая постоянна, однако нужно придать телу ускорение в 1 м/с².
Нужно сделать следующие расчеты: (F=10times9,8 =98 Н.)
Сила трения будет рассчитана по формуле: (F=0,5times98=49 Н.)
Сила ускорения будет рассчитана по формуле: (F=10times1=10 Н).
Общее натяжение: (F+F=49+10=59 Н.)
Нахождение силы натяжения на нескольких нитях
Один из способов нахождения силы натяжения нити — использовать вертикальные параллельные грузы при помощи блока.
Блок — простой механизм, который состоит из подвесного диска. Это помогает ему изменять направление силы натяжения веревки.
В обычном расположении блока кабельнитьверевка начинаются от подвешенного объекта вверх к блоку, потом вниз к иному объекту. Так создаются два разных участка веревки. В таком случае натяжение на всех участках становятся одинаковыми, если оба конца натягиваются силами различных величин.
Для системы масс, подвешенных вертикально в блоке, сила натяжения будет равна (T=frac{2g(m1)(m2)}{m2+m1)}). В данной формуле g будет ускорением силы тяжести, m1 — массой первого тела, m2 — массой второго тела.
Примечание 3
Во многих физических задачах блоки являются идеальными — не обладают массой, трением, не ломаются, не отделяются от нити, не деформируются.
Приведем пример: есть два груза, которые подвешены через блок на параллельных концах нити. Один груз обладает массой в 10 кг, а второй груз обладает массой в 5 кг. В данном случае нужно произвести расчет по следующим формулам:
(T=frac{2g(m1)(m2)}{m2+m1)})
(T=frac{2(9,8)(10)(5)}{5+10)}=frac{980}{15}=65,33 Н.)
Важно понимать, что из-за того, что один груз является более тяжелым, другие элементы будут равны, данная система будет ускоряться, значит, груз в 10 кг будет передвигаться вниз, заставляя второй объект идти вверх.
Другая формула — подвешиваем грузы, берем блоки с нитями, которые не параллельны. Блоки часто используют для того, чтобы направить силу натяжения в другую сторону. Если груз подвешивается вертикально к одному концу нити, а другой конец поддерживает груз в диагональной плоскости, то система блоков — непараллельная — формирует треугольную форму с углами в точках с первым грузом, вторым, а также самим блоком. В данном случае натяжение в веревке будет зависеть от силы тяжести, силы натяжения, которая будет параллельная диагональной части нити.
Пример 5
Приведем пример: есть система с объектом в 10 кг, подвешенным вертикально, соединяющимся с грузом в 5 кг, который находится на наклонной плоскости в 60° (нет трения). Для нахождения натяжения в нити нужно составить следующие уравнения:
- Груз, который подвешивают, намного тяжелее, трение не создается, потому что мы знаем, что груз ускоряется вниз. Натяжение в веревке тащит вверх, поэтому объект ускоряется по отношению к силе (равнодействующей) (F=m1times{g}-T=98-Т.)
- Груз на плоскости, которая находится под наклоном, ускоряется вверх. Так как трения нет у данной плоскости, натяжение тянет груз вверх по плоскости, вниз объект тянет собственный вес. Часть силы, которая тянет вниз по наклонной, будет вычисляться как (mgsinominus). Можно предположить, что тело ускоряется по отношению к равнодействующей силе: (F=T-m^{2}(g)sin60=T-5(9,8)(0,87)=T-42,14).
- Если сравнять оба уравнения, то получится следующее: (98-T=T-42,12). Вычисляем T, получается, что (2T=140,14. Так T=70,07 )Н.
Последняя формула — использование нескольких нитей для того, чтобы подвесить тело. Представим, что объект подвешивается на «Y-образной» системе нитей — две нити закрепляются на потолке, встречаются в центральной точке, из которой третья нить идет с объектом. Сила натяжения третьей нити проста — обычное натяжение в итоге действия силы тяжести или же m(g).
Натяжение на других нитях отличается, они обязаны составлять в совокупности силу, которая равна силе тяжести вверх в вертикальном положении, а также равны нулю в обоих горизонтальных направлениях. Однако нужно взять во внимание, что система покоится. Натяжение в нити зависит напрямую от массы подвешенных грузов, а также от угла, на который происходит наклон каждой нити от потолка.
Пример 6
Приведем пример: в системе Y-образной нижний груз обладает массой в 10 кг, подвешивается на двух нитях, угол одной из нитей составляет 30° с потолком. Угол второй нити составляет 60°. Если необходимо найти натяжение каждой нити, необходимо рассчитать вертикальную и горизонтальную части натяжения. Для того чтобы найти T1 (натяжение с наклоном в 30°), T2 (натяжение с наклоном в 60°), нужно рассчитать:
- По законам тригонометрии, соотношение между T=m(g) и Т1, Т2 будет равно косинусу угла между нитями и потолком. Для натяжения T1 будет (cos30=0,87). Для натяжения T2 будет (cos60=0,5).
- Нужно умножить натяжение в нижней нити на косинус всех углов, чтобы найти общее натяжение. (T1=0,87times{mg}=0,87times10(9,8)=85,26) Ньютонов. (T2=0,5times{mg}=0,5times10(9,8)=49) Ньютонов.
Примеры решения задач
Задача
Нерастяжимая, с малым весом нить может выдержать силу натяжения в T=4400 Н. Какое максимальное ускорение может быть, чтобы поднять груз с массой в 400 кг? Груз подвешивают на данную нить. Нужно, чтобы нить при этом не разорвалась, и не произошло падение груза.
На рисунке ниже изображены все силы, которые воздействуют на груз.
Запишем второй закон Ньютона. Объект считается материальной точкой, все силы прикладываются к центру масс объекта: (T+mg=ma).
Далее записываем проекции уравнения на ось Y: (T-mg=ma).
Получаем уравнение: (a=frac{T-mg}{m}).
Произведем расчеты: (a=frac{4400-400times9,8}{400}=1,2 м/с²).
Ответ: 1,2 м/с².
Содержание:
- Определение и формула силы натяжения нити
- Единицы измерения силы натяжения нити
- Примеры решения задач
Определение и формула силы натяжения нити
Определение
Силу натяжения определяют как равнодействующую сил $(bar{R})$, приложенных к нити, равную ей по модулю,
но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее
обозначают и просто $bar{F}$ и
$bar{T}$, и
$bar{N}$ . Математически определение для силы натяжения нити можно записать как:
$$bar{T}=-bar{R}(1)$$
где $bar{R}$ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).
Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.
Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая
нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют
закон Гука, при этом:
$$T=F_{u p r}=k Delta l(2)$$
где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.
Единицы измерения силы натяжения нити
Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н
В СГС: [T]=дин
Примеры решения задач
Пример
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением
можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?
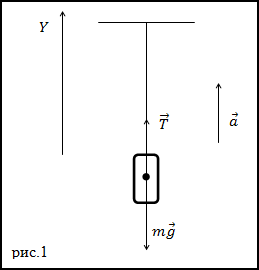
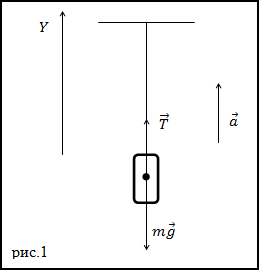
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона.
Тело будем считать материальной точкой, все силы приложенными к центру масс тела.
$$bar{T}+m bar{g}=m bar{a}(1.1)$$
где $bar{T}$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:
$$T-m g=m a(1.2)$$
Из выражения (1.2) получим ускорение:
$$a=frac{T-m g}{m}$$
Все данные в задаче представлены в единицах системы СИ, проведем вычисления:
$$a=frac{4400-400 cdot 9,8}{400}=1,2 mathrm{~m} / mathrm{c}^{2}$$
Ответ. a=1,2м/с2

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности,
расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с
центростремительным ускорением:
$$bar{T}+m bar{g}=m bar{a}(2.1)$$
Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:
$$
begin{array}{c}
X: quad T sin alpha=m a=m omega^{2} R(2.2) \
Y: quad-m g+T cos alpha=0
end{array}
$$
Из уравнения (2.3) получим формулу для модуля силы натяжения нити:
$$T=frac{m g}{cos alpha}(2.4)$$
Из рис.2 видно, что:
$$sin alpha=frac{R}{l} rightarrow cos alpha=sqrt{1-left(frac{R}{l}right)^{2}}$$
Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:
$$T=frac{m g}{sqrt{1-left(frac{R}{l}right)^{2}}}=frac{m g l}{sqrt{l^{2}-R^{2}}}$$
Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
$$T=frac{0,1 cdot 9,8 cdot 5}{sqrt{5^{2}-3^{2}}}=1,225(H)$$
Ответ. T=1,225 Н
Читать дальше: Формула силы тяги.
nkerom
Вопрос по физике:
Найдите максимальную силу натяжения нити, если верёвка может выдержать груз массой 5 кг. При подъеме его с ускорением 4 м/с^2
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
ckimp832
Fн = P
P = m*(g + a) = 5 кг * (10 м/с² +4 м/с²) = 70 Н
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.