2020-04-04
Источник тока с ЭДС $mathcal{E}$ и внутренним сопротивлением $r$ замыкают на реостат. При каком сопротивлении реостата на нем будет выделяться максимальная мощность? Чему она равна?
Решение:
Мощность, выделяющаяся на реостате, выражается формулой
$P = I^{2}R = frac{ mathcal{E}^{2}}{(R + r)^{2} }R$.
Это выражение стремится к нулю как при $R rightarrow 0$, так и при $R rightarrow infty$. Значит, оно должно быть максимально при некотором $R$. Кто научился хорошо дифференцировать, может попробовать найти максимум этого выражения с помощью производной. Мы поступим иначе. Преобразуем выражение для мощности, разделив на $R$ числитель и знаменатель:
$P = frac{ mathcal{E}^{2}}{R + 2r + frac{r^{2} }{R}}$.
Из неравенства о среднем арифметическом и среднем геометрическом следует, что минимум выражения $R + frac{r^{2}}{R}$, а значит максимум мощности, достигается при равенстве слагаемых, т.е. при
$R = r$.
Максимальная мощность при этом будет равна
$P_{max} = frac{ mathcal{E}^{2} }{4r}$.
Если бы мы не додумались до указанного преобразования, то могли бы пойти другим знакомым путем. Будем считать исследуемое выражение для $P(R)$ уравнением для $R$ при заданной $P$, тогда при $P = P_{max}$ это уравнение должно иметь одно решение, т.е. дискриминант должен обратиться в ноль. Проделайте вычисления самостоятельно и убедитесь, что получается правильный ответ. Мы же обозначим еще один подход к этой задаче.
Мощность во внешней цепи можно выразить не как функцию $R$, а как функцию силы тока $I$:
$P = mathcal{E} I – I^{2}r$
(мощность, переданная во внешнюю цепь, есть полная мощность источника минус тепловая мощность на внутреннем сопротивлении источника). Эта формула имеет даже более общий характер, чем формула $P(R)$, она применима при любой нагрузке внешней цепи. Зависимость $P(I)$ есть квадратичная функция с корнями $I_{1} = 0$ и $I_{2} = frac{ mathcal{E}}{r}$, имеющая при $I = frac{ mathcal{E}}{2r}$ максимальное значение $P_{max} = frac{ mathcal{E}^{2} }{4r}$.
Резисторы есть в любой электрической схеме. Но в разных схемах протекают различной величины ток. Не могут же одни и те же элементы работать при 0,1 А и при 100 А. Ведь при прохождении тока сопротивление греется. Чем выше ток, тем более интенсивный нагрев. Значит, и резисторы должны быть на разную величину тока. Так и есть. Отображает их способность работать при различных токах такой параметр, как мощность резистора. На деталях покрупнее она указывается прямо на корпусе. Для мелких корпусов есть другой метод определения (см. ниже).
Содержание статьи
- 1 Что такое мощность резистора
- 2 Стандартный ряд мощностей резисторов и их обозначение на схемах
- 3 Как определить по внешнему виду
- 3.1 Мощность SMD-резисторов
- 4 Как рассчитать мощность резистора в схеме
- 5 Как подобрать резистор на замену
Что такое мощность резистора
Мощность определяется как произведение силы тока на напряжение: P = I * U и измеряется в ваттах (закон Ома). Рассеиваемая мощность резистора — это максимальный ток, который сопротивление может выдерживать длительное время без ущерба для работоспособности. То есть, этот параметр надо выбирать для каждой схемы отдельно — по максимальному рабочему току.
Как определить мощность резистора по внешнему виду: надо знать соответствие размеров и мощностей
Физически рассеиваемая мощность резистора — это то количество тепла, которое его корпус может «отдать» в окружающую среду и не перегреться при этом до фатальных последствий. При этом, нагрев не должен слишком сильно влиять на сопротивление резистора.
Стандартный ряд мощностей резисторов и их обозначение на схемах
Обратите внимание, что резисторы одного номинала могут быть с разной мощностью рассеивания. Этот параметр зависит от технологии изготовления, материала корпуса. Есть определенный ряд мощностей и их графическое обозначение по ГОСТу.
| Вт | Условное обозначение не схемах |
|---|---|
| мощность резистора 0,05 Вт |
Как обозначается на схеме мощность рассеивания резистора 0,05 Вт |
| мощность резистора 0,125 Вт |
Мощность резистора 0,125 Вт на схеме |
| мощность резистора 0,025 Вт |
Как на схеме выглядит резистор мощностью 0,25 Вт |
| мощность резистора 0,5 Вт |
Так на схеме обозначается резистор мощностью 0,5 Вт |
| мощность резистора 1 Вт |
Мощность резистора 1 Вт схематически обозначается так |
| мощность резистора 2 Вт |
Рассеиваемая на резисторе мощность 2 Вт |
| мощность резистора 5 Вт |
Обозначение на схеме мощности резистора 5 Вт |
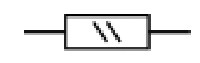
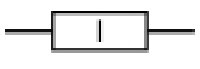
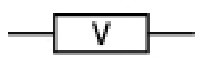
Графическое обозначение мощности резисторов на схеме — черточки и римские цифры, нанесенные на поверхность сопротивления. Самое малое стандартное значение 0,05 Вт, самое большое — 25 Вт, но есть и более мощные. Но это уже специальная элементная база и в бытовой аппаратуре не встречается.
Как обозначаются мощность маломощных резисторов надо просто запомнить. Это косые линии на прямоугольниках, которыми обозначают сопротивления на схемах. Количество косых черточек обозначает количество четвертей дюйма. При номиналах сопротивлений от 1 Вт на изображении ставятся римские цифры: I, II, III, V, VI и т.д. Цифра эта и обозначает мощность резистора в ваттах. Тут немного проще, так как соответствие прямое.
Как определить по внешнему виду
На принципиальной схеме указана нужная мощность резистора — тут все понятно. Но как определить мощность сопротивления по внешнему виду на печатной плате? Вообще, чем больше размер корпуса, тем больше тепла он рассеивает. На достаточно крупных по размеру сопротивлениях указывается номинальное сопротивление и его мощность в ваттах.
Тут есть некоторая путаница, но не все так страшно. На отечественных сопротивлениях рядом с цифрой ставят букву В. В зарубежных ставят W. Но эти буквы есть не всегда. В импортных может стоять V или SW перед цифрой. Еще в импортных может тоже стоять буква B, а в отечественных МЛТ может не стоять ничего или буква W. Запутанная история, конечно. Но с опытом появляется хоть какая-то ясность.
Как определить мощность резистора: стоит в маркировке
А ведь есть маленькие резисторы, на которых и номинал-то с трудом помещается. В импортных он нанесен цветными полосками. Как у них узнать мощность рассеивания?
В старом ГОСТе была таблица соответствий размеров и мощностей. Резисторы отечественного производства по прежнему делают в соответствии с этой таблицей. Импортные, кстати, тоже, но они по размерам чуть меньше отечественных. Тем не менее их также можно идентифицировать. Если сомневаетесь, к какой группе отнести конкретный экземпляр, лучше считать что он имеет более низкую способность рассеивать тепло. Меньше шансов, что деталь скоро перегорит.
| Тип резистора | Диаметр, мм | Длинна, мм | Рассеиваемая мощность, Вт |
|---|---|---|---|
| ВС | 2,5 | 7,0 | 0,125 |
| УЛМ, ВС | 5,5 | 16,5 | 0,25 |
| ВС | 5,5 | 26,5 | 0,5 |
| 7,6 | 30,5 | 1 | |
| 9,8 | 48,5 | 2 | |
| 25 | 75 | 5 | |
| 30 | 120 | 10 | |
| КИМ | 1,8 | 3,8 | 0,05 |
| 2,5 | 8 | 0,125 | |
| МЛТ | 2 | 6 | 0,125 |
| 3 | 7 | 0,125 | |
| 4,2 | 10,8 | 0,5 | |
| 6,6 | 13 | 1 | |
| 8,6 | 18,5 | 2 |
С размерами сопротивлений и их мощностью вроде понятно. Не все так однозначно. Есть резисторы большого размера с малой рассеивающей способностью и наоборот. Но в таких случаях, проставляют этот параметр в маркировке.
Мощность SMD-резисторов
SMD-компоненты предназначены для поверхностного монтажа и имеют миниатюрные размеры. Мощность резисторов SMD определяется по размерам. Также она есть в характеристиках, но необходимо знать серию и производителя. Таблица мощности СМД резисторов содержит наиболее часто встречающиеся номиналы.
Размеры SMD-резисторов — вот по какому признаку можно определить мощность этих элементов
| Код imperial | Код metrik | Длинна inch/mm | Ширина inch/mm | Высота inch/mm | Мощность, Вт |
|---|---|---|---|---|---|
| 0201 | 0603 | 0,024/0,6 | 0,012/0,3 | 0,01/0,25 | 1/20 (0,05) |
| 0402 | 1005 | 0,04/1,0 | 0,02/0,5 | 0,014/0,35 | 1/16 (0,062) |
| 0603 | 1608 | 0,06/1,55 | 0,03/0,85 | 0,018/0,45 | 1/10 (0,10) |
| 0805 | 2112 | 0,08/2,0 | 0,05/1,2 | 0,018/0,45 | 1/8 (0,125) |
| 1206 | 3216 | 0,12/3,2 | 0,06/1,6 | 0,022/0,55 | 1/4 (0,25) |
| 1210 | 3225 | 0,12/3,2 | 0,10/2,5 | 0,022/0,55 | 1/2 (0,50) |
| 1218 | 3246 | 0,12/3,2 | 0,18/4,6 | 0,022/0,55 | 1,0 |
| 2010 | 5025 | 0,20/2,0 | 0,10/2,5 | 0,024/0,6 | 3/4 (0,75) |
| 2512 | 6332 | 0,25/6,3 | 0,12/3,2 | 0,024/0,6 | 1,0 |
В общем-то, у этого типа радиоэлементов нет другого оперативного способа определения тока, при котором они могут работать, кроме как по размерам. Можно узнать по характеристикам, но их найти не всегда просто.
Как рассчитать мощность резистора в схеме
Чтобы рассчитать мощность резисторов в схеме, кроме сопротивления (R) необходимо знать силу тока (I). На основании этих данных можно рассчитать мощность. Формула обычная: P = I² * R. Квадрат силы тока умножить на сопротивление. Силу тока подставляем в Амперах, сопротивление — в Омах.
Если номинал написан в килоомах (кОм) или мегаомах (мОм), его переводим в Омы. Это важно, иначе будет неправильная цифра.
Схема последовательного соединения резисторов
Для примера рассмотрим схему на рисунке выше. Последовательное соединение сопротивлений характерно тем, что через каждый отдельный резистор цепи протекает одинаковый ток. Значит мощность сопротивлений будет одинаковой. Последовательно соединенные сопротивления просто суммируется: 200 Ом + 100 Ом + 51 Ом + 39 Ом = 390 Ом. Ток рассчитаем по формуле: I = U/R. Подставляем данные: I = 100 В / 390 Ом = 0,256 А.
По расчетным данным определяем суммарную мощность сопротивлений: P = 0,256² * 390 Ом = 25,549 Вт. Аналогично рассчитывается мощность каждого из резисторов. Например, рассчитаем мощность резистора R2 на схеме. Ток мы знаем, его номинал тоже. Получаем: 0,256А² * 100 Ом = 6,55 Вт. То есть, мощность этого резистора должна быть не ниже 7 Вт. Брать с более низкой мощностью точно не стоит — быстро перегорит. Если позволяет конструктив прибора, то можно поставить резистор большей мощности, например, на 10 Вт.
Есть резисторы серии МЛТ, в которых мощность рассеивания тепла указана сразу после названия серии без каких-либо букв. В данном случае — МЛТ-2 означает, что мощность этого экземпляра 2 Вт, а номинал 6,8 кОм.
При параллельном подключении расчет аналогичен. Нужно только правильно рассчитать ток, но это тема другой статьи. А формула расчета мощности резистора от типа соединения не зависит.
Как подобрать резистор на замену
Если вам необходимо поменять резистор, брать надо либо той же мощности, либо выше. Ни в коем случае не ниже — ведь резистор и без того вышел из строя. Происходит это обычно из-за перегрева. Так что установка резистора меньшей мощности исключена. Вернее, вы его поставить можете. Но будьте готовы к тому, что скоро его снова придется менять.
Примерно определить мощность резистора можно по размерам
Если место на плате позволяет, лучше поставить деталь с большей мощностью рассеивания, чем была у заменяемой детали. Или поднять резистор той же мощности повыше (можно вообще не подрезать выводы) — чтобы охлаждение было лучше. В общем, при замене резистора, мощность берем либо ту же, либо выше на шаг.
Лекция 8. Уравнение силового баланса
План лекции
8.1. Силовой баланс автомобиля
8.2. Силовой баланс автомобиля при различной нагрузке
8.3. Динамические факторы автомобиля
8.4. Динамическая характеристика автомобиля
8.5. Динамический паспорт автомобиля
8.1. Силовой баланс автомобиля
Представим уравнение движения автомобиля в следующем виде:
РТ = РД + РВ+РИ. (8. 1)
Рекомендуемые материалы
В такой форме оно называется уравнением силового баланса автомобиля и выражает соотношение между тяговой силой на ведущих колесах и силами сопротивления движению.
На основании уравнения (8. 1) строится график силового баланса, позволяющий оценивать тягово-скоростные свойства автомобиля.
При построении графика силового баланса (рис. 8.1) сначала строят тяговую характеристику автомобиля. Затем наносят зависимость силы сопротивления дороги от скорости. Если коэффициент сопротивления дороги — постоянная величина, то указанная зависимость представляет собой прямую линию, параллельную оси абсцисс, а при непостоянном коэффициенте сопротивления дороги — кривую параболической формы. После этого от кривой, характеризующей силу сопротивления дороги, откладывают вверх значения силы сопротивления воздуха при различных скоростях движения. Полученная зависимость называется графиком силового баланса автомобиля.
Кривая суммарного сопротивления дороги и воздуха РД + РВ определяет тяговую силу РТ, необходимую для движения автомобиля с постоянной скоростью. При любой скорости движения отрезок Р3, заключенный между кривыми РТ (на рис. 8.1 — РтШ) и РД + РВ, характеризует запас силы по тяге. Он может быть использован при данной скорости для разгона, преодоления дополнительного дорожного сопротивления (например, подъема) или перевозки дополнительного груза (буксировка прицепа). При одной и той же скорости движения запас силы по тяге на низших передачах больше, чем на высших. Следовательно, при увеличении передаточного числа трансмиссии запас силы по тяге возрастает. Именно поэтому движение в тяжелых дорожных условиях осуществляется на низших передачах.
Рис. 8.1. График силового баланса автомобиля:
•PTI, РТII, РТIII — тяговые силы на I, II, III передачах, PTI — тяговая сила на I передаче при уменьшенной подаче топлива; v1, — одно из возможных значений скорости автомобиля
С помощью графика силового баланса можно решать различные задачи, связанные с изучением тягово-скоростных свойств автомобиля. Рассмотрим некоторые из этих задач.
Определение максимальной скорости. Максимальная скорость vmax движения автомобиля определяется точкой пересечения кривой тяговой силы РТ на высшей передаче и суммарной кривой сил сопротивления РД + РВ. В этой точке запас силы по тяге и ускорение автомобиля j равны нулю. Скорость его движения максимальна, так как ее дальнейшее увеличение невозможно.
Определение максимальной силы сопротивления дороги.
Максимальная сила сопротивления дороги, которую преодолевает автомобиль, двигаясь равномерно с любой скоростью, определяется как разность тяговой силы и силы сопротивления воздуха:
Определение максимального преодолеваемого подъема.
Для нахождения максимального подъема, который может преодолеть автомобиль при заданной постоянной скорости на любой передаче, необходимо нанести на график суммарную кривую сил сопротивления качению и воздуха РK + РВ и определить максимальную силу сопротивления подъему:
Зная эту силу, можно найти максимальный угол подъема αmах.
Определение ускорения движения. Для нахождения ускорения, которое может развить автомобиль на заданной дороге при любой скорости, нужно определить силу сопротивления разгону:
Зная значение этой силы, можно найти ускорение, которое способен развить автомобиль при выбранной скорости движения на заданной дороге.
Определение возможности буксования ведущих колес. С этой целью находят силу сцепления Рсц колес с дорогой при известном коэффициенте сцепления <φх. Значение силы сцепления откладывают на оси ординат и на этом уровне проводят горизонталь.
В области, расположенной над проведенной прямой, Рсц < Рт, следовательно, трогание автомобиля с места на I передаче невозможно, а при движении неизбежна остановка.
В области, находящейся под данной прямой, выполняется условие Рсц > РТ. Следовательно, при полной нагрузке двигателя (при полной подаче топлива) безостановочное движение автомобиля без пробуксовки ведущих колес невозможно лишь на I передаче. Для движения без буксования ведущих колес на I передаче необходимо уменьшить подачу топлива и, следовательно, тяговую силу на ведущих колесах (см. кривую Р’T1 на рис. 8.1).
8.2. Силовой баланс автомобиля при различной нагрузке
Практическое применение рассмотренного выше силового баланса автомобиля затруднительно, так как для определения показателей тягово-скоростных свойств необходимо построить отдельные графики для разных значений нагрузки на автомобиль. Это связано с тем, что при изменении нагрузки сила сопротивления дороги РД и суммарная сила сопротивления дороги и воздуха РД + РВв изменяются и для их вычисления требуются дополнительные затраты времени.
Более универсальным является рассмотренный ниже метод силового баланса автомобиля при различной нагрузке. В этом случае строится только один график силового баланса для всех эксплуатационных нагрузок автомобиля.
В основу метода силового баланса автомобиля при различной нагрузке положено уравнение его движения (8.20), представленное в следующем виде:
или
где 
Безостановочное движение автомобиля возможно при выполнении условия
Для оценки тягово-скоростных свойств при различной нагрузке на автомобиль строится график его силового баланса (рис. 8.2).
Методика построения графика силового баланса такова:
• строят тяговую характеристику автомобиля
• на график тяговой характеристики наносят кривые свободной тяговой силы Рсв для различных передач;
• слева от графика тяговой характеристики автомобиля строят вспомогательный график для определения коэффициента сопротивления дороги ψ. С этой целью ось абсцисс продолжают влево и на нее в произвольном масштабе наносят шкалу коэффициента сопротивления дороги ψ;
• справа от графика тяговой характеристики автомобиля строят вспомогательный график для определения коэффициента сцепления колес с дорогой φх. Для этого ось абсцисс продолжают вправо и на нее в произвольном масштабе наносят шкалу коэффициента сцепления φх;
• из начала координат вспомогательных графиков проводят лучи, соответствующие различным значениям нагрузки на автомобиль.
Рис. 8.2. График силового баланса автомобиля при различной
нагрузке:
I — IV — передачи; O1 — начало координат левого и центрального графиков; О2 — начало координат правого графика; ψ1— ψ3, ψx1 ,— ψ хз — значения коэффициентов сопротивления и продольного сцепления различных дорог; vt — v3 — значения скорости автомобиля;———-тяговая сила РТ;———-свободная тяговая сила РСВ
Для определения углов наклона лучей нагрузки на левом вспомогательном графике задают какое-либо значение свободной тяговой силы Рсв, откладывают это значение на оси ординат и проводят горизонтальную прямую. Затем по формуле
находят значения коэффициента у для разных нагрузок (Н = 0 % при G = G0;
Н = 100 % при G = G а и т.д., где G — вес автомобиля при заданной нагрузке Н, представляющей собой долю груза, %, который может быть перевезен на данном автомобиле; G0 — вес снаряженного (порожнего) автомобиля; Gа, — вес автомобиля при полной нагрузке). Из точек, соответствующих найденным значениям коэффициента у, проводят вертикали до пересечения с горизонтальной линией, проходящей через точку, отвечающую выбранному значению свободной тяговой силы Рсв. Полученные точки пересечения соединяют с началом координат левого вспомогательного графика и у каждого луча указывают соответствующее значение нагрузки на автомобиль, % или пасс.
Для определения углов наклона лучей нагрузки на автомобиль на правом вспомогательном графике задают какое-либо значение тяговой силы РТ, откладывают это значение на оси ординат и проводят горизонтальную линию. Затем по формуле
находят значения коэффициента сцепления для разных нагрузок (Н = 0 % при < G 02; Н = 100 % при Ga2 и т.д., где G2 — вес, приходящийся на задние (ведущие) колеса автомобиля при заданной нагрузке; G02 и Gа2 — вес, приходящийся на ведущие колеса соответственно снаряженного автомобиля и автомобиля при полной нагрузке).
Вес автомобиля призаданной нагрузке
где Gгp — полезная нагрузка на автомобиль, Н (грузовые автомобили) или пасс, (легковые автомобили, автобусы). Вес на ведущие колеса при заданной нагрузке
где G02 и Ga2 — вес приходящийся на ведущие колеса соответственно снаряженного автомобиля и с полной нагрузкой, Н.
Через точки, соответствующие найденным значениям коэффициента сцепления φх при разных нагрузках на автомобиль и ведущие колеса, проводят вертикальные линии до пересечения с горизонталью, которая проходит через точку, отвечающую выбранному значению тяговой силы РТ. Полученные точки пересечения соединяют с началом координат правого вспомогательного графика и у соответствующих лучей указывают значения нагрузки на автомобиль, % или пасс. При расчете нагрузок используют значения G02 и Ga2 из технической характеристики автомобиля.
С помощью графика силового баланса автомобиля при различной нагрузке можно решить ряд задач по анализу и оценке тягово-скоростных свойств автомобиля. При этом из четырех параметров (скорость автомобиля v, нагрузка на автомобиль Н, коэффициент сопротивления дороги ψ и коэффициент сцепления колес с дорогой φх) можно определить два любых параметра по двум другим заданным. При этом найденные значения коэффициента сопротивления дороги ψ являются максимально возможными, а значения коэффициента сцепления φх — минимально необходимыми для движения автомобиля при различных нагрузках.
Метод силового баланса удобен для анализа тягово-скоростных свойств конкретного автомобиля. Сравнивать же разные автомобили этим методом затруднительно, так как значения тяговой силы у них могут отличаться в несколько раз, да и масса их также неодинакова.
Поэтому для сравнительной оценки тягово-скоростных свойств разных автомобилей удобнее пользоваться их динамическими факторами и динамическими характеристиками.
8.3. Динамические факторы автомобиля
У автомобиля различают динамический фактор по тяге и динамический фактор по сцеплению. Это безразмерные величины, выражаемые в долях единицы или процентах.
Динамическим фактором по тяге называется отношение разности тяговой силы и силы сопротивления воздуха к весу автомобиля:
Значения динамического фактора по тяге позволяют судить о тягово-скоростных свойствах конкретного автомобиля при разных нагрузках и сравнивать тягово-скоростные свойства различных автомобилей. При этом чем больше динамический фактор по тяге, тем лучше тягово-скоростные свойства и выше проходимость автомобиля: он способен развивать большие ускорения, преодолевать более крутые подъемы и буксировать прицепы большей массы.
Максимальные значения динамического фактора по тяге составляют 0,3…0,45 для автомобилей ограниченной проходимости и 0,6…0,8 — для автомобилей высокой проходимости.
Динамический фактор по тяге часто называют просто динамическим фактором.
Его значение ограничено вследствие наличия сцепления колес с дорогой. Для безостановочного движения автомобиля без пробуксовки ведущих колес необходимо выполнение следующего условия:
где D.сц — динамический фактор по сцеплению.
Динамическим фактором по сцеплению называется отношение разности силы сцепления и силы сопротивления воздуха к весу автомобиля:
Так как буксование ведущих колес обычно происходит при малой скорости движения и большой тяговой силе, то влиянием силы сопротивления воздуха можно пренебречь. Тогда динамический фактор по сцеплению
где G2 — вес, приходящийся на ведущие колеса.
Для установления связи между динамическим фактором и условиями движения представим уравнение движения автомобиля в следующем виде:
или
Разделив обе части последнего уравнения на вес G, получим уравнение силового баланса автомобиля в безразмерной форме:

При равномерном движении ускорение равно нулю. Тогда
8.4. Динамическая характеристика автомобиля
Динамической характеристикой автомобиля называется зависимость динамического фактора по тяге от скорости на различных передачах. Динамическая характеристика, представленная на рис. 8.3, свидетельствует о том, что динамический фактор по тяге на низших передачах имеет большую величину, чем на высших. Это связано с тем, что на низших передачах тяговая сила увеличивается, а сила сопротивления воздуха уменьшается.
Поскольку при равномерном движении D = ψ, ордината каждой точки кривых динамического фактора, приведенных на динамической характеристике, определяет значение коэффициента сопротивления дороги ψ.
Рис. 8.3. Динамическая характеристика автомобиля:
I—III — передачи; I’—I передача при уменьшенной подаче топлива; vmax — максимальная скорость автомобиля; v max(ψ)— максимальная скорость автомобиля для конкретных дорожных условий
Так, например, точка Dv, соответствующая значению динамического фактора при максимальной скорости vmах, определяет коэффициент сопротивления дороги ψv, которое может преодолеть автомобиль при этой скорости, а ординаты точек максимума кривых динамического фактора представляют собой максимальные значения коэффициента сопротивления дороги, преодолеваемого на каждой передаче.
С помощью динамической характеристики можно решать различные задачи по определению тягово-скоростных свойств автомобиля. Рассмотрим некоторые из этих задач.
Определение максимальной скорости движения автомобиля при заданном коэффициенте сопротивления дороги у. На оси ординат откладываем значение коэффициента сопротивления дороги ψ, характеризующее данную дорогу, и проводим прямую, параллельную оси абсцисс, до пересечения с кривой динамического фактора D. Точка пересечения и будет соответствовать максимальной скорости, которую может развить автомобиль при заданном коэффициенте сопротивления дороги ψ.
Определение максимального подъема, преодолеваемого на дороге с заданным коэффициентом сопротивления качению f Для нахождения максимального подъема, который может преодолеть автомобиль при постоянной скорости на любой передаче на дороге с коэффициентом сопротивления качению f на оси ординат откладываем значение коэффициента f и проводим прямую, параллельную оси абсцисс. Разность между максимальным значением динамического фактора Dmax на любой передаче и значением коэффициента f соответствует максимальному подъему, преодолеваемому на выбранной передаче:
Определение максимального ускорения автомобиля при заданном коэффициенте сопротивления дороги у. Для нахождения максимального ускорения jmax, которое может развить автомобиль на любой передаче, необходимо найти разность между максимальным значением динамического фактора на выбранной передаче и
значением коэффициента сопротивления дороги (Dmax – ψ). Зная эту разность, можно определить значение максимального ускорения по формуле (8. 2)
Определение возможности буксования ведущих колес. При решении данной задачи необходимо сопоставить динамические факторы по тяге и сцеплению. С этой целью определяют значение динамического фактора по сцеплению для заданного коэффициента сцепления φх. Найденное значение откладывают на оси ординат и проводят горизонтальную прямую.
В области, расположенной над проведенной прямой, Dcц < D, следовательно, трогание автомобиля с места на I передаче невозможно, а при его движении неизбежна остановка.
В области, находящейся под этой прямой, выполняется условие Dcц < D, следовательно, при полной нагрузке двигателя, или при полной подаче топлива, движение без пробуксовки ведущих колес невозможно лишь на I передаче. Для движения без буксования ведущих колес на I передаче необходимо уменьшить подачу топлива и динамический фактор по тяге (см. кривую I’ на рис. 8.3).
При определении тягово-скоростных свойств динамическая характеристика строится для автомобиля с полной нагрузкой.
8.5. Динамический паспорт автомобиля
Неудобство использования динамической характеристики автомобиля состоит в том, что для оценки тягово-скоростных свойств необходимо строить отдельные графики для каждого значения нагрузки на автомобиль.
Более универсальным и удобным является динамический паспорт автомобиля (рис. 8.4), который позволяет оценить тягово-скоростные свойства при различных нагрузках на автомобиль.
Динамическим паспортом автомобиля называется его динамическая характеристика с номограммой нагрузок и графиком контроля буксования.
Методика построения динамического паспорта автомобиля такова:
. строят динамическую характеристику автомобиля с полной нагрузкой;
• строят номограмму нагрузок, характеризующую изменение динамического фактора по тяге D в зависимости от нагрузки на автомобиль;
. строят график контроля буксования. Он включает в себя зависимости динамического фактора по сцеплению Dcц от нагрузки на автомобиль при разных значениях коэффициента сцепления колес с дорогой φх.
Рис. 8.4. Динамический паспорт автомобиля:
О — начало координат динамической характеристики; 0 — начало координат графика контроля буксования; А, В — характерные точки построения; DI,— DIV — динамический фактор по тяге на I—IV передачах; Н2 — искомая нагрузка; v1 v2 — значения скорости автомобиля;_______динамический фактор по тяге при разных нагрузках;———-динамический фактор по сцеплению при разных коэффициентах продольного сцепления
При построении номограммы нагрузок на автомобиль ось абсцисс его динамической характеристики продолжают влево и на ней в произвольном масштабе откладывают значения нагрузки на автомобиль, % (для грузовых автомобилей) или пасс, (для легковых автомобилей и автобусов). Из точки, соответствующей нулевой нагрузке, проводят вертикаль, на которой откладывают значения динамического фактора по тяге D0 для снаряженного автомобиля (без груза или без пассажиров) в масштабе, определяемом по формуле

Затем сплошными линиями соединяют одинаковые значения динамических факторов
График контроля буксования строят на номограмме нагрузок автомобиля. С помощью этого графика сопоставляют динамические факторы по тяге D и сцеплению D.cц с целью определения возможности буксования ведущих колес при различных нагрузках на автомобиль.
Лекция “15 Свойства вероятности” также может быть Вам полезна.
Для построения графика контроля буксования сначала рассчитывают динамические факторы по сцеплению при разных нагрузках на автомобиль. При этом используют следующие выражения:

где D0cц и Dаcц — динамические факторы по сцеплению соответственно снаряженного автомобиля и автомобиля с полной нагрузкой;

φх — коэффициент продольного сцепления (φх = 0,1…0,8).
Последовательно подставляя значения коэффициента сцепления φх в выражения (8.3), определяют динамические факторы по сцеплению D0cц и Dаcц Найденные значения динамических факторов по сцеплению откладывают на вертикалях D0 и Dа номограммы нагрузок в том же масштабе, что и динамические факторы по тяге, и их одинаковые значения соединяют штриховыми линиями, над которыми указывают соответствующие значения φх.
При решении задач по оценке тягово-скоростных свойств автомобиля из четырех параметров — скорости автомобиля v, нагрузки на автомобиль Н, коэффициентов сопротивления дороги ψ и сцепления колес с дорогой φх — можно определить два любых параметра по двум другим заданным. При этом найденные значения коэффициента сопротивления дороги ψ будут максимально возможными, а значения коэффициента сцепления φх — минимально необходимыми для движения автомобиля при различных нагрузках.
Электрическое сопротивление проводника происходит из-за взаимодействия электрона с ионами кристаллической решетки.
Сопротивление проводника зависит от:
- — его длины,
- — площади поперечного сечения
- — от вещества из которого он изготовлен,
а также сопротивление прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.
Чтобы посчитать зависимость сопротивления от вещества, из которого изготовляют проводник, надо вычислить его удельное сопротивление.
Удельное сопротивление — физическая величина которая определяет сопротивление проводника из данного вещества длиной 1м, и площадью поперечного сечения 1м^2.
- Удельное сопротивление обозначается буквой — p.
- Длина — l.
- Площадь поперечного сечения — S.
- Сопротивление проводника обозначим буквой R.
В итоге мы получим формулу:
R = p*l/S
Получим еще несколько разновидностей формул:
l = R*S/p ; S = p*l/R ; p = R*S/l
Единицей сопротивления является 1 Ом, следовательно единица удельного сопротивления будет:
1 Ом*1м^2/1м или 1 Ом*м, следуя из формулы p = R*S/l
Также площадь поперечного сечения можно выражать в квадратных миллиметрах, тогда мы получим такую формулу:
1 Ом*мм^2/м
Наименьшим удельным сопротивлением обладает серебро (0,016) и медь (0,017), следовательно они лучше проводят электричество.
Эбонит(10^20) и фарфор(10^19) имеют очень большое удельное сопротивление и почти не проводят электрический ток, их используют для изоляторов.
Формулы для расчета мощности тока
Измеряется электрическая мощность в ваттах (Вт). Ток в 1А и с напряжением в 1 В обладает мощностью в 1Вт. Для того, чтобы узнать, как определить мощность тока, необходимо воспользоваться следующей формулой: P=U*I (А), где U, I – это напряжение электрического поля и сила тока соответственно, а P – его мощность.
Чтобы понять, как правильно пользоваться формулой, рассмотрим небольшой пример. Допустим, подано напряжение на резистор в 150В и по нему идет ток в 0,2А. Какая на данном резисторе развивается мощность? P=150*0.2=30Вт.
Существует еще один способ вычисления мощности электрического тока. Если известно сопротивление цепи и сила тока, то необходимо воспользоваться законом Ома (применима формула для участка цепи): U=I*R (Б)
Теперь подставим формулу (Б) в формулу (А) и получим формулу (В): P=I 2 R (В). Предположим, что через реостат, сопротивление которого равно 5 Ом, проходит с силой 0,5А ток. Определить мощность, которая теряется в реостате? P=0.5 2 *5=1.25Вт.
Если сила тока нам неизвестна, но мы знаем напряжение и сопротивление, то тоже возможно определить мощность. Из закона Ома I=U/R, тогда пользуясь формулой (А) мощность тока равна: P=U 2 /R (Г)
Реостат имеет сопротивление в 5 Ом, а напряжение в нем 2,5В, тогда мощность согласно формуле (Г) будет равна: P=2.5 2 /5= 1.25Вт. Если вам известны любые два значения из формулы для закона Ома (если рассмотреть участок цепи), то всегда можно определить мощность тока.
Вспомнив определение мощности, можно записать еще одну формулу для её расчета: P=A/t (Д), где P – это мощность, А – работа электрического тока, а t – время, за которое совершается эта работа.
Выбирая тот или иной бытовой прибор в магазине, мы часто задаемся вопросом о том, сколько же денег нам придется заплатить за его использование. Особенно это касается обогревателя, работающего на электричестве. Иногда, пользуясь сварочным аппаратом или электродвигателем, мы даже не подозреваем о том, сколько он потребляет электроэнергии. Но как же узнать необходимые нам цифры, если данные о приборах не известны.
Расчёт сопротивления проводника. Реостаты
На прошлых уроках мы с вами говорили об электрическом сопротивлении. Давайте с вами вспомним, что это физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока.
Введя новую величину — сопротивление, мы с вами до сих пор не ответили на один очень важный вопрос: от каких факторов зависит сопротивление проводника?
Анализируя природу электрического сопротивления, можно высказать предположение, что сопротивление зависит от длины и толщины проводника, а также материала, из которого он изготовлен.
Как обычно, проверим справедливость этой гипотезы на опыте. Для этого используем цепь из источника тока, амперметра и панели с исследуемыми проводниками. На панели имеются укреплённая вверху проволока из нихрома (специальный сплав, из которого изготовляют спирали нагревательных приборов) с клеммами подключения на концах и в середине.
Ниже неё, посередине панели, располагаются два других нихромовых проводника сложены вместе. А в нижней части укреплена железная проволока такого же диаметра, как и верхние нихромовые. Для удобства поочерёдного включения левые концы всех проволок соединены друг с другом и к ним подведён один из проводов источника. Дотрагиваясь поочерёдно другим проводом, идущим от источника, до точек
В
,
С
,
D
и
E
мы можем включать в цепь любой из проводников.
Из чего можно сделать первый вывод: сопротивление проводника прямо пропорционально его длине.
Затем сравним силу тока в первом измерении (то есть в нихромовом проводе полной длины) с силой тока в двойном проводе, который имеет такую же длину, но обладает вдвое большим сечением.
Как видно, при удвоении сечения сила тока возросла вдвое, то есть при большем сечении (в два раза) сопротивление меньше также в два раза, что приводит нас к выводу о том, что сопротивление проводника обратно пропорционально площади его поперечного сечения.
Для чего в установке нижний, железный, провод вы, наверняка, уже догадались: он по длине и сечению одинаков с верхним, но изготовлен из другого материала.
Включив его в цепь, мы увидим резкое увеличение силы тока, то есть его проводимость гораздо больше, чем у нихромового проводника, а, следовательно, меньше сопротивление. Отсюда делаем третий вывод: сопротивление проводника зависит от вещества, из которого он изготовлен.
Теперь мы с вами получили возможность вывести формулу для расчёта сопротивления проводника. Не трудно понять, что в её правой части будет три члена: длина — в числителе (прямая пропорциональность), площадь поперечного сечения — в знаменателе (обратная пропорциональность) и, конечно же, специальный коэффициент, отражающий проводящие свойства вещества.
Таким образом, сопротивление проводника прямо пропорционально его длине, обратно пропорционально площади его поперечного сечения и зависит от материала проводника:
Коэффициент ρ
, стоящий в формуле, называют
удельным сопротивлениемвещества.
Иными словами, это характеристика не конкретного рассматриваемого проводника, а именно вещества, из которого он изготовлен.
Она равна сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м2.
В СИ удельное сопротивление измеряется в Ом-м
. Так как на практике длину проводников измеряют обычно в метрах, а площадь поперечного сечения в квадратных миллиметрах, то удельное сопротивление удобно записывать в виде:
Значения удельного сопротивления для различных веществ представлены в таблице:
Смысл приведённых в таблице удельных сопротивлений прост. Если для нихрома значение удельного сопротивления равно 1,1 ∙ 10−6, то это значит, что нихромовый проводник длиной 1 м и поперечным сечением в 1 мм2 обладает сопротивлением 1,1 Ом.
Будьте внимательны и всегда смотрите на единицу удельного сопротивления, когда пользуетесь табличными данными.
Значения удельного сопротивления веществ приведены для температуры 20 оС, так как сопротивление проводников зависит от температуры (с чем вы более подробно познакомитесь в старших классах). Отметим лишь то, что при повышении температуры удельное сопротивление возрастает, а при понижении уменьшается.
Так сенсацией начала ХХ в. стало открытие явления сверхпроводимости. Оно заключается в том, что при очень сильном охлаждении (примерно до −270 оС и ниже) сопротивление некоторых металлов резко снижалось до нуля. При этом сверхпроводящие металлы не нагревались даже при очень большой силе тока в них.
Очень часто на практике приходится менять силу тока в цепи, плавно увеличивая или уменьшая её.
Изменить силу тока можно, меняя сопротивление цепи. Приборы, которые позволяют сделать это плавно, называются
реостатами.
Продемонстрировать принцип работы реостата можно с помощью обычной проволоки, желательно никелиновой или нихромовой, так как они обладают большим удельным сопротивлением.
При включении в цепь такой проволоки один контакт неподвижен, а другой — может перемещаться вдоль проволоки. Амперметр показывает, как меняется сила тока в цепи при перемещении подвижного контакта. Очевидно, что чем больше часть проволоки, включённая в цепь, тем больше сопротивление проволоки и, следовательно, тем меньше сила тока в цепи.
На практике применяют самые разнообразные реостаты. Но общее для всех реостатов — это использование длинной проволоки с большим удельным сопротивлением.
Давайте рассмотрим поподробнее ползунковый реостат, с которым вы будете работать на уроках. Его внешний вид и условное обозначение на схемах представлены на рисунке.
В этом реостате никелиновая проволока, покрытая тонким слоем окалины, намотана на керамический цилиндр. Окалина позволяет изолировать витки друг от друга. По расположенному вверху металлическому стержню может перемещаться ползунок. Контакты ползунка прижаты к виткам обмотки, и в результате трения слой окалины под контактами стирается. Электрический ток в цепи проходит от витков проволоки к ползунку, а через него — в стержень, на конце которого находится зажим. Другой зажим соединён с одним из концов обмотки. Таким образом, ток проходит от одного зажима до другого через витки обмотки, число которых можно менять в зависимости от положения ползунка.
Пример решения задачи.
Задача.
При подключении к источнику тока с напряжением 6 В никелинового проводника поперечным сечением 0,3 мм2 по нему прошёл ток силой 0,3 А. Какова длина проводника?
Потребляемая мощность электроприборов: таблица с показателями
Для проведения вычислений вам необходимы элементарные знания электродинамике из школьного курса, связанные с мощностью, напряжением, током. Для того, чтобы рассчитать потребляемую мощность прибора, необходимо знать величину напряжения, а также силу источника. Мощность (Р) можно высчитать посредством перемножения силы тока на показатель электрического напряжения в сети.
Силой тока принято называть величину электрического заряда, проходящего через заданную площадь сети за единицу времени. Физическая величина, характеризующаяся электрическим полем, которое создает ток – это напряжение.
Используются следующие показатели:
- В качестве несистемной единицы измерения мощности иногда используют многие вольт-ампер;
- В данном случае силу указывают в автоматических выключателях.
Оно верно является максимальным значением, при котором происходит срабатывание прерывателя.
Определение мощности источника питания: способы расчетов
Для получения данного показателя вам пригодится значения силы тока, обозначаемо как (I) и напряжение, записываемо как (V) источник питания. Чтобы вычислить мощность (Р) необходимо перемножить между собой эти два значения. Данная сила тока – количество заряда, которое проходит через определенную поверхность за какой-то отрезок времени. Напряжение – это переменная величина, какую характеризует электрическое поле, что создается током.
Приблизительная мощность прибора равна произведению напряжения и силы тока. Формула выглядит как Р = I х V.
Как правило:
- Силу тока указывает на автоматических выключателях;
- Указанное значение – это максимальная сила тока, при котором включается прерыватель;
- Значение напряжения и силы тока обычно указывают на корпусе электроприбора или тэна.
Если там его нет, то следует поискать в документации к нему.
Расчет сил сопротивления
Фильтр нулевого сопротивления плюсы и минусы. Неудобная правда
С целью определения сил сопротивления потребуется применение третьего закона Ньютона. Такая величина, как сила сопротивления, будет численно равной силе, которую потребуется приложить с целью равномерного движения предмета по горизонтальной ровной поверхности. Это становится возможным с помощью динамометра.
Таким образом, искомая величина оказывается прямо пропорциональной массе тела
Стоит при этом учитывать во внимание, что для более точного подсчета потребуется выбрать $u$ коэффициент, зависимый от материала изготовления опоры. Также принимается во внимание материал изготовления самого предмета исследования
При расчете применяется постоянная $g$, чье значение 9,8 $м/с^2$.
В условиях движения тела на высоте, на него влияет сила трения воздуха, зависимая от скорости перемещения предмета. Искомую величину определяют на основании такой формулы (подходящей исключительно для тел с передвижением с небольшой скоростью):
$F = va$, где:
- $v$ – скорость движения предмета,
- $a$ – коэффициент сопротивления среды.
Как рассчитать потребление электроэнергии прибором
Показатель силы тока, а также напряжения некоторых распространенных электроприборов имеется в специализированных справочниках. Если у вас их нет, то дайте запрос и найдите в интернете, или онлайн-ресурсах.
Вычисляется сила тока по аналогичной формуле, как и напряжение. Для этого имеющиеся величины нужно разделить.
Например, вам нужно вычислить, какую мощность потребляет телевизор, потолочный вентилятор, или микроволновая печь, при этом, такой показатель, как их сила тока обозначена на корпусе прибора. Для возможности произвести расчет вам необходимо найти напряжение вентилятора и сопротивление. Узнать его вы можете в интернете, или у производителя. После чего, подставив в формулу значения, можно без труда вычислить мощность вентилятора.
Что нужно знать о мощности:
- Мощность – это скорость преобразования, передачи или потребления необходимой энергии. Обычно, вы оплачиваете электроэнергию согласно потребленной мощности.
- Измеряется мощность в ваттах (Вт).
- Мощность электроприбора – это показатель энергии, который потребляет данный прибор.
- Номинальная мощность – потребная величина, необходимая для правильной работы прибора.
- Ток бывает постоянным и переменным. Переменный ток может изменятся по величине или направлению. Он подается по электросетям. Определение – постоянный ток не изменяется по направлению или величине. Источником такого тока можно назвать аккумулятор или батарейку.
Стартовая мощность – это единица, необходимая для того, чтобы запустить двигатель или компрессор.
6.5.Сила упругости. Закон Гука.
При действии на тело внешних сил, возникает упругая и неупругая деформация.
П
x
x=0
ри упругой деформации тело после прекращения действия внешних сил полностью восстанавливает свою форму и размеры. При неупругой деформации форма и размеры тела не восстанавливаются.
Упругая деформация пружины.
При растяжении пружины (рис 2.14) на величину
относительно её равновесного состояния (х= 0) возникает упругая сила
, которая возвращает пружину в прежнее положение после прекращения действия внешней силы. Модуль упругой силы, возникающей прилинейном растяжении или сжатии пружины определяется законом Гука.
, (2.56)
где
– проекция силы упругости на осьx, знак минус учитывает противоположные направления силы
и перемещения пружины
.
Деформация стержня
Стержень длинной l
и сечениемSпри действии сил
и
перпендикулярно его торцам в противоположных направлениях деформируется (растягивается или сжимается) (рис 2.15). Деформация стержня определяется относительной величиной
(2.57)
где ∆l
=
l—l ,l—
длинна стержня после деформации.
Рис. 2.15
Опыт показывает, что
, (2.58)
где α – коэффициент упругости стержня,
=σ – нормальное напряжение, измеряемое в
(паскаль).
Наряду с коэффициентом упругости aдля характеристики упругих свойств тел при нормальных напряжениях используютмодуль Юнга
Е = 1/a, который, как и напряжение, измеряется в паскалях.
Относительное удлинение (сжатие) и модуль Юнга в соответствии с равенствами (2.13 и 2.14) определяется из соотношений:
,
. (2.59)
Модуль Юнга равен такому нормальному напряжению, при котором деформация стержня Dlравна его первоначальной длинеl. В действительности при таких напряжениях происходит разрушение стержня.
Решая уравнение (2.58) относительно F, и подставляя вместоe=Dl/l,a= 1/Е, получим формулу для определения силы деформирующей стержень с сечениемSна величину
, (2.60)
где
– постоянный для стержня коэффициент, который в соответствии с законом Гука соответствует коэффициенту упругости стержня при его сжатии и растяжении.
При действии на стержень касательного (тангенциального) напряжения
силы F1 иF2приложены параллельно противоположным граням площадьюSпрямоугольного стержня вызываютдеформацию сдвига (рис 2.16).
b
Рис. 2.16
Если действие сил равномерно распределено по всей поверхности соответствующей грани, то в любом сечении, параллельном этим граням, возникает тангенциальное напряжение
. Под действием напряжений тело деформируется так, что одна грань сместиться относительно другой на некоторое расстояниеа.
Если тело мысленно разбить на элементарные, параллельные рассматриваем граням слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев.
При деформации сдвига любая прямая, первоначально перпендикулярная к слоям, отклонится на некоторый угол φ. тангенс которого называется относительным сдвигом
, (2.61)
где b– высота грани. При упругих деформациях угол φ очень мал, поэтому можно считать, что
и
.
Опыт показывает, что относительный сдвиг пропорционален тангенциальному напряжению
, (2.62)
где G– модуль сдвига.
Модуль сдвига
зависит только от свойств материала и равен тангенциальному напряжению при угле φ = 45˚. Модуль сдвига так же, как и модуль Юнга измеряется в паскалях (Па). Сдвиг стержня на угол
вызывает сила
=GSφ, (2.63)
где G·S
– коэффициент упругости стержня при деформации сдвига.
Рассмотрим, как работает измеритель мощности в розетку
Если вам необходимо узнать, какой мощностью обладает тот или иной предмет, можно замерять с помощью прибора мультиметра силу тока и напряжение, а затем их просто перемножить. Есть и приборы, которые определяют и мощность. Они называются ваттметры. Показатель мощности рассчитывает встроенный калькулятор, и показатель сразу появляется на его дисплее.
Как пользоваться ваттметром и мультиметром:
- Вставляем прибор в розетку 220В;
- В ваттметр вставляем вилку прибора, который нам нужно замерять;
- Ждем, когда на дисплее появится требуемый показатель.
На задней панели прибора есть отсек под батарейки, идущие обычно в комплекте. На пластине рядом имеется информация с характеристиками самого ваттметра, его номер, а также вилка. На внешней стороне находится дисплей. Управление осуществляется 4 кнопками, возле которых размещена розетка для подключения бытовых приборов, оборудования и техники.
Когда прибор включен, на его экране, как у счетчика, появляются 3 информационных строчки: одна графическая и две цифровые.
С помощью четвертой кнопки Value вы сможете переключить и определить следующие измеряемые параметры:
- Напряжение сети;
- Мощность, которую потребляет подключенное устройство;
- Потребляемая прибором сила тока.
При установленном граничном показателе, относительно напряжению и току, одной из характеристик прибор будет давать сигнал. Это означает перегрузку.
Можно ли посчитать расход электроэнергии, зная примерную мощность
При самостоятельных расчетах не стоит забывать о небольшой мощности, которую потребляют некоторые устройства даже когда они не работают, но подключены к розетке. Его тоже нужно считать. Многие приборы оснащены индикатором, или у них есть светодиод, который тоже может потреблять некоторую мощность.
Осведомленность о потребляемой мощности прибора дает возможность существенно экономить электроэнергию.
Расчеты производят следующим образом:
- При вычислении мощности согласно формулы вы получаете приблизительное значение.
- В случае, когда вам нужен точный показатель мощности, лучше воспользуйтесь ваттметром. Любая мощность, будь то электрическая, тепловая или механическая, измеряется в ваттах. Для того, чтобы уметь экономить электроэнергию важно знать их потребляемую приборами мощность.
- Для вычисления разности двух мощностей следует вычитать одно такое значение из другого.
Когда вы оплачиваете счета за электроэнергию, вы платите, в сущности, за каждый потребленный вами киловатт. Для конвертирования показателя ватт в киловатты нужно разделить один показатель в ваттах на 1000, а потом умножить значение, получившееся в киловаттах на количество отработанных прибором часов. В результате вы получите требуемое значение, существующее как (кВт-ч). Если умножить его на стоимость 1 киловатта электроэнергии, вы сможете узнать, сколько вам придется заплатить за работу прибора. К примеру, если в вашем доме или квартире всего 10 лампочек и 100 Вт – мощность, потребляемая каждой лампой, то произведя расчет мы получим 10 х 100 в итоге выйдет 1000 Вт – суммарная мощность всех ламп. Если 1000 Вт вы поделите на 1000, то получите 1 кВт. Теперь не трудно подсчитать, что если, лампочки горели на протяжении 2000 часов в год, а один киловатт в час стоит 6 руб. То, за год вам придется заплатить 12000 руб.
Расчет падения напряжения
Любой проводник, кроме сверхпроводников, имеет сопротивление. Поэтому при достаточной длине кабеля или провода происходит падение напряжения. Нормы ПЭУ требуют, чтобы сечение жилы кабеля было таким при котором падение напряжения составляло не более 5%.
В первую очередь это касается низковольтных кабелей малого сечения. Расчет падения напряжения выглядит следующим образом:
R = 2*(ρ * L) / S
U пад = I * R
U % = (U пад / U лин) * 100
2 – коэффициент, обусловленный тем, что ток течет обязательно по двум жилам
R – сопротивление проводника, Ом
ρ — удельное сопротивление проводника, Ом*мм 2 /м
S – сечение проводника, мм 2
U пад – напряжение падения, В
U % — падение напряжения по отношению к U лин,%
Таблица 9. Удельное сопротивление распространенных металлических проводников (+)
Сопротивление цепи фаза – ноль
Таблица 1
| Сечение фазных жил мм2 | Сечение нулевой жилы мм2 | Полное сопротивление цепи фаза – ноль, Ом/км при температуре жил кабеля +65 градусов | |||||
| Материал жилы: | |||||||
| Алюминий | Медь | ||||||
| R фазы | R нуля | Z цепи (кабеля) | R фазы | R нуля | Z цепи (кабеля) | ||
| 1,5 | 1,5 | — | — | — | 14,55 | 14,55 | 29,1 |
| 2,5 | 2,5 | 14,75 | 14,75 | 29,5 | 8,73 | 8,73 | 17,46 |
| 4 | 4 | 9,2 | 9,2 | 18,4 | 5,47 | 5,47 | 10,94 |
| 6 | 6 | 6,15 | 6,15 | 12,3 | 3,64 | 3,64 | 7,28 |
| 10 | 10 | 3,68 | 3,68 | 7,36 | 2,17 | 2,17 | 4,34 |
| 16 | 16 | 2,3 | 2,3 | 4,6 | 1,37 | 1,37 | 2,74 |
| 25 | 25 | 1,47 | 1,47 | 2,94 | 0,873 | 0,873 | 1,746 |
| 35 | 35 | 1,05 | 1,05 | 2,1 | 0,625 | 0,625 | 1,25 |
| 50 | 25 | 0,74 | 1,47 | 2,21 | 0,436 | 0,873 | 1,309 |
| 50 | 50 | 0,74 | 0,74 | 1,48 | 0,436 | 0,436 | 0,872 |
| 70 | 35 | 0,527 | 1,05 | 1,577 | 0,313 | 0,625 | 0,938 |
| 70 | 70 | 0,527 | 0,527 | 1,054 | 0,313 | 0,313 | 0,626 |
| 95 | 50 | 0,388 | 0,74 | 1,128 | 0,23 | 0,436 | 0,666 |
| 95 | 95 | 0,388 | 0,388 | 0,776 | 0,23 | 0,23 | 0,46 |
| 120 | 35 | 0,308 | 1,05 | 1,358 | 0,181 | 0,625 | 0,806 |
| 120 | 70 | 0,308 | 0,527 | 0,527 | 0,181 | 0,313 | 0,494 |
| 120 | 120 | 0,308 | 0,308 | 0,616 | 0,181 | 0,181 | 0,362 |
| 150 | 50 | 0,246 | 0,74 | 0,986 | 0,146 | 0,436 | 0,582 |
| 150 | 150 | 0,246 | 0,246 | 0,492 | 0,146 | 0,146 | 0,292 |
| 185 | 50 | 0,20 | 0,74 | 0,94 | 0,122 | 0,436 | 0,558 |
| 185 | 185 | 0.20 | 0,20 | 0,40 | 0,122 | 0,122 | 0,244 |
| 240 | 240 | 0,153 | 0,153 | 0,306 | 0,090 | 0,090 | 0,18 |
Таблица 2
| Мощность трансформатора, кВ∙А | 25 | 40 | 69 | 100 | 160 | 250 | 400 | 630 | 1000 |
| Сопротивление трансформатора, Zт/3, Ом (Δ/Υ) | 0,30 | 0,19 | 0,12 | 0,075 | 0,047 | 0,03 | 0,019 | 0,014 | 0,009 |
Таблица 3
| I ном. авт. выкл, А | 1 | 2 | 6 | 10 | 13 | 16 | 20 | 25 | 32-40 | 50 и более |
| R авт., Ом | 1,44 | 0,46 | 0,061 | 0,014 | 0,013 | 0,01 | 0,007 | 0,0056 | 0,004 | 0,001 |
Таблица 4
| R цепи, Ом | 0,05 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,8 | 1,0 | 1,5 | 2 и более |
| Rдуги, Ом | 0,015 | 0,022 | 0,032 | 0,04 | 0,045 | 0,053 | 0,058 | 0,075 | 0,09 | 0,12 | 0,15 |
При проектировании групповой сети, если питающая и распределительная сеть уже проложены, целесообразно выполнить измерение сопротивления цепи фаза – ноль от трансформатора до шин группового щита. Это может значительно уменьшить вероятность ошибок при расчетах групповой сети. В этом случае сопротивление рассчитываем по формуле:
RL-N= Rрасп + Rпер.гр + Rавт.гр+ Rnгр∙Lnгр +Rдуги (2)
где, Rрасп – измеренное сопротивление цепи фаза – ноль линии, подключаемой к вводному автоматическому выключателю группового щитка, Ом; Rпер.гр – сопротивление переходных контактов в групповой линии, Ом; Rавт.гр – суммарное сопротивление автоматических выключателей – вводного группового щита и отходящей групповой линии, Ом; Rnгр – удельное сопротивление кабеля n-й групповой линии (по таблице 1), Ом/км; Lnгр – длина n-й групповой линии, км.
Рассмотрим процесс вычисления сопротивления цепи фаза – ноль схемы, показанной на Рис.1 при однофазном коротком замыкании фазы на ноль в конце групповой линии.
Исходные данные:
— трансформатор мощностью 630 кВ∙А подключен по схеме «треугольник – звезда» — по таблице 2 находим Zт/3=0,014 Ом;
— питающая сеть – кабель с алюминиевыми жилами длиной 80 метров имеет фазный проводник 150 мм2 и нулевой – 50 мм2. По таблице 1 находим удельное сопротивление кабеля 0,986 Ом/км. Вычисляем его сопротивление (длины кабелей выражаем в километрах): 0,986 Ом/км∙0,08 км=0,079 Ом;
— распределительная сеть – кабель с медными жилами длиной 50 метров и сечением жил 35 мм2. По таблице 1 находим удельное сопротивление кабеля 1,25 Ом/км. Вычисляем его сопротивление:
1,25 Ом/км∙0,05 км=0,0625 Ом;
— групповая сеть – кабель с медными жилами длиной 35 метров и сечением жил 2,5 мм2. По таблице 1 находим удельное сопротивление кабеля 17,46 Ом/км. Вычисляем его сопротивление:
17,46 Ом/км∙0,035 км=0,61 Ом;
— автоматический выключатель отходящий линии – 16 Ампер (с характеристикой срабатывания «С»), вводной автоматический выключатель группового щитка 32 Ампера, остальные автоматические выключатели в линии имеют номинальный ток более 50 Ампер. Вычисляем их сопротивление (по таблице 3) 0,01 Ом+0,004 Ом+3∙0,001 Ом=0,017 Ом;
— переходные сопротивления контактов учтем только в групповой линии (точки подключения кабеля групповой линии к щитку и к нагрузке). Получаем 2∙0,01 Ом=0,02 Ом.
Суммируем все полученные значения и получаем сопротивление цепи фаза – ноль без учета сопротивления дуги RL-N=0,014+0,079+0,0625+0,61+0,017+0,02=0,80 Ом.
Из таблицы 4 берем сопротивление дуги 0,075 Ом, и получаем окончательное значение искомой величины RL-N=0,80 Ом+0,075 Ом=0,875 Ом.
В Правилах устройства электроустановок (ПУЭ) задано наибольшее время отключения цепей при коротком замыкании в сетях с глухозаземленной нейтралью 0,2 секунды при напряжении 380 В и 0,4 секунды при напряжении 220В.
Для обеспечения заданного времени срабатывания защиты необходимо, что бы при коротком замыкании в защищаемой линии возникал ток, превышающий не менее чем в 3 раза номинальный ток плавкой вставки ближайшего предохранителя (для взрывоопасных помещений не менее чем в 4 раза) и не менее чем в 3 раза ток расцепителя автоматического выключателя, имеющего обратнозависимую от тока характеристику (для взрывоопасных помещений не менее чем в 6 раз). Для автоматических выключателей с комбинированным расцепителем (имеющим тепловой расцепитель для защиты от перегрузок и электромагнитный расцепитель для защиты от токов коротких замыканий) ток короткого замыкания должен превысить ток срабатывания электромагнитного расцепителя не менее, чем в 1,2 – 1,25 раза.
В настоящее время используются автоматические выключатели с различной кратностью токов срабатывания электромагнитного расцепителя к тепловому. Автоматические выключатели группы «В» имеют кратность в пределах от 3 до 5, группы «С» от 5 до 10, группы «D» от 10 до 20, группы «K» от 10 до 15 и группы «Z» от 2 до 3. При расчетах всегда берется максимальное значение кратности токов срабатывания расцепителей. Например для автоматического выключателя С16, ток короткого замыкания должен быть не менее 16 А∙10∙1,2=192 А (для автоматического выключателя С10 не менее10А∙10∙1,2=120 А и для С25 не менее 25 А∙10∙1,2=300 А). В приведенном выше примере мы получили сопротивление цепи фаза – ноль 0,875 Ом. При таком сопротивлении цепи ток короткого замыкания Iкз составит величину
Uф/ RL-N=220В/0,875 Ом=251 А. Следовательно групповая линия в приведенном примере защищена от токов коротких замыканий.
Максимальное сопротивление цепи фаза – ноль для автоматического выключателя С16 составит величину 220 В/192А=1,14 Ом. В приведенном примере сети (Рис. 1) сопротивление цепи от трансформатора до шин группового щита составит 0, 875 Ом — 0,61 Ом=0.265 Ом. Следовательно максимально возможное сопротивление кабеля групповой линии будет равно 1,14 Ом – 0, 265 Ом=0,875 Ом. Его максимальную длину L при сечении жил кабелей 2,5 мм2 определим при помощи таблицы 1.
L, км=0,875 Ом/(17,46 Ом/км)=0,050 км.
Всегда, когда есть возможность, следует рассчитывать групповую сеть с максимальным запасом по сопротивлению цепи фаза – ноль, особенно розеточную сеть. Часто нагрузки (утюг, чайник и другие бытовые приборы), в которых часто происходят замыкания, подключают к розетке через удлинитель. Начиная с определенной длины провода удлинителя, нарушается согласование параметров цепи с характеристиками аппаратов защиты, то есть ток короткого замыкания оказывается недостаточным для мгновенного отключения сети. Отключение аварийного участка осуществится только тепловым расцепителем через сравнительно большой промежуток времени (несколько секунд), в результате чего кабели могут нагреться до недопустимо высоких температур вплоть до воспламенения изоляции.
Проект электропроводки должен быть выполнен таким образом, что бы даже в случае воспламенения изоляции кабеля при коротком замыкании это не приводило к пожару. Именно поэтому возникли требования к прокладке скрытой электропроводки в стальных трубах в зданиях со строительными конструкциями, выполненными из горючих материалов. Во взрывоопасных зданиях целесообразно использовать более сложную защиту кабелей от воздействия токов короткого замыкания.
9 марта 2013 г.
К ОГЛАВЛЕНИЮ
Здравствуйте, друзья! Многие считают, что в физике самое сложное – это формулы, которые трудно запомнить, а вредные учителя почему-то заставляют учить их наизусть. По моему опыту, формулы сложно не столько запомнить, сколько применить, понять условие их применимости. Для этого надо конкретно разбираться, в идеале (недостижимом) – выводить, и бесполезно просто зазубривать. Ведь даже простые формулы, состоящие всего из трех буковок, и знаков умножить-разделить, бывают коварными.
Возьмем обычные школьные формулы электрической мощности, рассеиваемой на сопротивлении нагрузки, то есть на электроприборе.
На этом вопросе я часто ловлю школьников и студентов. Что же получается, физика нам врёт? Где правда, как действительно зависит мощность от сопротивления?
Не буду вас томить, уважаемые читатели. Никакого противоречия нет. Просто в формулах, приведенных выше, и сила тока, и напряжение, не являются постоянными, они тоже зависят от сопротивления.
Зависимость силы тока и напряжения от сопротивления – это уже другая формула, а именно закон Ома для полной цепи. Вот он:
В формулы закона Ома входят постоянные параметры – ЭДС и внутреннее сопротивление. Теперь берем любую из формул – тока или напряжения, и подставляем в любое из выражений для мощности, данное на первом рисунке. Результат получится одинаковым! Вот таким:
Как видите, это уже более хитрая формулка. Есть на чём поймать школьника! Такие задачки есть в школьном учебнике, но в стандартной программе они идут как усложненные.
Вот график этой зависимости.
Если внешнее сопротивление равно внутреннему сопротивлению источника, то мощность будет максимальной. Это так называемое условие согласования, оно часто применяется в электротехнике. Интерес также вызывают предельные случаи.
- Внешнее сопротивление мало по сравнению с внутренним. Сила тока, даваемая источником, не будет зависеть от внешнего сопротивления. Такой источник называют источником тока. Зависимость мощности от внешнего сопротивления будет близка к линейной.
- Внешнее сопротивление велико по сравнению с внутренним. Тогда напряжение, даваемое источником, не будет зависеть от внешнего сопротивления. Это источник напряжения. Зависимость мощности от сопротивления будет обратно пропорциональной. Кстати, стандартная электрическая розетка является источником напряжения.
Предельные случаи графика мне напоминают известную притчу о слепых мудрецах, которые ощупывали слона с разных сторон (вот она на Дзене). Объединив знания вместе, получаем отличного слона.
Вот бы все в жизни противоречия разрешались так же просто! Спасибо всем, кто дочитал до конца!