Как найти максимальную скорость бруска

          

2.3.3.1. На гладкой горизонтальной поверхности около стенки стоит симметричный брусок массы $m_1$ с углублением полусферической формы радиуса $R$. Из точки $A$ без трения и начальной скорости соскальзывает маленькая шайба массы $m_2$. Максимальная скорость бруска при его последующем движении равна …

Решение.

Давайте рассмотрим последовательные фазы взаимодействия бруска и шайбы.

На первом рисунке, при соскальзывании шайба действует на брусок силой, направленной к стенке,

тем самым прижимая брусок к ней. Начиная от положения равновесия, в котором шайба приобрела скорость равную

$m_2gR = frac{m_2v_0^2}{2}$, $v_0 = sqrt{2gR}$ (1)

шайба будет действовать на брусок силой, направленной вправо, разгоняя его.

Когда шайба окажется в высшей своей точке подъема скорость бруска станет равной $v_1^/$. Эта скорость не является максимальной для бруска так как при обратном движении шайбы (см. рисунок),

она по-прежнему будет действовать на брусок вправо, увеличивая его скорость. При обратном движении, шайба, проходя положение равновесия со скоростью $v_2$ сообщит бруску максимальную скорость $v_1$, так как начиная с этого момента шайба начинает действовать на брусок силой, направленной влево, тем самым уменьшая его скорость.

Запишем закон сохранения импульса в проекции на направление движения бруска (ось ОХ направлена вправо):

$m_2v_0 = m_1v_1 – m_2v_2$, (2)

и закон сохранения кинетической энергии (трения нет)

$m_2gR = frac{m_2v_0^2}{2} = frac{m_2v_2^2}{2} + frac{m_1v_1^2}{2}$. (3)

Запишем пару уравнений (2) и (3) в виде:

$m_2(v_0 + v_2) = m_1v_1$

$m_2(v_0^2 – v_2^2) = m_1v_1^2$.

Разделим нижнее уравнение на верхнее соответственно, получим

$v_0 – v_2 = v_1$, откуда $v_2 = v_0 – v_1$.

Сделаем подстановку в (2), преобразуем и получим

$v_1 = frac{2m_2v_0}{m_1 + m_2}$.

Окончательно, с учетом (1), имеем конечную формулу для определения максимальной скорости бруска

$v_1 = frac{2m_2}{m_1 + m_2} cdot sqrt{2gR}$

Ответ: максимальная скорость бруска при его последующем движении равна $v_1 = frac{2m_2}{m_1 + m_2} cdot sqrt{2gR}$

2014-06-01   

На гладкой горизонтальной поверхности около стенки покоится симметричный брусок массой $m_{1}$ с углублением полусферической формы радиуса $r$ (рис.). Из начального положения без трения соскальзывает маленькая шайба массой $m_{2}$.

Найти максимальную скорость бруска при его последующем движении.

Решение:

До тех пор пока шайба не окажется в наинизшем положении, брусок будет касаться стены. К этому моменту времени шайба приобретет скорость $v$, которую найдем из закона сохранения энергии: $v^{2}=2gr$. При последующем движении системы шайба будет «забираться» на правую половину бруска, все время ускоряя его вправо (рис.), пока наконец скорости шайбы и бруска не сравняются. Далее шайба относительно бруска начнет соскальзывать вниз, при этом, пока она опять не пройдет низшее положение, брусок все еще будет ускоряться. Таким образом, максимальная скорость бруска будет в моменты прохождения шайбой низшего положения при ее движении назад относительно бруска.

Чтобы найти максимальную скорость бруска, запишем закон сохранения импульса после того, как брусок «оторвется» от стены:

$m_{2}sqrt{2gr} = m_{1}v_{1} + m_{2}v_{2}$.

и закон сохранения энергии для моментов прохождения шайбой низшего положения:

$m_{2}gr = frac{m_{1}v^{2}_{1}}{2} + frac{m_{2}v^{2}_{2}}{2}$

Написанная система уравнений имеет два решения:

$1. v_{1}=0, v_{2}=sqrt{2gr}$,

$2. v_{1}=frac{2m_{1}}{m_{1}+m_{2}} sqrt{2gr}, v_{2}=frac{m_{2}-m_{1}}{m_{1}+m_{2}} sqrt{2gr}$.

Решение 1 отвечает моментам времени, когда шайба движется, а брусок находится в покое. Нас интересует решение 2, отвечающее тем моментам времени, когда брусок имеет максимальную скорость:

$v_{1max}=2m_{2} sqrt{2gr} /(m_{1} + m_{2})$.

Решение.

Проекция
скорости на направление нормали к стене
есть v_x.
При минимальной скорости бросания v₀
значение проекции скорости должно быть
равно v_кр.
В некоторый момент времени v_x
= v_кр
. (1) Запишем исходные кинематические
уравнения для тела, движущегося с
ускорением g:

Здесь
α
– угол с горизонтом, под которым был
брошен комок.

Из
формул (1) и ()
следует

v₀cosα
= v_кр . (4)

П

Рис. 12

ри том же значении α высота подъёма
в точке x = L есть решение уравнений (2^|)
и (3^|),
в которых принимается x = L, y = h:

Исключая
t, получим соотношение

(5)

Вспоминая,
что угол α определяется условием (4),
получим из (5) и (4)

(6)

Из
соотношения (6) находим выражение для
v₀:

При
подстановке данных получим v₀
= 11,65 м/с.

Пример
4.
Невесомый брусок начинает скользить
по наклонной плоскости, составляющей
угол

с горизонтом. Коэффициент трения зависит
от пройденного пути по закону μ = ax
, где a = 0,2 м^-1.
Какая максимальная скорость достигалась
бруском?

Решение.

При
решении этой задачи удобно скорость
бруска v рассматривать как функцию
координаты x, направленной вниз вдоль
плоскости. Тогда ускорение бруска можно
записать как

Силы,
действующие на брусок: это скатывающая
сила mgsinα
и сила трения –mg(cosα)μ
= – mg(cosα)ax..

Запишем
уравнение динамики:

(1)

Помножив
уравнение на dx/m
и взяв неопределённые интегралы от
обеих частей равенства, получим

(2)

Константу
определяем таким образом, чтобы при x
= 0 получалось v = 0. То есть константа
должна быть равна нулю. Чтобы найти
максимальную скорость, необходимо
рассмотреть условие максимума

(3)

Подставляя
(2) в (3), получим

откуда
находим .

Подставляя
эту величину x снова в выражение (2),
получим для максимальной скорости
бруска

Расчёт
даёт v_max
= 3,82 м/с.

Пример
5.
Тело некоторой массы m падает с высоты

h
= 200 м. На тело действует сила сопротивления,
зависящая от скорости по формуле , где
k = 0,004 м^-1,
v – скорость.

Какая
скорость будет достигнута телом спустя
время
?

Решение.

Так
как одна из сил (F_r)
дана как функция скорости, то в уравнении
динамики ускорение лучше записать как
.
Считая направление движения вниз
положительным, запишем уравнение
динамики

Переписав
уравнение в виде

где

,
мы получим соотношение между
дифференциалами. Левая часть соотношения
представляет собой дифференциал
выражения

.

Перейдя
от соотношения между дифференциалами
к соотношению между самими величинами,
запишем

.

Подбираем
константу такой, чтобы при t=0 получалось
v = 0 (тело только начинает набирать
скорость). Видим, что const = 0 .Окончательно
для функции v(t) получим

.

При
подстановке данных получаем:
=
50 м;
;
v = 42,7 м/с. В отсутствии силы сопротивления
скорость была бы равна (2gh)^1/2
= 63,2 м /с.

Пример
6 .
На носу покоящейся лодки длиной l= 4 м
стоит человек, держа на высоте h = 1,6 м
ядро массой m₁
= 2 кг. Человек бросает горизонтально
ядро вдоль лодки. Какую скорость по
горизонтали должен сообщить ядру
человек, чтобы ядро упало рядом с кормой
лодки? Масса человека с лодкой

m₂
= 100 кг.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

В этой статье представлены задачи, которые предлагались в последние годы на письменных вступительных экзаменах по физике в РГУ нефти и газа им. И.М.Губкина.

Эти задачи были отобраны по следующим критериям. Во-первых, при их решении используются подходы и методы, применение которых требует хорошего понимания физической сущности законов сохранения, что является сложным для многих абитуриентов. Во-вторых, преимущество отдавалось задачам, содержащим красивую физическую «изюминку» или подвох, что выделяет их в ряду аналогичных задач. В то же время, уровень сложности предлагаемых задач вполне «абитуриентский» (хотя и из верхнего эшелона), они не претендуют на высокое звание «олимпиадных».

Надеемся, что эта статья позволит вам глубже познакомиться с такой важной и нетривиальной темой, как закон сохранения механической энергии.

В первой группе из четырех задач внимание концентрируется на анализе возможных случаев, соответствующих различным соотношениям между исходными данными. Неумение увидеть скрытые в условии задачи возможности может привести к ошибочным результатам.

Задача 1. Груз массой m = 1,6 кг подвешен к потолку на упругом резиновом шнуре жесткостью k = 250 Н/м. Грузу резким толчком сообщают начальную скорость υ₀ = 1 м/с, направленную вертикально вверх. На какую максимальную высоту (отсчитывая от начальной точки) поднимется груз?

Наиболее часто встречающаяся ошибка состоит в том, что абитуриенты не обращают внимания на слова про резиновый шнур и решают задачу так, как будто груз висит на пружине. Однако шнур, в отличие от пружины, работает только на растяжение. Если шнур не растягивать, а «сжимать» (сближать его концы), то он теряет форму, изгибается, не оказывая никакого сопротивления.

Давайте и мы начнем решение со случая груза на пружине и посмотрим, не даст ли нам сам ответ (как это часто бывает) какую-нибудь подсказку, «сигнал» о том, что что-то не в порядке. Заодно поговорим о важном методическом приеме, помогающем существенно упрощать решение задач с вертикальными пружинами.

Запишем закон сохранения энергии системы, отсчитывая потенциальную энергию тяготения от начального положения груза (рис. 1):

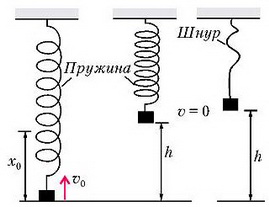
Рис. 1.

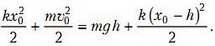
Здесь h — искомая высота, а x₀ — начальное растяжение пружины (шнура), которое находится из условия равновесия висящего груза:

 

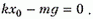
Раскрывая скобки в законе сохранения энергии и подставляя x₀, приходим к совсем короткому уравнению

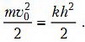
Заметим, что ускорение силы тяжести g вообще не вошло в конечное уравнение, как будто поле тяжести отсутствует. В чем причина? Здесь проявилось следующее свойство груза на пружине: если отсчитывать общую потенциальную энергию для равнодействующей силы тяжести и силы упругости от положения равновесия, то она принимает вид 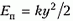, где 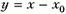 – смещение из этого положения. Действительно, равнодействующая сила в положении равновесия равна нулю, а при смещении груза на y возникает сила 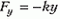, равная изменению силы упругости (сила тяжести не меняется). Поскольку сама равнодействующая такая же, как сила упругости, то и потенциальная энергия для нее такая же, как для чистой силы упругости. Это свойство часто используется молча, без всяких пояснений, например — при рассмотрении вертикальных колебаний груза на пружине.

Подставляя численные данные в последнее уравнение, находим искомую высоту:

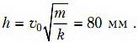
Вернемся к задаче со шнуром. Казалось бы, полученный ответ как в общем виде, так и в числовом выражении ничем не помогает нам заметить допущенную ошибку. Однако будем внимательны и, заподозрив подвох, проверим, остается ли шнур в растянутом состоянии до самого верхнего положения груза. Для этого вычислим начальное растяжение шнура x₀ и сравним его с h:

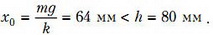
Видим, что груз при подъеме проходит точку, после которой шнур теряет свои упругие качества, изгибается, и сила упругости исчезает. Условие исчезновения силы упругости имеет вид

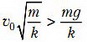 или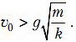

В таком случае задачу надо решать заново.

Упрощающий подход с объединением силы тяжести и силы упругости больше не действует (на некотором этапе движения сила упругости исчезает), и закон сохранения энергии надо записать так:

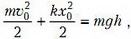
откуда (с учетом равенства 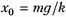) получим окончательный ответ:

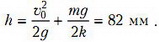
Задача 2. Груз подвешен к потолку на упругом резиновом шнуре. На груз дважды подействовали постоянной силой, направленной вертикально вверх и равной в первом случае F₁ = 3m·g/4, а во втором случае F₂ = m·g/4. Во сколько раз максимальная высота подъема груза (отсчитанная от начальной точки) в первом случае больше, чем во втором?

Решим задачу сначала в предположении, что сила упругости действует все время движения, т.е. как бы мысленно заменим шнур пружиной. Запишем закон сохранения (точнее – изменения) энергии, используя сокращенную запись для полной потенциальной энергии системы (см. задачу 1):

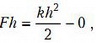
откуда найдем искомую высоту:

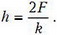
В рамках сделанного предположения отношение высот в обсуждаемых двух случаях равнялось бы отношению внешних сил:

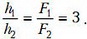
Однако, наученные горьким опытом, мы должны проверить, остается ли шнур растянутым до достижения грузом максимальной высоты. Для этого должно выполняться условие h < x₀, т.е.

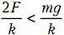 или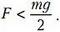

Это условие выполняется для второго случая, поэтому

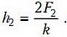
Для первого же случая (рис. 2) закон сохранения энергии надо написать заново (поскольку сила упругости на верхнем участке движения не действует, потенциальные энергии силы тяжести и силы упругости надо писать раздельно):

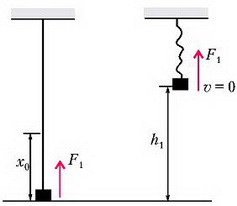
Рис. 2.

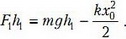
Подставляя 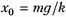, получим

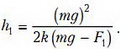
Тогда окончательно

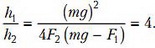
Задача 3. Однородный стержень длиной l = 2 м, двигаясь вдоль своей длины по гладкой горизонтальной поверхности, начинает пересекать границу, за которой поверхность становится шероховатой с коэффициентом трения μ = 0,2. Какое расстояние s проедет стержень с этого момента до остановки, если его начальная скорость υ₀ = 3 м/с?

Запишем закон сохранения энергии (теорему о кинетической энергии) в виде

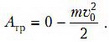
Вычислим работу силы трения A_тр в предположении, что сила трения в процессе движения все время возрастает, т.е. что стержень остановится до того, как целиком пересечет границу. В тот момент, когда стержень проехал расстояние x (рис. 3), сила трения, действующая на кусок стержня длиной x < l, равна

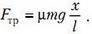
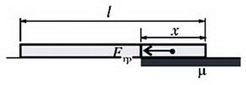
Рис. 3

Поскольку сила трения представляет собой линейную функцию пройденного расстояния, ее работу можно вычислить по формуле

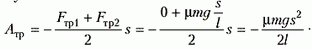
Подставив в уравнение закона сохранения энергии, получаем

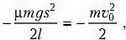
откуда

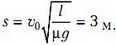
К сожалению, многие абитуриенты на этом заканчивают решение задачи, не заметив, что полученный ответ не имеет смысла, поскольку пройденное расстояние получилось больше длины стержня, а работа силы трения вычислялась в противоположном предположении. Правильное выражение для работы силы трения в случае s > l имеет вид

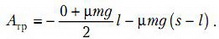
Тогда из закона сохранения энергии получаем

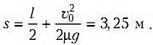
Конечно, можно поступить по-другому. Если сразу увидеть, что возможны разные случаи, то начать решение можно с выяснения того, какой случай реализуется. Например, найти минимальную скорость υ₁, при которой стержень полностью заедет на шероховатую поверхность:

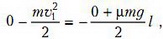
откуда

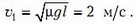
Поскольку υ₀ > υ₁, то ясно, что задний конец стержня обязательно пересечет границу.

Задача 4. В шар массой m₂ = 480 г попадает пуля массой m₁ = 20 г, летящая со скоростью υ₁ = 100 м/с по линии, проходящей через центр шара. Считая, что сила сопротивления движению пули в материале шара постоянна и равна F_c = 1650 Н, найдите конечную скорость шара. Диаметр шара d = 5 см.

Запишем для данного удара законы сохранения импульса и энергии, с учетом перехода механической энергии во внутреннюю за счет работы силы сопротивления:

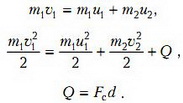
Исключая из этих уравнений конечную скорость пули

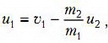
получим для конечной скорости шара u₂ квадратное уравнение

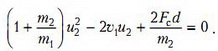
Решение этого уравнения

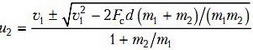
дает два положительных ответа: 2,5 м/с и 5,5 м/с. Какой из них выбрать?

Многие школьники привыкли, что один из ответов обычно получается отрицательным, и заранее отбрасывают решение с минусом перед квадратным корнем. Другие не знают, что делать с двумя положительными корнями, и выбирают наибольший (и получают неверный ответ!). На самом деле, надо вычислить скорость пули в каждом из случаев (используя написанную выше формулу, выражающую u₁ через u₂):

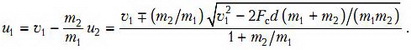
Видно, что если выбрать верхние знаки в формулах для u₂ и u₁ (плюс для шара и минус для пули), то скорость пули получится меньше, чем скорость шара: u₁ < u₂ (в данном конкретном случае u₁ отрицательна и равна u₁ = –32 м/с). Значит, пуля в этом случае оказывается с той же стороны от шара, с которой она подлетала. Это соответствует отскоку пули при ударе назад с потерей энергии Q (см. далее упражнение 4). Наоборот, если взять нижние знаки (минус для шара и плюс для пули), то скорость пули оказывается больше, чем скорость шара (в данном случае u₁ = 40 м/с), что соответствует ситуации, когда пуля пробивает шар насквозь и вылетает с другой стороны. Значит, правильный ответ для скорости шара соответствует меньшему корню: u₂ = 2,5 м/с.

В следующей задаче упор делается на выбор правильного условия, определяющего конечное состояние системы.

Задача 5. На гладкой горизонтальной плоскости лежат два бруска массами m₁ = 400 г и m₂ = 100 г, соединенные недеформированной пружиной. Первому бруску сообщают скорость υ₁ = 10 м/с в направлении второго бруска. Найдите минимальную скорость этого бруска в процессе дальнейшего движения.

Запишем законы сохранения импульса и энергии системы (рис. 4):

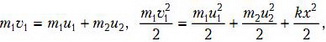
где х — деформация пружины.

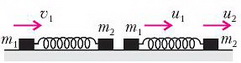
Рис. 4.

Главное для решения задачи – понять, чем интересующий нас момент, когда скорость бруска массой m₁ минимальна, отличается от всех остальных моментов движения. Для этого надо рассмотреть действующие на первый брусок силы.

Как только брусок массой m₁ придет в движение, пружина начнет сжиматься, и на него будет действовать сила упругости, направленная навстречу движению. Предположим, что скорость этого бруска не меняет направления, т.е. что u₁ все время положительна (позже нам придется проверить это предположение). Тогда скорость u₁ будет уменьшаться по модулю до тех пор, пока на брусок действует сжатая пружина. Когда пружина перейдет в растянутое состояние, сила упругости будет направлена по движению, и скорость бруска начнет возрастать. Минимальная скорость соответствует тому моменту, когда пружина снова (как до начала движения) придет в недеформированное состояние, т.е. когда x = 0. В этот же момент скорость второго бруска будет максимальной.

Система уравнений в этот момент

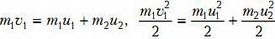
совпадает с системой уравнений для центрального упругого удара (т.е. пружина как бы осуществляет растянутый по времени упругий удар). Решение этой задачи хорошо известно, мы приведем его без вывода:

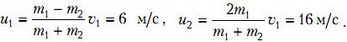
Если скорость u₂ всегда положительна, т.е. получен правильный ответ для максимальной скорости второго бруска при любом соотношении масс, то скорость u₁ остается положительной только при условии m₁ > m₂. Если m₁ < m₂, то в процессе движения скорость первого бруска меняет знак, и ответ для минимальной скорости такой: u₁ = 0.

Отметим интересное отличие этой задачи от центрального упругого удара, например, двух шаров. Шары после удара перестают взаимодействовать и разлетаются. В нашем же случае пружина, соединяющая бруски, после рассмотренного момента растягивается, первый брусок начинает тормозиться, второй — разгоняться. Через некоторое время скорость первого бруска достигнет максимального значения u’₁, а скорость второго — минимального u’₂. Пружина в этот момент опять не деформирована, т.е. эти скорости подчиняются той же самой системе уравнений. Поскольку скорости должны отличаться от найденных, они представляют собой второе решение этой системы, которое в задаче о центральном упругом ударе отбрасывают: u’₁ = υ₁, u’₂ = 0.

Последние две задачи связаны с движением по окружности. Первая из них иллюстрирует, как можно описать движение модельного твердого тела, состоящего из точечных масс, закрепленных на невесомом стержне. Вторая показывает, как использовать движущиеся системы отсчета в задачах на законы сохранения при движении по окружности.

Задача 6. Невесомый стержень, на концах которого закреплены два груза массой m = 0,5 кг каждый, может свободно вращаться вокруг горизонтальной оси. Ось делит стержень в отношении 1:3. Стержень приводят в горизонтальное положение и отпускают. С какой силой он действует на ось в вертикальном положении?

Если в вертикальном положении сила натяжения нижней части стержня T₁, а верхней T₂, то действующая на ось сила равна (рис. 5)

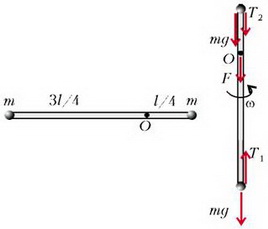
Рис. 5.

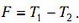
Силы натяжения стержней найдем из выражений второго закона Ньютона для грузов:

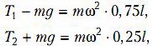
где l – длина стержня. Отметим, что написанные формулы годятся и в том случае, когда верхняя часть стержня находится в сжатом состоянии (T₂ < 0). Угловую скорость вращения ω найдем из закона сохранения энергии системы (уровень отсчета потенциальной энергии примем в точке подвеса):

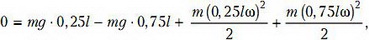
откуда

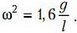
Окончательно получаем

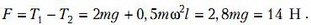
Задача 7. Демонстрационная установка состоит из наклонной плоскости, плавно переходящей в «мертвую петлю» радиусом R (рис. 6). Установка закреплена на тележке, стоящей на горизонтальной плоскости. Груз массой m₁ = 0,2 кг съезжает с высоты h = 3R, отсчитанной от нижней точки петли. Чему равна сила давления груза на поверхность в верхней точке петли? Трением пренебречь. Масса установки вместе с тележкой m₂ в 4 раза больше массы груза.

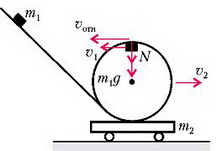
Рис. 6.

Чтобы найти силу давления (точнее, нормальную силу реакции N), надо записать второй закон Ньютона для верхней точки петли. Но тут возникает проблема: в системе отсчета, связанной с землей, траектория движения груза отлична от окружности, поскольку тележка с установкой движутся с переменной скоростью. Это значит, что радиус кривизны траектории груза может отличаться от R. Выход состоит в том, чтобы записать второй закон Ньютона в системе отсчета, связанной с тележкой, где движение происходит по окружности радиусом R. Однако есть возражение: тележка под действием силы давления груза движется с ускорением, а значит, связанная с ней система отсчета не является инерциальной. Это возражение справедливо для всех моментов движения, кроме тех, когда груз проходит нижнюю и верхнюю точки петли. В эти моменты сила давления направлена вертикально и ускорение тележки равно нулю, следовательно, силы инерции, которые действуют все остальное время, обращаются в ноль. Запишем второй закон Ньютона для верхней точки петли:

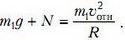
Здесь υ_отн — скорость груза относительно тележки, равная

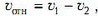
где υ₁ и υ₂ — проекции скоростей груза и тележки на горизонтальную ось. Эти скорости мы найдем из законов сохранения импульса и энергии:

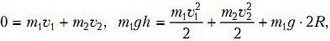
Откуда

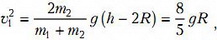
и

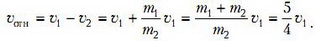
Подставляя υ_отн во второй закон Ньютона, получим

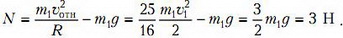
Упражнения

1. Груз массой 5 кг подвешен к потолку на упругом резиновом шнуре жесткостью 500 Н/м. Грузу дважды сообщают начальную скорость, направленную вертикально вверх. В первом случае эта скорость равна 0,5 м/с, во втором — 2 м/с. Во сколько раз максимальная высота подъема груза (отсчитанная от начальной точки) во втором случае больше, чем в первом?

2. Груз массой 2 кг подвешен к потолку на упругом резиновом шнуре. На груз дважды подействовали постоянной силой 15 Н, направленной в первом случае вертикально вверх, а во втором случае — вертикально вниз. На сколько процентов расстояние, пройденное грузом до остановки, во втором случае меньше, чем в первом?

3. Однородный стержень длиной 2 м, двигаясь вдоль своей длины по шероховатой горизонтальной поверхности, начинает пересекать границу, за которой поверхность становится гладкой. Скорость стержня в этот момент равна 1,6 м/с. Какое расстояние (в см) проедет стержень от этого момента до остановки, если коэффициент трения о шероховатую поверхность равен 0,2?

4. В шар массой 480 г попадает пуля массой 20 г, летящая со скоростью 100 м/с по линии, проходящей через центр шара. После удара пуля отскакивает назад, при этом при ударе выделяется 90 Дж тепла. Найдите конечную скорость шара.

5. Невесомый стержень, на конце которого закреплен груз массой 3 кг, а в середине — груз массой 4 кг, может свободно вращаться вокруг горизонтальной оси, проходящей через его свободный конец. Стержень приводят в верхнее положение и отпускают. С какой силой он будет действовать на ось в момент прохождения нижнего положения?

6. Два бруска массами 0,5 кг и 1 кг, лежащие на гладком полу, соединены пружиной жесткостью 900 Н/м. Вначале первый брусок упирается в стену, пружина не деформирована и расположена перпендикулярно стене. Второй брусок перемещают на 10 см в сторону первого и отпускают. Найдите максимальную скорость первого бруска в процессе дальнейшего движения.

7. Брусок стоит на гладкой горизонтальной плоскости. На бруске закреплен штатив, к которому на легкой нити подвешен груз массой 0,1 кг. Масса бруска вместе со штативом равна массе груза. Вначале нить с грузом удерживают в горизонтальном положении, затем отпускают. Найдите силу натяжения нити в момент, когда груз находится в нижней точке.

Ответы

1. n = 5.

2. δ = 25%.

3. s = 80 см.

4. u₂ = 5 м/с.

5. F = 320 Н.

6. υ_1max = 4 м/с.

7. Т = 5 H.