На чтение 4 мин Просмотров 3к. Опубликовано 25.11.2021
Содержание
- Ответ или решение 2
- Скорость движения рассчитывается по формуле
- Найдем уравнение скорости
- Ответ
- Уравнение скорости
- График скорости
- Некоторые частные случаи
- Заключение
Ответ или решение 2
![]()
Скорость движения рассчитывается по формуле
- Скорость движения равна производной формулы пути;
- чтобы найти максимальную скорость, нужно найти производную скорости;
- затем нужно определить точки максимума;
- подставить их в уравнение скорости.
Нам дано уравнение пути s = -10t 3 + 15t 2 + 2t
Найдем уравнение скорости
S` = — 10 * 3t 2 + 15 * 2t + 2 = — 30t 2 + 30t + 2
v = — 30t 2 + 30t + 2
Найдем точки максимума этой функции
Для этого найдем производную этой функции.
v`= — 30 * 2t + 30 = — 60t + 30
Приравняем ее к нулю.
Переносим 30 в правую часть, меняя знак.
Делим все уравнение на (- 30).
Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.
Берем любую точку, например, 0.
— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)
Берем например, точку 1.
— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)
Значит, t = 1/2 — это точка максимума.
Подставим это значение в уравнение скорости.
v = — 30t 2 + 30t + 2
v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.
Ответ: максимальная скорость движения равна 9,5.
![]()
Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.

- Попроси больше объяснений
- Следить
- Отметить нарушение
Vazgen1312 05.07.2019
Ответ

Ответ:
Объяснение:
Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)
1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²
S = 0 + 15*1/2 = 7,5 м
2. S = V*t = 15*3 = 45 м
3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.
Еще раз о том, что такое равноускоренное движение
Автомобиль за каждую секунду увеличивает свою скорость на  . Движется ли автомобиль равноускоренно?
. Движется ли автомобиль равноускоренно?
На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на 
 . Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).
. Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).
Уравнение скорости
Воспользовавшись уравнением, определяющим ускорение  , удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:
, удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:


Уравнение скорости в проекциях имеет вид:

Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.
К вопросу о направлении скорости и ускорения
В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.
Рассмотрим наиболее типичные примеры направления скорости и ускорения.
1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).

Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой
В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.
2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).

Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой
Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.
3. Скорость и ускорение взаимно перпендикулярны (рис. 3).

Рис. 3. Скорость и ускорение взаимно перпендикулярны
Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.
Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.
График скорости
График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.

Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения
Проанализируем различные графики.
Первый. Уравнение проекции скорости: 


Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:



График начинается в точке 
Где 

Рис. 5. График функции 
Это уравнение прямой, что подтверждается графиками, рассмотренными нами.
Некоторые частные случаи
Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость,  , равняется нулю, проекция ускорения больше нуля.
, равняется нулю, проекция ускорения больше нуля.
Запись этого уравнения  . А сам вид графика достаточно простой (график 1).
. А сам вид графика достаточно простой (график 1).

Рис. 6. Различные случаи равноускоренного движения
Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси .
.
Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси  . При этом модуль скорости постоянно возрастает, тело ускоряется.
. При этом модуль скорости постоянно возрастает, тело ускоряется.
График зависимости ускорения от времени
Равноускоренное движение – это движение, при котором ускорение тела не меняется.

Рис. 7. График зависимости проекций ускорения от времени
Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.
Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:

Произведение ускорения и времени –это изменение скорости за данное время.


Рис. 8. Изменение скорости
Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.
Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.
Заключение
На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.
- Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
- Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «class-fizika.narod.ru» (Источник)
- Интернет-портал «youtube.com» (Источник)
- Интернет-портал «fizmat.by» (Источник)
- Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)
1. Что такое равноускоренное движение?
2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:

3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при  ?
?
«>
Колебания и волны: скорости и ускорения
В этой статье мы вспомним кинематику: то, что скорость – производная координаты, а ускорение – производная скорости или вторая производная координаты. Заодно потренируемся брать производные от сложных функций.
Задача 1. Материальная точка совершает гармонические колебания по закону $x = 1,2 cos pi (frac+frac)$. Определить амплитуду, круговую частоту, период и начальную фазу колебаний. Найти амплитуды скорости и ускорения. Построить графики зависимости координаты. скорости и ускорения точки от времени.
Амплитуда равна $A=1,2$, круговая частота (или циклическая, или угловая) равна $omega=frac$, начальная фаза равна $psi_0=frac$, период колебаний – $T=frac=frac=3$ с.
Скорость – производная координаты. Возьмем производную:
Тогда $upsilon_= A omega=1,2frac=0,8pi=2,51$ м/с.
Ответ: амплитуда $A=1,2$, круговая частота $omega=frac$, начальная фаза $psi_0=frac$, период колебаний – $T=3$ с, $upsilon_=2,51$ м/с, $a_=5,26 $ м/с$^2$
Задача 2. Материальная точка совершает гармонические колебания с частотой $f= 0,5$ Гц. Амплитуда колебаний А =3 см. Определить скорость точки в момент времени, когда смещение $x= 1,5$ см.
Запишем закон колебаний. Так как не указано, по какому закону они совершаются, то выберем косинус.
Скорость – производная координаты. Возьмем производную:
$$upsilon=x^=-A omega sin (omega t+psi_0)$$
Ответ: $upsilon=-8,16$ см/с.
Задача 3. Написать закон гармонического колебания точки, если максимальное ускорение ее $a_= 49,3$ см/с2, период колебаний $T = 2$ с и смещение точки от положения равновесия в начальный момент времени $x_0 = 2,5$ см. Колебания совершаются по закону синуса.
В момент времени $t=0$ смещение равно 2,5 см:
$$x_0=Asin(psi_0)= 2,5$$
Выясним, какая у точки амплитуда колебаний. Для этого определим скорость (первую производную) и ускорение(вторую производную):
Кинематика

Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_ ) :

Определим скорость второго тела относительно первого ( v_ ) :

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:


Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:


Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ) , единицы измерения — м/с (км/ч).

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ) , единица измерения — м/с 2 .
В векторном виде:

где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:


где ( a_n ) – нормальное ускорение, ( a_ ) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_ ) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_ ) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_ ) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_ ) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_ ) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ( x=x(t) ) .

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):


При торможении (в проекциях на ось ОХ):


График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) < 0.
График скорости (проекции скорости) представляет собой зависимость скорости от времени:
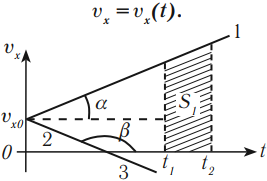
График скорости при равноускоренном движении – прямая.
График 1 направлен вверх, тело движется равноускоренно в положительном направлении оси ОХ, ( v_ ) > 0, ( a_x ) > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_ ) > 0, ( a_x ) < 0,
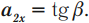
График 3 направлен вниз, тело движется равноускоренно против оси ОХ, ( v_ ) < 0, ( a_x ) < 0. По графику зависимости скорости от времени можно определить перемещение, пройденное телом за промежуток времени ( t_2-t_1 ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ( n ) -ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ) , единицы измерения – м/с 2 .
Важно! ( g ) = 9,8 м/с 2 , но при решении задач считается, что ( g ) = 10 м/с 2 .
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_ ) ;
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_=0 ) .



Скорость тела в любой момент времени:


Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.



Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:


Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ) , с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ) , под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_ ) , единицы измерения – м/с 2 .

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ) , единицы измерения – с.

где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ) , единицы измерения – с –1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ) , единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ) , единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:


Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:


Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ) , и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ) , то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ) , мгновенная скорость точки ( (p) ) , лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
Уравнение движения, графики равномерного прямолинейного движения
Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.
Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.

Составим таблицу перемещений за первые 4 секунды:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 30 | 40 | 50 | 60 |
Стартуя с точки x0=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end

Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 |
| x, м | 20 | 10 | 0 | -10 | -20 |
В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x0 в любой момент времени t.
п.2. Уравнение прямолинейного равномерного движения
Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.
- если направление вектора (overrightarrow) совпадает с направлением оси OX, то (v_x=vgt 0)
- если направление вектора (overrightarrow) противоположно направлению оси OX, то (v_x=-vlt 0)
- если (triangle xgt 0), перемещение (overrightarrow) произошло в направлении оси OX;
- если (triangle xlt 0), перемещение (overrightarrow) произошло противоположно направлению оси OX.
п.3. Удобная система отсчета для решения задачи о прямолинейном движении
При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.
При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.
Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.
п.4. График движения x=x(t)
Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).
В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).
- возрастает, если (v_xgt 0)
- убывает, если (v_xlt 0)
- постоянна (параллельна оси (t)), если (v_x= 0)
п.5. Как найти уравнение движения по графику движения?

п.6. График скорости vx=vx(t)
- расположена над осью (t), если (v_xgt 0)
- расположена под осью (t), если (v_xlt 0)
- совпадает с осью (t), если (v_x=0)
Для рассмотренного примера:
п.7. Как найти путь и перемещение по графику скорости?
Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости: 
Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.
Проекция перемещения может быть как положительной, так и отрицательной или равной 0.
п.8. Задачи
Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?
По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin x_1=x(5)=8cdot 5=40 text\ x_2=x(10)=8cdot 10=80 text end
б) Скорость (v_x=8) м/с — постоянная величина, её график:
$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text $$ Ответ: а) 40 м и 80 м; б) 40 м
Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?
а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).
Найдем скорость корабля (v_x): $$ v_x=frac=frac=18 (text) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.
б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.
в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text) $$
г) Переведем скорость в км/с: $$ 18000frac>>=frac>>=frac>>=5 text $$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с
Как найти максимальную скорость
Задачи физики и математики часто требуют найти максимальную скорость объекта на протяжении всего пути. Данный вид задач относится к разделу кинематики. Рассмотрим алгоритм нахождения максимальной скорости.

Инструкция
Запишите уравнение зависимости скорости от времени.
Найдите производную правой части уравнения и приравняйте её к нулю. Найдите момент времени t, в который производная равна нулю. Если функция периодическая, достаточно рассмотреть какой-либо один период.
Из полученных значений t выберите точки максимума функции. Точка максимума – это минус.
Посчитайте значение функции скорости в точках максимума. Выберите наибольшее.
Если задан конкретный промежуток времени, сравните значения функции скорости на граничных точках и в точках максимума. Выберите наибольшее из них.
Видео по теме
Полезный совет
Функцию зависимости скорости от времени можно получить, дифференцируя функцию пройденного пути, либо интегрируя функцию ускорения. Во втором случае понадобятся еще начальные условия.
Источники:
- как находится максимальная скорость
Максимальную скорость
Vamax
, развивающую проектируемым автомобилем
на горизонтальной дороге, определим
как по тяговой характеристике, так и по
динамической. Допускается небольшое
несовпадение максимальных скоростей,
определенным по двум разным характеристикам;
большое несовпадение (более 4%) говорит
о погрешности в ходе проведения тягового
расчета.
Используя данные
таблицы 15, на графике тяговой характеристики
(пункт 1.7.1) строим кривую, соответствующую
суммарной силе сопротивления движения
автомобиля (сила сопротивления дороги
Fψ
плюс сила сопротивления воздуха FB);
точка пересечения данной кривой (Fψ
+ FB)
и кривой, соответствующей полной окружной
силе FK0
на высшей передаче, позволяет определить
максимальную скорость Va
max на дороге без
уклона: опустив линию на горизонтальную
ось (I = 0), по которой
отложена скорость Va
автомобиля. Если кривые Fψ
+ FB и
FK0
на высшей передаче не пересеклись, то
Vamax
соответствует максимальной скорости
по кривой FK0
на высшей передаче (данная Vamax
называется максимальной кинематической
скоростью, определяемой передаточными
числами трансмиссии и максимальной
частотой вращения коленчатого вала
двигателя); запас окружной силы FK0
в данном случае (кривые Fψ
+ FB и
FK0
не пересеклись) может быть использован
для достижения Vamax
при движении автомобиля на подъеме.
Аналогично определяется
Vamax
по динамической характеристике: используя
данные таблицы 15 на графике динамической
характеристики (пункт 1.7.2) строится для
высшей передачи кривая ψ = fV
(i=0) – безразмерного
фактора сопротивления движению
автомобиля. Точка пересечения кривой
ψ и кривой динамического фактора D
(движущего фактора) определяет Vamax,
если кривее не пересеклись, то Vamax
(кинематическая) соответствует максимуму
скорости по кривой D на
высшей передаче.
Максимально возможные
скорости движения автомобиля, определенные
по тяговой и динамической характеристикам,
должны быть равны между собой, и
соответствовать той максимальной
скорости Va
max, которая была
определена в техническом задании на
проектирование (см. пункт 1.2). Результаты
расчетов заносим в таблицу 16.
Таблица 16 – Максимальная
скорость Vаmax
автомобиля
|
Условия определения |
Vаmax |
Погрешность |
|
Тяговая характеристика |
92 |
0% |
|
Динамическая |
92 |
0% |
|
Мощносной баланс |
92 |
0% |
При движении автомобиля
на подъем (уклон дороги i)
максимальную скорость, по динамической
характеристике, в данных дорожных
условиях определяют следующим образом:
величину уклона i складывают
с коэффициентом сопротивления качению
колес fV
и ищут точку пересечения кривой i+fV
с кривой D – полученная
точка позволяет определить: какую
максимальную скорость развивает
проектируемый автомобиль и на какой
передаче в КПП.
Определяется максимальная
скорость автомобиля при преодолении
уклона в 5% и максимального уклона по
таблице 15. Найденные значения скоростей
не должны быть меньше значений, приведенных
в таблице 17.
Таблица 17 – Максимальные
скорости автомобилей
-
Максимальная скорость,
км/чГрузовые автомобили
полноприводные
неполноприводные
автопоезда
На горизонтальной
дороге, i = 080
90
80
На подъеме в 5%,
i
= 0,0540
45
25
На максимальном
подъеме i max5
12
8
Максимальная скорость
при преодолении уклона в 5%
Vаmax
= 40км/ч
Максимальная скорость
при преодолении максимального уклона
Vаmax
=7 км/ч
что соответствует
рекомендациям.
1.8
Путь и время разгона автомобиля
Считаем, что разгон
начинается с минимальной устойчивой
скорости
Vamin
(соответствующей nemin
– минимальной устойчивой частоте
вращения коленчатого вала ДВС) на
передаче, используемой для трогания
автомобиля с места. Разгон осуществляется
при полной подаче топлива т.е. двигатель
работает по ВСХ (имеем наибольшую
интенсивность разгона).
Ускорение, как известно,
можно определить по формуле:
аx![]()
(45)
где dVa
– приращение скорости за промежуток
времени dt.
Тогда
dt![]()
(46)
откуда время разгона
t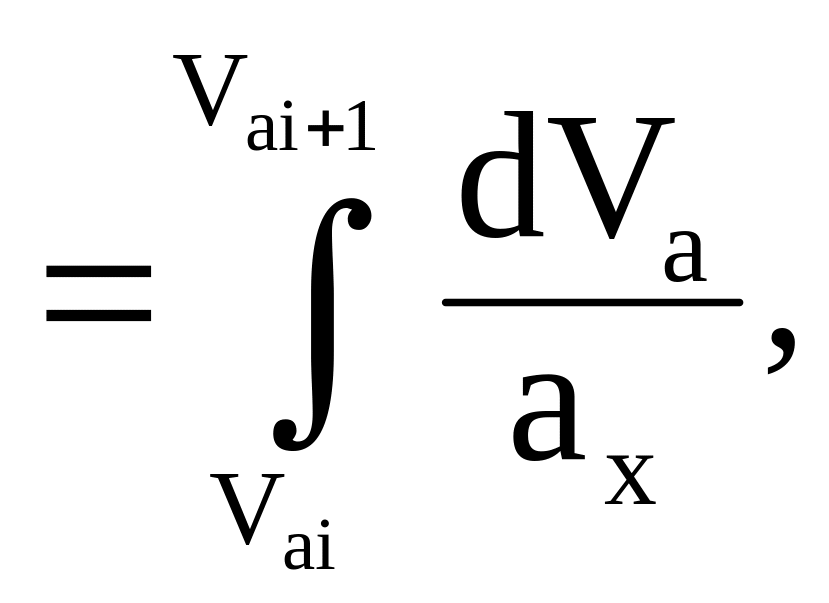
(47)
Считаем, что в небольшом
интервале скоростей ΔVai=Vai+1-Vai
движение является равноускоренным
со средним ускорением аmi
, тогда время движения в данном
интервале, между двумя точками, определим
по формуле:
![]()
(48)
где ∆Vai
– изменение скорости между двумя
точками, м/с;
Дальнейшие результаты
расчётов сведены в таблицу 18.
аmi
– среднее ускорение между двумя точками
![]()
(49)
Дальнейшие результаты
расчётов сведены в таблицу
Путь, проходимый за
время движения между двумя точками:
∆S=Vmi·∆ti
(50)
где Vmi
– средняя скорость в рассматриваемом
интервале
![]()
(51)
Дальнейшие результаты
расчётов сведены в таблицу 18.
Потери скорости за
время переключения ∆Vn
определим по формуле:
![]()
,
м/с (52)
где tn=1c
– время переключения передач
δi+1
– коэффициент учёта вращающихся масс
Путь, проходимый
автомобилем, за время переключения tn
c К-ой на К+1 передачу:
∆Sn=(Vкmax–
0,5∆Vnк-(к+1))·tn,
м (53)
где Vкmax
– скорость, соответствующая моменту
переключения
Таблица 18 – Разгон
автомобиля
Разгон автомобиля на
первой передаче
|
Пара- метр |
Раз-мер- ность |
№ точки |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||
|
Va |
км/ч |
3,0 |
3,86 |
4,71 |
5,57 |
6,43 |
7,28 |
8,14 |
9 |
|
Va |
м/с |
0,83 |
1,07 |
1,31 |
1,55 |
1,79 |
2,02 |
2,26 |
2,5 |
|
∆Vi |
м/с |
– |
0,24 |
0,24 |
0,24 |
0,24 |
0,23 |
0,24 |
0,24 |
|
ax |
м/с2 |
0,748 |
0,816 |
0,869 |
0,899 |
0,908 |
0,899 |
0,866 |
0,818 |
|
ami |
м/с2 |
– |
0,872 |
0,843 |
0,884 |
0,904 |
0,904 |
0,883 |
0,842 |
|
∆ti |
с |
– |
0,31 |
0,29 |
0,27 |
0,27 |
0,25 |
0,27 |
0,29 |
|
t |
с |
– |
0,31 |
0,6 |
0,87 |
1,14 |
1,39 |
1,66 |
1,95 |
|
Vmi |
м/с |
– |
0,95 |
1,19 |
1,43 |
1,67 |
1,91 |
2,14 |
2,38 |
|
∆Si |
м |
– |
0,3 |
0,35 |
0,39 |
0,45 |
0,48 |
0,58 |
0,69 |
|
S |
м |
– |
0,3 |
0,65 |
1,04 |
1,49 |
1,97 |
2,55 |
3,24 |
Разгон автомобиля на
второй передаче
-
Параметр
Размерность
№ точки
9
10
11
12
13
14
Va
км/ч
8,68
9,67
11,15
12,64
14,13
15,61
Va
м/с
2,41
2,69
3,1
3,51
3,93
4,34
∆Vi
м/с
(0,09)
0,28
0,41
0,41
0,42
0,41
ax
м/с2
0,895
0,923
0,936
0,925
0,892
0,836
ami
м/с2
–
0,91
0,93
0,93
0,91
0,87
∆ti
с
(1,5)
0,31
0,44
0,44
0,46
0,47
t
с
3,45
3,76
4,2
4,64
5,1
5,57
Vmi
м/с
–
2,55
2,9
3,31
3,72
4,14
∆Si
м
3,68
0,79
1,28
1,46
1,71
1,95
S
м
6,92
7,71
8,99
10,45
12,16
14,11
Разгон автомобиля на
третьей передаче
-
Параметр
Размерность
№ точки
15
16
17
18
19
Va
км/ч
15,23
16,26
18,43
20,6
22,76
Va
м/с
4,23
4,52
5,12
5,72
6,32
∆Vi
м/с
(0,11)
0,29
0,6
0,6
0,6
ax
м/с2
0,785
0,796
0,788
0,759
0,71
ami
м/с2
–
0,791
0,792
0,77
0,735
∆ti
с
(1,5)
0,37
0,76
0,78
0,82
t
с
7,07
0,44
8,2
8,98
9,8
Vmi
м/с
–
4,38
4,82
5,42
6,02
∆Si
м
(6,43)
1,62
3,66
4,23
4,94
S
м
20,54
22,16
25,82
30,05
34,99
Разгон автомобиля на
четвёртой передаче
-
Параметр
Размерность
№ точки
20
21
22
23
24
Va
км/ч
22,31
22,42
25,41
28,4
31,39
Va
м/с
6,193
6,23
7,06
7,89
8,72
∆Vi
м/с
(0,123)
0,037
0,83
0,83
0,83
ax
м/с2
0,63
0,634
0,618
0,593
0,552
ami
м/с2
–
0,632
0,626
0,606
0,573
∆ti
с
(1,5)
0,06
1,33
1,37
1,45
t
с
11,3
11,36
12,69
14,06
15,51
Vmi
м/с
–
6,21
6,65
7,48
8,31
∆Si
м
(9,39)
0,37
8,85
10,25
12,05
S
м
44,38
44,75
53,6
63,85
75,9
Разгон автомобиля на
пятой передаче
-
Параметр
Размерность
№ точки
25
26
27
28
Va
км/ч
30,91
34,24
38,27
42,3
Va
м/с
8,586
9,51
10,63
11,75
∆Vi
м/с
(0,134)
0,924
1,12
1,12
ax
м/с2
0,465
0,47
0,443
0,408
ami
м/с2
–
0,47
0,46
0,43
∆ti
с
(1,5)
1,97
2,43
2,6
t
с
17,01
18,98
21,41
24,01
Vmi
м/с
–
9,05
10,07
11,19
∆Si
м
(12,98)
17,83
24,47
29,09
S
м
88,88
106,71
131,18
160,27
Разгон автомобиля на
шестой передаче
-
Параметр
Размерность
№ точки
29
30
31
32
Va
км/ч
41,79
45,12
50,43
55,72
Va
м/с
11,61
12,53
14,01
15,48
∆Vi
м/с
(0,142)
0,92
1,48
1,47
ax
м/с2
0,34
0,333
0,313
0,285
ami
м/с2
–
0,336
0,323
0,299
∆ti
с
(1,5)
2,74
4,58
4,92
t
с
25,51
28,25
32,83
37,75
Vmi
м/с
–
12,07
13,27
14,75
∆Si
м
(17,52)
33,07
60,78
72,57
S
м
177,79
210,86
271,64
344,21
Разгон автомобиля на
седьмой передаче
-
Параметр
Размерность
№ точки
33
34
35
36
Va
км/ч
55,18
58,17
65,01
71,86
Va
м/с
15,33
16,16
18,06
19,96
∆Vi
м/с
(0,151)
0,83
1,9
1,9
ax
м/с2
0,225
0,225
0,204
0,174
ami
м/с2
–
0,225
0,215
0,189
∆ti
с
(1,5)
3,69
8,84
10,05
t
с
39,25
42,94
51,78
61,83
Vmi
м/с
–
15,75
17,11
19,01
∆Si
м
(23,11)
58,12
151,25
191,05
S
м
367,32
425,44
576,69
767,74
Разгон автомобиля на
восьмой передаче
-
Параметр
Размерность
№ точки
37
38
39
40
Va
км/ч
71,26
74,28
83,02
92
Va
м/с
19,795
20,63
23,06
25,56
∆Vi
м/с
(0,165)
0,84
2,43
2,5
ax
м/с2
0,125
0,12
0,097
0,064
ami
м/с2
–
0,123
0,109
0,081
∆ti
с
(1,5)
6,83
22,29
30,86
t
с
63,33
70,16
92,45
123,31
Vmi
м/с
–
20,21
21,85
24,31
∆Si
м
29,82
138,03
487,04
750,21
S
м
797,56
935,59
1422,63
2172,84
По данным таблицы 18
строим графики пути и времени разгона
автомобиля, по которым определяем:
1) время разгона до
скорости 60 км/ч
t60=45с
2) путь проходимый АТС
до достижения Vamax
– Sv
Sv=2172,84м
3) время разгона с места
на пути 1000м – t1000
t1000=72c
1.9
Мощностной баланс
Расчет мощностного
баланса, проведем на высшей передаче.
Уравнение мощностного
баланса имеет вид:
NK=NB+
N+
Nia
(54)
где NК
– мощность, подведенная к ведущим
колесам:
NK
= Nе
Т, кВт
(55)
где Ne –
эффективная мощность двигателя (таб.2),
кВт;
ηТ – КПД
трансмиссии;
Nк=73,34,38·0,82=60,14
кВт
Дальнейшие результаты
расчётов сведены в таблицу 19
N
– мощность, затрачиваемая на преодоление
сопротивления дороги;
Nψ=Fψ·Va,
кВт (56)
где Fψ
– сила сопротивления дороги (таблица
15), Н;
Va –
скорость автомобиля (таблица 15),м/с;
Nψ=2900·8,5=24650Вт=24,65кВт
Дальнейшие результаты
расчётов сведены в таблицу 19
NВ
– мощность, затрачиваемая на преодоление
сопротивления воздуха:
NВ =
FB
Va,
кВт (57)
где FB
– сила сопротивления воздуха (таблица
15),Н;
NВ=51,8·5,047=261Вт=0,261кВт
Дальнейшие результаты
расчётов сведены в таблицу 12
Nia
– мощность, которая может быть затрачена
на разгон автомобиля.
Таблица 19 – Мощносной
баланс автомобиля на высшей передаче
|
ne, об/мин |
Va, км/ч |
Va, м/с |
Ne, кВт |
NК, кВт |
NВ, кВт |
NК кВт |
N, кВт |
|
700 |
30,59 |
8,5 |
73,34 |
60,14 |
1,95 |
58,19 |
24,65 |
|
900 |
39,32 |
10,92 |
102,57 |
84,11 |
4,13 |
79,98 |
32,54 |
|
1100 |
48,06 |
13,35 |
133,01 |
109,07 |
7,53 |
101,54 |
40,72 |
|
1300 |
56,8 |
15,78 |
162,73 |
133,44 |
12,43 |
121,01 |
49,71 |
|
1500 |
65,54 |
18,21 |
190,05 |
155,84 |
19,1 |
136,74 |
59,36 |
|
1700 |
74,28 |
20,63 |
212,82 |
174,51 |
27,79 |
146,72 |
69,52 |
|
1900 |
83,02 |
23,06 |
229,83 |
188,46 |
38,81 |
149,65 |
80,94 |
|
2100 |
92 |
25,56 |
239,66 |
196,52 |
52,91 |
143,61 |
94,06 |
По данным таблицы 19
строим график мощностного баланса
автомобиля на высшей передаче и определяем
Vаmax
– точка пересечения кривых Nψ
и Nк-Nв
Vаmax=92
км/ч
1.10
Топливная экономичность
Построим топливную
характеристику установившегося движения
– зависимость путевого расхода топлива
Qs от скорости
движения Vа и
определим эксплуатационный расход
топлива проектируемого автомобиля,
(все расчёты будем вести на высшей
передаче).
Путевой расход будет
определяться по зависимости:
![]()
,
л/100 км (58)
где geN
– средний удельный эффективный расход
топлива при максимальной мощности
двигателя, г/кВтч;
geN
= (1,05 … 1,1) gemin
(59)
где gemin
– минимальный удельный расход топлива,
г/кВтч;
gemin
= 180 … 240 г/кВтч;
geN
=1,05·180=189 г/кВтч
KИ
– коэффициент использования мощности
двигателя;
KИ =
1, 2 + 0,14 · U – 1.8 · U2
+ 1,46 · U3
(60)
![]()
(61)
![]()
Дальнейшие результаты
расчётов сведены в таблицу 20
KИ =
1,2 + 0,14 · 0,442 – 1,8 · 0,442 2 + 1,46 · 0,442 3=
1,036
Дальнейшие результаты
расчётов сведены в таблицу 20
KЕ
– коэффициент использования частоты
вращения коленчатого вала двигателя;
KЕ
= 1,25 – 0,99 · Е + 0,98 · Е2 – 0,24 · Е3
(62)
![]()
(63)
где ne,
Va –
текущая соответственно частота вращения
коленчатого вала и скорость АТС;
nN,
VaN –
соответственно частота вращения
коленчатого вала и скорость автомобиля
при максимальной мощности двигателя;
![]()
Дальнейшие результаты
расчётов сведены в таблицу 20
KЕ
= 1,25 – 0,99·0,333 + 0,98·0,3332 –
0,24·0,3333=1,018
Дальнейшие результаты
расчётов сведены в таблицу 20
N
и NВ – см. таблицу
19
T
– плотность топлива, кг/м3 : для
дизельного топлива;
T=835
кг/м3
Va,
км/ч – см. таблицу 15
![]()
л/100 км
Дальнейшие результаты
расчётов заносим в таблицу 20 и строим
топливную характеристику автомобиля,
по которой определяем:
1) расход топлива при
скорости 80км/ч и 60км/ч
расход топлива при
скорости 80км/ч равен 35,5 л/100 км
расход топлива при
скорости 60км/ч равен 30,2 л/100 км
2) эксплуатационный
расход (э.р.) топлива
э.р. = 1,1·QP
(64)
где QP
– путевой расход при расчетной скорости
VP
![]()
;
(65)
![]()
км/ч;
QP=32,4
л/100 км;
э.р. = 1,1·32,4=35,64 л/100 км;
3) контрольный расход
топлива Qк –
минимальный расход по топливной
характеристике
Qк=28
л/100 км
Таблица 20 – Топливная
экономичность автомобиля на высшей
передаче
-
Va,
км/чNК,
кВтN
+ NВ,кВт
U
E
KИ
KЕ
QS
,л/100кмч
30,59
60,14
26,6
0,442
0,333
1,036
1,018
25,32
39,32
84,11
36,67
0,436
0,427
1,04
0,987
26,43
48,06
109,07
48,25
0,442
0,522
1,036
0,966
27,74
56,8
133,44
62,14
0,466
0,617
1,022
0,956
29,5
65,54
155,84
78,46
0,504
0,712
1,001
0,955
31,59
74,28
174,51
97,31
0,558
0,807
0,972
0,963
33,85
83,02
188,46
119,75
0,635
0,902
0,937
0,978
36,48
92
196,52
146,97
0,748
1
0,909
1
40,08
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тема: Найти максимальную скорость движения тела на промежутке (Прочитано 9321 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Help!!! Помогите!
Нужно решить задачу по применению производной в механике.
Закон движения задан уравнением: S(t)= -t^3+3*t^2+9*t+3.
Необходимо найти максимальную скорость движения тела.
Вроде бы всё просто: скорость – производная S, нашла её, но вот дальше загвоздка: как определить максимальную скорость движения тела?
Может быть решение и элементарно, но школу закончила 10 лет назад, вспоминала сейчас весь курс, перелопатила кучу информации, но НИГДЕ не нашла пример нахождения максимальной скорости. Везде просто нужно найти скорость в определенный момент времени 
« Последнее редактирование: 03 Июня 2011, 17:25:32 от kms_fima »

Может найти точку максимума,это и будет наибольшая скорость.

Человек переживает свою индивидуальность в терминах воли, а это означает, что существование его личности тождественно его способности выражать в этом мире свою волю. Progoff.
Если построить график скорости, то видно, что она имеет вид параболы и имеет только точку минимума. Ветви параболы уходят вверх до бесконечности.

Сомнения очень правильные.
Поскольку у Вас минимум, а не то что надо, ищем значения на концах
заданого интервала и выбираем подходящее.

А если интервал не задан, как в этом примере? Просто опечатка?потому что получается, что скорость возрастает до бесконечности…

Если построить график скорости, то видно, что она имеет вид параболы и имеет только точку минимума. Ветви параболы уходят вверх до бесконечности.
Почему вверх?
Максимальная скорость =12

Решение задач – практическое искусство; научиться ему можно, только подражая хорошим образцам и постоянно практикуясь….
Если построить график скорости, то видно, что она имеет вид параболы и имеет только точку минимума. Ветви параболы уходят вверх до бесконечности.
Почему вверх?
Максимальная скорость =12
Спасибо большое))))))) у меня уже голова квадратная была, не на тот график глянула..Построила заново – всё получилось! Ещё раз спасибо огромное!






