Как найти максимальную скорость груза на пружине

Найти частоту и максимальную скорость, которую имеет груз, совершающий колебания на пружине жѐсткостью 20 Н/м, если его масса 5 кг.

Амплитуду колебаний можем найти из выражения закона Гука. Поскольку  сила, которая действует на пружину равна силе тяжести, то можем записать уравнение:

$mg=kA$   где m, g, k , A –  масса, ускорение земного притяжения, эжесткость пружины, амплитуда колебаний.    Откуда амплитуда:

Уравнение гармонических колебаний:     $x(t)=Asin(wt+phi_0)$  

Максимальная скорость груза в процессе колебаний равна произведению амплитуды на круговую частоту:

Спрятать решение

Спрятать критерии

Для определения
характера движения механической системы
нужно:

– составить уравнение
движения системы исходя из законов
динамики или закона сохранения энергии;

– сравнить с
уравнением (1.1.3)
;

– если оно приводится
к такому виду, то можно однозначно
утверждать, что данная система является
гармоническим осциллятором, частота
ω₀которого равна корню квадратному
из коэффициента прих.

Колебания груза на пружине

Рассмотрим
колебания груза на пружине, при условии,
что пружина
не деформирована за пределы упругости.

П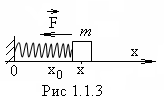окажем,
что такой груз будет совершать
гармонические колебания относительно
положения равновесия (рис.1.1.3).

Действительно,
согласно закону Гука, сжатая или
растянутая пружина создаёт гармоническую
силу:

где
–коэффициент жёсткости пружины,

–координата
положения равновесия,

х–координата
груза (материальной точки) в момент
времени
,

– смещение от
положения равновесия.

Поместимначало
отсчета координаты в положение равновесия
системы. В этом случае.

Если пружину
растянуть на величину х, после чего
отпустить в момент времениt=0,
то уравнение движения груза согласно
второму закону Ньютона примет вид

–kx
=ma, или
,
и

(1.1.6)

Это уравнение
совпадает по виду с уравнением движения
(1.1.3) системы, совершающей гармонические
колебания, его решение будем искать в
виде:

.
(1.1.7)

Подставим (1.17) в
(1.1.6), имеем:

то есть выражение (1.1.7) является
решением уравнения (1.1.6) при условии,
что

Если
в начальный момент времени положение
груза было произвольным, то уравнение
движения примет вид:

.

Р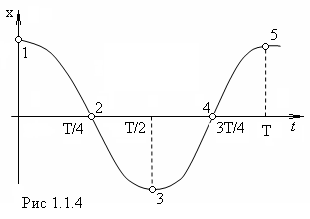ассмотрим,
как меняется энергия груза, совершающего
гармонические колебания в отсутствие
внешних сил (рис.1.14).

• Если
  в момент
  времени t=0
  : грузу сообщить смещение
  х=А, то его
  полная энергия станет равной потенциальной
  энергии деформированной пружины
  ,
  кинетическая энергия равна нулю (точка
  1).

На
груз действует сила F= -kx, стремящаяся
вернуть его в положение равновесия,
поэтому груз движется с ускорением и
увеличивает свою скорость, а, следовательно,
и кинетическую энергию. Эта сила сокращает
смещение груза х, потенциальная энергия
груза убывает, переходя в кинетическую.
Система «груз – пружина» замкнутая,
поэтому её полная энергия сохраняется,
то есть:

.
(1.1.8)

• В момент временигруз находитсяв положении равновесия(точка 2), его потенциальная энергия
  равна нулю, а кинетическая максимальна.

Максимальную
скорость груза найдём из закона сохранения
энергии (1.1.8):

За счёт запаса
кинетической энергии груз совершает
работу против упругой силы –и пролетает положение равновесия.
Кинетическая энергия постепенно
переходит в потенциальную.

• При
  груз имеетмаксимальное отрицательное
  смещение –А,кинетическая
  энергияW_k=0, груз останавливается и начинает
  движение к положению равновесия под
  действием упругой силыF=
  –kx.

Далее движение
происходит аналогично.

5. Маятники

Под маятником
понимают твёрдое тело, которое
совершает под действием силы тяжести
колебания вокруг неподвижной точки или
оси.

Различают физический
и математический маятники.

Математический
маятник – это идеализированная
система, состоящая из невесомой
нерастяжимой нити, на которой подвешена
масса, сосредоточенная в одной материальной
точке.

например,
математическим маятником, является
шарик на длинной тонкой нити.

Отклонение
маятника от положения равновесия
характеризуется углом φ, который образует
нить с вертикалью(рис.1.15).

При отклонении
маятника от положения равновесия
возникает момент внешних сил (силы
тяжести)
:

,

где m– масса,

– длина маятника

Этот момент
стремится вернуть маятник в положение
равновесия (аналогично квазиупругой
силе) и направлен противоположно смещению
φ, поэтому в формуле стоит знак
«минус».

Уравнение динамики
вращательного движения для маятника
имеет вид:

Iε=,

где
–момент инерции
математического маятника,

–
угловое
ускорение

Или
.

Рассмотрим случай
малых колебаний,поэтомуsin
φ ≈φ, обозначим,

имеем:
,
или
,

и окончательно

=0
–этоуравнение гармонических
колебаний,

его решение:.

Частота колебаний
математического маятника определяется
только его длиной и ускорением силы
тяжести, – и не зависит от
массы маятника.

Период равен:
.

_{Если колеблющееся
тело нельзя представить, как материальную
точку, то маятник называют физическим
(рис.1.1.6).}

_{Физический
маятник – твердое
тело, которое может вращаться под
действием своей силы тяжести вокруг
неподвижной горизонтальной оси О, не
проходящей через центр тяжести тела.}

_{Ось О называют
осью качания маятника.}

_{Центр тяжести
маятника совпадает с его центром масс.}

_{Точка подвеса
маятника– точка О пересечения оси
качания маятника и перпендикулярной
оси качания.}

_{Уравнение его
движениязапишем в виде:}

.

_{В случае малых
колебаний}
,
или
=0
_{, где}

_{Это уравнение
движения тела, совершающего гармонические
колебания.}

_{Частота
колебаний физического маятника
зависит от его массы, длины и момента
инерции относительно оси, проходящей
через точку подвеса.}

_{Обозначим .}

<sub>Величина

называется приведённой длинной
физического маятника – это
длина математического маятника, период
колебаний которого совпадает с периодом
данного физического маятника.</sub>

_{Точка на
прямой, соединяющей точку подвеса с
центром масс, лежащая на расстоянии
приведённой длины от оси вращения,
называется центром качания физического
маятника (О’).}

_{Если маятник
подвесить в центре качания, то приведённая
длина и период колебаний будут теми же,
что и в точке О.}

_{Таким образом,
точка подвеса и центр качания
обладают свойствами взаимности:
при переносе точки подвеса в
центр качения прежняя точка подвеса
становится новым центром качения.}

_{Период
колебания:}

_{Математический
маятник, который качается с таким же
периодом, как и рассматриваемый
физический, называется изохронным
данному физическому маятнику.}

Общие выводы.
Рассмотренные примеры

• относятся к
  свободным колебаниям без трения,
  которые происходят в системе,
  предоставленной самой себе после того,
  как она была тем или иным способом
  выведена из состояния равновесия.

• свободные колебания
  любого осциллятора в отсутствие
  трения будут гармоническими, если
  действующая в нем сила (или момент
  силы) являетсяквазиупругой,
  т. е. силой, направленной к положению
  равновесия и зависящей от смещения из
  этого положениялинейно.

• квазиупругий
  характер силы (или момента силы) служит
  и критериеммалых колебаний.

• частота и период
  свободных колебаний без трения зависят
  только от свойств самого осциллятора.

• Амплитуда колебаний
  и начальная фаза определяются начальными
  условиями.

Рассмотрим еще
один пример на малые колебания.

Пример.Частица
массыт совершает колебания
в силовом поле, где ее потенциальная
энергия зависит от координаты хкакгдеU₀и α —
постоянные. Найдем частоту ω₀малых колебаний частицы около положения
равновесиях = 0.

Согласно основному
уравнению динамики,

/

Так как колебания
малые, то
и
предыдущее уравнение можно привести к
виду

^/

^{Отсюда следует,
что .}

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Теория периодичности относится к общей физике. Повторяемость некоторых процессов в течение времени определяют с помощью различных величин, например, угла, напряжённости, температуры. Для изучения явления удобно использовать маятник. Одним из его видов является пружина с грузом. Колебания в такой системе зависят от периода, частоты и амплитуды. Узнать эти параметры можно, зная начальные условия и уравнения, описывающие механическую работу.

Общие сведения

Колебания — это изменения какой-либо величины в точности или приблизительно повторяющиеся во времени. Если рассматривать процесс, с точки зрения механики, то он описывается положением тела. Повторение в точности является периодическим. Математически это можно записать формулой: x (t + T) = x (t), где T — время, в течение которого совершается одно полное колебание (период). Число циклов принято обозначать буквой N. Его находят как отношение времени к периоду: N = t / T.

При исследовании процесса не всегда бывает удобно оперировать временем, поэтому часто используют число колебаний за единицу времени. Эта величина называется частотой. Находят её количество по формуле: f = 1 / T. Доказать справедливость приведённого равенства просто. Число колебаний зависит от времени и частоты: N = f * t. Отсюда: f = N / t = (t / T) / t = 1 / T.

Очень важно не только понимать суть характеристик колебания, но и знать единицы его измерения. Вот основные из них:

• период — секунды (с);
• частота — герцы (Гц);
• число колебаний — безразмерная величина.

Если в течение времени меняется и координата, то периодически будет изменяться и скорость. Значит: vx (t + T) = Vx (t).

Исходя из верности равенства, можно сказать, что условие периодичности будет справедливо и для проекции, то есть изменения ускорения. Отсюда следует, что сила действующая на тело тоже будет переменной: Fx (t + T) = Fx (t).

При процессе также происходит изменение потенциальной и кинетической энергий. Действительно, так как в процессе колебания скорость не является постоянной величиной, то соответственно будет меняться кинетическая работа. Потенциальная же энергия зависит от координат. Например, если рассмотреть период колебаний пружинного маятника, то за это время тело переместится из нижнего положения в верхнее и вернётся обратно. Значит, координата физического объекта изменится от нуля до какого-то граничного значения.

Следует отметить, что периодичные движения обязательно будут происходить в той системе, в которой есть положение равновесия. Причём оно должно быть устойчивым. То есть существует равнодействующая сила, стремящаяся привести объект в положение, соответствующее покою. Поэтому для поддержания отклонений нужна дополнительная сила. Колебательную систему (осциллятор) под действием вынужденной периодической силы называют вынужденной.

Пружинный маятник

Это устройство является простейшим примером свободных колебаний. В его состав входит кронштейн, пружина и груз. В качестве последнего может выступать любое физическое тело. Масса пружины по сравнению с грузом считается малой и при исследованиях не учитывается.

При изучении такой системы важной задачей является измерение периода движения тела, подвешенного к пружине. Определение понятию пружинного маятника, которое даётся в учебниках по физике довольно обобщённое. Считается, что это конструкция, в которой тело, имеющее массу m, подвешено на упругой пружине обладающей жёсткостью K. При этом из состояния равновесия систему может вывести упругая сила F = — k * x, где: x- расстояние от середины пружинного элемента до поверхности прикреплённого к нему груза.

Можно выделить два достаточных условия возникновения свободных колебаний:

Во время отклонения тела от положения равновесия должна возникать возвращающая сила.

Силы сопротивления (трения) должны быть малы по сравнению со стремящей вернуть энергией тело назад.

Суть изучения гармонических колебаний состоит в определении их частоты движения или периода. В пружинном маятнике, впрочем, как и в любой колебательной системе, параметры зависят от ряда характеристик. Из основных величин, описывающих процесс, можно выделить: массу груза и жёсткость. Поэтому задача и состоит в выяснении, как период зависит от этих двух параметров.

Во время экспериментов регулировать массу довольно легко. Для этого можно взять эталонные гири и, соединяя их, увеличивать вес. Жёсткость же пружины можно изменить, добавляя параллельно или последовательно к ней другое сжимающееся тело. Чтобы выяснить, как будет изменяться характеристика растягивающегося элемента, нужно знать, что же представляет собой параметр. Так, под жёсткостью тела понимают отношение силы упругости к удлинению: k0 = F / Δ L. Измеряется величина в ньютонах, делённых на метр (Н/м).

Исходя из правила, если соединить две пружины параллельно и деформировать их, то можно утверждать, что первый и второй элемент растянется на одинаковую длину ΔL. Значит, возникнет две одинаково направленных силы упругости. Отсюда равнодействующая будет равняться: K = 2F/ ΔL = 2k0. Для последовательного же соединения длина всей системы увеличится на 2 ΔL. Сила упругости будет равна F. Соответственно, жёсткость будет изменяться по формуле: K = F / 2ΔL = k0 / 2.

Зависимость периода

При проведении эксперимента можно исследовать пять различных комбинаций поведения груза на пружине — два варианта связаны с весом и три с жёсткостью. Чтобы выполнить опыт самостоятельно нужно будет взять вертикальный кронштейн, две одинаковые пружины и два равных по весу груза. Так как в реальности период будет довольно маленький, то для его измерения можно взять время, например, пятидесяти колебаний, а потом полученный результат разделить на это число. Подсчёт времени удобно выполнять с помощью секундомера.

Вычисленные результаты нужно занести в таблицу. Примерный порядок чисел должен получиться таким:

k m	m0	2m0
k0 / 2	0,68	0,93
k0	0,46	0,64
2k0	0.34	0,47

Эти данные можно проанализировать. Выводы будут следующими:

• с ростом массы физического тела период цикличности увеличивается;
• по мере увеличения жёсткости период колебаний уменьшается.

Приведённые утверждения, возможно, описать и количественно. Исходя из результатов, величины, стоящие в ячейке m0k0 и 2m02ko почти совпадают. С точки зрения физики, так и должно быть. Если взять грузик на пружине и измерить характеристику, а потом добавить к нему точно такую же систему, то период не поменяется. Это и можно наблюдать во время опыта. Значит, период движения зависит от того каким будет отношение массы к жёсткости.

По аналогии можно рассмотреть, как влияет жёсткость. Из эксперимента, видно, что если её увеличить дважды на одну и ту же величину, то она возрастёт в четыре раза, а значение обратное частоте уменьшится на это же число. Отсюда можно предположить, что период будет обратно пропорционален корню квадратному из жёсткости.

Объединив эти две гипотезы можно сделать заключение. Что период амплитуды колебаний груза на пружине будет прямо пропорционален корню квадратного из отношения массы к жёсткости: T = √(m / k). Проверить это утверждение можно по теории размерности. Подставив в формулу единицы измерения, получим: √(m / k) = √(кг / (Н/м)) = √(кг * м / Н). Учитывая, что ньютон — это отношение метра к секунде в квадрате или килограмму, умноженному на метр и делённому на секунду, размерное равенство примет вид: √(кг * м/Н) = √(c² * м/м) = √с² = с.

Для написания полной формулы в равенство нужно вести ещё коэффициент. Он будет равняться 2p. Значит, период колебаний пружинного маятника количественно описывается выражением: T = 2p * √ (m / k).

Примеры решения задач

Практические задания помогают лучше разобраться в теоретическом материале и запомнить нужные для решения формулы. Существуют различные примеры, с помощью которых можно довольно быстро проработать весь изученный курс. Вот два задания с подробным описанием решения на вычисления параметров пружинных колебаний тела. Разобравшись в них, можно переходить к самостоятельному вычислению более сложных примеров.

Задание № 1. Груз, подвешенный к пружине, перемещается циклически по вертикальной оси. За восемь секунд он совершил тридцать два колебания. Определить частоту. Итак, по условию задания дано время t = 8 c и число полного перемещения тела N = 32. Чтобы решить эту задачу нужно воспользоваться формулой нахождения периода: T = t / N. Все величины для этого есть: T = 8 c / 32 = 1 / 4 = 0,25 секунды. Частота связана с периодом выражением: f = 1 / T. После подстановки чисел получится ответ равный четырём герцам.

Задание № 2. Грузик совершает колебания на пружине с жёсткостью сто ньютон на метр. При этом максимальная скорость движения составляет два метра в секунду. Вычислить массу тела учитывая, что максимальная амплитуда отклонения от точки покоя составляет десять сантиметров. Силой трения пренебречь.

При решении примера нужно рассуждать следующим образом. Когда будет максимальное растяжение пружины, то скорость груза равна нулю: V1 = 0. Значит, кинетическая энергия тоже будет нулевой: Ek1 = 0.

В этот момент останется только потенциальная энергия вытянутой пружины Ep1. В положении равновесия скорость тела максимальная и равняется V = 2 м/с. Так как пружина в этот момент нерастянута и несжатая, то Ep = 0.

По закону сохранения энергии: Ek1 + Ep1 = Ek + Ep. Кинетическая работа при растянутой пружине равняется нулю, так же как и потенциальная в состоянии покоя, значит, Ep1 = (k * L²) / 2, где L — удлинение, а k — жёсткость. Энергию же можно найти так: Ek = mV² / 2. Так как тело совершает колебания около положения равновесия, то вытянутость пружины будет равняться амплитуде.

Перед тем как непосредственно переходить к составлению итоговой формулы и вычислениям необходимо все значения измерений привести в соответствии с СИ. Так, амплитуда указана в сантиметрах, поэтому её нужно перевести в метры. Теперь можно переходить к составлению отношения и подстановки данных: (k * L ²) / 2 = mV ² / 2. Отсюда: m = (k * L) / V ² = (100 Н/м * 0,1 ² м) / 2 ² м/с = 1 / 4 = 0,25 килограмма.

Предыдущая

ФизикаФормула тонкой линзы – свойства, применение и расчеты

Следующая

ФизикаТепловое движение – доказательство явления, виды и признаки