Формула скорости волны в физике
Формула скорости волны
Определение
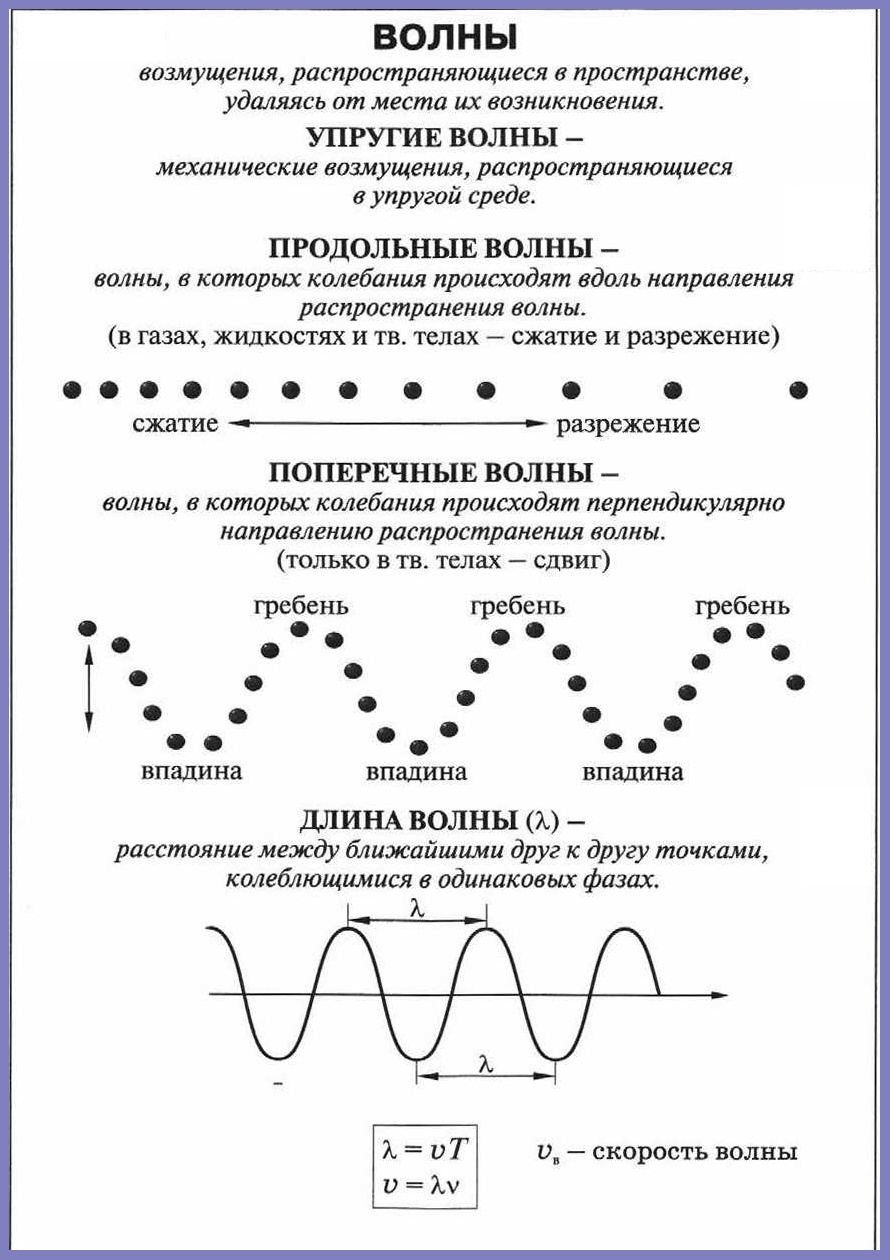
Фронт волны (волновая поверхность) – это геометрическое место точек среды, для которых в некоторый момент времени фаза волны
имеет одно и то же значение.
Скоростью волны называют скорость, с которой движется фронт волны.
Формула фазовой скорости волны
Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),]
где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).]
Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right),]
где $T$ – период колебаний точек в волне.
Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны.
Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны – это не то же самое, что скорость колебания частиц среды в волне.
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как:
[v=sqrt{frac{K}{rho }}left(4right),]
где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение:
[v=sqrt{frac{gamma p}{rho }}left(5right),]
где $gamma $ – показатель адиабаты; $p$ – давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна:
[v=sqrt{frac{E}{rho }}left(6right),]
где $E$ – модуль Юнга вещества стержня.
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как:
[v=sqrt{frac{G}{rho }left(7right),}]
где $G$ – модуль сдвига среды; $rho $ – плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн.
Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой:
[u=v-frac{dv}{dlambda }left(8right).]
Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
Примеры задач с решением
Пример 1
Задание. За время равное $t=20$ c волне совершается $N=$100 колебаний, при этом расстояние между соседними максимумами волны составляет 1 м. Какова скорость распространения волны?
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
[v=frac{lambda }{T} left(1.1right).]
Найдем период колебаний как время одного полного колебания:
[T=frac{t}{N} left(1.2right).]
Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.]
Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).]
Ответ. $v=5frac{м}{с}$
Пример 2
Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды?
Решение. Фазовую скорость движения волны найдем как:
[v=frac{lambda }{T}=lambda nu left(2.1right),]
где период – величина обратная частоте колебаний:
[T=frac{1}{nu }left(2.2right).]
Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).]
Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }]
Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
[{left(frac{dxi }{dt}right)}_{max}=left|2omega right|left(2.4right).]
Циклическую частоту найдем как:
[omega =2pi nu ,]
тогда:
[{left(frac{dxi }{dt}right)}_{max}=left|2cdot 2pi nu right|=4pi nu .]
Вычислим максимальную скорость колебаний частиц:
[{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).]
Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$
Читать дальше: формула скорости свободного падения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
1 |
|
Скорость распространения волны и максимальная скорость колебаний частиц воздуха08.07.2011, 18:03. Показов 38203. Ответов 34
Добрый вечер уважаемые участники форума. Применять уравнение звуковой волны для решения этой задачи?Или формулу можно выудить другими методами? Миниатюры
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
08.07.2011, 18:03 |
|
34 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
09.07.2011, 15:30 |
2 |
|
скорость=длина волны*частота
0 |
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
09.07.2011, 15:56 [ТС] |
3 |
|
6a6ka, Знаю, что связь длины электромагнитной волны с периодом
Как найти максимальную скорость пока не понимаю.Как тут рассуждать, когда скорость будет максимальна?
0 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
09.07.2011, 16:10 |
4 |
|
макс. скорость колебания=амплитуда*цикл частота
0 |
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
09.07.2011, 16:19 [ТС] |
5 |
|
6a6ka, Вы ничего не написали по поводу моих формул в предыдущем моём посте. Почему в нашем случае нельзя пользоваться формулой Что мешает?
0 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
09.07.2011, 16:24 |
6 |
|
Формула в посте выше – только для электромагнитных волн.
0 |
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
09.07.2011, 16:33 [ТС] |
7 |
|
6a6ka, То есть Вы хотите сказать, что формула Почему Вы написали, что умножить на частоту, а не поделить?
0 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
09.07.2011, 16:41 |
8 |
|
Да. Где скорость – скорость распространения волны. Для электромагнитных волн – это скорость света c. В моем посте не ошибка – внимательно прочитайте, что именно там за величины.
0 |
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
09.07.2011, 18:24 [ТС] |
9 |
|
6a6ka, Прошу прощение, там действительно всё верно у Вас.Это я продурил чуток
В посте №2 Вы писали, что макс. скорость=амплитуда*2*Пи*частота , а в посте №4 макс. скорость колебания=амплитуда*цикл частота Чему тут можно верить, а чему нет?
0 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
09.07.2011, 18:38 |
10 |
|
Циклическая частота обозначается омегой и равна 2*Пи*собс. частота. Собственная частота дана в условии.
0 |
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
09.07.2011, 18:50 [ТС] |
11 |
|
6a6ka, Для чего нам определять циклическую частоту?Какие соображения должны быть по этому поводу?
0 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
09.07.2011, 19:06 |
12 |
|
Эта формула справедлива только для механических колебаний.
0 |
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
09.07.2011, 19:18 [ТС] |
13 |
|
V=A*w*cos(wt), скорость макс., если cos равен 1. 6a6ka, Объясните пожалуйста почему косинус равен единице в силу чего? В каком случае скорость будет максимальна и почему?
0 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
09.07.2011, 20:03 |
14 |
|
Представьте себе пружинный маятник без каких-либо потерь энергии. У него можно выделить три основных положения: крайнее верхнее, крайнее нижнее, серединное.
0 |
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
12.07.2011, 12:56 [ТС] |
15 |
|
6a6kin, Не сказано какой именно маятник в условии.Пока не понимаю почему применяется формула для гармонических колебаний маятника?
0 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
12.07.2011, 13:55 |
16 |
|
В задаче вообще ничего про маятник не сказано. Вообще, маятник – физическая модель колебаний. Просто свойства колебаний проявляются через физические свойства маятника. К примеру, коэфф. пропорциональности равен коэфф. упругости пружины.
0 |
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
12.07.2011, 14:04 [ТС] |
17 |
|
6a6kin,
Непонятно только как единицы измерения дадаут м/с.
0 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
12.07.2011, 14:09 |
18 |
|
А – амплитуда, [А] = 1 м
0 |
|
42 / 8 / 0 Регистрация: 30.03.2010 Сообщений: 350 |
|
|
12.07.2011, 14:12 [ТС] |
19 |
|
6a6kin, Циклическая частота в рад/с. Что такое 1/с или речь идёт про
0 |
|
232 / 102 / 6 Регистрация: 18.04.2010 Сообщений: 294 |
|
|
12.07.2011, 14:34 |
20 |
|
Собственно, разницы нет, т.к. w=2*pi/T=2*pi*nu=const/сек. Добавлено через 3 минуты Численно циклическая частота равна числу циклов (колебаний, оборотов) за Из вики
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
12.07.2011, 14:34 |
|
Помогаю со студенческими работами здесь Найти амплитуду колебаний и фазовую скорость волны пределите: длину волны, фазу колебаний, смещение, скорость и ускорение точки Скорость распространения поперечной волны Чем квант-фотон отличается от электромагнитной волны и почему у них в пустоте одинаковая скорость распространения? Найти амплитуду напруженности магнитного поля волны и фазовую скорость волны Определить скорость а-частицы, если ее дебройлевская длина волны совпадает с дебройлевской длиной волны протона Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 20 |
Задачи на Механические волны с решениями
Формулы, используемые на уроках «Задачи на Механические волны».
Название величины |
Обозначение |
Единица измерения |
Формула |
Длина волны |
λ |
м |
λ = vT ;λ = v / v |
Скорость волны |
v |
м/с |
v = λ / T ;v = λv |
Период колебаний |
T |
с |
T = λ / v ;T = t / N |
Частота колебаний |
v |
Гц |
v = v / λ ;v = N / t |
Число колебаний |
N |
N = t / T ;N = vt |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Лодка качается на волнах, распространяющихся со скоростью 4 м/с, и за 10 с совершает 20 колебаний. Каково расстояние между соседними гребнями волн?
Задача № 2.
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Задача № 3.
Скорость звука в эбоните 2400 м/с, а в кирпиче — 3600 м/с. В каком веществе звуковому сигналу требуется большее время для распространения? Во сколько раз?
Задача № 4.
Расстояние между ближайшими гребнями волн в море 6 м. Лодка качается на волнах, распространяющихся со скоростью 2 м/с. Какова частота ударов волн о корпус лодки?
Задача № 5.
Наблюдатель, находящийся на расстоянии 2 км 150 м от источника звука, слышит звук, пришедший по воздуху, на 4,8 с позднее, чем звук от того же источника, пришедший по воде. Определите скорость звука в воде, если скорость звука в воздухе равна 345 м/с.
Задача № 6.
Охотник выстрелил, находясь на расстоянии 170 м от лесного массива. Через сколько времени после выстрела охотник услышит эхо?
Задача № 7.
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.
Задача № 8.
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?
Задача № 9.
Длина волны в воздухе 17 см (при скорости 340 м/с). Найти скорость распространения звука в теле, в котором при той же частоте колебаний длина волны равна 1,02 м.
Задача № 10.
ОГЭ
Расстояние между гребнями волн в море λ = 5 м. При встречном движении катера волна за t = 1 с ударяет о корпус катера N1 = 4 раза, а при попутном — N2 = 2 раза. Найти скорость катера и волны.
Задача № 11.
ОГЭ
Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду А = 0,25 мм, распространяются в воздухе. Длина волны λ = 70 см. Найти скорость распространения колебаний v и максимальную скорость частиц среды.
Краткая теория для решения Задачи на Механические волны.
Это конспект по теме «ЗАДАЧИ на Механические волны». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на
- Посмотреть конспект по теме ДИНАМИКА: вся теория для ОГЭ (шпаргалка)
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.

Если бросить камень в воду водоема, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется.
Кроме скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней. ИЛИ Расстояние между ближайшими друг к другу точками, колеблющимися в одинаковых фазах, называется длиной волны.
Она равна расстоянию между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разрежениями в продольной волне.
Поскольку скорость волны – величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней: λυTТак как период Т и частота v связаны соотношением T = 1 / v, то скорость волны: υ = λ / Т = λ v
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Скорость упругой волны тем больше, чем плотнее среда и чем выше температура.
Величины, характеризующие волну: длина волны, скорость волны, период колебаний, частота колебаний.
Единицы измерения в системе СИ:
длина волны [λ] = 1 м скорость распространения волны [ v ] = 1м/с период колебаний [ T ] = 1c
частота колебаний [ v ] = 1 Гц

Абсолютно все в этом мире происходит с какой-либо скоростью. Тела не перемещаются моментально, для этого требуется время. Не являются исключением и волны, в какой бы среде они не распространялись.
Если вы бросите камень в воду озера, то возникшие волны дойдут до берега не сразу. Для продвижения волн на некоторое расстояние необходимо время, следовательно, можно говорить о скорости распространения волн.
Скорость волны зависит от свойств среды, в которой она распространяется. При переходе из одной среды в другую, скорость волн меняется. Например, если вибрирующий железный лист засунуть концом в воду, то вода покроется рябью маленьких волн, однако скорость их распространения будет меньше, чем в железном листе.
Это несложно проверить даже в домашних условиях. Только не порежьтесь о вибрирующий железный лист. .
Длина волны
None Если зарисовать волну в виде рисунка или графика, то длиной волны будет являться расстояние между любыми ближайшими гребнями либо впадинами волны, либо между любыми другими ближайшими точками волны, находящимися в одинаковой фазе.
Так как длина волны это расстояние, пройденное ею, то и найти эту величину можно, как и любое другое расстояние, умножив скорость прохождения на единицу времени. Таким образом, длина волны связана со скоростью распространения волны прямо пропорционально. Найти длину волны можно по формуле:
λ=vT ,где λ длина волны, v скорость волны, T период колебаний.
А учитывая, что период колебаний обратно пропорционален частоте этих же колебаний: T=1⁄υ, можно вывести связь скорости распространения волны с частотой колебаний:
v=λυ .
[custom_ads_shortcode1]
Частота колебаний в разных средах
Частота колебаний волн не меняется при переходе из одной среды в другую. Так, например, частота вынужденных колебаний совпадает с частотой колебаний источника. Частота колебаний не зависит от свойств среды распространений. При переходе из одной среды в другую меняется лишь длина волны и скорость ее распространения.
Эти формулы справедливы как для поперечных, так и для продольных волн. При распространении продольных волн длина волны будет расстоянием между двумя ближайшими точками с одинаковым растяжением или сжатием. Она также будет совпадать с расстоянием, пройденным волной за один период колебаний, поэтому формулы будут полностью подходить и в этом случае.
[custom_ads_shortcode2]
Нужна помощь в учебе?
Предыдущая тема: Распространение колебаний в среде и волны: продольные и поперечные
Следующая тема: Источники звука и звуковые колебания: что это и как происходит
| Твитнуть | Нравится | Нравится |
Все неприличные комментарии будут удаляться.
Геометрическое место точек среды, для которых в некоторый момент времени фаза волны имеет одно и то же значение, называют волновой поверхностью или фронтом волны. ОпределениеСкорость перемещения фронта волны называется скоростью волны.
Если рассматривается одномерный случай гармонической волны, то уравнение волновой поверхности имеет вид:
[Ф_s=omega t-kx+varphi left(1right),] где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Условию (1) в каждый момент времени соответствует только одна точка оси X c координатой, равной:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).] Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне вырождается в точку. Из выражения (2) видно, что волновые поверхности с течением времени перемещаются в веществе со скоростью:
[frac{dx}{dt}=frac{omega }{k}=frac{lambda }{T}=v left(3right).] Для гармонических волн скорость движения поверхности волны совпадает со скоростью распространения волны. Скорость, определенная выражением (3) называют фазовой скоростью. В случае гармонической волны скорость распространения энергии совпадает с фазовой скоростью волны.
Скорость волны зависима от среды и типа волны. Скорость волны не надо путать со скоростью колебания частиц среды в волне.
[custom_ads_shortcode3]
Фазовая скорость распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях равна:
[v=sqrt{frac{K}{rho }}left(4right),] где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) справедлива, если избыточное давление много меньше, чем равновесное давление невозмущенного газа. Для определения скорости распространения продольных волн в газе используют формулу:
None Фазовая скорость распространения продольных волн в твердом теле:
[v=sqrt{frac{E}{rho }}left(6right),] где $E$ – модуль Юнга вещества стержня.
[custom_ads_shortcode1]
Фазовая скорость распространения поперечных волн
Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде можно вычислить как:
[v=sqrt{frac{G}{rho }left(7right),}] где $G$ – модуль сдвига среды; $rho $ – плотность вещества. Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
[custom_ads_shortcode2]
Групповая скорость волн
Для диспергирующих волн помимо фазовой скорости волны следует использовать такое понятие как групповая скорость. Если фазовая скорость зависит от частоты и в среде распространяются волны сложного негармонического характера, то при помощи групповой скорости характеризуют распространение волн.
Групповой скоростью называют скорость движения группы (цуга) волн, которые создают в каждый момент времени локализованный в пространстве волновой пакет. Любая реальная волна является суперпозицией гармонических волн. Скорость с которой такая волна распространяется в веществе, имеющем дисперсию на равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой: [u=v-frac{dv}{dlambda }left(8right).] Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тога фазовая и групповая скорости равны и не зависят от длины волны.
[custom_ads_shortcode3]
Примеры задач с решением
None Решение: Зная, что звук – продольная волна, за основу решения задачи примем формулу вычисления фазовой скорости продольной волны в газе:
[v=sqrt{frac{gamma p}{rho }}left(1.1right).] Будем считать азот идеальным газом. Тогда используем уравнение Менделеева – Клапейрона:
[pV=frac{m}{mu }RTleft(1.2right),] где $mu $ – молярная масса газа. Для азота она равна ${mu }_{N_2}=28cdot {10}^{-3}frac{кг}{моль}$; $R=8,31 frac{Дж}{мольcdot К}$ – универсальная газовая постоянная; $T$ – термодинамическая температура газа. Разделим обе части выражения (1.2) на объем:
None [frac{p}{rho }=frac{RT}{mu }left(1.4right),] подставим полученное отношение в (1.1) скорость звука найдем как:
None [gamma =frac{i+2}{i}=frac{7}{5},] так как молекула двух атомная имеет три степени свободы поступательного движения и две вращательного (рис.1).
Вычислим скорость звука в азоте:
[v=sqrt{frac{7}{5}cdot frac{8,31cdot 300}{28cdot {10}^{-3}}}approx 350 left(frac{м}{с}right).] Ответ: $v=350frac{м}{с}$Пример 2Задание: Какова скорость распространения волны в упругой среде, если разность фаз точек, которые находятся на расстоянии $Delta x,$ равна $Delta varphi $ при частоте колебаний равной $nu $?
Решение: Рассмотрим уравнение одномерной плоской волны:
None [{varphi }_1=omega t-kx_1+varphi ;; {varphi }_2=omega t-kx_2+varphi left(2.3right).] Найдем их разность:
None [omega =2pi nu left(2.5right).] Выражение (2.4) преобразуем к виду:
None [v=frac{2 pi nu Delta x}{Delta varphi }(frac{м}{с}).] Ответ: $v=frac{2 pi nu Delta x}{Delta varphi }frac{м}{с}$Читать дальше: скорость движения.
None Скоростью волны называют скорость, с которой движется фронт волны. Рассмотрим одномерный случай для гармонической волны. Уравнение волновой поверхности при это запишем как:
[Ф_s=omega t-kx+varphi left(1right),] где${ Ф}_s$ – фаза волны; $k=frac{2pi }{lambda }$ – волновое число; $lambda $ – длина волны; $omega $ – циклическая частота; $varphi $ – начальная фаза. Уравнению (1) в каждый момент времени соответствует только одна точка оси X координата которой, равна:
[x=frac{omega t+varphi -Ф_s}{k}left(2right).] Разным значениям фазы волны $Ф_s$ соответствуют разные волновые поверхности, каждая из которых в одномерной волне превращается в точку. Из формулы (2) видно, что волновые поверхности перемещаются в среде со скоростью:
None Если волны гармонические, то скорость движения волновой поверхности равна скорости распространения волны. Скорость, которую определяет выражение (3) является фазовой скоростью.
Фазовая скорость гармонической волны совпадает со скорость распространения энергии волны. Скорость волны зависит от вещества, в котором распространяется волна и типа волны. Скорость волны – это не то же самое, что скорость колебания частиц среды в волне.
[custom_ads_shortcode1]
Формула для вычисления фазовой скорости распространения продольных волн
Скорость распространения продольных упругих волн в однородных в газах или жидкостях может быть вычислена как: [v=sqrt{frac{K}{rho }}left(4right),] где $K$ – модуль объемной упругости вещества; $rho =const$ – плотность среды. В газах формула (4) выполняется, если избыточное давление много меньше, равновесного давление газа в невозмущенном состоянии.
Для нахождения скорости распространения продольных волн в газе применяют выражение: [v=sqrt{frac{gamma p}{rho }}left(5right),] где $gamma $ – показатель адиабаты; $p$ – давление газа.
Продольные механические волны могут распространяться в твердых телах, их фазовая скорость равна: [v=sqrt{frac{E}{rho }}left(6right),] где $E$ – модуль Юнга вещества стержня.
[custom_ads_shortcode2]
Формула для фазовой скорости распространения поперечных волн
Поперечные механические волны способны распространяться только в твердых телах. Скорость ($v$) распространения поперечных волн в бесконечной изотропной среде при этом можно найти как: [v=sqrt{frac{G}{rho }left(7right),}] где $G$ – модуль сдвига среды; $rho $ – плотность вещества.
Упругие свойства и плотность твердого тела зависит от химического состава вещества, и она несущественно изменяется при изменении давления и температуры. Поэтому в большинстве случаев скорость распространения волны можно считать постоянной.
[custom_ads_shortcode3]
Формула для групповой скорости волн
Кроме фазовой скорости для описания распространения диспергирующих волн применяют понятие групповой скорости. При этом фазовая скорость может зависеть от частоты, при этом в веществе распространяются волны сложного негармонического характера, тогда с групповую скорость проще использовать, как характеристику скорости распространения волн. Групповой скоростью называют скорость перемещения группы (цуга) волн, которые создают в каждый момент времени, локализованный в пространстве, волновой пакет. Любая реальная волна представляет собой суперпозицию гармонических волн. Скорость, с которой такая волна распространяется в веществе, имеющем дисперсию, равна фазовой скорости накрадывающихся волн. Распространение волны определяют перемещением энергии колебаний, которую переносит группа вол от источника.
Групповая скорость ($u$) связана с фазовой скоростью ($v$) формулой: [u=v-frac{dv}{dlambda }left(8right).] Если дисперсия отсутствует, то $frac{dv}{dlambda }=0$, тогда фазовая и групповая скорости равны и не зависят от длины волны.
[custom_ads_shortcode1]
Примеры задач с решением
None Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для вычисления фазовой скорости волны вида:
None [T=frac{t}{N} left(1.2right).] Используя формулу (1.2) скорость будем вычислять, применяя формулу:
[v=frac{lambda N}{t}.] Вычислим искомую скорость:
[v=frac{1cdot 100}{20}=5left(frac{м}{с}right).] Ответ. $v=5frac{м}{с}$Пример 2Задание. Уравнение плоской волны, которая распространяется вдоль положительного направления оси X, имеет вид: $xi left(x,tright)=2{cos left[omega left(t-frac{x}{v}right)right] }left(мright).$ Частота колебаний $nu =450$Гц, длина волны $lambda =0,8 $м. Какова скорость распространения волны, какой будет максимальная скорость колебания частиц среды? Решение. Фазовую скорость движения волны найдем как:
None [T=frac{1}{nu }left(2.2right).] Вычислим фазовую скорость:
[v=450cdot 0,8=360 left(frac{м}{с}right).] Скорость колебания частиц равна:
[frac{dxi }{dt}=frac{d}{dt}left(2{cos left[omega left(t-frac{x}{v}right)right] }right)=-2omega {sin left[omega left(t-frac{x}{v}right)right]left(2.3right). }] Максимальное значение скорости колебаний частиц в волне из (2.3) равно:
None [omega =2pi nu ,] тогда:
None [{left(frac{dxi }{dt}right)}_{max}=4pi cdot 450=5,65cdot {10}^3left(frac{м}{с}right).] Ответ. $v=360 frac{м}{с}$, ${left(frac{dxi }{dt}right)}_{max}=5,65cdot {10}^3frac{м}{с}$Читать дальше: формула скорости свободного падения.
Источники:
- www.sites.google.com
- www.nado5.ru
- www.webmath.ru
- www.webmath.ru
Волновое уравнение
Содержание:
- Что такое волновое уравнение
-
Общий вид
- Составляющие уравнения
- Операторы уравнения
-
Решение уравнения
- Формула Д’Аламбера
- Формула Пуассона-Парсенваля
- Формула Кирхгофа
- Решение в сферических координатах
- Волновое уравнение механических волн
- Примеры задач и решение
Что такое волновое уравнение
Определение
Волновое уравнение — линейное гиперболическое уравнение в частных производных, описывающее колебательные процессы в сплошных средах и электромагнетизме:
(triangle u;=;frac1{v^2}cdotfrac{partial^2u}{partial t^2})
Где (triangle) — оператор Лапласа, u=u(x,t) — дифференцируемая функция, (xinmathbb{R}^n) — аргумент функции u в виде n-мерной переменной, t — время, v — фазовая скорость.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Волновые уравнения в математической физике применяются для описания малых поперечных колебаний струны и мембраны, акустических процессов в газообразных, жидких и твёрдых средах, электромагнитных и гравитационных волн.
Общий вид
Составляющие уравнения
При работе с физическими процессами в трёхмерном пространстве волновое уравнение получается из уравнения плоской волны.
Если мы имеем уравнение плоской волны:
(A(overrightarrow r,;t);=;A_0cos(wt;-;(overrightarrow k,overrightarrow r);+;varphi_0))
Где (A(x,;t);) — возмущение в точке x в момент времени t, (A_0) — волновая амплитуда, (omega) — круговая частота, (overrightarrow k) — волновой вектор, (overrightarrow k;=;overrightarrow k(x,y,z)) — радиус-вектор в точке (x, y, z, varphi_0) — начальная фаза колебаний.
Если мы продифференцируем его по переменным x, y, z и t, то получим систему уравнений в частных производных:
(frac{partial^2A(overrightarrow r,t)}{{partial t}^2}=-omega^2A_0cos(wt-(overrightarrow r,t)+varphi_0)=-omega^2A(overrightarrow r,t), (1))
(frac{partial^2A(overrightarrow r,t)}{{partial x}^2}=-k_x^2A_0cos(wt-(overrightarrow r,t)+varphi_0)=-k_x^2A(overrightarrow r,t), (2))
(frac{partial^2A(overrightarrow r,t)}{{partial y}^2}=-k_y^2A_0cos(wt-(overrightarrow r,t)+varphi_0)=-k_y^2A(overrightarrow r,t), (3))
(frac{partial^2A(overrightarrow r,t)}{{partial z}^2}=-k_z^2A_0cos(wt-(overrightarrow r,t)+varphi_0)=-k_z^2A(overrightarrow r,t). (4))
При сложении уравнений (2), (3), (4) получаем:
(frac{partial^2A(overrightarrow r,t)}{{partial x}^2}+frac{partial^2A(overrightarrow r,t)}{{partial y}^2}+frac{partial^2A(overrightarrow r,t)}{{partial z}^2}=-k^2A(overrightarrow r,t). (5))
Из уравнений (1) и (5) следует, что:
(frac{k^2}{omega^2}=frac1{v^2}. (6))
Следовательно:
(frac{partial^2A(overrightarrow r,t)}{{partial x}^2}+frac{partial^2A(overrightarrow r,t)}{{partial y}^2}+frac{partial^2A(overrightarrow r,t)}{{partial z}^2}=frac1{v^2}cdotfrac{partial^2u}{partial t^2}. (7))
Таким образом, мы получаем общее волновое уравнение из суммы уравнений плоской волны в частных производных.
Для уравнений в n-мерных пространствах для построения берется система дифференциальных уравнений в частных производных по времени t и по каждому из n измерений.
Для одномерного пространства данное уравнение называется уравнением колебания струны и имеет следующую характеристику:
(frac{partial^2u}{{partial x}^2}=frac1{v^2}cdotfrac{partial^2u}{{partial t}^2}. (8))
Из описанного выше мы можем сделать вывод, что в общем случае для решения волновых задач необходимо применение численных методов. Тем не менее, для некоторых случаев существуют аналитические решения уравнений.
Операторы уравнения
С применением оператора Лапласа уравнение (7) принимает привычный нам вид:
(triangle u;=;frac1{v^2}cdotfrac{partial^2u}{partial t^2}.)
Оператором Д’Аламбера (square) называется следующая разность:
(square=bigtriangleup-frac1{v^2}cdotfrac{partial^2}{partial t^2}. (9))
Тогда волновое уравнение можно представить в виде:
(square u=0. (10))
Решение уравнения
В математической физике существуют несколько частных случаев волновых уравнений, для которых существуют аналитические решения:
- формула Д’Аламбера;
- формула Пуассона-Парсенваля;
- формула Кирхгофа.
Формула Д’Аламбера
Рассмотрим формулу Д’Аламбера, являющейся частным случаем волновых уравнений в одномерном пространстве:
(u_{tt}=a^2u_{tt}+f.)
Где f=f(x,t) — вынуждающая внешняя сила, (u(x,0);=;varphi(x),;u_t(x,0)=psi(x)) — начальные условия.
Тогда решение формулы Д’Аламбера имеет вид:
(u(x,t);=;frac{varphi(x+at)+varphi(x-at)}2+frac1{2a}int_{x-at}^{x+at}psi(alpha)operatorname dalpha+frac1{2a}int_0^tint_{x-a(t-tau)}^{x+a(t-tau)}f(s,tau)operatorname dsdtau. (11))
Формула Пуассона-Парсенваля
Частным случаем волнового уравнения для поверхности или плоскости является формула Пуассона-Парсенваля.
Рассмотрим уравнение:
(u_{tt};=;a^2triangle u+f)
Где (u(x,0)=varphi(x),;u_t(x,0)=psi(x)) — начальные условия.
Тогда решение формулы Пуассона-Парсенваля имеет следующий вид:
(u(overline x,t)=u(x_1,x_2,t)=frac1{2pi a}int_0^tiintlimits_{tau<(at-tau)}frac{f(y_1,y_2,;tau)dy_1dy_2dtau}{sqrt{a^2{(t-tau)}^2-{(y_1-x_1)}^2-{(y_2-x_2)}^2}}+fracpartial{partial t}frac1{2mathrm{πa}}iintlimits_{tau<at}frac{varphi(y_1,y_2,;)dy_1dy_2}{sqrt{a^2t^2-{(y_1-x_1)}^2-{(y_2-x_2)}^2}}+frac1{2mathrm{πa}}iintlimits_{tau<at}frac{psi(y_1,y_2,;)dy_1dy_2}{sqrt{a^2t^2-{(y_1-x_1)}^2-{(y_2-x_2)}^2}}. (12))
Формула Кирхгофа
В трёхмерном пространстве частным случаем волновых уравнений, для которых существует аналитическое решение, является формула Кирхгофа.
Мы имеем уравнение следующего вида:
(frac{partial^2}{partial t^2}-a^2bigtriangleup u;=;f (13))
Где (u=u(x,t), f=f(x,t), u,;f;inmathbb{R}^ntimesmathbb{R}^+, bigtriangleup) — оператор Лапласа, при начальных условиях:
({left.uright|}_{t=0}=varphi_0(overline x),;frac{partial u}{partial t}=varphi_1(overline x))
Мы получим следующее решение уравнения:
(u(x,t);=;fracpartial{partial t}left[frac1{4mathrm{πa}^2mathrm t}iintlimits_Svarphi_0(y)d^2S_nright]+frac1{4mathrm{πa}^2mathrm t}iintlimits_Svarphi_1(y)d^2S_n+frac1{4mathrm{πa}^2}underset{left|x-yright|<at}{intintint}frac{f(y,t-{displaystylefrac{vert x-yvert}a}}{vert x-yvert}d^3y (14))
Где (S:;vert x-yvert=at ) — сфера, по которой осуществляется интегрирование.
Решение в сферических координатах
Стандартное волновое уравнение в сферических координатах имеет следующий вид:
(frac{partial^2}{partial r^2}+frac2rfrac{partial V}{partial r}+frac1{r^2}bigtriangleup_1V+k^2V=0. (15))
Требуется найти решение данного в обычной форме:
(V=f(r)Y(theta,varphi). (16))
Используя в изначальном уравнении данную формулу, а также воспользовавшись методом разделения переменных, получаем:
(frac{f”(r)}{f(r)}+frac2rfrac{f'(r)}{f(r)}+frac1{r^2}frac{triangle_1Y(theta,varphi)}{Y(theta,varphi)}+k^2=0. (17))
Посредством преобразований получаем следующую систему уравнений:
(left{begin{array}{l}triangle_1Y+lambda Y=0,\f”(r)+frac2rf'(r)+(k^2-fraclambda{r^2})f(r)=0.end{array}right. (18))
Тогда, для любых (lambda_n=n(n+1),;ninmathbb{Z}+) имеет место:
({f”}_n(r)+frac2r{f’}_n(r)+(k^2-frac{n(n+1)}{r^2})f_n(r)=0. (19))
Для удобства дальнейших вычислений произведём замену функции f(r) на R(r):
(f_n(r)=frac1{sqrt r}R_n(r). (20))
Получим:
(R”_n(r)+frac1rR’_n+(k^2-frac{{(n+{displaystylefrac12})}^2}{r^2})R_n(r)=0 (21))
Где (R_n(r)=Z_{n+frac12}(kr), а Z_{n+frac12}(r)) — решение уравнения Басселя с параметром (p=n+frac12.)
Тогда мы получаем следующее выражение:
(V=frac{Z_{n+{displaystylefrac12}}(kr)}{sqrt r}Y_n(theta,varphi),;Ninmathbb{Z}+ (22))
Волновое уравнение механических волн
Определение
Механические волны — упругие возмущения, распространяемые в упругой среде.
Рассматривают поперечные и продольные механические волны.
В продольных волнах колебания, несущие эту волну, осуществляется по вектору, параллельном направлению движения. Они возможны в газообразной, жидкой и твёрдой среде. Особенностью поперечных волн является возможность их наличия исключительно при возможности деформации сдвига в твёрдых средах.
В условиях распространения в бесконечной натянутой струне поперечная монохроматическая волна может быть описана следующим выражением (уравнением бегущей струны):
(xi(t,z)=Acdotcosomega(t-frac zv) (23))
Где (xi(t,z)) — смещение частицы из положения равновесия в струне, z — расстояние от начала струны до точки равновесного положения частицы в струне, v — скорость распространения колебаний.
Примеры задач и решение
Задача 1
Найти скорость распространения звуковой волны, если частота колебаний равна (nu)=400Гц, а амплитуда (A=10^{-4}м) и длина волны (lambda)=0,8м. Также определить максимальную скорость частиц в данной среде.
Решение
Ввиду недостаточно строгого определения условий, сделаем допущение, что волна является плоской.
Тогда, сориентировав ее распространение по оси X, получим следующее уравнение:
(xi(t,x)=Acosomega(t-frac xv).)
Зная, что длина волны равна (lambda=frac vnu,) получаем, что скорость волны равна:
(v=lambdanu=0,8cdot400=320;(м/с).)
Исходя из того, что скорость есть первая производная расстояния по времени, имеем:
(frac{dxi}{dt}=frac d{dt}(Acosomega(t-frac xnu))=-Aomegasinomega(t-frac xnu),) следовательно:
(maxfrac{dxi}{dt}=2pinu A=2picdot400cdot10^{-4}=0,25(м/с).)
Ответ:
- (v=320 м/с;)
- (maxfrac{dxi}{dt}=0,25 м/с.)
Задача 2
Скорость распространения волны по упругой струне составляет (nu)=10 м/с. Амплитуда колебаний точек в струне составляет A=0,05 м, период колебаний составляет Т=1 с. Сформулировать уравнение волны.
Решение
Так как в общем случае при распространении по оси X уравнение поперечной механической волны имеет вид:
(xi(t,z)=Acdotcosomega(t-frac xv))
то, найдя циклическую частоту по формуле (omega=frac{2pi}T=2pi;(рад/с),) получаем:
(xi(t,z)=0,05cdotcos2pi(t-frac x10) (м))
Ответ: (xi(t,z)=0,05cdotcos2pi(t-frac x10)) м.