поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,653 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,904 -
разное
16,900
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
где длине волны
![]() соответствует максимальное значение
соответствует максимальное значение
спектральной плотности энергетической
светимости абсолютно черного тела,![]() – постоянная Вина.
– постоянная Вина.
Квантовая гипотеза
Планка устанавливает пропорциональность
между энергией кванта излучения и
частотой колебаний
![]() ,
,
где
![]() – постоянная Планка.
– постоянная Планка.
Формула Планка
для спектральной плотности энергетической
светимости абсолютно черного тела имеет
вид
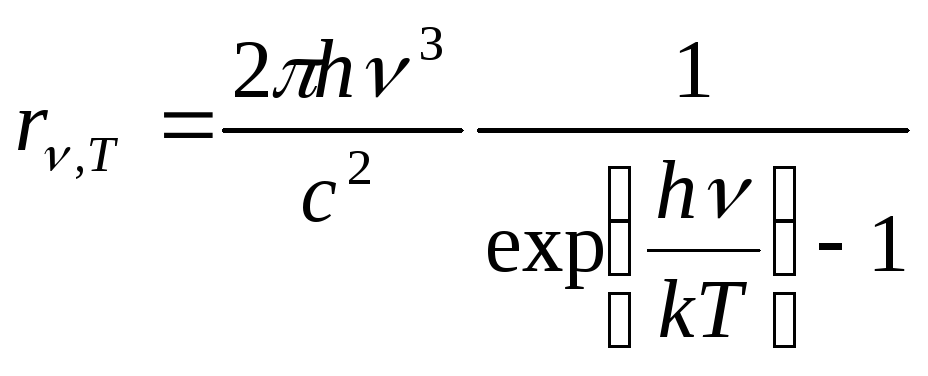 .
.
Уравнение Эйнштейна
для внешнего фотоэффекта
![]() ,
,
где
![]() – работа выхода электрона из металла,
– работа выхода электрона из металла,![]() – максимальная кинетическая энергия
– максимальная кинетическая энергия
электрона.
Красная граница
фотоэффекта может быть определена по
формулам
![]() ,
,
![]() .
.
Величина запирающего
напряжения вычисляется по формуле
![]() .
.
Масса фотона
определяется при помощи формул Планка
и Эйнштейна
![]() ,
,
а его импульс равен
![]() .
.
Давление света,
падающего нормально на некоторую
поверхность, определяется по формуле
![]() ,
,
где
![]() – энергия всех фотонов, падающих на
– энергия всех фотонов, падающих на
единицу площади поверхности за единицу
времени (энергетическая освещенность
поверхности),![]() – коэффициент отражения света от
– коэффициент отражения света от
поверхности,![]() – объемная плотность энергии излучения.
– объемная плотность энергии излучения.
Изменение длины
волны коротковолнового излучения при
его рассеянии на свободных (или
слабосвязанных) электронах (эффект
Комптона) определяется по формуле
![]() ,
,
где
![]() – угол рассеяния,
– угол рассеяния,![]() – комптоновская длина волны (для рассеяния
– комптоновская длина волны (для рассеяния
фотона на электроне![]() ).
).
Длина волны
коротковолновой границы сплошного
рентгеновского спектра определяется
по формуле
![]() ,
,
где
![]() – напряжение на рентгеновской трубке.
– напряжение на рентгеновской трубке.
Примеры решения задач
Задача 1. Излучение
Солнца близко по своему спектральному
составу к излучению абсолютно черного
тела, для которого максимум испускательной
способности приходится на длину волны
![]() .
.
Найти массу, теряемую Солнцем ежесекундно
за счет излучения. Оценить время, за
которое масса Солнца уменьшится на 1%.
Решение
Воспользуемся
законом смещения Вина и определим
температуру поверхности Солнца
![]() .
.
(2.1.1)
Тогда энергетическая
светимость Солнца по закону Стефана –
Больцмана и при помощи (2.1.1) запишется
в виде
![]() .
.
(2.1.2)
Умножая (2.1.2) на
площадь излучающей поверхности и время,
находим энергию, излучаемую Солнцем
![]() .
.
(2.1.3)
Для определения
массы, теряемой Солнцем вследствие
излучения, воспользуемся формулой
Эйнштейна для взаимосвязи массы и
энергии, что с учетом (2.1.3) позволит
записать
![]() .
.
(2.1.4)
Учитывая, что
площадь излучающей поверхности (сферы)
![]() ,
,
из (2.1.4) находим
![]()
Чтобы оценить
время уменьшения массы Солнца на 1%,
предположим, что в течение этого времени
энергия, излучаемая Солнцем, не изменяется,
тогда
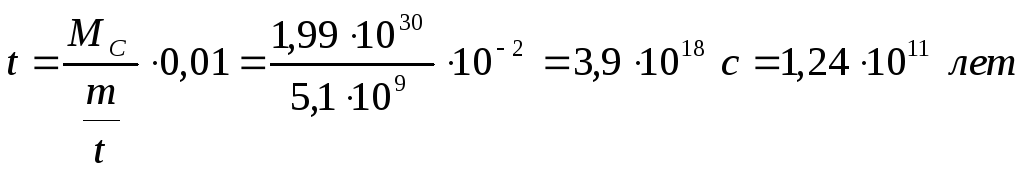 .
.
Задача 2. Определить
установившуюся температуру
![]() зачерненного шарика, расположенного
зачерненного шарика, расположенного
на половине расстояния от Земли до
Солнца. Температуру поверхности Солнца
принять равной![]() .
.
Решение
Очевидно, что
находясь в состоянии теплового равновесия,
шарик должен получать в единицу времени
такую же энергию излучения от Солнца,
которую сам излучает в окружающее
пространство. Тогда, обозначая мощность
солнечного излучения, упавшего на шарик
через
![]() ,
,
а мощность, излученную шариком – через![]() ,
,
имеем
![]() .
.
(2.1.5)
Предполагая, что
Солнце излучает как абсолютно черное
тело, выражение для мощности солнечного
излучения можно записать в виде
![]() ,
,
(2.1.6)
где
![]() – температура поверхности Солнца,
– температура поверхности Солнца,![]() – площадь поверхности Солнца. Долю
– площадь поверхности Солнца. Долю
мощности солнечного излучения,
приходящуюся на поверхность шарика,
найдем из пропорции
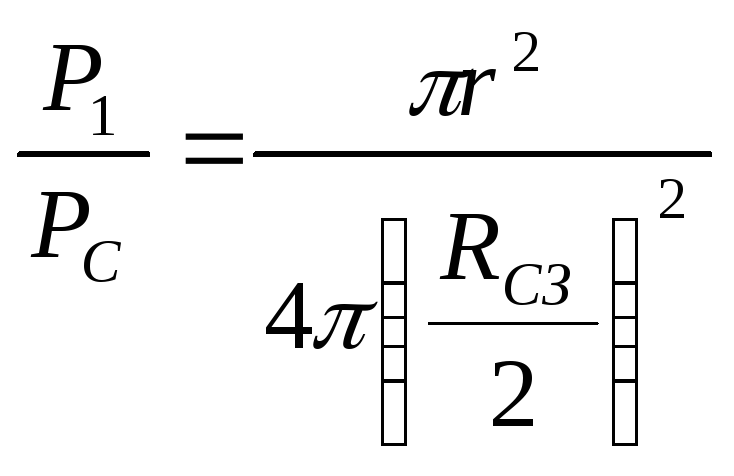 ,
,
(2.1.7)
где
![]() – площадь круга радиуса
– площадь круга радиуса![]() ,
,
равного радиусу шарика,![]() – расстояние от Земли до Солнца. Из
– расстояние от Земли до Солнца. Из
(2.1.6), (2.1.7) находим
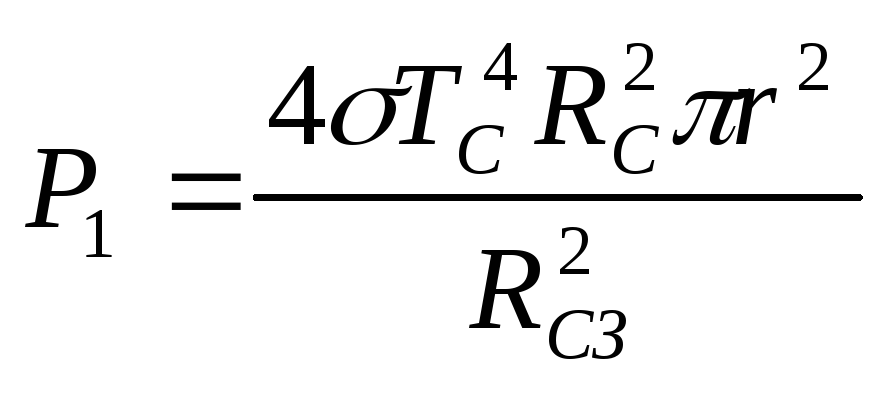 .
.
(2.1.8)
Определим теперь
мощность излучения шарика, предполагая,
что он тоже излучает как абсолютно
черное тело, а температура всех его
точек одинакова. Тогда получим
![]() .
.
(2.1.9)
Из (2.1.5), (2.1.8), (2.1.9)
следует
![]() .
.
Используя табличные
данные, получаем ответ
![]() .
.
Задача 3. Медный
шарик, удаленный от других тел, под
действием света, падающего на него,
зарядился до потенциала
![]() .
.
Определить длину волны света.
Решение
Согласно уравнению
Эйнштейна для фотоэффекта максимальная
кинетическая энергия фотоэлектронов
равна
![]() .
.
(2.1.10)
Вследствие вылета
электронов с шарика под действием света
он приобретает положительный заряд, в
результате чего вокруг него создается
электрическое поле, тормозящее движение
вылетевших электронов. Шарик будет
заряжаться до тех пор, пока максимальная
кинетическая энергия фотоэлектронов
не станет равной работе тормозящего
электрического поля при перемещении
электронов на бесконечно большое
расстояние. Так как потенциал бесконечно
удаленной точки равен нулю, по теореме
о кинетической энергии получаем
![]() ,
,
что с учетом
(2.1.10) позволяет найти длину волны света
![]() .
.
(2.1.11)
Подставляя в
(2.1.11) числовые значения (работа выхода
электронов из меди равна
![]() ),
),
находим
![]() .
.
Задача 4. Плоская
поверхность освещается светом с длиной
волны
![]() .
.
Красная граница фотоэффекта для данного
вещества![]() .
.
Непосредственно у поверхности создано
однородное магнитное поле с индукцией![]() ,
,
линии которого параллельны поверхности.
На какое максимальное расстояние от
поверхности смогут удалиться фотоэлектроны,
если они вылетают перпендикулярно
поверхности?
Решение
Воспользуемся
уравнением Эйнштейна для фотоэффекта
и определим максимальную скорость
вылетающих фотоэлектронов
![]() .
.
(2.1.12)
Используя формулу
для красной границы фотоэффекта
![]() ,
,
выражение (2.1.12)
можно записать в виде
![]() .
.
(2.1.13)
После вылета с
поверхности электроны попадает в
перпендикулярное к вектору скорости
однородное магнитное поле, следовательно,
движутся в нем по окружности, и их
максимальное удаление от поверхности
будет равно радиусу этой окружности.
Радиус окружности можно найти, применяя
второй закон Ньютона и используя формулу
Силы Лоренца
![]() .
.
(2.1.14)
Тогда из (2.1.13),
(2.1.14) находим максимальное удаление
электронов от поверхности
![]() .
.
Вычисления дают
![]()
![]() .
.
Задача 5. Катод
фотоэлемента освещают монохроматическим
светом. При задерживающем напряжении
между катодом и анодом
![]() ток в цепи прекращается. При изменении
ток в цепи прекращается. При изменении
длины волны света в![]() раза потребовалось подать на электроды
раза потребовалось подать на электроды
задерживающую разность потенциалов![]() .
.
Определить работу выхода электронов
из материала катода.
Решение
Используя уравнение
Эйнштейна для фотоэффекта и формулу
для задерживающего напряжения, получаем
![]() ,
,
(2.1.15)
![]() ,
,
(2.1.16)
где длины волн
связаны условием
![]() .
.
(2.1.17)
Решая систему
уравнений (2.1.15) – (2.1.17), находим
![]() .
.
Задача 6. Определить,
с какой скоростью должен двигаться
электрон, чтобы его импульс был равен
импульсу фотона с длиной волны
![]() .
.
Решение
Предварительно
сравним энергию фотона с энергией покоя
электрона
![]() ,
,
![]() .
.
Вычисления
показывают, что энергия фотона больше
энергии покоя электрона, следовательно,
при решении задачи необходимо использовать
формулы специальной теории относительности.
Приравнивая формулы импульса фотона и
релятивистского электрона, получаем
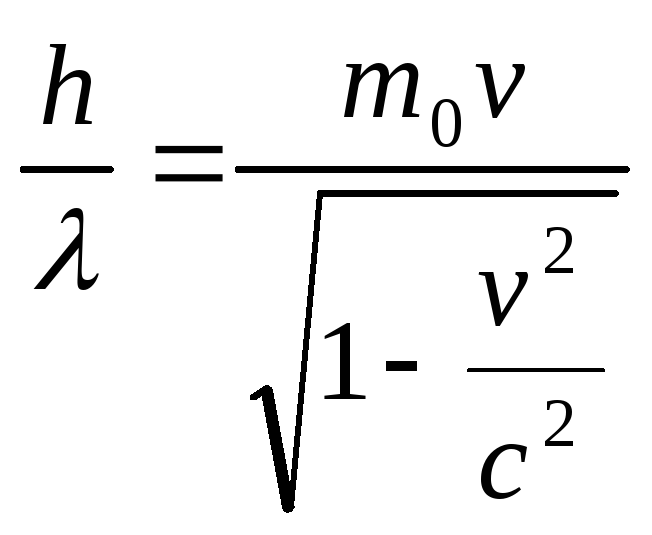 .
.
(2.1.18)
Решая (2.1.18)
относительно скорости электрона,
получаем
![]()
![]() .
.
Задача 7. В космосе
движется пылинка плотностью
![]() ,
,
поглощающая весь падающий на нее свет.
Зная мощность излучения Солнца![]() ,
,
найти радиус пылинки, при котором ее
гравитационное притяжение к Солнцу
компенсируется силой светового давления.
Решение
Согласно условию
задачи сила всемирного тяготения должна
уравновешиваться силой светового
давления, поэтому
![]() .
.
(2.1.19)
По закону всемирного
тяготения
![]() ,
,
(2.1.20)
где массу пылинки
можно записать в виде
![]() ;
;
(2.1.21)
здесь
![]() – радиус пылинки,
– радиус пылинки,![]() – расстояние от пылинки до Солнца.
– расстояние от пылинки до Солнца.
Сила светового
давления равна
![]() ,
,
(2.1.22)
где проекция
поверхности пылинки на плоскость,
перпендикулярную солнечным лучам, имеет
площадь
![]() ,
,
(2.1.23)
а давление связано
с мощностью излучения
![]() ,
,
пронизывающего поверхность пылинки
формулой
![]() .
.
(2.1.24)
Мощность излучения,
приходящуюся на пылинку, можно выразить
через мощность солнечного излучения
при помощи пропорции
![]() .
.
(2.1.25)
Исключая из системы
(2.1.19) – (2.1.25) неизвестные, получаем
формулу для радиуса пылинки
![]() .
.
Подстановка
числовых значений дает
![]() .
.
Задача 8. В результате
столкновения фотона и протона, летевших
по взаимно перпендикулярным направлениям,
протон остановился, а длина волны фотона
изменилась на
![]() .
.
Чему был равен импульс фотона? Скорость
протона считать![]() .
.
Решение
Воспользуемся для
решения задачи законами сохранения
импульса и энергии. Пусть первоначальный
импульс фотона
![]() направлен по оси
направлен по оси
![]() ,
,
импульс протона
![]() – по оси
– по оси![]() ,
,
а импульс фотона после рассеяния![]() образует с осью
образует с осью![]() угол
угол![]() (рис. 2.1.1). Учитывая, что движение протона
(рис. 2.1.1). Учитывая, что движение протона
по условию можно описывать классическими
формулами, по закону сохранения энергии
имеем
![]() .
.
(2.1.26)
Р ис.
ис.
2.1.1
Закон сохранения
импульса в проекциях на оси
![]() и
и![]() дает
дает
![]() ,
,
![]() .
.
(2.1.27)
Изменение длины
волны рассеянного фотона по условию
удовлетворяет формуле
![]() .
.
(2.1.28)
Выразим из (2.1.27)
![]() и
и![]() ,
,
возведем эти уравнения в квадрат, сложим
и воспользуемся основным тригонометрическим
тождеством. В результате получим
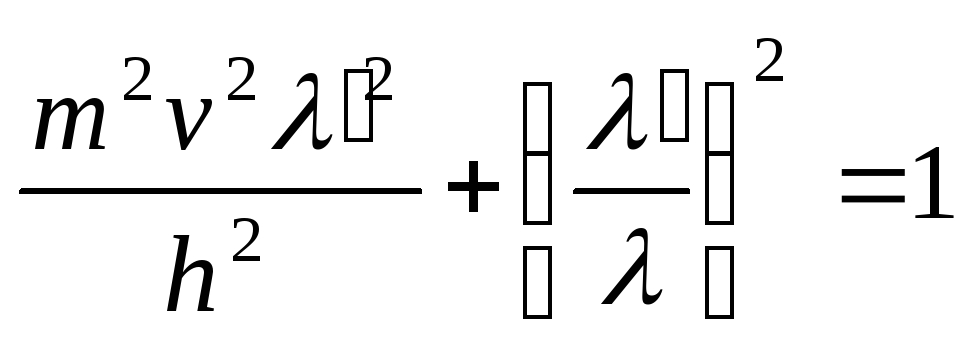 .
.
(2.1.29)
Исключая из
(2.1.26), (2.1.29)
![]() при помощи (2.1.28), преобразуем эти уравнения
при помощи (2.1.28), преобразуем эти уравнения
к виду
![]() ,
,
(2.1.30)
![]() .
.
(2.1.31)
Исключая теперь
из системы (2.1.30), (2.1.31) скорость протона,
находим длину волны фотона до рассеяния
![]() ,
,
после чего определяем
первоначальный импульс фотона
![]() .
.
Задача 9. Узкий
пучок монохроматического рентгеновского
излучения падает на рассеивающее
вещество. При этом длины волн смещенных
составляющих излучения, рассеянного
под углами
![]() и
и![]() ,
,
отличаются друг от друга в![]() раза. Считая, что рассеяние происходит
раза. Считая, что рассеяние происходит
на свободных электронах, найти длину
волны падающего излучения.
Решение
Воспользуемся
формулами изменения длины волны при
комптоновском рассеянии для двух углов
рассеяния, упомянутых в условии
![]() ,
,
![]() .
.
(2.1.32)
Деля второе
уравнение (2.1.32) на первое, получаем
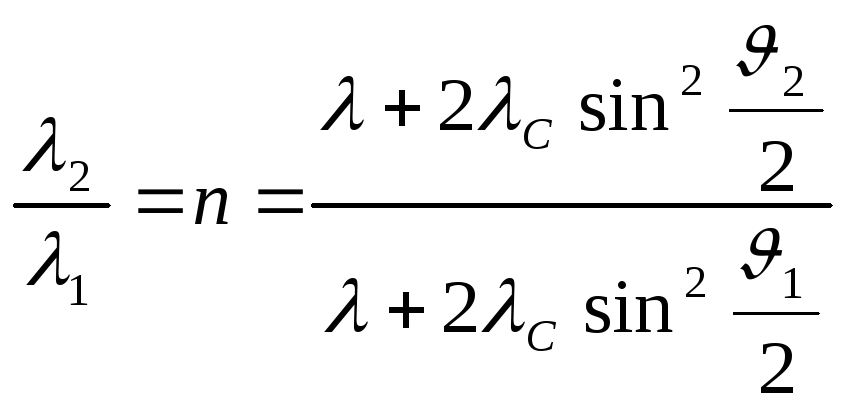 .
.
(2.1.33)
Решая (2.1.33), находим
длину волны падающего на вещество
излучения
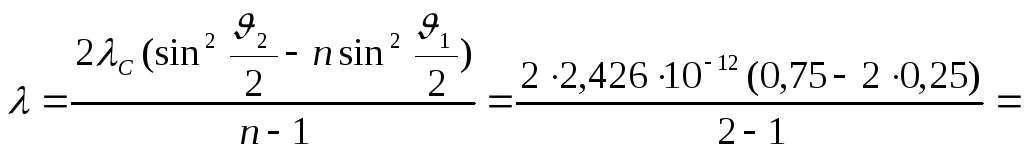
![]() .
.
Задача 10. Фотон с
энергией, в
![]() раза превышающей энергию покоя электрона,
раза превышающей энергию покоя электрона,
рассеялся назад на неподвижном свободном
электроне. Найти радиус кривизны
траектории электрона отдачи в магнитном
поле с индукцией![]() ,
,
предполагая, что линии индукции
перпендикулярны вектору скорости
электрона.
Решение
Запишем выражение
изменения длины волны света при
комптоновском рассеянии
![]() .
.
(2.1.34)
Перейдем в (2.1.34)
от длин волн к энергиям при помощи
соотношения
![]() и учтем, что угол рассеяния
и учтем, что угол рассеяния![]() .
.
В результате получим
![]() ,
,
(2.1.35)
где
![]() – энергия покоя электрона. С учетом того,
– энергия покоя электрона. С учетом того,
что![]() ,
,
находим из (2.1.35) энергию рассеянного
фотона
![]()
и кинетическую
энергию электрона отдачи
![]() .
.
(2.1.36)
Как известно,
радиус окружности, по которой электрон
движется в магнитном поле, определяется
по формуле
![]() ,
,
(2.1.37)
где с учетом
релятивистского характера движения
электрона
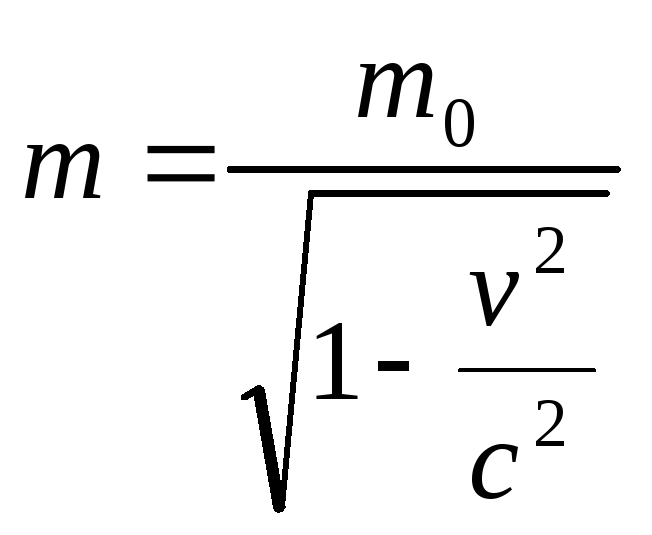 .
.
(2.1.38)
Используя
релятивистскую формулу кинетической
энергии
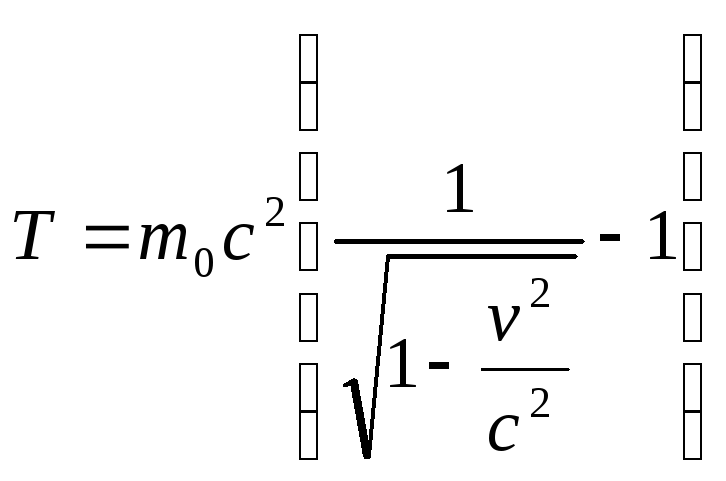 ,
,
из (2.1.36) после
алгебраических преобразований можно
получить
![]() ,
,
что после подстановки
в (2.1.37), (2.1.38) позволяет найти радиус
кривизны траектории электрона
![]() .
.
(2.1.39)
Подстановка в
(2.1.39) числовых значений дает
![]() .
.
Задача 11. При
увеличении напряжения на рентгеновской
трубке в
![]() раза длина волны коротковолновой границы
раза длина волны коротковолновой границы
сплошного рентгеновского спектра
изменилась на![]() .
.
Найти первоначальное напряжение на
трубке.
Решение
Применим формулу
длины волны коротковолновой границы
сплошного рентгеновского спектра для
случаев до и после изменения напряжения
на трубке
![]() ,
,
![]() .
.
(2.1.40)
Вычитая из первого
уравнения (2.1.40) второе, находим
![]() ,
,
откуда следует
формула первоначального напряжения на
трубке
![]() .
.
По уравнению Эйнштейна , где V – частота излучения (Гц), h – постоянная планка (h = 6,62*10⁻³⁴ Дж*с),
– работа выхода (Дж),
– максимальная энергия излучения (Дж). Распишим кинетическую энергию:
. Частоту также расписываем как:
, где с – скорость света (c = 3*10⁸ м/с), Y – длина волны (м). Тогда подставив получим:
Производим преорразования и выражаем находимую скорость:
В системе СИ: 200 нм = 200*10⁻⁹ м; 4,5 эВ = 4,5*1,6*10⁻¹⁹ = 7,2*10⁻¹⁹ Джоуль; масса электрона m(e) = 9,1*10⁻³¹ кг. Подставляем численные данные и вычисляем:
Ниже размещены условия задач и отсканированные решения. Если вам нужно решить задачу на эту тему, вы можете найти здесь похожее условие и решить свою по аналогии. Загрузка страницы может занять некоторое время в связи с большим количеством рисунков. Если Вам понадобится решение задач или онлайн помощь по физике- обращайтесь, будем рады помочь.
Явление фотоэффекта заключается в испускании веществом электронов под действием падающего света. Теория фотоэффекта разработана Эйнштейном и заключается в том, что поток света представляет собой поток отдельных квантов(фотонов) с энергией каждого фотона hn. При попадании фотонов на поверхность вещества часть из них передает свою энергию электронов. Если этой энергия больше работы выхода из вещества, электрон покидает металл. Уравнение эйнштейна для фотоэффекта:  где
где  — максимальная кинетическая энергия фотоэлектрона.
— максимальная кинетическая энергия фотоэлектрона.
Длина волны красной границы фотоэффекта для некоторого металла составляет 307 нм. Максимальная кинетическая энергия фотоэлектронов – 1 эВ. Найти отношение работы выхода электрона к энергии падающего фотона.

Частота света красной границы фотоэффекта для некоторого металла составляет 6*1014 Гц, задерживающая разность потенциалов для фотоэлектронов – 2В. Определить частоту падающего света и работу выхода электронов.

Работа выхода электрона из металла составляет 4,28эВ. Найти граничную длину волны фотоэффекта.

На медный шарик радает монохроматический свет с длиной волны 0,165 мкм. До какого потенциала зарядится шарик, если работа выхода электрона для меди 4,5 эВ?

Работа выхода электрона из калия составляет 2,2эВ, для серебра 4,7эВ. Найти граничные длину волны фотоэффекта.

Длина волны радающего света 0,165 мкм, задерживающая разность потенциалов для фотоэлектронов 3В. Какова работа выхода электронов?
Красная граница фотоэффекта для цинка 310 нм. Определить максимальную кинетическую энергию фотоэлектронов, если на цинк падает свет с длиной волны 200нм.

На металл с работой выхода 2,4эВ падает свет с длиной волны 200нм. Определить задерживающую разность потенциалов.

На металл падает свет с длиной волны 0,25 мкм, задерживающая разность потенциалов при этом 0,96В. Определить работу выхода электронов из металла.

При изменении длины волны падающего света максимальные скорости фотоэлектронов изменились в 3/4 раза. Первоначальная длина волны 600нм, красная граница фотоэффекта 700нм. Определить длину волны после изменения.


Работы выхода электронов для двух металлов отличаются в 2 раза, задерживающие разности потенциалов – на 3В. Определить работы выхода.

Максимальная скорость фотоэлектронов равно 2,8*108 м/с. Определить энергию фотона.
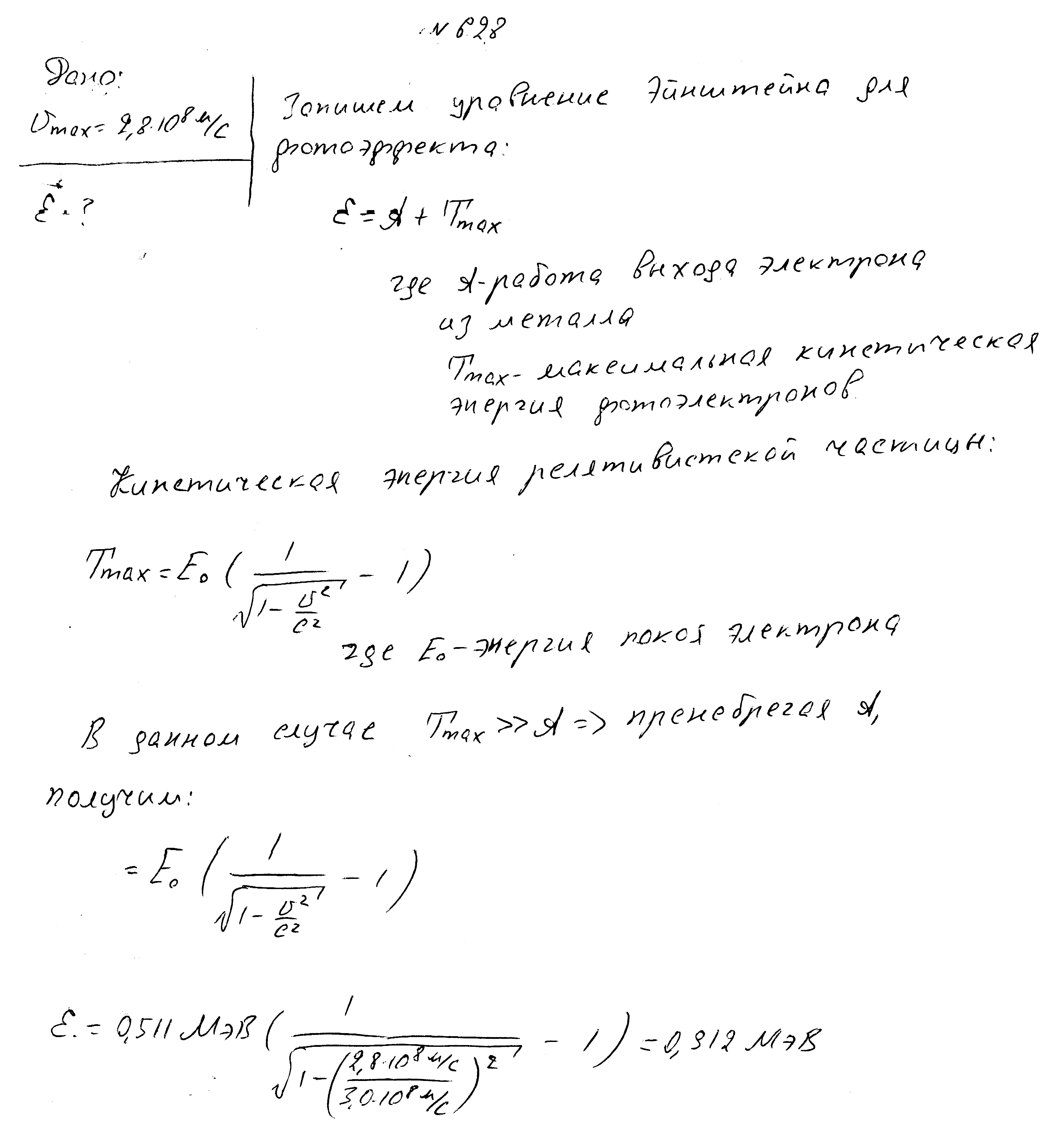
Энергии падающих на металл фотонов равны 1,27 МэВ. Найти максимальную скорость фотоэлектронов.

Максимальная скорость фотоэлектронов равно 0,98с, где с – скорость света в вакууме. Найти длину волны падающего света.
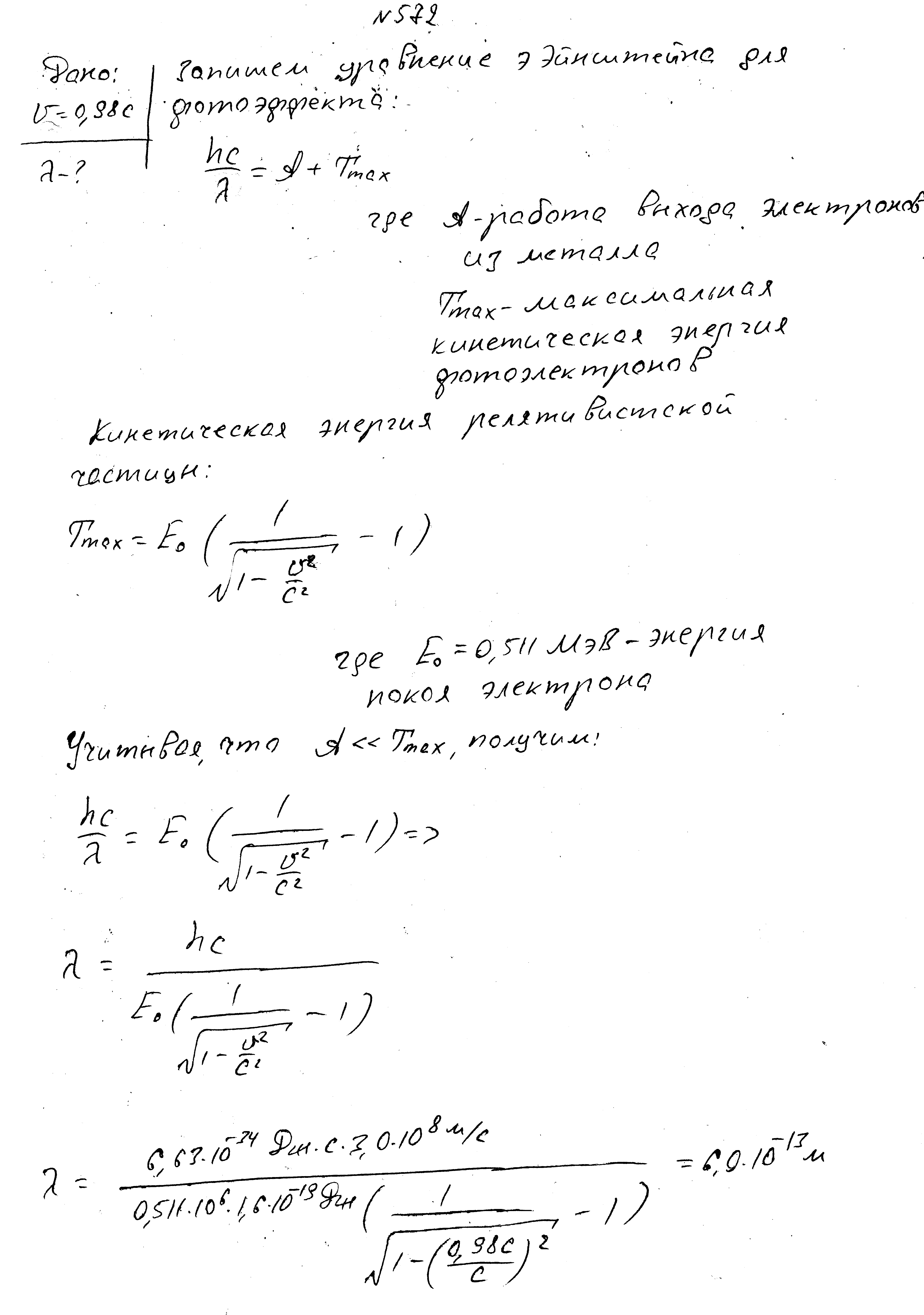
Энергия фотона в пучке света, падающего на поверхность металла, равно 1,53 МэВ. Определить максимальную скорость фотоэлектронов.
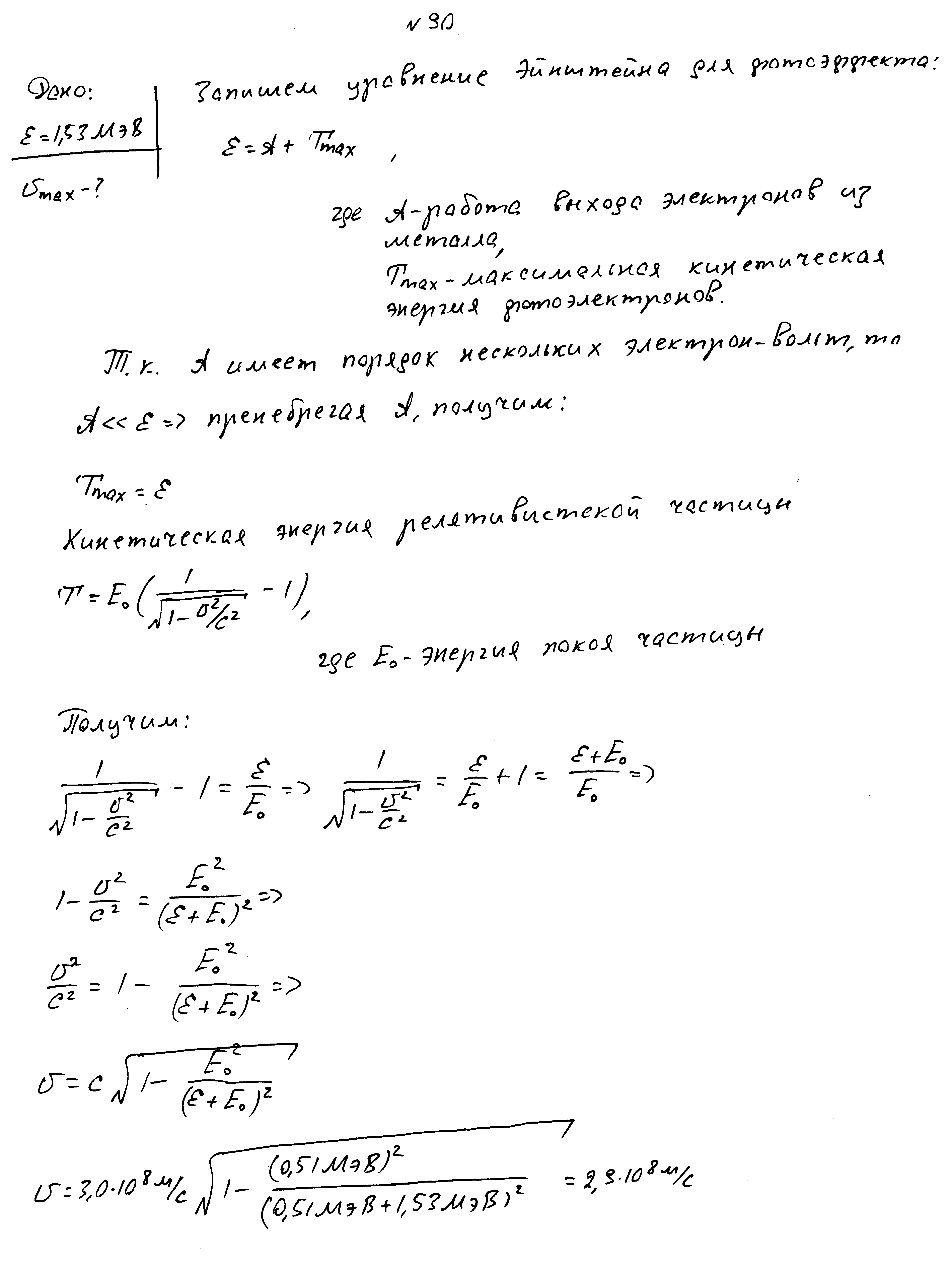
На шарик из металла падает свет с длиной волны 0,4 мкм, при этом шапик заряжается до потенциала 2В. До какого потенциала зарядится шарик, если длина волны станет равной 0,3 мкм?

После изменения длины волны падающего света в 1,5 раза задерживающая разность потенциалов изменилась с 1,6В до 3В. Какова работа выхода?
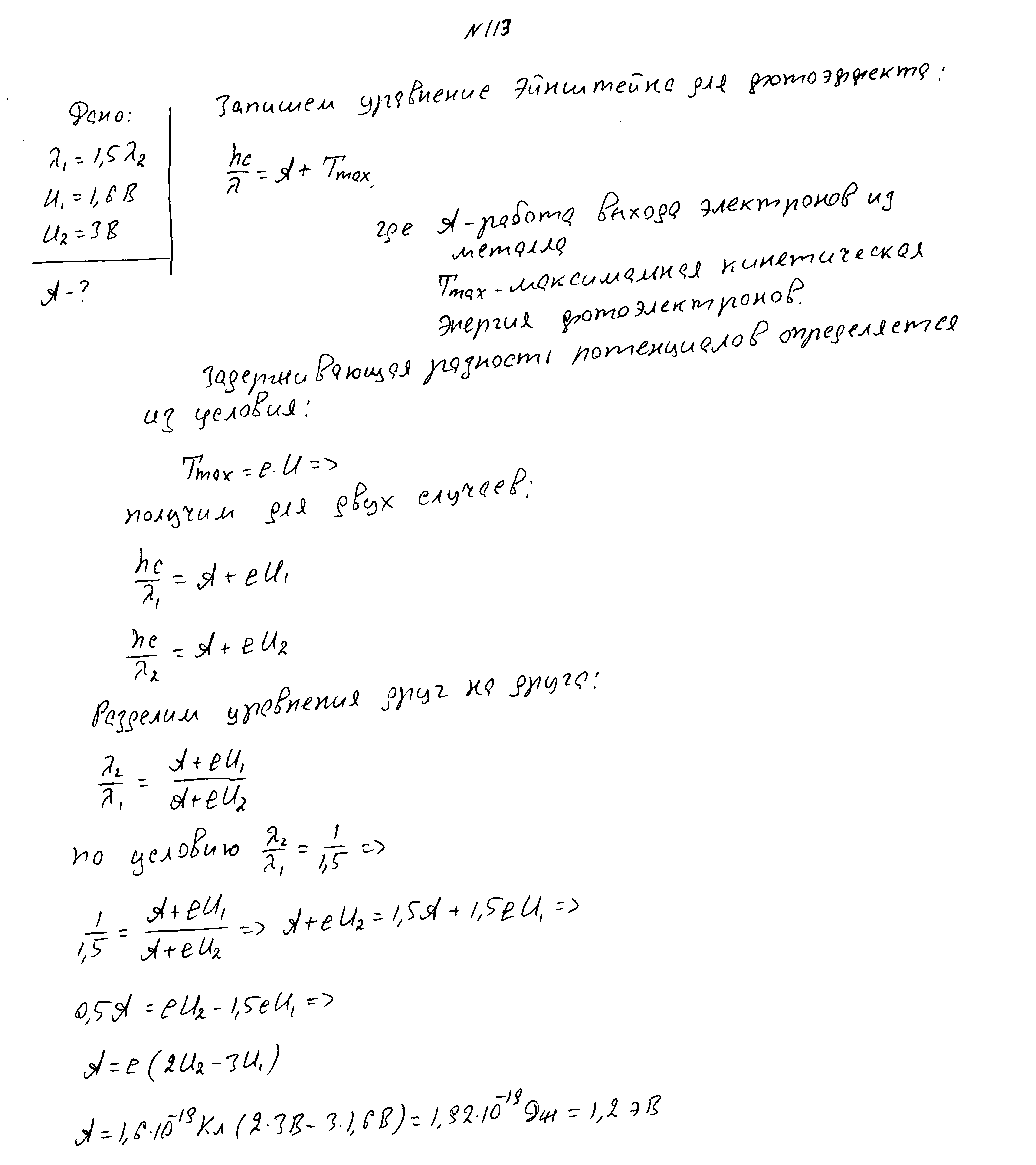
Красная граница фотоэффекта 560нм, частота падающего света 7,3*1014 Гц. Найти максимальную скорость фотоэлектронов.
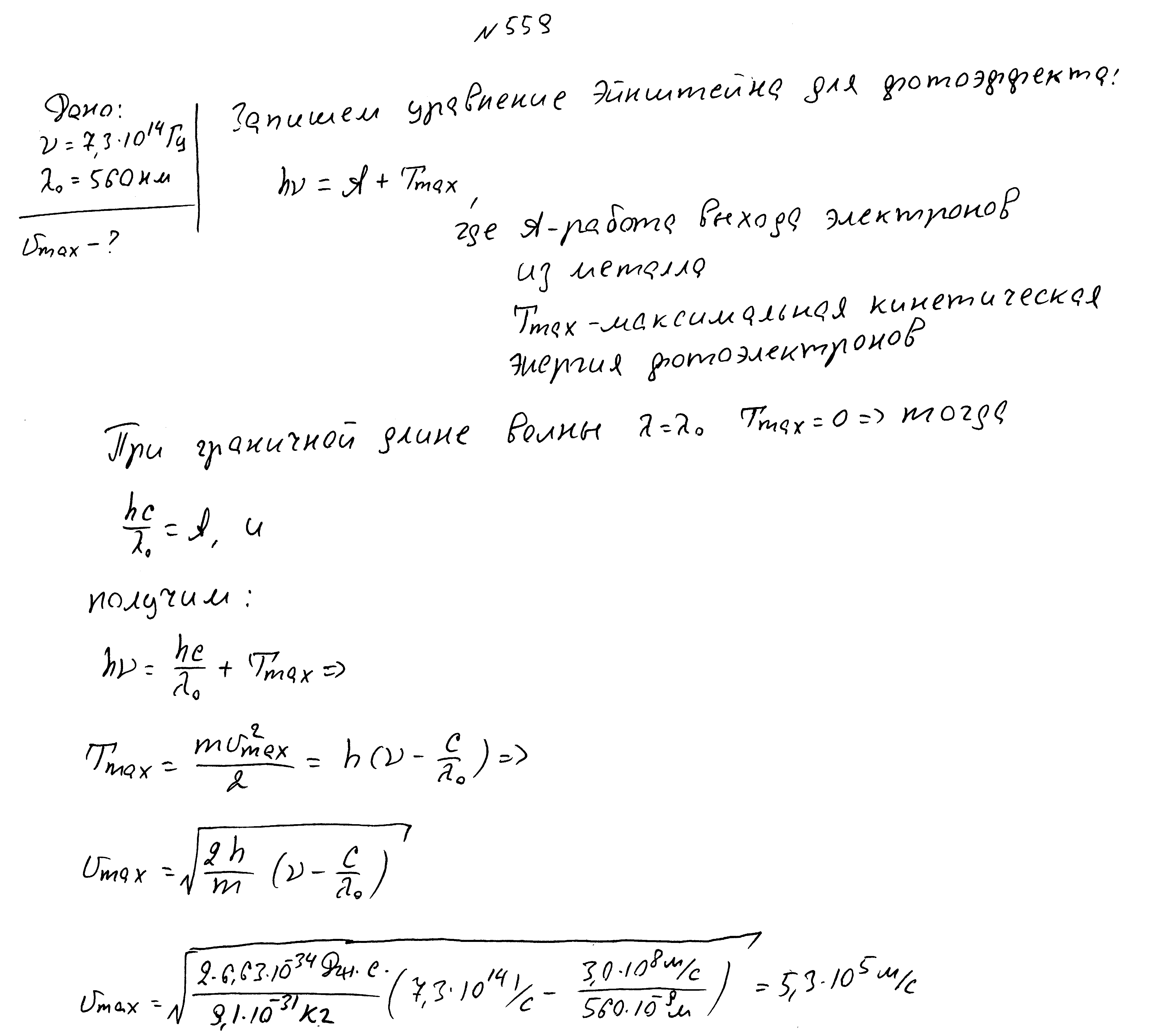
Красная граница фотоэффекта 2800 ангстрем, длина волны падающего света 1600 ангстрем. Найти работу выхода и максимальную кинетическую энергию фотоэлектрона.

Задерживащая разность потенциалов 1,5В, работа выхода электронов 6,4*10-19 Дж. Найти длину волны падающего света и красную границу фотоэффекта.

Работа выхода электронов из металла равна 3,3 эВ. Во сколько раз изменилась кинетическая энергия фотоэлектронов. если длина волны падающего света изменилась с 2,5*10-7м до 1,25*10-7м?
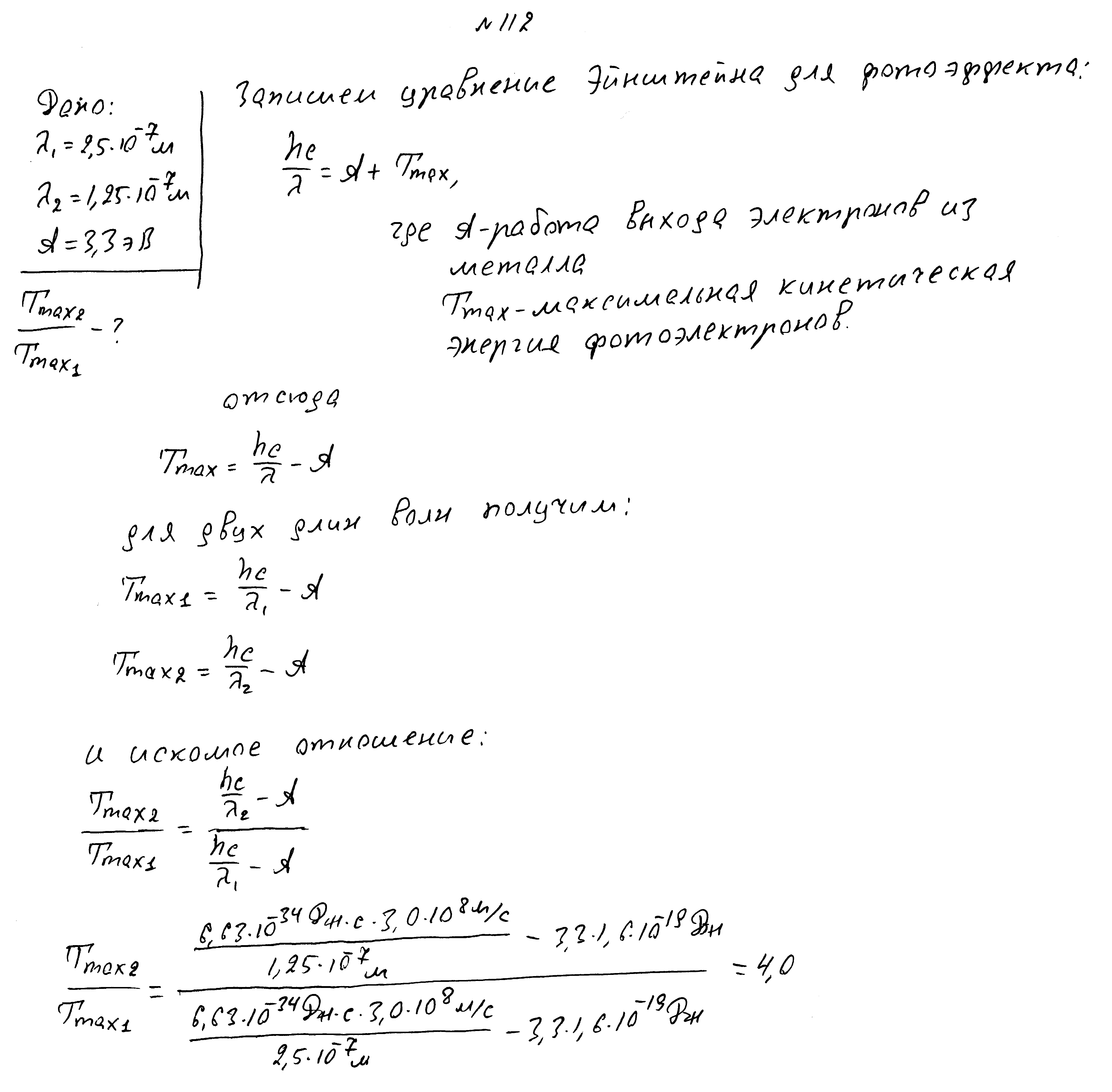
Найти максимальную скорость фотоэлектронов для видимого света с энергией фотона 8 эВ и гамма излучения с энергией 0,51 МэВ. Работа выхода электронов из металла 4,7 эВ.
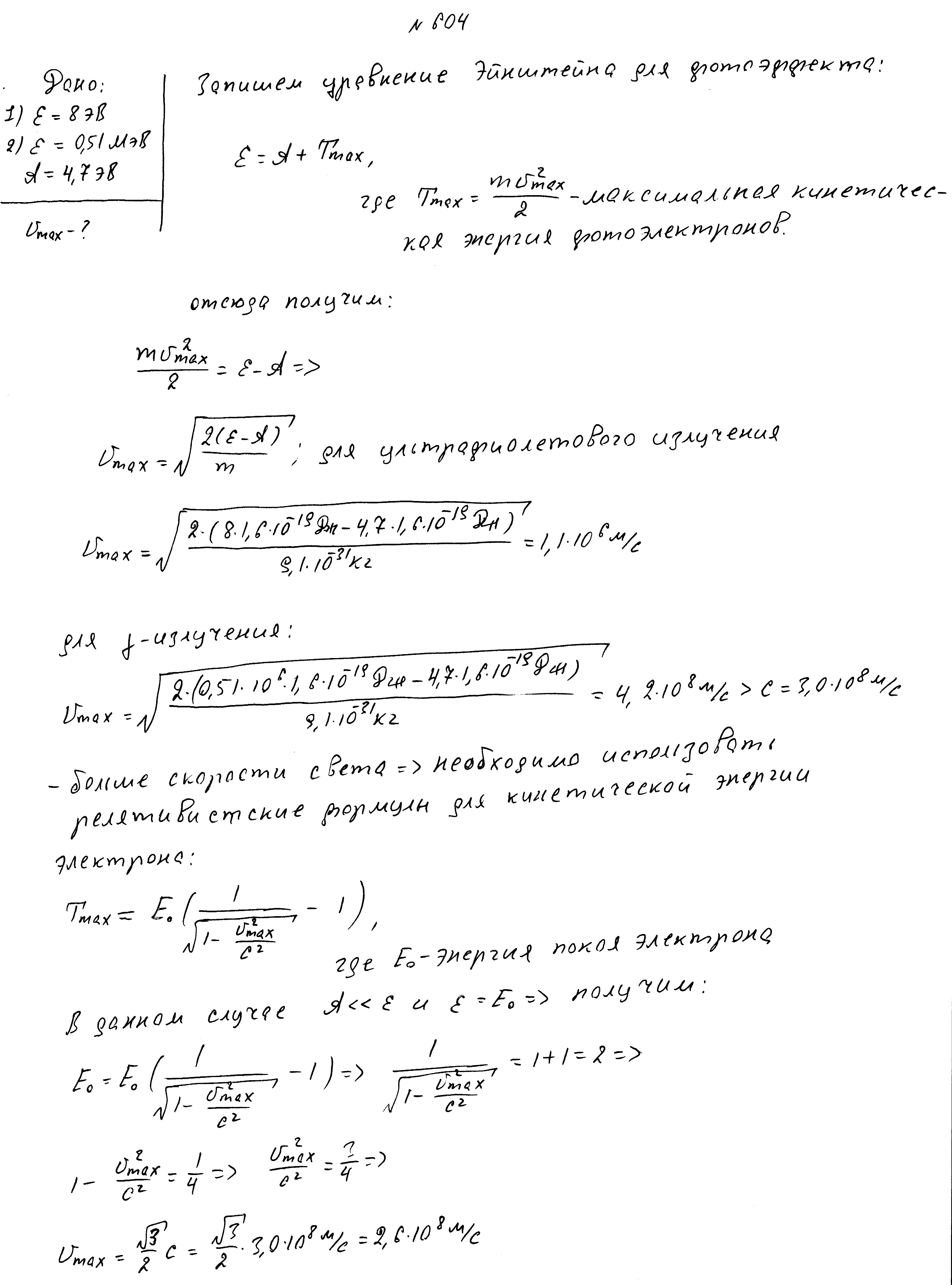
Фототок прекращается при задерживающей разности потенциалов 3,7 В. Работа выхода электронов равна 6,3 эВ. Какая работа выхода электронов у другого металла, если там фототок прекращается при разности потенциалов, большей на 2,3В.
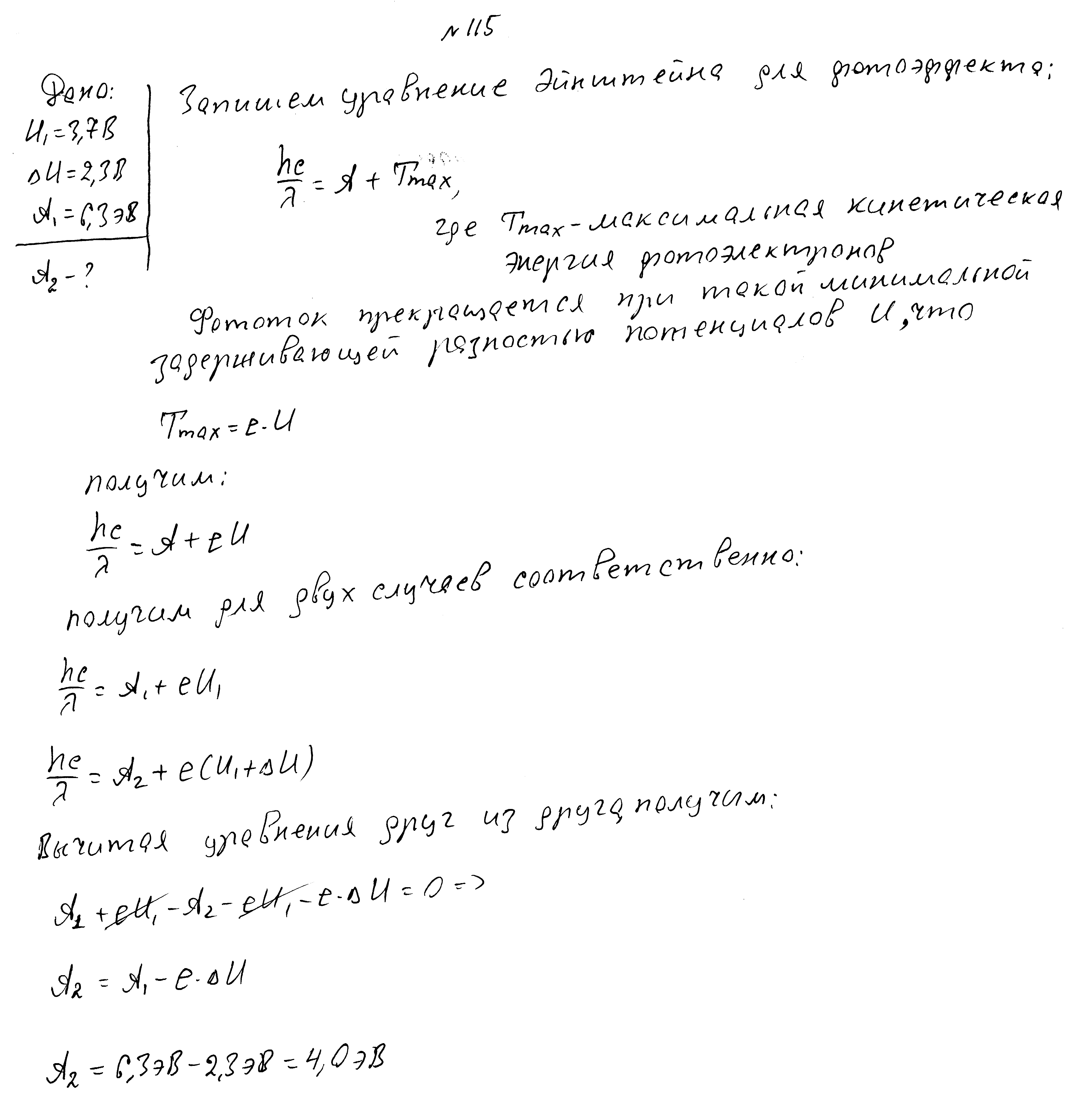
Работа выхода электронов из металла 4,5 эВ, энергия падающих фотонов 4,9 эВ. Чему равен максимальный импульс фотоэлектронов?
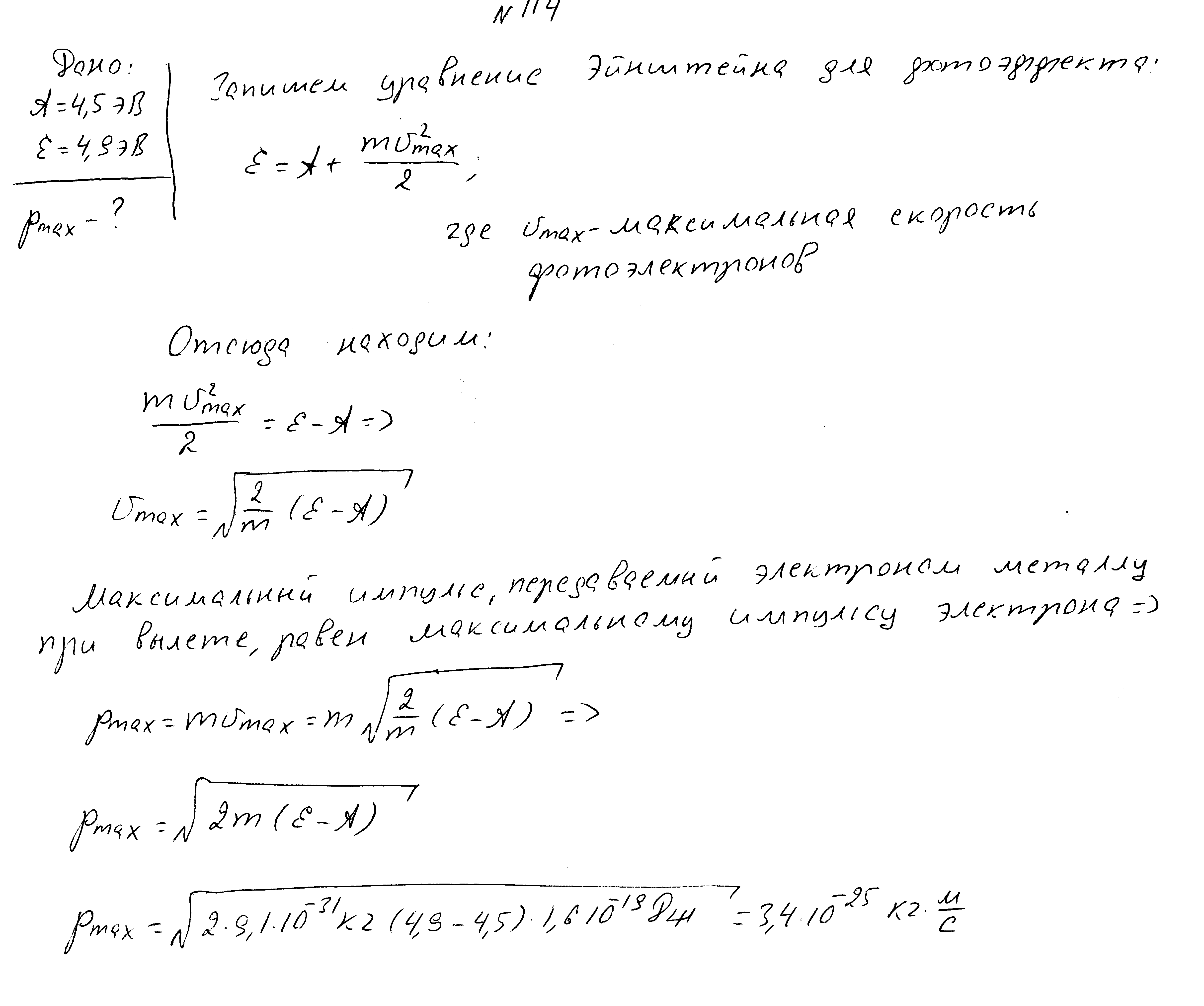
Красная граница фотоэффекта 2900 ангстрем, максимальная скорость фотоэлектронов 108 м/с. Найти отношение работы выхода электронов к энергии палающих фотонов.
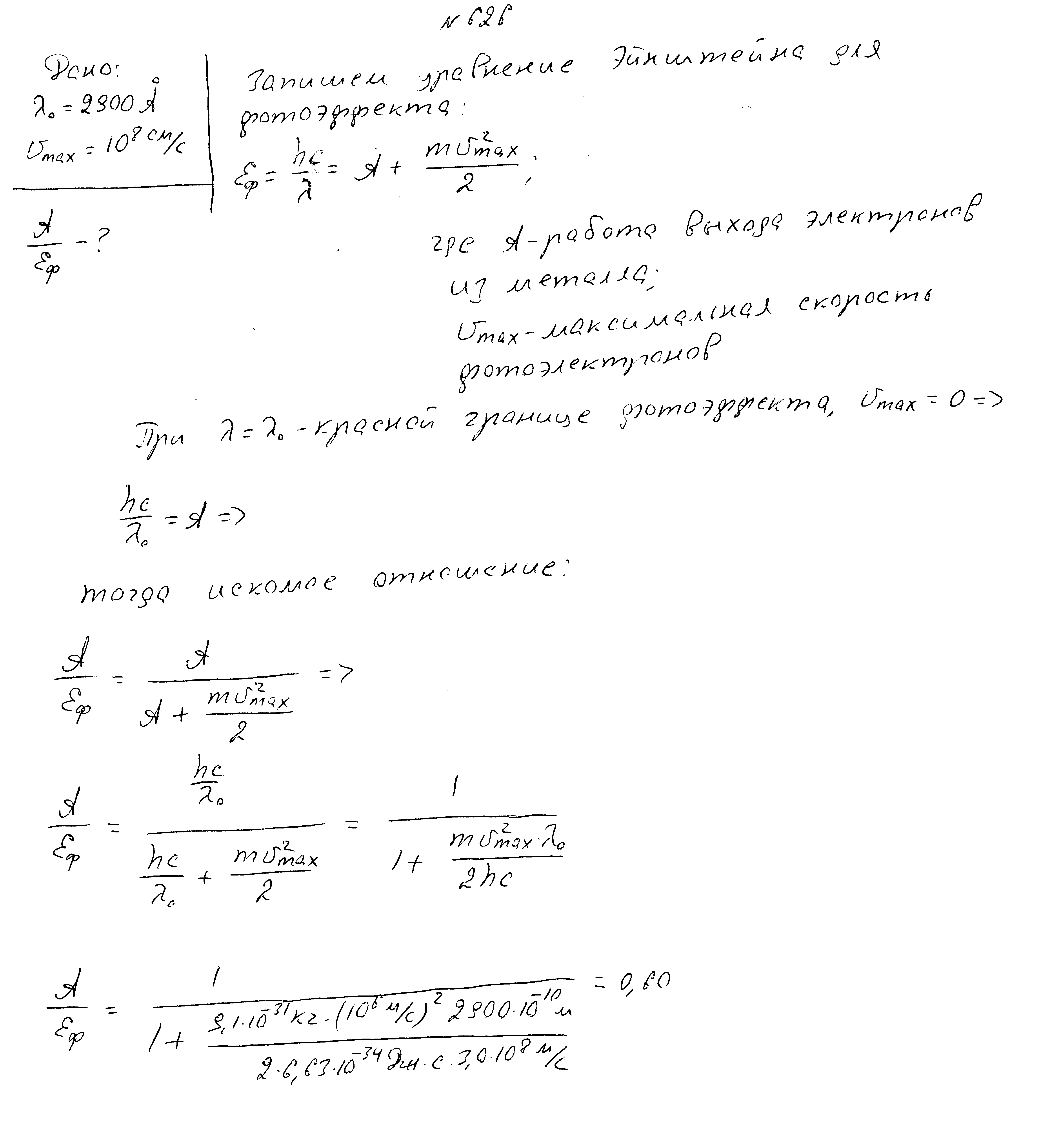
Длина волны падающего света 400нм, красная граница фотоэффекта равна 400нм. Чему равна максимальная скорость фотоэлектронов?
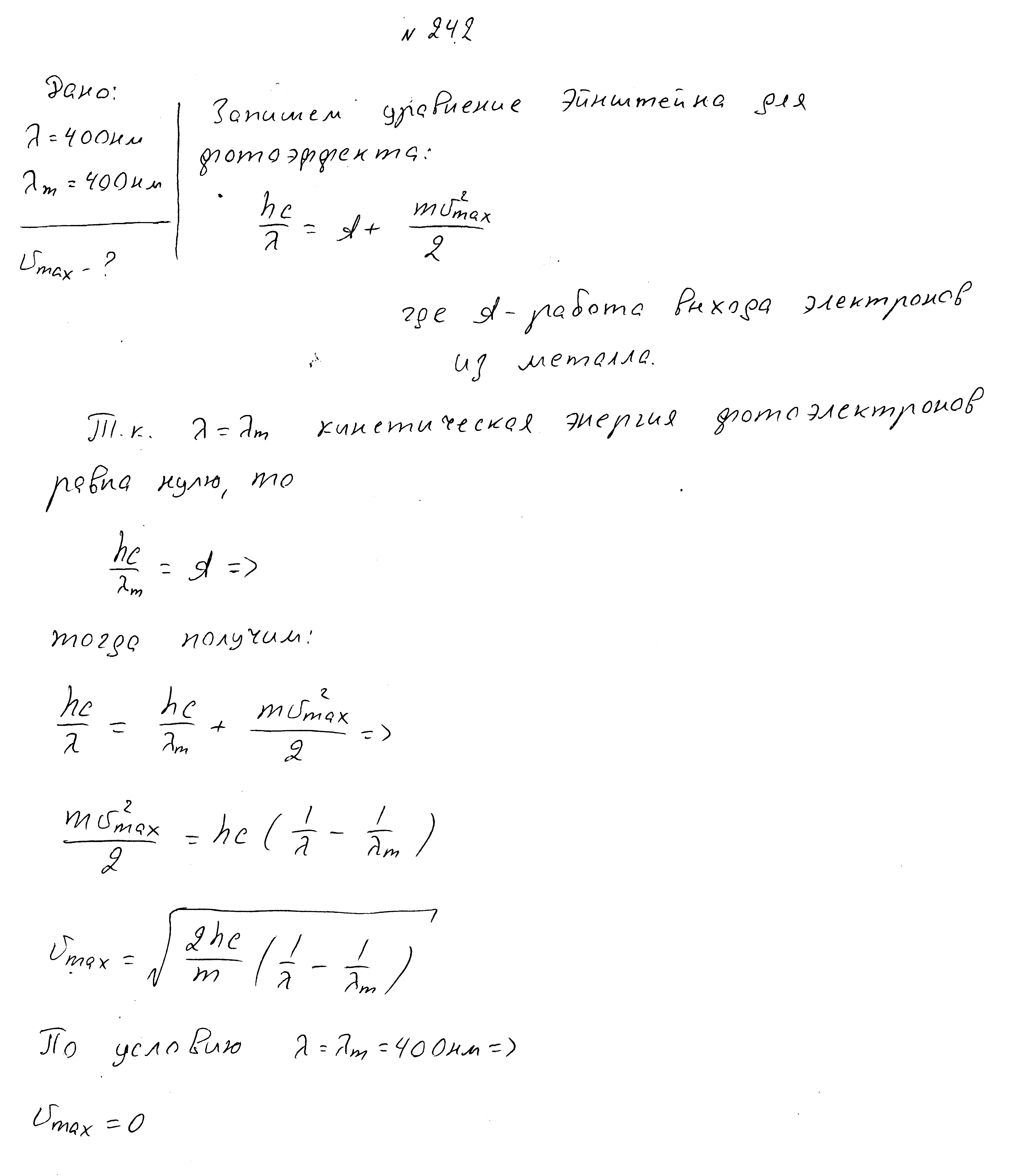
Длина волны падающего света 300нм, работа выхода электронов 3,74 эВ. Напряженность задерживающего электростатического поля 10 В/см.Какой максимальный путь фотоэлектронов при движении в направлении задерживающего поля?
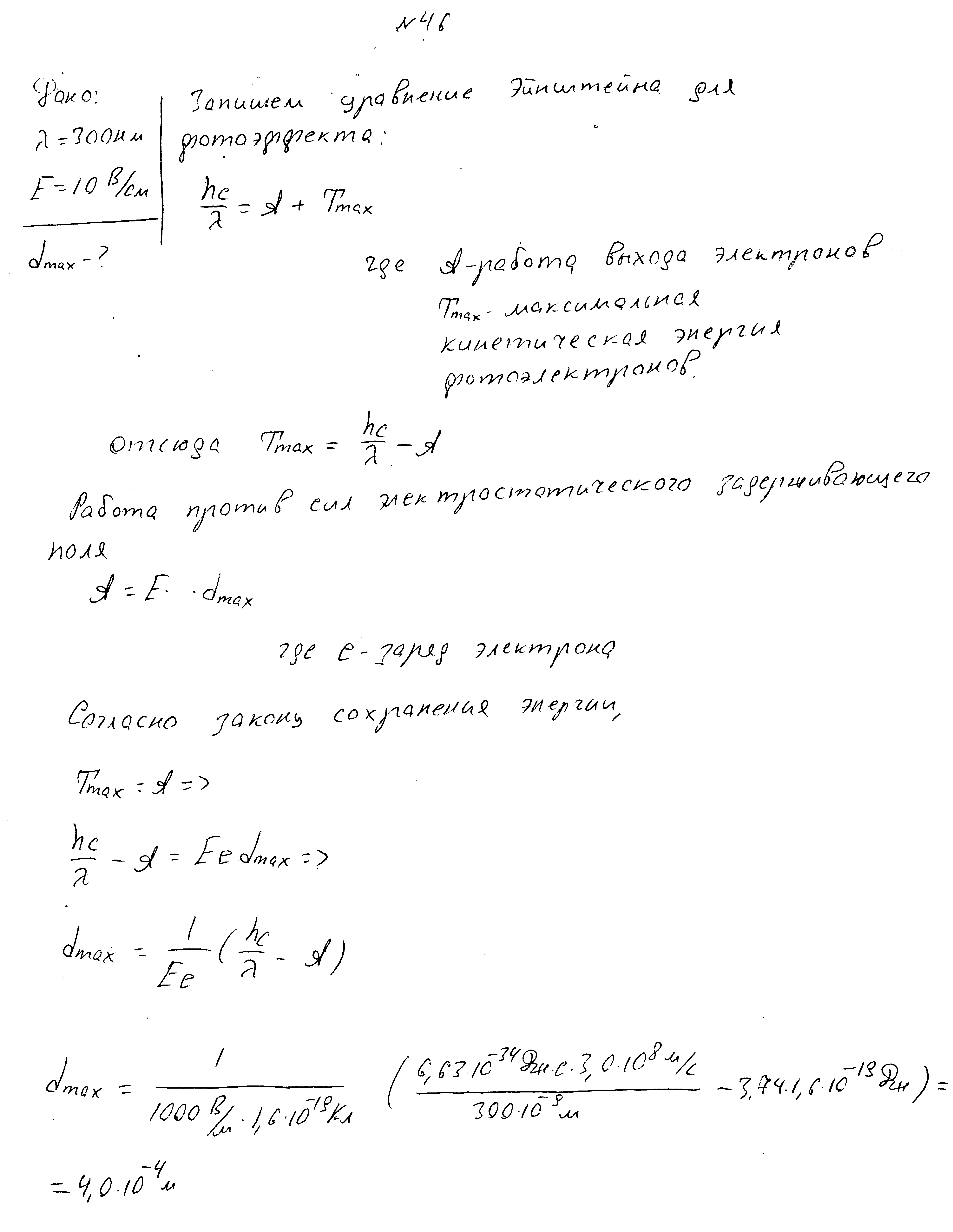
Длина волны падающего света 100 нм, работа выхода электронов 5,30эВ. Найти максимальную скорость фотоэлектронов.
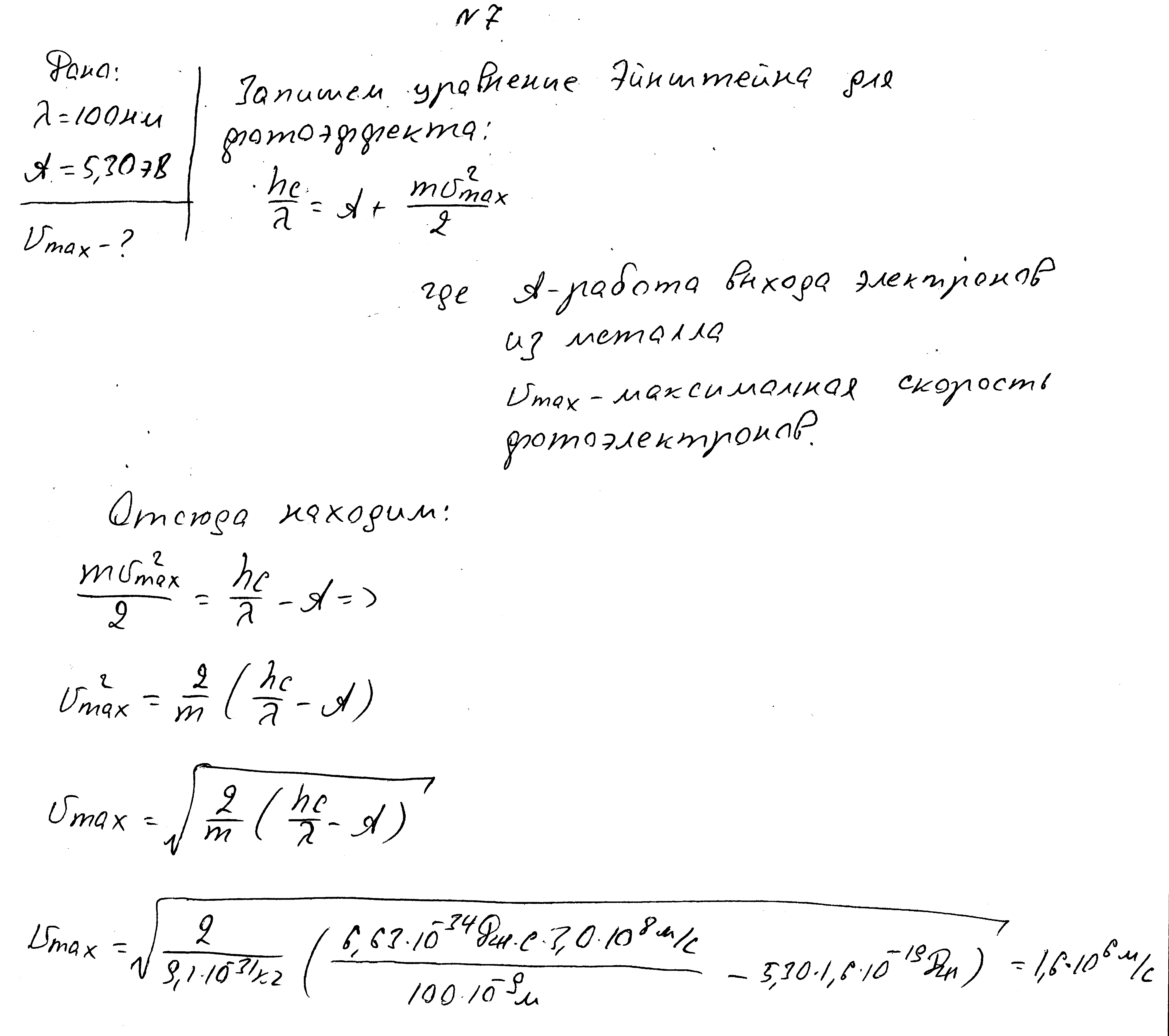
При длине волны радающего света 491нм задерживающая разность потенциалов 0,71В. Какова работа выхода электронов? Какой стала длина волны света, если задерживающая разность потенциалов стала равной 1,43В?
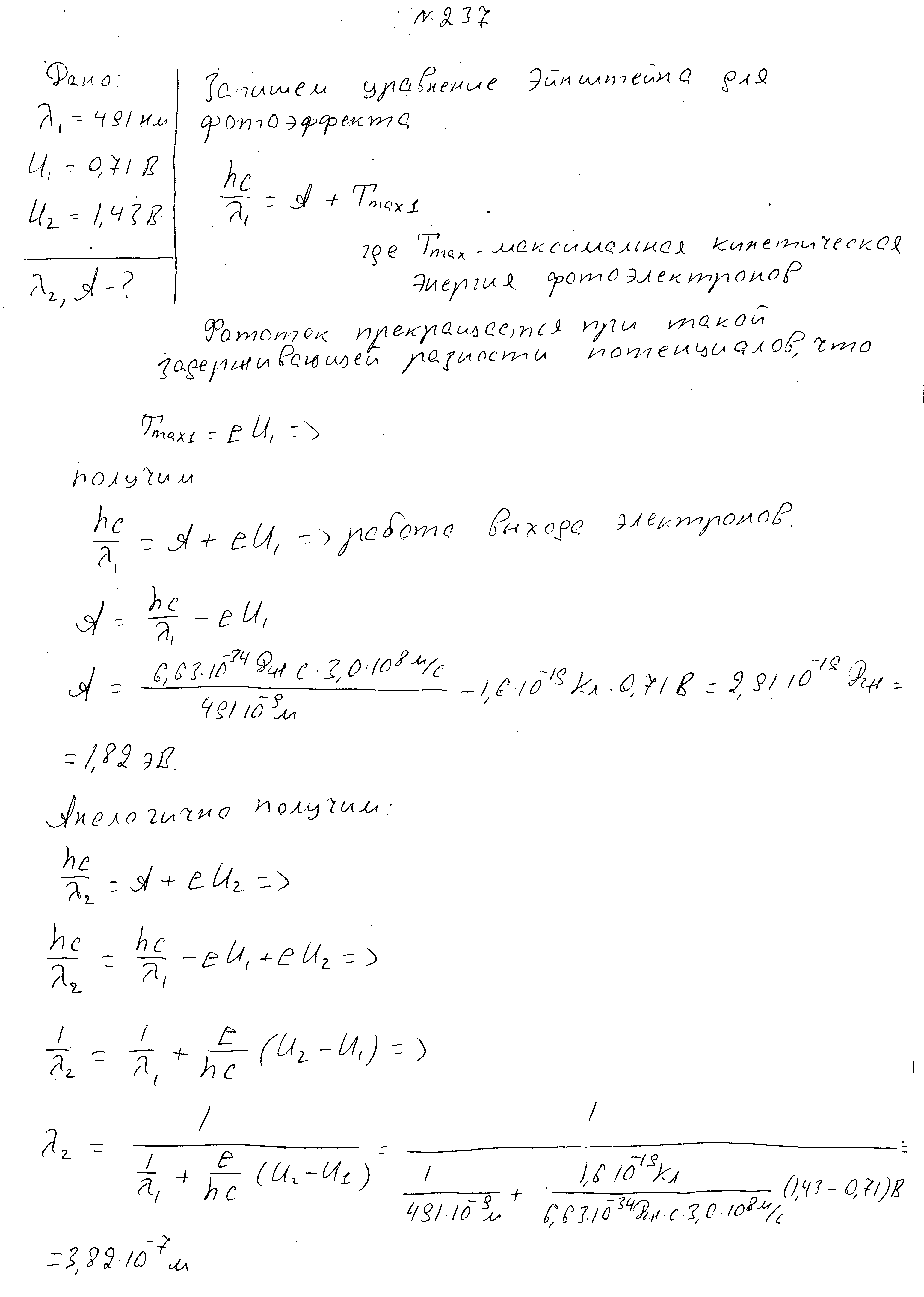
Кинетическая энергия фотоэлектронов 2,0 эВ, красная граница фотоэффекта 3,0*1014 Гц. Определить энергию фотонов.

Красная граница фотоэффекта 0,257 мкм, задерживающая разность потенциалов 1,5В. Найти длину волны падающего света.
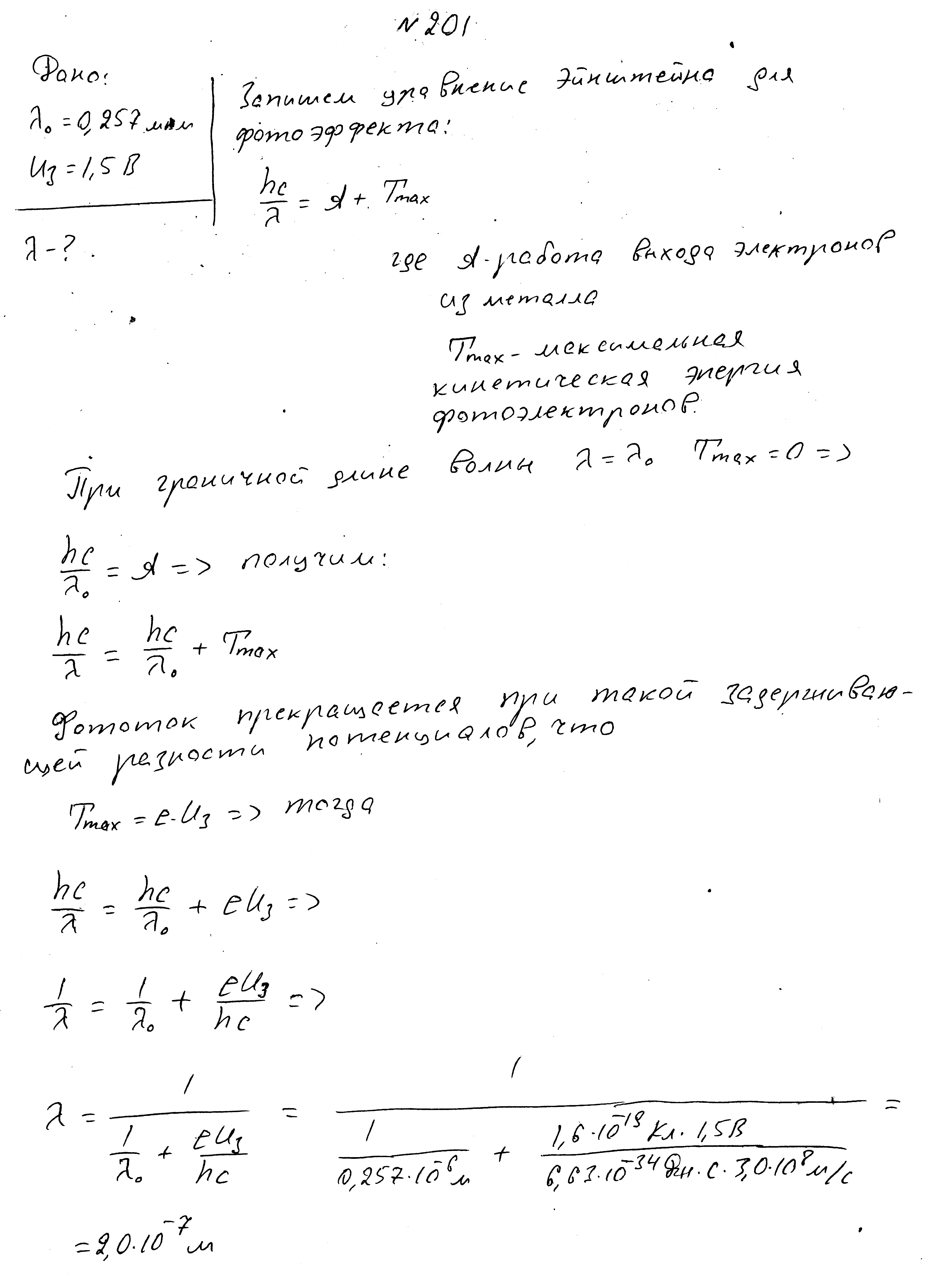
Красная граница фотоэффекта 2850 ангстрем. Минимальное значение энергии фотона, при котором возможен фотоэффект?

Ниже вы можете посмотреть обучаюший видеоролик на тему фотоэффекта и его законов.
