Тема .
№27 МКТ. Термодинамика (Расчетная задача высокого уровня сложности)
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
№27 мкт. термодинамика (расчетная задача высокого уровня сложности)
.01МКТ
.02Термодинамика
.03Влажность. Водяной пар
.04Тепловые явления
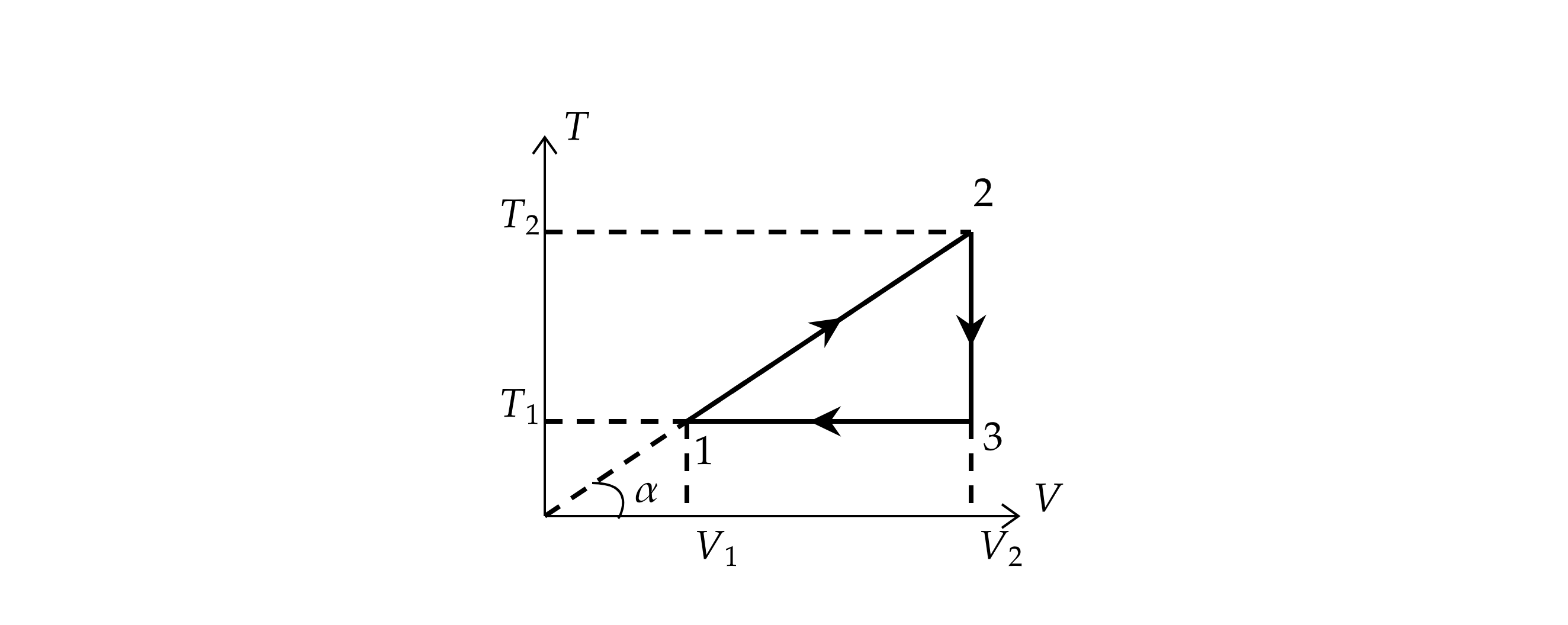
Решаем задачу:
Показать ответ и решение
1) По уравнению Менделеева-Клапейрона:
где
– количество вещества, 
– давление газа.
Тогда
Так
как по условию 
, где 
– некоторый постоянный коэффициент.
Тогда для процесса 1-2:
То
есть давление постоянно. Тогда по закону Гей-Люссака:
2) Так как 1-2 – изобара, то работа газа равна:
3)
Работа газа за цикл равна:
так
как в процессе 2-3 объём постоянен, то работа равна нулю, при этом 
. При этом газ получает
количество теплоты в процессе 1-2, значит, КПД равно:
Количество теплоты в процессе 1-2 можно найти по первому началу термодинамики:
где
– изменение внутренней энергии.
Изменение внутренней энергии равно:
Откуда:
КПД
Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»
- Подробности
- Обновлено 13.08.2018 14:05
- Просмотров: 712
«Физика – 10 класс»
При решении многих задач на газовые законы требуется построение графиков, изображающих разного рода процессы. На графиках обозначаем точки, определяющие состояния системы. Имеем в виду, что можно изобразить только равновесные процессы, при которых каждое промежуточное состояние равновесное, т. е. температура и давление одинаковы во всех точках данного объёма.
Задача 1.
Постройте изобары для водорода массой 2 г при нормальном атмосферном давлении р0 в координатах р, Т; р, V; V, Т.
Р е ш е н и е.
На графиках зависимости р от Т и р от V изобара представляет собой прямую, параллельную либо оси Т, либо оси V (рис. 10.5, а и б). Так как 
то графиком зависимости V от Т является прямая, проходящая через начало отсчёта. Учитывая, что m = 0,002 кг, М = 0,002 кг/моль, R = 8,31 Дж/(моль • К) и р0 = 105 Па, можно записать: V = ВТ, где 
В частности, при Т = 100 К V ≈ 8 • 10-3 м3. График зависимости V от Т показан на рисунке (10.5, в).
Задача 2.
Выведите уравнение Клапейрона при переходе газа из состояния 1 (Р1, V1, Т1) в состояние 2 (р2, V2, Т2) (рис. 10.6, а).
Р е ш е н и е.
Переведём газ из состояния 1 в состояние 2, совершив два процесса: изотермический из состояния 1 в состояние 1′, поддерживая постоянную температуру T1, и изобарный из состояния 1′ в состояние 2, поддерживая постоянным давление р2 (рис. 10.6, б).
Согласно закону Бойля—Мариотта запишем: P1V1 = p2V’, согласно закону Гей-Люссака 
Выразив из первого и второго уравнений V’ и приравняв правые части полученных равенств, запишем:
Перенеся параметры с индексом 1 в левую часть, а параметры с индексом 2 в правую, получим уравнение Клапейрона 
Для вывода уравнения мы использовали два экспериментально установленных закона: изотермический и изобарный.
Задача 3.
На графике (рис. 10.7) показан переход газа, взятого в количестве 2 моль, из состояния А в состояние В. Определите изменение температуры газа, а также максимальное значение температуры при этом переходе.
Р е ш е н и е.
По графику видно, что сначала газ нагревался при постоянном давлении, а затем давление уменьшалось при постоянном объёме, при этом температура уменьшалась. Обратим внимание на то, что произведение давления на объём в состояниях А и В одно и то же и равно 4000 Па • м3.
Согласно закону Менделеева—Клапейрона 
ΔТ = 0.
Начертим изотермы, проходящие через отмеченные состояния. Согласно графикам максимальная температура соответствует промежуточному состоянию 1′, для которого V = 4 л, а давление 4 • 106 Па. Тогда Т = 962 К.
Задача 4.
На рисунке (10.8, а) изображён график перехода газа из состояния А в состояние В в координатах р, V. Постройте график этого перехода в координатах р, Т и V, Т.
Р е ш е н и е.
Сначала построим график перехода в координатах р, Т. Поставим точку, соответствующую состоянию А газа (рис. 10.8, б). Процесс А—1 изотермический. При этом давление газа уменьшается. Процесс 1—2 изобарный. Построим отрезок, параллельный оси абсцисс. Процесс 2—В изохорный, при этом температура газа уменьшается. Начертим изохору, проходящую через точку 2. Конечное состояние соответствует давлению рB.
Аналогично строим переход в координатах V, Т (рис. 10.8, в). При процессе А—1 объём газа увеличивается при постоянной начальной температуре. При процессе 1—2 объём увеличивается при постоянном давлении. Изобара проходит через начало координат. Конечное состояние соответствует объёму VB. Затем процесс изохорный, при этом температура газа понижается.
Источник: «Физика – 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Основные положения МКТ. Тепловые явления – Физика, учебник для 10 класса – Класс!ная физика
Почему тепловые явления изучаются в молекулярной физике —
Основные положения молекулярно-кинетической теории. Размеры молекул —
Примеры решения задач по теме «Основные положения МКТ» —
Броуновское движение —
Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел —
Идеальный газ в МКТ. Среднее значение квадрата скорости молекул —
Основное уравнение молекулярно-кинетической теории газов —
Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» —
Температура и тепловое равновесие —
Определение температуры. Энергия теплового движения молекул —
Абсолютная температура. Температура — мера средней кинетической энергии молекул —
Измерение скоростей молекул газа —
Примеры решения задач по теме «Энергия теплового движения молекул» —
Уравнение состояния идеального газа —
Примеры решения задач по теме «Уравнение состояния идеального газа» —
Газовые законы —
Примеры решения задач по теме «Газовые законы» —
Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»
72,7% бесплатных материалов
964 руб. средняя цена курсовой работы
351 руб. средняя цена домашнего задания
119 руб. средняя цена решённой задачи
160 руб. средняя цена лабораторной работы
174 руб. средняя цена реферата
168 руб. средняя цена доклада
1610 руб. средняя цена ВКР
664 руб. средняя цена диссертации
596 руб. средняя цена НИР
357 руб. средняя цена отчёта по практике
276 руб. средняя цена ответов (шпаргалок)
201 руб. средняя цена лекций
222 руб. средняя цена семинаров
280 руб. средняя цена рабочей тетради
188 руб. средняя цена презентации
67 руб. средняя цена перевода
137 руб. средняя цена изложения
150 руб. средняя цена сочинения
308 руб. средняя цена статьи
Гарантия возврата средств
Сообщение от maks.runner
Помогите решить, желательно с подробными действиями, чтобы было понятно)) спасибо…
С одним молем идеального одноатомного газа совершают цикл, который на диаграмме PV изображается окружностью. Нижней точке окружности соответствует давление 100 кПа, верхней 200 кПа. Максимальный объем в цикле равен 16,6 л. Минимальный объем равен 8,3 л. Найти максимальную температуру.
maks.runner, хорошей новостью является то, что в заданных условиях
а далее мне эта задачка видится, чисто алгебраической и это новость, – так себе, поскольку как математик математику признаюсь, что моё счастье форуме состоит в том, что меня за мои математические труды на этом форуме ещё не бьют. 
Попробую порассуждать, а Вам решать, что верно, а что нет. В числовом виде P(V) окружностью не является, это эллипс который графически выглядит как окружность. Чтобы сохранить уравнение окружности примем по оси V масштабный коэффициент A=100/8,3. То есть координата X =AV. А по оси Y масштаб останется равным единице: Y=P
Радиус окружности равен r=50 (R занято универсальной газовой постоянной)), Yc=150, Xc=12,45 A, – то есть тоже 150. Забавное совпадение. Уравнение окружности:
распадается на два уравнения, верхней и нижней полуокружности, соответственно:
и
Вернёмся к P и V:
и
вспомнив хорошую новость умножим обе части обоих уравнений на
и получим две кривые температуры (в смысле функции)) :
и
индексы символизируют верхнюю и нижнюю часть полуокружности (не верхнее и нижнее значение температуры))
Обе являются функциями только V.
Теперь необходимо продифференцировать, приравнять к нулю и найти значения объёмов при которых наблюдается экстремум. Рискну предсказать, что один соответствует минимуму, а один максимуму T. Это выяснится подстановкой в уравнение состояния (PV=RT), хотя и на глаз будет видно: меньшему объёму соответствует большая температура. Отнеситесь критически и в бой. Удачи.
ps: признайтесь, где такие задачи задают? 
Добавлено через 9 минут
Сообщение от IGPIGP
и получим две кривые температуры (в смысле функции)) :
и
кривые таки, потому, что радиус выразил криво. Надо бы:
и
просмотрите всё внимательно, может, что-то и пригодится. 
Добавлено через 9 часов 18 минут
Вот здесь:
Сообщение от IGPIGP
…Чтобы сохранить уравнение окружности примем по оси V масштабный коэффициент A=100/8,3…
и тут:
Сообщение от IGPIGP
… Xc=12,45 A, – то есть тоже 150…
неточно. Не учёл, что объём в литрах. Перевод в М3 приведёт к тому что:
…Чтобы сохранить уравнение окружности примем по оси V масштабный коэффициент A=100000/8,3…
и
…Xc=(12,45E-3) A, – то есть тоже 150…
2
2018-04-16 
Найти максимально возможную температуру идеального газа в каждом из нижеследующих процессов:
а) $p = p_{0} – alpha V^{2}$; б) $p = p_{0} e^{ – beta V}$,
где $p_{0}, alpha$ и $beta$ — положительные постоянные, $V$ — объем одного моля газа.
Решение:
(a) $p = p_{0} – alpha V^{2} = p_{0} – alpha left ( frac{RT}{p} right )^{2}$ (так как, $V = RT/p$ для одного моля газа)
Таким образом, $T = frac{1}{R sqrt{ alpha} } p sqrt{p_{0} – p } = frac{1}{R sqrt{ alpha } } sqrt{ p_{0}p^{2} – p^{3} }$ (1)
Для $T_{max}, frac{d(p_{0}p^{2} – p^{3} ) }{dp}$ должно быть равным нулю
что дает, $p = frac{2}{3} p_{0}$ (2)
Следовательно, $T_{max} = frac{1}{R sqrt{ alpha} } frac{2}{3} p_{0} sqrt{p_{0} – frac{2}{3}p_{0} } = frac{2}{3} left ( frac{p_{0} }{R} right ) sqrt{ frac{p_{0} }{3 alpha} }$
(б) $p = p_{0} e^{ – beta V} = p_{0}e^{ – beta RT/p }$
$frac{ beta RT}{p} = ln frac{p_{0} }{p}$, $T = frac{p}{ beta R} ln frac{p_{0} }{p}$ (1)
Для $T_{max}$ условие равно $frac{dT}{dp} = 0$, что дает
$p = frac{p_{0} }{e}$
Следовательно, используя это значение $p$ в уравнении (1), получаем
$T_{max} = frac{p_{0} }{e beta R}$
