1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
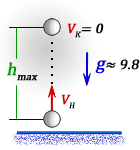
h max
– максимальная высота достигнутая телом за время t
Vк – конечная скорость тела на пике, равная нулю
Vн – начальная скорость тела
t – время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула максимальной высоты (h max):
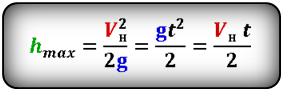
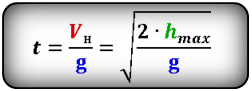
Формула времени за которое тело достигло максимальную высоту (t):
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
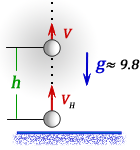
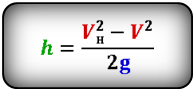
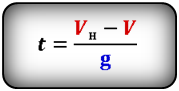
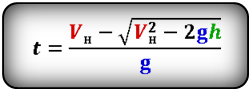
h – расстояние пройденное телом за время t
Vн – начальная скорость тела
V – скорость тела в момент времени t
t – время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула скорости тела в момент времени t (V):
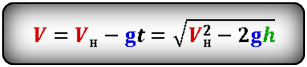
Формула начальной скорости тела (Vн):
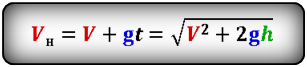
Формулы высоты тела в момент времени t (h):
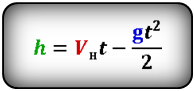
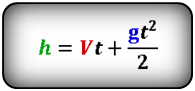
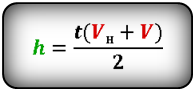
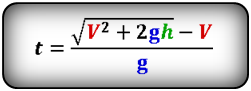
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,660 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,971 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Знаток
(301),
на голосовании
12 лет назад
Голосование за лучший ответ
МАГ
Мастер
(1104)
12 лет назад
v = V0-g*t
на макс. высоте скорость равна нулю, и значит она достигается в момент времени t=V0/g=1 c
подставь это время в формулу высоты
h = V0*t-g*t^2/2
и получим h=5 м
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t – frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 – gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 – 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
Один из вариантов решения.
За тело отсчета выберем начальное положение мяча, ось 0Y направим вверх, тогда h0 = 0 (рис. 1). При свободном падении тел можно использовать уравнение проекции скорости и уравнение движения
[ upsilon _{y} =upsilon _{0y} +g_{y} cdot t, ; ; ; y=y_{0} +upsilon _{0y} cdot t+frac{g_{y} cdot t^{2}}{2}, ]
где y0 = h0 = 0, υ0y = υ0, gy = –g (см. рис. 1). Тогда
[ upsilon _{y} =upsilon _{0} -gcdot t, ; ; ; (1) ; ; ; ; y=upsilon _{0} cdot t-frac{gcdot t^{2} }{2}. ; ; ; (2) ]
Так как высота бросания мяча равна высоте, на которую мяч упал назад, то время подъема мяча вверх t1 равно времени падения мяча вниз t2, т.е. t1 = t2. Если t0 = 2 c, то
t0 = t1 + t2 = 2⋅t1 и t1 = t0/2. (3)
Найдем значение начальной скорости υ0. Воспользуемся уравнениями (1) и (3), при этом учтем, что скорость на максимальной высоте υk = 0 (t = t1):
υy(t1) = υ0 – g⋅t1 = 0, υ0 = g⋅t1 = g⋅t0/2. (4)
Максимальную высоту подъема мяча hmax можно найти, используя уравнения (2), (3) и (4) для t = t1:
[ h_{max } =yleft(t_{1} right)=upsilon _{0} cdot t_{1} -frac{gcdot t_{1}^{2} }{2} =frac{gcdot t_{0} }{2} cdot frac{t_{0} }{2} -frac{gcdot t_{0}^{2} }{8} =frac{gcdot t_{0}^{2} }{8}, ]
hmax = 5 м.
