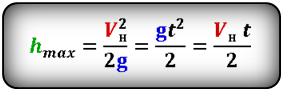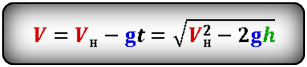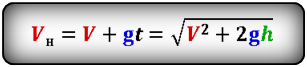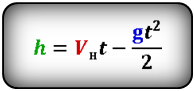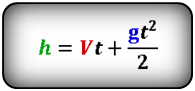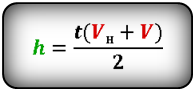1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
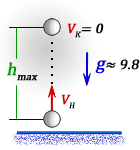
h max
– максимальная высота достигнутая телом за время t
Vк – конечная скорость тела на пике, равная нулю
Vн – начальная скорость тела
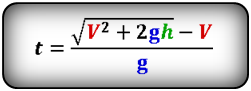
t – время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 – ускорение свободного падения
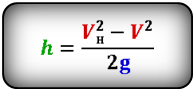
Формула максимальной высоты (h max):
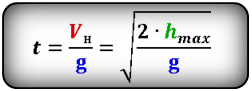
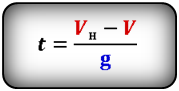
Формула времени за которое тело достигло максимальную высоту (t):
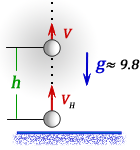
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h – расстояние пройденное телом за время t
Vн – начальная скорость тела
V – скорость тела в момент времени t
t – время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула скорости тела в момент времени t (V):
Формула начальной скорости тела (Vн):
Формулы высоты тела в момент времени t (h):
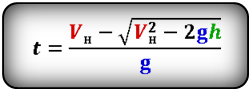
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
Шар массой m, летящий горизонтально со скоростью v0 , сталкивается с неподвижной призмой массой M, стоящей на столе, и после абсолютно
упругого удара движется вертикально вверх. Определите максимальную высоту, на
которую поднимается шар, и расстояние, на которое переместится призма, если
коэффициент трения между ней и поверхностью стола равен μ.
Решение.
Систему отсчета свяжем
с поверхностью Земли и будем считать ее инерциальной.
Начало координат выберем
в точке столкновения. Ось OX
направим горизонтально, ось OY
– вертикально вверх.
Высоту поднятия шара и
перемещение призмы можно определить, если известны их скорости v1 и v2
в конце столкновения.
Для определения этих
скоростей рассмотрим физическую систему «шар – призма». Можно выделить два
состояния этой системы: начало о конец столкновения. Будем считать, что при
столкновении взаимодействия шара с призмой и призмы с поверхностью стола
происходят мгновенно и одновременно. Фактически это означает, что мы будем
рассматривать столкновение шара с системой «призма – поверхность стола».
Отметим, что допущение об одновременности и мгновенности взаимодействия
выполняется, если жесткость материала призмы больше и сравнима с жесткостью
материала шара, а их размеры также сравнимы между собой.
Поскольку выделенная
физическая система взаимодействует с материальными объектами, не входящими в
нее, то она является незамкнутой. Если не учитывать взаимодействие с воздухом,
то по горизонтали на физическую систему внешние силы не действуют.
Поэтому проекция полного импульса системы
на это направление сохраняется, т.е. (p1)x
= (p2)x , где
p1
= mv0 , p2
= mv1 + Mv2 .
Если спроецировать
векторные величины на ось OX,
получим: mv0
= Mv2 .
По условию задачи
рассматриваемая система консервативная, поэтому при переходе из начального
состояния в конечное в ней выполняется закон сохранения механической энергии.
Таким образом система «шар
– призма» математически описывается следующей системой уравнений.
Решение этой системы
дает скорости v1 и v2 ,
где v1 – скорость шара, v2
– скорость призмы сразу после столкновения.
Для определения
максимальной высоты, на которую поднимается шар, рассмотрим физическую систему «шар
после удара – гравитационное поле Земли». Можно выделить два состояния этой
систем: начальное – непосредственно после столкновения и конечное – в момент
времени, когда шар достиг максимальной высоты. Если не учитывать взаимодействие
шара с воздухом, то рассматриваемая физическая система является замкнутой и
консервативной и может быть описана законом сохранения механической энергии.
Если нулевой уровень
потенциальной энергии системы выбрать на горизонтали, проходящей через точку
столкновения, то начальная энергия системы E1 будет равна.
В конечном состоянии E2
.
Заметим, что полученная
формула является решением задачи при условии, если m/M < 1.
Если в физическую
систему включить только «шар после удара», то получим незамкнутую физическую
систему, которая может быть описана законами кинематики и динамики или теоремой
об изменении кинетической энергии.
В первом случает (если
не учитывать взаимодействие с воздухом) физическая система может быть описана
следующими законами.
Если перейти к
скалярной форме и учесть, что в верхней точке скорость шара равна нулю, получим
максимальную высоту поднятия шара.
При использовании
энергетического подхода ∆Ek
= A , где A – работа силы тяжести.
Таким образом,
независимо от выбора физической системы и законом, описывающих ее, получается
одно и тоже выражение для максимальной высоты подъема шара, хотя физическое
обоснование в этих случаях разное. Это свидетельствует о том, что высота, на
которую поднялся шар после столкновения, найдена правильно.
Для определения
перемещения призмы рассмотрим физическую систему «призма после столкновения».
Можно выделить два состояния этой системы: начальное – непосредственно после
столкновения и конечное – в момент
остановки призмы.
Выделенная физическая
система является незамкнутой, т.к. на нее действуют: сила тяжести Mg , обусловленная взаимодействием с
гравитационным полем Земли, сила реакции N и сила трения Fтр , обусловленные взаимодействием с поверхностью стола (взаимодействие
призмы с воздухом не учитываем).
Таким образом, про кинематико-динамическом подходе система может быть описана
следующими законами.
Если перейти к
скалярной форме и учесть, что Fтр = μN
, в скорость призмы в конце движения v
= 0, получим l.
Можно использовать для
описания этой физической системы энергетический подход.
Работа силы тяжести и
силы реакции опоры равны нулю, поэтому работа внешних сил A = Aтр = Fтр cos180° = –μMgl. C учетом того, что v2 =
(mv0)/M найдем
l.
Совпадение
результатов свидетельствует о правильности решения задачи.
Ответ:  .
.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник – это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Уравнение движения математического маятника
Математический маятник – классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ – угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ – начальная фаза колебаний; ${varphi }_0$ – амплитуда колебаний; ${omega }_0$ – циклическая частота.
Колебания гармонического осциллятора – это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ – кинетическая энергия маятника; $E_p$ – потенциальная энергия маятника; $v$ – скорость движения маятника; $x$ – линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол – смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ – максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ – максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Движение тела, брошенного вертикально вверх
Тело, брошенное вертикально вверх, движется равномерно замедленно с начальной скоростью u0 и ускорением
a = -g.
Перемещение тела за время t представляет собой высоту подъема h.
Для этого движения справедливы формулы:
Если:
u0 — начальная скорость движения тела ,
u — скорость падения тела спустя время t,
g — ускорение свободного падения, 9.81 (м/с²),
h — высота на которую поднимется тело за время t,
t — время,
То, движение тела, брошенного вертикально вверх описывается следующими формулами:
Высота подъема тела за некоторое время, зная конечную скорость
[ h = frac{u_0 + u}{2} t ]
Высота подъема тела за некоторое время, зная ускорение свободного падения
[ h = u_0 t – frac{g t^2}{2} ]
Скорость тела через некоторое время, зная ускорение свободного падения
[ u = u_0 – gt ]
Скорость тела на некоторой высоте, зная ускорение свободного падения
[ u = sqrt{ u_0^2 – 2gh} ]
Максимальная высота подъема тела, зная первоначальную скорость и ускорение свободного падения
Тело, брошенное вертикально вверх, достигает максимальной высоты в тот момент, когда его скорость обращается в ноль. Поднявшись на максимальную высоту тело начинает свободное падение вниз.
[ h_{max} = frac{u_0^2}{2g} ]
Время подъема на максимальную высоту подъема тела, зная первоначальную скорость и ускорение свободного падения
[ t_{hmax} = frac{u_0}{g} ]
Примечание к статье: Движение тела, брошенного вертикально вверх
- Сопротивление воздуха в данных формулах не учитывается.
- Ускорение свободного падения имеет приведенное значение (9.81 (м/с²)) вблизи земной поверхности. Значение g на других расстояниях от поверхности Земли изменяется!
Движение тела, брошенного вертикально вверх |
стр. 409 |
|---|
Куклин Андрей
Высший разум
(189385)
1 год назад
1)Время движения становится меньше
2) В верхней точке a = g = 10 м/с^2.
3) m*Vo^2/2 – A = m*g*h, h = (m*Vo^2/2 – A)/m*g = (0,2*10^2/2 – 4)/0,2*10 = 3 м.
kafoЗнаток (480)
1 год назад
Мне кажется, у вас ошибка, ведь во втором подзадании сказано округлить до десятых, а такое не пишут спроста. Могу ошибаться, ведь я ученик, по ОГЭ обычно пишут “округлить”, если это необходимо
Куклин Андрей
Высший разум
(189385)
костя федотов, Ну, напиши 10,0. Хотя дано g = 10 м/с^2.