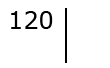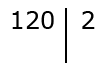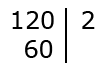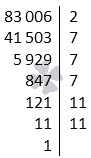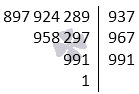Как найти максимальные множители числа - Сайт, где вы сможете решить свои вопросы

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given a positive integer ‘n'( 1 <= n <= 10¹⁵). Find the largest prime factor of a number.

Input: 6
Output: 3
Explanation
Prime factor of 6 are- 2, 3
Largest of them is '3'

Input: 15
Output: 5

The approach is simple, just factorise the given number by dividing it with the divisor of a number and keep updating the maximum prime factor. See this to understand more.

C++

#include <iostream>

#include<bits/stdc++.h>

using namespace std;

long long maxPrimeFactors(long long n)

{

long long maxPrime = -1;

while (n % 2 == 0) {

maxPrime = 2;

n >>= 1;

}

while (n % 3 == 0) {

maxPrime = 3;

n=n/3;

}

for (int i = 5; i <= sqrt(n); i += 6) {

while (n % i == 0) {

maxPrime = i;

n = n / i;

}

while (n % (i+2) == 0) {

maxPrime = i+2;

n = n / (i+2);

}

if (n > 4)

maxPrime = n;

return maxPrime;

}

int main()

{

long long n = 15;

cout << maxPrimeFactors(n) << endl;

n = 25698751364526;

cout << maxPrimeFactors(n);

}

C

#include <math.h>

#include <stdio.h>

long long maxPrimeFactors(long long n)

{

long long maxPrime = -1;

while (n % 2 == 0) {

maxPrime = 2;

n >>= 1;

}

while (n % 3 == 0) {

maxPrime = 3;

n = n / 3;

}

for (int i = 5; i <= sqrt(n); i += 6) {

while (n % i == 0) {

maxPrime = i;

n = n / i;

}

while (n % (i + 2) == 0) {

maxPrime = i + 2;

n = n / (i + 2);

}

if (n > 4)

maxPrime = n;

return maxPrime;

}

int main()

{

long long n = 15;

printf("%lldn", maxPrimeFactors(n));

n = 25698751364526;

printf("%lld", maxPrimeFactors(n));

return 0;

}

Java

import java.io.*;

import java.util.*;

class GFG {

static long maxPrimeFactors(long n)

{

long maxPrime = -1;

while (n % 2 == 0) {

maxPrime = 2;

n >>= 1;

}

while (n % 3 == 0) {

maxPrime = 3;

n = n / 3;

}

for (int i = 5; i <= Math.sqrt(n); i += 6) {

while (n % i == 0) {

maxPrime = i;

n = n / i;

}

while (n % (i + 2) == 0) {

maxPrime = i + 2;

n = n / (i + 2);

}

if (n > 4)

maxPrime = n;

return maxPrime;

}

public static void main(String[] args)

{

Long n = 15l;

System.out.println(maxPrimeFactors(n));

n = 25698751364526l;

System.out.println(maxPrimeFactors(n));

}

Python3

import math

def maxPrimeFactors (n):

maxPrime = -1

while n % 2 == 0:

maxPrime = 2

n >>= 1

while n % 3 == 0:

maxPrime = 3

n=n/3

for i in range(5, int(math.sqrt(n)) + 1, 6):

while n % i == 0:

maxPrime = i

n = n / i

while n % (i+2) == 0:

maxPrime = i+2

n = n / (i+2)

if n > 4:

maxPrime = n

return int(maxPrime)

n = 15

print(maxPrimeFactors(n))

n = 25698751364526

print(maxPrimeFactors(n))

C#

using System;

class GFG {

static long maxPrimeFactors(long n)

{

long maxPrime = -1;

while (n % 2 == 0) {

maxPrime = 2;

n >>= 1;

}

while (n % 3 == 0) {

maxPrime = 3;

n = n / 3;

}

for (int i = 5; i <= Math.Sqrt(n); i += 6) {

while (n % i == 0) {

maxPrime = i;

n = n / i;

}

while (n % (i + 2) == 0) {

maxPrime = i + 2;

n = n / (i + 2);

}

if (n > 4)

maxPrime = n;

return maxPrime;

}

public static void Main()

{

long n = 15L;

Console.WriteLine(maxPrimeFactors(n));

n = 25698751364526L;

Console.WriteLine(maxPrimeFactors(n));

}

PHP

<?php

function maxPrimeFactors($n)

{

$maxPrime = -1;

while ($n % 2 == 0)

{

$maxPrime = 2;

$n >>= 1;

}

while ($n % 3 == 0) {

$maxPrime = 3;

$n=$n/3;

}

for ($i = 3; $i <= sqrt($n); $i += 2)

{

while ($n % $i == 0)

{

$maxPrime = $i;

$n = $n / $i;

}

while ($n % ($i+2) == 0) {

$maxPrime = $i+2;

$n = $n / ($i+2);

}

if ($n > 4)

$maxPrime = $n;

return $maxPrime;

}

$n = 15;

echo maxPrimeFactors($n), "n";

$n = 25698751364526;

echo maxPrimeFactors($n), "n";

?>

Javascript

<script>

function maxPrimeFactor(n) {

let maxPrime = -1;

while(n % 2 == 0) {

n = n / 2;

maxPrime = 2;

}

while(n % 3 == 0) {

n = n / 3;

maxPrime = 3;

}

for (let i = 5; i <= Math.sqrt(n); i += 6) {

while (n % i == 0) {

maxPrime = i;

n = n / i;

}

while (n % (i + 2) == 0) {

maxPrime = i + 2;

n = n / (i + 2);

}

return n > 4 ? n : maxPrime;

}

document.write(maxPrimeFactor(15));

document.write(maxPrimeFactor(25698751364526));

</script>

Time complexity:
Auxiliary space:

Method 2:

Follow the steps below for the implementation:

Initialize variables largest_prime to -1, i to 2, and n to the input integer.
Start a while loop that continues as long as i * i <= n. This loop will iterate through all possible factors of n.
In the while loop, start another while loop that continues as long as n % i == 0. This inner loop will divide n by i until n is no longer divisible by i.
In the inner loop, set largest_prime to i, and update n by dividing it by i.
At the end of the inner loop, increment i by 1.
After the outer loop, if n > 1, set largest_prime to n. This is because n could be a prime number larger than any of its factors.
Return largest_prime.

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>

using namespace std;

int maxPrimeFactors(long long n)

{

int largest_prime = -1;

int i = 2;

while (i * i <= n) {

while (n % i == 0) {

largest_prime = i;

n = n / i;

}

i = i + 1;

}

if (n > 1) {

largest_prime = n;

}

return largest_prime;

}

int main()

{

long long n = 15;

cout << maxPrimeFactors(n) << endl;

n = 25698751364526;

cout << maxPrimeFactors(n) << endl;

return 0;

}

Python3

def gcd(a, b):

while(a > 0 and b > 0):

if (a > b):

a = a % b

else:

b = b % a

if (a == 0):

return b

return a

def pollard_rho(n):

if n == 1:

return []

if n % 2 == 0:

return [2] + pollard_rho(n // 2)

x = 2

y = 2

d = 1

while d == 1:

x = (x*x + 1) % n

y = (y*y + 1) % n

d = gcd(abs(x-y), n)

if d == n:

return pollard_rho(n)

else:

return pollard_rho(d) + pollard_rho(n // d)

n = 15

print(pollard_rho(n))

Time complexity: O(sqrt(n)).
Auxiliary space: O(1)

Method 3: (Trial Division)

Trial Division is a simple algorithm for finding the prime factors of a given number. It works by dividing the number by all possible prime factors starting from 2, and adding each prime factor to a list of factors until the number becomes 1.

Follow the steps below for the implementation:

Initialize an variable to hold the largest prime factor.
Divide the given number by with all of its prime factors and compare them with factor variable and also decrement the number.
If remaining number is greater than one, then compare it again with factor variable, otherwise skip it.
Finally, return the factor which contains .

Below is the implementation of the above approach:

Python3

def max_prime_factor(n):

factor = 0

d = 2

while d*d <= n:

if (n % d) == 0:

factor = max(factor, d)

n //= d

d += 1

if n > 1:

factor = max(factor, n)

return factor

n = 15

print(max_prime_factor(n))

n = 25698751364526

print(max_prime_factor(n))

Time complexity: O(log(sqrt(n)) = O(log(n)), because in each iteration, n becomes n//d.
Auxiliary space: O(1), as it uses a constant amount of memory for storing the variables factor and d.

Last Updated :
09 May, 2023

Like Article

Save Article

Источник

Разложение натурального числа на простые множители

Перед тем как приступить к рассмотрению принципа разложения чисел, сформулируем определение простого множителя числа.

Определения

Простое число — это целое число больше 1, единственные делители которого равны 1 и
самому себе.

Фактор значения

— это целое число, которое можно равномерно разделить на другое число.

Первые несколько простых чисел — это 2, 3, 5, 7, 11, 13, 17, 19, 23 и 29. Числа, содержащие более двух множителей, называются составными числами. Число 1 не простое и не составное.

Простые числа могут использоваться по ряду причин. Например, некоторые типы криптографии будут использовать простые числа. Для каждого простого числа, например: «p», существует простое число, которое больше p, называемое p ‘. Это математическое доказательство, которое было продемонстрировано в древние времена греческим математиком Евклидом, подтверждает идею о том, что не существует «наибольшего» простого числа. По мере того, как набор натуральных чисел N = {1, 2, 3, …} продолжается, простые числа, как правило, становятся менее частыми, и их значение труднее найти.

Определения

Простой множитель — это числовое значение, которое представлено в виде простого числа.

Если, рассмотреть составное число, то можно сделать вывод, что его можно преобразовать и представить в виде простых чисел.

Рассмотрим пример разложения чисел:

[4=2 cdot 2]

[6=2 cdot 3]

[8=2 cdot 2 cdot 2]

При разложении числа могут повторяться, как в третьем примере. Чтобы исключить повтор, их лучше всего скомпоновать и представить в виде степени.

Пример: 24 = 2 · 2 · 2 · 3 = 23 · 3.

Рассмотрим другой пример разложения числа на множители. Возьмем число 609840 и распишем его на составные множители.

Запишем следующее выражение: [609840=2 cdot 2 cdot 2 cdot 2 cdot 3 cdot 3 cdot 5 cdot 7 cdot 11 cdot 11 ], преобразуем его в канонический вид и получим пример: [609840=2^{4} cdot 3^{2} cdot 5 cdot 7 cdot 11^{2}].

Применяя каноническое уравнение, можно определить значение всех делителей и их количество.

Основные свойства простых чисел:

Существует несколько свойств простых чисел. Большая часть из них считается доказанной, остальную часть, так и оставили недоказанной.

Среди доказанных свойств, можно выделить следующие:

Множество простых числовых значений, является бесконечным. Иными словами, простые числа не имеют наибольшего значения.
Если значение p – минимальный простой делитель числа n. Из этого следует доказательство, p2 ≤ n.

В случае, если p — делитель составного числа n, тогда должен быть другой делитель q, для числового значения n.

Значение n, должно быть представлено, как произведение числовых множителей p и q.

Делителей меньше значения p не должно быть, так как данный множитель является наименьшим простым делителем. Из данного условия составим неравенство:

[q geq p . Rightarrow p cdot p leq p cdot q, text { т. e. } p 2 leq p q text { или } p 2 leq n .]

Данное свойство, принято использовать для проверки на простой множитель.

Если есть простой делитель любого составного числа, и квадрат числа является меньшим или равен ему. В этом случае не требуется определять другие делители. Для того чтобы доказать, что проверяемое значение является простым.

Достаточно будет провести проверку на делимость значения n на простые делители p [Rightarrow]p2 ≤ n.

Из данного значения n нужно извлечь корень и обязательно округлить его до целого числа. Затем нужно перебрать все делители до числа, полученного при вычислении. Если не один из них не подходит, значит простых делителей не существует, следовательно, проверяемое число — простое.

Пример:

Проверим число 37. Вычислим квадратный корень этого числа и округлим до целого значения. [sqrt{37} approx 6]

Далее нужно проверить значения на признак делимости, а именно на 2,3,4,5,6. После проверки, делаем вывод, что ни одно из значений 37 не делится. Из этого следует, что данное значение является простым.

Натуральные значения, выражаются в виде суммы из двадцати слагаемых.

«Теорема Ферма» Когда число p является простым и значение n на него нельзя разделить[Rightarrow]np — 1 — 1 всегда делится на p.

Пример:

Число 34 нельзя разделить на 3. Однако 343-1 — 1 = 342 — 1 = 1156 — 1 = 1155[Rightarrow]делится на 3.

Недоказанные свойства простых чисел:

Любое из четного значения, можно представить в виде суммы двух и более простых чисел. Например: 18=10+8, 65=11+54, 108=70+38.
Каждое максимальное значение нечетного числа, возможно расписать в виде суммы трех и более простых чисел.
Максимальные значения простых чисел, можно выразить как сумма четырех нечетных значений.
Четное значение можно расписать как разность двух и более простых значений.

Составим алгоритм, для разложения на простые множители чисел:

Последовательность действий при разложении числа на простые множители:

Чтобы разложить число на простые множители нужно знать несколько основных правил и действий.

Число, которое нужно расписать на множители, нужно проверить по таблице простых чисел. А именно, определить не является ли оно простым.
В случае, если число не является простым, пользуемся таблицей и подбираем самое наименьшее значение. Оно должно равняться числу, на которое можно поделить значение. Деление должно быть без остатка.
Далее проверяем, по этой же таблице, простых чисел, полученное значение. Оно не должно быть простым.
Если условие соблюдается, то поочередно подбираем наименьшее значение из таблицы. При делении на данное значение, вычисленное частное должно делиться без дробного остатка.
Повторяем последние два пункта до тех пор, пока окончательный ответ, не будет равняться единичному значению.

Решим несколько примеров:

Пример №1:

Согласно задания нужно разложить на простые множители число 102.

Решение примера начнем с поиска минимального делителя для значения 102. Для этого нужно воспользоваться таблицей чисел простых значений. Затем последовательно определяем самое малое значение из таблицы, при делении на которое, ответ получится без дробного остатка.

Подбираем значение 2 и проводим деление заданного значения 102 на него и получаем выражение:

102:2 = 51.

Если число 102 разделить на 2, то получим ответ равный без остатка. Из этого следует, что два, является первым определенным простым множителем.

Следующим действием, будем проводить проверку частного простого числа. Значение 51, является составным числом. Берем наименьший делитель, равный двум. Но число 51, без остатка на два не делится. Поэтому переходим к следующему пункту алгоритма.

Берем следующее значение по таблице простых чисел — это 3. Проводим вычисление и получаем следующее выражение:

51:3 = 17

После вычисления примера получаем целое значение, без остатка. И это означает, что число три, является вторым множителем. Поэтому, можно сделать вывод, что число 51 записывается в виде произведения из трех множителей.

102 = 2 · 51 = 2 · 3 · 17

Проводим проверку значения, не является ли оно простым числом. Значение 17 — простое. Поэтому минимальным числом, на которое оно будет делится будет именно само числовое значение 17.

17:17 = 1

Так как полученный ответ равен единичному значению, то разложение на множители считается завершенным.

Запишем окончательное решение: 102 = 2 · 3 · 17.

В математике существует еще один вариант разложения на множители. Весь алгоритм решения записывается в виде столбика. Для этого применяются две колонки, которые разделены прямой линией.

Этот способ имеет следующий алгоритм решения:

сверху вниз, с левой стороны от вертикальной черты записывается заданное число;

затем записываем полученные частные значения;

по правую сторону от линии, нужно записать минимальные значения простых делителей.

Пример №2:

Записываем заданное число 120 и проводим по правую сторону вертикальную линию.

С правой стороны записывается простой делитель, наименьшего значения:

Проводим вычисление: делим число 120 на делитель 2 и получаем частное равное 60. Вычисленное значение нужно записать под числом 120 с левой стороны от вертикальной прямой.

Определяем делитель наименьшего значения. Далее записываем его с правой стороны от черты под предыдущим делителем и вычисляем значение.

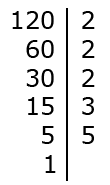
Вычисления нужно производит до тех пор, пока ответ не будет равен единице.

Разложение будет окончено, только тогда, когда окончательный ответ получится равным единичному значению.

Окончательный ответ записывается в строку:

120 = 23 · 3 · 5.

Примеры разложения чисел на простые множители

При решении задач данного типа, всегда нужно помнить и придерживаться основного алгоритма решения.

Пример №1:

Число 78 разложить на простые множители.

Для начала пересматриваем все простые числа, входящие в состав числа 78.

Берем число 2 и проводим вычисление: [78 div 2=39].

Так как ответ при вычислении получается без остатка, то это значит, что значение 2 будет первым простым делителем. Дадим ему обозначение [p_{1}].

Запишем выражение следующего вида: [a_{1}=a div p_{1}=78 div 2=39]

Из этого следует следующее равенство [a=p_{1} cdot a_{1}]. Подставим значения в уравнение: [78=2 cdot 39].

Находим простой делитель [p_{2}] числа [a_{1}], которое равняется 39.

Перебираем все простые числа: [39div2=19]. Деление получается с остатком, поэтому число два, не будет являться простым делителем. Далее берем число три: [39div3=13].

Следовательно [p_{2}] будет являться наименьшим простым делителем для числа 39.

Запишем равенство: [a=p_{1} cdot p_{2} cdot a_{2}=2 cdot 3 cdot 13=78].Получаем следующее значение [a_{2}=13], оно естественно не равняется единице. Поэтому нужно проводить расчет далее, согласно алгоритму.

Применяем снова перебор чисел. Он необходим для, того чтобы найти наименьший делитель числа 13. Берем значение три и подставляем в пример: [13div3=4] (остаток равен 1). Из решения видно,что 13 нельзя разделить на назначения 5,7,11, так как [13div5=2] (остаток 3), [13div7=1]

(остаток равный 6) и [13 div 11=1] (остаток 2). Проведя все решения, можно сделать вывод, что число 13 равняется простым.

Продолжим решение и запишем следующую формулу:

[a_{3}=a_{2} div p_{3}]

[13 div 13=1 Rightarrow a_{3}=1]

Так как ответ равен единице, значит решение окончено. И множители будут записаны в следующем выражении: [78=2 cdot 3 cdot 13]

Нет времени решать самому?

Наши эксперты помогут!

Пример №2:

Для решения возьмем число 86006 и разлом его множители. Разложим на простые множители значение [p_{1}=2]

[a_{1}=a div p_{1}=83006 div 2=41503]

Для проверки берем значения 2,3,5 и предполагаем, что они не простые числа.

[a_{1}=41503 Rightarrow 7 ] простой делитель, так как [ 41503div 7=5929. ]

Произведя расчеты получаем следующие действия: [p_{2}=7 . a_{2}=a_{1} div p_{2}=41503 div 7=5929]

Значение 83006 можно разложить на следующие множители [2 cdot 7 cdot 5929]

Определяем простой делитель наименьшего значения для [a_{3}=847 Rightarrow 7].

[a_{4}=a_{3} div p_{4}=847 div 7=121], из этого следует, что [83006=2 cdot 7 cdot 7 cdot 7 cdot 121]

Числовое значение 11 будем применять, для определения делителя [a_{4}=121 Rightarrow p_{5}=11].

Получаем следующее выражение: [a_{5}=11 text { значение } p_{6}=11] и будет являться наименьшим простым делителем.

Следовательно: [a_{6}=a_{5} p_{6}=11 div 11=1 Rightarrow a_{6}=1]

Окончательный ответ в решении равен единице. Это означает окончание расчета.

И множители числа будут записаны в следующем выражении:

[83006=2 cdot 7 cdot 7 cdot 7 cdot 11 cdot 11]

Преобразуем уравнение, так как имеются одинаковые множители, в каноническое.

[83006=2 cdot 7^{2} cdot 11^{2}]

Пример №3:

Нужно разложить на составные множители число 897 924 289.

Решение начинаем с разбора простых множителей. Свой расчет начинаем со значения 2. Окончание перебора множителей будет число 937.

Отсюда следует, что: [p_{1}=937 a_{1}=a div p_{1}=897924289 div 937=958297] и [ 897924289=937 cdot 958297 .]

Далее перебираем наименьшие простые числа. Для начала берем число 937. Так как 967 является простым делителем, его можно считать простым числом.

Значение 991 не имеет не одного простого делителя, поэтому, оно будет также являться простым числом.

Запишем подкоренное выражение [sqrt{991}] и определим его примерное значение. [sqrt{991}<40^{2}].

Из решения, можно сделать вывод, что [p_{3}=991 text { и } a_{3}=a_{2} div p_{3}=991 div 991=1].

Расчет согласно алгоритма завершен, поскольку ответ равен один.

Записываем окончательный ответ к задаче: [897924289=937 cdot 967 cdot 991]

Применение при решении задач, признаков делимости для разложения на множители

При разложении чисел на множители, всегда необходимо использовать алгоритмы решения. Однако имеются случаи, когда разложить нужно число небольшого значения. Для этого можно применять обычные таблицы умножения или делимости.

Разберем несколько примеров:

Нужно разложить на простые множители число со значением равным 10. Применяем таблицу умножения и записываем, что [2 cdot 5=10]. Числа 2 и 5 являются простыми значениями. Поэтому их можно назвать и простыми множителями для 10.

Рассмотрим еще одно значение равное 48. Снова воспользуемся таблицей перемножения данных. Запишем выражение: [48=6 cdot 8].

Данные значения, не является простыми множителя, потому что их можно разложить: [6=2cdot3 ] и [8=2cdot4]. Правильное разложение будет выглядеть следующим образом: [48=6 cdot 8=2 cdot 3 cdot 2 cdot 4 text {. }]

Преобразуем уравнение и запишем его канонический вид: [48=2^{4} cdot 3]

Для разложения значения 3400, нужно воспользоваться признаком делимости числа. Для данного значения это 10 и 100. Распишем число: [3400=34 cdot 100], отсюда можно выполнить следующее действие 100 разделить на 10 и записать, что [100=10 cdot 10 Rightarrow 3400=34 cdot 10 cdot 10 .] Применяя основные признаки делимости значений, получаем выражение: [3400=34 cdot 10 cdot 10=2 cdot 17 cdot 2 cdot 5 cdot 2 cdot 5 .]

Все числа относятся к простым множителям. Запишем выражение в виде канонического разложения.

[3400=2^{5} cdot 5^{2} cdot 17]

Источник

Схематическая иллюстрация факторизации числа 525.

Факториза́цией натурального числа называется его разложение в произведение простых множителей. Существование и единственность (с точностью до порядка следования множителей) такого разложения следует из основной теоремы арифметики.

В отличие от задачи распознавания простоты числа, факторизация предположительно является вычислительно сложной задачей. В настоящее время неизвестно, существует ли эффективный не квантовый алгоритм факторизации целых чисел. Однако доказательства того, что не существует решения этой задачи за полиномиальное время, также нет.

Предположение о том, что для больших чисел задача факторизации является вычислительно сложной, лежит в основе широко используемых алгоритмов (например, RSA). Многие области математики и информатики находят применение в решении этой задачи. Среди них: эллиптические кривые, алгебраическая теория чисел и квантовые вычисления.

История[править | править код]

Задача поиска эффективных способов разложения целых чисел на множители интересовала математиков с давних времён, особенно специалистов в области теории чисел. Существуют предположения о том, что Ферма был одним из первых, кто предложил метод разложения, заключающийся в том, чтобы представить число в виде разности квадратов $n=x^{2}-y^{2}$ , а затем, вычисляя , попытаться найти нетривиальный делитель . Данный способ позволяет находить два мало различающихся по величине делителя числа быстрее, чем простой перебор делителей^[1].

Создание алгоритма RSA стимулировало бурные исследования в области факторизации целых чисел.

Далее Лежандр обнаружил, что при таком подходе достаточно получить сравнение $x^{2}equiv y^{2}mod n$ , и использовал для этого цепные дроби. Также Эйлером и Гауссом были предложены некоторые способы нахождения чисел, связанных этим сравнением^[1].

Одним из ключевых моментов в развитии факторизации целых чисел было создание алгоритма RSA, что возобновило интерес учёных в данном направлении, так как имело практическое применение в области шифрования. Этот алгоритм был предложен в 1977 году тремя учёными Рональдом Ривестом, Ади Шамиром и Леонардом Адлеманом из Массачусетского технологического института и назван по первым буквам фамилий авторов методом RSA. Он основан на идее криптографии с открытым ключом и для взлома системы необходимо выполнить разложение числа на простые сомножители. На момент публикации алгоритма RSA были известны методы, которые позволяли факторизовать числа, состоящие не более чем из 25—30 цифр, а наиболее известным и применяемым все ещё оставался метод Ферма. Метод RSA позволяет факторизовать числа^{[уточнить]} из 100 и более десятичных знаков. Создатели, в свою очередь, пообещали за факторизацию числа из 129 десятичных знаков символические сто долларов США^[2].

На популярность задачи факторизации также повлияла публикация в 1977 году в журнале Scientific American Мартина Гарднера «Новый алгоритм шифрования, для взлома которого потребуются миллионы лет».^[3] Столь громкое название было воспринято в качестве вызова всему математическому сообществу. В результате этой гонки было предложено несколько новых и нестандартных идей факторизации^[2].

Эпопея с разложением 129-значного числа завершилась в 1994 году, когда коллектив под руководством А. Ленстры, используя 1600 компьютеров, подготовил за 220 дней систему линейных уравнений, содержавшую более полумиллиона неизвестных. Решение этой системы суперкомпьютером заняло два дня. Несмотря на то, что в то время уже были известны методы решета числового поля, данный результат был получен с помощью алгоритма квадратичного решета^[2].

Алгоритмы факторизации[править | править код]

Как правило, на вход таких алгоритмов подаётся число , которое необходимо факторизовать, состоящее из $N=[log _{2}n]+1$ символов (если представлено в двоичном виде)^[4]. При этом алгоритм ищет первый простой делитель, после чего, при необходимости, можно запустить алгоритм заново для дальнейшей факторизации. Также, прежде чем начинать факторизацию большого числа, следует убедиться в том, что оно не простое. Для этого достаточно пройти тест числа на простоту. Эта задача детерминированно разрешима за полиномиальное время^[5].

В зависимости от сложности алгоритмы факторизации можно разбить на две группы. Первая группа — экспоненциальные алгоритмы, сложность которых экспоненциально зависит от длины входящих параметров (то есть от длины самого числа в бинарном представлении). Вторая группа — субэкспоненциальные алгоритмы.

Вопрос о существовании алгоритма факторизации с полиномиальной сложностью на классическом компьютере является одной из важных открытых проблем современной теории чисел. В то же время факторизация с полиномиальной сложностью возможна на квантовом компьютере с помощью алгоритма Шора (класс BQP)^[6].

Экспоненциальные алгоритмы[править | править код]

Перебор возможных делителей[править | править код]

Сложность $O({sqrt {n}}log ^{2}n)$ или .

Один из самых простых и очевидных алгоритмов факторизации, заключающийся в том, чтобы последовательно делить факторизуемое число на натуральные числа от до . Формально достаточно делить только на простые числа в этом интервале, однако, для этого необходимо знать их множество. На практике составляется таблица простых чисел и производится проверка небольших чисел (например, до $2^{16}$ ). Для очень больших чисел алгоритм не используется в силу низкой скорости работы^[7].

Метод факторизации Ферма[править | править код]

Сложность O(n) или .

Идея алгоритма заключается в поиске таких чисел и , что факторизуемое число n представимо в виде: $n=A^{2}-B^{2}=(A-B)(A+B)$ . Как и метод пробного деления, обычно не применяется на практике для факторизации больших чисел, так как имеет экспоненциальную сложность. Метод реализуем без операции деления, а только лишь с операциями сложения и вычитания^[9]. Если n=pq , при условии того, что и — простые числа, не сильно различающиеся по величине, то метод Ферма факторизует n достаточно быстро^[10].

Пример модификации алгоритма^[11]

ρ-алгоритм Полларда[править | править код]

Сложность $O(n^{{1/4}})$ .

Алгоритм Полларда является вероятностным алгоритмом, позволяющим находить делитель составного числа , работающим со сложностью, зависящей лишь от величины делителя, но не величины факторизуемого числа . Это обуславливает удобство применимости данного алгоритма в тех случаях, когда другие алгоритмы, сложность которых зависит от , становятся неэффективны^[12]. Примечателен также тем, что существует вариант реализации такого алгоритма, при котором достаточно в памяти хранить всего 3 целых числа^[13].

Алгоритм Ленстры[править | править код]

Сложность $O(n^{{1/3}}log ^{2}n)$ .

Несмотря на относительно неплохую эффективность среди экспоненциальных алгоритмов, в алгоритме Ленстры есть необходимость неоднократно вычислять квадратный корень в одном из шагов алгоритма, что является более трудоёмким, чем сложение или вычитание^[15].

Пример модификации алгоритма^[16]

Пусть r,s,n — натуральные числа, удовлетворяющие условиям $1leq r<s<n;;n^{{1/3}}<s;;gcd(r,s)=1$

Шаг 1. С помощью обобщённого алгоритма Евклида найти $r^{*}in mathbb{N} ,rr^{*}equiv 1mod s$ . Найти такое, что $r'equiv r^{*}nmod s,0leq r'<s$ .

Шаг 2. Для очередного значения найти числа $a_{i},b_{i},c_{i}$ по следующим правилам:

$a_{0}=s,;b_{0}=0,;c_{0}=0$
$a_{1}=rr'mod s,0<a_{1}leq s,;b_{1}=1,;c_{1}equiv {frac {n-rr'}{s}}r^{*}(mod s)$

при igeq 2 :

$a_{i}=a_{{i-2}}-q_{i}a_{{i-1}},;;b_{i}=b_{{i-2}}-q_{i}b_{{i-1}},;;c_{i}=c_{{i-2}}-q_{i}c_{{i-1}}(mod s)$

$q_{i}$ — частное от деления $a_{{i-2}}$ на $a_{i-1}$ , за исключением случая, когда нечётно и остаток от деления равен нулю.

Шаг 3. Для очередного выбора $a_{i},b_{i},c_{i}$ найти все целые числа , удовлетворяющие условиям

$c=c_{i}mod s$ ,

если четное,

$2a_{i}b_{i}leq cleq {frac {n}{s^{2}}}+a_{i}b_{i},;;$ если нечетное.

Шаг 4. Для каждого c из шага 3 решить в целых числах систему уравнений

$left{{begin{array}{rcl}xa_{i}+yb_{i};;;;;;&=&c\(xs+r)(ys+r')&=&n\end{array}}right.$

Если и окажутся неотрицательными целыми числами, то добавить xs+r

Шаг 5. Если $a_{i}=0$ , то алгоритм заканчивает работу. Иначе, возвращаемся на шаг 2 к следующему значению .

Алгоритм Полларда — Штрассена[править | править код]

Сложность $O(n^{{1/4}}log ^{4}n)$ .

Данный алгоритм имеет оценку сложности схожую с методом квадратичных форм Шенкса (что является наилучшей среди детерминированных алгоритмов факторизации), однако требует выделение ${displaystyle O(n^{1/4}log n)}$ памяти. Он может использоваться непосредственно для факторизации не очень больших целых чисел, а также в качестве вспомогательного алгоритма в субэкспоненциальном методе Диксона^[17] и для ускорения вычислений второго этапа метода факторизации с помощью эллиптических кривых.^[18]

Краткое описание алгоритма^[15]

Метод квадратичных форм Шенкса[править | править код]

Гарантированная сложность ${displaystyle O(n^{1/4+varepsilon })}$ и при верности гипотезы Римана ${displaystyle O(n^{1/5+varepsilon })}$ .

В отличие от алгоритма Полларда – Штрассена не требует выделения больших объёмов памяти, к тому же имеет достаточно простые расчётные формулы^[19].

P-1 алгоритм Полларда[править | править код]

Сложность $O(n^{{1/2}}log ^{c}n)$ ^[20].

Несмотря на экспоненциальную оценку сложности, алгоритм во всех случаях быстро находит небольшие простые делители , потому что они являются степенно-гладкими для небольшой границы гладкости . В практических задачах данный алгоритм обычно используется до применения субэкспоненциальных алгоритмов факторизации, чтобы отделить небольшие простые делители числа ^[20].

Оценка сложности по стадиям^[21]

Метод Лемана[править | править код]

Сложность $O(n^{{1/3}})$ .

В настоящее время алгоритм представляет скорее исторический, чем практический интерес, так как этот алгоритм был первым детерминированным алгоритмом со сложностью выполнения быстрее, чем .

Пример модификации алгоритма^[24]

Субэкспоненциальные алгоритмы[править | править код]

Для обозначения сложности принята L-нотация^[4]:

${displaystyle L_{n}(alpha ,;c):=O(exp((c+o(1))(log n)^{alpha }(log log n)^{1-alpha })),}$

где — число подлежащее факторизации, и — некоторые константы.

Алгоритм Диксона[править | править код]

Сложность $L_{n}(1/2,;2{sqrt {2}})$ .

Факторизация методом непрерывных дробей[править | править код]

Сложность $L_{n}(1/2,;{sqrt {2}})$ ^[26].

Метод квадратичного решета[править | править код]

Сложность $L_{n}(1/2,;1)$ ^[26].

Данный метод с использованием нескольких многочленов эффективен и достаточно легко реализуем на компьютере. Есть основания полагать, что он является наилучшим из известных алгоритмов факторизации для $n<10^{{110}}$ (не считая метод факторизации с помощью эллиптических кривых, который в некоторых случаях может работать быстрее. Для чисел $n>10^{{110}}$ алгоритмы решета числового поля сработают быстрее, чем метод квадратичного решета^[27].

Факторизация Ленстры с помощью эллиптических кривых[править | править код]

Сложность $L_p(1/2,;sqrt{2})$ , где — наименьшее простое, которое делит ^[28].

Параметры a,x,y выбираются случайно. Значения w,v следует выбирать эмпирически, рассмотрев некоторую серию возрастающих значений^[28]. На практике при заданных n,v,w алгоритм заключается в том, чтобы выполнить алгоритм с одной кривой. Это повторяется до тех пор, пока не разложится на множители или пока время, отведённое для алгоритма, не закончится.

Существуют модификации алгоритма, позволяющие работать с несколькими кривыми одновременно^[28].

Описание алгоритма^[28]

На вход алгоритма поступает число , которое необходимо факторизовать, параметры , зависящие от , кроме того, задаются такие, что $P=(x:y:1)in {mathbb {V}}_{n}$ и для $bequiv y^{2}-x^{3}-axmod n$ выполнено условие $6(4a^{3}+27b^{2})in (mathbb{Z } /nmathbb{Z } )^{*}$ . Алгоритм находит натуральный делитель числа n,1<d<n .

Для каждого , полагается

$e(r)=max{m|min Z_{{geq 0}},r^{m}leq v+2{sqrt {v}}+1}$

А также

$k=prod limits _{{2leq rleq w}}r^{{e(r)}}$ , — простые.

Пусть $P=(x:y:1in {mathbb {V}}_{n})$ . Тогда лежит на эллиптической кривой $E_{{a,b}}$ над , определённой уравнением $Y^{2}=X^{3}+aX+b$ . Необходимо вычислить точку по правилам арифметики над эллиптическими кривыми. Если в ходе вычисления найден делитель числа , то разложилось на множители. Если найден , а делитель не найден, то алгоритм завершает работу и выдаёт сообщение о неудачной попытке факторизации.

Решето числового поля[править | править код]

В настоящее время самыми эффективными алгоритмами факторизации являются вариации решета числового поля^[29]:

Применение в криптографии[править | править код]

Предполагаемая большая вычислительная сложность задачи факторизации лежит в основе криптостойкости некоторых алгоритмов шифрования с открытым ключом, таких как RSA. Более того, если известен хотя бы один из параметров ключей RSA, то система взламывается однозначно, кроме того, существует множество алгоритмов восстановления всех ключей в системе, обладая какими-то данными^[31].

Текущее состояние[править | править код]

В марте 1994 года с помощью двойной вариации множественного полиномиального QS командой математиков под руководством Ленстры было разложено на множители 129-разрядное (428-битовое) число. Вычисления выполнялись добровольцами в Интернете — в течение восьми месяцев трудились 600 человек и 1600 компьютеров. Компьютеры соединялись по электронной почте, передавая свои результаты в центральное хранилище, где выполнялся окончательный анализ. В этих вычислениях использовались QS и теория пятилетней давности, NFS мог бы ускорить выполнение расчётов. Группа учёных сделала вывод о том, что широко используемые 512-битовые модули RSA могут быть вскрыты организацией, готовой потратить несколько миллионов долларов и подождать несколько месяцев^[32].

С целью развития искусства разложения на множители RSA Data Security, Inc. в марте 1991 года объявило о программе RSA Factoring Challenge (состязание RSA по разложению на множители). Состязание состоит в разложении на множители ряда трудных чисел, каждое из которых является произведением двух простых чисел примерно одинакового размера. Каждое простое число было выбрано конгруэнтным 2 по модулю 3. Всего было предложено 42 числа, по одному в диапазоне от 100 до 500 разрядов с шагом в 10 разрядов (плюс одно дополнительное, 129-разрядное число. Подробнее: RSA Factoring Challenge^[en]^[32].

Примечания[править | править код]

↑ ¹ ² Ященко, 1999, с. 107.
↑ ¹ ² ³ Ишмухаметов, 2011, с. 7—8.
↑ Gardner M. A New Kind of Cipher that Would Take Millions of Years to Break (англ.) // Scientific American — New York City: NPG, 1977. — Vol. 237, 237, Iss. 2, 2. — P. 120—124, 120—125. — 5 p. — ISSN 0036-8733; 1946-7087 — doi:10.1038/SCIENTIFICAMERICAN0877-120
↑ ¹ ² Василенко, 2003, с. 9.
↑ Василенко, 2003, с. 48.
↑ Ишмухаметов, 2011, с. 52.
↑ Нестеренко, 2012, с. 142—143.
↑ Кнут, 2007, с. 424.
↑ Ишмухаметов, 2011, с. 52—54.
↑ Василенко, 2003, с. 57.
↑ Кнут, 2007, с. 431.
↑ Ишмухаметов, 2011, с. 64.
↑ Ишмухаметов, 2011, с. 63.
↑ Ишмухаметов, 2011, с. 62.
↑ ¹ ² Василенко, 2003, с. 73.
↑ Василенко, 2003, с. 69.
↑ Василенко, 2003, с. 73—74.
↑ 20 Years of ECM.
↑ JASON E. GOWER AND SAMUEL S. WAGSTAFF, JR. SQUARE FORM FACTORIZATION // MATHEMATICS OF COMPUTATION. Архивировано 24 августа 2017 года.
↑ ¹ ² Василенко, 2003, с. 62.
↑ Ишмухаметов, 2011, с. 57.
↑ Ишмухаметов, 2011, с. 55.
↑ Ишмухаметов, 2011, с. 56.
↑ Нестеренко, 2012, с. 151.
↑ Черемушкин, 2002, с. 78.
↑ ¹ ² Василенко, 2003, с. 87.
↑ Василенко, 2003, с. 92.
↑ ¹ ² ³ ⁴ Василенко, 2003, с. 113.
↑ Шнайер, 2002, 11.4.
↑ ¹ ² Василенко, 2003, с. 93.
↑ Черемушкин, 2002, с. 87.
↑ ¹ ² Шнайер, 2002, par.11.4.

Литература[править | править код]

на русском языке

Коблиц Н. Курс теории чисел и криптографии — 2-е издание — М.: Научное издательство ТВП, 2001. — 254 с. — ISBN 978-5-85484-014-9, 978-5-85484-012-5
Черемушкин А. В. Лекции по арифметическим алгоритмам в криптографии — М.: МЦНМО, 2002. — 104 с. — ISBN 978-5-94057-060-8
Василенко О. Н. Теоретико-числовые алгоритмы в криптографии — М.: МЦНМО, 2003. — 328 с. — ISBN 978-5-94057-103-2
Ишмухаметов Ш. Т. Методы факторизации натуральных чисел: учебное пособие — Казань: Казанский университет, 2011. — 190 с.
Нестеренко А. Ю. Теоретико-числовые методы в криптографии — М.: Московский государственный институт электроники и математики, 2012. — 224 с. — ISBN 978-5-94506-320-4
Кнут, Д. Искусство программирования = The Art of Computer Programming. — Москва: Вильямс, 2007. — Т. 2. — 832 с. — ISBN 978-5-8459-0081-4.
Введение в криптографию / Ященко, В. В.. — Москва: МЦНМО, 1999. — 272 с. — ISBN 5-900916-40-5.
Шнайер, Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — Москва: Триумф, 2002. — 816 с. — 3000 экз. — ISBN 5-89392-055-4.

на английском языке

Bressoud, D. M. Factorization and Primality Testing. — N. Y.: Springer-Verlag, 1989. — 260 p. — ISBN 0-387-97040-1.
Mahoney, M. S. The Mathematical Career of Pierre de Fermat. — 2. — Princeton: Princeton Univercity Press, 1994. — P. 324—332. — 438 p. — ISBN 0-691-03666-7.

Источник

0 / 0 / 0

Регистрация: 04.12.2014

Сообщений: 15

Найти наибольший простой множитель заданного числа

12.03.2016, 10:53. Показов 8670. Ответов 6

Простые множители 13195 – 5, 7, 13 и 29.
Каким является наибольший простой множитель заданного числа N?

Входные данные:
Первая строка содержит число T(1 ≤ T ≤ 100), которое обозначает количество тестов. Далее следуют T строк, каждая из которых содержит целое число N(2 ≤ N ≤ 1012).

Выходные данные:
Для каждого теста вывести наибольший простой множитель числа N.

Пример ввода Пример вывода
10 5
17 17

Модератор

13084 / 10361 / 6201

Регистрация: 18.12.2011

Сообщений: 27,704

12.03.2016, 11:10

0 / 0 / 0

Регистрация: 04.12.2014

Сообщений: 15

12.03.2016, 11:18

[ТС]

чет не то выходит

skipaq

70 / 70 / 52

Регистрация: 24.01.2013

Сообщений: 198

12.03.2016, 11:20

Страшноватенько правда…

C++

int main(){
    int n,p;
    cout << "Enter n: " << endl;
    cin >> n ;
    for (p = n; p > 0; p--) {
        if (n % p == 0) {
            if (p < n) {
                if (p == 1) {
                     cout << n << endl;
                     break;
                }
                cout << p << endl;
                break;
            }
 
        }
    }
    system("pause");
    return 0;
}

SpBerkut

Объявлятель переменных

1210 / 399 / 316

Регистрация: 24.09.2011

Сообщений: 1,249

12.03.2016, 12:38

Сообщение от skipaq

Страшноватенько правда…

И неверно, к тому же.

C++

int getMaxPrimeDivider(int x) {
    if (x<4) return x;
    if (!(x & x-1)) return 2;   // Если х степень двойки, то выдаём 2.
    while (!(x & 1)) x/=2;      // Делим на 2 пока делится
    int d = 3;                  // Делитель
    while (x>1) {               // Пока есть что делить
        while (!(x%d))          // Пока это что-то делится на текущий делитель
            x/=d;               // Делим
        d+=2;                   // Увеличиваем делитель на 2
    }
    return d-2;                 // Выводим
}

70 / 70 / 52

Регистрация: 24.01.2013

Сообщений: 198

12.03.2016, 18:02

Прошу прощения, что-то я совсем не по условию писал.. У меня программа просто выдаёт наибольший множитель, если его нет выдаёт само число. Хз, как я читал условие -( буду дома – подправлю =D

TheCalligrapher

Вездепух

10873 / 5878 / 1603

Регистрация: 18.10.2014

Сообщений: 14,672

12.03.2016, 18:17

Применить простейший алгоритм факторизации

C++

unsigned n = ...;
unsigned max_factor = 1;
 
unsigned d = 2;
while (d < n)
  if (n % d == 0) {
    // Сейчас d - простой делитель
    max_factor = d;
    n /= d;
  }
  else
    ++d;
  
if (n != 1)
  // Сейчас n - простой делитель
  max_factor = n;
 
std::cout << max_factor << std::endl;

Этот алгоритм порождает факторы по возрастанию. Последний фактор – наибольший.

Источник

Загрузить PDF

Любое натуральное число можно разложить на произведение простых множителей. Если вы не любите иметь дело с большими числами, такими как 5733, научитесь раскладывать их на простые множители (в данном случае это 3 x 3 x 7 x 7 x 13). Подобная задача часто встречается в криптографии, которая занимается проблемами информационной безопасности. Если вы еще не готовы создать собственную систему безопасной электронной почты, для начала научитесь раскладывать числа на простые множители.

1
Узнайте, что такое разложение числа на множители. Разложение числа на произведение множителей представляет собой процесс его “разбиения” на более мелкие части. При перемножении эти части, или множители, дают первоначальное число.
- Например, число 18 можно разложить на следующие произведения: 1 x 18, 2 x 9, или 3 x 6.
2

Вспомните, что такое простые числа. Простое число делится без остатка лишь на два числа: на само себя и на 1. Например, число 5 можно представить в виде произведения 5 и 1. Это число нельзя разложить на другие множители. Цель разложения числа на простые множители заключается в том, чтобы представить его в виде произведения простых чисел. Это особенно удобно при операциях с дробями, так как позволяет сравнивать и упрощать их.^[1]
3
Начните с исходного числа. Выберите составное число больше 3. Нет смысла брать простое число, так как оно делится лишь на само себя и единицу.
- Пример: разложим на произведение простых чисел число 24.
4
Разложим данное число на произведение двух множителей. Найдем два меньших числа, произведение которых равно исходному числу. Можно использовать любые множители, но проще взять простые числа. Один из хороших способов состоит в том, чтобы попробовать поделить исходное число сначала на 2, затем на 3, потом на 5 и проверить, на какие из этих простых чисел оно делится без остатка.
- Пример: если вы не знаете множителей для числа 24, попробуйте поделить его на малые простые числа. Так вы обнаружите, что данное число делится на 2: 24 = 2 x 12. Это хорошее начало.
- Поскольку 2 является простым числом, его хорошо использовать при разложении четных чисел.
5
Начните строить дерево множителей. Эта простая процедура поможет вам разложить число на простые множители.^[2] Для начала проведите от исходного числа две “ветки” вниз. На конце каждой ветки напишите найденные множители.
- Пример:
- 24
- /
- 2 12
6
Разложите на множители следующую строку чисел. Взгляните на два новых числа (вторая строка дерева множителей). Оба ли они относятся к простым числам? Если одно из них не является простым, также разложите его на два множителя. Проведите еще две ветки и напишите два новых множителя в третьей строке дерева.
- Пример: 12 не является простым числом, поэтому его следует разложить на множители. Используем разложение 12 = 2 x 6 и запишем его в третьей строке дерева:
- 24
- /
- 2 12
- /
- 2 x 6
7
Продолжайте двигаться вниз по дереву. Если один из новых множителей окажется простым числом, проводите от него одну “ветку” и пишите на ее конце это же число. Простые числа не раскладываются на меньшие множители, поэтому просто переносите их на уровень ниже.
- Пример: 2 является простым числом. Просто перенесите 2 из второй в третью строку:
- 24
- /
- 2 12
- / /
- 2 2 6
8
Продолжайте раскладывать числа на множители, пока у вас не останутся одни простые числа. Проверяйте каждую новую строку дерева. Если хоть один из новых множителей не является простым числом, разложите его на множители и запишите новую строку. В конце концов у вас останутся одни простые числа.
- Пример: 6 не является простым числом, поэтому его также следует разложить на множители. В то же время 2 представляет собой простое число, и мы переносим две двойки на следующий уровень:
- 24
- /
- 2 12
- / /
- 2 2 6
- / / /
- 2 2 2 3
9
Запишите последнюю строку в виде произведения простых множителей. В конце концов у вас останутся одни простые числа. Когда это случится, разложение на простые множители завершено. Последняя строка представляет собой набор простых чисел, произведение которых дает исходное число.
- Проверьте ответ: перемножьте стоящие в последней строке числа. В результате должно получиться исходное число.
- Пример: в последней строке дерева множителей содержатся числа 2 и 3. Оба этих числа являются простыми, поэтому разложение завершено. Таким образом, разложение числа 24 на простые множители имеет следующий вид: 24 = 2 x 2 x 2 x 3.
- Порядок множителей не имеет значения. Разложение можно записать также в виде 2 x 3 x 2 x 2.
10
При желании упростите ответ с помощью степенной записи. Если вы знакомы с возведением чисел в степень, можно записать полученный ответ в более простом виде. Помните, что внизу записывается основание, а надстрочное число показывает, сколько раз это основание следует умножить на само себя.
- Пример: сколько раз встречается число 2 в найденном разложении 2 x 2 x 2 x 3? Три раза, поэтому выражение 2 x 2 x 2 можно записать в виде 2³. В упрощенной записи получаем 2³ x 3.
Реклама

1
Найдите наибольший общий делитель двух чисел. Наибольшим общим делителем (НОД) двух чисел называется максимальное число, на которое оба числа делятся без остатка. В приведенном ниже примере показано, как с помощью разложения на простые множители найти наибольший общий делитель чисел 30 и 36.
- Разложим оба числа на простые множители. Для числа 30 разложение имеет вид 2 x 3 x 5. Число 36 раскладывается на простые множители следующим образом: 2 x 2 x 3 x 3.
- Найдем число, которое встречается в обоих разложениях. Перечеркнем это число в обоих списках и напишем его с новой строки. Например, 2 встречается в двух разложениях, поэтому запишем 2 в новой строке. После этого у нас остается 30 = 2 x 3 x 5 и 36 = 2 x 2 x 3 x 3.
- Повторяйте это действие, пока в разложениях не останется общих множителей. В оба списка входит также число 3, поэтому в новой строке можно записать 2 и 3. После этого вновь сравните разложения: 30 = ~~2 x 3~~ x 5 и 36 = 2 x 2 x 3 x 3. Как видно, в них не осталось общих множителей.
- Чтобы найти наибольший общий делитель, следует найти произведение всех общих множителей. В нашем примере это 2 и 3, поэтому НОД равен 2 x 3 = 6. Это наибольшее число, на которое делятся без остатка числа 30 и 36.
2
С помощью НОД можно упрощать дроби. Если вы подозреваете, что какую-то дробь можно сократить, используйте наибольший общий делитель. По описанной выше процедуре найдите НОД числителя и знаменателя. После этого поделите числитель и знаменатель дроби на это число.^[3] В результате вы получите ту же дробь в более простом виде.
- К примеру, упростим дробь ³⁰/₃₆. Как мы установили выше, для 30 и 36 НОД равен 6, поэтому поделим числитель и знаменатель на 6:
- 30 ÷ 6 = 5
- 36 ÷ 6 = 6
- ³⁰/₃₆ = ⁵/₆
3
Найдем наименьшее общее кратное двух чисел. Наименьшее общее кратное (НОК) двух чисел — это наименьшее число, которое делится без остатка на оба данных числа. Например, НОК 2 и 3 является 6, поскольку это наименьшее число, которое делится на 2 и 3. Ниже приведен пример нахождения НОК с помощью разложения на простые множители:
- Начнем с двух разложений на простые множители. Например, для числа 126 разложение можно записать как 2 x 3 x 3 x 7. Число 84 раскладывается на простые множители в виде 2 x 2 x 3 x 7.
- Сравним, сколько раз каждый множитель встречается в разложениях. Выберите тот список, где множитель встречается максимальное число раз, и обведите это место. Например, число 2 встречается один раз в разложении для числа 126 и дважды в списке для 84, поэтому следует обвести 2 x 2 во втором списке множителей.
- Повторите это действие для каждого множителя. Например, 3 встречается чаще в первом разложении, поэтому следует обвести в нем 3 x 3. Число 7 встречается по одному разу в обоих списках, так что обводим 7 (неважно в каком списке, если данный множитель встречается в обоих списках одинаковое число раз).
- Чтобы найти НОК, перемножьте все обведенные числа. В нашем примере наименьшим общим кратным чисел 126 и 84 является 2 x 2 x 3 x 3 x 7 = 252. Это наименьшее число, которое делится на 126 и 84 без остатка.
4
Используйте НОК для сложения дробей. При сложении двух дробей необходимо привести их к общему знаменателю. Для этого найдите НОК двух знаменателей. Затем умножьте числитель и знаменатель каждой дроби на такое число, чтобы знаменатели дробей стали равны НОК. После этого можно сложить дроби.
- Например, необходимо найти сумму ¹/₆ + ⁴/₂₁.
- С помощью приведенного выше метода можно найти НОК для 6 и 21. Оно равно 42.
- Преобразуем дробь ¹/₆ так, чтобы ее знаменатель равнялся 42. Для этого необходимо поделить 42 на 6: 42 ÷ 6 = 7. Теперь умножим числитель и знаменатель дроби на 7: ¹/₆ x ⁷/₇ = ⁷/₄₂.
- Чтобы привести вторую дробь к знаменателю 42, поделим 42 на 21: 42 ÷ 21 = 2. Умножим числитель и знаменатель дроби на 2: ⁴/₂₁ x ²/₂ = ⁸/₄₂.
- После того как дроби приведены к одинаковому знаменателю, их можно легко сложить: ⁷/₄₂ + ⁸/₄₂ = ¹⁵/₄₂.
Реклама

Примеры задач

Попробуйте решить приведенные ниже задачи самостоятельно. Если вы считаете, что получили правильный ответ, выделите мышкой место после двоеточия в условии задачи. Последние задачи наиболее сложные.
Найдите разложение на простые множители для числа 16: 2 x 2 x 2 x 2
Запишите ответ в степенной форме: 2⁴
Найдите разложение на простые множители для числа 45: 3 x 3 x 5
Запишите ответ в степенной форме: 3² x 5
Найдите разложение на простые множители для числа 34: 2 x 17
Найдите разложение на простые множители для числа 154: 2 x 7 x 11
Найдите разложение на простые множители для чисел 8 и 40, а затем определите их наибольший общий делитель: разложение на простые множители числа 8 имеет вид 2 x 2 x 2 x 2; разложение на простые множители числа 40 имеет вид 2 x 2 x 2 x 5; НОД двух чисел 2 x 2 x 2 = 6.
Найдите разложение на простые множители для чисел 18 и 52 и найдите их наименьшее общее кратное: разложение на простые множители числа 18 имеет вид 2 x 3 x 3; разложение на простые множители числа 52 имеет вид 2 x 2 x 13; НОК двух чисел составляет 2 x 2 x 3 x 3 x 13 = 468.

Советы

Каждое число имеет характерное для него единственное разложение на простые множители. Неважно, каким образом вы находите это разложение, в конце должен получиться один и тот же ответ. Это называется основной теоремой арифметики.^[4]
Вместо того чтобы каждый раз переписывать простые числа в новой строке дерева множителей, можно оставлять их на месте и просто обводить. По окончании разложения в него войдут все обведенные простые множители.
Всегда проверяйте полученный ответ. Вы можете допустить ошибку и не заметить этого.
Будьте готовы к заданиям с подвохом. Если вас просят найти разложение на простые множители простого числа, нет необходимости проводить какие-либо вычисления.^[5] Например, для числа 17 разложением на простые множители будет 17; это число не раскладывается на другие простые множители.
Наибольший общий делитель и наименьшее общее кратное можно найти для трех и более чисел.

Предупреждения

Дерево множителей позволяет определить лишь простые, а не все возможные множители.

Об этой статье

Эту страницу просматривали 8197 раз.

Была ли эта статья полезной?

Источник

C++

C

Java

Python3

C#

PHP

Javascript

Method 2:

C++

Python3

Method 3: (Trial Division)

Python3

Разложение натурального числа на простые множители

Примеры разложения чисел на простые множители

Применение при решении задач, признаков делимости для разложения на множители

История[править | править код]

Алгоритмы факторизации[править | править код]

Экспоненциальные алгоритмы[править | править код]

Перебор возможных делителей[править | править код]

Метод факторизации Ферма[править | править код]

ρ-алгоритм Полларда[править | править код]

Алгоритм Ленстры[править | править код]

Алгоритм Полларда — Штрассена[править | править код]

Метод квадратичных форм Шенкса[править | править код]

P-1 алгоритм Полларда[править | править код]

Метод Лемана[править | править код]

Субэкспоненциальные алгоритмы[править | править код]

Алгоритм Диксона[править | править код]

Факторизация методом непрерывных дробей[править | править код]

Метод квадратичного решета[править | править код]

Факторизация Ленстры с помощью эллиптических кривых[править | править код]

Решето числового поля[править | править код]

Применение в криптографии[править | править код]

Текущее состояние[править | править код]

Примечания[править | править код]

Литература[править | править код]

Найти наибольший простой множитель заданного числа

Примеры задач

Советы

Предупреждения

Об этой статье

Была ли эта статья полезной?

Вам также может понравиться

Как открыть найти фирму

Как найти каналы на мтс тарелке

Размазанное изображение на мониторе как исправить

Добавить комментарий Отменить ответ