Ответ:
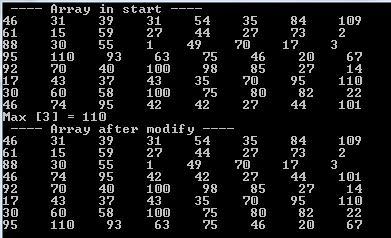
Условие – Найти максимальный элемент матрицы. Строку, содержащую
максимальный элемент, поменять с последней строкой матрицы.
Нумерация в матрице начинается с 0.
С++ на Code Blocks 16
Объяснение:
#include <iostream>
#include <time.h>
using namespace std;
int main()
{
int n = 8; // можно ввести любую размерность квадратной матрицы
int a[n][n];
int Nmax, Nind, i, j = 0 ;
int d;
// Заполним матрицу случайными числами в диапазоне [0 ,100)
// и сразу её выведем
cout << ” —- Array in start —- ” << endl;
srand(time(0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = rand()%111;
cout <<a[i][j] ;
cout<< ” “;
}
cout << ” ” << endl;
}
// Поиск максимального элемента матрицы. Для оптимизации, можно было это произвести на этапе заполнения матрицы
// но для наглядности, напишем отдельно
Nmax = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++){
if (Nmax < a[i][j]) {
Nmax = a[i][j];
Nind = i;
}
}
}
cout<< “Max [“<< Nind<<“] = “<< Nmax << endl;
// Меняем строки местами
for (int j = 0; j < n; j++) {
d = a[n-1][j];
a[n-1][j]=a[Nind][j];
a[Nind][j] = d;
}
cout << ” —- Array after modify —- ” << endl;
// Выводим полученную матрицу
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++){
cout << a[i][j] ;
cout<< ” “;
}
cout << ” ” << endl;
}
return 0;
}

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 |
#include "stdafx.h" #include<iostream> #include<iomanip> using namespace std; //создает матрицу размер size int** matrix_constructor(int size) { int** matrix_new = new int* [size]; for (int i = 0; i < size; i++) matrix_new[i] = new int[size]; return matrix_new; } //удаляем матрицу void matrix_destructor(int** matrix, int size) { for (int i = 0; i < size; i++) delete matrix[i]; delete matrix; } заполняет матрицу : если random_fill == true - случайно, иначе вводит ручками void matrix_fill(int** matrix, int size, bool random_fill = true) { if(random_fill) { srand((unsigned)time(NULL)); for (int i = 0; i < size; i++) for (int j = 0; j < size; j++) { int temp = matrix[i][j] = rand() % 80 + 10; if(temp > 70) matrix[i][j] = 0; else matrix[i][j] = temp; } } else { for(int i = 0; i < size; i++) { for(int j = 0; j < size; j++) { cout<<"Enter {"<<i<<":"<<j<<"}"<<"element"; cin>>matrix[i][j]; } cout<<endl; } } } //печатаем матрицу void matrix_print(int** matrix, int size) { for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) cout<<matrix[i][j]<<" "; cout<<endl; } cout<<endl; } void matrix_copy(int** orignal, int** copy, int size) { for (int i = 0; i < size; i++) for (int j = 0; j < size; j++) copy[i][j] = orignal[i][j]; } //первый пункт задания void matrix_action1(int** matrix, int size) { int maximal_index[2], //строка и столбец максимального элемента minimal_last_row = matrix[size - 1][0], //минимальный элемент последней строки maximal = matrix[0][0]; //максимальный элемент матрицы int** copy = matrix_constructor(size);//делаем matrix_copy(matrix, copy, size);////////копию матрицы for (int i = 0; i < size; i++) { for (int j = 0; j < size; j++) { if(copy[i][j] > maximal) //если текущий больше максимального { maximal = copy[i][j];//значит максимальным становится текущий maximal_index[0] = i;//строка maximal_index[1] = j;//стролбец } if(i == size - 1)//если мы на последней строке, то ищем минимум if(copy[i][j] < minimal_last_row) minimal_last_row = copy[i][j]; } } //заменяем все элементы до максимального на минимум последней строки for (int i = 0; i <= maximal_index[0]; i++) for (int j = 0; j <= (i == maximal_index[0] ? maximal_index[1] : size - 1); j++) copy[i][j] = minimal_last_row; matrix_print(copy, size);//выводи отредактированную матрицу matrix_destructor(copy, size);//удаляем ее } //второй пункт задания void matrix_action2(int** matrix, int size) { int counter_temp = 0;//временный счетчик нулей int** copy = matrix_constructor(size);//делаем копию matrix_copy(matrix, copy, size);//матрицы for (int i = 0; i < size; i++) { int counter_null = 0;//счетчик нулей в текущей строке for (int j = 0; j < size; j++) { if(!copy[i][j]) counter_null++;//если ноль, то увеличиваем счетчик if(counter_temp == 2) copy[i - 1][j] = 0;//если временный счетчик равен 2, значик в предыдущей строке было 2 нуля, значит обнуляем все ее элементы } counter_temp = counter_null; } matrix_print(copy, size);//выводи отредактированную матрицу matrix_destructor(copy, size);//удаляем ее } int main() { int size; int** matrix; cout<<"Matrix size : "; cin>>size; matrix = matrix_constructor(size); matrix_fill(matrix, size); matrix_print(matrix, size); matrix_action1(matrix, size); matrix_action2(matrix, size); matrix_destructor(matrix, size); getchar(); getchar(); return 0; } |
Я создал два динамических массива, двумерный и одномерный (arrA[n][m] и arrB[n])
Помогите найти ошибку в цикле. В некоторых строках находит максимальный элемент, во других же находит мусор.
int maxv = A - 1, nextv; // A - минимальный возможный элемент массива при генерации
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (maxv < (nextv = arrA[i][j]))
{
maxv = nextv;
arrB[i] = maxv;
}
}
}
задан 18 дек 2016 в 11:57
1
У вас после того, как в строке найден максимальный элемент, он и остается в maxv… Эту переменную надо инициализировать для каждой строки:
int maxv = A - 1, nextv; // A - минимальный возможный элемент массива при генерации
for (int i = 0; i < n; i++)
{
maxv = A - 1;
for (int j = 0; j < m; j++)
{
if (maxv < (nextv = arrA[i][j]))
{
maxv = nextv;
arrB[i] = maxv;
}
}
}
Но без этой переменной можно и обойтись совсем 🙂
ответ дан 18 дек 2016 в 12:06
HarryHarry
214k15 золотых знаков117 серебряных знаков227 бронзовых знаков
Вообще то это должен быть комментарий, но пока мне не дозволено (не хватает рейтинга), чтобы их оставлять.
Ваша проблема в том, что Вы не производите сброс maxv перед входом во внутренний цикл, если конечно я правильно понял задачу.
ответ дан 18 дек 2016 в 12:08
Александр МуксимовАлександр Муксимов
1,6422 золотых знака15 серебряных знаков21 бронзовый знак
Вообще для таких вещей есть отладчик. Но вот исправленный вариант:
int maxv = A - 1, nextv; // На самом деле эти переменные не нужны
for (int i = 0; i < n; i++)
{
arrB[i] = arrA[i][0];
for (int j = 1; j < m; j++)
{
if (arrB[i] < arrA[i][j])
{
arrB[i] = arrA[i][j];
}
}
}
Необходимости использовать дополнительные переменные тут нет.
ответ дан 18 дек 2016 в 12:05
c4pQc4pQ
7475 серебряных знаков17 бронзовых знаков
Ответ:
Условие – Найти максимальный элемент матрицы. Строку, содержащую
максимальный элемент, поменять с последней строкой матрицы.
Нумерация в матрице начинается с 0.
С++ на Code Blocks 16
Объяснение:
#include <iostream>
#include <time.h>
using namespace std;
int main()
{
int n = 8; // можно ввести любую размерность квадратной матрицы
int a[n][n];
int Nmax, Nind, i, j = 0 ;
int d;
// Заполним матрицу случайными числами в диапазоне [0 ,100)
// и сразу её выведем
cout << ” —- Array in start —- ” << endl;
srand(time(0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = rand()%111;
cout <<a[i][j] ;
cout<< ” “;
}
cout << ” ” << endl;
}
// Поиск максимального элемента матрицы. Для оптимизации, можно было это произвести на этапе заполнения матрицы
// но для наглядности, напишем отдельно
Nmax = 1;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++){
if (Nmax < a[i][j]) {
Nmax = a[i][j];
Nind = i;
}
}
}
cout<< “Max [“<< Nind<<“] = “<< Nmax << endl;
// Меняем строки местами
for (int j = 0; j < n; j++) {
d = a[n-1][j];
a[n-1][j]=a[Nind][j];
a[Nind][j] = d;
}
cout << ” —- Array after modify —- ” << endl;
// Выводим полученную матрицу
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++){
cout << a[i][j] ;
cout<< ” “;
}
cout << ” ” << endl;
}
return 0;
}
В этой статье мы научимся находить максимальное значение в списке на Python. Для всестороннего понимания вопроса мы рассмотрим использование некоторых встроенных функций, простые подходы, а также небольшие реализации известных алгоритмов.
Сначала давайте вкратце рассмотрим, что такое список в Python и как найти в нем максимальное значение или просто наибольшее число.
В Python есть встроенный тип данных под названием список (list). По своей сути он сильно напоминает массив. Но в отличие от последнего данные внутри списка могут быть любого типа (необязательно одного): он может содержать целые числа, строки или значения с плавающей точкой, или даже другие списки.
Хранимые в списке данные определяются как разделенные запятыми значения, заключенные в квадратные скобки. Списки можно определять, используя любое имя переменной, а затем присваивая ей различные значения в квадратных скобках. Он является упорядоченным, изменяемым и допускает дублирование значений. Например:
list1 = ["Виктор", "Артем", "Роман"]
list2 = [16, 78, 32, 67]
list3 = ["яблоко", "манго", 16, "вишня", 3.4]
Далее мы рассмотрим возможные варианты кода на Python, реализующего поиск наибольшего элемента в списке, состоящем из сравниваемых элементов. В наших примерах будут использоваться следующие методы/функции:
- Встроенная функция
max() - Метод грубой силы (перебора)
- Функция
reduce() - Алгоритм Heap Queue (очередь с приоритетом)
- Функция
sort() - Функция
sorted() - Метод хвостовой рекурсии
№1 Нахождение максимального значения с помощью функции max()
Это самый простой и понятный подход к поиску наибольшего элемента. Функция Python max() возвращает самый большой элемент итерабельного объекта. Ее также можно использовать для поиска максимального значения между двумя или более параметрами.
В приведенном ниже примере список передается функции max в качестве аргумента.
list1 = [3, 2, 8, 5, 10, 6]
max_number = max(list1)
print("Наибольшее число:", max_number)
Наибольшее число: 10Если элементы списка являются строками, то сначала они упорядочиваются в алфавитном порядке, а затем возвращается наибольшая строка.
list1 = ["Виктор", "Артем", "Роман"]
max_string = max(list1, key=len)
print("Самая длинная строка:", max_string)
Самая длинная строка: Виктор№2 Поиск максимального значения перебором
Это самая простая реализация, но она немного медленнее, чем функция max(), поскольку мы используем этот алгоритм в цикле.
В примере выше для поиска максимального значения нами была определена функция large(). Она принимает список в качестве единственного аргумента. Для сохранения найденного значения мы используем переменную max_, которой изначально присваивается первый элемент списка. В цикле for каждый элемент сравнивается с этой переменной. Если он больше max_, то мы сохраняем значение этого элемента в нашей переменной. После сравнения со всеми членами списка в max_ гарантировано находится наибольший элемент.
def large(arr):
max_ = arr[0]
for ele in arr:
if ele > max_:
max_ = ele
return max_
list1 = [1,4,5,2,6]
result = large(list1)
print(result) # вернется 6
№3 Нахождение максимального значения с помощью функции reduce()
В функциональных языках reduce() является важной и очень полезной функцией. В Python 3 функция reduce() перенесена в отдельный модуль стандартной библиотеки под названием functools. Это решение было принято, чтобы поощрить разработчиков использовать циклы, так как они более читабельны. Рассмотрим приведенный ниже пример использования reduce() двумя разными способами.
В этом варианте reduce() принимает два параметра. Первый — ключевое слово max, которое означает поиск максимального числа, а второй аргумент — итерабельный объект.
from functools import reduce
list1 = [-1, 3, 7, 99, 0]
print(reduce(max, list1)) # вывод: 99
Другое решение показывает интересную конструкцию с использованием лямбда-функции. Функция reduce() принимает в качестве аргумента лямбда-функцию, а та в свою очередь получает на вход условие и список для проверки максимального значения.
from functools import reduce
list1 = [-1, 3, 7, 99, 0]
print(reduce(lambda x, y: x if x > y else y, list1)) # -> 99
№4 Поиск максимального значения с помощью приоритетной очереди
Heapq — очень полезный модуль для реализации минимальной очереди. Если быть более точным, он предоставляет реализацию алгоритма очереди с приоритетом на основе кучи, известного как heapq. Важным свойством такой кучи является то, что ее наименьший элемент всегда будет корневым элементом. В приведенном примере мы используем функцию heapq.nlargest() для нахождения максимального значения.
import heapq
list1 = [-1, 3, 7, 99, 0]
print(heapq.nlargest(1, list1)) # -> [99]
Приведенный выше пример импортирует модуль heapq и принимает на вход список. Функция принимает n=1 в качестве первого аргумента, так как нам нужно найти одно максимальное значение, а вторым аргументом является наш список.
№5 Нахождение максимального значения с помощью функции sort()
Этот метод использует функцию sort() для поиска наибольшего элемента. Он принимает на вход список значений, затем сортирует его в порядке возрастания и выводит последний элемент списка. Последним элементом в списке является list[-1].
list1 = [10, 20, 4, 45, 99]
list1.sort()
print("Наибольшее число:", list1[-1])
Наибольшее число: 99№6 Нахождение максимального значения с помощью функции sorted()
Этот метод использует функцию sorted() для поиска наибольшего элемента. В качестве входных данных он принимает список значений. Затем функция sorted() сортирует список в порядке возрастания и выводит наибольшее число.
list1=[1,4,22,41,5,2]
sorted_list = sorted(list1)
result = sorted_list[-1]
print(result) # -> 41
№7 Поиск максимального значения с помощью хвостовой рекурсии
Этот метод не очень удобен, и иногда программисты считают его бесполезным. Данное решение использует рекурсию, и поэтому его довольно сложно быстро понять. Кроме того, такая программа очень медленная и требует много памяти. Это происходит потому, что в отличие от чистых функциональных языков, Python не оптимизирован для хвостовой рекурсии, что приводит к созданию множества стековых фреймов: по одному для каждого вызова функции.
def find_max(arr, max_=None):
if max_ is None:
max_ = arr.pop()
current = arr.pop()
if current > max_:
max_ = current
if arr:
return find_max(arr, max_)
return max_
list1=[1,2,3,4,2]
result = find_max(list1)
print(result) # -> 4
Заключение
В этой статье мы научились находить максимальное значение из заданного списка с помощью нескольких встроенных функций, таких как max(), sort(), reduce(), sorted() и других алгоритмов. Мы написали свои код, чтобы попробовать метод перебора, хвостовой рекурсии и алгоритма приоритетной очереди.