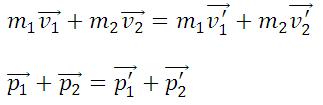Решение. 1 эВ – 1,6∙10-19 Дж, 4,9 эВ = 7,84∙10-19 Дж, 4,5 эВ= 7,2∙10-19 Дж.
Запишем формулу Эйнштейна для фотоэффекта и определим скорость фотоэлектрона:
[ E=A+{{E}_{K}}(1),{{E}_{K}}=frac{mcdot {{upsilon }^{2}}}{2}(2),E=A+frac{mcdot {{upsilon }^{2}}}{2},frac{mcdot {{upsilon }^{2}}}{2}=E-A,upsilon =sqrt{frac{2cdot (E-A)}{m}}(3). ]
Где: m – масса электрона, m = 9,1∙10-31 кг.
Максимальный импульс pmax, передаваемый поверхности металла рассчитаем по формуле
[ begin{align}
& {{p}_{max }}=mcdot upsilon (4),={{p}_{max }}=mcdot sqrt{frac{2cdot (E-A)}{m}},{{p}_{max }}=sqrt{frac{{{m}^{2}}cdot 2cdot (E-A)}{m}}, \
& {{p}_{max }}=sqrt{2cdot mcdot (E-A)}(5). \
& {{p}_{max }}=sqrt{2cdot 9,1cdot {{10}^{-31}}cdot (7,84cdot {{10}^{-19}}-7,2cdot {{10}^{-19}})}=3,4cdot {{10}^{-25}}. \
end{align} ]
Ответ: 3,4∙10-25 кг∙м/с.
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:
|
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695
На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730
Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520
Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.1k
Спрятать решение
Решение.
Согласно постулатам Бора, свет излучается при переходе атома на более низкие уровни энергии, при этом фотоны несут энергию, равную разности энергий начального и конечного состояний. Таким образом, испущенный фотон имел нес энергию
Согласно уравнению фотоэффекта, максимальная кинетическая энергия вылетающих фотоэлектронов связана с энергией фотона и работой выхода соотношением
Работа выхода связана с частотой красной границы соотношением:
Таким образом, максимально возможный импульс фотоэлектрон равен
Ответ: 
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае — постулаты Бора, уравнение Эйнштейна для фотоэффекта); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, и обозначений величин, используемых в условии задачи); III) проведены необходимые математические преобразования, приводящие к правильному ответу; IV) представлен правильный ответ. |
3 |
| Правильно записаны все необходимые положения теории, физические законы, закономерности и проведены необходимые преобразования. Но имеются следующие недостатки.
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. ИЛИ Лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты, не заключены в скобки, рамку и т. п.). ИЛИ В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца. ИЛИ Отсутствует пункт IV, или в нём допущена ошибка. |
2 |
| Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа. ИЛИ В решении отсутствует одна из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В одной из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла. | 0 |
| Максимальный балл | 3 |
Раздел кодификатора ФИПИ/Решу ЕГЭ:
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,658 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,962 -
разное
16,905
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Лабораторная работа № 2
Тема: Изучение закона сохранения импульса
Цель: экспериментально проверить справедливость закона сохранения импульса тел при прямом упругом соударении
Оборудование: 1. Два металлических шарика разной массы.
2. Рама для подвеса шариков.
3. Измерительная линейка.
Теория
Величина, равная произведению массы материальной точки на ее скорость, называется импульсом.
p=mυ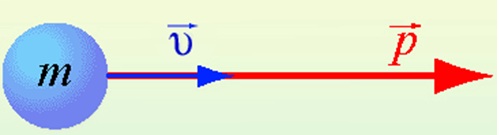 
p — импульс тела
m — масса тела
υ — скорость тела
Импульс тела направлен в ту же сторону, что и скорость тела.
Единицей измерения импульса в СИ является 1 кг·м/с.
Изменение импульса тела происходит при взаимодействии тел, например, при ударах.
Для системы материальных точек полный импульс равен сумме импульсов. При этом следует иметь в виду, что импульс – это векторная величина, и поэтому в общем случае импульсы складываются как векторы, т.е. по правилу параллелограмма.
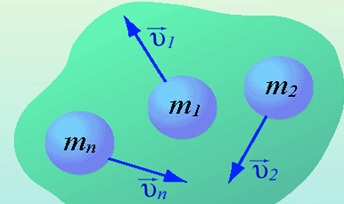
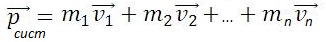
Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой. Замкнутая система – это система тел, которые взаимодействуют только друг с другом.
Закон сохранения импульса: в замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
m1, m2 — массы взаимодействующих тел, кг
υ1, υ2 — скорости тел до столкновения, м/с
υ’1, υ’2 — скорости тел после столкновения, м/с
Закон сохранения импульса можно сформулировать и так: если на тела системы действуют только силы взаимодействия между ними («внутренние силы»), то полный импульс системы тел не изменяется со временем, т.е. сохраняется. Этот закон применим к системе, состоящей из любого числа тел. Отметим еще раз, что импульс – величина векторная, поэтому сохранение полного импульса означает сохранение не только его величины, но и направления.
Закон сохранения импульса выполняется при распаде тела на части и при абсолютно неупругом ударе, когда соударяющиеся тела соединяются в одно. Если распад или удар происходят в течение малого промежутка времени, то закон сохранения импульса приближенно выполняется для этих процессов даже при наличии внешних сил, действующих на тела системы со стороны тел, не входящих в нее, т.к. за малое время внешние силы не успевают значительно изменить импульс системы.
Под ударом в механике понимается кратковременное взаимодействие двух или более тел, возникающее в результате их соприкосновения (соударение шаров, удар молота о наковальню и др.). Самым простым является прямой (центральный) удар, то есть такой удар, при котором скорости соударяющихся тел до удара направлены по линии, соединяющей центры тел. При соударении взаимодействие длится такой короткий промежуток времени (иногда измеряемый тысячными долями секунды) и возникают столь большие внутренние силы взаимодействия, что внешними силами можно пренебречь и систему соударяющихся тел можно считать замкнутой и применять к ней закон сохранения импульса.
В зависимости от упругих свойств тел соударения могут протекать весьма различно. Принято выделять два крайних случая: абсолютно упругий и абсолютно неупругий удары.
Абсолютно упругим называется удар, при котором после взаимодействия тела полностью восстанавливают свою форму. Таких ударов в природе не существует, так как всегда часть энергии затрачивается на необратимую деформацию тел. Однако для некоторых тел, например стальных закаленных шаров, потерями механической энергии при столкновении можно пренебречь и считать удар абсолютно упругим. В случае центрального абсолютно упругого удара двух тел с массами m1, m2 и скоростями υ1, υ2 до удара и υ′1, υ′2 после удара можно записать закон сохранения импульса тел:
Абсолютно неупругим называется удар, при котором после соприкосновения тел они не восстанавливают полностью свою форму, соединяются вместе и движутся как единое целое с одной скоростью. При этом ударе часть их механической энергии переходит в работу деформации тел (внутреннюю энергию). Столкновение двух шаров из пластилина, когда после столкновения шары слипаются и движутся вместе, является примером абсолютно неупругого удара. В случае центрального абсолютно неупругого удара двух тел с массами m1, m2 движущихся со скоростями υ1, υ2 до удара и υ′ после удара можно записать законы сохранения импульса тел:
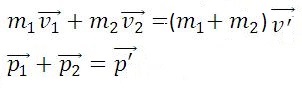
Закон сохранения импульса служит основой для объяснения обширного круга явлений природы, применяется в различных науках:
- Закон строго выполняется в явлениях отдачи при выстреле, явлении реактивного движения, взрывных явлениях и явлениях столкновения тел.
- Закон сохранения импульса применяют: при расчетах скоростей тел при взрывах и соударениях; при расчетах реактивных аппаратов; в военной промышленности при проектировании оружия; в технике – при забивании свай, ковке металлов и т.д
Описание работы
Установка состоит из двух стальных шаров, на длинных подвесах и измерительной линейки под шарами. Центры масс соприкасающихся шарв лежат на одном уровне от точки подвеса. Отведя один из шаров (например, большей массы) в сторону и отпустив его, можно произвести прямой (центральный) удар шаров.
Если до столкновения один из шаров покоился υ2=0, то выражение закона сохранения импульса упростится. При прямом ударе оба шара после столкновения движутся по одной прямой, поэтому от векторной формы записи закона сохранения импульса можно перейти к алгебраической и учитывая, что после столкновения оба шара движутся в одном направлении, получим:
m1∙υ1= m1∙υ′1 + m2∙υ′2
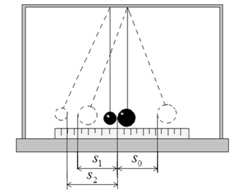
рис. 2
Для определения скорости первого шара υ1 до удара и скоростей шаров υ′1 и υ′2 после удара воспользуемся законом сохранения механической энергии. Потенциальная энергия шара в положении максимального отклонения равняется его кинетической энергии при ударе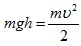 
, отсюда 
.
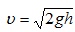Высоту подъёма шара можно определить по его максимальному отклонению s от положения равновесия (рис.3,а).
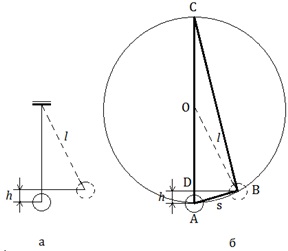
рис. 3
Треугольник АВС прямоугольный (опирается на диаметр). Катет АВ является средней пропорциональной величиной между гипотенузой АС=2l и своей проекцией на гипотенузу АD (рис.3,б): АВ2=АС·AD то есть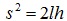 
, откуда 
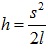. Следовательно, величины скоростей можно выразить так: 
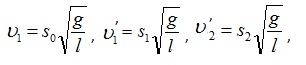где S0, S1 – максимальные отклонения первого шара до и после удара; S2 – максимальное отклонение второго шара после удара.
Запишем уравнение закона сохранения через выражения скоростей:
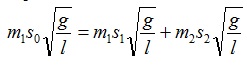или m1∙S0= m1∙S1 + m2∙S2.
Таким образом, проверка закона сохранения импульса в данной работе сводится к проверке справедливости последнего уравнения.
При малых углах отклонения шара от положения равновесия S0, S1 и S2 можно заменить соответствующими величинами, отсчитанными по горизонтальной шкале.
Выполнение работы.
1. Перенесите рисунок 2 в отчет по работе.
2. Подготовьте в тетради таблицу для записи результатов измерений и вычислений:
|
№ |
m1, |
m2, |
S0, |
S1, |
S2, |
m1∙S0, |
m1∙S1, |
m2∙S2, |
m1∙S1 + m2∙S2, |
|
1 |
|||||||||
|
2 |
|||||||||
|
3 |
3. Определите массы шаров m1 и m2. Запишите их результат в таблицу.
4. Отрегулируйте подвеску шаров так, чтобы их центры и точка касания находились на одной горизонтальной линии.
5. Отклоните шар большей массы на 3 см от положения расновесия (S0) и затем отпустите его. Заметьте максимальное отклонение шара большей массы после удара (S1). Повторите опыт 5 раз и найдите среднее значение отклонения S1ср. Запишите его в таблицу (S1).
6. Повторите опыт, но теперь заметьте после удара максимальное отклонение шара с меньшей массой (S2). Повторите опыт 5 раз, и найдите среднее значение отклонения S2ср. Запишите его в таблицу (S2).
7. Повторите опыт, отклоняя шар большей массы на 4 см и 5 см. Результаты измерений запишите в таблицу.
8. Используя значения S0, S1 и S2, вычислите импульс шара до удара m1∙S0 и сумму импульсов шаров после удара m1∙S1 + m2∙S2 и внесите в таблицу их результаты.
9. Сравните импульс шара до удара с суммой импульсов шаров после удара. Запишите вывод по полученным результатам работы.
10. Ответьте на контрольные вопросы.
Контрольные вопросы
1. Что называется импульсом материальной точки? По какой формуле он находится? В каких единицах он измеряется?
2. Импульс – величина векторная или скалярная?
3. Запишите формулу и формулировку закона сохранения импульса.
4. При каких условиях выполняется закон сохранения импульса?
5. Какое соударение называется абсолютно упругим?
6. Для каких видов соударений выполняется закон сохранения импульса?
Вариант выполнения измерений.
1. Определяем массы шариков m1 и m2 при помощи динамометра (или весов) и записываем в таблицу:
m1=62 г
m2=27,5 г
2. Отклоняем большой шар от положения расновесия на 3 см и отпускаем его.
S0=3 см=30 мм
Замечаем его максимальное отклонение после удара. Повторяем опыт 5 раз, находим среднее значение отклонения и записываем в таблицу S1ср.
S1=13мм S1=15мм S1=18мм S1=14мм S1=16мм
S1ср=(13мм+15мм+18мм+14мм+16мм)/5=15,2 мм
3. Повторяем этот же опыт, но теперь замечаем после удара отклонение шара меньшей массы. Повторяем опыт 5 раз, находим среднее значение и записываем в таблицу S2ср.
S2=31мм S2=34мм S2=36мм S2=35мм S2=32мм
S2ср=(31мм+34мм+36мм+35мм+32мм)/5=34мм
4. Повторяем опыт, отклоняя шар большей массы на 4 см и 5 см.
S0=4 см=40 мм
S1=18 мм S1=19 мм S1=23 мм S1=22 мм S1=18 мм
S1ср=(18 мм+19 мм+23 мм+22 мм+18 мм)/5=20 мм
S2=43 мм S2=44 мм S2=46 мм S2=47 мм S2=45 мм
S2ср=(43 мм + 44 мм + 46 мм + 47 мм + 45 мм)/5=45 мм
S0=5 см=50 мм
Результаты измерений записываем в таблицу.
|
№ |
m1, |
m2, |
S0, |
S1, |
S2, |
m1∙S0, |
m1∙S1, |
m2∙S2, |
m1∙S1 + m2∙S2, |
|
1 |
62,0 |
27,5 |
30 |
15 |
34 |
||||
|
2 |
62,0 |
27,5 |
40 |
20 |
45 |
||||
|
3 |
62,0 | 27,5 | 50 | 25 | 56 |
