Построение
эпюр поперечной силы и изгибающего
момента для балок
Пример
1.
Построить
эпюры внутренних усилий Qy,
Mx
для балки (см. рис.).
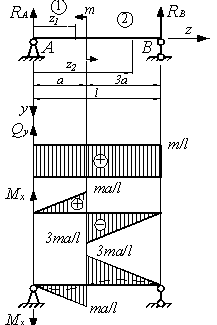
а)
б)
Решение.
1.
Определение опорных реакций
Из
уравнений равновесия
![]()
находим
![]()
.
2.
Определение Qy,
Mx
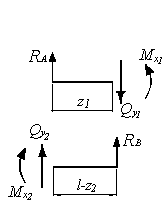
методом сечений (рис. б) и построение
эпюр
Из
уравнений равновесия отсеченных частей
балки находим
![]()
![]()
По
полученным значениям строим эпюры (рис.
а). Отметим, что сосредоточенный момент
не повлиял на характер эпюры Qy.
На эпюре моментов сосредоточенный
момент вызвал скачок на величину этого
момента. Наклон прямых на эпюре моментов
одинаков, что соответствует правилу
Журавского.
Пример
2.
Построить
эпюры Qy,
Mx
для балки (см. рис. а).

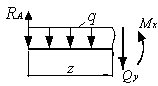
а)
б)
Решение.
1.
Определение опорных реакций
Из
уравнений равновесия
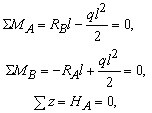
находим
![]()
.
2.
Определение Qy,
Mx
методом сечения и построение эпюр
Из
уравнения равновесия отсеченной части
балки (рис. б) находим
![]()
.
Как
видно, график-эпюра
–
прямая линия, а
– квадратичная парабола. Полагая
![]()
и
![]()
,
находим значения усилий в этих точках.
При
значения внутренних усилий
![]()
а при
:
![]()
Отметим, что в шарнирах моменты всегда
равны нулю. На эпюре
при
![]()
перерезывающая сила
![]()
.
Это признак экстремума на эпюре моментов.
Вычислим при
![]()
максимум изгибающего момента
![]()
Откладываем
полученное значение на графике-эпюре
и проводим через три точки параболу. По
правилу зонтика и дождика выпуклость
параболы обращена к верху, а на перевернутой
эпюре моментов – к низу.
Эпюра моментов напоминает изогнутую
ось балки, изображенную на рис. а
пунктиром.
Пример
3.
Построить
эпюры Qy,
Mx
для балки (см. рис. а).
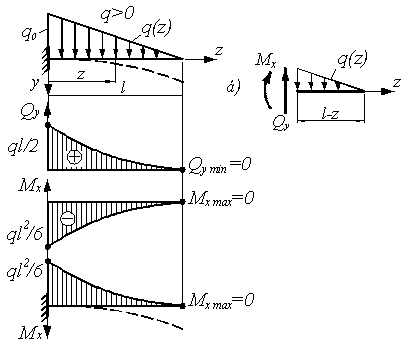
а)
б)
Решение.
Методом
сечений (рис. б)
находим
![]()
![]()
Поскольку
![]()
то эпюра
–
квадратичная парабола, а
![]()
–
кубическая.
При
,
![]()
.
При
имеем
![]()
.
Эпюра
испытывает экстремум при
![]()
,
когда
![]()
Выпуклость эпюры
определяется знаком ее второй производной:
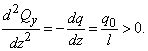
Так как
вторая производная возрастает, то
выпуклость направлена вниз.
Экстремум
эпюры моментов
имеет место в сечении, где
![]()
,
т.е. на конце консоли при
![]()
.
В этом сечении
![]()
.
Выпуклость кривой
определяется по знаку второй производной,
то есть по правилу зонтика:
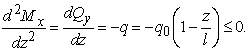
В нашем
случае выпуклость направлена вверх.
Пример
4.
Построить
эпюры перерезывающих сил и изгибающих
моментов Qy,
Mx
для балки (см. рис. а), если
![]()
,
интенсивность нагрузки
![]()
.


а)
б)
Решение.
1.
Определение опорных реакций из уравнений
равновесия
Составим
два независимых уравнения равновесия
моментов относительно опор A,
B:
![]()
Находим
опорные реакции
![]()
.
Для
статической проверки составляем третье
зависимое уравнение равновесия в
проекции на вертикальную ось:
![]()
.
Подставляем в это уравнение значения
найденных реактивных сил и получаем
![]()
Следовательно,
опорные реакции определены правильно.
2.
Определение Qy,
Mx
методом сечения и построение их эпюр
Балка
имеет два участка
![]()
и
![]()
с различными аналитическими выражениями
внутренних силовых факторов.
На
первом участке (рис. б) методом
сечений с учетом
![]()
находим

Эпюра
−
квадратичная парабола, а
− кубическая.
При
![]()
имеем
![]()
,
а при
![]()
имеем
![]()
.
Согласно дифференциальным зависимостям
Журавского экстремум эпюры
имеет место в сечении
![]()
,
где
![]()
,
экстремум эпюры
в сечении, где
![]()
,
что дает
![]()
,
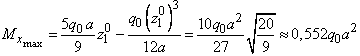
.
На
втором участке (рис. б) методом
сечений получаем
![]()
![]()
При
![]()
![]()
.
Эпюра
− постоянна, а
− наклонная прямая. Максимальный момент
определяется по формуле
![]()
.
3.
Расчет на прочность
Условие
прочности записываем в виде
![]()
Пример
6.
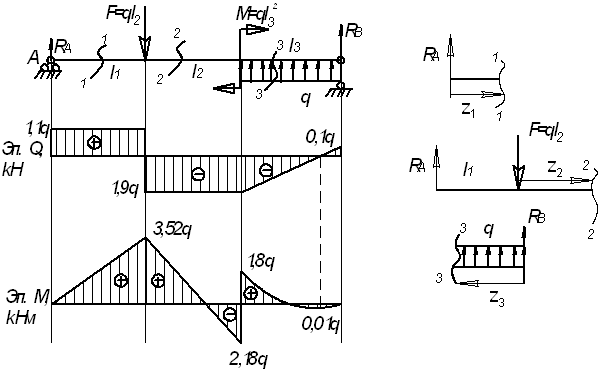
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М.
Дано:
l1=3,8 м; l2=3,6
м; l3=1,4 м, F=3,8q;
M=14,44q
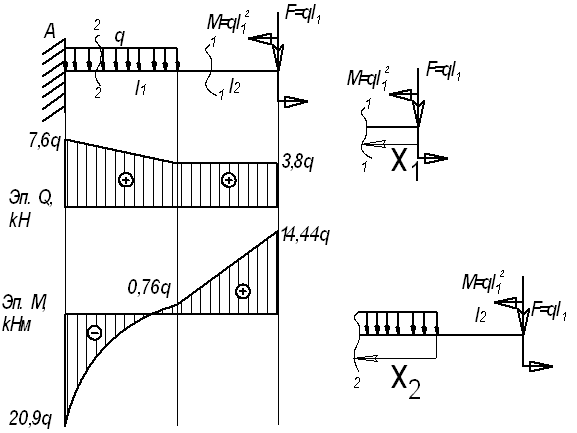
Решение.
Рассмотрим
сечение 1-1:
![]()
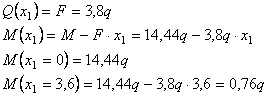
Рассмотрим
сечение 2-2:
![]()

Пример
7.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М.
Дано:
l1=3,8 м; l2=3,6
м; l3=1,4 м, F=3,8q;
M=12,96q
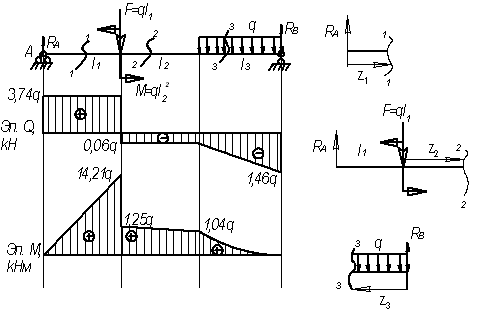
Решение.
Находим
реакции опор
![]()
![]()
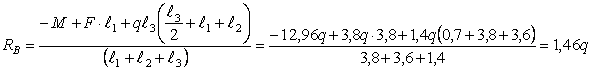
![]()
![]()
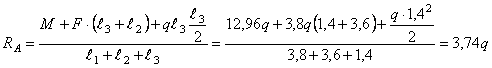
Проверка
![]()
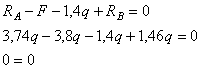
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим сечение 3-3:

Пример
8.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М.
Дано:
l1=2 м; l2=3,4
м; l3=2 м, F=3,4q;
M=4q
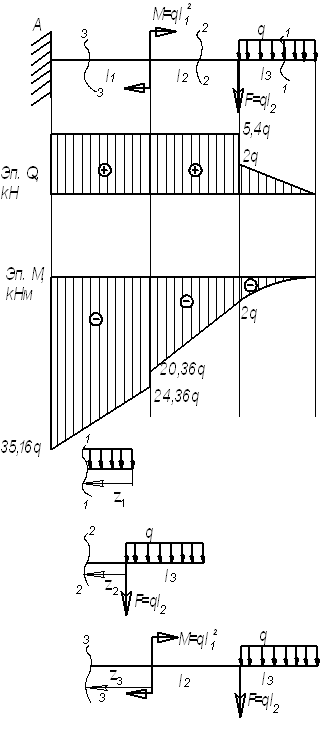
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 3-3:
![]()
![]()
![]()
![]()
![]()
Пример
9.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=2 м; l2=3,4
м; l3=2 м, F=2q;
M=11,56q
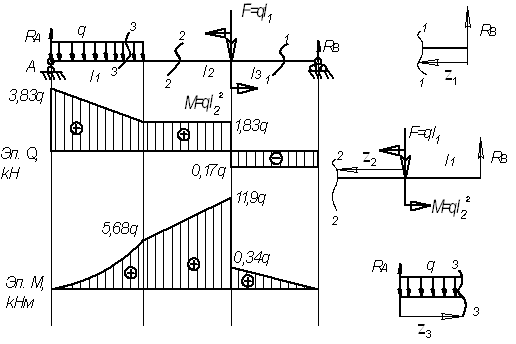
Решение.
Находим
реакции опор
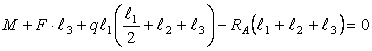
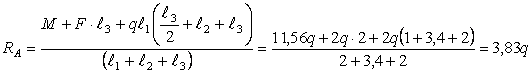
![]()
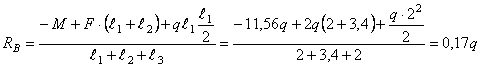
Проверка
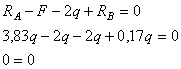
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим сечение 3-3:
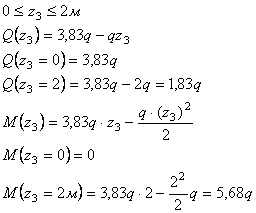
Пример
10.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=2,3 м; l2=3,4
м; l3=1,8 м, F=3,4q;
M=2,65q
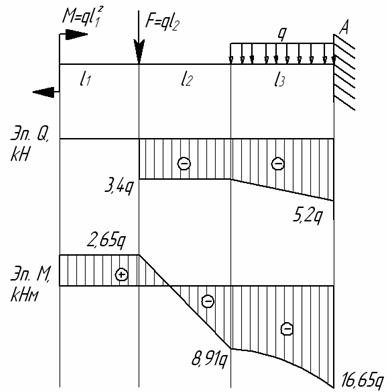
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 3-3:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример 11.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=2,3 м; l2=3,4
м; l3=1,8 м, F=1,8q;
M=2,65q
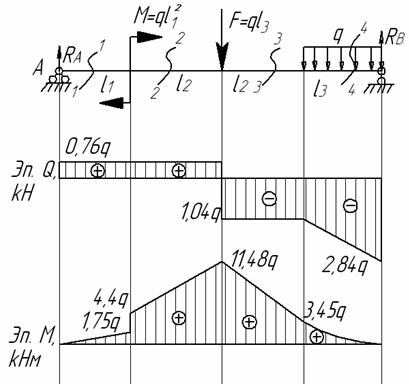
Решение.
Находим
реакции опор
![]()
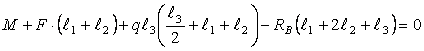

![]()
![]()
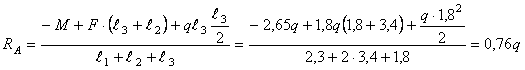
Проверка
![]()
![]()
![]()
0=0
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 3-3:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 4-4:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пример
12.
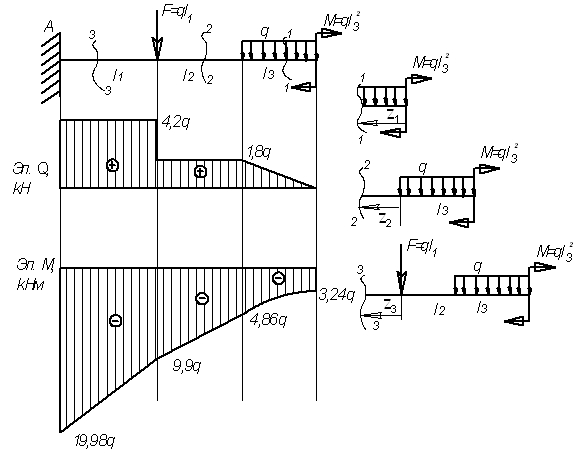
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=2,4 м; l2=2,8
м; l3=1,8 м, F=2,4q;
M=3,24q
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
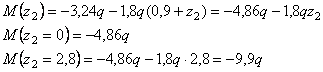
Рассмотрим
сечение 3-3:
![]()
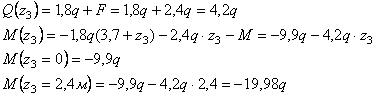
Пример
13.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=2,4 м; l2=2,8
м; l3=2 м, F=2,8q;
M=7,84q
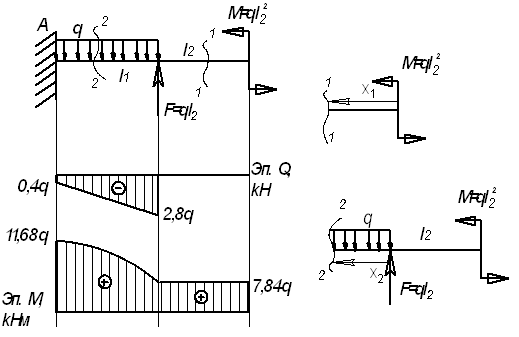
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
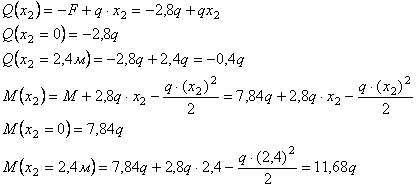
Пример
14.
Для
заданной балки (см.рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=3,2 м; l2=3
м; l3=2 м, F=3,2q;
M=10,24q
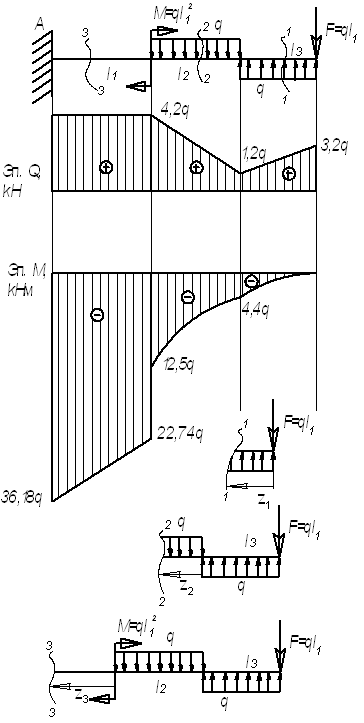
Решение.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
15.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=3,2 м; l2=3
м; l3=2 м, F=3q;
M=10,24q
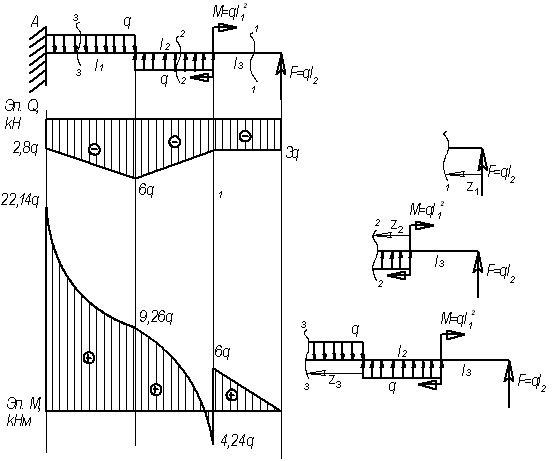
Решение.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
16.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=3,2 м; l2=3
м; l3=2 м, F=3q;
M=4q
Решение.
Находим
реакции опор
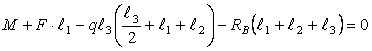
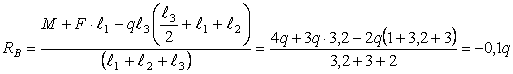
![]()
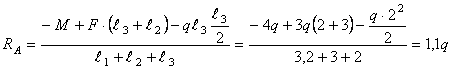
Проверка
![]()
![]()
![]()
0=0
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:

Рассмотрим
сечение 2-2:

Рассмотрим
сечение 3-3:

Пример
17.
Для
заданной балки (см. рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=3,2 м; l2=2,4
м; l3=2 м, F=3,2q;
M=10,24q
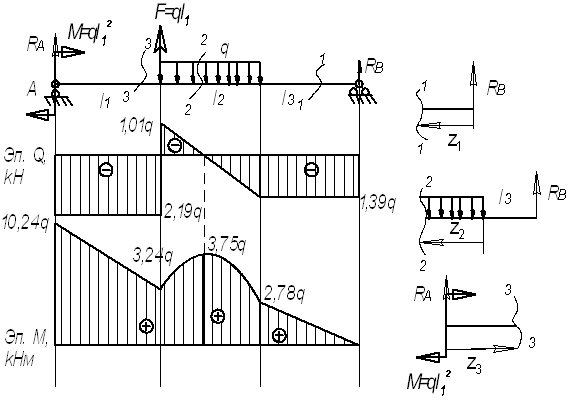
Решение.
Находим
реакции опор

Проверка
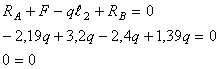
Реакции
опор найдены правильно.
Рассмотрим
сечение 1-1:
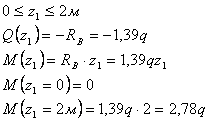
Рассмотрим
сечение 2-2:
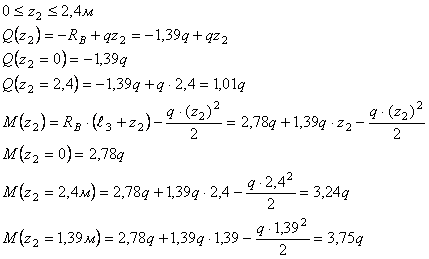
Рассмотрим
сечение 3-3:

Пример
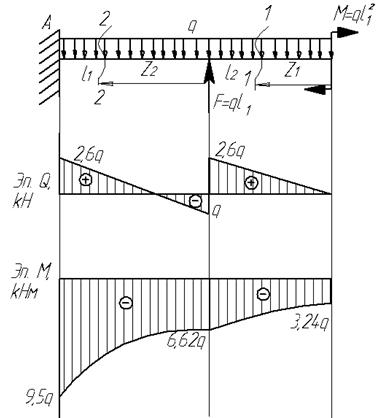
18.
Для
заданной балки (см.рис.) построить эпюры
от силы Q и от момента
М
Дано:
l1=3,6 м; l2=2,6
м; F=3,6q;
M=3,24q
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
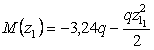
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
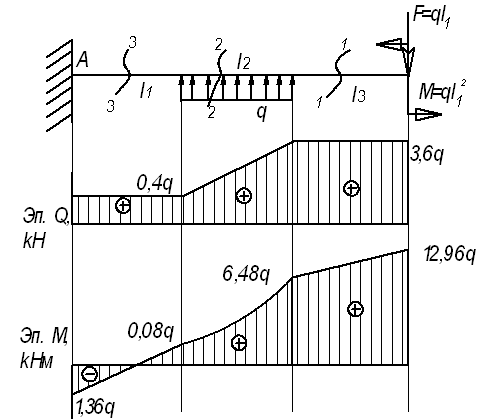
Пример
19.
Для
заданной балки (см.рис.) построить эпюры
от силы Q и от
момента М
Дано:
l1=3,6 м; l2=3,2
м; l3=1,8 м, F=3,6q;
M=12,96q
Решение.
Рассмотрим
сечение 1-1:
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 2-2:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассмотрим
сечение 3-3:
![]()
![]()
![]()
![]()
![]()
![]()
Пример
20.
Построить
эпюры Qy
и Мх для балки с консолью.
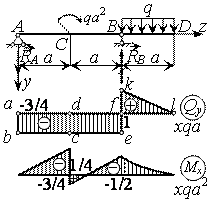
Решение.
1.
Определение опорных реакций. Составляем
уравнения равновесия:
![]()
,
RA![]()
a
–
qa2
–
qa![]()
/2
= 0,
откуда
![]()
,
![]()
,
RВ
a
– qa2–
qa![]()
a/2
= 0,
откуда
![]()
.
Проверка:
![]()
,
RA
– RB
+ qa
= 3qa/4 –
7qa/4 + qa
º
0.
2.
Построение эпюр поперечной силы и
изгибающего момента.
Э п ю
р а Qy.
В сечении А происходит скачок вниз
на величину реакции RA
и QA
= –RA.
На всем протяжении участков АС и СВ
распределенная нагрузка отсутствует
(q = 0), поэтому эпюра
Qy
представляется отрезком прямой,
параллельной оси абсцисс. Наличие пары
сил на эпюре Qy
не отражается. В сечении В происходит
скачок вверх, равный по величине
приложенной реакции RB,
и правее этого сечения имеем QBD
= QBC
+RB=
-3qa/4 + 7qa/4
= qa. На участке BD
поперечная сила изменяется по линейному
закону (Qy
= Qo–qz)
от Qo
= QBD
= qa до QD
= QBD
– qa = 0. По условию
загружения балки в сечении D
нет сосредоточенной силы, поэтому QD=0.
Совпадение значений QD,
полученных независимо друг от друга,
служит проверкой правильности построения
эпюры Qy.
Э п ю
р а Мх. Она строится по
формуле Мх = Мо +
![]()
.
На опоре А нет пары сил, поэтому МА
=0. На участке АС момент изменяется
по линейному закону. Находим момент в
сечении, бесконечно близком слева от
точки С: МСА = Мо
+
![]()
=
-3 qa
/4
= -3qa2/4. По двум
точкам (А и С) строим наклонную
прямую. Пара сил, приложенная в сечении
С, вызывает растяжение нижних волокон
балки при движении слева направо, поэтому
на эпюре Мх скачок вниз и
в бесконечно близком сечении справа
от точки С изгибающий момент
равен: MCB
= MCA
+ qa2 = qa2/4.
Находим момент в сечении В: MB
= MCB
+
![]()
=
qa2/4 – 3qa2/4
= –qa2/2 и по двум
точкам строим наклонную прямую. На
участке BD момент
изменяется по квадратичному закону,
достигая в сечении D
значения, равного MD
= MB
+
![]()
=
–qa2/2 + (1/2)qa
=
0. С другой стороны, по условию загружения
балки на свободном конце MD
= 0. Совпадение результатов служит
проверкой правильности построения
эпюры Мх. По двум точкам
(В и D) приближенно
строим параболу, обращенную выпуклостью
вниз (в направлении нагрузки q).
Вершина параболы совпадает с точкой D,
так как QD
= 0.
Пример
21.
Построить
эпюры Qy
и Мх для простой консоли,
изображенной на рисунке.
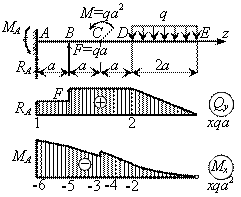
Решение.
1.
Определение опорных реакций. Составляем
уравнения равновесия:
,
MA
+ F
+ M –
q
a![]()
a
= 0,
откуда
MA
= 6qa2;
![]()
,
RA
= q
a
– F = qa.
2.
Построение эпюр поперечной силы и
изгибающего момента.
Э п ю
р а Qy.
В сечении А имеем QA
= RA
(скачок на величину и в направлении
реакции RA
= qa). На участке АВ
погонной нагрузки нет, поэтому поперечная
сила постоянна. В сечении В поперечная
сила меняется скачком от QBA
= QA
= qa до QBC
= QBA
+ F = 2qa
(скачок на величину и в направлении силы
F = qa).
На участках ВС и CD
поперечная сила опять сохраняет
постоянное значение, т.е. QBC
= QCD
= 2qa. На участке DE
поперечная сила изменяется по линейному
закону от QD
= 2qa до QE
= QD
– q
a
= 0.
Э п ю
р а Мх. В сечении А
приложен момент МА,
вызывающий растяжение верхних волокон,
поэтому на эпюре изгибающего момента
происходит скачок вверх на величину
момента MA
= 6qa2.
На
участке АВ Мх изменяется
по линейному закону. Вычисляем момент
в сечении В MB
= MA
+
= -6qa2 + qa×a
= -5qa2 и проводим
наклонную прямую. Аналогично на участках
ВС и СD. В
бесконечно близком сечении слева от
точки С момент равен MСB
= MB
+
=
-5qa2 + 2qa
= -3qa2.
В сечении
С на эпюре Мх скачок
вверх, равный приложенной паре сил M
= qa2, и правее
этого сечения имеем MCD
= MCB
– qa2 = -3qa2
– qa2 = -4qa2.
Момент
в сечении D MD
= MCD
+
= -4qa2 + 2qa
= -2qa2.
На
участке DE изгибающий
момент изменяется по закону квадратной
параболы, обращенной выпуклостью вниз
(в сторону погонной нагрузки q).
В сечении Е по условию загружения
балки МЕ = 0. По двум точкам
D и Е приближенно
строим параболу.
Пример
22.
Построить
эпюры Qy
и Мх для балки.
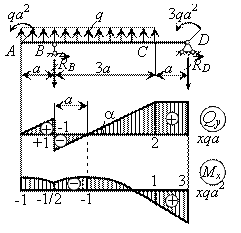
Решение.
1.
Определение опорных реакций. Составляем
уравнения равновесия:
,
q
a
+ qa2
+ 3qa2–RD
a
= 0,
откуда
RD
= 2qa;
![]()
,
RB
a
+ qa2
+3qa2–q
a![]()
a
= 0,
откуда
RB
= 2qa.
П р о в е р к а
,
q×4a
– RB
– RD
= 4qa –
2qa – 2qa
= 0.
2.
Построение эпюр поперечной силы и
изгибающего момента.
Э п ю
р а Qy. Строится по формуле
Qy = Qo ±
qz. В данном случае перед вторым
слагаемым следует взять знак “плюс”,
так как погонная нагрузка положительна
(см. правила построения эпюр). На участках
АВ и ВС эпюра Qy
изображается прямой, наклоненной вверх
(в направлении погонной нагрузки q),
а на участке CD поперечная сила
постоянна (q = 0). В сечениях В и D
на балку действуют сосредоточенные
силы RA и RD,
поэтому на эпюре Qy возникают
скачки. Вычисляем значения поперечной
силы в характерных точках QA
= 0,
QBA
= QA
+ q×a
= qa,
QBC
= QBA
– RB
= qa – 2qa
= –qa,
QC
= QBC
+ q
a
= –qa + 3qa
= 2qa и строим эпюру
Qy.
Э п ю
р а Мх. Она строится по
формуле Мх = Мо +
.
На участках с погонной нагрузкой (АВ
и ВС) изгибающий момент изменяется
по закону квадратной параболы Mx
= Mo + Qoz +
0,5qz2, обращенной выпуклостью
вверх (в сторону погонной нагрузки q).
В сечениях А и D,
где приложены сосредоточенные пары, на
эпюре Мх наблюдаются
скачки, причем момент qa2
вызывает растяжение сверху (при обходе
слева направо), поэтому в сечении А
скачок направлен вверх, а момент 3qa2
вызывает растяжение снизу (при обходе
справа налево), поэтому в сечении D
скачок происходит вниз. На участке АВ
парабола строится по двум точкам А
и В, а на участке ВС – по трем
точкам (к крайним точкам В и С
добавляется точка экстремума). Положение
точки экстремума определяется из условия
zo
= QBC
/![]()
.
Согласно дифференциальной зависимости
=
dQ/dz
= q, поэтому zo
= qa/q
= 0. Вычисляем значения момента в
характерных точках:
MA
= –qa2, MB
= MA
+
= –qa2 + (1/2)![]()
a
= –qa2/2,
Mmax
= MB
+
= –qa2/2
– (1/2)
a
= –qa2,
MC
= Mmax
+
= –qa2
+ (1/2)
qa
a
= qa2
и строим эпюру Мх.
Пример
23.
По
заданной эпюре поперечной силы Qy
установить нагрузку, действующую на
двухопорную балку, и ее опорные реакции.
Построить также эпюру изгибающего
момента, учитывая, что на правой опоре
С приложена пара сил.
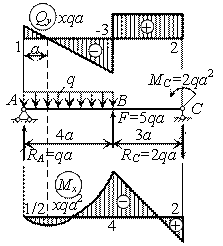
Решение.
Скачки
на эпюре Qy
свидетельствуют о приложенных в этих
сечениях сосредоточенных силах. Приняв
направление обхода слева направо,
получим: реакция в точке А равна RA
= qa и направлена вверх;
в сечении В приложена сосредоточенная
сила F = 5qa,
направленная вверх; наконец, реакция
RB
= 2qa и направлена вниз.
На участке АВ поперечная сила
изменяется по линейному закону, что
связано с наличием погонной нагрузки,
интенсивность которой определяется
как тангенс угла наклона прямой qy
= dQ/dz = (-3qa – qa)/4a = –q.
Знак “минус” означает, что нагрузка
направлена вниз. Для определения
неизвестной пары сил М, приложенной
в сечении С, составим уравнение
моментов относительно этой точки:
![]()
,
–RA![]()
a
– F
a
+ q
a
a
+ MC
= 0,
откуда MC
= 2qa2 и направлен
против часовой стрелки.
Эпюру
Мх строим по формуле Мх
= Мо +
.
На участке АВ изгибающий момент
изменяется по квадратичному закону. На
концевой шарнирной опоре А нет пары
сил, поэтому МА = 0. В
сечении, где Qy
= 0, изгибающий момент принимает
экстремальное значение:
Mmax
= MA
+
=
(1/2)qa
= qa2/2.
Находим
момент в сечении В: MB
= Mmax
+
=
qa2/2- (1/2)3qa
a
= -4qa2 и по трем
точкам приближенно строим параболу,
обращенную выпуклостью вниз. На участке
ВС изгибающий момент изменяется
по линейному закону от MB
= -4qa2 до MC
= MB
+
=
-4qa2 + 2qa
a
= 2qa2. По условию
загружения балки также имеем MC
=2qa2. Совпадение
значений МС, найденных
независимо друг от друга, свидетельствует
о правильности построения эпюры Мх.
Пример
24.
По
заданной эпюре изгибающего момента
построить эпюру поперечной силы и
определить нагрузку, действующую на
балку. Криволинейный участок эпюры Мх
очерчен по квадратной параболе, а кружком
отмечена ее вершина.
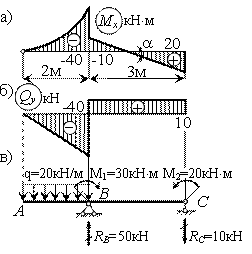
Решение.
На
участке АВ изгибающий момент
изменяется по квадратичному закону:
Mx
= Mo
+ Qoz
– 0,5qz2. Так как
вершина параболы совпадает с точкой
А, то Мо =МА
=0 и Qo
= 0. Следовательно, Мх =
-0,5qz2. Момент в
бесконечно близком сечении слева от
опоры В, судя по приведенной
эпюре, равен МВА = -40 кНм.
С другой стороны, МВА =
-0,5q(2)2.
Следовательно, q = 20
кН/м. Парабола обращена выпуклостью
вниз, поэтому и погонная нагрузка
направлена вниз.
В
сечении В изгибающий момент
изменяется скачком от МВА
= -40 кНм до МВС = -10 кНм, что
свидетельствует о наличии пары сил М1
= 30 кНм, вызывающей растяжение нижних
волокон (при обходе слева направо), т.е.
направленной по часовой стрелке. На
опоре С приложена пара сил с моментом
М2 = 20 кНм, вызывающая растяжение
снизу (при обходе справа налево), т.е.
направленная против часовой стрелки.
На
участке ВС поперечная сила постоянна
и равна тангенсу угла наклона прямой,
т.е. QBC = dM/dz =
=
(20 + 10)/3 = 10 кН. На участке АВ поперечная
сила изменяется по линейному закону
(Qy = Qo – qz)
от Qo
= QA
= 0 до QBA
= –q
= -40 кН. По скачкам на эпюре Qy
находим величины и направления реакций:
RB
= 50 кН (направлена вверх) RC
= 10 кН (направлена вниз).
Пример
25.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис.1).
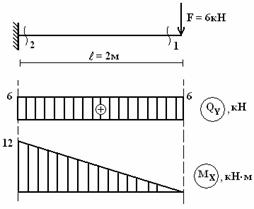
Рис.1
Решение.
1)
Проведем две оси, параллельные оси балки
(одну для эпюры QY,
вторую для эпюры MX).
2) Балка
имеет один участок загружения.
3) Строим
эпюру QY.
Сделаем сечение (1), отбросим жесткую
заделку. Учитывая правило знаков, получим
![]()
.
В сечении (2) получим
![]()
.
Силы
![]()
,
так как сила F
поворачивает оставшуюся часть балки
вокруг сечения по часовой стрелке
(рис.2,а).
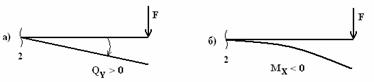
Рис. 2
Положительные
значения поперечной силы откладывают
всегда выше оси.
Соединим
их прямой линией, поставим знак, эпюру
заштрихуем, обозначим.
4) Строим
эпюру МХ. Сделав сечение и отбросив
часть с жесткой заделкой, сосчитаем
момент от силы F относительно
сделанного сечения. Получим
![]()
.
Для эпюры изгибающих моментов принимается
следующее правило: значения моментов
откладываются от оси в сторону растянутого
волокна. Из рис.2,б, следует, что сила F
растягивает верхние волокна, поэтому
полученное значение МХ откладываем
выше оси. Соединяем отложенные значения
прямой линией. Знак на эпюре изгибающих
моментов можно не ставить. Эпюру штрихуем
и обозначаем (рис.1).
5)
Проверка эпюр. К балке не приложена
распределенная нагрузка, следовательно,
на графиках QY
и МХ имеем прямые линии, причем
на эпюре QY
это прямая, параллельная оси. На свободном
конце балки приложена сосредоточенная
сила F = 6кН
![]()
в этом сечении на эпюре QY
образовался скачок, равный 6.
Пример
26.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис.).
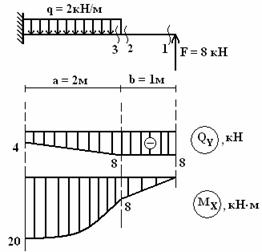
Решение.
1)
Проводим оси для построения эпюр.
2) Делим
балку на два участка загружения.
3) Строим
эпюру QY.
1-й
участок:
![]()
;
![]()
.
Откладываем
значения ниже оси, соединяем прямой
линией.
2-й
участок:
![]()
;
![]()
.
Значение
![]()
откладываем ниже оси, соединяем прямой
линией.
Ставим
знаки, эпюру штрихуем и обозначаем.
4) Строим
эпюру МХ.
1-й
участок:
![]()
;
![]()
.
Откладываем
значения
![]()
ниже оси, так как сила F
растягивает нижние волокна, соединяем
прямой линией.
2-й
участок:
![]()
;
![]()
.
Значения
![]()
откладываем ниже оси и соединяем
параболой. При этом выпуклость параболы
должна быть обращена в сторону действия
распределенной нагрузки. Это правило
называют «правилом паруса». Роль паруса
здесь играет эпюра, а роль ветра –
нагрузка.
5)
Проверка эпюр. На участке балки с
распределенной нагрузкой получаем на
эпюре QY
наклонную прямую, на эпюре MX
– параболу. В сечении с приложенной
сосредоточенной силой F
= 8 кН на эпюре QY
образовался скачек равный 8.
Пример
27.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис.).
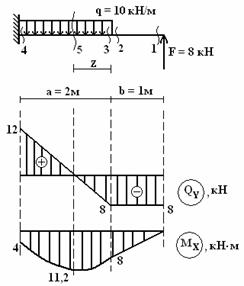
Решение.
1)
Проводим оси для построения эпюр.
2) Делим
балку на два участка загружения.
3) Строим
эпюру QY.
1-й
участок.
;
.
Откладываем
значения ниже оси, соединяем прямой
линией.
2-й
участок.
;
![]()
.
Откладываем
![]()
ниже оси, а
![]()
– выше оси, соединяем прямой линией (см.
рис.).
4) Строим
эпюру МХ.
1-й
участок:
;
![]()
.
Откладываем
ниже оси, соединяем с нулем прямой
линией.
2-й
участок:
Из
рисунка следует, что эпюра поперечных
сил QY
на этом участке пересекает ось, то есть
в некотором сечении (5) сила
![]()
.
Отсюда следует, что в сечении (5) изгибающий
момент МХ достигает экстремального
значения (максимума или минимума). Таким
образом, на этом участке следует
просчитать момент в трех точках.
![]()
.
![]()
.
Определим
экстремальное значение момента. Выясним
сначала, на каком расстоянии Z от
правой границы участка находится сечение
(5), в котором поперечная сила равна нулю.
![]()
.
Найдем
значение момента.
![]()
.
Откладываем
значения
![]()
ниже оси и соединяем параболой по правилу
«паруса», то есть выпуклостью вниз (см.
рис.).
5)
Проверка эпюр. Все линии на эпюрах
соответствуют приложенным нагрузкам,
силе F = 8 кН соответствует
скачок, равный 8 на эпюре QY.
Пример
28.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис. 1).
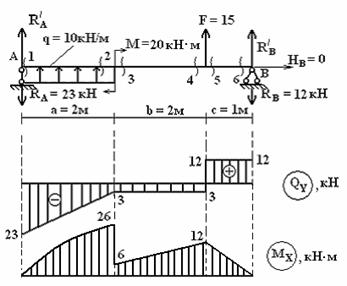
Рис.1
Решение.
1) Расчет
балки с шарнирным закреплением следует
начинать с определения реакций связей.
Расставим эти реакции. В шарнирно
–подвижной опоре А возникает одна
вертикальная реакция R¢A.
В шарнирно-неподвижной опоре В, вообще
говоря, возникает две реакции –
вертикальная R¢B
и горизонтальная НВ, однако,
поскольку в случае вертикального
плоского изгиба все силы действуют
перпендикулярно оси балки, горизонтальная
реакция НВ всегда будет равна
нулю, поэтому в дальнейшем показывать
ее на схеме балки не будем. Вертикальные
реакции найдем из уравнений статики.
![]()
;
![]()
.
![]()
;
![]()
.
При
записи уравнений использовалось
следующее правило знаков: если сила
поворачивает балку вокруг т.А (т.В) по
часовой стрелке, то момент от этой силы
берется со знаком «+».
Для
проверки найденных реакций используем
уравнение статики:
![]()
(сумма всех вертикальных сил должна
быть равна нулю). При этом силы, изображенные
на схеме балки направленными вверх,
берем со знаком «+».
![]()
.
Подставим
сюда найденные значения реакций со
своими знаками.
– 23 + 10
× 2 + 15 – 12 = 0; 35 – 25
=0; 0 = 0.
Поскольку
направления вертикальных реакций
поначалу были взяты произвольно, то
полученные в результате знаки «-» у
реакций RA,
RB
показывают, что мы не угадали направление
реакций, в действительности они направлены
вниз. Удобно изменить направление этих
реакций на обратное и в дальнейшем
считать эти реакции положительными
(см. рис.1).
2)
Проводим оси для построения эпюр.
3) Делим
балку на три участка загружения.
4) Так
как все реакции в закреплениях балки
найдены, то, сделав сечение, можно
отбрасывать любую (обычно более
загруженную) часть балки .
5) Строим
эпюру QY.
1-й
участок.
![]()
(отбросили правую часть балки),
![]()
(отбросили левую часть балки).
Пару
сил М = 20 кНм при вычислении QY,
естественно, не учитываем.
Откладываем
значения от оси, соединяем прямой линией.
2-й
участок.
![]()
;
![]()
.
3-й
участок.
![]()
;
![]()
.
6) Строим
эпюру МХ.
1-й
участок:
![]()
;
![]()
.
Чтобы
не ошибиться в знаке изгибающего момента,
сечение, в котором он определяется,
следует представлять защемленным, а
опоры – отброшенными (рис.2):
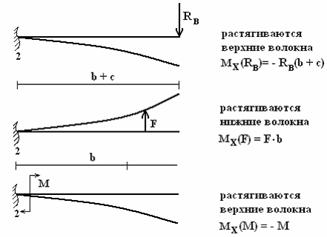
Рис.2
Откладываем
значения от оси и соединяем параболой
по правилу «паруса», то есть направленной
выпуклостью вверх.
2-й
участок:
![]()
![]()
.
Откладываем
значения выше оси, соединяем прямой
линией.
3-й
участок:
![]()
![]()
.
Отложенные
от оси значения соединяем прямой линией
(рис.1).
6)
Проверка эпюр. Все линии на эпюрах
соответствуют действующим нагрузкам.
К балке приложены три сосредоточенные
силы – RA,
F, RB.
На эпюре QY
получили три скачка
на опоре А – равный RA
= 23, на границе 2-го и 3-го участков –
равный F = 3 + 12 = 15, на опоре
В – равный RB
= 12. К балке приложена пара сил М = 20. На
эпюре МХ на границе 1-го и 2-го
участков имеем скачок, равный М = (26 – 6)
= 20.
Пример
29.
Построить
эпюры поперечных сил QY
и изгибающего момента MX
(см. рис.).
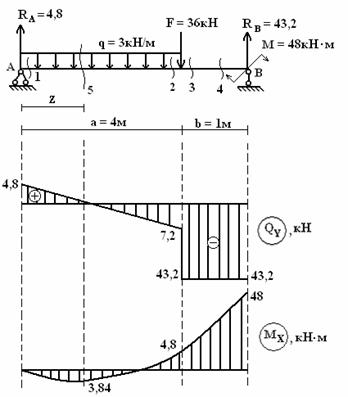
Решение.
1) Найдем
реакции опор RA,
RB.
;
![]()
;
![]()
.
Проверка:
![]()
![]()
.
Обе
реакции получились положительными, то
есть мы угадали их направление, они
действительно направлены вверх.
2) Балка
имеет два участка загружения.
3) Строим
эпюру QY.
1-й
участок.
![]()
;
![]()
.
Откладываем
значения от оси и соединяем прямой
линией.
2-й
участок.
![]()
;
![]()
.
Откладываем
значения от оси и соединяем прямой (см.
рис.).
4) Строим
эпюру МХ.
1-й
участок:
Из эпюры
сил следует, что на этом участке будет
возникать экстремальный момент, поэтому
будем определять МХ в трех сечениях.
(отбрасываем правую часть балки);
![]()
(отбрасываем левую часть балки).
Находим
координату Z сечения (5):
![]()
.
Находим
экстремальный момент.
![]()
.
Откладываем
значения от оси и соединяем параболой
по правилу «паруса», то есть выпуклостью
вниз.
2-й
участок.
![]()
;
![]()
.
Отложенные
от оси значения соединяем прямой (см.
рис.).
5)
Проверка эпюр.
Линии
эпюры соответствуют приложенным
нагрузкам. К балке приложены три
сосредоточенные силы – RA,
F, RB
на эпюре QY
в соответствующих сечениях имеем скачки.
К балке
на опоре В приложена пара сил М: на эпюре
МХ имеем на правом конце скачок,
равный М = 48.
Пример
30.
Дана
балка с действующими на нее нагрузками
(рис. а). Требуется определить
внутренние усилия – поперечную силу Q
и изгибающий момент М в балке,
построить графики их изменения вдоль
оси стержня (эпюры Q и М).
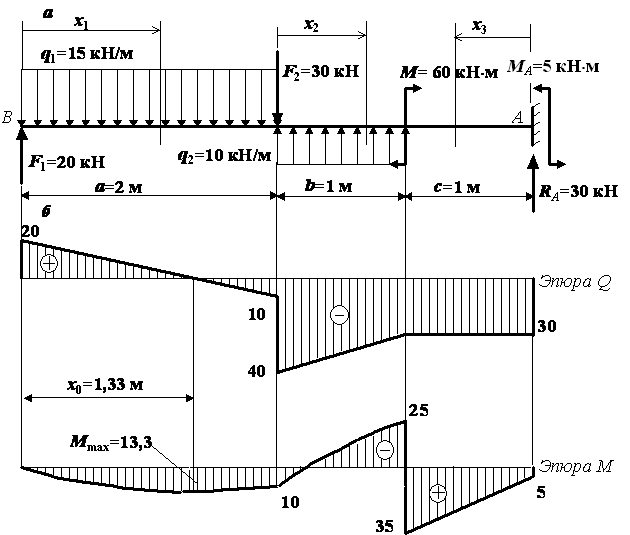
Решение.
Прежде
всего найдем опорные реакции. Балка
имеет жесткое защемление на правом
конце (В балке с заделкой можно строить
эпюры Q и М без определения
опорных реакций, рассматривая все силы
с одной стороны от сечения – со свободного
конца. Но студенту, только начинающему
осваивать построение эпюр, рекомендуем
все же реакции находить. Это дополнительная
проверка правильности решения задачи)
и в этом закреплении при заданной
вертикальной нагрузке возникают две
опорные реакции: вертикальная реакция
RA и реактивный момент MA.
Горизонтальная реакция при действии
вертикальной нагрузки равна нулю. Это
следует из уравнения равновесия “сумма
проекций всех сил на горизонтальную
ось равна нулю”. Определим RA
и MA, используя два других
уравнения статики. Желательно составлять
такие уравнения, в каждое из которых
входит только одна неизвестная. В данном
случае такими уравнениями являются
“сумма проекций всех сил на вертикальную
ось (ось z) равна нулю” и “сумма
моментов всех сил относительно точки
А равна нулю”:
![]()
;
![]()
;
![]()
;
![]()
Из
первого уравнения найдем RA
= 30 кН, из второго – МА
=5 кНм. Полученные положительные знаки
опорных реакций подтверждают выбранные
нами направления опорных реакций: RA
– вверх, а МА – против
часовой стрелки. Для проверки рекомендуем
использовать любое другое уравнение
равновесия, например
![]()
:
– 30×2
– 15×2×1
– 60 + 10×1×2,5
+ 30×4+5 = – 150 + 150 = 0.
Теперь
определяем внутренние усилия: поперечную
силу Q и изгибающий момент М. В
соответствии с методом сечений рассекаем
балку на каждом участке (в данной задаче
их три) произвольным сечением и
рассматриваем все силы, расположенные
с одной стороны от сечения: слева или
справа. Удобно рассматривать все силы
с той стороны от сечения, где сил меньше.
Начало отсчета координаты x на каждом
участке можно выбирать произвольным
образом. Например, на рис. а начало
отсчета x на каждом участке – свое
и находится в начале участка. Запишем
выражения для Q и М на каждом
участке.
Участок
1:
![]()
.
Рассмотрим
силы, расположенные слева от сечения.
По определению поперечной силы и с
учетом правила знаков для Q :
![]()
.
Здесь
![]()
– равнодействующая равномерно
распределенной нагрузки, действующей
слева от сечения.
По
определению изгибающего момента и с
учетом правила знаков для М :
![]()
,
где во
втором слагаемом
![]()
– плечо равнодействующей равномерно
распределенной нагрузки (![]()
),
взятой слева от сечения (равнодействующая
приложена по середине длины отсеченной
части балки x1).
Для
построения эпюр найдем значения Q
и М на границах участка:
в начале
участка (х1 = 0)
![]()
,
а
![]()
;
в конце
участка (![]()
)
![]()
;
![]()
.
Участок
2:
![]()
.
Снова
рассмотрим все силы, расположенные
слева от сечения.
![]()
;
![]()
.
Граничные
значения Q и М:
в начале
участка (![]()
)
![]()
;
,
в конце
участка (![]()
)
![]()
;
![]()
.
Участок
3:
![]()
.
Теперь
рациональнее рассмотреть все силы
справа от сечения. Тогда
![]()
;
![]()
.
Из этих
выражений следует, что поперечная сила
на третьем участке – постоянная величина,
а изгибающий момент меняется по линейному
закону и на границах участка имеет
следующие значения:
в начале
участка (![]()
)
![]()
,
в конце
участка (![]()
)
![]()
.
Запишем
результаты определения внутренних
усилий в таблицу, сосчитав численные
значения Q и М на границах участков
(табл. 1).
Таблица 1

Из
таблицы видно, что поперечная сила на
первом участке меняет свой знак, т. е.
график Q пересекает нулевую линию.
Это значит, что изгибающий момент на
этом участке имеет экстремум. Найдем
максимальное значение М на этом
участке. Сначала определим то значение
координаты х1, при котором
поперечная сила равна нулю. Обозначим
это значение координаты х0
(см. рис. ).
![]()
х0 = 1,33 м.
Чтобы
найти максимальное значение изгибающего
момента, подставим х0 в выражение
для М на первом участке:
![]()
кНм.
По
результатам вычислений в таблице строим
эпюры Q и М на каждом участке
(см. рис. б). Не забываем после
построения эпюр проанализировать
результаты по тем правилам проверки
правильности построения эпюр, которые
перечислены ранее.
Расчет балки на прогиб нужно проводить практически для любой конструкции, чтобы проверить ее надежность и прочность. Под влиянием внешних, внутренних факторов, природных явлений балка подвержена деформации.
Балку сравнивают со стержнем, закрепленным на опорах. Чем больше опор, тем сложнее провести расчет самостоятельно. Основная нагрузка считается путем сложения сил, перпендикулярно направленных к сечению.
Данный расчет – основы сопромата, помогает определить наивысшую деформацию. Значения показателей должны входить в рамки допустимых величин.
Виды балок
При возведении зданий используется балки разных конфигураций, размеров, профиля, характера сечения. Их изготавливают из металла и дерева. Для любого вида используемого материала нужен индивидуальный расчёт изгиба.
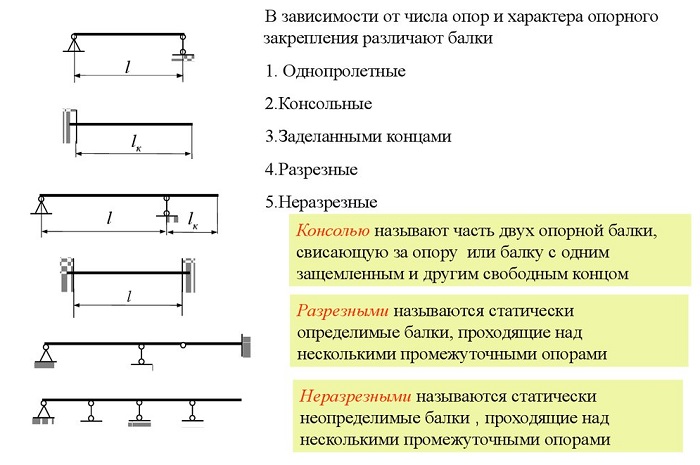
Виды балок:
-
Деревянные – их используют в основном при строительстве индивидуальных построек. Они применяются при возведении полов, потолков, несущих перекрытий. Дерево – капризный материал и подвержено деформации. Для определения максимального изгиба, существенны такие параметры: используемый профиль, размер, нагрузка, характер поперечного сечения.
-
Металлические – такие балки изготавливают из сплава металлов и сечение у них сложное. Поэтому особое внимание уделяется жесткости, а также прочности соединений. Балки из металла применяются в возведении многоэтажек, сооружений, требующих высокой прочности.
Прочность и жесткость балки
При проектировании следует учесть изгиб балок, чтобы конструкция была надежная, качественная, прочная и практичная.
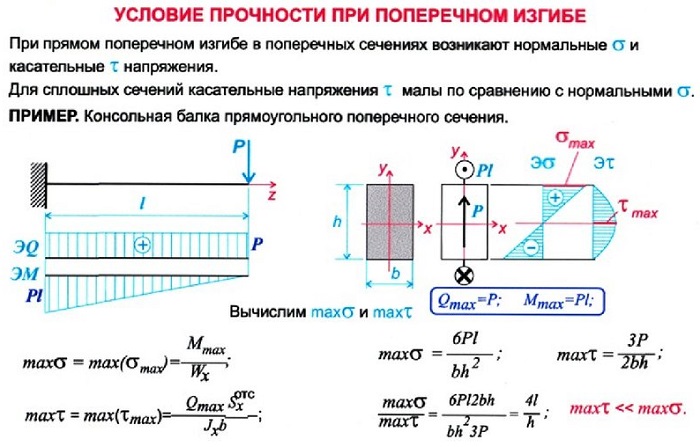
На эти параметры влияют следующие факторы:
-
величина наружных нагрузок, их положение;
-
параметры, характер, нахождение поперечного сечения;
-
продольные величины;
-
материал;
-
число опор, метод их закрепления.
Выделяют 2 метода исчисления: простой – применяется увеличительный коэффициент, и точный – дополнительно включает пограничные подсчеты.
Построение эпюр балки
Эпюра распределения величины нагрузки на объект:
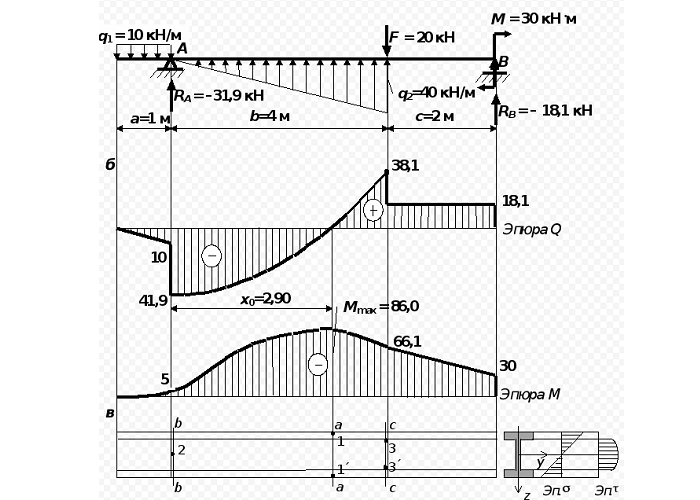
Расчет на жесткость
Алгоритм исчисления:
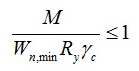
В формуле обозначены:
-
M – max момент, возникающий в брусе;
-
Wn,min – момент сопротивления сечения (табличный показатель);
-
Ry – сопротивление на изгиб (расчётный показатель);
-
γc – показатель условий труда (табличный показатель).
Такой расчет не трудоемок, но для более верного значения требуется следующее:
-
рабочий план объекта;
-
определение характеристик балки, характер сечения;
-
определение max нагрузки, воздействующей на брус;
-
оценка точки max прогиба;
-
проверка прочности max изгибающего момента.
Расчет моментов инерции и сопротивления сечения
Алгоритм исчисления:
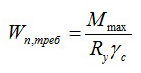
Где:
-
J – момент инерции сечения;
-
W – момент сопротивления.
Для определения данных параметров необходимо учитывать сечение по грани разреза. Если момент инерции возрастает, величина жесткости также возрастает.
Нахождение максимальной нагрузки и прогиба
Формула для вычисления:
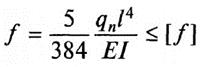
Здесь обозначены:
-
q – нагрузка равномерно-распределенная;
-
E – гибкость (табличный показатель);
-
l – длина;
-
I – момент инерции сечения.
Нагрузки учитываются статические и периодические.
Расчет на прогиб и его особенности
Он необходим для всех перекрытий при высоких эксплуатационных нагрузках.

При применении соответствующих коэффициентов, придерживаются следующего:
-
балка, держащаяся на одной жесткой и одной шарнирной опоре, подвергающаяся воздействию сосредоточенной нагрузки;
-
балка, держащаяся на жесткой и шарнирной опоре, подвергающаяся воздействию распределенной нагрузки;
-
нагрузка консольного типа;
-
воздействие комплексной нагрузки.
Пример расчет балки на прогиб
Рассмотрим задачу из курса сопромата.
Дано: балка четырехугольного сечения 20 на 30 см; поперечная сила Q = 19 кН; изгибающий момент М = 28 кНм.
Необходимо рассчитать напряжение: нормальное и в пределе К, отдаленной на 11 см от оси, узнать прочность бруса из дерева, при [σ] = 10 МПа, [τ] = 3 МПа.
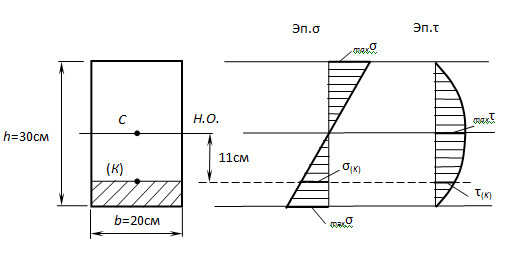
Решение.
Чтобы узнать σ(К), τ(К), σmax, τmax
определяем значение осевого момента инерции общего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсеченного ряда и статического момента середины сечения Smax:
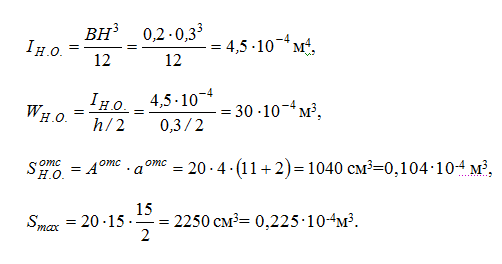
Из этого следует:
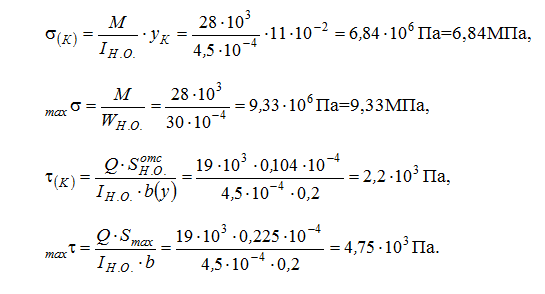
Определение прочности по нормальному напряжению:
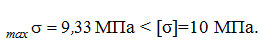
Определение прочности по касательному напряжению:
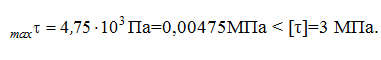
Задача решена.
При проектировании конструкций важно соблюдать все физико-механические вычисления на прочность. Удобно и качественно произвести расчеты может онлайн, что существенно сократит временные сроки.
Калькулятор выполняет подробный подсчет на основе формул, эпюр усилий, подбирает номер сечения металлической балки из прокатных профильных, двутавровых материалов, а также из металлических труб.
Расчет балки на изгиб — «вручную»!
Опубликовано 28 Апр 2013
Рубрика: Механика | 98 комментариев
 Расчет балки на изгиб «вручную», по-дедовски, позволяет познать один из важнейших, красивейших, четко математически выверенных алгоритмов науки сопротивление материалов. Использование многочисленных программ типа «ввел исходные данные…
Расчет балки на изгиб «вручную», по-дедовски, позволяет познать один из важнейших, красивейших, четко математически выверенных алгоритмов науки сопротивление материалов. Использование многочисленных программ типа «ввел исходные данные…
…– получи ответ» позволяет современному инженеру сегодня работать гораздо быстрее, чем его предшественникам сто, пятьдесят и даже двадцать лет назад. Однако при таком современном подходе инженер вынужден полностью доверять авторам программы и со временем перестает «ощущать физический смысл» расчетов. Но авторы программы – это люди, а людям свойственно ошибаться. Если бы это было не так, то не было бы многочисленных патчей, релизов, «заплаток» практически к любому программному обеспечению. Поэтому, мне кажется, любой инженер должен уметь иногда «вручную» проверить результаты расчетов.
Справка (шпаргалка, памятка) для расчётов балок на изгиб представлена ниже на рисунке.
 Давайте на простом житейском примере попробуем ей воспользоваться. Допустим, я решил сделать в квартире турник. Определено место – коридор шириной один метр двадцать сантиметров. На противоположных стенах на необходимой высоте напротив друг друга надежно закрепляю кронштейны, к которым будет крепиться балка-перекладина – пруток из стали Ст3 с наружным диаметром тридцать два миллиметра. Выдержит ли эта балка мой вес плюс дополнительные динамические нагрузки, которые возникнут при выполнении упражнений?
Давайте на простом житейском примере попробуем ей воспользоваться. Допустим, я решил сделать в квартире турник. Определено место – коридор шириной один метр двадцать сантиметров. На противоположных стенах на необходимой высоте напротив друг друга надежно закрепляю кронштейны, к которым будет крепиться балка-перекладина – пруток из стали Ст3 с наружным диаметром тридцать два миллиметра. Выдержит ли эта балка мой вес плюс дополнительные динамические нагрузки, которые возникнут при выполнении упражнений?
Чертим схему для расчета балки на изгиб. Очевидно, что наиболее опасной будет схема приложения внешней нагрузки, когда я начну подтягиваться, зацепившись одной рукой за середину перекладины.
 Исходные данные:
Исходные данные:
F1 = 900 н – сила, действующая на балку (мой вес) без учета динамики
b1 = 0 м
b2 = 0,6 м
b3 = 1,2 м
d = 32 мм – наружный диаметр прутка, из которого сделана балка
E = 206000 н/мм^2 — модуль упругости материала балки стали Ст3
[σи] = 250 н/мм^2 — допустимые напряжения изгиба (предел текучести) для материала балки стали Ст3
Граничные условия:
Мx (0) = 0 н*м – момент в точке z = 0 м (первая опора)
Мx (1,2) = 0 н*м– момент в точке z = 1,2 м (вторая опора)
V (0) = 0 мм – прогиб в точке z = 0 м (первая опора)
V (1,2) = 0 мм – прогиб в точке z = 1,2 м (вторая опора)
Расчет:
1. Для начала вычислим момент инерции Ix и момент сопротивления Wx сечения балки. Они нам пригодятся в дальнейших расчетах. Для кругового сечения (каковым является сечение прутка):
Ix = (π*d^4)/64 = (3.14*(32/10)^4)/64 = 5,147 см^4
Wx = (π*d^3)/32 = ((3.14*(32/10)^3)/32) = 3,217 см^3
2. Составляем уравнения равновесия для вычисления реакций опор R1 и R2:
Qy = -R1+F1-R2 = 0
Мx (0) = F1*(0-b2) -R2*(0-b3) = 0
Из второго уравнения: R2 = F1*b2/b3 = 900*0.6/1.2 = 450 н
Из первого уравнения: R1 = F1-R2 = 900-450 = 450 н
3. Найдем угол поворота балки в первой опоре при z = 0 из уравнения прогиба для второго участка:
V (1.2) = V (0)+U (0)*1.2+(-R1*((1.2-b1)^3)/6+F1*((1.2-b2)^3)/6)/
/(E*Ix) = 0
U (0) = (R1*((1.2-b1)^3)/6 -F1*((1.2-b2)^3)/6)/(E*Ix)/1,2 =
= (450*((1.2-0)^3)/6 -900*((1.2-0.6)^3)/6)/
/(206000*5,147/100)/1,2 = 0,00764 рад = 0,44˚
4. Составляем уравнения для построения эпюр для первого участка (0<z<b2):
Поперечная сила: Qy (z) = -R1
Изгибающий момент: Мx (z) = -R1*(z-b1)
Угол поворота: Ux (z) = U (0)+(-R1*((z-b1)^2)/2)/(E*Ix)
Прогиб: Vy (z) = V (0)+U (0)*z+(-R1*((z-b1)^3)/6)/(E*Ix)
z = 0 м:
Qy (0) = -R1 = -450 н
Мx (0) = 0
Ux (0) = U (0) = 0,00764 рад
Vy (0) = V (0) = 0 мм
z = 0,6 м:
Qy (0,6) = -R1 = -450 н
Мx (0,6) = -R1*(0,6-b1) = -450*(0,6-0) = -270 н*м
Ux (0,6) = U (0)+(-R1*((0,6-b1)^2)/2)/(E*Ix) =
= 0,00764+(-450*((0,6-0)^2)/2)/(206000*5,147/100) = 0 рад
Vy (0,6) = V (0)+U (0)*0,6+(-R1*((0,6-b1)^3)/6)/(E*Ix) =
= 0+0,00764*0,6+(-450*((0,6-0)^3)/6)/ (206000*5,147/100) = 0,003 м
Балка прогнется по центру на 3 мм под тяжестью моего тела. Думаю, это приемлемый прогиб.
5. Пишем уравнения эпюр для второго участка (b2<z<b3):
Поперечная сила: Qy (z) = -R1+F1
Изгибающий момент: Мx (z) = -R1*(z-b1)+F1*(z-b2)
Угол поворота: Ux (z) = U (0)+(-R1*((z-b1)^2)/2+F1*((z-b2)^2)/2)/(E*Ix)
Прогиб: Vy (z) = V (0)+U (0)*z+(-R1*((z-b1)^3)/6+F1*((z-b2)^3)/6)/(E*Ix)
z = 1,2 м:
Qy (1,2) = -R1+F1 = -450+900 = 450 н
Мx (1,2) = 0 н*м
Ux (1,2) = U (0)+(-R1*((1,2-b1)^2)/2+F1*((1,2-b2)^2)/2)/(E*Ix) =
= 0,00764+(-450*((1,2-0)^2)/2+900*((1,2-0,6)^2)/2)/
/(206000*5,147/100) = -0.00764 рад
Vy (1,2) = V (1,2) = 0 м
6. Строим эпюры, используя данные полученные выше.
7. Рассчитываем напряжения изгиба в наиболее нагруженном сечении – посередине балки и сравниваем с допустимыми напряжениями:
σи = Mx max/Wx = (270*1000)/(3,217*1000) = 84 н/мм^2
σи = 84 н/мм^2 < [σи] = 250 н/мм^2
По прочности на изгиб расчет показал трехкратный запас прочности – турник можно смело делать из имеющегося прутка диаметром тридцать два миллиметра и длиной тысяча двести миллиметров.
Таким образом, вы теперь легко можете произвести расчет балки на изгиб «вручную» и сравнить с результатами, полученными при расчете по любой из многочисленных программ, представленных в Сети.
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
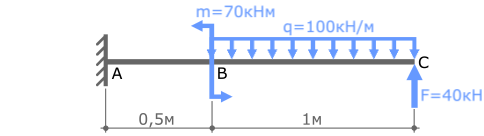
Пример решения задачи на построение эпюры внутренних изгибающих моментов Mx для стальной консольной балки нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.
Задача
Рассмотрим порядок построения эпюры изгибающих моментов Mx для консольной балки закрепленной в жесткой заделке.
Другие примеры решений >
Помощь с решением задач >
Пример решения
Ранее для данной балки уже были рассмотрены примеры определения опорных реакций и построения эпюры поперечных сил Qy.
Покажем найденные опорные реакции и выбранную систему координат.
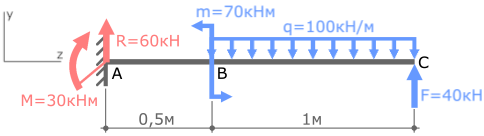
Для построения эпюры изгибающих моментов Mx запишем их выражение по каждому силовому участку и рассчитаем их значения на границах участков. При этом воспользуемся методом сечений.
Наш видеоурок построения эпюр внутренних силовых факторов для балки:
Другие видео
Нумерацию силовых участков балки, сечения и другие вспомогательные обозначения примем из расчета эпюры Qy.
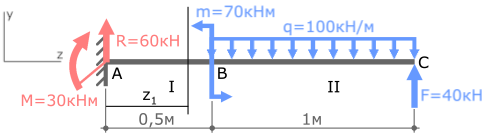
Рассмотрим I силовой участок:
Выбрав левую часть балки, отбросим ненадолго правую, и запишем имеющиеся данные.
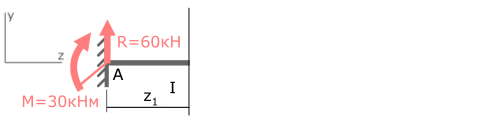
I с.у. (AB) 0 ≤ z1≤ 0,5м
Внутренний изгибающий момент в указанном сечении равен сумме всех внешних моментов, воздействующих на рассматриваемую часть балки.
Здесь на момент в рассматриваемом сечении влияют только опорные реакции M и R, то есть сумма моментов состоит из двух слагаемых.
По правилу знаков момент, который стремится сжать верхние слои балки, принимается положительным, следовательно:
MxI=Σmi=M+R∙z1=30+60z1
В выражении переменная z1 в первой степени, поэтому эпюра Mx на первом участке будет иметь вид прямой линии.
Рассчитаем значения MxI на границах участка, т.е. при z1=0 и при z1=0,5м
MxI (z1=0)=30кНм
MxI (z1=0,5м)=60кНм
Переходим на второй силовой участок:
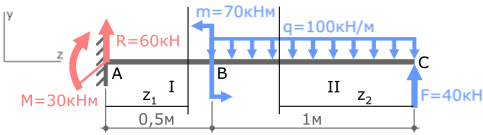
Рассекаем балку в произвольном месте участка и рассматриваем её правую часть.
Эта часть балки изгибается силой F и распределенной нагрузкой q.
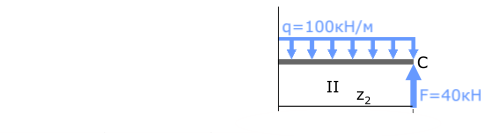
II с.у. (BC) 0 ≤ z2 ≤ 1м
MxII=Σmi=-q∙z2(z2/2)+F∙z2= -50∙z22+40∙z2
Получено выражение с переменной z2 во второй степени, значит, эпюра Mx на втором участке будет иметь вид параболы.
Видео про построение эпюр:
Другие видео
Для построения параболы требуется как минимум три точки. Этими точками будут значения Mx на границах и в середине II силового участка, то есть при z2=0, z2=1м и z2=0,5м.
MxII(z2=0)=0
MxII(z2=0,5м)=7,5кНм
MxII(z2=1м)= -10кНм
По полученным данным строим эпюру изгибающих моментов Mx (готовую эпюру Qy перенесем из ранее рассмотренной задачи)
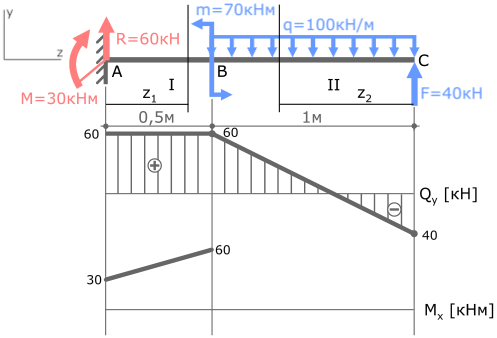
I с.у. (AB) 0 ≤ z1 ≤ 0,5м.
MxI=30+60z1 (прямая)
MxI(z1=0)=30кНм
MxI(z1=0,5м)=60кНм
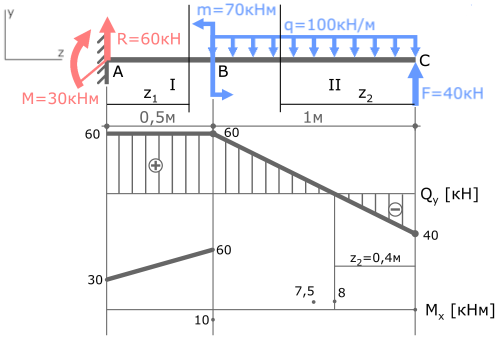
II с.у. (BC) 0 ≤ z2 ≤ 1м
MxII= -50z22+40z2 (парабола)
MxII(z2=0)=0
MxII(z2=0,5м)=7,5кНм
MxII(z2=1м)= -10кНм
Прежде чем соединять отмеченные точки эпюры параболой, обратите внимание на эпюру поперечных сил Qy.
Qy — первая производная от Mx. Поэтому в том месте, где Qy пересекает базовую линию (т.е. Qy=0) на эпюре Mx будет экстремум.
Видео про расчет экстремума эпюры:
Другие видео
Рассчитаем значение экстремума эпюры Mx на II участке балки.
Для этого:
- Выражение QyII приравняем к нулю
QyII=100z2-40=0 - Выразим из него z2
z2=40/100=0,4м - Подставим z2 в выражение для MxII
MxIIэкстр(z2=0,4м)= -50∙0,42+40∙0,4=8кНм
Отметив эту точку в области эпюры где Qy=0 соединим ее с тремя другими параболой.
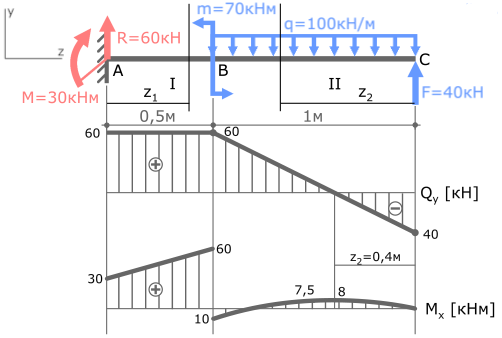
Эпюра изгибающих моментов построена. Проверка эпюры Mx.
Расчеты на прочность >
Другие примеры решения задач >
Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

Балки в доме
При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.
Содержание
- 1 Виды балок
- 1.1 Деревянные
- 1.2 Стальные
- 2 Прочность и жесткость балки
- 3 Расчет на жесткость
- 4 Расчет моментов инерции и сопротивления сечения
- 5 Определение максимальной нагрузки и прогиба
- 6 Особенности расчета на прогиб
- 7 Пример подсчета прогиба
Виды балок
Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.
Деревянные
Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Деревянные перекрытия
Для расчета максимального прогиба следует учитывать:
- Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
- Форма поперечного сечения и другие геометрические характеристики.
- Различные виды нагрузки на материал.
Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.
Конструкции из древесины хвойных пород
Стальные
Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Стальные перекрытия
Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:
- электросварка;
- заклепки;
- болты, винты и другие виды резьбовых соединений.
Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.
Для проведения расчета балки на прогиб может помочь видео:
Прочность и жесткость балки
Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.
Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.
Существует два основных метода расчета прочности и жесткости:
- Простой. При использовании данного метода применяется увеличительный коэффициент.
- Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.
Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.
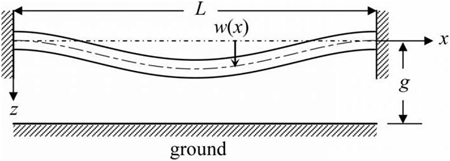
Расчет балок на прогиб
Расчет на жесткость
Для расчета прочности балки на изгиб применяется формула:
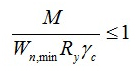
Где:
M – максимальный момент, который возникает в балке;
Wn,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.
Ry является расчетным сопротивлением стали при изгибе. Зависит от вида стали.
γc представляет собой коэффициент условий работы, который является табличной величиной.
Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:
- Составление расчетной схемы объекта.
- Расчет размеров балки и ее сечения.
- Вычисление максимальной нагрузки, которая воздействует на балку.
- Определение точки приложения максимальной нагрузки.
- Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
- Вычисление значения жесткости или максимально прогиба балки.
Чтобы составить расчетную схему, потребуются такие данные:
- размеры балки, длину консолей и пролет между ними;
- размер и форму поперечного сечения;
- особенности нагрузки на конструкцию и точно ее приложения;
- материал и его свойства.
Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.
Расчет моментов инерции и сопротивления сечения
Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:
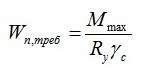
Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.
Определение максимальной нагрузки и прогиба
Для точного определения прогиба балки, лучше всего применять данную формулу:
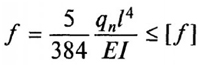
Где:
q является равномерно-распределенной нагрузкой;
E – модуль упругости, который является табличной величиной;
l – длина;
I – момент инерции сечения.
Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.
Особенности расчета на прогиб
Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:
- Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
- Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
- Варианты нагружения консольного стержня, который закреплен жестко.
- Действие на конструкцию сложной нагрузки.
Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.
Пример подсчета прогиба
Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:
- материал изготовления – древесина;
- плотность составляет 600 кг/м3;
- длина составляет 4 м;
- сечение материала составляет 150*200 мм;
- масса перекрывающих элементов составляет 60 кг/м²;
- максимальная нагрузка конструкции составляет 249 кг/м;
- упругость материала составляет 100 000 кгс/ м²;
- J равно 10 кг*м².
Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:
- вес одного метра балки;
- вес м2 перекрытия;
- расстояние, которое оставляется между балками;
- временная нагрузка;
- нагрузка от перегородок на перекрытие.
Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.
Если подставить все эти значения в формулу, то получится:
q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.
Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].
Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.
Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.
Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.
