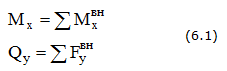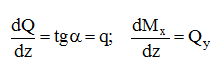В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).


Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
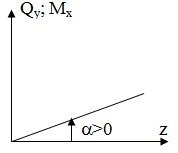
Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
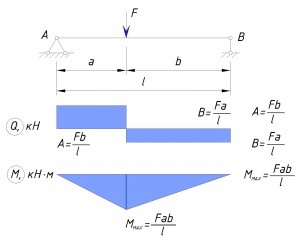
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:


Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
Построение эпюр для консольной балки
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:

Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:

Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:


Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:


На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки
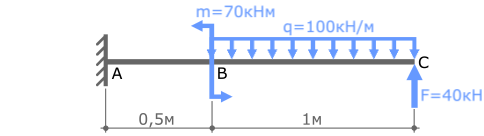
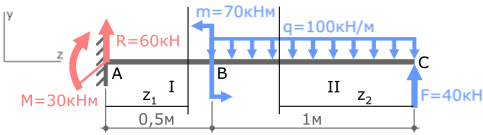
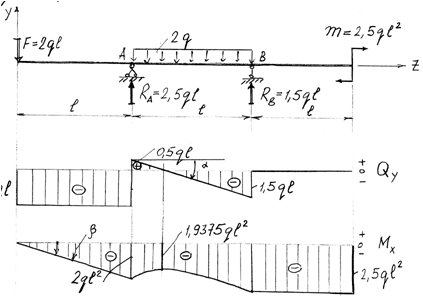
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

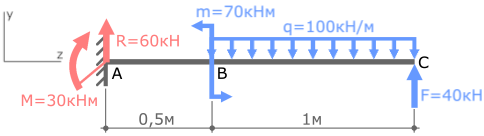
Определим реакции опор:

Рассчитываем первый участок:
Строим эпюры на первом участке:

Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:
Определение экстремума:


Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
Пример решения задачи на построение эпюры внутренних изгибающих моментов Mx для стальной консольной балки нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.
Задача
Рассмотрим порядок построения эпюры изгибающих моментов Mx для консольной балки закрепленной в жесткой заделке.
Другие примеры решений >
Помощь с решением задач >
Пример решения
Ранее для данной балки уже были рассмотрены примеры определения опорных реакций и построения эпюры поперечных сил Qy.
Покажем найденные опорные реакции и выбранную систему координат.
Для построения эпюры изгибающих моментов Mx запишем их выражение по каждому силовому участку и рассчитаем их значения на границах участков. При этом воспользуемся методом сечений.
Наш видеоурок построения эпюр внутренних силовых факторов для балки:
Другие видео
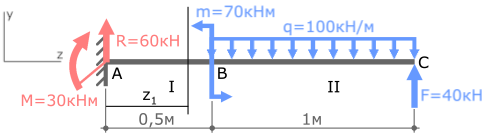
Нумерацию силовых участков балки, сечения и другие вспомогательные обозначения примем из расчета эпюры Qy.
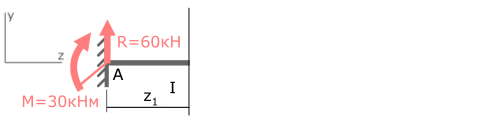
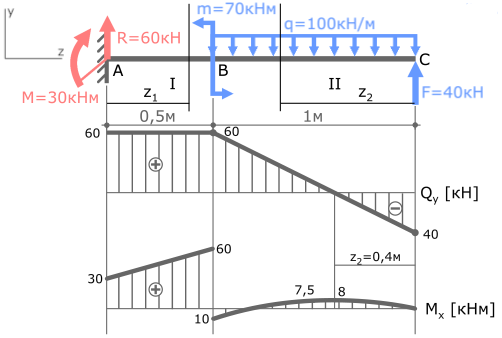
Рассмотрим I силовой участок:
Выбрав левую часть балки, отбросим ненадолго правую, и запишем имеющиеся данные.
I с.у. (AB) 0 ≤ z1≤ 0,5м
Внутренний изгибающий момент в указанном сечении равен сумме всех внешних моментов, воздействующих на рассматриваемую часть балки.
Здесь на момент в рассматриваемом сечении влияют только опорные реакции M и R, то есть сумма моментов состоит из двух слагаемых.
По правилу знаков момент, который стремится сжать верхние слои балки, принимается положительным, следовательно:
MxI=Σmi=M+R∙z1=30+60z1
В выражении переменная z1 в первой степени, поэтому эпюра Mx на первом участке будет иметь вид прямой линии.
Рассчитаем значения MxI на границах участка, т.е. при z1=0 и при z1=0,5м
MxI (z1=0)=30кНм
MxI (z1=0,5м)=60кНм
Переходим на второй силовой участок:
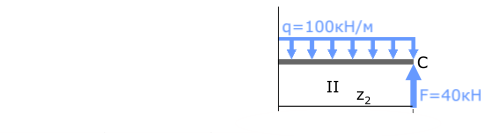
Рассекаем балку в произвольном месте участка и рассматриваем её правую часть.
Эта часть балки изгибается силой F и распределенной нагрузкой q.
II с.у. (BC) 0 ≤ z2 ≤ 1м
MxII=Σmi=-q∙z2(z2/2)+F∙z2= -50∙z22+40∙z2
Получено выражение с переменной z2 во второй степени, значит, эпюра Mx на втором участке будет иметь вид параболы.
Видео про построение эпюр:
Другие видео
Для построения параболы требуется как минимум три точки. Этими точками будут значения Mx на границах и в середине II силового участка, то есть при z2=0, z2=1м и z2=0,5м.
MxII(z2=0)=0
MxII(z2=0,5м)=7,5кНм
MxII(z2=1м)= -10кНм
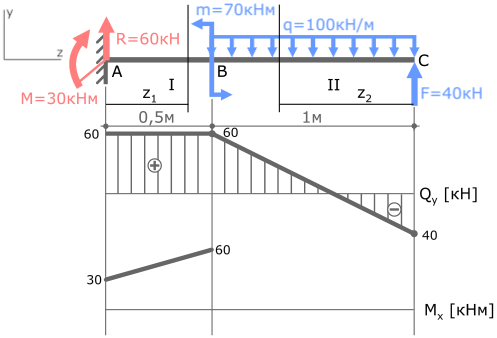
По полученным данным строим эпюру изгибающих моментов Mx (готовую эпюру Qy перенесем из ранее рассмотренной задачи)
I с.у. (AB) 0 ≤ z1 ≤ 0,5м.
MxI=30+60z1 (прямая)
MxI(z1=0)=30кНм
MxI(z1=0,5м)=60кНм
II с.у. (BC) 0 ≤ z2 ≤ 1м
MxII= -50z22+40z2 (парабола)
MxII(z2=0)=0
MxII(z2=0,5м)=7,5кНм
MxII(z2=1м)= -10кНм
Прежде чем соединять отмеченные точки эпюры параболой, обратите внимание на эпюру поперечных сил Qy.
Qy — первая производная от Mx. Поэтому в том месте, где Qy пересекает базовую линию (т.е. Qy=0) на эпюре Mx будет экстремум.
Видео про расчет экстремума эпюры:
Другие видео
Рассчитаем значение экстремума эпюры Mx на II участке балки.
Для этого:
- Выражение QyII приравняем к нулю
QyII=100z2-40=0 - Выразим из него z2
z2=40/100=0,4м - Подставим z2 в выражение для MxII
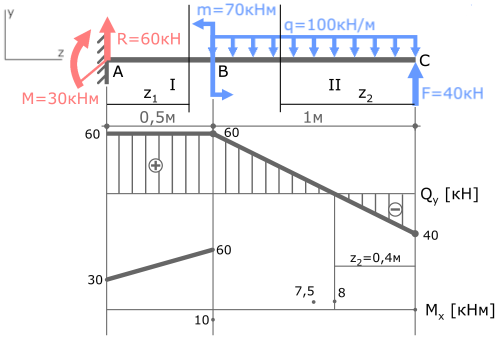
MxIIэкстр(z2=0,4м)= -50∙0,42+40∙0,4=8кНм
Отметив эту точку в области эпюры где Qy=0 соединим ее с тремя другими параболой.
Эпюра изгибающих моментов построена. Проверка эпюры Mx.
Расчеты на прочность >
Другие примеры решения задач >
Дифференциальные
зависимости между интенсивностью
распределенной нагрузки, поперечной
силой и изгибающим моментом и изложенные
выше следствия из этих зависимостей
позволяют не только контролировать
правильность построения эпюр внутренних
силовых факторов при изгибе, но и строить
эпюры поперечных сил и изгибающих
моментов по “характерным”
сечениям. Этот метод существенно
отличается от аналитического метода,
так как в результате его применения
нельзя получить уравнения распределения
внутренних силовых факторов в пределах
рассматриваемого участка изгибаемого
элемента конструкции. С помощью этого
метода можно получить лишь численные
значения поперечной силы и изгибающего
момента в том или ином сечении. Однако
такой подход в сочетании с использованием
следствий из дифференциальных зависимостей
между интенсивностью распределенной
нагрузки, поперечной силой и изгибающим
моментом позволяет быстро и качественно
строить эпюры различной сложности.
“Характерными”
будем называть поперечные сечения,
расположенные бесконечно близко к
границам участка изгибаемого элемента
конструкции.
Рассмотрим
применения этого метода на примере.
Пример
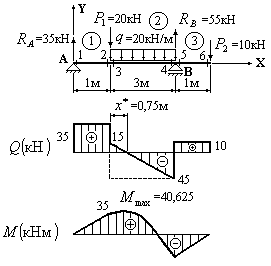
2.8. Построить
эпюры поперечных сил
и изгибающих моментов
для изображенной на рис.2.16,а балки по
методу“характерных”
сечений.
Рис.2.16
Решение:
1. Определяем
опорные реакции. Для этого составим два
уравнения равновесия:
;
(а)
.
(б)
Из
уравнения (а) находим величину реакции
:
кН.
Из
уравнения (б) находим величину реакции
:
кН.
Выполняем
проверку. Для этого составим уравнение
проекций всех сил, действующих на балку,
на вертикальную ось
:
.
2.
Разбиваем балку на участки и проставляем
“характерные”
сечения 1
6 на границах участков.
3.
Определяем величины для поперечной
силы в каждом из “характерных”
сечений:
кН;
кН;
кН;
кН;
кН;
кН.
Откладываем
от базисной линии найденные значения
для поперечной силы в каждом из
“характерных”
сечений и соединяем полученные точки,
руководствуясь следствиями из
дифференциальных зависимостей между
интенсивностью распределенной нагрузки,
поперечной силой и изгибающим моментом.
На участке №1
распределенная нагрузка отсутствует.
Следовательно, на основании первого
следствия из дифференциальных зависимостей
поперечная сила будет постоянной.
Соединяем точки, соответствующие
значениям поперечной силы, найденным
в сечениях №1 и №2, горизонтальной
прямой. На втором участке действует
распределенная нагрузка постоянной
интенсивности. Следовательно, на
основании следствия №2 из дифференциальных
зависимостей поперечная сила должна
меняться по линейному закону. Поэтому
соединяем точки соответствующие
значениям поперечной силы, найденным
в сечениях №3 и №4 наклонной прямой. На
участке №3 распределенная нагрузка так
же, как и на участке №1, отсутствует.
Следовательно, на основании первого
следствия из дифференциальных зависимостей
поперечная сила будет постоянной.
Соединяем точки, соответствующие
значениям поперечной силы, найденным
в сечениях №5 и №6 горизонтальной прямой.
При
построении эпюры поперечных сил следует
обращать внимание на возможные скачки
в тех сечениях, в которых приложены
сосредоточенные силы. Так, в сечениях
№2 и №3 значения для поперечной силы
отличаются на величину силы
.
В сечениях №4 и №5 значения для поперечной
силы отличаются на величину реакции.
В сечении №6 также наблюдается скачок
на величину силыв направлении ее действия при построении
эпюры слева направо.
4.
Находим значения для изгибающих моментов
в “характерных”
сечениях:
;
кНм;
кНм;
кНм;
кНм;
.
Откладываем
от базисной линии найденные значения
для изгибающих моментов в “характерных”
сечениях и соединяем полученные точки,
руководствуясь следствиями из
дифференциальных зависимостей между
интенсивностью распределенной нагрузки,
поперечной силой и изгибающим моментом.
На
участке №1 распределенная нагрузка
отсутствует. Следовательно, на основании
первого следствия из дифференциальных
зависимостей изгибающий момент будет
меняться по линейному закону. Соединяем
точки, соответствующие значениям
изгибающих моментов, найденным в сечениях
№1 и №2, наклонной прямой. На втором
участке действует распределенная
нагрузка постоянной интенсивности.
Следовательно, на основании следствия
№2 из дифференциальных зависимостей
изгибающий момент должен меняться по
закону квадратной параболы. При этом
на основании следствия №4 выпуклость
на эпюре изгибающих моментов должна
быть обращена навстречу распределенной
нагрузке, т.е. вверх. Соединяем точки,
соответствующие значениям изгибающих
моментов, найденным в сечениях №3 и №4
параболой, обращенной выпуклостью
вверх. На участке №3 распределенная
нагрузка так же, как и на участке №1,
отсутствует. Следовательно, на основании
первого следствия из дифференциальных
зависимостей изгибающий момент будет
меняться по линейному закону. Поэтому
соединяем точки, соответствующие
значениям изгибающих моментов, найденных
в сечениях №5 и №6 наклонной прямой.
Скачков на эпюре изгибающих моментов
не наблюдается, так как отсутствуют
сосредоточенные моменты, приложенные
к балке. Следует обратить внимание, что
в сечениях, в которых имеются скачки на
эпюре поперечных сил, на эпюре изгибающих
моментов должны быть изломы.
Найдем
величину максимального изгибающего
момента
.
На втором участке балки поперечная сила
меняет знак, пересекая базисную линию.
Сечение, в котором поперечная сила равна
нулю, также считается“характерным”.
В этом сечении изгибающий момент
достигает экстремальной величины на
рассматриваемом участке. Для рассматриваемой
балки изгибающий момент будет максимальным
на основании дифференциальной зависимости
(2.15), так как интенсивность распределенной
нагрузки
.
Для определения
максимального изгибающего момента
сначала определим координату сечения,
в котором момент максимален. Для этого
на эпюре поперечных сил сформируем два
треугольника (контур одного из
треугольников показан пунктиром). Один
из рассматриваемых треугольников имеет
неизвестный катет длиной
,
который и следует определить. Выделенные
треугольники подобны по трем углам.
Составим пропорцию:,
решая которую относительно,
получимм.
Максимальный
изгибающий момент можно определить
двумя способами:
1.
Помещая начало координат в точке А балки
на левом ее конце, вычислим координату
сечения, в котором изгибающий момент
достигает максимальной величины:
м,
составляем выражение для изгибающего
момента в указанном сечении и подставляем
в это выражение координатум.
Получим:
кНм.
2.
Используя следствие №5 из дифференциальных
зависимостей между интенсивностью
распределенной нагрузки, поперечной
силой и изгибающим моментом, максимальный
изгибающий момент найдем, прибавив к
значению изгибающего момента в сечении
№3 площадь эпюры поперечной силы
на участке длиной
м:
кНм.
Последний способ
определения изгибающих моментов в
некоторых случаях может оказаться
предпочтительнее, так как существенно
экономит время.
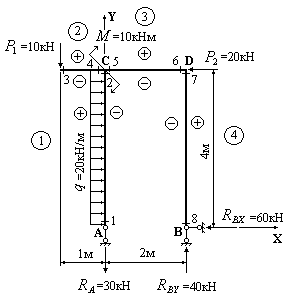
Пример
2.8. Используя
метод “характерных”
сечений, построить эпюры распределения
поперечных[
сил
,
изгибающих моментови продольных сил
для
статически определимой рамы, изображенной
на рис. 2.17.
Решение:
1.Определяем опорные
реакции:
;
(а)
;
(б)
.
(в)
Рис.2.17
Из
уравнения (а) находим реакцию
:
кН.
Из
уравнения (б) находим реакцию
:
кН.
Из
уравнения (в) находим реакцию
:
кН.
Реакции получились
положительными. Следовательно, их
направления выбраны верно.
Выполним
проверку. Для этого составим сумму
проекций всех сил на ось
.
Эта сумма должна тождественно равняться
нулю:
.
2.
Расставляем реакции, разбиваем раму на
участки, выбираем точку наблюдения,
расставляем знаки на каждом участке
для поперечных сил и изгибающих моментов
и расставляем номера “характерных”
сечений таким образом, чтобы нумерация
сечений производилась слева направо.
При этом знак «+» должен находиться над
участком, знак «»
– под участком.
3.
Определяем значения поперечных
сил в “характерных”
сечениях рамы:
;
кН;
кН;
кН;
кН;
кН;
кН;
кН.
Строим эпюру
поперечных сил (Рис.2.18):
Рис.2.18
4. Определяем
значения для изгибающих моментов в
“характерных”сечениях рамы:
;
кНм;
;
кНм;
кНм;
кНм;
кНм;
.
Строим эпюру
изгибающего момента (Рис.2.19):
Рис.3.19
5. Выполняем
статическую проверку. Статическая
проверка состоит а кинематической
проверке расновесия узлов рамы. Вырежем
сечениями №2, №4 и №5 первый узел С и
изобразим его на рис. 2.20,а. Приложим к
узлу моменты, характеризующие влияние
отброшенной части рамы на узел. Эти
моменты численно равны значениям
изгибающих моментов соответственно в
сечениях №2, №4 и №5. Направление действия
этих моментов определяется правилом
знаков для изгибающего момента. Значения
моментов на рис 2.20 приведены в кНм.
Рис.2.20
Рассматривая
равновесие узла С, выделенного из рамы
сечениями №2, №4 и №5, составляем уравнение
для суммы моментов относительно центра
узла. В данном случае следует учитывать,
что на узел С действует внешний заданный
момент М.
. (а)
Как видно из
уравнения (а) узел С находится в равновесии.
Выполним проверку узла D,
выделенного из рамы сечениями №6 и №7
(Рис.2.20,б). Составим сумму моментов,
действующих на узел D:
.
(б)
Как видно из
уравнения (б) узел Dтакже
находится в равновесии.
6. Определяем
величину продольной силы в стержнях
рамы. Для этого вырежем сечениями №2,
№4 и №5 узел Cи изобразим
его на рис. 2.21,а. Приложим к узлуC
продольные усилияи поперечные силы
,
характеризующие влияние отброшенной
части рамы на узел. Эти усилия численно
равны значениям соответственно продольных
и поперечных сил в сечениях №2, №4 и №5.
Направление действия этих усилий
определяется правилом знаков для
продолных усилий и поперечных сил.
Значения поперечных сил на рис 2.21
приведены в кН.
Составим суммы
проекций сил, приложенных к узлу
C, на осии
:
(в)
(г)
Рис.2.21
Рассматривая
уравнение (в), обнаруживаем, что в этом
уравнении две неизвестных продольных
силы
и
.
Решить это уравнение относительно
усилийи
невозможно. Найдем сначала усилие
,
рассмотрев равновесие участка рамы,
ограниченного сечениями №3 и №4
(Рис.2.22).
Рис.2.22
Составим для
изображенного на рис.2.22 стержня условие
равновесия приложенных к стержню сил,
на ось
:
,
(д)
откуда
.
Но усилие
,
так как в сечение №3 отсутствуют силы,
действующие вдоль участка стержня 3-4
(Рис.2.17). Следовательно,усилие.
Теперь можно определить остальные
продольные усилия, действующие в узле
C. Из уравнения (в) находим:
кН.
Из уравнения
(г) найдем усилие
:
кН.
Найдем продольные
усилия в сечениях №6 и №7. Для этого
составим уравнения равновесия сил,
приложенных к узлу Dна
горизонтальную и вертикальную оси
координат Х и Y (Рис.2.21,б). При
составлении этих уравнений не следует
забывать, что к узлуD приложена
сосредоточенная сила.
;
(е)
.
(ж)
Из уравнения
(е) находим продольную силу в сечении
№6:
кН.
Из уравнения
(ж) находим продольную силу в сечении
№7:
кН.
Откладываем
найденные значения для продольной силы
и строим эпюру продольных усилий
(Рис.2.23).
Рис.2.23
Приведенные
примеры построения эпюр поперечных сил
и изгибающих моментов для балок и эпюр
поперечных сил, изгибающих моментов и
продольных усилий для рам позволяют
получить наглядное представление о
преимуществах и недостатках метода
“характерных”сечений. К числу преимуществ этого
метода можно отнести простоту определения
внутренних силовых факторов. К числу
недостатков – отсутствие аналитических
законов распределения внутренних
силовых факторов по длине элементов
конструкции. Однако, использования
дифференциальных зависимостей между
интенсивностью распределенной нагрузки,
поперечной силой и изгибающим моментом
для анализа поведения распределения
внутренних усилий и следствий из них в
значительной мере компенсирует последний
недостаток. Сделанный вывод позволяет
рекомендовать метод построения эпюр
распределения внутренних силовых
факторов по“характерным’сечениям в учебную практику.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Изгибающий момент – внутренний силовой фактор
Здравствуйте. Здорово, что Вы проявляете интерес к нашему проекту SoproMats, спасибо! Эта статья будет посвящена внутреннему силовому фактору – изгибающему моменту. Фактору, который возникает в поперечных сечениях балок, работающих на изгиб. Здесь поделимся информацией как он обозначается, измеряется, определяется и т.д. В общем все, что нужно знать об изгибающем моменте. Также в конце статьи поделимся ссылочками, на важные материалы про изгибающий момент.
Что такое изгибающий момент?
Изгибающий момент – это внутренний силовой фактор, возникающий в элементах конструкций, деталях, работающих на изгиб: такие конструктивные элементы как балка, рама, плита и т.д.
Зачем нужен?
Зная изгибающий момент в сечении, а также геометрические размеры этого сечения, можно определить нормальное напряжение в его конкретной точке и исследовать ее напряженно-деформированное состояние. Определение изгибающих моментов является неотъемлемой частью любого прочностного расчета деталей, работающих на изгиб. Для наглядной визуализации распределения изгибающих моментов строят эпюры, которые позволяют выявить наиболее подверженные к разрушению места балки. Как правило, то сечение, в котором изгибающий момент имеет максимальное значение, является самым опасным у балки. За редкими исключениями. Поэтому так важно уметь определять эту величину.
Как обозначается?
Изгибающий момент обозначается буквой M с индексом, который указывает на название оси, относительного которой происходит изгиб. Обычно это ось x, поэтому в этой статье будем использовать такое обозначение — Mx.
Как определяется?
Для определения этой величины используется метод сечений. По которому считается, что если балка находится в равновесии, то и отдельные части балки также будут находится в равновесии, если действие каждой части друг на друга, заменить равными силовыми факторами. Используя этот метод в совокупности с уравнениями равновесия статики, можно определить изгибающий момент в любом сечении, более подробно посмотрим этот процесс на примере ниже.
В чем измеряется?
Данная величина измеряется в Н·м. В расчетах, в основном, используется размерность — кН·м, и этот вариант будем использовать в этой статье. Иногда считают в кгс·м и т·м.
Статьи про изгибающие моменты:
Как построить эпюру изгибающего момента? В материале этой статьи написано, как можно построить эпюру различными методами.
Источник
Тема 2.5. Изгиб
Изгибом называется вид нагружения бруса, при котором к нему прикладывается поперечная нагрузка, лежащая в плоскости проходящей через продольную ось (рис.1). Брус, работающий при изгибе, называется балкой.
Изгиб называется плоским или прямым, если плоскость действия нагрузки проходит через главную центральную ось инерции сечения (рис.1).
Рис.1. Прямой изгиб
Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым (рис.2). При наличии поперечной силы Qy изгиб называется поперечным. Строго говоря, к простым видам сопротивления относится лишь чистый изгиб; поперечный изгиб относят к простым видам сопротивления условно, так как в большинстве случаев (для достаточно длинных балок) действием поперечной силы при расчетах на прочность можно пренебречь.
Далее будем рассматривать плоский изгиб, то есть все силы будем прилагать в плоскости симметрии балки.
Рис.2. Чистый изгиб
Осваивать расчет балок и рам удобно, рассматривая по очереди следующие вопросы:
— Определение внутренних усилий в балках и построение эпюр внутренних усилий.
— Проверка прочности балок.
— Определение перемещений и проверка жесткости балок.
§2.Построение эпюр поперечной силы и изгибающего момента
Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.
Эпюра внутренней силы – график, показывающий изменение этой силы по длине балки.
Для построения эпюр балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.
Последовательно на каждом участке вводится скользящая система координатных осей (начало координат совмещается с началом участка) и для произвольного сечения составляются выражения для определения поперечной силы и изгибающего момента. Затем по этим выражениям в пределах каждого участка строятся графики (эпюры) внутренних сил.
Перед тем, как определять внутренние усилия (поперечные силы и изгибающие моменты) и строить эпюры, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 3 показаны эти закрепления. Для неподвижной (рис 3,б) и подвижной (рис. 3,в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 6.5,а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 3,б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис.3,в).
Рис.3. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре;
в – в шарнирно-подвижной опоре.
После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений.
Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силу можно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).
Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.
Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.
Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.
Поперечная сила Q в каком-либо поперечном сечении балки численно равная алгебраической сумме на ось у внешних сил действующих на балку по одну сторону от рассматриваемого сечения, а изгибающий момент M равен алгебраической сумме моментов сил, относительно центра тяжести сечения.
Взаимосвязь между нагрузкой и очертаниями эпюр поперечных сил Q и изгибающих моментов M:
Указанные закономерности позволяют упростить построения эпюр поперечных сил и изгибающих моментов (в сложнoзагруженных балках) и обойтись без составления уравнений для каждого участка.
Для определения максимальных значений изгибающих моментов дополнительно подсчитываются моменты в сечениях, где поперечные силы равны нулю. Построение без составления эпюр уравнений дает особенно значительный эффект для балок, нагруженных сложной нагрузкой, имеющих много участков нагружения.
Источник
iSopromat.ru
Внутренние поперечная сила и изгибающий момент возникают в поперечных сечениях балки при её изгибе под действием внешних нагрузок.
Поперечным изгибом называется такой вид деформирования бруса, при котором внешние нагрузки действуют перпендикулярно к его продольной оси. Деформация изгиба заключается в искривлении оси бруса.
Брус с прямой осью, работающий на изгиб, называется балкой. Если плоскость действия внешних нагрузок проходит через ось балки и одну из главных центральных осей поперечного сечения, изгиб называется прямым. В этом случае ось балки искривляется в плоскости действия нагрузок и является плоской кривой.
В сечениях балки возникают два внутренних силовых фактора: изгибающий момент Мх и поперечная сила Qy
Дифференциальные зависимости между q, Qy и Мх имеют вид:
Изгиб называется чистым, если в сечении балки возникает только изгибающий момент Мх.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Определение максимального изгибающего момента.



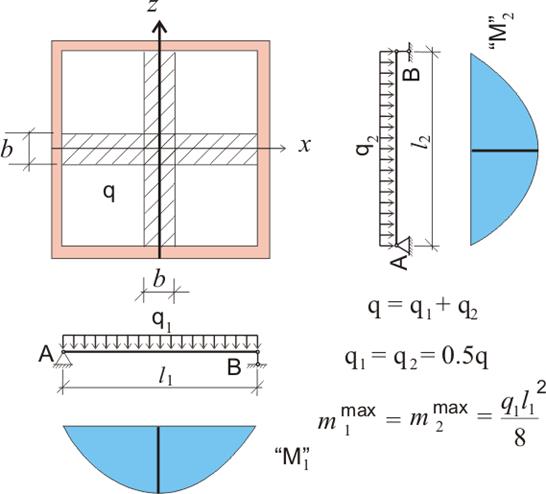
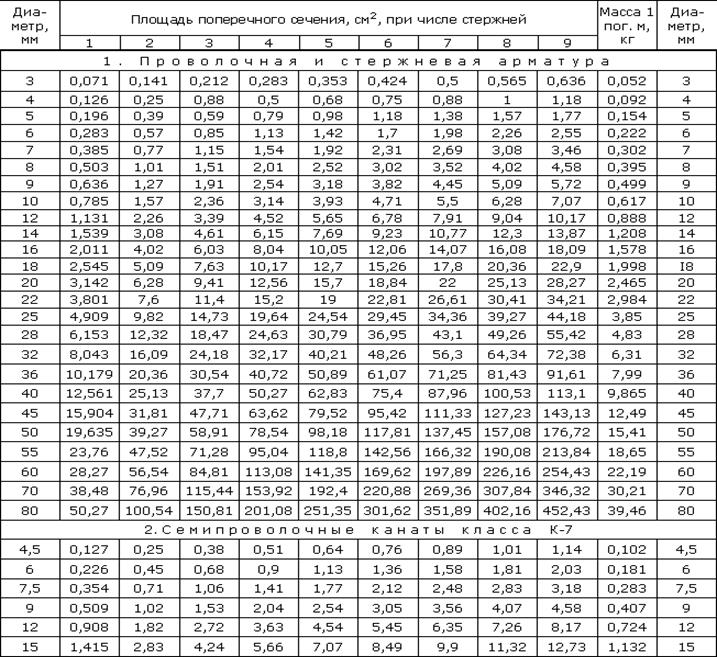
Если бы наша плита опиралась только на 2 стены, то такую плиту можно было бы рассматривать как балку на двух шарнирных опорах (ширину опорных площадок пока не учитываем), при этом ширина балки для удобства расчетов принимается b = 1 м.
Однако в данном случае у нас плита опирается на 4 стены. А это значит, что рассматривать одно поперечное сечение балки относительно оси х недостаточно, ведь мы можем рассматривать нашу плиту также как балку относительно оси z. А еще это означает, что сжимающие и растягивающие напряжения будут не в одной плоскости, нормальной к оси х, а в двух плоскостях. Если рассчитывать балку с шарнирными опорами с пролетом l1 относительно оси х, то получится, что на балку действует изгибающий момент m1 = q1l12/8. При этом на балку с шарнирными опорами с пролетом l2 будет действовать точно такой же момент m2, так как пролеты у нас равны. Но расчетная нагрузка у нас одна:
и если плита квадратная, то мы можем допустить, что:
Это означает, что арматуру, укладываемую параллельно оси х, и арматуру, укладываемую параллельно оси z, мы можем рассчитывать на одинаковый изгибающий момент, при этом момент этот будет в два раза меньше, чем для плиты, опирающейся на две стены. Таким образом максимальный расчетный изгибающий момент составит:
М = 775 х 52/16 = 1219.94 кгс·м
2. Подбор сечения арматуры.
Рассчитать сечение арматуры как в продольном, так и в поперечном направлении можно по любой из предлагаемых методик (по старой методике, по новому СНиПу, другим способом), результат будет приблизительно одинаковым. Но при использовании любой из методик необходимо помнить о том, что высота расположения арматуры будет разная, например, для арматуры, располагаемой параллельно оси х, можно предварительно принять h01 = 13 см, а для арматуры, располагаемой параллельно оси z, можно предварительно принятьh02 = 11 см, так как диаметра арматуры мы пока не знаем.
По старой методике:
А01 = M/bh201Rb = 1219.94/(1·0.132·1170000) = 0.0617
А02 = M/bh201Rb = 1219.94/(1·0.112·1170000) = 0.08617
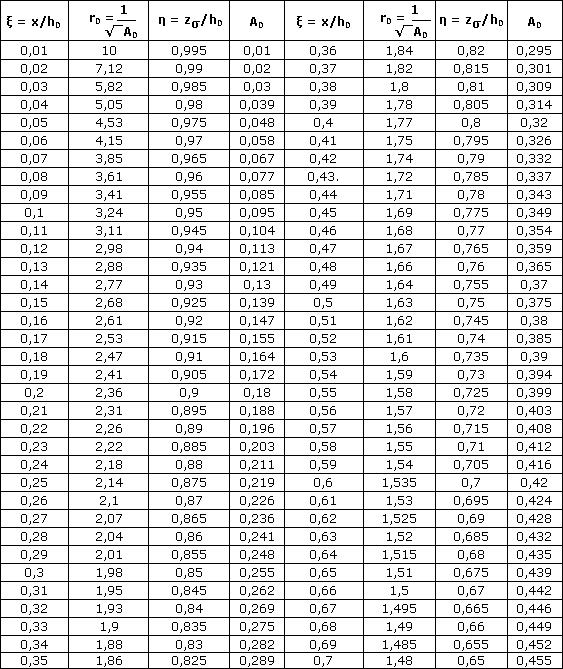
Теперь по вспомогательной таблице 1(170):
мы можем найти η1 = 0.967 и ξ1 = 0.066. η2 = 0.956 и ξ2 = 0.091. И тогда требуемая площадь сечения арматуры:
Fa1 = M/ηh01Rs = 1219.94/(0.967·0.13·36000000) = 0.0002696 м2 или 2.696 см2.
Fa2 = M/ηh02Rs = 1219.94/(0.956·0.11·36000000) = 0.000322 м2 или 3.22 см2.
Если мы для унификации примем и продольную и поперечную арматуру диаметром 10 мм и пересчитаем требуемое сечение поперечной арматуры при h02 = 12 см,
А02 = M/bh201Rb = 1219.94/(1·0.122·1170000) = 0.0724, η2 = 0.963
Fa2 = M/ηh02Rs = 1219.94/(0.963·0.12·36000000) = 0.000293 м2 или 2.93 см2.
то для армирования 1 погонного метра мы можем использовать 4 стержня продольной арматуры и 4 стержня поперечной арматуры. Таким образом получится сетка с ячейкой 250х250 мм. Площадь сечения арматуры для 1 погонного метра составит 3.14х2 = 6.28 см2. Подбор сечения арматуры удобно производить по таблице 2 (см. ниже). На всю плиту потребуется 40 стержней длиной 5.2-5.4 метра. Также для армирования плиты можно использовать 6 стержней продольной арматуры и 6 стержней поперечной арматуры диаметром 8 мм. Площадь сечения арматуры для 1 погонного метра составит 3.02х2 = 6.04 см2. Размеры ячейки при этом будут
Это был простой расчет (даже если Вам так не кажется), его можно усложнить с целью уменьшения количества арматуры. Так как максимальный изгибающий момент действует только в центре плиты, а при приближении к опорам-стенам момент стремится к нулю, то остальные погонные метры кроме центральных можно армировать арматурой меньшего диаметра (размер ячейки для арматуры диаметром 10 мм увеличивать не стоит, так как наша распределенная нагрузка является в достаточной степени условной) или увеличивать шаг арматуры (для арматуры диаметром 8 мм). Для этого нужно определять значения моментов на каждом следующем погонном метре и определять для каждого погонного метра требуемое сечение арматуры и размер ячейки. Но все равно конструктивно использовать арматуру с шагом более 250 мм не стоит, поэтому экономия от таких расчетов будет не большой.
Примечание: существующие методики расчета плит перекрытия, опирающихся по контуру, для панельных домов предполагают использование дополнительного коэффициента, учитывающего пространственную работу плиты (так как под воздействием нагрузки плита будет прогибаться) и концентрацию арматуры в центре плиты. Использование такого коэффициента позволяет уменьшить сечение арматуры еще на 10-15%, однако для железобетонных плит, изготавливаемых не на заводе, а на стройплощадке, использование дополнительного коэффициента я считаю не обязательным. Во-первых, потребуются дополнительные расчеты на прогиб, на раскрытие трещин, на процент минимального армирования. А во-вторых, чем больше арматуры, тем меньше будет прогиб посредине плиты и тем проще его будет устранить или замаскировать при финишной отделке.

Как проверить процент армирования и соблюдение граничных условий, рассказывается отдельно, здесь на этом останавливаться не буду.
Источник
Сопромат для чайников, основные расчетные формулы
Итак, давайте разбираться, зачем понадобилось ломать школьную линейку, оставляя детей без школьных принадлежностей, и чем это может нам помочь. Пришло время добавить к наглядности несколько формул, тут все будет почти так же просто и понятно, как и в первой части сопромата для чайников, но понадобятся знания математики на уровне 4-5 классов и начальные знания по геометрии.
4. Реакции опор.
5. Уравнения статического равновесия (проекции сил).
Вроде все просто, но на самом деле мы воспользовались всеми основными аксиомами статики:
2. Механическое состояние тела не изменится, если освободить тело от связей и приложить к тем же точкам тела силы, равные действовавшим на них силам реакций связей. В данном случае мы заменили опоры опорными реакциями.
3. Если тело под воздействием системы сил находится в состоянии равновесия (покоя) или продолжает двигаться с постоянной скоростью, то такая система сил, является уравновешенной.
Таким образом мы можем составить первых два уравнения, удовлетворяющие условиям статического равновесия системы:
Примечание: так как горизонтальных сил в данном случае нет, то и горизонтальная опорная реакция R H лев = 0, при замене опорных связей на реактивные силы не показана для упрощения восприятия.
4. Две силы, приложенные к некоему телу, считаются уравновешенными тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны.
5. Не нарушая равновесного состояния тела, к нему можно приложить или отнять от него любую уравновешенную систему сил.
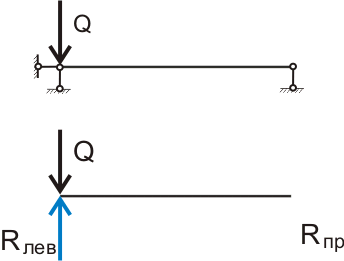
4.1. Определение опорных реакций.
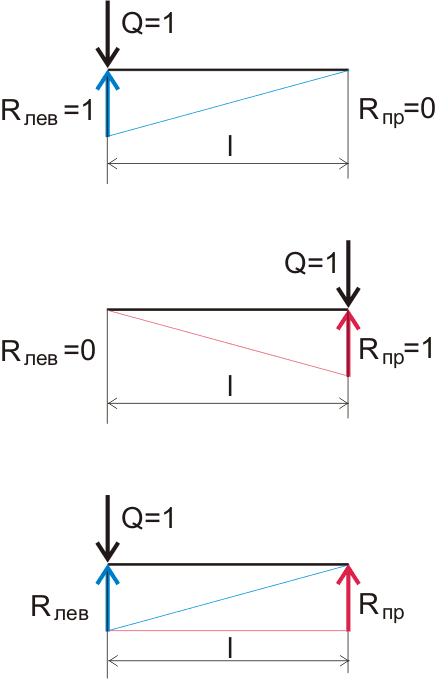
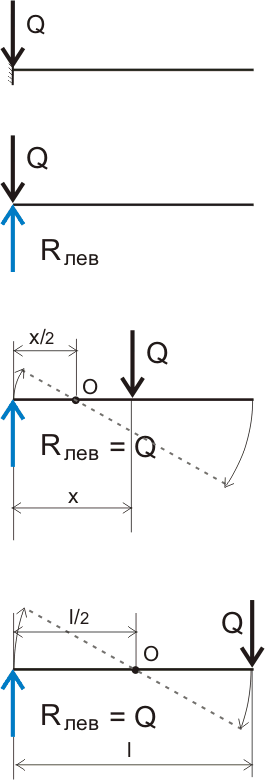
Теперь немного усложним задачу. Наша линейка (то есть балка) лежит на двух опорах и когда мы давим на линейку пальцем между опорами, а говоря по-научному, прикладываем сосредоточенную нагрузку, то реакция возникает на обеих опорах. Так как статическое равновесие системы мы можем наблюдать даже и невооруженным глазом, то логично предположить, что суммарная реакция опор численно равна приложенной нагрузке. Определить значение реакций опор можно простым графическим методом (по линиям влияния):
Рисунок 5.2. Графическое отображение изменения реакций опор в зависимости от расстояния приложения нагрузки.
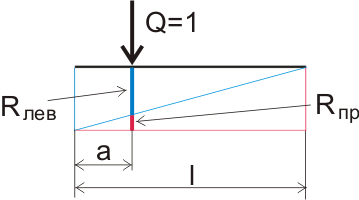
Рисунок 5.3. Графическое определение реакций опор.
Определить реакцию опор можно и математическими формулами, описывающими пропорциональность прямоугольных треугольников: Если нагрузка приложена на расстоянии а от опоры при общей длине балки l, то реакция на правой опоре будет:
Rпр = В = Qа/l (4.1)
а реакция на левой опоре будет:
Конечно при расчетах все пользуются формулами, но наглядность треугольников нам еще пригодится.
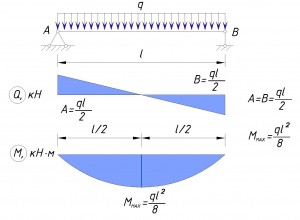
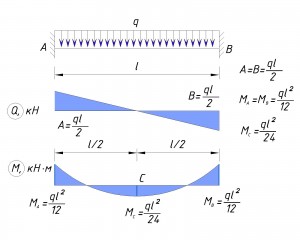
При определении реакции опор от действия распределенной нагрузки, сначала определяется равнодействующая сила, т.е. распределенная нагрузка сводится к сосредоточенной, а потом определяются реакции опор в зависимости от точки приложения сосредоточенной нагрузки. Если распределенная нагрузка является равномерно распределенной и приложена по всей длине балки, то реакции опор будут А = В = ql/2. Как определить реакции опор в других случаях, надеюсь, станет понятно из дальнейшего описания.
6. Уравнения изгибающего момента, третье уравнение статического равновесия системы
Если мы положим 20 см линейку на книги и надавим пальцем посредине, то линейка прогнется на некоторое расстояние, если мы возьмем 40 см линейку такого же сечения и из такого же материала, обопрем ее на книги, уложенные на расстоянии 40 см, и приложим к линейке точно такую же нагрузку, то расстояние, на которое прогнется линейка, будет больше, в чем же дело? ведь ни нагрузка, ни материал балки, ни сечение балки не изменились, изменилась только длина балки.
Все мы помним Архимеда и его радость при открытии принципа рычага, так вот этот принцип действует везде, суть его сводится к следующему: чем больше рычаг, тем меньшую силу можно приложить для совершения одной и той же работы.
М = Ах (0≤ х 7. Балка на двух шарнирных опорах.
7.1. Для балки, на которую действует сосредоточенная нагрузка посредине балки, определить изгибающий момент в любой точке поперечного сечения на левом участке балки проще простого: нужно умножить реакцию одной из опор на расстояние от этой опоры до точки приложения нагрузки (на участке балки от х=0 до х= l/2). В математическом выражении это будет выглядеть так:
М=(Q/2)x (7.1)
Так как в данном случае реакция каждой из опор равна половине от действующей нагрузки. Максимальное значение изгибающего момента также будет посредине, т.е. на расстоянии l/2 от начала балки и будет составлять:
M=(Q/2)(l/2) = Ql/4 (7.2)
Полное уравнение моментов, на участке где l/2 2 /8 (7.4)
Вывести данную формулу в общем-то несложно. Распределенная нагрузка рассматривается как очень много сосредоточенных нагрузок, приложенных на одинаковом расстоянии друг от друга. Далее для каждой нагрузки можно построить свою эпюру изгибающих моментов, а потом эти эпюры сложить или сразу строить эпюру, учитывающую действие сосредоточенных нагрузок. Чем больше будет сосредоточенных нагрузок, тем менее ломаным будет низ эпюры. Чтобы каждый раз не рисовать огромное количество эпюр используется интегральное вычисление, для этого его и придумали. Так как у нас на правой или на левой половине балки действуют две силы: реакция опоры и распределенная нагрузка, то значение изгибающего момента в некотором поперечном сечении балки можно определить, решив уравнение:
в данном случае значение распределенной нагрузки сначала сводится к сосредоточенной нагрузке, действующей на некотором участке х, а затем умножается на плечо силы х/2. Таким образом посредине балки значение изгибающего момента будет составлять:
Пример расчета балки на действие равномерно распределенной нагрузки по всей длине балки приводится отдельно. Если неравномерно распределенная нагрузка действует не по всей длине балки, то вам сюда.
8. Консольная балка.
Если взять ту же линейку, один конец линейки всунуть между книгами, а лучше между кирпичами, а второй конец оставить на весу, то мы получим модель консольной балки. Особенность консольной балки в том, что у нее только одна опора, причем жесткое защемление не позволяет балке свободно вращаться вокруг этой опоры. Так как опора только одна, то где бы мы ни приложили нагрузку к балке реакция опоры всегда будет равна приложенной нагрузке. Если мы как и в случае с балкой на шарнирных опорах попробуем убрать опору, заменив ее реакцией, то условие равновесия системы не будет соблюдаться, две равные по значению, противоположно направленные силы, не лежащие на одной прямой, будут вращать балку вокруг некоторой точки «о»:
Рисунок 8.1. Возникновение вращающего момента при приложении равных сил в разных точках.
Как видно из рисунка 8.1 и понятно из описания природы момента, чем больше расстояние между точками приложения сил, тем больше будет вращающий момент. Чтобы соблюсти условие равновесия системы нам необходимо приложить к балке другой вращающий момент, т.е. еще одну пару сил, которая будет пытаться вращать балку в противоположную сторону.
Изгибающий момент, возникающий на жесткой опоре консольной балки при действии сосредоточенной нагрузки:
Изгибающий момент, возникающий на жесткой опоре консольной балки при действии распределенной нагрузки по всей длине балки:
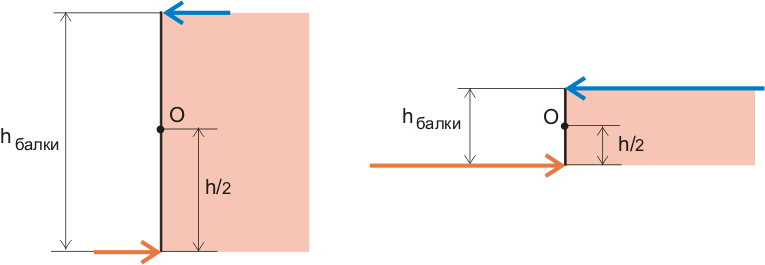
На схеме это можно изобразить с помощью условного обозначения изгибающего момента (известного нам из первой части), но нас сейчас интересует конкретика. Так как балка у нас имеет вполне осязаемые высоту и ширину, то логично было бы приложить эти силы к балке, или, выражаясь более точно, к поперечному сечению балки и тут даже глазом, невооруженным сопроматом, видно, что чем больше высота балки, тем меньшие силы можно прикладывать к самому верху и к самому низу балки, чтобы значение момента было одинаковым:
Рисунок 8.2. Увеличение значения сил при уменьшении высоты балки при одинаковом вращающем моменте.
При этом верхняя сила пытается балку растянуть, а нижняя сила пытается балку сжать. Вроде бы ничего сложного тут нет, все достаточно просто и понятно, но на самом деле мы открыли самую главную тайну сопромата:
Изгибающий момент, действующий на любую строительную конструкцию в некоторой точке, можно рассматривать как пару сил, действующих на поперечное сечение балки в этой точке.
9. Метод сечений
Такой подход позволяет нам при решении задач рассматривать не всю балку, а только ее часть, заменив отсутствующую часть парой сил, действующих на поперечное сечение балки. Так, например, мы могли бы не рассматривать всю балку (рисунок 7.2), а только правую половину, заменив левую половину моментом или парой сил.
А если в рассматриваемом поперечном сечении действуют касательные напряжения, определяемые по эпюре поперечных сил, и(или) нормальные напряжения, определяемые по эпюре нормальных сил, то для того, чтобы отсеченная часть балки находилась в равновесии, мы должны все эти нагрузки приложить к рассматриваемому поперечному сечению.
В этом и состоит суть метода сечений:
Таким образом, решая перечисленные выше уравнения, мы определяем значения внешнего изгибающего момента и теперь пришло время узнать, какой же будет на это реакция материала.
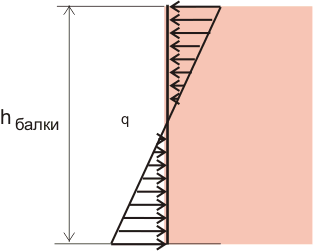
В данном случае мы приложили силы к самому верху и к самому низу балки (рисунок 8.2), но мы можем прикладывать эти силы в любых точках поперечного сечения балки, главное чтобы не изменялось значение внешнего момента. Сосредоточенные силы можно заменить распределенной нагрузкой, которая будет создавать такой же изгибающий момент, причем значение распределенной нагрузки может изменяться в зависимости от высоты балки и графически может быть обозначено так:
Рисунок 8.3. Изменение распределенной нагрузки по высоте балки.
Почему распределение нормальных напряжений по высоте поперечного сечения балки имеет такой странный вид, мы сейчас и узнаем.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Если имеется в виду распределенная нагрузка на погонный метр, то распределенная нагрузка 1кг/1м равна распределенной нагрузке 2кг/2м, что в итоге все равно дает 1кг/м. А сосредоточенная нагрузка измеряется просто в килограммах или Ньютонах.
Формулы это хорошо! но как и какими формулами расчитать конструкцию для навеса а самое главное какой металл (профильную трубу) размером должен быть.
Если Вы обратили внимание, то данная статья посвящена исключительно теоретической части, а если Вы еще и проявите сообразительность, то без особого труда найдете примера расчета конструкций в соответсвующем разделе сайта: Расчет конструкций. Для этого достаточно перейти на главную страницу и найти там этот раздел.
Не во всех формулах описываются все учавствующие переменные ((
Так же есть путаница с обозначениями, сперва иксом обозначается расстояние от левой опы до приложенной силы Q, а двумя абзацами ниже иск это уже функция, потом выводятся формули и поехала путаница.
Я конечно понимаю, что это не труд какой-то оплачиваемый, но тем не менее. Если идёт формула, то под ней должно быть описание всех её переменых, у Вас же нужно это выискивыть сверху из контекста. А кое где и вообще нет и в контексте упоминания. Я отнюдь не жалуюсь. Я говорю о недостатках работы (за которую уже кстати Вас благодарил). Что касается переменных икс как функции и потом введении ещё одной переменной икс как отрезка, без указаний всех переменный под выводимой формулой вводит путаницу дело тут не в устоявшихся обозначениях, а в целесообразности ведения такого изложения материала.
Кстати вас арказм не уместен, потому как вы излагаете всё на одной странице и без указания всех переменных непонятно, что вы вообще имеете в виду. К примеру в программировании всегда указываются все перменные. Кстати если Вы делаете это всё для народа, то Вам не мешало бы узнать про то какой вклад в математику внёс Кисилёв как педагог, а не как математик, может тогда Вы поймёте о чём я говорю.
Добрый день!
Ниже формулы 1.2 приводится формула реакции опор для равномерной нагрузки по всей длине балки А=В=ql/2. Мне кажется, что должно быть А=В=q/2, или я чего-то не понимаю?
В тексте статьи все правильно, ведь равномерно распределенная нагрузка означает, какая нагрузка приложена на участке длины балки, и измеряется распределеннная нагрузкка в кг/м. Чтобы определить реакцию опроры, мы сначала находим, чему будет равна суммарная нагрузка, т.е. по всей длине балки.
Разница между сосредоточенной и распределенной нагрузкой описывается в вводной статье, ссылка на которую в самом начале статьи, рекомендую ознакомиться.
Не понятно, зачем рассказывать азы сопромата тем, кто строит или проектирует. Если они в вузе не поняли сопромат у грамотных педагогов, то их и близко нельзя допускать до проектирования, а популярные статьи только еще больше их запутают, так как часто содержат грубые ошибки.
Каждый должен быть профессионалом в своей области.
Кстати, изгибающие моменты в приведенных выше простых балках должны иметь положительный знак. Отрицательный знак, проставленный на эпюрах, противоречит всем общепринятым нормам.
1. Далеко не все, кто строит, учились в ВУЗах. И почему-то такие люди, занимающиеся ремонтом в своем доме, за подбор сечения перемычки над дверным проемом в перегородке не хотят платить профессионалам. Почему? спросите у них.
2. Опечаток хватает и в бумажных изданиях учебников, но путают людей не опечатки, а слишком абстрагированное изложение материала. В данном тексте тоже, возможно, есть опечатки, но в отличие от бумажных источников они будут исправлены сразу после того, как будут обнаружены. А вот насчет грубых ошибок, вынужден вас огорчить, здесь их нет.
3. Если вы считаете, что эпюры моментов, построенные снизу оси должны иметь только положительный знак, то мне вас жаль. Во-первых, эпюра моментов достаточно условна и она лишь показывает изменение значения момента в поперечных сечениях изгибаемого элемента. При этом изгибающий момент вызывает в поперечном сечении как сжимающие так и растягивающие напряжения. Раньше было принято строить эпюру сверху оси, в таких случаях положительный знак эпюры был логичным. Затем для наглядности эпюру моментов стали строить так, как показано на рисунках, однако положительный знак эпюр сохранился по старой памяти. Но в принципе, как я уже сказал это не имеет принципиального значения для определения момента сопротивления. В статье по этому поводу сказано: «В данном случае значение момента считается отрицательным, если изгибающий момент пытается вращать балку по часовой стрелке относительно рассматриваемой точки сечения. В некоторых источниках считается наоборот, но это не более чем вопрос удобства». Впрочем объяснять это инженеру нет необходимости, лично я много раз сталкивался с различными вариантами отображения эпюр и никогда проблем это не вызывало. Но по всей видимости статью вы не читали, а ваши высказывания подтверждают, что даже основ сопромата вы не знаете, пытаясь подменить знание некими общепринятыми нормами, да еще и «всеми».
Уважаемый доктор Лом!
Вы невнимательно прочитали мое сообщение. Я говорил об ошибках в знаке изгибающих моментов «в приведенных выше примерах», а не вообще – для этого достаточно открыть любой учебник по сопротивлению материалов, технической или прикладной механике, для вузов или техникумов, для строителей или машиностроителей, написанный полвека назад, 20 лет назад или 5 лет. Во всех без исключения книгах правило знаков для изгибающих моментов в балках при прямом изгибе одно и то же. Это я и имел в виду, говоря об общепринятых нормах. А с какой стороны балки откладывать ординаты – это уже другой вопрос. Поясню свою мысль.
Знак на эпюрах ставят для того, чтобы определить направление внутреннего усилия. Но при этом необходимо договориться, какой знак – какому направлению соответствует. Эта договоренность и является так называемым правилом знаков.
Берем несколько книг, рекомендуемых в качестве основной учебной литературы.
1) Александров А.В. Сопротивление материалов, 2008, с. 34 – учебник для студентов строительных специальностей: «изгибающий момент считать положительным, если он изгибает элемент балки выпуклостью вниз, вызывая растяжение нижних волокон.». В приведенных примерах (во втором параграфе), очевидно, растягиваются нижние волокна, так почему знак на эпюре отрицательный? Или утверждение А. Александрова является чем-то особенным? Ничего подобного. Смотрим дальше.
2) Потапов В.Д. и др. Строительная механика. Статика упругих систем, 2007, с. 27 – вузовский учебник для строителей: «момент считается положительным, если он вызывает растяжение нижних волокон балки».
3) А.В. Дарков, Н.Н. Шапошников. Строительная механика, 1986, с. 27 – широко известный учебник также для строителей: «при положительном изгибающем моменте верхние волокна балки испытывают сжатие (укорочение), а нижние – растяжение (удлинение);». Как видим, правило то же самое. Может быть у машиностроителей все совсем по другому? Опять же нет.
4) Г.М. Ицкович. Сопротивление материалов, 1986, с. 162 – учебник для учащихся машиностроительных техникумов: «Внешняя сила (момент), изгибающая эту часть (отсеченную часть балки) выпуклостью вниз, т.е. таким образом, что сжатые волокна находятся сверху, дает положительный изгибающий момент».
Список можно продолжить, но зачем? Любой студент, сдавший сопромат хотя бы на 4, это знает.
Вопрос, с какой стороны стержня откладывать ординаты эпюры изгибающих моментов, – это уже другое соглашение, которое может полностью заменить выше приведенное правило знаков. Поэтому при построении эпюр М в рамах знак на эпюрах не ставят, так как локальная система координат связана со стержнем, и меняет свою ориентацию при изменении положения стержня. В балках же все проще: это или горизонтальный или наклоненный под небольшим углом стержень. В балках эти два соглашения дублируют друг друга (но не противоречат при правильном понимании). И вопрос, с какой стороны откладывать ординаты, определялся не «раньше, а потом», как Вы пишите, а сложившимися традициями: строители всегда строили и строят эпюры на растянутых волокнах, а машиностроители – на сжатых (до сих пор!). Я бы мог объяснить, почему, но и так много написал. Если бы на эпюре М в приведенных задачах стоял знак «плюс», или вообще не стояло никакого знака (с указанием, что эпюра построена на растянутых волокнах – для определенности), то дискуссии вообще бы не было. А то, что знак М не влияет на прочность элементов при строительстве садового домика, так об этом никто и не спорит. Хотя и здесь можно выдумать особые ситуации.
Вообще, эта дискуссия не плодотворна в виду тривиальности задачи. Каждый год, когда ко мне приходит новый поток студентов, приходится им объяснять эти простые истины, или подправлять мозги, запутанные, что греха таить, отдельными преподавателями.
Отмечу, что из Вашего сайта я почерпнул и полезную, интересную информацию. Например, графическое сложение линий влияния опорных реакций: интересный прием, который не встречал в учебниках. Доказательство здесь элементарное: если сложить уравнения линий влияния, получим тождественно единицу. Наверное, сайт будет полезен умельцам, затеявшим строительство. Но все же, на мой взгляд, лучше пользоваться литературой, опирающейся на СНИП. Есть популярные издания, содержащие не только формулы сопромата, но и нормы проектирования. Там даны простые методики, содержащие и коэффициенты перегрузки, и сбор нормативных и расчетных нагрузок и др.
отличный сайт, спасибо вам! Будьте добры, подскажите, если у меня точечая нагрузка 500 Н каждые полметра на балке длиной 1.4 м, могу я рассчитывать как равномерно распределеную нагрузку в 1000 Н/м? и чему тогда будет равно q?
я знаю как рассчитывать, спасибо, не знаю вот какую схему взять правильней, 2 нагрузки через 0,45-0,5-0,45м или 3 через 0,2-0,5-0,5-0,2м условие сая знаю как рассчитывать, спасибо, не знаю вот какую схему взять правильней, 2 нагрузки через 0,45-0,5-0,45м или 3 через 0,2-0,5-0,5-0,2м условие самые неблагоприятные положения, опора на концах.
Если вы ищете наиболее неблагоприятное положение нагрузок, к тому же их может быть не 2 а 3, то в целях надежности имеет смысл просчитать конструкцию по обоим указанным вами вариантам. Если навскидку, то вариант с 2 нагрузками представляется наиболее неблагоприятным, но как я уже говорил, желательно проверить оба варианта. Если запас прочности важнее точности расчета, то можете принять распределенную нагрузку 1000 кг/м и умножить ее на дополнительный коэффициент 1.4-1.6, учитывающий неравномерность распределения нагрузки.
спасибо большое за подказку, ещё один вопрос: а если указанная мной нагрузка будет приложена не на балку, а на прямоугольную плоскость в 2 ряда, кот. жестко защемлена с одной большей стороны посередине, как тогда будет выглядеть эпюра или как тогда считать?
Ваше описание слишком неопределенно. Я понял так, что вы пытаетесь рассчитать нагрузку на некий листовой материал, уложенный в два слоя. Что означает «жестко защемлена с одной большей стороны посередине» я так и не понял. Возможно вы имеете в виду, что опираться этой листовой материал будет по контуру, но что тогда означает посредине? Не знаю. Если листовой материал будет защемлен на одной из опор на небольшом участке посредине, то такое защемление вообще можно не учитывать и считать балку шарнирной. Если это однопролетная балка (не важно листовой это материал или профиль металлопроката) с жестким защемлением на одной из опор, то ее так и следует рассчитывать (см. статью «Расчетные схемы для статически неопределимых балок») Если это некая плита, опертая по контуру, то принципы расчета такой плиты можно посмотреть в соответствующей статье. Если листовой материал будет укладываться в два слоя и эти слои имеют одинаковую толщину, то расчетную нагрузку можно уменьшить в два раза.
Однако листовой материал помимо всего прочего следует проверить на местное сжатие от сосредоточенной нагрузки.
Какие усилия действуют на шарнирную балку с равнораспределенной нагрузкой?
вернулась я к вам, потому что ответа так и не нашла. Попробую объясниь понятнее. Это типа балкона 140*70 cм. Сторона 140 прикручена к стене 4 болтами посередине в виде квадрата 95*46mm. Само дно балкона состоит из перфорированного по центру(50*120) листа алюминиевого сплава и под низом приварены 3 прямоугольные полые профиля, кот. начинаются от точки крепления со стеной и расхoдятся в разные стороны одна паралельно боковой стороне, т.е. прямо, а две другие разные стороны, в углы противоположно закрепленой стороны По кругу есть бардюр 15 см высотой; на балконе могут находится 2 человека по 80 кг в самых неблагоприятных положениях + равнораспределеная нагрузка в 40 кг. Балки в стену не закреплены, всё держится на болтах. Так вот, как мне расчитать какой взять профиль и толщину листа, чтобы дно не дифoрmировалось? Это ведь нельзя считать балкой, всё ведь происходит в плоскости? или как?
Здравствуйте. Будьте добры Приведите пример (задачу) с размерностью Q q L,M в разделе. Рисунок №1.2. Графическое отображение изменения реакций опор в зависимости от расстояния приложения нагрузки.
Здравствуйте! Помогите, пожалуйста. У меня консольная балка, на нее по всей длине действует распределенная нагрузка, на крайнюю точку «снизу вверх» действует сосредоточенная сила. На расстоянии 1м от края балки крутящий момент М. Мне нужно построить эпюры поперечной силы и моментов. Не знаю как определить распределенную нагрузку в точке приложения момента. Или ее не нужно считать в этой точке?
Распределенная нагрузка потому и распределенная, что распределена по всей длине и для некоторой точки можно определить только значение поперечных сил в сечении. Это означает, что на эпюре сил никакого скачка не будет. А вот на эпюре моментов, если момент изгибающий, а не вращающий, скачок будет. Как будут выглядеть эпюры от каждой из указанных вами нагрузок вы можете посмотреть в статье «Расчетные схемы для балок» (ссылка есть в тексте статьи перед п.3)
А как же приложенная к крайней точке балки сила F? Из-за нее не будет скачка на эпюре поперечных сил?
Будет. В крайней точке (точке приложения силы) правильно построенная эпюра поперечных сил изменит свое значение с F на 0. Да это и так должно быть понятно, если вы внимательно прочитали статью.
Спасибо Вам, Доктор Лом. Врубился, как делать, все получилось. У вас очень полезные познавательные статьи! Пишите больше, премного Вам благодарен!
У вас задача обратного порядка, когда уже известны реакции опор, а по ним нужно определить нагрузку и тогда вопрос более правильно сформулировать так:» при какой равномерно распределенной нагрузке на перекрытие опорные реакции будут составлять 36 000 кг при шаге между опорами 6 м по оси х и по оси z?»
Ответ: «4 тонны на м^2»
Решение: сумма опорных реакций 36х4=144 т, площадь перекрытия 6х6=36 м^2, тогда равномерно распределенная нагрузка 144/36 =4 т/м^2. Это следует из уравнения (1.1), настолько простого, понять, как можно его не понять, очень трудно. И это действительно, очень простая задача.
Две (три, десять) одинаковых балок (стопка) свободно сложенные друг на друга (концы не заделаны) выдержат большую нагрузку, чем одна?
Спасибо.
Доказываю это конструкторам на примере десантников и стопки кирпичей, тетрадь/одинокий лист.
Не сдаются бабушки.
Армированный бетон у них подчиняется другим законам, нежели дерево.
Посмотрите статью «Многопролетные неразрезные балки.»
А энто в какой же хвормуле не сходится? в 4.6, в 4.7, али в другой какой? Поточнее надобно мыслю выражать.
Я оформил нашу переписку в отдельную статью «Определение нагрузки на конструкции», все ответы там.
Потребовалось узнать, во сколько увеличится изгибающий момент, если случайно выбить одну из промежуточных балок. Увидел квадратичную зависимость от расстояния, следовательно в 4 раза. Не пришлось лопатить учебник. Большое спасибо.
Для неразрезных балок со множеством опор, все намного сложнее, так как момент будет не только в пролете но и на промежуточных опорах (смотрите статьи по неразрезным балкам). Но для предварительной оценки несущей способности можно использовать указанную квадратичную зависимость.
Ага. Вы все-таки хотите сделать подпорную стенку на время монтажа септика и, судя из вашего описания, собираетесь это сделать после того, как котлован будет выкопан. В этом случае нагрузка на доски будет создаваться осыпавшимся во время монтажа грунтом и потому будет минимальна и никаких особых расчетов не требуется.
Если же вы собираетесь засыпать и утрамбовать грунт обратно до монтажа септика, то расчет действительно нужен. Вот только расчетную схему вы приняли не правильную. В вашем случае доску, крепящуюся к 3 балкам 100х100, следует рассматривать как двухпролетную неразрезную балку, пролеты у такой балки будут около 90 см, а значит и максимальная нагрузка, которую сможет выдержать 1 доска, будет значительно больше, чем определенная вами, хотя при этом следует еще учесть и неравномерность распределения нагрузки от грунта в зависимости от высоты. А заодно и проверить несущую способность балок работающих по длинной стороне 4.5 м.
В принципе на сайте есть расчетные схемы, подходящие для вашего случая, а вот информации по расчету свойств грунта пока нет, впрочем это уже далеко не основы сопромата, да и по моему мнению вам такой точный расчет не нужен. Но в целом ваше стремление к пониманию сути процессов весьма похвально.
Спасибо доктор! Мысль вашу понял, надо будет еще почитать ваш материал. Да септик нужно впихнуть так чтобы не произошло обрушения. Опалубка при этом должна выдержать, т.к. рядом на расстоянии 4м еще и фундамент и можно все это запросто обрушить. Поэтому я так беспокоюсь. Еще раз спасибо, вы меня обнадежили.
Док, в конце статьи, где вы приводите пример определения момента сопротивления, в обоих случаях забыли разделить на 6. Разница все равно получится в 7,5 раз, но цифры будут другие (0,08 и 0,6) а не 0,48 и 3,6
Верно, была такая ошибка, исправил. Спасибо за внимательность.
добрый день. У меня такой вопрос, как можно посчитать нагрузку на балку. если с одной стороны закрепление жесткое с другой нет закрепленя. длина балки 6 метров. Вот надо посчитать какая должна быть балка, лучше монорельса. макс нагрузка на не закрепленной стороне 2 тонны. заранее спасибо.
Посчитайте, как консольную. Больше подробностей в статье «Расчетные схемы для балок».
Если бы я не изучал сопрамат, то я бы, честно говоря ничего не понял. Если вы пишите популярно, то вы и расписывайте популярно. А то у вас вдруг что-то появляется непонятно откуда, что за х? почему х? почему вдруг x/2 и чем он отличается от l/2 и l? Вдруг появилась q. откуда? Может опечатка и нужно было обозначить Q. Неужели нельзя потробно описать. И момент про производные. Вы понимаете, что вы описываете то, что только вы понимаете. И тот кто читает это впервые он этого не поймет. Поэтому стоило либо расписать подробно, либо вообще удалить этот абзац. Я сам со второго раза понял о чем речь.
Тут, к сожалению, ничем помочь не могу. Популярнее сущность неизвестных величин излагается только в начальных классах средней школы, и я полагаю, что хотя бы этот уровень образования читатели имеют.
Внешняя сосредоточенная нагрузка Q так же отличается от равномерно распределенной нагрузки q, как и внутренние усилия Р от внутренних напряжений р. Более того, в данном случае рассматривается внешняя линейная равномерно распределенная нагрузка, а между тем внешняя нагрузка может быть распределенной и по плоскости и по объему, при этом распределение нагрузки далеко не всегда бывает равномерным. Тем не менее любую распределенную нагрузку обозначаемую маленькой литерой, всегда можно привести к равнодействующей силе Q.
Впрочем, изложить все особенности строительной механики и теории сопротивления материалов в одной статье физически невозможно, для этого есть другие статьи. Почитайте, возможно, что-то прояснится.
Доктор! Не могли бы вы сделать пример расчета монолитного железобетонного участка как балку на 2х шарнирных опорах, при отношении сторон участка больше 2х
В разделе «Расчет железобетонных конструкций» всяких примеров хватает. К тому же постичь глубокую суть вашей формулировки вопроса я так и не смог, особенно вот это: «при отношении сторон участка больше 2х»
добрый. я первый раз встретил сапромат на вашем сайте заинтерисовался. пытаюсь разобраться в основах но понять эпюры Q не получается с М все понятно и ясно и их отличие тоже. Для распределенной Q я на веревку положил например танковый трак или каму что удобно. а на сосредоточенную Q я подвесил яблоко все логично. как на пальцах посмотреть эпюруQ. прошу не цетировать пословицу мне она не подходит я уже женат. спасибо
Добрый день, объясните пожалуйста почему допустимая опорная реакция в балке в 2 раза больше допустимой поперечноя силы Q по эпюре
Ваш вопрос мне не понятен, так как опорная реакция соответствует значению поперечной силы по эпюре Q. А о допустимости речь можно вести только тогда, когда проверяется на прочность существующая конструкция, а на данном этапе, пока параметры балки не известны, любая нагрузка или напряжение будут допустимыми.
Здравствуйте «Чтобы не углубляться в абстракции математики рассмотрим наглядный пример:» а где сам пример?
Работаю инженером развертки сетей ИТ(не по профессии). Одна из причин моего ухода с проектирования были расчеты по формулам из области сопромата и термеха(приходилось искать подходящее по рук-вам Мельникова, Муханова итд.. :)) В институте, к лекциям по относился несерьезно. В результате получил пробелы. К моим пробелам в расчетах Гл. спецы относились безразлично, так как сильным всегда удобно когда выполняют их указания. В результате, моя мечта быть профессионалом в области проектирования не сбылась. Всегда беспокоила неуверенность в расчетах(хотя интерес был всегда), соответственно платили копейки.
Спустя годы, мне уже 30, но в душе остается осадок. Лет 5 назад, такого открытого ресурса в интернете не существовало. Когда я вижу что все понятно изложено, хочется вернуться и учиться заново!)) Сам материал просто бесценный вклад в развитие таких как я))), а их возможно и тысячи. Думаю что они как и я будут Вам сильно признательно. СПАСИБО за проделанную работу!
Не отчаивайтесь, учиться никогда не поздно. Часто в 30 лет жизнь только начинается. Рад, что смог помочь.
Не очень понял как решение уравнения 1.5 дает нам ноль. Если подставить l=x, то нулю равно только третье слагаемое В(x-l), а два других нет. Как же тогда М равно 0?
Понял. Я почему-то рассматриваю сечение именно в точке приложения силы. Невижу необходимости рассматривать сечение между точками нагрузок так как оно испытывает меньшее воздействие чем последующая точка сосредоточенной нагрузки. Я неспорю просто мне нужно пересмотреть тему занова
Иногда есть необходимость определить значение момента, поперечной силы других параметров не только в точке приложения сосредоточенной силы, но и для других поперечных сечений. Например при расчете балок переменного сечения.
Отличная статья. В памяти все восстановилось. Сегодня она была очень кстати!
Здравствуйте доктор. Скажите пожалуйста, каким образом в графическом методе определения реакций, мы определяем значение, т.е. длину прилежащего катета, т.е. длину линии обозначающую реакцию опоры?
Огромное Вам спасибо за работу. Вы очень сильно помогаете многим, в том числе и мне, людям.Всё изложено просто и доходчиво
Здравствуйте! Спасибо за статью, всё намного понятнее и интереснее, чем в учебнике, я остановился на построении эпюры «Q» отображения изменения сил, ни как не могу понять почему эпюра слева устремляется к верху, а с права к низу, как я понял силы что на левой и на правой опоре действую зеркально, то есть сила балки (синяя) и реакции опоры (красная) должны отображаться с обеих сторон, можете объяснить?
День добрый! Проконсультируйте см картинка https://yadi.sk/i/CCBLk3Nl3TCAP2. Железобетонная монолитная опора с консолями. Если я консоль делаю не обрезанную, а прямоугольную то по калькулятору сосредоточенная нагрузка на краю консоли 4т при прогибе 4мм, а какая нагрузка будет на эту обрезанную консоль на картинке. Как в таком случае рассчитывается сосредоточенная и распределенная нагрузка при моем варианте. С Уважением.
Сергей, посмотрите статью «Расчет балок равного сопротивления изгибающему моменту», это конечно не ваш случай, но общие принципы расчета балок переменного сечения там изложены достаточно наглядно.
Помогите рассчитать предельную длину консольной балки до достижения жёсткой заделки напряжений равной пределу текучести материала
Добрый день. Строим качель. Хотелось бы узнать какую надо балку для качели при нагрузке в 250кг. Сечение балки у нас 85 мм? Спасибо за помощь.
Для того, чтобы ответить на ваш вопрос, нужно знать расстояние между опорами и что имеется в виду под сечением балки 85 мм. Это диаметр трубы или площадь сечения трубы или еще что-то?
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Источник
Эпюра — это вид графика, показывающий распределение нагрузки по стержню. Эпюра необходима, чтобы вычислить максимальные напряжения в стержне и на основе этих данных подобрать сечение для конструкции. Как построить эпюру подробно расписано в курсе сопротивления материалов, мы же остановимся на самых необходимых эпюрах для проектирования балок.
Из эпюры балки нам необходимо будет вычислить максимальный изгибающий момент, поперечную силу, опорные реакции стержня. Эти данные нам понадобятся для подбора сечения и проверочного расчета элемента конструкции.
Рассмотрим самые распространенные эпюры балки:
1) Балка имеет шарнирное закрепление по двум сторонам и равномерно-распределенную нагрузку.
Здесь и далее Q — Это поперечная сила, M — изгибающий момент.
Как видим максимальная поперечная нагрузка на балку находится в опорах балки, а максимальный момент в центре балки.
К полезной нагрузке можно прибавить и вес балки т.к. он, как правило, также равномерно распределен по длине балки.
2) Балка имеет шарнирное закрепление по двум сторонам и сосредоточенную нагрузку.
Этот вариант загрузки можно применить к подкрановой балке, хотя чаще всего подкрановая балка имеет несколько пролетов.
Максимальная поперечная сила возникает по всей длине участка от точки приложения силы до ближайшей опоры, причем чем ближе к опоре, тем больше поперечная сила. В расчетах этот показатель необходим чтобы рассчитать стенку балки на устойчивость и подобрать ребра жесткости в случае необходимости.
Максимальный момент возникает в точке приложения силы. Чем ближе точка приложения силы к центру балки, тем выше момент, поэтому если точка приложения нагрузки движется по балке, то подбор сечения необходимо сделать для приложения нагрузки по центру балки.
Эта эпюра не учитывает вес балки, но ее вес также необходимо считать. Для этого можно отдельно построить эпюру моментов для веса балки и сложить показатели в одинаковых точках.
3) Балка защемлена в опорах и равномерно-нагружена по всей длине
При защемлении в узлах максимальный момент в балке в 2-а раза ниже, чем в балке с равномерно-распределённой, однако необходимо сделать жесткий узел с колонной, что создает некоторые сложности. Кроме того момент от балки будет передаваться на колонны, как и момент с колонн будет передаваться на балку.
В расчетных программах необходимо быть внимательным и контролировать закрепление балок т.к. если расчет балки и подбор сечения будет произведен для жестко закрепленной балки, а в реальности узлы будут шарнирными, то балка будет посчитана не правильно и запас прочности может быть не достаточен.
4) Двухпролетная балка с шарнирными опорами и равномерно-распределенной нагрузкой
В данной схеме мы видим, что максимальный момент находиться на средней опоре, причем больше растянута верхняя часть балки.
Максимальная поперечная сила также находится в точке «В».
При расчете многопролетных балок необходимо учитывать то, что все пролеты могут быть не загружены равномерно, в этом случае эпюра 2-х пролетной балки выглядит следующим образом:
Как видим момент в пролете увеличился, все остальные параметры уменьшились, поэтому момент в пролете для расчета надо брать по этому варианту загружения.
_____________________________________________________________________
Как подобрать сечение стальной балки читайте в статье Расчет балки
Как правильно закрепить балку на колонне читайте в статье Опорные узлы балки