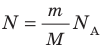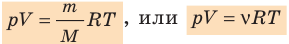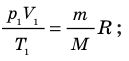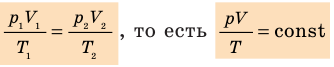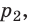Или с учетом химической формулы газа: p = M/V М = M/22,4, где M — молекулярная масса, V М — молярный объем.
Как считать объем газа?
Молярный объём V m — это отношение объёма данной порции вещества к его количеству. Численно молярный объём равен объёму (1) моль вещества. Обрати внимание! Молярный объём любого газа при нормальных условиях (давлении (101,3) кПа и температуре (0) °С) равен (22,4) дм³/моль.
Вычисление объёма газа по его количеству Преобразуем формулу молярного объёма — выразим из неё V : V ( X ) = n ( X ) ⋅ V m — объём газа равен произведению его количества на молярный объём. Пример: вычисли объём (н.у.) метана количеством (1,5) моль. V ( CH 4 ) = n ( CH 4 ) ⋅ V m = 1,5 ⋅ 22,4 = 33,6 дм³.
Вычисление количества газа по его объёму Выразим из формулы молярного объёма n : n ( X ) = V ( X ) V m — количество газа можно вычислить, если его объём разделить на молярный объём. Пример: вычисли количество водорода, соответствующее при н.у. его объёму (11,2) дм³.
Сколько литров в 1 м3 газа?
Кубометр газа — это сколько? — 1 кубометр сжиженного углеводородного газа — это 1000 литров. Не стоит путать кубометр и тонну газа, т.к. они неравнозначны: количество литров зависит от плотности газа, которая может колебаться от 0,51 до 0,56 (соответственно 1000 литров сжиженного газа — это 510-560 кг).
Как измеряют объем природного газа?
Для учета потребления природного газа и передачи показаний счетчика все еще используются кубометры (м 3 ), однако, согласно правилам Кабинета министров № 78 «Правила торговли и использования природного газа », в расчетах за природный газ необходимо использовать киловатт-часы (кВт·ч).
Сколько кубометров газа в 1 кг?
1 кг жидкого пропана объемом около 1,9 л образует около 500 литров газа. Соответственно 1 кг зимней смеси будет иметь объем 0,25х1,7 + 0,75х1,9 = 1,85 л и образует в нормальных условиях газ объемом 0,25х370 + 0,75х500 = 467,5 л (0,4675 м3).
Что такое объем газа?
V — объем газа — пространство, заполняемое газом. Ввиду отсутствия заметного притяжения между молекулами газа, он занимает весь предоставленный ему объем. Формулы, где встречается объем газа: Уравнение Менделеева — Клайперона Давление газа. Уравнение Клайперона. Объединенный газовый закон (при m = const; ν = const) Концентрация молекул газа. Плотность вещества. Работа газа при изобарном процессе,
Как измерить куб газа?
Приведение к нормальным и стандартным условиям — Единицей измерения объема газа является кубический метр (м³). Измеренный объем приводится к нормальным физическим условиям. Нормальные физические условия: давление 101 325 Па, температура 273,16 К (0 °С).
Стандартные условия: давление 101 325 Па, температура 293,16 К (+20 °С). В настоящее время эти обозначения выходят из употребления. Поэтому в дальнейшем следует указывать те условия, к которым относятся объемы и другие параметры газа. Если эти условия не указываются, то это значит, что параметры газа даны при 0 °С (273,16 °К) и 760 мм рт.
ст. (1,033 кгс/см²). Иногда объем газа (особенно в иностранной литературе и нормах) при пользовании системой СИ приводится к 288,16 °К (+15 °С) и давлению 1 бар (105 Па). Если известен объем газа при одних условиях, то пересчитать его в объемы при других условиях можно с помощью коэффициентов, приведенных следующей таблице.
Как перевести объем газа в литры?
Как перевести пропан-бутан из килограммов в литры ? ❓ Для того, чтобы посчитать количество литров в одном килограмме газа нужно воспользоваться формулой: Литр =Килограмм/Плотность Пример: Известно, что в баллоне 50 литров залито 21 килограмм газа, у которого испытательная плотность равна 0,567.
Чтобы посчитать литры нужно 21 разделить на 0,567. Получится 37,04 литра газа. Как перевести пропан-бутан из литров в килограммы? Для того, чтобы посчитать сколько килограммов содержится в одном литре газа нужно воспользоваться формулой: Килограмм= Литр*Плотность Пример: Известно, что в автомобиль заправлено 100 литров газа плотностью 0,567.
Чтобы посчитать какое количество килограммов газа, нужно 100 умножить на 0,567. Получится 56,7 кг газа. Уважаемые клиенты! Рекомендуем Вам 👓 наиболее популярные сезонные товары по низким ценам: Газовые баллоны 🛠️ Газовые комплекты ☘️ Газовая плита Гефест ПГТ-1+ баллон 5л Турист Полный комплект(баллон, редуктор, плита) для выездов на природу, на дачу. Рекомендован автотуристам.3 490 Комплект газовый Кемпинг ПГТ 1Б-В ( газ.горелка + баллон 8 литров), Крым Высота: 365 мм, Диаметр: 265 мм, Рабочее давление: 1,6 Мпа Товар распродан Таганок НЗГА Дачник Н-1 Объем, л 5. Тепловая мощность горелки, кВт: 1,8 Товар распродан Посмотреть все Газовые плиты здесь Посмотреть Газовые баллоны и все для подключения здесь
Какой объем газа в баллоне 50 литров?
Сколько м3 пропана в 1 баллоне на 5, 12, 27, 50 литров? — Мы произвели специальные расчеты, условно переводящие пропан-бутан в газообразное состояние. При стандартных условиях (100 кПа, 288 К) из 1кг сжиженного газа образуется 0,526 м³ пропана или 0,392 м³ бутана.
| Ёмкость баллона (л) | 5 | 12 | 27 | 50 |
|---|---|---|---|---|
| Вместимость (кубометров горючего газа) | 0,95 | 2,59 | 5,38 | 10,01 |
| Объём жидкого пропана (литров) | 4,3 | 10,2 | 22,9 | 42,5 |
Следует иметь в виду, что теплотворная способность пропан-бутановой смеси в три раза выше, чем у природного газа (метана).
В чем измеряется количество газа?
Соответственно, количество газа, как правило, измеряют в кубических метрах (м³), редко — в единицах массы, килограммах или тоннах (в основном — технологических газов).
Сколько тонн в кубометре газа?
Перевод 1 тонны СПГ в кубометры (м 3 ). — 1 тонна СПГ — это примерно 1,38 тыс м 3 природного газа после регазификации. Примерно — потому что плотность газа и компонентный на разных месторождения разная. Формулу Менделеева — Клайперона никто не отменял. Кроме метана в состав природного газа могут входить: этан, пропан, бутан и некоторые другие вещества.
- Плотность газа изменяется в интервале 0,68 — 0,85 кг/м³, но зависит не только от состава, но и от давления и температуры в месте расчета плотности газа.
- Стандартные условия для температуры и давления – это установленные стандартом физические условия, с которыми соотносят свойства веществ, зависящие от этих условий.
Национальный институт стандартов и технологий (NIST) устанавливает температуру 20 °C (293,15 K) и абсолютное давление 1 атм (101.325 кПа), и этот стандарт называют нормальной температурой и давлением (NTP). Плотность компонентов газа сильно различается:
Метан — 0,668 кг/м³, Этан — 1,263 кг/м³, Пропан — 1,872 кг/м³.
Поэтому, в зависимости от компонентного состава изменяется и количество м 3 газа при переводе из тонн. Перевод 1 м³ СПГ в 1 м³ регазифицированного природного газа Пропорции тоже зависят от компонентного состава. В среднем принимается соотношение 1: 600.1 м³ СПГ — это примерно 600 м 3 природного газа после регазификации.
Процесс сжижения идет ступенями, на каждой из которых газ сжимается в 5-12 раз, затем охлаждается и передается на следующую ступень. Собственно сжижение происходит при охлаждении после последней стадии сжатия. Процесс сжижения таким образом требует значительного расхода энергии — до 25 % от ее количества, содержащегося в сжиженном газе.
Ныне применяются 2 техпроцесса:
конденсация при постоянном давлении (компримирование), что довольно неэффективно из-за энергоемкости, теплообменные процессы: рефрижераторный — с использованием охладителя и турбодетандерный/дросселирование с получением необходимой температуры при резком расширении газа.
В процессах сжижения газа важна эффективность теплообменного оборудования и теплоизоляционных материалов. При теплообмене в криогенной области увеличение разности температурного перепада между потоками всего на 0,5ºС может привести к дополнительному расходу мощности в интервале 2 — 5 кВт на сжатие каждых 100 тыс м 3 газа.
каскадный цикл с последовательным использованием в качестве хладагентов пропана, этилена и метана путем последовательного снижения их температуры кипения, цикл с двойным хладагентом — смесью этана и метана, расширительные циклы сжижения.
Известно 7 различных технологий и методы сжижения природного газа:
- для производства больших объемов СПГ лидируют техпроцессы AP-SMR™, AP-C3MR™ и AP-X™ с долей рынка 82% компании Air Products, технология Optimized Cascade, разработанная ConocoPhillips, использование компактных GTL-установок, предназначенных для внутреннего использования на промышленных предприятиях, локальные установки производства СПГ могут найти широкое применение для производства газомоторного топлива ( ГМТ ), использование морских судов с установкой сжижения природного газа ( FLNG ), которые открывают доступ к газовым месторождениям, недоступным для объектов газопроводной инфраструктуры, использование морских плавающих платформ СПГ, к примеру, которая строится компанией Shell в 25 км от западного берега Австралии.
- Объем газа зависит от температуры и давления, поэтому при расчетах следует брать объем газа при нормальных условиях.
- Нормальными условиями считается температура 0 градусов и давление 101,325 кПа.
- Молярный объем 1 моля газа при нормальных условиях всегда одинаков и равен 22,41 дм 3 /моль.
- Этот объем называется молярным объемом идеального газа.
В чем измеряется газ при продаже?
Цены на природный газ — Основное использование единицы — при котировке оптовых цен на топливо (как правило, на англо-американских рынках), в основном, газа. Одна тысяча кубических метров природного газа содержит около 360 термов, Газовые счётчики измеряют объём газа; поэтому газовые компании используют коэффициент пересчёта объёма в теплотворную способность ; размерность такого коэффициента в англоязычных странах обычно терм/Ccf (100 кубических футов).
- кубометр в России; 100 кубических футов (Ccf) в США; киловатт-час в Великобритании.
Как правильно измерять расход газа?
Ультразвуковые расходомеры к содержанию — Принцип действия ультразвуковых расходомеров основан на измерении величины ультразвуковых колебаний, которые распространяются в потоке измеряемого вещества. Приборы для измерения количества вещества называются расходометрическими счётчиками.
1.скоростные счётчики, принцип действия которых основан на суммировании числа оборотов помещённого в поток жидкости вращающегося элемента.2.объёмные счетчики, принцип действия которых основан на суммировании объёмов вещества, вытесненного из измерительной камеры прибора.
Наибольшее распространение получили скоростные счётчики.
Сколько кг газа в 50 литровом баллоне?
При покупке бытовых пропановых баллонов часто возникает вопрос: какой будет расход пропана? При ответе на данный вопрос необходимо знать объем газа в баллоне. Сколько газа в баллонах? Баллон объемом 50 литров, В баллоне находится 21,5 кг*. Баллон объемом 27 литров, Чтобы определить сколько газа потребляет ваша газовая плита, необходимо обратиться к технической документации плиты. Например, у газовой плиты гефест ПГ 900 с 4 конфорками максимальный расход газа 486 г/ч (или 0,486 кг/час). Следовательно, если включены все 4 конфорки на максимум, то баллона 50 литров хватит на 44 часа (количество газа в баллоне 21,5 кг делим на расход 0,486 кг/час). Расход газа котлом рассчитывается аналогично расходу газа в газовых плитах. Из нюансов следует отметить, что расход сильно зависит от степени утепления вашего дома, а также от температуры окружающей среды. Чем меньше утеплен дом и чем ниже температура на улице, тем больше необходимо котлу затратить энергии (сжечь газ), чтобы нагреть помещения до необходимой температуры.
Сколько это 1000 кубометров газа?
Энергетический эквивалент природного газа
| тысяча кубометров природного газа → миллион кубометров природного газа | 0.001 |
|---|---|
| тысяча кубометров природного газа → тысяча кубических футов природного газа | 35.96 |
| тысяча кубометров природного газа → кубометр природного газа | 1,000 |
Сколько кг газа в 40 литровом баллоне?
Объем и вес технических газов в стандартных баллонах
| Газ | Объем баллона | Вес газа |
|---|---|---|
| Аргон технический | 40 л | 7,5 кг |
| Углекислота | 40 л | 20-24 кг |
| Пропан | 50 л | 21,5 кг |
| Ацетилен | 40 л | 5 кг |
Как найти объем газа по массе?
Молярный объем газа — Молярный объем газа – это отношение объема вещества к количеству этого вещества. Эту величину вычисляют при делении молярной массы вещества на его плотность по следующей формуле: Vm=M/p, где Vm – молярный объем, М – молярная масса, а p – плотность вещества. Рис.2. Молярный объем формула. В международной системе Си измерение молярного объема газообразных веществ осуществляется в кубических метрах на моль (м 3 /моль) Молярный объем газообразных веществ отличается от веществ, находящихся в жидком и твердом состоянии тем, что газообразный элемент количеством 1 моль всегда занимает одинаковый объем (если соблюдены одинаковые параметры).
То есть, в 1 моле любого газа (кислород, водород, воздух) объем равен 22,41 дм 3 /м. Рис.3. Молярный объем газа при нормальных условиях.
Как рассчитать расход газа через трубу?
Уравнение состояния: P =ρг·Rг·T·z, (6) где Rг = R/M. Для расчета массового расхода газа по трубопроводу основной яв- ляется формула. ρ = ρг/ρв – относительная плотность газа по воздуху.
Как определить первоначальный объем газа?
Данные задачи: P2 (конечное давление) = 1,5Р1 (начальное давление); ΔV (уменьшение объема) = 30 мл; процесс считаем изотермическим. Для нахождения первоначального объема взятого газа будем использовать пропорцию: P1 * V1 = P2 * V2. Подставим значение переменных: P1 * V1 = 1,5P1 * (V1 — 30). V1 = 1,5V1 — 45.0,5V1 = 45 и V1 = 45 / 0,5 = 90 мл. Ответ: Первоначально заданный газ занимал объем 90 мл.
Здравствуйте, уважаемые читатели!
Я продолжаю сегодня тему об оптимальных способах выполнения заданий ЕГЭ по химии, позволяющих с минимальными затратами времени и энергии достичь требуемого результата.
Вторая разновидность 28 задачи затрагивает только реакции с участием газов. Чаще всего предлагаются несложные процессы, связанные с использованием водорода, кислорода, азота, галогенов, а также газообразных соединений этих веществ. Популярны реакции гидрирования и сгорания газообразных углеводородов.
В отличие от задач на термохимию, в этой разновидности 28 задачи нужно самостоятельно составить уравнение реакции. В таблице представлены уравнения наиболее часто встречающихся в 28 задаче реакций:
Наряду с разнообразием химизма реакций, этот тип задач отличается и разнообразием усложнений. Крайне редко, но могут встречаться задачи на избыток-недостаток, выход реакции, наличие примесей в исходных веществах.
Ниже представлено видео с типовым решением рассматриваемого типа задач (начиная со 2 минуты):
Действия, которые предлагает сделать педагог:
1. написать уравнение реакции
2. перевести данные задачи в моли
3. по уравнению реакции найти количество неизвестного вещества
4. найти массу (объем) неизвестного вещества.
Ниже я предложу свое решение этой задачи, основанное на том же принципе, что и задача на термохимию (см. предыдущую статью). Составляется пропорция, главное в которой – одинаковые размерности числителя и знаменателя. Считаю использование в данной задаче пересчета на моли и обратно ненужным, и, более того, даже вредным: увеличивается количество промежуточных расчетов, возрастает возможность количественных ошибок. Моли хороши для задач, в которых задействовано несколько реакций. Во всех остальных случаях это – “Стрелять из пушки по воробьям…”
Задача 1 (из видео)
Рассчитайте массу газа, образующегося при взаимодействии с избытком кислорода 30, 24 л (н.у.) оксида азота (2). Запишите число с точностью до десятых.
Решение.
1. 2NO+O2=2NO2
2.Пусть левая часть пропорции посвящена известному вeществу – NO, правая неизвестному веществу -NO2. В числителе левой дроби указываем данные условия задачи – 30,24 л, в знаменателе -данные из уравнения (коэффициент перед формулой NO, умноженный на молярный объем 22,4 л). В числителе правой дроби указываем данные задачи – х г, в знаменателе – данные уравнения( коэффициент перед формулой NO2), умноженный на молярную массу, 46 г) :
Откуда х= 30,24*2*46/44,8=62,1 г
Задача 2 (из видео)
Какой объем кислорода требуется для полного сгорания 10 л ацетилена?
Решение:
1. 2С2Н2+5О2=4СО2+2Н2О
2. Пропорция (левая часть – посвящена С2Н2, правая – О2):
Откуда х=10*5/2=25 л
Задача 3.
При разложении нитрата меди(II) образовалось 12 л оксида азота(IV). Чему равен объём образовавшегося кислорода? Объёмы газов измерены при одинаковых условиях.
Решение.
1. 2Cu(NO3)2=2CuO+4NO2+O2
2. Пропорция(левая часть – для NO2, правая часть – для О2):
х= 12/4=3 л.
Задача 4.
Рассчитайте максимально возможный объём (н. у.) аммиака, который может быть получен исходя из 40 л водорода и 30 л азота? Ответ укажите в литрах с точностью до десятых.
Решение.
1.N2+3H2=2NH3
2. Поскольку в условии даны объемы двух исходных веществ, это – задача на избыток-недостаток. Это усложнение можно решить как устно, так и письменно. Сделаем это письменно:
а) V(N2) (по условию)/коэффициент перед азотом по уравнению=30/1=30
V(Н2) (по условию)/коэффициент перед водородом по уравнению=40/3=13
13 меньше 30, следовательно, Н2 – в недостатке. Далее решаем по недостатку.
б) Пропорция(левая часть – для Н2, правая часть – для NH3):
40л/(3*22,4 л)= Хл/(2*22,4 л)
х=40*2/3=26,7л
Как можно видеть из приведенных примеров, старая добрая пропорция при грамотном ее использовании (РАЗМЕРНОСТИ ЧИСЛИТЕЛЯ И ЗНАМЕНАТЕЛЯ ДОЛЖНЫ БЫТЬ ОДИНАКОВЫ) – прекрасный инструмент для решения задач, в которых задействована только одна реакция. По самым скромным подсчетам использование пропорций вместо молей позволяет в два раза сократить объем расчетов при одновременном снижении вероятных ошибок.
В следующей статье я покажу, как аналогичным образом решать задачу 29. А кроме того, поделюсь, как можно получить в ней ответ вообще без написания уравнения реакций .
Всего доброго!
Как найти объём выделившегося газа
В учебном курсе химии часто встречаются задачи, в которых требуется вычислить объем газа, выделившегося в результате химической реакции. Почти все задачи такого типа можно решить по следующему алгоритму.

Вам понадобится
- – таблица Менделеева;
- – ручка;
- – бумага для записей.
Инструкция
К примеру, вам требуется найти объем выделившегося водорода в результате реакции ортофосфорной кислоты и карбоната натрия. Самое главное для решения – правильно составить уравнение реакций. Если вы сомневаетесь, как реагируют данные в вашей задаче вещества, посмотрите в справочной литературе свойства химических веществ, участвующих в реакции.
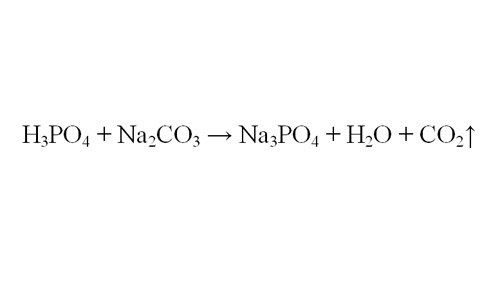
Расставьте коэффициенты в уравнении, чтобы число атомов элементов в левой и правой части уравнения совпадали. Теперь вы видите, в каком соотношении реагируют вещества. По известному количеству любого из них вы можете определить количество молей выделившегося газа. Например, если в реакцию вступило 4 моля ортофосфорной кислоты, получится 6 молей углекислого газа.
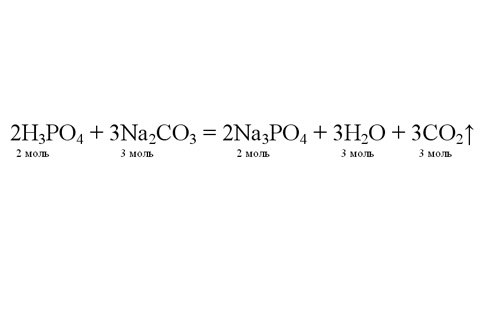
Зная количество молей газа, найдите его объем. По закону Авогадро 1 моль любого газа в нормальных условиях занимает 22,4 литра объема. Объем 6 молей газа будет равен: 6*22,4 = 134,4 литра.
Если в условии не дано количество реагента или продукта реакции, найдите из его других данных. При известной массе одного из веществ вы вычислите его количество молей по формуле: v = m/M, где v – количество вещества, моль; m – масса вещества, г; M – молярная масса вещества, г/моль. Молярную массу вы получите, сложив атомные веса элементов, составляющих вещество, из таблицы Менделеева. Например, молярная масса H3PO4: М = 3*1+31+16*4 = 98 г/моль.
Массу или количество нетрудно рассчитать из концентрации вещества, если известен объем раствора. Из молярности определите количество молей растворенного вещества по уравнению: v = V*Cм, где V – объем раствора, л; См – молярная концентрация, моль/л. Нормальность раствора связана с молярностью выражением: Сн = z*Cм, г моль-экв/л, где z – эквивалент реагента, количество протонов водорода, которое он может принять или отдать. Например, эквивалент H3PO4 – 3.
Также массу растворенного вещества вы можете найти из титра раствора: m = T*V, где Т – титр раствора, г/л; V – объем раствора. Или из плотности: m = p*V, где р – плотность раствора, г/мл.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Законы идеальных газов. Изопроцессы
Здесь рассматривается модель идеального газа, типичные процессы, которые с ней производятся: изотермический, изобарный, изохорный.
В статье рассматривается модель идеального газа и типичные процессы, которые с ней производятся: изотермический, изобарный, изохорный. Основную часть статьи представляют собой задачи с решениями, а в конце есть домашние задания.
Введение
В первую очередь хочется поговорить про идеальный газ. Что же он из себя представляет и почему он идеален?
Идеальный газ — теоретическая математическая модель газа, в которой пренебрегают размерами частиц и не учитывают силы взаимодействия между ними, предполагая, что их средняя кинетическая энергия много больше энергии их взаимодействия. Считается, что столкновения частиц газа между собой и со стенками сосуда абсолютно упругие.
Существует модель классического идеального газа, свойства которого описываются законами классической физики, и модель квантового идеального газа, подчиняющегося законам квантовой механики. Обе модели идеального газа справедливы для реальных классических и квантовых газов при достаточно высоких температурах и разряжениях.
В реальных же газах при некоторых расчетах мы не можем пренебрегать вышеуказанными приближениями. Например, вы можете столкнуться с газом Ван-дер-Ваальса, в уравнении которого есть поправка на объем и давление.
Какими величинами можно охарактеризовать состояние идеального газа?
Считая, что нам известен химический состав газа и его масса, для описания его состояния мы можем воспользоваться такими параметрами, как объем V, занимаемый газом, давление Р, температура Т. Связь между этими параметрами идеальных газов отражают четыре основных закона: закон Бойля — Мариотта, закон Гей-Люссака, закон Шарля и закон Клапейрона — Менделеева. Пользуясь уравнениями, описывающими эти законы, можно решать практически любые задачи, в которых нас интересует физическое состояние идеального газа.
Среди различных газовых процессов можно выделить такие, в которых одна из величин (T, P или V) поддерживается постоянной.
Изотерма
Изотермическими называются процессы, в которых температура постоянна: Т = const. Такие процессы, описывает закон Бойля — Мариотта:
P₁V₁ = P₂V₂,
где индексы 1 и 2 относятся к начальному и конечному состояниям газа.
Одним из основополагающих знаний про изопроцессы, в частности, для понимания темы и для решения задач, является вид графиков этих процессов в разных координатах.

Задача. Посредине узкой, запаянной с обоих концов горизонтальной трубки (рис. 2) находится столбик ртути длиной h = 25 см. Ртуть разделяет в трубке два столба воздуха длиной l₀ = 1 м каждый. Давление воздуха 76 см. рт. ст., температура остается постоянной. На какое расстояние х переместится столбик ртути, если трубку поставить вертикально?

Решение. Рассмотрим отдельно два столбика воздуха в стоящей вертикально трубке и применим закон Бойля — Мариотта к каждому из них (площадь сечения трубки S):
(1) P₀l₀S = P₁(l₀ + x)S,
(2) P₀l₀S = P₁(l₀ – x)S.
Из условия механического равновесия столбика ртути следует, что при вертикальном положении трубки давление в нижнем столбе воздуха равно
P₂ = P₁ + ρgh,
(ρ — плотность ртути). Подставив это значение P₂ в (2), получим квадратное уравнение, решив которое, найдем, что

(Отрицательное значение корня не имеет смысла).
Интересно отметить, что при вычислении неизвестного х нам не нужны сведения о плотности ртути ρ, а также о соотношениях между единицами давления. Дело в том, что по определению давление Р, которое создает 1 см. рт. ст., равно P = ρg · 1 см. Следовательно, P / ρg = 76 см без каких-либо дополнительных пересчетов.
Изобара
В изобарных процессах постоянно давление (P = const). Закон, описывающий этот процесс, называется законом Гей-Люсакка:
V₁ / T₁ = V₂ / T₂.
Графики при изобарном процессе:

Изохора
При изохорном процессах постоянным поддерживается объем газа (V = const), и закон, описывающий этот процесс, носит название закона Шарля:
P₁ / T₁ = P₂ / T₂.

Примеры

Рассмотрим теперь одну графическую задачу.
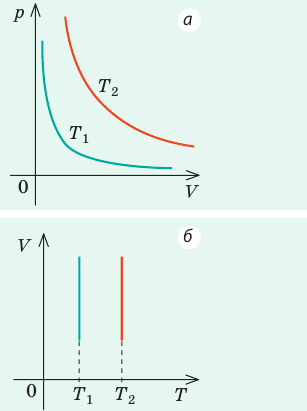
Задача. С идеальным газом происходит циклический процесс, график которого в координатах «давление-объем» приведен на рисунке (участок графика 2–3 — изотерма). Построить графики зависимости P(T) и V(T) для этого процесса.
Решение. Исследуем отдельно все участки процесса: 1–2, 2–3 и 3–1. Как видно из данного в условии графика, процесс 1–2 является изохорическим с ростом давления.

Поэтому на графиках P(T) и V(T) ему отвечают прямая, продолжение которой проходит через начало координат, и горизонтальная прямая соответственно, причем и давление, и температура в этом процессе растут (участки 1–2).
Процесс 2–3 является изотермическим (это говорится в условии) с ростом объема газа и убыванием давления. Поэтому на графиках P(T) и V(T) ему отвечают вертикальные прямые: убывающая на графике P(T) и растущая на графике V(T) (участки 2–3). Как следует из рисунка, процесс 3–1 является изобарическим, в нем объем газа убывает. Поэтому ему отвечают горизонтальная прямая на графике P(T) и прямая, продолжение которой проходит через начало координат, на графике V(T). Поскольку, совершив процесс 1–2–3–1, газ возвращается в первоначальное состояние, все графики должны быть замкнуты. Это значит, что соответствующие прямые должны попасть в начальную точку 1 (участки 3–1).
Рассмотрим еще несколько задач.
Задача. Определить температуру газа, находящегося в закрытом сосуде, если при нагревании газа на ΔT = 1 °С давление газа увеличивается на величину, составляющую α часть от первоначального давления (α = 0,004).
Решение. Так как объем сосуда в рассматриваемом процессе не меняется, то давление и температура газа в нем связаны законом Шарля. Из этого закона для начального и конечного состояния газа имеем:

Решая это уравнение, находим:

Задача. Во фляжке вместимостью 0,5 л находится 0,3 л воды. Турист пьет из неё воду, плотно прижав губы к горлышку так, что во фляжку не попадает наружный воздух. Сколько воды удастся выпить туристу, если он может понизить давление оставшегося во фляжке воздуха до 80 кПа.
Решение. Согласно условию задачи, исходный объем воздуха во фляжке V₁ = 0,2 л, а исходное давление равно атмосферному P₁ = 100 кПа. Если считать процесс поглощения воды туристам изотермическим, то, конечно, объем воздуха можно найти из закона Бойля-Мариотта:

Таким образом, объем воздуха во фляжке увеличится на 0,05 л = 50 см³ — именно такой объем воды и сможет выпить турист.
Из сказанного ясно, что параметры, определяющие состояние данной массы газа, неизменного химического состава (Р, V и Т) и связаны друг с другом. Если известны две величины, можно найти третью.
Уравнение, определяющее связь температуры, объема и давления, называют уравнением состояния газа, или, в честь открывших его ученых, уравнением Менделеева-Клапейрона. Подробнее о нем мы расскажем в следующей статье.
Задачи для самостоятельного решения
Задачи разделены на 3 уровня Л — легкий, С — средний, П — повышенный.
Задача 1. (Л). При увеличении давления в 1.5 раза объем газа уменьшился на 30 мл. Найти первоначальный объем газа. (90 мл)
Задача 2. (Л). Какой объем займет газ при температуре 77 ℃, если при температуре 27 ℃ его объем был 6л? (7 л)
Задача 3. (C). С идеальным газом происходит процесс, график которого в координатах «давление-объем» приведен на рисунке. Определить отношение максимальной и минимальной абсолютных температур газа в течение всего процесса. Все необходимые величины приведены на рисунке, k и n — известные числа. (T₃ / T₁ = nk)

Задача 4. (C). Построить эквивалентные графики в P(T) и V(T) координатах.

Задача 5. (П). Водяной паук Серебрянка строит в воде воздушный домик, перенося на лапках и брюшке пузырьки атмосферного воздуха и помещая их под купол паутины, прикрепленный концами к водяным растениям. Сколько рейсов надо сделать пауку, чтобы на глубине 50 см построить домик объемом 1 см³, если каждый раз он берет 5 мм³ воздуха под атмосферным давлением? (N = 210 раз)
А.Ю. Рудь
Список литературы
- Буховцев Б. Законы идеальных газов // Квант. №5. Квант. М., 1972.
- Гельфгат И.М. 1001 задача по физике с решениями. М., 1998.
- Савельев И.В. Курс общей физики. Т.1. Механика, колебания и волны, молекулярная физика. М., 1970.
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
Уравнение состояния идеального газа – основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 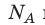
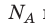
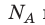
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
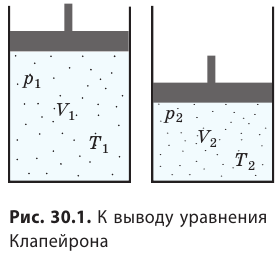
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (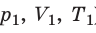
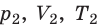
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 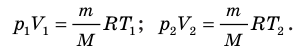
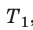
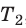
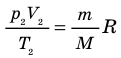
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (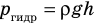
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (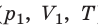
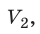
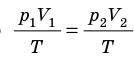
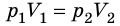
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 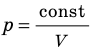
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (
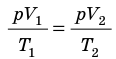
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния () в состояние (), то есть объем газа не изменяется (рис. 30.6). В этом случае имеет место равенство . После сокращения на V получим:
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
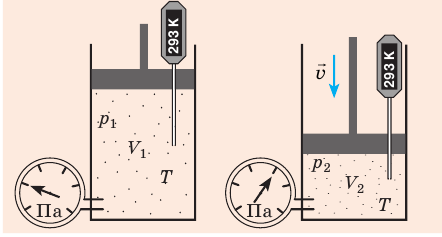
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:, но использовать закон Бойля — Мариотта нельзя, так как вследствие диссоциации (распада) молярная масса и число молей водорода увеличились в 2 раза:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: Разделив уравнение (2) на уравнение (1) и учитывая, что получим: где Найдем значение искомой величины:
Ответ: примерно в 2,7 раза.
Пример №2
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона): — универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнение состояния идеального газа
теория по физике 🧲 молекулярная физика, МКТ, газовые законы
Уравнение состояния идеального газа было открыто экспериментально. Оно носит название уравнения Клапейрона — Менделеева. Это уравнение устанавливает математическую зависимость между параметрами идеального газа, находящегося в одном состоянии. Математически его можно записать следующими способами:
Уравнение состояния идеального газа
Внимание! При решении задач важно все единицы измерения переводить в СИ.
Пример №1. Кислород находится в сосуде вместимостью 0,4 м 3 под давлением 8,3∙10 5 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода равна 0,032 кг/моль.
Из основного уравнения состояния идеального газа выразим массу:
Уравнение состояния идеального газа следует использовать, если газ переходит из одного состояния в другое и при этом изменяется его масса (количество вещества, число молекул) или молярная масса. В этом случае необходимо составить уравнение Клапейрона — Менделеева отдельно для каждого состояния. Решая систему уравнений, легко найти недостающий параметр.
Подсказки к задачам
Важна только та масса, что осталась в сосуде. Поэтому:
| Давление возросло на 15% | p2 = 1,15p1 |
| Объем увеличился на 2% | V2 = 1,02V1 |
| Масса увеличилась в 3 раза | m2 = 3m1 |
| Газ нагрелся до 25 о С | T2 = 25 + 273 = 298 (К) |
| Температура уменьшилась на 15 К (15 о С) | T2 = T1 – 15 |
| Температура уменьшилась в 2 раза | |
| Масса уменьшилась на 20% | m2 = 0,8m1 |
| Выпущено 0,7 начальной массы | |
| Какую массу следует удалить из баллона? | Нужно найти разность начальной и конечной массы: |
| Газ потерял половину молекул | |
| Молекулы двухатомного газа (например, водорода), диссоциируют на атомы | |
| Озон (трехатомный кислород) при нагревании превращается в кислород (двухатомный газ) | M (O3) = 3Ar (O)∙10 –3 кг/моль M (O2) = 2Ar (O)∙10 –3 кг/моль |
| Открытый сосуд | Объем V и атмосферное давление pатм остаются постоянными |
| Закрытый сосуд | Масса m, молярная масса M, количество вещества ν, объем V, число N и концентрация n частиц, плотность ρ— постоянные величины |
| Нормальные условия | Температура T0 = 273 К Давление p0 = 10 5 Па |
| Единицы измерения давления | 1 атм = 10 5 Па |
Пример №2. В баллоне содержится газ под давлением 2,8 МПа при температуре 280 К. Удалив половину молекул, баллон перенесли в помещение с другой температурой. Определите конечную температуру газа, если давление уменьшилось до 1,5 МПа.
2,8 МПа = 2,8∙10 6 Па
1,5 МПа = 1,5∙10 6 Па
Так как половина молекул была выпущена, m2 = 0,5m1. Объем остается постоянным, как и молярная масса. Учитывая это, запишем уравнение состояния идеального газа для начального и конечного случая:
Преобразим уравнения и получим:
Приравняем правые части и выразим искомую величину:
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
Алгоритм решения
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На высоте 200 км давление воздуха составляет примерно 10 –9 от нормального атмосферного давления, а температура воздуха Т – примерно 1200 К. Оцените плотность воздуха на этой высоте.
Уравнение состояния идеального газа
Содержание:
Уравнение состояния идеального газа получило название «уравнение Менделеева-Клапейрона». Давление смеси химически невзаимодействующих газов равно сумме их парциальных давлений: закон Дальтона.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Уравнение состояния идеального газа
Уравнение состояния идеального газа – это p = nkT называется уравнением Менделеева Клапейрона и оно даёт взаимосвязь трёх важнейших макроскопических параметров, описывающих состояние идеального газа давления, объёма и температуры. Поэтому уравнение Менделеева Клапейрона называется ещё уравнением состояния идеального газа.
Термодинамические параметры газа
В предыдущих главах было показано, что при описании свойств газа можно пользоваться величинами, характеризующими молекулярный мир (микромир), например энергией молекулы, скоростью ее движения, массой и т. п. Числовые значения таких величин мы можем определять только с помощью расчета. Все такие величины принято называть микроскопическими (от греческого «микрос» — малый).
Однако для описания свойств газов можно пользоваться и такими величинами, числовые значения которых находят простым измерением с помощью приборов, например давлением, температурой и объемом газа. Значения таких величин определяются совместным действием огромного числа молекул, поэтому они называются макроскопическими (от греческого «макрос» — большой).
Соотношение (4.1): устанавливает связь между микроскопическими и макроскопическими величинами для газов. Поэтому формулу (4.1) называют основным уравнением молекулярно-кинетической теории газов. Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа. Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
Если взять определенную массу газа т, то при постоянных р, V и Т газ будет находиться в равновесном состоянии. Когда происходят изменения этих параметров, то в газе протекает тот или иной процесс. Если этот процесс состоит из ряда непрерывно следующих друг за другом равновесных состояний газа, то он называется равновесным процессом. Равновесный процесс должен протекать достаточно медленно, так как при быстром изменении параметров давление и температура не могут иметь соответственно одинаковые значения во всем объеме газа. В этой главе рассматриваются только равновесные процессы в газах, при которых масса газа остается постоянной.
Когда процесс в газе заканчивается, то газ переходит в новое состояние, а его параметры приобретают новые постоянные числовые значения, вообще говоря, отличные от их значений в начале процесса. Если же при постоянной массе газа значения всех его параметров в начале и в конце процесса окажутся одинаковыми, то процесс называется круговым или замкнутым.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом. Газовый закон, выражающий связь между всеми тремя параметрами газа, называется объединенным газовым законом.
Отметим еще, что такого процесса в газе, при котором изменялся бы только один параметр газа, не существует, так как значения этих параметров взаимосвязаны. Примером сказанного является закон Шарля, выражающий связь между р и Т.
Объединенный газовый закон. Приведение объема газа к нормальным условиям
Связь между давлением, объемом и температурой определенной массы газа устанавливается с помощью соотношения (4.9):
Поскольку обозначает число молекул в единице объема газа, то , где N — общее число молекул, V — объем газа. Тогда получим
Так как при постоянной массе газа N остается неизменным, — постоянное число, т. е.
Поскольку значения р, V и Т в (5.2) относятся к одному и тому же состоянию газа, можно следующим образом сформулировать объединенный газовый закон: при постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Следовательно, если числовые значения параметров в начале процесса, происходящего с какой-либо определенной массой газа, обозначить через р1 , V1 и Т1, а их значения в конце процесса соответственно через р2 , V2 и Т2, то
Формулы (5.2) и (5.3) представляют собой математическое выражение объединенного газового закона.
На практике иногда нужно установить, какой объем V0 займет имеющаяся масса газа при нормальных условиях, т. е. при Т0=273 К и при р0=1,013 . 10 5 Па. Если значения параметров для этой массы газа в каком-либо произвольном состоянии, отличном от нормального, обозначить через р, V и Т, то на основании (5.3) получаем , или
Формула (5.4) позволяет приводить объем заданной массы газа к нормальным условиям.
Молярная газовая постоянная. Определение числового значения постоянной Больцмана
Формула (5.1) справедлива для любой массы газа, в которой содержится N молекул. Если применить эту формулу к одному молю какого-либо газа, то N нужно заменить постоянной Авогадро NA, а V — объемом одного моля Vмоль
Так как в одном моле любого газа содержится одно и то же число молекул NA, то произведение имеет одинаковое значение для всех газов, т. е. не зависит от природы газа. Произведение обозначается R и называется молярной газовой постоянной. Таким образом,
Числовое значение R можно найти, если применить (5.5) к состоянию одного моля газа при нормальных условиях, так как при этом м 3 /моль (§ 3.6). Действительно,
Это числовое значение R в СИ необходимо запомнить, так как им часто пользуются при расчетах и при решении задач.
Теперь легко найти числовое значение постоянной Больнмана . Из (5.6) получаем . Подставляя сюда числовые значения R и , вычисляем :
Уравнение Клапейрона — Менделеева. Плотность газа
Выясним, как будет выглядеть соотношение (5.1), если в него ввести молярную газовую постоянную R. Так как N — полное число молекул в массе газа т, а — число молекул в одном моле, то
где — число молей в массе газа /т. Поэтому
Поскольку , а равно массе газа т, деленной на массу одного моля газа , то получаем
Соотношение (5.7) называется уравнением Клапейрона — Менделеева или уравнением состояния для произвольной массы идеального газа. Для одного моля идеального газа уравнение Клапейрона — Менделеева принимает вид
С помощью формулы (5.7) легко выяснить, какими величинами определяется плотность газа. Так как , то из (5.7) имеем
Зависимость средней квадратичной скорости молекул газа от температуры
Выясним теперь, как можно с помощью вычислений находить среднюю квадратичную скорость движения молекул газа . Поскольку средняя кинетическая энергия поступательного движения молекул газа равна (3/2) , то можно написать , откуда
Отметим, что под т в формуле (5.10) подразумевается масса одной молекулы в кг. Так как , получим . Поскольку а есть масса одного моля газа (§ 3.6), имеем
Наконец, из (5.9) следует, что , поэтому
Среднюю квадратичную скорость можно находить по любой из формул (5.10)—(5.12). Из функции Максвелла можно получить формулы для средней арифметической скорости и наивероятнейшей скорости. Средняя арифметическая скорость
Наконец, наивероятнейшую скорость вычисляют так:
(Используя график функции Максвелла (рис. 3.3), поясните, почему меньше , а меньше
Изохорический процесс
Процессы, при которых масса газа и один из его параметров остаются постоянными, называются изопроцессами (от греческого «изос» — равный, одинаковый). Поскольку имеется три параметра газа, существует три различных изопроцесса. Первый из них (изохорический) рассмотрен выше (§ 4.3). Процесс в газе, который происходит при постоянной массе и неизменном объеме, называется изохорическим (от греческого «хора» — пространство). Графики для этого процесса называются изохорами (рис. 4.3).
Отметим, что к любому изопроцессу применим объединенный газовый закон и формулы (5.3), (5.7) и (5.8) с учетом того, что один из параметров остается постоянным. При изохорическом процессе постоянным остается объем V, поэтому формула (5.3) после сокращения на V принимает вид
Итак, изохорический процесс подчиняется закону Шарля: при постоянной-массе газа и неизменном объеме давление газа прямо пропорционально его абсолютной температуре. Это видно и из уравнения Клапейрона — Менделеева (5.7):
Так как V, т, и R остаются постоянными, то из (5.7) следует, что р пропорционально Т. Отметим, что закон Шарля можно формулировать и так, как это было сделано в § 4.3.
Изобарический- процесс
Процесс в газе, который происходит при постоянной массе и неизменном давлении, называется изобарическим (от греческого «барос» — тяжесть). Этот процесс был изучен французским физиком Л. Гей-Люссаком в 1802 г.
Поскольку при изобарическом процессе р постоянно, то после сокращения на р формула (5.3) принимает вид
Формула (5.16) является математическим выражением закона Гей-Люссака: при постоянной массе газа и неизменном давлении объем газа прямо пропорционален его абсолютной температуре. (Это видно и из уравнения Клапейрона — Менделеева (5.7): так как р, т, и R постоянны, то объем V пропорционален Т.)
На рис. 5.1 схематически изображен опыт Гей-Люссака. Колба с газом помещается в сосуд с водой и льдом.
В пробку вставлена трубка, изогнутая таким образом, что свободный конец ее горизонтален. Газ в колбе отделен от окружающего воздуха небольшим столбиком ртути в трубке. Температуру газа определяют по термометру, а объем — по положению столбика ртути. Для этого на трубке нанесены деления, соответствующие определенному внутреннему объему трубки (при градуировке трубки можно учесть и расширение сосуда при нагревании, но оно сравнительно мало’).
Сначала по положению столбика ртути 1 определяют — объем газа при 0°С. Затем газ нагревают (столбик ртути перемещается в положение 2), в процессе нагревания записывают значения объема и температуры и строят график, который называется изобарой.
Оказывается, что изобара представляет собой прямую линию (рис. 5.2, а), которая пересекается с осью абсцисс в точке А.
Из подобия треугольников на рис. 5.2, а следует
Обозначив через , получим
Здесь — коэффициент объемного расширения газа (гл. 13).
Если повторять этот опыт для разных газов или для разных масс газа, то все графики будут пересекаться в точке А, соответствующей t=—273°С (рис. 5.2, б), т. е. коэффициент одинаков для всех газов. Это означает, что расширение газа при изобарическом процессе не зависит от его природы.
Отметим, что для газов коэффициенты и в формулах (4.2а) и (5.17) численно одинаковы, поэтому обычно пользуются одним .
Изотермический процесс
Процесс в газе, который происходит при постоянной температуре, называется изотермическим.
Изотермический процесс в газе был изучен английским ученым Р. Бойлем и французским ученым Э. Мариоттом. Установленная ими опытным путем связь получается непосредственно из формулы (5.3) после сокращения на Т:
Формула (5.18) является математическим выражением закона Бойля — Мариотта: при постоянной массе газа и неизменной температуре давление газа обратно пропорционально его объему. Иначе говоря, в этих условиях произведение объема газа на соответствующее давление есть величина постоянная:
Соотношение (5.19) можно получить и из (5.7) или (5.8), так как при постоянном Г справа в формулах (5.7) и (5.8) стоит постоянная величина. График зависимости р от V при изотермическом процессе в газе представляет собой гиперболу и называется изотермой. На рис. 5.3 изображены три изотермы для одной и той же массы газа, но при разных температурах Т.
Отметим еще, что из формулы (5.9) непосредственно вытекает, что при изотермическом процессе плотность газа изменяется прямо пропорционально давлению:
(Подумайте, как проверить закон Бойля — Мариотта на опыте.)
Внутренняя энергия идеального газа
Как отмечалось, силы взаимодействия молекул в идеальном газе отсутствуют. Это означает, что молекулярно-потенциальной энергии у идеального газа нет. Кроме того, атомы идеального газа представляют собой материальные точки, т. е. не имеют внутренней структуры, а значит, не имеют и энергии, связанной с движением и взаимодействием частиц внутри атома. Таким образом, внутренняя энергия идеального газа представляет собой только сумму знамений кинетической энергии хаотического движения всех его молекул:
Поскольку у материальной точки вращательного движения быть не может, то у одноатомных газов (молекула состоит из одного атома) молекулы обладают только поступательным движением. Так как среднее значение энергии поступательного движения молекул определяется соотношением(4.8): , то внутренняя энергия одного моля одноатомного идеального газа выразится формулой , где — постоянная Авогадро. Если учесть, что , то получим:
Для произвольной массы одноатомного идеального газа имеем
Если молекула газа состоит из двух жестко связанных атомов (двухатомный газ), то молекулы при хаотическом движении приобретают еще и вращательное движение, которое происходит вокруг двух взаимно перпендикулярных осей. Поэтому при одинаковой температуре внутренняя энергия двухатомного газа больше, чем одноатомного, и выражается формулой
Наконец, внутренняя энергия многоатомного газа (молекула содержит три или больше атомов) в два раза больше, чем у одно-атомного при той же температуре:
поскольку вращение молекулы вокруг трех взаимно перпендикулярных осей вносит в энергию теплового движения такой же вклад, как поступательное движение молекулы по трем взаимно перпендикулярным направлениям.
Отметим, что формулы (5.23) и (5.24) теряют силу для реальных газов при высоких температурах, так как при этом в молекулах возникают еще колебания атомов, что ведет к увеличению внутренней энергии газа. (Почему это не относится к формуле (5.22)?)
Работа газа при изменении его объема
Физический смысл молярной газовой постоянной. Опыт показывает, что сжатый газ в процессе своего расширения может выполнять работу. Приборы и агрегаты, действия которых основаны на этом свойстве газа, называют пневматическими. На этом принципе действуют пневматические молотки, механизмы для закрывания и открывания дверей на транспорте и т. д.
Представим себе цилиндр с подвижным поршнем, заполненный газом (рис. 5.4).
Пока давление газа внутри цилиндра и окружающего наружного воздуха одинаковы, поршень неподвижен. Пусть при этом температура газа и окружающей среды равна а давление равно р.
Будем теперь медленно нагревать газ в цилиндре до температуры . Газ при этом начинает изобарически расширяться (внешнее давление р остается постоянным), и поршень переместится из положения 1 в положение 2 на расстояние . При этом газ совершит работу против внешней силы. Сила F, совершающая эту работу, будет равна рS, где S — площадь сечения цилиндра. Из механики известно, что работа выражается формулой , или . Так как есть приращение объема газа в процессе его изобарического нагревания от до , имеем
Нетрудно сообразить, что при изохорическом процессе работа газа равна нулю, так как никакого изменения объема, занятого газом, в этом случае не происходит. Вообще следует помнить, что газ выполняет работу только в процессе изменения своего объема, т. е. при . Отметим, что при расширении газа работа газа положительна; при сжатии газа положительную работу выполняют внешние силы, а работа газа в этом случае отрицательна.
Выясним, как можно определить работу газа по графику зависимости р от V в том или ином газовом процессе. При изобарическом процессе график зависимости р от V представляет собой прямую линию, параллельную оси абсцисс, так как р постоянно. Из рис. 5.5 видно, что работа газа в этом случае численно равна заштрихованной площади.
Выясним, как найти работу газа при изотермическом процессе. На рис. 5.6 изображена изотерма идеального газа. При таком процессе газ выполняет работу, так как в этом случае отлично от нуля. Формулу (5.25) здесь применять нельзя, так как она верна при постоянном давлении р, а в изотермической процессе р изменяется. Однако можно взять такое малое приращение объема , при котором изменением давления можно пренебречь. Тогда приближенно можно считать, что при увеличении объема газа на давление остается постоянным. Работу при этом можно вычислять по формуле . На рис. 5.6 она выражается заштрихованной площадью.
Разбивая интервал на множество интервалов , настолько малых, что работу на каждом из них можно вычислять по формуле , полную работу газа найдем как сумму элементарных работ . Это означает, что работа газа будет равна сумме площадей, подобных заштрихованной площади на рис. 5.6. Следовательно, работа газа при изотермическом процессе выражается площадью, ограниченной двумя ординатами и , отрезком оси абсцисс и графиком зависимости р от V.
Можно строго доказать, что работа газа при любом процессе выражается площадью, ограниченной двумя ординатами, отрезком оси абсцисс и графиком того процесса в координатах V и р.
Выясним теперь физический смысл молярной газовой постоянной R. Применяя формулу (5.25) к одному молю идеального газа, получим
Но из уравнения Клапейрона — Менделеева (5.8) для одного моля можно записать для двух состояний газа:
Подставляя это выражение в (5.26), будем иметь , или
Из (5.27) следует, что молярная газовая постоянная численно равна работе, совершаемой одним молем идеального газа при его изобарическом нагревании на один кельвин.
Из соотношения видно, что постоянная Больцмана показывает, сколько работы в среднем приходится на одну молекулу идеального газа при изобарическом нагревании на один кельвин.
Услуги по физике:
Лекции по физике:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
[spoiler title=”источники:”]
http://natalibrilenova.ru/uravnenie-sostoyaniya-idealnogo-gaza/
[/spoiler]