Как найти максимальный объем конуса - Сайт, где вы сможете решить свои вопросы

Ответ:

V = 6224,272 * √3 π см³

Объяснение:

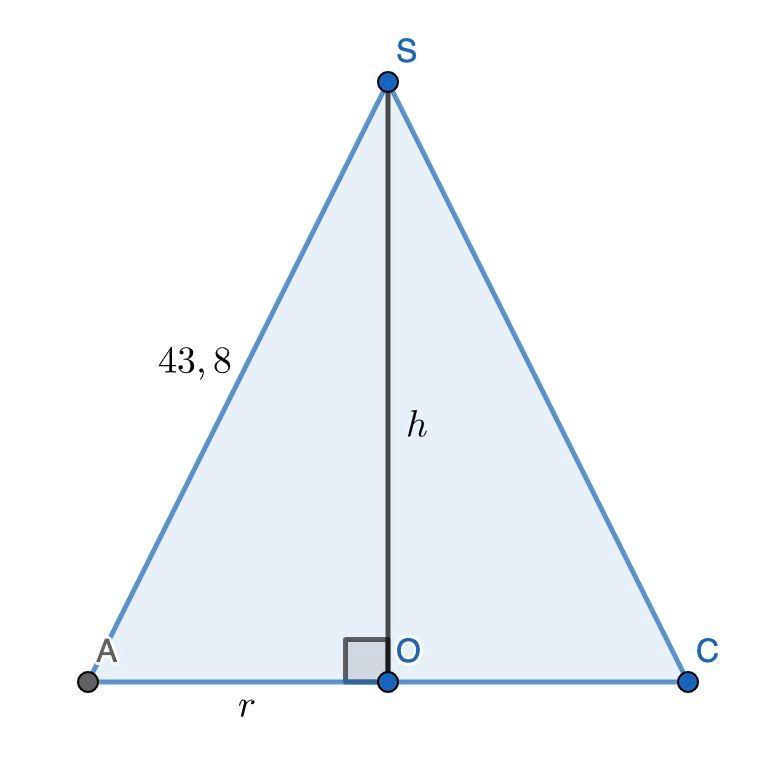
Рассмотрим осевое сечение конуса (см. рис.). SO — высота конуса (h), AO — радиус (r), AS — образующая конуса (43,8 см). Тогда по теореме Пифагора r² + h² = 43,8².

Объём конуса вычисляется по формуле $V=dfrac{1}{3}pi r^2h$ . Из предыдущего уравнения r² = 43,8² – h². Подставим это в уравнение объёма:

$V=dfrac{1}{3}pi (43{,}8^2-h^2)h=dfrac{43{,}8^2pi}{3}h-dfrac{pi}{3}h^3$

Найдём максимальное значение с помощью производной:

$V'(h)=dfrac{43{,}8^2pi}{3}-pi h^2\V'(h)=0Leftrightarrow dfrac{43{,}8^2pi}{3}=pi h^2Leftrightarrow h=pmdfrac{43{,}8}{sqrt{3}}$

Будем рассматривать только положительные значения h, так как отрицательной высота быть не может. При $0<h<dfrac{43{,}8}{sqrt{3}} V'(h)>0$ , при $h>dfrac{43{,}8}{sqrt{3}} V'(h)<0$ . Значит, $h=dfrac{43{,}8}{sqrt{3}}$ — точка максимума. При данном значении h объём конуса максимален.

$V_{max}=dfrac{1}{3}pileft(43{,}8^2-dfrac{43{,}8^2}{3}right)cdotdfrac{43{,}8}{sqrt{3}}=dfrac{1}{3}pi cdotdfrac{2}{3}cdot 43{,}8cdot 43{,}8cdotdfrac{43{,}8}{3}sqrt{3}=\=14{,}6cdot 2cdot 14{,}6cdot 14{,}6sqrt{3}pi=6224{,}272sqrt{3}pi$

Приложения:

Источник

Пифагор: h^2=l^2-r^2, где ^ – степень, r – радиус основания.

Объём конуса: V=1/3*pi*r^2*koren(l^2-r^2).

Обозначим для удобства x=r^2, x > 0.
Объём наибольший, когда функция y(x)=x*koren(l^2-x) имеет наибольшее значение. При этом f(x)=x^2*(l^2-x) тоже будет максимально.

Приравниваем к 0 производную:

(x^2*l^2-x^3)’=0, 2x*l^2-3x^2=0, x=2/3*l^2.

Итак, максимальный объем при r^2=2/3*l^2.
Осталось подставить это в формулу для V.

Анастасия СерыхУченик (88)

8 лет назад

“Объём наибольший, когда функция y(x)=x*koren(l^2-x)”-а куда делось 1/3pi?

Alexander Alenitsyn
Высший разум
(754455)
Функция у (х) отличается от объема только постоянным множителем, поэтому значение х, при котором объём максимальный, то же самое, при котором у (х) максимальна.

Источник

Пускай $%x$% – радиус основания конуса. Тогда его высота равна $%R+sqrt{R^2-x^2}$%,
$%V=frac{1}{3}pi x^2left(R+sqrt{R^2-x^2}right)$%. Далее стандартно: находим производную, приравниваем её к нулю и получаем, что $$V_{max}=frac{32}{81}pi R^3$$ при $$x=frac{2sqrt{2}}{3}R.$$

ссылка

отвечен
18 Дек ’14 15:47

EdwardTurJ
50●13●96●197

10|600
символов нужно
символов осталось

Источник

Найти наибольший объем конуса

	28.10.2013, 02:49
Найти наибольший объем конуса, образующая которого имеет данную длину l.
1 2 3 4 5 Категория: Задачи на доказательство \| Добавил: alexlat
Просмотров: 4201 \| Загрузок: 0 \| Рейтинг: 5.0/1

Добавлять комментарии могут только зарегистрированные пользователи.

[

Регистрация

Вход

]

Статистика

Источник

30 / 17 / 0

Регистрация: 21.10.2012

Сообщений: 346

Определить размеры конуса наибольшего объема

21.09.2013, 22:09. Показов 10184. Ответов 24

Определить размеры конуса наибольшего объема при условии, что его боковая поверхность S равна 10 см^2

4216 / 3411 / 396

Регистрация: 15.06.2009

Сообщений: 5,818

30.09.2013, 22:56

Сообщение было отмечено как решение

Решение

Площадь боковой поверхности:
$https://www.cyberforum.ru/cgi-bin/latex.cgi?S=pi r l=pi r sqrt{r^2+h^2}$

Целевая функция (метод множителей Лагранжа):
$https://www.cyberforum.ru/cgi-bin/latex.cgi?Phi (r,h,lambda )=frac{1}{3}pi r^2h+lambda (S-pi r sqrt{r^2+h^2})$

Частные производные (это для ТС задача)
$https://www.cyberforum.ru/cgi-bin/latex.cgi?left{begin{matrix}partial Phi /partial r=0\ partial Phi /partial h=0\ partial Phi /partial lambda =0end{matrix}right.$
После элементарной школьной алгебры первые два уравнения сводятся к

а из третьего уравнения (которое и есть исходное ограничение):
$https://www.cyberforum.ru/cgi-bin/latex.cgi?r^2=frac{S}{pi sqrt{3}}$

1765 / 969 / 180

Регистрация: 24.02.2013

Сообщений: 2,784

Записей в блоге: 12

30.09.2013, 23:54

Сообщение от Даниил 007

Но все же, возможно ли в ручную решить эту “недетскую” системку трех нелинейных уравнений, или же это из разряда фантастики ?

В ручную лично я давно ничего не решаю.Для этого существуют матпакеты.
Маткад, например, символьно решить вышеназванную систему из трех уравнений не смог.Помогать ему, естественно, не стал – решил численно (Маткад).
P.S.Ну, вот Том Ардер говорит, что система просто решается….

4216 / 3411 / 396

Регистрация: 15.06.2009

Сообщений: 5,818

01.10.2013, 02:34

Сообщение от Nacuott

Маткад, например, символьно решить вышеназванную систему из трех уравнений не смог

Mathcad 14, решение есть.

Миниатюры

Изображения

Вложения

30 / 17 / 0

Регистрация: 21.10.2012

Сообщений: 346

01.10.2013, 20:40

[ТС]

Сообщение от Том Ардер

Площадь боковой поверхности:
$https://www.cyberforum.ru/cgi-bin/latex.cgi?S=pi r l=pi r sqrt{r^2+h^2}$

Целевая функция (метод множителей Лагранжа):
$https://www.cyberforum.ru/cgi-bin/latex.cgi?Phi (r,h,lambda )=frac{1}{3}pi r^2h+lambda (S-pi r sqrt{r^2+h^2})$

а из третьего уравнения (которое и есть исходное ограничение):
$https://www.cyberforum.ru/cgi-bin/latex.cgi?r^2=frac{S}{pi sqrt{3}}$

Огромное Вам спасибо, что пролили истину на эту задачу, но меня мучает еще один вопрос:
Вот нашли мы радиус и высоту, а как доказать, что при этих радиусе и высоте объем конуса будет наибольшим, то есть как доказать, что это максимумы целевой функции ?

4216 / 3411 / 396

Регистрация: 15.06.2009

Сообщений: 5,818

01.10.2013, 22:21

Сообщение от Даниил 007

как доказать, что это максимумы целевой функции ?

Исследовать вторые производные, если нужно строгое формальное доказательство.

Источник

Определить размеры конуса наибольшего объема

Решение

Вам также может понравиться

Как в твиттере найти твит по слову

Как найти угол между двумя гранями пирамиды

Как найти работу без опыта с обучением

Добавить комментарий Отменить ответ