Как найти максимальный путь по графику

Задача
о максимальном пути формулируется
следующим об­разом: в заданной сети
G=(V,E,c)
с
выделенным узлом s,
для
ка­ждого узла vV
найти
s-v-путь,
имеющий максимальную длину среди всех
возможных s-v-путей
в сети G.

Отметим,
что имеет смысл решать эту задачу лишь
в сетях, не содержащих контуров
положительной длины. Рассмотрев тогда
сеть, отличающуюся от исходной только
изменением знаков ве­сов дуг, получим
сеть, в которой нет контуров отрицательной
длины. Применяя к новой сети алгоритм
Форда-Беллмана, можно построить кратчайшие
s-v-пути,
которые будут путями макси­мальной
длины в исходной сети.

Впрочем,
задачу о максимальном пути в общем
случае можно решать и непосредственно,
заменяя в алгоритме Форда-Беллмана
строку 6 на строку

6′
for
wV
do
D[v]
:= max(D[v], D[w]+A[w,v]);

Разумеется,
решая таким образом задачу о максимальном
пути, вес несуществующих дуг следует
положить равным -∞.

Важный
частный случай сети с неотрицательными
весами дуг в предположении отсутствия
контуров положительной длины сводится
к случаю отсутствия контуров в сети.
Следовательно, задача о максимальном
пути в частном случае может быть реше­на
алгоритмом 6.6, в котором +∞
заменяется на

-∞
(строка 3), а min
на
шах (строка 6). Несложное доказательство
корректности исправленного таким
образом алгоритма 6.6 мы предоставляем
читателю.

Отметим,
что замена всех минимумов в алгоритме
Дейкстры (строки 7 и 10) на максимумы не
позволяет получить алгоритм решения
задачи о максимальном пути. Для примера
достаточно рассмотреть сеть, изображенную
на рис.6.5. Здесь модификация алгоритма
Дейкстры, при которой все минимумы
заменены на максимумы неправильно
определит путь максимальной длины от
узла s
до
узла 2.

Итак,
алгоритм Форда-Беллмана и алгоритм 6.6
легко могут быть модифицированы для
вычисления длин максимальных

s-v-
*1
путей. Сами же пути с помощью вычисленных
Задача о максимальном пути в бесконтурной
сети имеет большое практическое значение.
Она является важнейшим зве­ном в
методах сетевого планирования работ
по осуществлению некоторого проекта.

Многие
крупные проекты, такие как строительство
дома, из­готовление станка, разработка
автоматизированной системы бух­галтерского
учета и т.д., можно разбить на большое
количество различных операций (работ).
Некоторые из этих операций могут
выполняться одновременно, другие —
только последовательно: одна операция
после окончания другой. Например, при
строи­тельстве дома можно совместить
во времени внутренние отде­лочные
работы и работы по благоустройству
территории, однако возводить стены
можно только после того, как будет готов
фун­дамент.

Задачи
планирования работ по осуществлению
некоторого проекта состоят в определении
времени возможного окончания как всего
проекта в целом, так и отдельных работ,
образующих проект; в определении резервов
времени для выполнения отдель­ных
работ; в определении критических работ,
то есть таких ра­бот, задержка в
выполнении которых ведет к задержке
выполне­ния всего проекта в целом; в
управлении ресурсами, если тако­вые
имеются и т.п.

Здесь
мы разберем основные моменты одного из
методов се­тевого планирования,
называемого методом
критического пути (МКП).

Метод
был разработан в конце пятидесятых
годов Дюпоном и Ремингтоном Рандом для
управления работой химических заво­дов
фирмы “Дюпон де Немур” (США).

Пусть
некоторый проект W
состоит
из работ v₁…,v_n.
для
каж­дой работы v_k
известно, или может быть достаточно
точно оценено время ее выполнения t(v_k).
Кроме
того, для каждой работы v_k
известен,
возможно пустой, список ПРЕДШ(v_к)
работ, непо­средственно предшествующих
выполнению работы v_k.
Иначе
го­воря, работа v_k
может
начать выполняться только после
заверше­ния всех работ, входящих в
список ПРЕДШ(v_к).

Для
удобства, в список работ проекта W
добавим
две фиктив­ные работы s
и
t,
где
работа s
обозначает
начало всего проекта W,
а
работа t
—
завершение работ по проекту W.
При
этом будем считать, что работа s
предшествует
всем тем работам vW,
для
которых список ПРЕДШ(v)
пуст, иначе говоря, для всех таких работ
vW
положим
ПРЕДШ(v)={s}.
Положим далее ПРЕДШ(s)
= Ø,
ПРЕДШ(t)={vW
:
v
не
входит ни в один список ПРЕДШ(w)},
то есть считаем, что работе t
предшествуют
все те работы, которые могут выполняться
самыми последними. Время выполнения
работ s
и
t
естественно
положить равными нулю; t(s)=t(t)=0.

Весь
проект W
теперь
удобно представить в виде сети G=(V,E,c),
где
сеть G=(V,E,c)
определим
по правилам:

1. V=W,
   то
   есть множеством узлов объявим множе­ство
   работ;

2. E={(v,w)
   :
   v
   ПРЕДШ(w)},
   то есть отношение предшествования
   задает дуги в сети;

3. c(v,w)=t(w).

Так
построенную сеть G
часто
называют сетевым графиком выполнения
работ по проекту W.
Легко
видеть, что списки смеж­ностей этой
сети ПРЕДШ[v]
совпадают с заданными для проекта
списками предшествующих работ ПРЕДШ(v).

Понятно,
что сетевой график любого проекта не
может содер­жать контуров. Действительно,
пусть узлы v_kl,v_k2,…,v_kr=v_k1
обра­зуют
контур в сети G.
Это
означает, что работа v_k2
не
может на­чаться раньше, чем будет
завершена работа v_k1
работа
v_k3
—
раньше, чем завершится работа v_k2,
и
т.д., и, наконец, v_kr
=
v_k|
-—
раньше, чем будет завершена работа
v_kr-1.
Но
тогда никакая из работ v_k1…,v_kr
никогда
не сможет быть выполнена. А каждый
ре­альный проект должен допускать
возможность его завершения. Следовательно,
в сетевом графике нет контуров.

Отсутствие
контуров в сети G
позволяет
пронумеровать рабо­ты проекта W
таким
образом, чтобы для каждой дуги (v_i,
v_j)
сети
G
выполнялось
условие i<j
(лемма
6.3). Напомним, что осущест­вить такую
нумерацию узлов сети G
можно
с помощью алгорит­ма 6.5 ТОПСОРТ. Поэтому
в дальнейшем будем считать, что уз­лы
в сети G
топологически
отсортированы.

n	Наименование работы	Предшествующие работы	Время выполнения
1	Закладка фундамента	Нет	4
2	Возведение коробки задания	1	8
3	Монтаж электропроводки	2	2
4	Сантехмонтаж	2	3
5	Настил крыши	2	4
6	Отделочные работы	3,4	5
7	Благоустройство территории	5	2

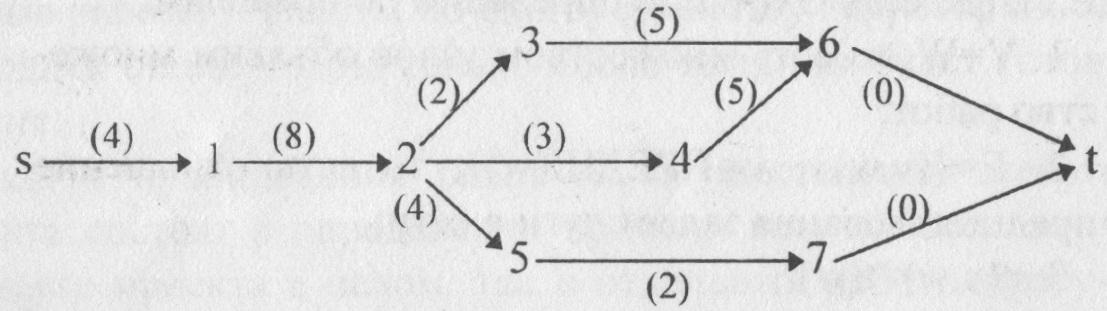Рис
6.6 Проект
строительства дома и его сетевой график

Конечной
целью построения сетевой модели является
получе­ние информации о возможных
сроках выполнения как отдельных работ,
так и о возможном сроке выполнения всего
проекта в це­лом.

Обозначим
через РВЫП(v)
(соответственно PHAЧ(v))
наибо­лее
ранний возможный срок выполнения работы
v
(соответственно
наиболее
ранний возможный срок начала рабо­ты
v).
Удобно
считать, что РВЫП(s)=PHAЧ(s)=0.
Поскольку
на­чать выполнять работу v
можно
только после того, как будут вы­полнены
все работы, предшествующие данной работе
v,
то
полу­чим следующие формулы для расчета
значений PHAЧ(v)
и
РВЫП(v):

PHAЧ(v)
=
max{
РВЫП(w):
wПРЕДШ(v)},

РВЫП(v)
= PHAЧ(v)
+
t(v).

Легко
видеть, что значение РВЫП(v)
равно длине максималь­ного s-v-пути
в сети G.
Поэтому,
для вычисления значений РВЫП(v)
можно использовать алгоритм 6.6 вычисления
длин минимальных путей в бесконтурной
сети, в котором все миниму­мы заменены
на максимумы. При этом значение РВЫП(t)
дает
наиболее ранний возможный срок завершения
всего проекта в целом.

Ради
полноты приведем здесь формальную
запись алгоритма, непосредственно
вычисляющего характеристики РНАЧ и
РВЫП.

АЛГОРИТМ
6.7.

(*
расчет наиболее ранних возможных сроков
начала и выполне­ния работ *)

Данные:
Сетевой график G
работ
V, заданный списками ПРЕДШ(v),
vV.

Результаты:
Наиболее ранние возможные сроки начала
и выпол­нения работ PHAЧ[v],
РВЫП[v],
vV.

1. begin

2. for
   k:=0 to
   n+1
   do PHAЧ[v_k]:=PBЫП[v_k]:=0;

3. for
   k:=1
   to n+1
   do

4. begin

5. for
   vПРЕДШ(v_к)
   do

6. PHAЧ[v_k]:=max(PBЫП[v],
   PHAЧ[v_k]);

7. PBЫП[v_k]:=PHAЧ[v_k]+t[v_k];

8. end;

9. end

Здесь,
в алгоритме 6.7,
узлы
сетевого графика s
и
t
обозначены
соответственно через v₀
и
v_n+1.

Значения
РВЫП(v)
и PHAЧ(v)
для
сетевого графика, изобра­женного
ранее на рис.6.6, приведены на рис. 6.7. Из
найденных значений следует, что этот
проект не может быть завершен ранее чем
через 20 единиц времени.

Пусть
Т — плановый срок выполнения проекта
W.
Ясно,
что Т должно удовлетворять неравенству
Т ≥ PBЫП(v_n+1).

Через
ПВЫП(v)
(соответственно ПНАЧ(у)) обозначим
наибо­лее
поздний допустимый срок выполнения
(начала)
работы v,
то
есть такой срок, который не увеличивает
срок Т реализации всего проекта. Например,
для работы 3 сетевого графика из рис.
6.6 имеем РНАЧ(3)=12, РВЫП(3)=14, но ясно, что
начать работу 3 можно на единицу времени
позже, поскольку это не повлияет на срок
выполнения всего проекта, а вот задержка
в реализации этой же работы на 2 единицы
приведет к увеличению срока выполне­ния
всего проекта на 1 единицу времени.

АЛГОРИТМ
6.8.

(*
Расчет наиболее поздних сроков начала
и окончания работ *) Данные: Сетевой
график G
работ
V, заданный списками ПРЕДШ[v],
vV,
плановый срок окончания проекта — Т.
Результаты: Наиболее поздние допустимые
сроки выполнения и начала работ ПВЫП[v]
и ПНАЧ[v].

1. begin

2. for
   vV
   do ПВЫП[v]:=Т;

3. for
   k:=n+1 downto
   1
   do

4. begin

5. ПНАЧ[v_k]
   := ПВЫП[v_k]
   –
   t(v_k);

6. for
   vПРЕДШ(v)
   do

7. ПВЫП[v]
   :=
   min(ПВЫП[v],
   ПНАЧ[v_k]);

8. end;

9. end.

Прямо
из определений получаем справедливость
равенств ПНАЧ(v_n+1)=ПВЫП(v_n+1)=Т.
Поскольку произвольная работа v
должна
быть завершена до начала всех наиболее
поздних допус­тимых сроков тех работ
w,
которым
предшествует работа v,
то
получаем следующие формулы:

ПВЫП(v)=min{ПНАЧ(w):
по всем w
таким,
что ПРЕДШ(w)v},

ПНАЧ(v)=ПВЫП(v)-t(v).

Вычислять
значения ПВЫП(v)
и ПНАЧ(v)
можно,
двигаясь по узлам сети G
от
v_n+1
к
v₀.
Все
детали вычисления названных ха­рактеристик
приведены выше в алгоритме 6.8.

Найденные
значения возможных и допустимых сроков
выпол­нения работ позволяют определить
резервы времени для выпол­нения той
или иной работы. В сетевом планировании
рассматри­вают несколько различных
и по-своему важных видов резерва работ.
Мы здесь ограничимся лишь полным
резервом
(иногда его называют суммарным)
времени выполнения работ. Он определя­ется
по формуле:

PE3EPB(v)=ПНАЧ(v)-PHAЧ(v).

Значение
PE3EPB(v)
равно
максимальной задержке в выпол­нении
работы v,
не
влияющей на плановый срок Т. Понятно,
что справедливо и такое равенство

РЕЗЕРВ(v)=ПВЫП(v)-РВЫП(v).

Работы	РНАЧ	РВЫП	ПНАЧ	ПВЫП	Резерв
0	0	0	0	0	0
1	0	4	0	4	0
2	4	12	4	12	0
3	12	14	13	15	1
4	12	15	12	15	0
5	12	16	14	18	2
6	15	20	15	20	0
7	16	18	18	20	2
8	20	20	20	20	20

Рис 6.7.
Численные характеристики сетевого
графика

Работы,
имеющие нулевой резерв времени, называются
кри­тическими.
Через любую такую работу проходит
некоторый мак­симальный s-t-путь
в сети G.
Поэтому
такой метод нахождения критических
работ и называют методом критического
пути. Кри­тические работы характеризуются
тем, что любая задержка в их выполнении
автоматически ведет к увеличению времени
выпол­нения всего проекта.

Численные
значения введенных характеристик
сетевых гра­фиков для проекта из
рис.6.6 даны на рис. 6.7. Расчеты выполне­ны
при Т=20. Критическими работами этого
проекта являются работы с номерами
0,1,2,4,6,8, которые и образуют в сети G
кри­тический
путь.

Исследование
сетевых графиков на этом мы завершим.
Отме­тим только, что помимо рассмотренных
нами характеристик, час­то рассматривают
и большое число других, связанных,
например, с неопределенностью во времени
выполнения работ, с управле­нием
ресурсами и т.д. Достаточно обширный и
содержательный материал по этому поводу
можно найти в книге [8].

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Improve Article

Save Article

Like Article

Read

Discuss

Improve Article

Save Article

Like Article

Given a directed graph G with N vertices and M edges. The task is to find the length of the longest directed path in Graph.
Note: Length of a directed path is the number of edges in it. 
Examples: 
 

Input: N = 4, M = 5 
 

Output: 3 
The directed path 1->3->2->4 
Input: N = 5, M = 8 
 

Output: 3 

Simple Approach: A naive approach is to calculate the length of the longest path from every node using DFS. 
The time complexity of this approach is O(N²). 
Efficient Approach: An efficient approach is to use Dynamic Programming and DFS together to find the longest path in the Graph. 
Let dp[i] be the length of the longest path starting from the node i. Initially all positions of dp will be 0. We can call the DFS function from every node and traverse for all its children. The recursive formula will be: 
 

dp[node] = max(dp[node], 1 + max(dp[child1], dp[child2], dp[child3]..)) 
 

At the end check for the maximum value in dp[] array, which will be the longest path in the DAG.
Below is the implementation of the above approach:
 

C++

#include <bits/stdc++.h>

using namespace std;

void dfs(int node, vector<int> adj[], int dp[], bool vis[])

{

    vis[node] = true;

    for (int i = 0; i < adj[node].size(); i++) {

        if (!vis[adj[node][i]])

            dfs(adj[node][i], adj, dp, vis);

        dp[node] = max(dp[node], 1 + dp[adj[node][i]]);

    }

}

void addEdge(vector<int> adj[], int u, int v)

{

    adj[u].push_back(v);

}

int findLongestPath(vector<int> adj[], int n)

{

    int dp[n + 1];

    memset(dp, 0, sizeof dp);

    bool vis[n + 1];

    memset(vis, false, sizeof vis);

    for (int i = 1; i <= n; i++) {

        if (!vis[i])

            dfs(i, adj, dp, vis);

    }

    int ans = 0;

    for (int i = 1; i <= n; i++) {

        ans = max(ans, dp[i]);

    }

    return ans;

}

int main()

{

    int n = 5;

    vector<int> adj[n + 1];

    addEdge(adj, 1, 2);

    addEdge(adj, 1, 3);

    addEdge(adj, 3, 2);

    addEdge(adj, 2, 4);

    addEdge(adj, 3, 4);

    cout << findLongestPath(adj, n);

    return 0;

}

Java

import java.util.ArrayList;

class Graph

{

    int vertices;

    ArrayList<Integer> edge[];

    Graph(int vertices)

    {

        this.vertices = vertices;

        edge = new ArrayList[vertices+1];

        for (int i = 0; i <= vertices; i++)

        {

            edge[i] = new ArrayList<>();

        }

    }

    void addEdge(int a,int b)

    {

        edge[a].add(b);

    }

    void dfs(int node, ArrayList<Integer> adj[], int dp[],

                                    boolean visited[])

    {

        visited[node] = true;

        for (int i = 0; i < adj[node].size(); i++)

        {

            if (!visited[adj[node].get(i)])

                dfs(adj[node].get(i), adj, dp, visited);

            dp[node] = Math.max(dp[node], 1 + dp[adj[node].get(i)]);

        }

    }

    int findLongestPath( int n)

    {

        ArrayList<Integer> adj[] = edge;

        int[] dp = new int[n+1];

        boolean[] visited = new boolean[n + 1];

        for (int i = 1; i <= n; i++)

        {

            if (!visited[i])

                dfs(i, adj, dp, visited);

        }

        int ans = 0;

        for (int i = 1; i <= n; i++)

        {

            ans = Math.max(ans, dp[i]);

        }

        return ans;

    }

}

public class Main

{

    public static void main(String[] args)

    {

        int n = 5;

        Graph graph = new Graph(n);

        graph.addEdge( 1, 2);

        graph.addEdge( 1, 3);

        graph.addEdge( 3, 2);

        graph.addEdge( 2, 4);

        graph.addEdge( 3, 4);

        graph.findLongestPath(n);

        System.out.println( graph.findLongestPath( n));

    }

}

Python3

def dfs(node, adj, dp, vis):

    vis[node] = True

    for i in range(0, len(adj[node])): 

        if not vis[adj[node][i]]:

            dfs(adj[node][i], adj, dp, vis)

        dp[node] = max(dp[node], 1 + dp[adj[node][i]])

def addEdge(adj, u, v):

    adj[u].append(v)

def findLongestPath(adj, n):

    dp = [0] * (n + 1)

    vis = [False] * (n + 1)

    for i in range(1, n + 1): 

        if not vis[i]:

            dfs(i, adj, dp, vis)

    ans = 0

    for i in range(1, n + 1): 

        ans = max(ans, dp[i])

    return ans

if __name__ == "__main__":

    n = 5

    adj = [[] for i in range(n + 1)]

    addEdge(adj, 1, 2)

    addEdge(adj, 1, 3)

    addEdge(adj, 3, 2)

    addEdge(adj, 2, 4)

    addEdge(adj, 3, 4)

    print(findLongestPath(adj, n))

C#

using System;

using System.Collections.Generic;

class Graph

{

    public int vertices;

    public List<int> []edge;

    public Graph(int vertices)

    {

        this.vertices = vertices;

        edge = new List<int>[vertices + 1];

        for (int i = 0; i <= vertices; i++)

        {

            edge[i] = new List<int>();

        }

    }

    public void addEdge(int a, int b)

    {

        edge[a].Add(b);

    }

    public void dfs(int node, List<int> []adj,

                    int []dp, Boolean []visited)

    {

        visited[node] = true;

        for (int i = 0; i < adj[node].Count; i++)

        {

            if (!visited[adj[node][i]])

                dfs(adj[node][i], adj, dp, visited);

            dp[node] = Math.Max(dp[node], 1 +

                                dp[adj[node][i]]);

        }

    }

    public int findLongestPath( int n)

    {

        List<int> []adj = edge;

        int[] dp = new int[n + 1];

        Boolean[] visited = new Boolean[n + 1];

        for (int i = 1; i <= n; i++)

        {

            if (!visited[i])

                dfs(i, adj, dp, visited);

        }

        int ans = 0;

        for (int i = 1; i <= n; i++)

        {

            ans = Math.Max(ans, dp[i]);

        }

        return ans;

    }

}

class GFG

{

    public static void Main(String[] args)

    {

        int n = 5;

        Graph graph = new Graph(n);

        graph.addEdge( 1, 2);

        graph.addEdge( 1, 3);

        graph.addEdge( 3, 2);

        graph.addEdge( 2, 4);

        graph.addEdge( 3, 4);

        graph.findLongestPath(n);

        Console.WriteLine(graph.findLongestPath(n));

    }

}

Javascript

<script>

function dfs(node, adj, dp, vis)

{

    vis[node] = true;

    for (var i = 0; i < adj[node].length; i++) {

        if (!vis[adj[node][i]])

            dfs(adj[node][i], adj, dp, vis);

        dp[node] = Math.max(dp[node], 1 + dp[adj[node][i]]);

    }

}

function addEdge(adj, u, v)

{

    adj[u].push(v);

}

function findLongestPath(adj, n)

{

    var dp = Array(n+1).fill(0);

    var vis = Array(n+1).fill(false);

    for (var i = 1; i <= n; i++) {

        if (!vis[i])

            dfs(i, adj, dp, vis);

    }

    var ans = 0;

    for (var i = 1; i <= n; i++) {

        ans = Math.max(ans, dp[i]);

    }

    return ans;

}

var n = 5;

var adj = Array.from(Array(n+1), ()=>Array());

addEdge(adj, 1, 2);

addEdge(adj, 1, 3);

addEdge(adj, 3, 2);

addEdge(adj, 2, 4);

addEdge(adj, 3, 4);

document.write( findLongestPath(adj, n));

</script>

Time Complexity: O(N+M) 
Auxiliary Space: O(N) 
 

?list=PLqM7alHXFySEaZgcg7uRYJFBnYMLti-nh
 

Last Updated :
30 Dec, 2021

Like Article

Save Article

Ответ или решение 2

Скорость движения рассчитывается по формуле

• Скорость движения равна производной формулы пути;
• чтобы найти максимальную скорость, нужно найти производную скорости;
• затем нужно определить точки максимума;
• подставить их в уравнение скорости.

Нам дано уравнение пути s = -10t 3 + 15t 2 + 2t

Найдем уравнение скорости

S` = — 10 * 3t 2 + 15 * 2t + 2 = — 30t 2 + 30t + 2

v = — 30t 2 + 30t + 2

Найдем точки максимума этой функции

Для этого найдем производную этой функции.

v`= — 30 * 2t + 30 = — 60t + 30

Приравняем ее к нулю.

Переносим 30 в правую часть, меняя знак.

Делим все уравнение на (- 30).

Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.

Берем любую точку, например, 0.

— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)

Берем например, точку 1.

— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)

Значит, t = 1/2 — это точка максимума.

Подставим это значение в уравнение скорости.

v = — 30t 2 + 30t + 2

v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.

Ответ: максимальная скорость движения равна 9,5.

Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.

• Попроси больше объяснений
• Следить
• Отметить нарушение

Vazgen1312 05.07.2019

Ответ

Ответ:

Объяснение:

Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)

1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²

S = 0 + 15*1/2 = 7,5 м

2. S = V*t = 15*3 = 45 м

3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.

Еще раз о том, что такое равноускоренное движение

Автомобиль за каждую секунду увеличивает свою скорость на . Движется ли автомобиль равноускоренно?

На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на Часто равноускоренным называют такое движение, при котором тело двигается с постоянным ускорением . Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).

Уравнение скорости

Воспользовавшись уравнением, определяющим ускорение , удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:

Уравнение скорости в проекциях имеет вид:

Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.

К вопросу о направлении скорости и ускорения

В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.

Рассмотрим наиболее типичные примеры направления скорости и ускорения.

1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).

Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой

В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.

2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).

Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой

Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.

3. Скорость и ускорение взаимно перпендикулярны (рис. 3).

Рис. 3. Скорость и ускорение взаимно перпендикулярны

Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.

Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.

График скорости

График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.

Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения

Проанализируем различные графики.

Первый. Уравнение проекции скорости:

Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:

График начинается в точке

Где

Рис. 5. График функции

Это уравнение прямой, что подтверждается графиками, рассмотренными нами.

Некоторые частные случаи

Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость, , равняется нулю, проекция ускорения больше нуля.

Запись этого уравнения . А сам вид графика достаточно простой (график 1).

Рис. 6. Различные случаи равноускоренного движения

Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси.

Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси . При этом модуль скорости постоянно возрастает, тело ускоряется.

График зависимости ускорения от времени

Равноускоренное движение – это движение, при котором ускорение тела не меняется.

Рис. 7. График зависимости проекций ускорения от времени

Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.

Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:

Произведение ускорения и времени –это изменение скорости за данное время.

Рис. 8. Изменение скорости

Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.

Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.

Заключение

На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.

1. Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
2. Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
3. Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «class-fizika.narod.ru» (Источник)
2. Интернет-портал «youtube.com» (Источник)
3. Интернет-портал «fizmat.by» (Источник)
4. Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)

1. Что такое равноускоренное движение?

2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:

3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при ?

«>

1. Нахождение пути по графику зависимости скорости от времени

Покажем, как можно найти пройденный телом путь с помощью графика зависимости скорости от времени.

Начнем с самого простого случая – равномерного движения. На рисунке 6.1 изображен график зависимости v(t) – скорости от времени. Он представляет собой отрезок прямой, параллельной осн времени, так как при равномерном движении скорость постоянна.

Фигура, заключенная под этим графиком, – прямоугольник (он закрашен на рисунке). Его площадь численно равна произведению скорости v на время движения t. С другой стороны, произведение vt равно пути l, пройденному телом. Итак, при равномерном движении

путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени.

Покажем теперь, что этим замечательным свойством обладает и неравномерное движение.

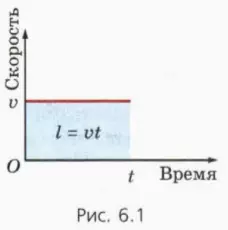
Пусть, например, график зависимости скорости от времени имеет вид кривой, изображенной на рисунке 6.2.

Разобьем мысленно все время движения на столь малые промежутки, чтобы в течение каждого из них движение тела можно было считать практически равномерным (это разбиение показано штриховыми линиями на рисунке 6.2).

Тогда путь, пройденный за каждый такой промежуток, численно равен площади фигуры под соответствующим ком графика. Поэтому и весь путь равен площади фигур заключенной под всем графиком. (Использованный нами прием лежит в основе интегрального исчисления, основы которого вы будете изучать в курсе «Начала математического анализа».)

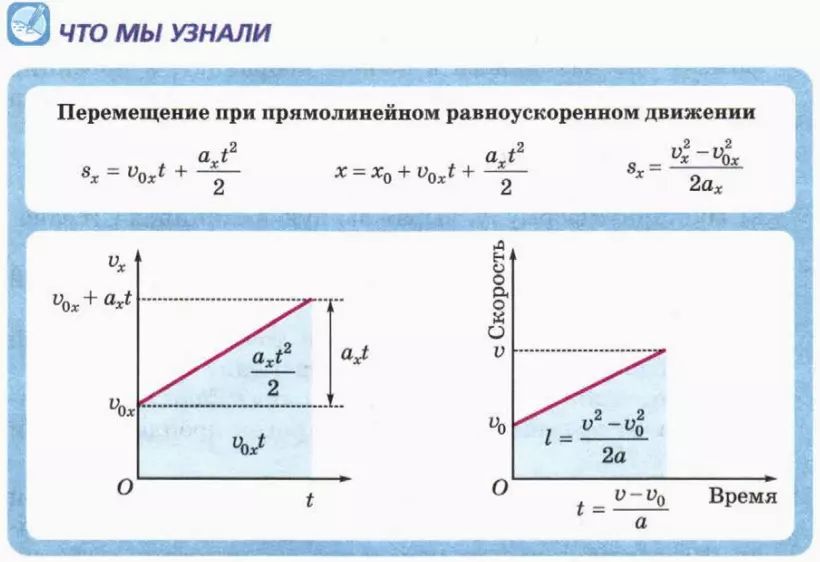
2. Путь и перемещение при прямолинейном равноускоренном движении

Применим теперь описанный выше способ нахождения пути к прямолинейному равноускоренному движению.

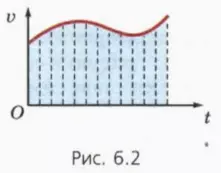
Начальная скорость тела равна нулю

Направим ось x в сторону ускорения тела. Тогда a_x = a, v_x = v. Следовательно,

v = at.     (1)

На рисунке 6.3 изображен график зависимости v(t).

? 1. Используя рисунок 6.3, докажите, что при прямолинейном равноускоренном движении без начальной скорости путь l выражается через модуль ускорения a и время движения t формулой

l = at²/2.     (2)

Главный вывод:

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату времени движения.

Этим равноускоренное движение существенно отличается от равномерного.

На рисунке 6.4 приведены графики зависимости пути от времени для двух тел, одно из которых движется равномерно, а другое – равноускоренно без начальной скорости.

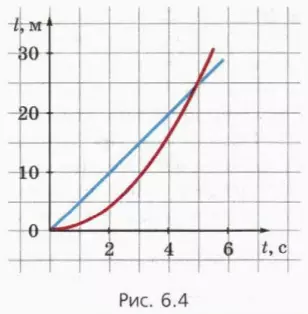
? 2. Рассмотрите рисунок 6.4 и ответьте на вопросы.
а) Каким цветом изображен график для тела, движущегося равноускоренно?
б) Чему равно ускорение этого тела?
в) Чему равны скорости тел в тот момент, когда они прошли одинаковый путь?
г) В какой момент времени скорости тел равны?

? 3. Тронувшись с места, автомобиль за первые 4 с проехал расстояние 20 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какое расстояние проедет автомобиль:
а) за 8 с? б) за 16 с? в) за 2 с?

Найдем теперь зависимость проекции перемещения s_x от времени. В данном случае проекция ускорения на ось x положительна, поэтому s_x = l, a_x = a. Таким образом, из формулы (2) следует:

s_x = a_xt²/2.     (3)

Формулы (2) и (3) очень похожи, что приводит порой к ошибкам при решении простых задач. Дело в том, что значение проекции перемещения может быть отрицательным. Так будет, если ось x направлена противоположно перемещению: тогда s_x < 0. А путь отрицательным быть не может!

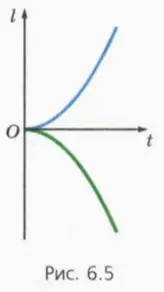
? 4. На рисунке 6.5 изображены графики зависимости от времени пути и проекции перемещения для некоторого тела. Какой цвет у графика проекции перемещения?

Начальная скорость тела не равна нулю

Напомним, что в таком случае зависимость проекции скорости от времени выражается формулой

v_x = v_0x + a_xt,     (4)

где v_0x – проекция начальной скорости на ось x.

Мы рассмотрим далее случай, когда v_0x > 0, a_x > 0. В этом случае снова можно воспользоваться тем, что путь численно равен площади фигуры под графиком зависимости скорости от времени. (Другие комбинации знаков проекции начальной скорости и ускорения рассмотрите самостоятельно: в результате получится та же общая формула (5).

На рисунке 6.6 изображен график зависимости v_x(t) при v_0x > 0, a_x > 0.

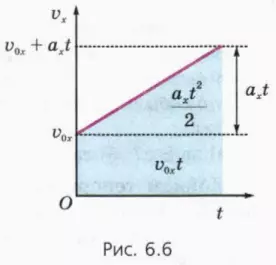
? 5. Используя рисунок 6.6, докажите, что при прямолинейном равноускоренном движении с начальной скоростью проекция перемещения

s_x = v_0x + a_xt²/2.     (5)

Эта формула позволяет найти зависимость координаты x тела от времени. Напомним (см. формулу (6), § 2), что координата x тела связана с проекцией его перемещения s_x соотношением

s_x = x – x₀,

где x₀ — начальная координата тела. Следовательно,

x = x₀ + s_x,     (6)

Из формул (5), (6) получаем:

x = x₀ + v_0xt + a_xt²/2.     (7)

6. Зависимость координаты от времени для некоторого тела, движущегося вдоль оси x, выражается в единицах СИ формулой x = 6 – 5t + t².
а) Чему равна начальная координата тела?
б) Чему равна проекция начальной скорости на ось x?
в) Чему равна проекция ускорения на ось x?
г) Начертите график зависимости координаты x от времени.
д) Начертите график зависимости проекции скорости от времени.
е) В какой момент скорость тела равна нулю?
ж) Вернется ли тело в начальную точку? Если да, то в какой момент (моменты) времени?
з) Пройдет ли тело через начало координат? Если да, то в какой момент (моменты) времени?
и) Начертите график зависимости проекции перемещения от времени.
к) Начертите график зависимости пути от времени.

3. Соотношение между путем и скоростью

При решении задач часто используют соотношения между путем, ускорением и скоростью (начальной v₀, конечной v или ими обеими). Выведем эти соотношения. Начнем с движения без начальной скорости. Из формулы (1) получаем для времени движения:

t = v/a.      (8)

Подставим это выражение в формулу (2) для пути:

l = at²/2 = a/2(v/a)² = v²/2a.     (9)

Главный вывод:

при прямолинейном равноускоренном движении без начальной скорости пройденный телом путь пропорционален квадрату конечной скорости.

? 7. Тронувшись с места, автомобиль набрал скорость 10 м/с на пути 40 м. Движение автомобиля считайте прямолинейным равноускоренным. Не вычисляя ускорения автомобиля, определите, какой путь от начала движения проехал автомобиль, когда его скорость была равна: а) 20 м/с? б) 40 м/с? в) 5 м/с?

Соотношение (9) можно получить также, вспомнив, что путь численно равен площади фигуры, заключенной под графиком зависимости скорости от времени (рис. 6.7).

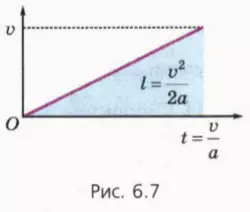
Это соображение поможет вам легко справиться со следующим заданием.

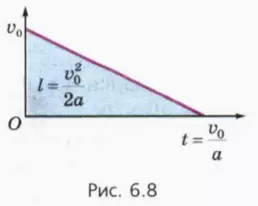
? 8. Используя рисунок 6.8, докажите, что при торможении с постоянным ускорением тело проходит до полной остановки путь l_т = v₀²/2a, где v₀ – начальная скорость тела, a – модуль ускорения.

В случае торможения транспортного средства (автомобиль, поезд) путь, пройденный до полной остановки, называют тормозным путём. Обратите внимание: тормозной путь при начальной скорости v₀ и путь, пройденный при разгоне с места до скорости v₀ с тем же по модулю ускорением a, одинаковы.

? 9. При экстренном торможении на сухом асфальте ускорение автомобиля равно по модулю 5 м/с². Чему равен тормозной путь автомобиля при начальной скорости: а) 60 км/ч (максимальная разрешенная скорость в городе); б) 120 км/ч? Найдите тормозной путь при указанных скоростях во время гололеда, когда модуль ускорения равен 2 м/с². Сравните найденные вами значения тормозного пути с длиной классной комнаты.

? 10. Используя рисунок 6.9 и формулу, выражающую площадь трапеции через ее высоту и полусумму оснований, докажите, что при прямолинейном равноускоренном движении:
а) l = (v² – v₀²)/2a, если скорость тела увеличивается;
б) l = (v₀² – v²)/2a, если скорость тела уменьшается.

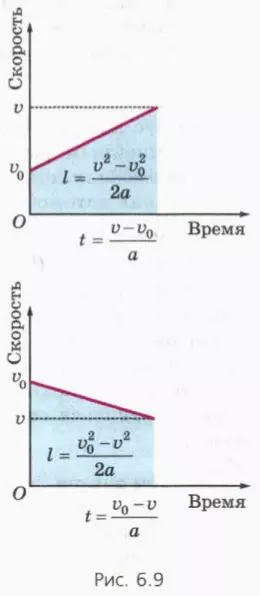
? 11. Докажите, что проекции перемещения, начальной и конечной скорости, а также ускорения связаны соотношением

s_x = (v_x² – v_0x²)/2ax     (10)

? 12. Автомобиль на пути 200 м разогнался от скорости 10 м/с до 30 м/с.
а) С каким ускорением двигался автомобиль?
б) За какое время автомобиль проехал указанный путь?
в) Чему равна средняя скорость автомобиля?

Лютый опыт

Дополнительные вопросы и задания

13. От движущегося поезда отцепляют последний вагон, после чего поезд движется равномерно, а вагон – с постоянным ускорением до полной остановки.
а) Изобразите на одном чертеже графики зависимости скорости от времени для поезда и вагона.
б) Во сколько раз путь, пройденный вагоном до остановки, меньше пути, пройденного поездом за то же время?

14. Отойдя от станции, электричка какое-то время ехала равноускоренно, затем в течение 1 мин – равномерно со скоростью 60 км/ч, после чего снова равноускоренно до остановки на следующей станции. Модули ускорений при разгоне и торможении были различны. Расстояние между станциями электричка прошла за 2 мин.
а) Начертите схематически график зависимости проекции скорости электрички от времени.
б) Используя этот график, найдите расстояние между станциями.
в) Какое расстояние проехала бы электричка, если бы на первом участке пути она разгонялась, а на втором – тормозила? Какова была бы при этом ее максимальная скорость?

15. Тело движется равноускоренно вдоль оси x. В начальный момент оно находилось в начале координат, а проекция его скорости была равна 8 м/с. Через 2 с координата тела стала равной 12 м.
а) Чему равна проекция ускорения тела?
б) Постройте график зависимости v_x(t).
в) Напишите формулу, выражающую в единицах СИ зависимость x(t).
г) Будет ли скорость тела равна нулю? Если да, то в какой момент времени?
д) Побывает ли тело второй раз в точке с координатой 12 м? Если да, то в какой момент времени?
е) Вернется ли тело в начальную точку? Если да, то в какой момент времени, и чему будет равен пройденный при этом путь?

16. После толчка шарик вкатывается вверх по наклонной плоскости, после чего возвращается в начальную точку. На расстоянии b от начальной точки шарик побывал дважды через промежутки времени t₁ и t₂ после толчка. Вверх и вниз вдоль наклонной плоскости шарик двигался с одинаковым по модулю ускорением.
а) Направьте ось x вверх вдоль наклонной плоскости, выберите начало координат в точке начального положения шарика и напишите формулу, выражающую зависимость x(t), в которую входят модуль начальной скорости шарика v0 и модуль ускорения шарика a.
б) Используя эту формулу и тот факт, что на расстоянии b от начальной точки шарик побывал в моменты времени t₁ и t₂ составьте систему двух уравнений с двумя неизвестными v₀ и a.
в) Решив эту систему уравнений, выразите v₀ и a через b, t₁ и t₂.
г) Выразите весь пройденный шариком путь l через b, t₁ и t₂.
д) Найдите числовые значения v₀, a и l при b = 30 см, t₁ = 1с, t₂ = 2 с.
е) Постройте графики зависимости v_x(t), s_x(t), l(t).
ж) С помощью графика зависимости sx(t) определите момент, когда модуль перемещения шарика был максимальным.