Как найти максимальный разрез - Сайт, где вы сможете решить свои вопросы

Максимальный разрез.

Максимальный разрез графа — это разрез, размер которого не меньше размера любого другого разреза. Задача определения максимального разреза для графа известна как задача о максимальном разрезе.

Задачу можно сформулировать следующим образом. Следует найти подмножество вершин S, такое, что число рёбер между S и его дополнением было бы настолько велико, насколько это возможно.

Существует расширенная версия, задача о взвешенном максимальном разрезе. В этой версии каждому ребру приписано вещественное число, его вес, и целью является максимизация не числа рёбер, а общего веса рёбер между S и его дополнением. Задача о взвешенном максимальном разрезе часто, но не всегда, ограничивается неотрицательными весами, поскольку отрицательные веса могут изменить природу задачи.

Вычислительная сложность[править | править код]

Следующая задача разрешимости, связанная с максимальным разрезом, широко изучалась в теоретической информатике:

Задан граф G и целое число k, определить, имеется ли разрез в G размером, не меньшим k.

Известно, что эта задача NP-полная. NP-полноту задачи можно показать, например, приведением от задачи максимальной 2-выполнимости^[en] (задача максимальной выполнимости^[en] с ограничениями)^[1]. Взвешенная версия задачи разрешимости входит в 21 NP-полную задачу Карпа^[2]. Карп показал NP-полноту путём приведения от задачи разбиения^[en].

Канонический оптимизационный вариант вышеупомянутой задачи разрешимости известен как «задача о максимальном разрезе» и определяется следующим образом:

Пусть задан граф G, нужно найти максимальный разрез.

Алгоритмы полиномиального времени[править | править код]

Так как задача о максимальном разрезе является NP-трудной, нет алгоритмов полиномиального времени для задачи о максимальном разрезе для общих графов.

Для планарных графов, однако, задача о максимальном разрезе двойственна задаче китайского почтальона (задаче поиска кратчайшего обхода с обходом всех рёбер по меньшей мере один раз), в том смысле, что рёбра, не принадлежащие максимальному разрезу графа G, двойственны рёбрам, которые проходятся многократно в оптимальном обходе двойственного графа для графа G. Оптимальный обход образует самопересекающуюся кривую, которая разбивает плоскость на два подмножества, подмножество точек, для которых порядок относительно кривой чётен, и подмножества точек, порядок которых нечётен. Эти два подмножества образуют разрез, в который входят все рёбра, двойственные рёбрам, которые появляются нечётное число раз в обходе. Задача о китайском почтальоне может быть решена за полиномиальное время, и эта двойственность позволяет задачу максимального разреза решать для планарных графов за полиномиальное время^[3]. Известно, однако, что задача максимальной бисекции NP-трудна^[4].

Аппроксимационные алгоритмы[править | править код]

Задача о максимальном разрезе является APX-сложной (Пападимитроу и Яннакакис доказали MaxSNP-полноту данной задачи^[5]), что означает, что не существует аппроксимационной схемы полиномиального времени (PTAS) как угодно близкой к оптимальному решению, если только не P = NP. Таким образом, любой аппроксимационный алгоритм полиномиального времени даёт аппроксимационный коэффициент, строго меньший единицы.

Существует простой вероятностный 0,5-аппроксимационный алгоритм — для любой вершины бросаем монету с целью решить, к какой части разреза отнести данную вершину^[6]^[7]. Ожидается, что половина рёбер являются разрезающими. Этот алгоритм может быть дерандомизирован с помощью метода условных вероятностей. Таким образом, существует простой детерминированный полиномиального времени алгоритм с 0,5-аппроксимацией^[8]^[9]. Один такой алгоритм начинает с произвольного разбиения вершин заданного графа G=(V,E) и передвигает одну вершину за один шаг из одной части разреза в другую, улучшая решение на каждом шаге до тех пор, пока улучшение возможно. Число итераций алгоритма не превосходит |E| , поскольку алгоритм улучшает разрез по меньшей мере на одно ребро. Когда алгоритм прекращает работу, по меньшей мере половина рёбер, инцидентных любой вершине, принадлежат разрезу, в противном случае перенос вершины улучшил бы разрез (увеличил бы размер разреза). Таким образом, разрез включает по меньшей мере рёбер.

Полиномиального времени аппроксимационный алгоритм для задачи о максимальном разрезе с лучшим известным аппроксимационным коэффициентом — это метод Геманса и Вильямсона, использующий полуопределённое программирование и вероятностное округление. Метод даёт аппроксимационный коэффициент , где ${displaystyle alpha ={tfrac {2}{pi }}min _{0leq theta leq pi }{tfrac {theta }{1-cos theta }}}$ ^[10]^[11].
Если гипотеза уникальной игры^[en] верна, это лучший возможный аппроксимационный коэффициент для максимального разреза^[12].
Если не принимать такие недоказанные допущения, было доказано, что NP-трудно аппроксимировать значение максимального разреза с коэффициентом, лучшим ${displaystyle {tfrac {16}{17}}approx 0{,}941}$ ^[13]^[14].

См. также[править | править код]

Наименьший разрез
Наименьший k-разрез

Примечания[править | править код]

↑ Garey, Johnson, 1979.
↑ Karp, 1972.
↑ Hadlock, 1975.
↑ Jansen, Karpinski, Lingas, Seidel, 2005.
↑ Papadimitriou & Yannakakis, 1991.
↑ Mitzenmacher, Upfal, 2005, с. Sect. 6.2.
↑ Motwani, Raghavan, 1995, с. Sect. 5.1.
↑ Mitzenmacher, Upfal, 2005, с. Sect. 6.3..
↑ Khuller, Raghavachari, Young, 2007.
↑ Gaur, Krishnamurti, 2007.
↑ Ausiello, Crescenzi и др., 2003.
↑ Khot, Kindler, Mossel, O’Donnell, 2007.
↑ Håstad, 2001.
↑ Trevisan, Sorkin, Sudan, Williamson, 2000.

Литература[править | править код]

Giorgio Ausiello, Pierluigi Crescenzi, Giorgio Gambosi, Viggo Kann, Alberto Marchetti-Spaccamela, Marco Protasi. Complexity and Approximation: Combinatorial Optimization Problems and Their Approximability Properties. — Springer, 2003.

Задача о максимальном разрезе (оптимизационная версия) — задача ND14 в Приложении B (стр. 399).

Michael R. Garey, David S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. — W. H. Freeman, 1979. — ISBN 0-7167-1045-5.

Задача о максимальном разрезе (задача разрешимости) — задача ND16 в Приложении A2.2.

Максимальный двудольный подграф (задача разрешимости) — задача GT25 в Приложении A1.2.

Daya Ram Gaur, Ramesh Krishnamurti. LP rounding and extensions // Handbook of Approximation Algorithms and Metaheuristics. — Chapman & Hall/CRC, 2007.
Michel X. Goemans, David P. Williamson. Improved approximation algorithms for maximum cut and satisfiability problems using semidefinite programming // Journal of the ACM. — 1995. — Vol. 42, no. 6. — P. 1115–1145. — doi:10.1145/227683.227684.
F. Hadlock. Finding a Maximum Cut of a Planar Graph in Polynomial Time // SIAM J. Comput.. — 1975. — Vol. 4, no. 3. — P. 221–225. — doi:10.1137/0204019.
Johan Håstad. Some optimal inapproximability results // Journal of the ACM. — 2001. — Vol. 48, no. 4. — P. 798–859. — doi:10.1145/502090.502098.
Klaus Jansen, Marek Karpinski, Andrzej Lingas, Eike Seidel. Polynomial Time Approximation Schemes for MAX-BISECTION on Planar and Geometric Graphs // SIAM Journal on Computing. — 2005. — Vol. 35, no. 1. — doi:10.1137/s009753970139567x.
Richard M. Karp. Reducibility among combinatorial problems // Complexity of Computer Computation / R. E. Miller, J. W. Thacher. — Plenum Press, 1972. — P. 85–103.
Subhash Khot, Guy Kindler, Elchanan Mossel, Ryan O’Donnell. Optimal inapproximability results for MAX-CUT and other 2-variable CSPs? // SIAM Journal on Computing. — 2007. — Vol. 37, no. 1. — P. 319–357. — doi:10.1137/S0097539705447372.
Samir Khuller, Balaji Raghavachari, Neal E. Young. Greedy methods // Handbook of Approximation Algorithms and Metaheuristics / Teofilo F. Gonzalez. — Chapman & Hall/CRC, 2007.
Michael Mitzenmacher, Eli Upfal. Probability and Computing: Randomized Algorithms and Probabilistic Analysis. — Cambridge, 2005.
Rajeev Motwani, Prabhakar Raghavan. Randomized Algorithms. — Cambridge, 1995..
Alantha Newman. Max cut // Encyclopedia of Algorithms / Ming-Yang Kao. — Springer, 2008. — P. 1. — ISBN 978-0-387-30770-1. — doi:10.1007/978-0-387-30162-4_219.
Christos H. Papadimitriou, Mihalis Yannakakis. Optimization, approximation, and complexity classes // Journal of Computer and System Sciences. — 1991. — Vol. 43, no. 3. — P. 425–440. — doi:10.1016/0022-0000(91)90023-X.
Luca Trevisan, Gregory Sorkin, Madhu Sudan, David Williamson. Gadgets, Approximation, and Linear Programming // Proceedings of the 37th IEEE Symposium on Foundations of Computer Science. — 2000. — P. 617–626.

Литература для дополнительного чтения[править | править код]

Francisco Barahona, Martin Grötschel, Michael Jünger, Gerhard Reinelt. An application of combinatorial optimization to statistical physics and circuit layout design // Operations Research. — 1988. — Vol. 36, no. 3. — P. 493–513. — doi:10.1287/opre.36.3.493. — JSTOR 170992.

Ссылки[править | править код]

Pierluigi Crescenzi, Viggo Kann, Magnús Halldórsson, Marek Karpinski, Gerhard Woeginger (2000), “Maximum Cut”, in “A compendium of NP optimization problems”.
Andrea Casini, Nicola Rebagliati (2012), “A Python library for solving Max Cut”

Источник

Пример максимального разреза

Для графика , максимальный разрез – это разрез, размер которого, по крайней мере, равен размеру любого другого разреза. То есть это разделение вершин графа на два дополнительных множества S и T, так что количество ребер между множеством S и множеством T является как можно большим. Проблема поиска максимального разреза в графе известна как проблема максимального разреза.

Проблема может быть сформулирована просто следующим образом. Требуется такое подмножество S набора вершин, чтобы количество ребер между S и дополнительным подмножеством было как можно большим. Эквивалентно, требуется двудольный подграф графа с максимально возможным количеством ребер.

Существует более общая версия проблемы, которая называется взвешенный Max-Cut,, где каждое ребро связано с действительным числом, его весом, а цель – чтобы максимизировать общий вес ребер между S и его дополнением, а не количество ребер. Взвешенная задача Max-Cut, допускающая как положительные, так и отрицательные веса, может быть тривиально преобразована в задачу взвешенного минимального сокращения, перевернув знак во всех весах.

Содержание

1 Вычислительная сложность
2 Алгоритмы
- 2.1 Полиномиальные алгоритмы
- 2.2 Планарные графы
- 2.3 Аппроксимационные алгоритмы
3 Приложения
- 3.1 Теоретическая физика
- 3.2 Конструкция схемы
4 См. Также
5 Примечания
6 Ссылки
7 Внешние ссылки

Вычислительная сложность

Следующая проблема решения, связанная с максимальными сокращениями, имеет широко изучался в теоретической информатике :

Для графа G и целого числа k определите, существует ли разрез размера не менее k в G.

Эта проблема известна как NP- полный. Легко увидеть, что проблема в NP : ответ «да» легко доказать, представив достаточно большой разрез. NP-полнота проблемы может быть продемонстрирована, например, сокращением от максимальной 2-выполнимости (ограничение задачи максимальной выполнимости ). Взвешенная версия проблемы решения была одной из 21 NP-полной проблемы Карпа ; Карп показал NP-полноту путем редукции из проблемы разбиения.

Канонический вариант оптимизации вышеупомянутой проблемы решения обычно известен как задача максимального сокращения или максимального сокращения и определяется как:

Для данного графа G найдите максимальный разрез.

Известно, что вариант оптимизации NP-Hard. Противоположная проблема, задача поиска минимального разреза, как известно, эффективно решается с помощью алгоритма Форда – Фулкерсона.

Алгоритмы

Полиномиальные алгоритмы

Поскольку задача Max-Cut является NP-сложной, алгоритмы с полиномиальным временем для Max-Cut в общих графах не известны.

Планарные графы

Однако в планарных графах проблема максимального отсечения двойственна задаче проверки маршрута (проблема поиска кратчайший обход, который посещает каждое ребро графа по крайней мере один раз), в том смысле, что ребра, которые не принадлежат максимальному набору разрезов графа G, являются двойниками ребер, которые удваиваются в оптимальном инспекционном туре по дуальный график из G. Оптимальный обзорный тур формирует самопересекающуюся кривую, которая разделяет плоскость на два подмножества, подмножество точек, для которых число витков кривой является четным и подмножество, для которого номер намотки нечетный; эти два подмножества образуют разрез, который включает в себя все ребра, чьи двойники появляются нечетное количество раз в маршруте. Задача проверки маршрута может быть решена за полиномиальное время, и эта двойственность позволяет решить задачу максимального разреза также за полиномиальное время для плоских графов. Однако известно, что проблема максимального деления пополам является NP-трудной.

Алгоритмы аппроксимации

Задача Max-Cut – APX-hard, что означает отсутствие полинома схема аппроксимации по времени (PTAS), сколь угодно близкая к оптимальному решению, для нее, если P = NP. Таким образом, каждый известный алгоритм полиномиальной аппроксимации достигает коэффициента аппроксимации строго меньше единицы.

Существует простой рандомизированный 0,5- алгоритм аппроксимации : для каждой вершины подбросьте монетку, чтобы решить, какой половине раздела ее назначить. В ожидании половина кромок – это обрезанные кромки. Этот алгоритм может быть дерандомизирован с помощью метода условных вероятностей ; следовательно, существует также простой детерминированный алгоритм 0,5-аппроксимации с полиномиальным временем. Один из таких алгоритмов начинается с произвольного разбиения вершин данного графа G = (V, E) { displaystyle G = (V, E)}и многократно перемещает одну вершину за раз. от одной стороны перегородки к другой, улучшая решение на каждом этапе, пока больше нельзя будет делать улучшения этого типа. Количество итераций не более | E | { displaystyle | E |} | E | , потому что алгоритм улучшает разрез по крайней мере на одно ребро на каждом шаге. Когда алгоритм завершается, по крайней мере половина ребер, инцидентных каждой вершине, принадлежит разрезу, иначе перемещение вершины улучшит разрез. Следовательно, разрез включает не менее | E | / 2 { displaystyle | E | / 2} |E|/2 ребер.

Алгоритм полиномиального приближения для Max-Cut с наиболее известным коэффициентом аппроксимации – это метод Гоеманса и Уильямсона, использующий полуопределенное программирование и рандомизированное округление, что позволяет коэффициент аппроксимации α ≈ 0,878, { displaystyle alpha приблизительно 0,878,}, где

α = 2 π min 0 ≤ θ ≤ π θ 1 – cos ⁡ θ. { displaystyle alpha = { frac {2} { pi}} min _ {0 leq theta leq pi} { frac { theta} {1- cos theta}}.} ${ displaystyle alpha = { frac {2} { pi}} min _ {0 leq theta leq pi} { frac { theta} {1- cos theta}}.}$

Если гипотеза об уникальных играх верна, это наилучший возможный коэффициент приближения для максимального сокращения. Было доказано, что без таких недоказанных допущений NP-сложно аппроксимировать максимальное значение отсечки с коэффициентом аппроксимации лучше 16 17 ≈ 0,941 { displaystyle { tfrac {16} {17}} приблизительно 0,941 } ${ tfrac {16} {17}} приблизительно 0,941$ .

Существует расширенный анализ 10 эвристик для этой проблемы, включая реализацию с открытым исходным кодом.

Приложения

Теоретическая физика

В статистической физике и неупорядоченных системах задача Max Cut эквивалентна минимизации Гамильтониан модели спинового стекла, проще всего модель Изинга. Для модели Изинга на графе G и только взаимодействий ближайших соседей гамильтониан равен

H [s] = – ∑ ij ∈ E (G) J ijsisj { displaystyle H [s] = – sum _ {ij in E (G)} J_ {ij} s_ {i} s_ {j}} ${ displaystyle H [s] = - sum _ {ij in E (G)} J_ {ij} s_ {i} s_ {j}}$

Здесь каждая вершина i графа представляет собой узел вращения, который может принимать значение вращения si = ± 1. { displaystyle s_ {i} = pm 1.} ${ displaystyle s_ {i} = pm 1.}$ Конфигурация вращения разделяет V (G) { displaystyle V (G)} V (G) на два набора, те, у которых есть вращение вверх V + { displaystyle V ^ {+}} $V ^ {+}$ и те, у которых замедлено вращение V -. { displaystyle V ^ {-}.} ${ displaystyle V ^ { -}.}$ Мы обозначаем δ (V +) { displaystyle delta (V ^ {+})} ${ displaystyle delta (V ^ {+})}$ набор ребер которые соединяют два набора. Затем мы можем переписать гамильтониан как

H [s] = – ∑ ij ∈ E (V +) J ij – ∑ ij ∈ E (V -) J ij + ∑ ij ∈ δ (V +) J ij = – ∑ ij ∈ E (G) J ij + 2 ∑ ij ∈ δ (V +) J ij = C + 2 ∑ ij ∈ δ (V +) J ij { displaystyle { begin {align} H [s] = – sum _ {ij in E (V ^ {+})} J_ {ij} – sum _ {ij in E (V ^ {-})} J_ {ij} + sum _ {ij in delta (V ^ {+})} J_ {ij} \ = – sum _ {ij in E (G)} J_ {ij} +2 sum _ {ij in delta (V ^ { +})} J_ {ij} \ = C + 2 sum _ {ij in delta (V ^ {+})} J_ {ij} end {align}}} ${ displaystyle { begin {align} H [s] = - sum _ {ij in E (V ^ {+})} J_ {ij} - sum _ {ij in E (V ^ {-})} J_ {ij} + sum _ {ij in delta (V ^ {+})} J_ {ij} \ = - sum _ {ij in E (G)} J_ {ij} +2 sum _ {ij in delta (V ^ {+})} J_ {ij} \ = C + 2 sum _ {ij in delta (V ^ {+})} J_ {ij} end {align}}}$

Минимизация этой энергии эквивалентно задаче минимального разреза или путем установки весов графа как wij = – J ij, { displaystyle w_ {ij} = – J_ {ij},} ${ displaystyle w_ {ij} = - J_ {ij},}$ проблема максимального разреза.

Проектирование схемы

Проблема максимального разреза имеет приложения в проекте СБИС.

См. Также

Минимальный разрез
Минимальный k-разрез
Поперечное перемещение нечетного цикла, что эквивалентно запросу самого большого двудольного индуцированного подграфа

Примечания

Ссылки

Ausiello, Giorgio; Крещенци, Пьерлуиджи; Гамбози, Джорджио; Канн, Вигго; Маркетти-Спаккамела, Альберто; Протаси, Марко (2003), Сложность и аппроксимация: комбинаторные задачи оптимизации и их свойства аппроксимации, Springer.

Максимальный разрез (оптимизационная версия) – это проблема ND14 в Приложении B (стр. 399).

Гарей, Майкл Р. ; Джонсон, Дэвид С. (1979), Компьютеры и несговорчивость: Руководство по теории NP-полноты, W.H. Freeman, ISBN 978-0-7167-1045-5 .

Максимальный разрез (версия решения) – это проблема ND16 в Приложении A2.2.

Максимальный двудольный подграф ( версия решения) – это проблема GT25 в Приложении A1.2.

Гаур, Дайя Рам; Кришнамурти, Рамеш (2007), «LP округление и расширения», в Гонсалес, Теофило Ф. (ред.), Справочник по алгоритмам приближения и метаэвристики, Chapman Hall / CRC.
Goemans, Michel X. ; Уильямсон, Дэвид П. (1995), «Улучшенные алгоритмы аппроксимации для задач максимального сокращения и выполнимости с использованием полуопределенного программирования», Журнал ACM, 42(6): 1115–1145, doi : 10.1145 / 227683.227684, S2CID 15794408.
Хэдлок, Ф. (1975), «Нахождение максимального разреза плоского графа за полиномиальное время “, SIAM J. Comput., 4(3): 221–225, doi : 10.1137 / 0204019.
Håstad, Johan (2001),” Some оптимальные результаты несовместимости », Журнал ACM, 48(4): 798–859, doi : 10.1145 / 502090.502098, S2CID 5120748.
Янсен, Клаус; Карпинский, Марек ; Лингас, Анджей; Зайдель, Эйке (2005), «Схемы аппроксимации полиномиального времени для MAX-BISECTION на плоских и геометрических графах», SIAM Journal on Computing, 35(1): 110–119, CiteSeerX 10.1.1.62.5082, doi : 10.1137 / s009753970139567x.
Карп, Ричард М. (1972), «Сводимость среди комбинаторных задач “, Миллер, RE; Тэчер, Дж. У. (ред.), Сложность компьютерных вычислений, Plenum Press, стр. 85–103.
Хот, Субхаш ; Киндлер, Гай; Моссель, Эльханан; О’Доннелл, Райан (2007), «Оптимальные результаты несовместимости для MAX-CUT и других CSP с двумя переменными?», Журнал SIAM по вычислениям, 37(1): 319–357, doi : 10.1137 / S0097539705447372.
Хуллер, Самир; Рагхавачари, Баладжи; Янг, Нил Э. (2007), «Жадные методы», в Гонсалес, Теофило Ф. (ред.), Справочник по алгоритмам приближения и метаэвристики, Chapman Hall / CRC.
Митценмахер, Майкл ; Упфал, Эли (2005), Вероятность и вычисления: рандомизированные алгоритмы и вероятностный анализ, Кембридж.
Мотвани, Раджив ; Рагхаван, Прабхакар (1995), рандомизированные алгоритмы, Cambridge.
Newman, Alantha (2008), «Max cut», в Kao, Ming-Yang (ed.), Encyclopedia of Algorithms, Springer, pp. 489–492, doi : 10.1007 / 978-0-387-30162-4_219, ISBN 978-0-387-30770-1 .
Пападимитриу, Христос H. ; Яннакакис, Михалис (1991), «Оптимизация, аппроксимация и классы сложности», Журнал компьютерных и системных наук, 43 (3): 425–440, doi : 10.1016 / 0022-0000 (91) 90023-X.
Тревизан, Лука ; Соркин Григорий; Судан, Мадху; Уильямсон, Дэвид (2000), «Гаджеты, аппроксимация и линейное программирование», Труды 37-го симпозиума IEEE по основам информатики: 617–626.
; Гупта, Свати; Зильберхольц, Джон (2018), «Что лучше всего работает, когда? Систематическая оценка эвристики для Max-Cut и QUBO», INFORMS Journal on Computing, 30 (3): 608–624, doi : 10.1287 / ijoc.2017.0798.

Внешние ссылки

Пьерлуиджи Крещенци, Вигго Канн, Магнус Халльдорссон, Марек Карпински, Герхард Вегингер (2000), “Максимальный разрез” «, в « Сборник задач оптимизации NP ».
Андреа Казини, Никола Ребальати (2012), « Библиотека Python для решения Max Cut »

Источник

Модель Изинга#

Автор(ы):

Синченко Семен

В этой лекции познакомимся с моделью Изинга, которая изначально была разработана для описания магнетизма, но оказалась настолько удачной и универсальной, что сегодня к решению именно этой задачи стараются свести многие проблемы реального мира, причем не только из физики. В следующем блоке подробно покажем, как к гамильтонианам типа Изинга, или, по-другому, “спиновым стеклам” могут быть сведены задачи комбинаторной оптимизации и квантовой химии. Так что знакомство с этой удивительной моделью, а также описывающим ее гамильтонианом нам просто необходимо!

Note

Специальные квантовые компьютеры компании D-Wave сконструированы так, что они могут решать вообще только одну задачу – нахождения основного состояния гамильтонианов типа Изинга. Но эта задача настолько распространена и важна, что эти компьютеры стали первыми в мире коммерческими квантовыми компьютерами! Кстати, далее этим компьютерам у нас посвящена отдельная лекция.

Ближайшее время посвятим довольно много времени объяснению этой модели. Это может показаться скучным и занудным, но это важно для понимания того, как это все работает и как решать с помощью вариационных квантовых алгоритмов реальные задачи!

Задача Изинга в одномерном случае#

Note

Ниже попробуем на пальцах объяснить модель Изинга. Пробовать будем через цепочку атомов антиферромагнетика во внешнем магнитном поле. Ели вы плохо помните физику и вам это объяснение покажется сложным, то не расстраивайтесь – дальше также объясним задачу Изинга как задачу о поиске максимального разреза в графе – известную задачу комбинаторной оптимизации.

Пусть у нас есть, например, цепочка атомов, которые обладают магнитным моментом. Например, цепочка атомов антиферромагнетика. И мы прикладываем к этой цепочке внешнее магнитное поле.

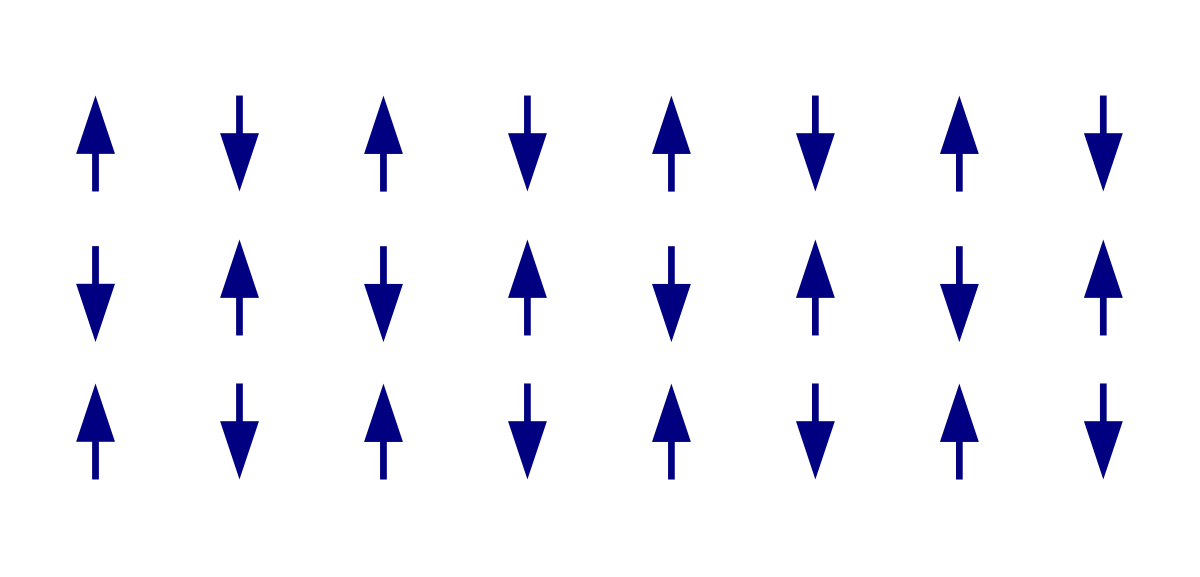
Тогда, если поле маленькое, наши атомы будут стараться выстроиться в антиферромагнитный порядок, когда соседние из них имеют моменты, направленные в разные стороны. Но если поле уже большое, то оно будет стремиться “повернуть” моменты по своему направлению. А если еще вспомнить, что магнитный момент атома является квантовой величиной и может быть в суперпозиции состояний в одну сторону и в противоположную, то не очень маленькое, но и не слишком большое поле будет переводить часть атомов именно в такие суперпозиции.

Fig. 85 Иллюстрация антиферромагнитного порядка#

Reminder о квантовой физике

В квантовой механике есть фундаментальное уравнение, которое описывает динамику квантовых систем. Оно называется уравнением Шредингера: (imath hbar frac{partial Psi}{partial t} = hat{H} Psi), где (hat{H}) – это оператор Гамильтона, или гамильтониан. Также его называют оператором полной энергии системы, так как в общем случае он равен сумме операторов кинетической и потенциальной энергии. Начиная с этой лекции будем очень часто обращаться к этому оператору, но в целом в нем нет ничего принципиально сложного. Это такой же эрмитов оператор, как и другие. А наблюдаемая величина, которую получаем при измерении этого оператора – это энергия системы.

Давайте теперь запишем гамильтониан такой системы. Для представления магнитных моментов будем использовать оператор (sigma^z) – другими словами, спин в направлении оси (Z). Если кто-то забыл, как выглядит оператор (sigma^z), то рекомендуем еще раз просмотреть раздел про операторы Паули первой лекции. Далее будем очень активно использовать эти матрицы для представления задач реального мира!

Для начала, в случае если внешнего поля нет, мы должны записать взаимодействие соседних атомов. Так как у нас антиферромагнетик, минимальная энергия достигается в случае, если каждый спин противонаправлен с соседними. Это просто оператор (sigma^z_j sigma^z_{j+1}), который действует на все пары соседних спинов. Ну и сразу введем некоторую константу обменного взаимодействия (J), чтобы потом нам было удобно сравнивать ее с внешним полем. В итоге, для цепочки из (N) спинов, получаем:

[
hat{H}_{h=0} = J sum_{i=0}^{N-1} sigma^{z}_i sigma^{z}_{i+1}
]

А теперь давайте добавим внешнее поле (h). В этом случае поле просто действует на все спины и пытается выстроить их в зависимости от своего направления, например, вниз. Тогда полный гамильтониан такой системы можно записать в виде:

[
hat{H}_{hneq 0} = J sum_{i=0}^{N-1} hat{sigma}^{z}_ihat{sigma}^{z}_{i+1} – hsum_{i=0}^N hat{sigma}^{z}_i
]

Задача Изинга как задача о максимальном разрезе в графе#

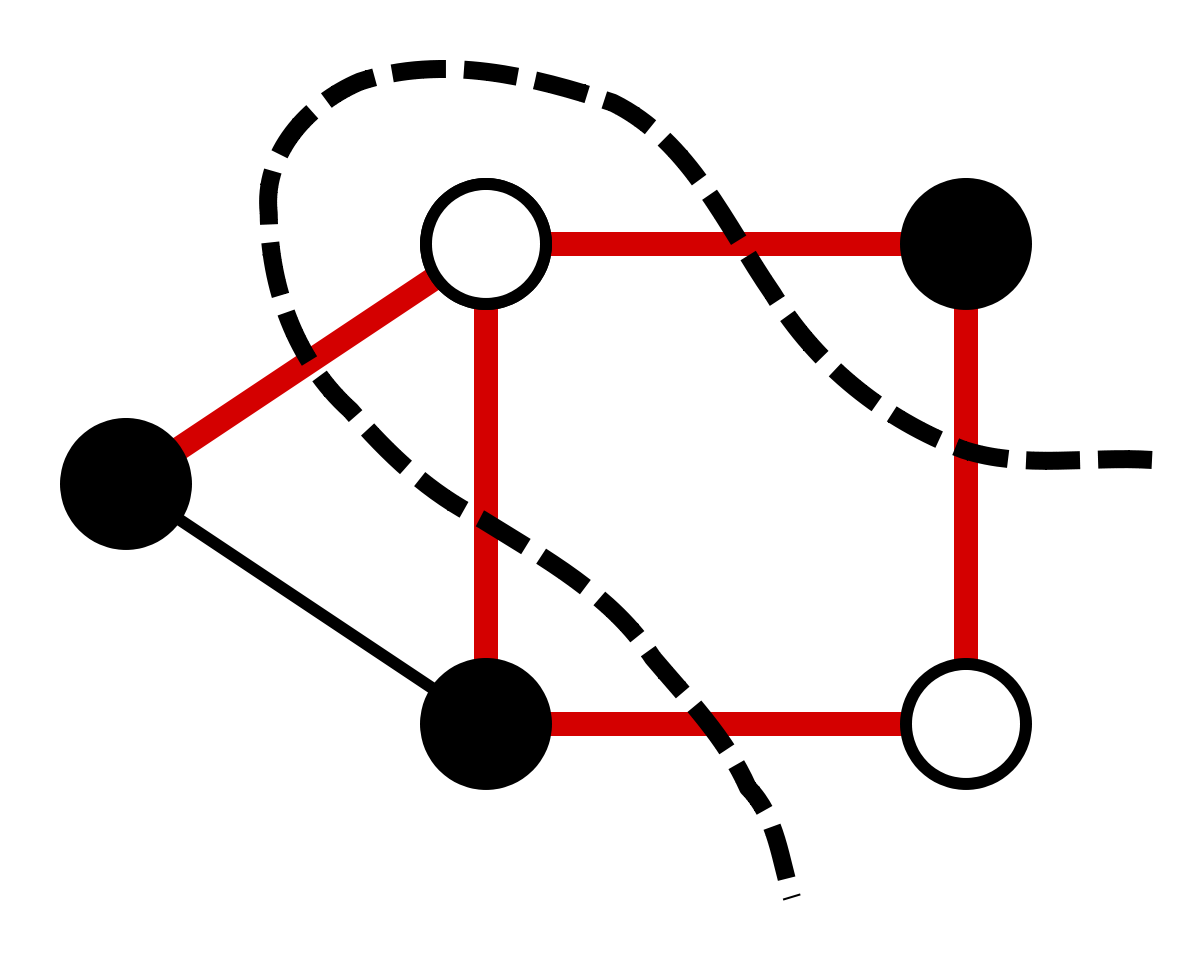
Задача о максимальном разрезе в графе – это очень известная задача комбинаторики. Она относится к классу (NP)-трудных, и к ней можно свести все другие (NP) задачи. При этом ее формулировка одна из самых простых среди всего класса задач. Формулируется она следующим образом.

Нам дан граф – набор вершин (V) и связывающих их ребер (E). Нам надо найти такое разделение вершин (V) на два непересекающихся набора (V_1, V_2), что число ребер между вершинами из разных наборов будет максимально.

Fig. 86 Иллюстрация задачи о максимальном разрезе в графе#

Теперь давайте представим, что каждой вершине нашего графа сопоставили кубит. Для этих кубитов можем производить измерения по оси (Z), чтобы понять, как направлен тот или иной спин. И давайте запишем вот такой гамильтониан и внимательно на него посмотрим:

[
hat{H} = sum_{u,v in E} hat{sigma}^z_u hat{sigma}^z_v
]

Тут суммирование (u,v in E) идет по всем ребрам графа, а (u,v) – вершины инцидентные ребрам. Если вспомнить, что собственные значения (sigma^z) это (pm 1) для, соответственно, спина “вверх” и спина “вниз”, то не трудно понять, в каком случае у нас будет минимум энергии этого гамильтониана. А будет он тогда, когда максимальное число пар вершин (u,v) имеют разную ориентацию своих спинов. Ведь если они имеют одинаковую направленность (причем не важно, (+1) или (-1)), их произведение будет равно (1), но если направленность разная, то их произведение даст нам (-1). Таким образом, минимум энергии такого гамильтониана достигается тогда, когда мы разбили наши вершины на две группы – спин “вверх” и спин “вниз” – причем число ребер между этими группами максимальное. А это в чистом виде формулировка задачи о максимальном разрезе в графе!

Note

Тематика квантовой физики мало обсуждалась в первых лекциях, но нам пока достаточно знать лишь то, что для любая физическая система (включая квантовую) стремится в состояние с минимальной энергией. Например, тело, подброшенное вверх, стремится упасть на землю, а возбужденный атом стремится релаксировать в невозбужденное состояние.

При этом из квантовой физики помним, что для реальных физических систем наиболее вероятными являются состояния с минимальной энергии и системы стремятся в эти состояния прийти. Теперь для простоты предположим, что наш граф – это просто цепочка, то есть ребра есть лишь между соседними в одномерном пространстве вершинами. Ну и теперь давайте сформулируем нашу задачу о максимальном разрезе чуточку сложнее – нам надо найти не просто максимальный разрез, а такой разрез, который самый большой при наименьшем числе вершин в наборе (V_1). И поскольку теперь у нас два вклада в стоимость, то нам нужны коэффициенты, которые покажут, что важнее. Пусть это будут (J) и (h). Тогда гамильтониан соответствующей модели Изинга можно записать так:

[
hat{H} = J sum_{i=0}^{N-1} hat{sigma}^{z}_ihat{sigma}^{z}_{i+1} – hsum_{i=0}^N hat{sigma}^{z}_i
]

Как видно, это тот же самый гамильтониан, который получили и для моделирования антиферромагнетиков. То есть задача об основном состоянии цепочки антиферромагнитных частиц во внешнем поле эквивалентна задаче о максимальном разрезе в графе-цепочке при некотором штрафе за одно из выделенных направлений спинов. Эквивалентность в данном случае значит, что:

решив задачу о максимальном разрезе, можно найти и основное состояние физической системы;
как-то смоделировав физическую систему, подождав пока она релаксирует, после чего измерив ее, получим конфигурацию, отвечающую решению задачи о максимальном разрезе.

Note

Одномерная цепочка атомов, или поиск максимального разреза в графе-цепочке, является простым случаем и не является (NP)-задачей. Однако уже в двумерном случае эта задача становится сильно сложнее, как и, например, если в цепочке атомов ферромагнетика добавим взаимодействие не только соседних спинов, но и взаимодействие с соседями соседа. Аналогично, модель вида Изинга сильно усложняется при добавлении недиагональных (off-diagonal elements) элементов гамильтониана, например, когда внешнее поле направлено в другом направлении и второй член гамильтониана принимает вид (hsum_{i=N} sigma^{x}_i). Более подробное исследование данной модели приводится в этой продвинутой лекции.

Модель Изинга на чистом NumPy#

Давайте попробуем реализовать одномерный гамильтониан Изинга на чистом NumPy/SciPy в виде разреженной матрицы. Для этого вспомним, что действуя оператором (sigma^z) на (i)-й кубит, одновременно действуем единичным оператором на все остальные, а потом перемножаем все операторы произведением Кронекера. Из лекций по линейной алгебре помним также об ассоциативности произведения Кронекера, чем и воспользуемся:

import numpy as np
from scipy import sparse
from scipy.sparse import linalg as sl

def sigmaz_k(k: int, n: int) -> (sparse.csr_matrix):
    left_part = sparse.eye(2 ** k)
    right_part = sparse.eye(2 ** (n - 1 - k))

    return sparse.kron(
        sparse.kron(
            left_part,
            sparse.csr_matrix(np.array([[1, 0,], [0, -1,],]))
        ),
        right_part
    )

А теперь можем реализовать и сам оператор Изинга:

def ising(j: float, h: float, n: int) -> (sparse.csr_matrix):
    res = sparse.csr_matrix((2 ** n, 2 ** n), dtype=np.complex64)

    for i in range(n - 1):
        res += j * sigmaz_k(i, n) * sigmaz_k(i + 1, n)
        res -= h * sigmaz_k(i, n)

    res -= h * sigmaz_k(n - 1, n)

    return res

Если внешнего поля нет, спины выстраиваются в полный антиферромагнитный порядок, в чем легко убедиться. Создадим оператор для такой модели и, например, 10 спинов (или 10 вершин в графе, если говорим в терминах Max-Cut):

op = ising(1, 0, 10)
solution = sl.eigs(op, which="SR", k=1, return_eigenvectors=True)
print(f"Energy: {solution[0][0]}")

Energy: (-9.000000000000018-2.208468631860285e-16j)

Note

Тут пользуемся функциями из ARPACK – набором рутин для линейной алгебры разреженных систем. Более подробно о способах и алгоритмах классических решений задачи о собственных значениях расскажем в одной из следующих лекций, полностью посвещнной этой теме. Пока же просто используем эту рутину как “черный ящик”. Более подробное описание этой функции и ее аргументов можно посмотреть в документации библиотеки SciPy.

Эта энергия соответствует антиферромагнитному порядку, в этом легко убедиться, нарисовав спины и формулу на бумажке. Внимательный читатель заметил, что в этот раз вернули также и первый собственный вектор, который в нашем случае является волновой функцией основного состояния. А как знаем, квадраты элементов вектора волновой функции дают нам вероятности соответствующих битовых строк (если для вас это все звучит дико, то очень рекомендуем вернуться к лекции про кубит). Давайте посмотрим на эту битовую строку, иначе на порядок наших спинов в решении (или на разбиение вершин графа на два подмножества в терминах Max-Cut):

def probs2bit_str(probs: np.array) -> (str):
    size = int(np.log2(probs.shape[0]))
    bit_s_num = np.where(probs == probs.max())[0][0]

    s = f"{bit_s_num:b}"
    s = "0" * (size - len(s)) + s

    return s

probs = solution[1] * solution[1].conj()
print(probs2bit_str(probs))

Теперь давайте попробуем добавить внешнее поле с коэффициентом, равным удвоенному значению константы обменного взаимодействия. В терминах комбинаторной задачи, добавляем штраф, равный (2) умножить на число спинов, направленных вверх.

def external_field(j: float, h: float, n: int) -> (None):
    op = ising(j, h, n)
    solution = sl.eigs(op, which="SR", k=1, return_eigenvectors=True)
    print(f"Energy: {solution[0][0]}")

    probs = solution[1] * solution[1].conj()
    print(probs2bit_str(probs))

external_field(1, 2, 10)

Energy: (-11.000000000000007-1.05712250567288e-16j)
0101010010

Видим, что теперь наш антиферромагнитный порядок уже не полный. В целом, данная модель довольно интересная, так как при некотором отношении (frac{h}{J}) у нас происходит фазовый переход от полной упорядоченности, а при дальнейшем росте (h) приходим к одинаковой ориентации всех спинов, в чем легко убедиться, взяв, например, (h = 100):

external_field(1, 100, 10)

Energy: (-991.0000000000039-3.488261257113687e-14j)
0000000000

Заключение#

В этой лекции на базовом уровне познакомились с моделью Изинга – очень важным концептом в квантовом машинном обучении. Узнали, что:

модель Изинга изначально была создана для объяснения магнетизма;
нахождение решений для модели Изинга в общем случае – (NP)-полная задача;
модель Изинга также может быть сформулирована в терминах задачи о максимальном разрезе в графе (и наоборот);
в классической модели Изинга существуют интересные фазовые переходы;
модель Изинга легко реализовать в коде, используя SciPy, но размерность задачи растет очень быстро.

Источник

4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ		191
Пусть Sk обозначает множество скобок, содержащих ровно k литералов, тогда:
∑ ∑	(1 2 k)	∑ ∑
n1 =	(1 2 k)^zj:
k Cj2Sk		k Cj2Sk

По лемме 22 имеем	∑ ∑ kz^j:
E n2
	k Cj2Sk

Следовательно,

	n + n	2	∑ ∑	(1 2 k) +	k
E	1		z^j:
2		2

kCj2Sk

Простое вычисление показывает, что (1 2 k) + k 3/2 для всех натуральных k и, значит,

E	n1 + n2		3	∑ ∑	3	∑
				z^j =		z^j:
2	4	k Cj2Sk	4
							j

4.4.2Максимальный разрез в графе

Задачи полуопределенного и векторного программирования. Использование эффективных алгоритмов для решений этих задач в вероятностном алгоритме решения задачи о максимальном разрезе в графе. Раздел основан на статье [GW95].

192	Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

Определение 4.4.2. Матрица X 2 Rn n является положительно полуопределенной если

8a 2 Rn; aTXa 0:

Обозначение: X 0.

Для симметрической X 2 Rn n следующее эквивалентно:

•X 0;

•X имеет неотрицательные собственные значения;

•X = V TV для некоторого V 2 Rm n, где m n.

Задача 21. «Полуопределенное программирование»².

∑

cijxij

i;j

∑

8k aijkxij

i;j

X = (xij)

8i; j xij

! max(min)

= bk;

= xji:

²В англоязычной литературе SDP, semideﬁnite programming.

4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ

193

Хотя задача 21 «SDP», несмотря на свою схожесть с линейным программированием, к нему не сводится, для нее существуют эффективные полиномиальные алгоритмы (модификации метода внутренней точки для ЛП), находящие приближенное решение с некоторой аддитивной ошибкой ϵ и временем, ограниченным полиномом по длине входа и O(log(1ϵ )).

Заметим, что, так как решение задачи 21 «SDP» может быть иррациональным числом, от численных методов точного (рационального) решения ждать и невозможно, хотя продолжаются попытки построить эффективный алгоритм нахождения точного решения алгебраическими методами.

Далее нам также пригодится эквивалентная формулировка задачи 21 «SDP» в виде задачи 22:

Задача 22. «Векторное программирование»³.

∑

cij(vi vj) ! max(min)

i;j

∑

aijk(

j) = bk;

i;j

8i vi 2 Rn:

Эквивалентность задач 21 «SDP» и 22 «VP» следует из факторизации положительно полуопределенной матрицы X в виде X = V TV , т. е. xij = vi vj, где vi и vj — соответствующие колонки матрицы V .

Преобразование решения задачи 22 «VP» в решение задачи 21 «SDP» тривиально (одно матричное умножение), обратное не совсем — требуется разложение Холецкого , и это преобразование неоднозначно, но ничего принципиально сложного в этом нет — это классическая задача линейной алгебры.

³В англоязычной литературе VP, vector programming.Cholesky factoriza on или Cholesky decomposi on.

194	Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

Вероятностное округление при нахождении аппроксимации максимального разреза

Определение 4.4.3. Пусть есть неориентированный граф G = (V; E). Разрезом (сечением, cut) называется разбиение множества вершин V на непересекающиеся множества S и T . т. е. V = S [ T

и S T = .

Определение 4.4.4. Для неориентированного графа G = (V; E) и разреза (S; T ) ребро e = (v; t) счита-

ется пересекающим разрез, если v 2 S, а t 2 T .

Определение 4.4.5. Для графа G = (V; E) размером разреза (S; T ) считается число ребер, пересекающих этот разрез.

Если граф — взвешенный, т. е. каждому ребру e 2 E соответствует некоторый вес we, то разме-

ром разреза (S; T ) считается сумма весов ребер пересекающих этот разрез:

∑

R(S; T ) =	we:
	e=(v;t)2E: v2S;t2T

Задача 23. «Максимальный разрез/MAX-CUT».

Для взвешенного неориентированного графа G = (V; E) с весами we > 0 найти разрез (S; T ) с максимальным весом R(S; T ).

Упражнение 4.4.2. Докажите, что для простого, невзвешенного графа в задаче 23 «MAX-CUT» можно применить простую стратегию, дающую вероятностный 0:5-приближенный алгоритм: для каждой вершины с вероятностью 1/2 отнести ее к множеству S и с вероятностью 1/2 — к множеству T .

Упражнение 4.4.3. Студент предлагает для задачи 23 «MAX-CUT» приближенный алгоритм с точностью 12 : положить первую вершину в одну часть, последнюю — в другую, затем по-очереди добавлять оставшиеся вершины, к множеству, с которым у этой вершины меньше ребер-связей.

Прав ли студент?

i<j 2

4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ

195

Наша цель — построить алгоритм с лучшими оценками точности приближения. Для этого сформулируем задачу 23 «MAX-CUT» как задачу целочисленного программирования.

Задача 24. «MAX-CUT(ЦП)»

G = (V; E) — входной граф, jV j = n;

W = (wij) — веса ребер, n n матрица. Для отсутствующего между vi и vj ребра — wij = 0;

yi — принадлежность вершины части разреза:

vi 2 S ! yi = 1, vi 2 T ! yi = 1. Ребро (vi; vj) 2 (S; T ) , yiyj = 1.

R(S; T ) — Вес разреза (S; T ). R(S; T ) = ∑ 1 yiyj wij:

Задача целочисленного квадратичного программирования:

∑	yiyj
1	wij ! max
ZЦП =		2
i<j

8i yi 2 f 1; 1g:

Видно, что постановка задачи 24 «MAX-CUT(ЦП)» внешне похожа на задачу 22 «VP», однако целочисленные ограничения в задаче 24 «MAX-CUT(ЦП)» делают ее существенно сложнее для решения. Рассмотрим следующую релаксацию задачи 24 «MAX-CUT(ЦП)».

196

Глава 4.

ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

Задача 25. «MAX-CUT(VP)»

∑

1 vi

! max

V P

i<j

Rn:

Эту задачу мы уже можем решать эффективно (см. выше), осталось разобраться, можно ли использовать решение задачи 25 «MAX-CUT(VP)» для нахождения решения (возможно приближенного) зада-

чи 24 «MAX-CUT(ЦП)».

Сначала заметим, что для оптимумов задач 24 «MAX-CUT(ЦП)» и 25 «MAX-CUT(VP)» выполняется

ZЦП ZV P :

Этот факт следует из того, что задача 25 «MAX-CUT(VP)» содержит задачу 24 «MAX-CUT(ЦП)» как частный случай.

Используя полученное решение задачи 25 «MAX-CUT(VP)» для вероятностного округления, получаем алгоритм 34 (концептуально аналогичный рассмотренному ранее алгоритму 33 «вероятностный MAXSAT»).

Нам понадобится небольшой технический факт.

Лемма 23.

min		2	0:878:
	cos )
0< (1

4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ

197

Доказательство. Рассмотрим график нашей функции на различных интервалах (Рис. 4.5). Функция имеет сингулярности в точках 0 и 2 , а на интервале (0; 2 ) функция выпуклая и имеет один минимум. Судя по построенным графикам, на интервале (0; 2 ) функция не меньше 0:878.

Чтобы убедиться в этом, найдем минимум (по равенству нулю производной) и вычислим значение функции в точке минимума. Воспользуемся системой компьютерной алгебры Maxima: возьмем производную и с помощью метода Ньютона найдем ее единственный нуль в интересующем нас интервале.

<load(”newton”);

<y:2*x/%pi/(1-cos(x));

<x0:newton(diff(y,x),3); > 2.331122370414422B0

<y(x0),numer;

> 0.87856720578485

Таким образом, можно даже утверждать, что

min		2	> 0:8785672057848:

0< (1	cos )

Теперь оценим качество алгоритма.

Теорема 20. Пусть (S ; T ) — оптимальный разрез для задачи 23 «MAX-CUT», тогда для математического ожидания величины разреза (S′; T ′), полученного вероятностным алгоритмом 34 «SDPокругление MAX-CUT», выполняется

E[R(S′; T ′)] 0:878 R(S ; T ):

198	Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ
	Рис. 4.5: График функции (1	2
	cos )

4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ

199

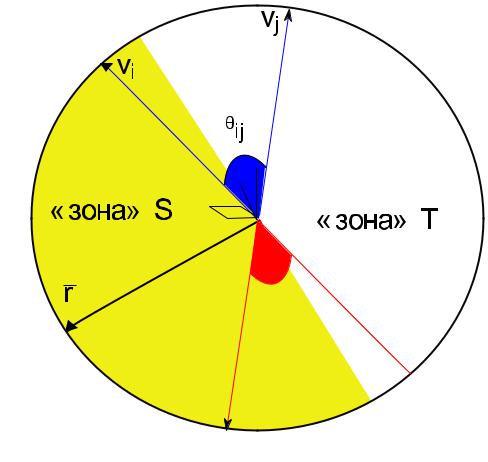
Рис. 4.6: Вектора в вероятностном округлении «MAX-CUT»

200	Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

Алгоритм 34 «SDP-округление MAX-CUT»

Вход: Формулировка задачи 23 «MAX-CUT» в виде задачи 24 «MAX-CUT(ЦП)» (v1; : : : ; vn) решения релаксации 25 «MAX-CUT(VP)»

случайно выбираем r из равномерного распределения векторов единичной длины

S T

for all i 2 f1::ng do if vi r 0 then

S S [ fig else

T T [ fig end if

end for

Выход: (S,T) — приближенное решение (23).

Доказательство. Возьмем некоторые i и j и соответствующие им векторы решения релаксации vi и vj. Затем оценим вероятность того, что при вероятностном округлении соответствующие вершины попадут в разные части разреза. Получим

		P(yi ̸= yj) = P(yiyj = 1) =	ij	;

где ij — угол между векторами vi и vj.
Отсюда, используя определение математического ожидания:			∑
E	∑	1 yiyj	wij =	∑	2 P(yi	̸= yj)	wij =	ij	wij:
i<j	2	i<j	2		i<j

С другой стороны, значение решения релаксации 25 «MAX-CUT(VP)» тоже можно выразить через углы ij:

ZV P = ∑	1				∑	1 cos
v	v		ij
	i	j	wij =	wij:
	2		2

4.4. ВЕРОЯТНОСТНОЕ ОКРУГЛЕНИЕ

201

Теперь оценим минимальное качество решения, используя лемму 23:

∑

E[R(S′; T ′)]

wij

R(S ; T )

∑

cos ij

min

cos )

0:878:

ZV P

wij

0< (1

i<j

202

Глава 4. ВЕРОЯТНОСТНЫЕ АЛГОРИТМЫ И ИХ АНАЛИЗ

Рис. 4.7: Карта-памятка раздела 4.4.2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Представим, что у нас есть диграф и две вершины — источник и сток. У каждого ребра есть вес, который называется его пропускной способностью. Нам нужно пропустить как можно больше материала через диграф от источника к стоку. Это называется потоком, а взвешенный диграф — сетью. Таким образом мы строим сетевой поток.

Например, источник — это

, а сток —

Первое число, выделенное красным на каждом ребре — это значение потока, а второе — пропускная способность. В этом случае поток не оптимальный, так как через сеть можно пропустить больше вещей, чем

единиц.

Количество потока на ребре не может превышать его пропускную способность. Еще общее количество потока в вершину должно быть равно общему количеству потока из этой вершины, за исключением источника и стока. В итоге поток проходит через вершины, которые не создают и не потребляют поток.

Общее объем потока, который проходит через сеть, называется величиной потока. Это количество можно найти, если посчитать:

Общий поток, который выходит из источника
Общий поток, который входит в сток

Многие реальные проблемы можно смоделировать с помощью сетей потоков. Например, источник — это место, где мы добываем сырье. Его нужно доставить на завод — сток. Края — это различные маршруты, по которым мы можем отправить сырье, а мощность — сколько материала можно доставить по этим маршрутам.

Если предположить, что транспортная сеть — это ограничивающий фактор, то нас интересует, сколько сырья мы можем доставить на фабрику.

Многие несвязанные проблемы теории графов можно преобразовать в проблемы сетевых потоков.

Источник

Вычислительная сложность[править | править код]

Алгоритмы полиномиального времени[править | править код]

Аппроксимационные алгоритмы[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Литература для дополнительного чтения[править | править код]

Ссылки[править | править код]

Содержание

Вычислительная сложность

Алгоритмы

Полиномиальные алгоритмы

Планарные графы

Алгоритмы аппроксимации

Приложения

Теоретическая физика

Проектирование схемы

См. Также

Примечания

Ссылки

Внешние ссылки

Модель Изинга#

Задача Изинга в одномерном случае#

Задача Изинга как задача о максимальном разрезе в графе#

Модель Изинга на чистом NumPy#

Заключение#

4.4.2Максимальный разрез в графе

Вам также может понравиться

Как исправить ошибку в документе об образовании

Сталкер ушедшая душа вылет в забытой лаборатории как исправить

Как исправить пересоленную рыбу скумбрию

Добавить комментарий Отменить ответ