Пример решения задачи по определению угла отклонения стержня от вертикали при его вращении как функцию угловой скорости и реакций опор в заданных точках.
Задача
С невесомым валом AB шарнирно скреплен однородный стержень OD длиной l и массой m1, имеющий на конце груз массой m2.
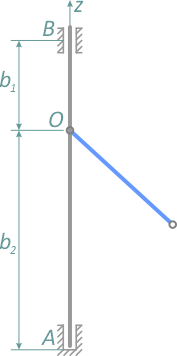
Вал и стержень вращаются вокруг оси OZ с постоянной угловой скоростью ω. Известны b1 и b2 – расстояния от опор до точки крепления стержня (рисунок 1.4).
Рисунок 1.4
Требуется определить угол отклонения стержня от вертикали — α, как функцию угловой скорости и реакции опор A и B.
Другие примеры решений >
Помощь с решением задач >
Решение
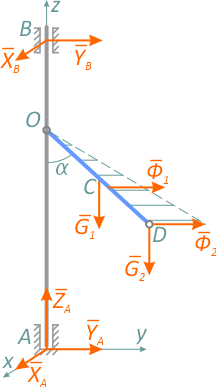
Применим принцип Даламбера для данной системы. Проведем вращающиеся вместе с валом и стержнем оси координат Axyz так, чтобы стержень OD находился в плоскости yAz. Внешние силы: G1, G2; реакции опор: xA, yA, zA, xB, yB; силы инерции Φ1 и Φ2 (рисунок 1.5).
Рисунок 1.5
Отклонение стержня от вертикали происходит за счет сил инерции. Определенной угловой скорости соответствует свой угол отклонения. Величина силы инерции стержня определяется из формулы
и направлена перпендикулярно к оси вращения, в сторону, противоположную ускорению центра масс стержня.
Эпюра распределения сил инерции стержня представляет собой треугольник (элементарные силы инерции частичек стержня возрастают с удалением от точки O к точке D, т.к. растет их ускорение с увеличением радиуса вращения). Результирующая таких сил приложена на расстоянии 2/3 длины стержня от точки O (см. раздел «Статика», распределенные нагрузки).
Сила инерции точечной массы
Напишем для равновесия стержня при данной угловой скорости ω уравнение моментов относительно точки O – точки крепления стержня:
подставляем данные:
определяем угол:
Для определения реакций опор вала составим уравнения равновесия:
— вращающие моменты отсутствуют, система вращается по инерции, с постоянной угловой скоростью.
Из имеющихся пяти уравнений, подставляя данные задачи, можно найти пять неизвестных реакций в опорах A и B.
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
не одна скорость же не задана в условии
Но скорость все-таки вычисляется и мне не хватает думалки понять как или ее, действительно, не найти?
Вот представьте себе, что шарик, который ударяется о стержень, летел до удара медленно-медленно, и вообразите, какой будет максимальный угол отклонения. Теперь представьте, что он летел быстро-быстро, и прикиньте, будет ли максимальный угол отклонения такой же или какой-то другой. Можно даже представить себе сначала не шар и висящий стержень, а просто два шара, летящий и неподвижный.
Начальное состояние всей этой системы вашим условием не задаётся однозначно, потому что не указана скорость шара. Порой бывает и так, что ответ не зависит от такого параметра, поэтому его задание необязательно. Однако в этой задаче такой случай не кажется вероятным, поэтому следует задаться начальной скоростью шара. Если вдруг ответ от неё всё-таки не зависит, то она просто везде сократится в выкладках при выписывании ответа.
Итак, в условие стоит добавить фразу: шар врезается в стержень перпендикулярно стержню, и его скорость перед ударом имеет известную величину 


Во-первых, разве скорость стержня до удара не 0? Во-вторых, что такое “скорость стержня после удара”? Он же после удара вертится, его верхний конец вообще на месте, а скорости остальных его точек разные.
Далее вы пишете какие-то формулы, не понимая их смысла. Не надо переписывать кучу формул. Надо писать, что какой буквой означено и откуда берётся каждое из уравнений: какие законы вы применяете и почему вы вправе их применить.
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
ДОМАШНЕЕ ЗАДАНИЕ ПО КУРСУ ОБЩЕЙ ФИЗИКИ. ТЕМА «ЗАКОНЫ СОХРАНЕНИЯ. КОЛЕБАНИЯ. ВОЛНЫ» (Н.А. Гладков, А.С. Романов) (книга).pdf
Скачиваний:
54
Добавлен:
24.05.2015
Размер:
539.19 Кб
Скачать

Все задачи этого раздела решаютcя в два этапа. В задачах 2- 1, 2-2, 2-4 расчет следует начинать с определения минимальной скорости V0m. После этого проводится второй этап расчета при скорости V0, значения которой представлены в табл. 4, 5, 7. Аналогичным образом, в задаче 2-3 расчет следует начинать с определения минимальной угловой скорости ω0m. После этого проводится второй этап расчeта с угловой скоростью ω0, значение которой представлено в табл. 6. На втором этапе расчeта в зависимости от варианта задания определяют либо угловую скорость ωк, либо максимальный угол ϕmax, а также изменение энергии E. В задаче 2-3 в некоторых вариантах на втором этапе расчета требуется определить скорость кубика V0 после удара.
Задача 2-1
|
Однородный жeсткий стержень |
|||
|
длиной l = 1 м и массой M = 1 кг сво- |
|||
|
бодно висит на горизонтальной идеаль- |
|||
|
но гладкой оси вращения О, как пока- |
|||
|
зано на рис. 13. |
|||
|
Ось |
вращения |
перпендикулярна |
|
|
плоскости рисунка. Малый шарик мас- |
|||
|
сой m = 0,1 кг, летящий горизонтально |
|||
|
со скоростью V0, движется в плоско- |
|||
|
сти рисунка и ударяет в стержень. При |
|||
|
этом взаимодействие шарика со стерж- |
|||
|
нем может происходить в виде: |
|||
|
Рис. 13 |
а) |
абсолютно |
упругого удара |
|
(АУУ); |
|||
б) неупругого удара (НУУ); в) абсолютно неупругого удара (АНУУ).
Сразу после удара стержень вращается с угловой скоростью w0, а шарик приобретает скорость Vк и продолжает двигаться в плоскости рисунка.
При решении задачи используются также следующие обозначения:
24
Таблица 4
V0m — минимальная начальная скорость шарика, а ω0m — соответственно минимальная угловая скорость стержня, при которой стержень после удара совершает полный оборот;
ωк — угловая скорость стержня при прохождении им крайней верхней точки;
ϕmax — максимальный угол отклонения стержня от положения равновесия;
E — потери механической энергии при ударе.
Другие исходные данные и искомые величины для каждого варианта задания представлены в табл. 4. Расчет следует начинать с определения характерного значения V0m.
|
Номер |
Задано |
Вид |
Определить |
|||||||
|
варианта |
взаимодействия |
|||||||||
|
V0 |
Vк |
АУУ |
НУУ |
АНУУ |
ωк |
ϕm |
V0m |
E |
||
|
1 |
0,5V0m |
— |
— |
— |
+ |
— |
+ |
+ |
+ |
|
|
2 |
2V0m |
— |
— |
— |
+ |
+ |
— |
+ |
+ |
|
|
3 |
0,5V0m |
0 |
— |
+ |
— |
— |
+ |
+ |
+ |
|
|
4 |
2V0m |
0 |
— |
+ |
— |
+ |
— |
+ |
+ |
|
|
5 |
0,5V0m |
— |
+ |
— |
— |
— |
+ |
+ |
— |
|
|
6 |
2V0m |
— |
+ |
— |
— |
+ |
— |
+ |
— |
|
Задача 2-2
Однородный жeсткий вертикальный стержень длиной l = 1 м и массой М = 1 кг, движущийся поступательно в плоскости рисунка с постоянной горизонтальной скоростью V0, налетает на край массивной преграды (рис. 14). После удара стержень вращается вокруг оси O, перпендикулярной плоскости рисунка. Ось вращения стержня совпадает с ребром преграды и проходит через точку контакта стержня с преградой, так что точка контакта лежит выше центра тяжести стержня. Потерями механической энергии при вращении стержня после удара пренебречь.
При решении задачи используются также следующие обозначения:
25
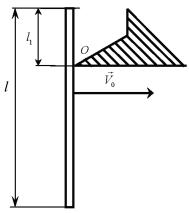
Таблица 5
Рис. 14
l1 — расстояние от верхнего конца стержня до точки контакта; ω0 — угловая скорость стержня сразу после удара о ребро пре-
грады;
V0m — минимальная горизонтальная скорость стержня, а ω0m — соответственно минимальная угловая скорость стержня, при которой он после удара способен коснуться горизонтальной поверхности преграды;
ϕmax — максимальный угол поворота стержня после удара; ωк — угловая скорость стержня в момент его удара о горизон-
тальную поверхность преграды.
Другие исходные данные и искомые величины для каждого варианта задания представлены в табл. 5.
Расчет следует начинать с определения характерной скорости V0m.
|
Номер |
Задано |
Определить |
|||||
|
варианта |
|||||||
|
l1 |
V0 |
ω0 |
ωк |
ϕmax |
V0m |
||
|
7 |
0,1l |
1,4V0m |
+ |
+ |
— |
+ |
|
|
8 |
0,1l |
0,5V0m |
+ |
— |
+ |
+ |
|
|
9 |
0,2l |
1,5V0m |
+ |
+ |
— |
+ |
|
|
10 |
0,2l |
0,6V0m |
+ |
— |
+ |
+ |
26
Окончание табл. 5
|
Номер |
Задано |
Определить |
|||||
|
варианта |
|||||||
|
l1 |
V0 |
ω0 |
ωк |
ϕmax |
V0m |
||
|
11 |
0,4l |
1,2V0m |
+ |
+ |
— |
+ |
|
|
12 |
0,4l |
0,8V0m |
+ |
— |
+ |
+ |
|
|
13 |
0,3l |
1,1V0m |
+ |
+ |
— |
+ |
|
|
14 |
0,3l |
0,4V0m |
+ |
— |
+ |
+ |
|
|
15 |
0,25l |
1,3V0m |
+ |
+ |
— |
+ |
Задача 2-3
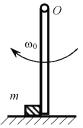
Однородный жесткий стержень длиной l = 0,5 м и массой М = 0,5 кг может свободно без трения вращаться вокруг горизонтальной оси О. При прохождении стержнем вертикального положения с угловой скоростью ω0, он своим нижним концом ударяет по маленькому кубику массой m = 0,1 кг, кото-
рый после удара движется в плоскости рисунка (рис. 15).
При этом взаимодействие стержня с кубиком может происходить в виде:
а) абсолютно упругого удара (АУУ); б) неупругого удара (НУУ);
в) абсолютно неупругого удара (АНУУ).
При решении задачи используются также следующие обозначения: Рис. 15
ω0 — угловая скорость стержня сразу после взаимодействия с кубиком;
ω0m — минимальная угловая скорость ω0, при которой стержень после удара совершит полный оборот вокруг оси O при заданном типе взаимодействия;
ω0m — угловая скорость стержня сразу после взаимодействия
с кубиком, при условии, что начальная угловая скорость стержня была равна ω0m;
ωк — угловая скорость стержня в крайней верхней точке после удара;
ϕm — максимальный угол отклонения стержня от положения равновесия после удара;
27

V0 — скорость кубика после удара;
E — потери механической энергии при ударе стержня по ку-
бику.
Другие исходные данные и искомые величины для каждого варианта задания представлены в табл. 6.
Расчет следует начинать с определения минимальной угловой скорости стержня ω0m.
|
Таблица 6 |
|||||||||||
|
Номер |
Задано |
Вид взаимо- |
Определить |
||||||||
|
варианта |
действия |
||||||||||
|
ω0 |
V0 |
АУУ |
НУУ |
АНУУ |
ω0m |
ωк |
ϕm |
V0 |
E |
||
|
16 |
0,5ω0m |
— |
+ |
— |
— |
+ |
— |
+ |
+ |
— |
|
|
17 |
1,2ω0m |
— |
+ |
— |
— |
+ |
+ |
— |
+ |
— |
|
|
18 |
0,4ω0m |
ω0l |
— |
+ |
— |
+ |
— |
+ |
— |
+ |
|
|
19 |
1,5ω0m |
ω0l |
— |
+ |
— |
+ |
+ |
— |
— |
+ |
|
|
20 |
0,6ω0m |
— |
— |
— |
+ |
+ |
— |
+ |
+ |
+ |
|
|
21 |
2ω0m |
— |
— |
— |
+ |
+ |
+ |
— |
+ |
+ |
Задача 2-4
Физический маятник, состоящий из однородного шара радиусом R = 3 см и массой М = 0,4кг, жестко соединенного с однородным жестким стержнем длиной 4R и массой M, подвешен к горизонтальной оси O, проходящей через верхний конец стержня перпендикулярно плоскости рисунка (рис. 16).
|
Рис. 16 |
Маятник может свободно без трения |
|
|
вращаться вокруг оси O. Шарик массой |
||
m = 0,05 кг движется горизонтально в плоскости рисунка со скоростью V0 вдоль горизонтальной прямой, проходящей через центр шара, и ударяет в шар. При этом взаимодействие шарика с маятником может происходить в виде:
а) абсолютно упругого удара (АУУ);
28
б) неупругого удара (НУУ); в) абсолютно неупругого удара (АНУУ).
При решении задачи используются также следующие обозначения:
ω0 — угловая скорость физического маятника сразу после удара шарика;
V0m — минимальная скорость шарика, при которой маятник после удара, приобретая угловую скорость ω0m, совершает полный оборот;
ωк — угловая скорость физического маятника в верхней точке; ϕmax — максимальный угол отклонения физического маятника
от положения равновесия;
Vк — скорость шарика после удара;
E — потери механической энергии при ударе шарика по маятнику.
Другие исходные данные и искомые величины для каждого варианта задания представлены в табл. 7.
Расчет следует начинать с определения минимальной скорости шарика V0m.
Таблица 7
|
Номер |
Задано |
Виды |
Определить |
|||||||
|
варианта |
взаимодействия |
|||||||||
|
V0 |
Vк |
АУУ |
НУУ |
АНУУ |
ωк |
ϕm |
V0m |
E |
||
|
22 |
0,5V0m |
— |
+ |
— |
— |
— |
+ |
+ |
— |
|
|
23 |
2V0m |
— |
+ |
— |
— |
+ |
— |
+ |
— |
|
|
24 |
0,4V0m |
0 |
— |
+ |
— |
— |
+ |
+ |
+ |
|
|
25 |
1,2V0m |
0 |
— |
+ |
— |
+ |
— |
+ |
+ |
|
|
26 |
0,8V0m |
— |
— |
— |
+ |
— |
+ |
+ |
+ |
|
|
27 |
1,4V0m |
— |
— |
— |
+ |
+ |
— |
+ |
+ |
|
|
28 |
0,6V0m |
— |
+ |
— |
— |
— |
+ |
+ |
— |
|
29

Основные зависимости к задачам раздела 2. Уравнение динамики вращательного движения механической системы относительно неподвижной оси OZ:
dLdtz = Mz.
Здесь Lz — сумма моментов импульсов всех частей механической системы относительно оси OZ; Mz — сумма моментов всех внешних сил, действующих на систему, относительно оси OZ. Если Mz = 0, то из этого уравнения следует закон сохранения момента импульса относительно оси OZ:
Lz = const.
Момент силы относительно оси z определяется по формуле
Mz = Fτ R,
где — проекция вектора внешней силы на направление каса-
Fτ F
тельной к окружности с центром на оси z, лежащей в плоскости перпендикулярной оси OZ, и проходящей через точку приложения
вектора ; — радиус этой окружности (плечо проекции силы ).
F R Fτ
Момент импульса твердого тела, вращающегося относительно неподвижной оси OZ с угловой скоростью ω,
Lz = Iz ω,
где Iz — момент инерции твердого тела относительно оси OZ. Момент импульса твердого тела массой m, движущегося по-
ступательно со скоростью V , перпендикулярно неподвижной оси OZ, относительно этой оси равен
где h — плечо импульса твердого тела, равное длине отрезка, проведенного от оси вращения перпендикулярно прямой, совпадающей
с направлением вектора скорости центра масс тела .
Vc
Докажем справедливость данной формулы на примере поступательного движения однородного прямолинейного стержня массой m и длиной l (см. задачу 2-2), который движется со скоростью V . Момент импульса этого стержня относительно оси OZ (ось OZ
30

Рис. 17
проходит через точку О перпендикулярно плоскости, изображенной на рис. 17, и направлена на нас) будет складываться в результате интегрирования моментов импульсов dLz от элементарных частей стержня массой dm
где y — координата элементарной части стержня длиной dу. Тогда
dm = ρSdу,
31

где ρ — плотность материала стержня; S — площадь его поперечного сечения.
Начало координат оси ОY расположено в точка О, где находится выступ (ребро) преграды. Момент импульса стержня относительно оси ОZ будет, согласно (2.2), вычисляться по формуле
|
l−l1 |
l1 |
|
|
Lz = |
ρV Sуdy − ρV Sуdy. |
(2.3) |
00
На рис. 17 введены следующие обозначения: l1 — длина стержня над выступом;
h — расстояние от выступа (точка О) до центра масс стержня (точка С);
l/2 — расстояние от края стержня до центра масс.
Перед вторым интегралом в формуле (2.3) стоит знак минус, потому что проекции моментов импульсов нижней и верхней частей стержня относительно оси ОZ имеет разные знаки. После интегрирования получаем:
|
Lz = ρV S |
(l−l1)2 |
− |
ρV S |
l12 |
. |
|
2 |
2 |
После преобразований имеем:
l
Lz = ρV Sl 2 −l1 .
|
Поскольку ρSl = m, а |
l |
−l1 = h, в итоге имеем выражение |
||
|
2 |
||||
|
Lz = mV h, |
(2.4) |
которое совпадает с формулой (2.1).
Кинетическая энергия твердого тела, вращающегося относительно неподвижной оси OZ:
ЕK = Iz2ω2 .
Моменты инерции некоторых однородных твердых тел массой m простой формы:
32

сплошного кругового цилиндра с радиусом R относительно его
оси
I = 0,5mR2;
сплошного шара с радиусом R относительно оси, проходящей через центр шара
I = 0,4mR2;
тонкого стержня длиной l относительно оси, перпендикулярной стержню и проходящей через его центр масс
I = 121 ml2.
Теорема Штейнера:
Ioz = Icz +ma2,
где Icz — момент инерции твердого тела, относительно оси, проходящей через центр масс; Ioz — момент инерции относительно оси OZ, параллельной CZ; a — расстояние между осями CZ и OZ.
Пример решения задачи 2-1
Однородный жeсткий стержень длиной l и массой М свободно висит на горизонтальной гладкой оси вращения OZ, как показано на рис. 13. Ось вращения перпендикулярна плоскости рисунка. Малый шарик массой m, летящий горизонтально со скоростью V0, движется в плоскости рисунка, ударяет в стержень и застревает в нeм. Найти изменение импульса механической системы (МС) стержень — шарик и потерю механической энергии МС за время удара.
Решение. При ударе шарика о стержень со стороны опоры оси на ось вращения действует дополнительная сила (реакция опоры), удерживающая эту ось на месте. Поэтому МС оказывается незамкнутой, так как реакция опоры является внешней силой по отношению к рассматриваемой МС.
Воспользуемся законом сохранения момента импульса данной МС относительно оси вращения ОZ для расчeта угловой скорости вращения стержня сразу после удара ω0. Это возможно, так как, во-первых, интервал времени взаимодействия (удара) шарика со
33
стержнем настолько незначителен, что углом поворота стержня вокруг оси вращения за этот интервал времени можно пренебречь, а во-вторых, момент внешней силы (реакции опоры) относительно оси вращения равен нулю в силу равенства нулю плеча этой силы относительно оси ОZ.
Момент импульса МС до удара равен моменту импульса шарика относительно оси ОZ:
|
L0 |
= mV0 |
2l |
. |
(2.5) |
|
|
3 |
|||||
Момент импульса МС после удара складывается из моментов импульсов шарика и стержня относительно оси О:
|
Lк = mω0 |
4l2 |
+Iz ω0, |
(2.6) |
|
|
9 |
||||
где Iz — момент инерции стержня относительно оси z, который вычисляется в соответствии с теоремой Штейнера.
Приравнивая (2.5) и (2.6), после преобразований находим начальную угловую скорость вращения стержня:
|
ω0 = |
V0 |
24m |
. |
|
|
l (16m+7M) |
Импульс МС до удара направлен горизонтально и равен начальному импульсу шарика:
Импульс МС после удара направлен горизонтально и равен
|
Pк = mω0 |
2l |
+MVC, |
(2.8) |
|
|
3 |
||||
где mω0(2l/3) — импульс шарика после удара, а скорость центра масс стержня равна VC = ω0l/3.
Вычитая выражение (2.7) из (2.8), получаем изменение импульса P = Pк −P0 системы стержень — шарик за время удара:
|
P = mω0 |
2l |
+M ω0 |
l |
−mV0 = |
mV0 |
|
. |
|||||
|
3 |
3 |
7+16m/M |
Из последней формулы следует, что импульс МС за время удара увеличился.
34
Решить систему полученных уравнений.2. Провести анализ решения (проверить размерность и лишние корни, рассмотреть характерные случаи, установитьобласть применимости).3. Получить численный результат.7.3. Примеры решения задач7.3.1. Законы сохранениямомента импульса и механической энергииЗадача 7.1Вокруг горизонтальной оси, проходящей через точку закрепления математического маятника массой m и длиной l, может вращаться без трения однородный стержень массой M и длиной L ≥ l,шарнирно закрепленный в той же точке (см. рис. 7.2). Маятник отпускают из горизонтального положения.
Найти максимальный уголотклонения стержня αmax после абсолютно упругого соударения cмаятником.Глава 7. Законы сохранения момента импульса и механической энергии239РешениеI. Выберем лабораторную инерциmπ/2 lальную систему отсчета, жестко связанную с точкой подвеса математическогомаятника и стержня. Направим горизонтальную ось вращения за плоскость чер- M, Lтежа (см. рис. 7.2).Выберем четыре момента времени:Рис. 7.2t1 – момент начала движения математического маятника, t2 – момент непосредственно перед соударениеммаятника со стержнем, t3 – момент сразу после соударения, t4 – момент, соответствующий максимальному отклонению стержня.
Втечение временного интервала (t1, t2) сохраняется механическаяэнергия математического маятника. В промежутке времени (t2, t3)сохраняются механическая энергия и момент импульса системытел «маятник + стержень». Импульс системы тел в этом промежутке не сохраняется, поскольку в точке подвеса стержня во время соударения возникают дополнительные силы, импульс которых отличен от нуля. В промежутке времени (t3, t4) сохраняется механическая энергия стержня вследствие отсутствия сил трения.Потенциальные энергии математического маятника и стержня будем считать равными нулю при их вертикальной ориентации.II.
Запишем закон сохранения механической энергии (7.17)для математического маятника на интервале времени (t1, t2):2J1ω1mgl =.(7.25)2Здесь mgl – потенциальная энергия маятника в его исходном гори2J1ω1– кинетиче2ская энергия маятника непосредственно перед соударением (в момент времени t2), J1 – момент инерции маятника относительно осивращения, ω1 – его угловая скорость перед соударением.Для временного интервала (t2, t3) закон сохранения моментаимпульса (7.4) и механической энергии (7.17) для системы тел «маятник + стержень» имеют вид:J1ω1 = J 2ω2 + J1ω3 ,(7.26)зонтальном положении (в момент времени t1),МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ240222JωJ1ω1Jω(7.27)= 2 2 + 1 3 ,222где J2 – момент инерции стержня, ω2 и ω3 – угловые скорости вращения стержня и маятника сразу после соударения.Запишем также закон сохранения механической энергии(7.17) для стержня на интервале времени (t3, t4):2J 2ω2MgL(1 − cos α max ) .=(7.28)22Моменты инерции маятника J 1 и стержня J 2 относительновыбранной оси вращения равны:J1 = ml 2 ,(7.29)1J 2 = ML 2 .(7.30)3III.
Решая систему уравнений (7.25) – (7.30) относительно искомого максимального угла отклонения стержня, получаем:⎛⎞⎜⎟⎜⎟L⎟24α max = arccos⎜1 −⋅.(7.32)2⎜ ⎛⎟2l⎞⎜ ⎜ 3 + M ⎛⎜ L ⎞⎟ ⎟⎟⎟⎜ ⎜⎟ml⎝⎠⎠⎝ ⎝⎠Поскольку α max не может превышать π / 2 , то на соотношения масс M / m и длин L / l стержня и математического маятниканакладывается условие:24L⋅ <1,(7.33)22⎛⎞ lML⎞⎛⎜3 + ⎜ ⎟ ⎟⎜m ⎝ l ⎠ ⎟⎠⎝при нарушении которого стержень ударится о потолок.На рис. 7.3 изображены области значений отношений длин имасс маятника и стержня, при которых максимальный угол отклонения стержня в результате соударения с математическим маятником меньше или равен π / 2 .
Кривая, изображенная на рис. 7.3 соответствует значениям отношений длин l / L и масс m / M маятника и стержня, при которых стержень принимает горизонтальноеположение, не соударяясь с потолком. Область значений отноше-Глава 7. Законы сохранения момента импульса и механической энергии241ний длин и масс, расположенная выше изображенной кривой, соответствует случаю соударения стержня с потолком.l/L10.8α max = π / 20.60.4α max < π / 20.2000.40.8 1.2m/M1.62Рис. 7.3На рис. 7.4 изображены зависимости максимального угла отклонения стержня после соударения от отношения длин маятника истержня α max (l / L ) при различных значениях отношения их масс(m / M ) .α max ,°90m/M = 210,5600,30,130000.20.40.60.81l/LРис. 7.4Как видим, при увеличении отношения длин маятника истержня максимальный угол отклонения стержня возрастает, при-МЕХАНИКА.
МЕТОДИКА РЕШЕНИЯ ЗАДАЧ242чем скорость возрастания увеличивается с увеличением отношениямасс маятника и стержня.На рис. 7.5 изображены зависимости максимального угла отклонения стержня после соударения от отношения масс маятника истержня α max (m / M ) при различных значениях отношения их длин(l / L) .α max ,°90l/L = 10,30,5600,2300,1000.40.8 1.2m/M1.62Рис. 7.5Как видим, при увеличении отношения масс маятника истержня максимальный угол отклонения стержня возрастает, причем скорость возрастания увеличивается с увеличением отношениядлин маятника и стержня.⎛⎞⎜⎟⎜⎟L⎟24⋅.Ответ: α max = arccos⎜1 −⎜ ⎛2 2 l ⎟⎞⎜ ⎜ 3 + M ⎛⎜ L ⎞⎟ ⎟⎟⎟⎜ ⎜⎟ml⎝ ⎠ ⎠⎝ ⎝⎠Задача 7.2На гладкой горизонтальной поверхности лежат небольшаяшайба массой m и тонкий однородный стержень длиной L и массойM. Шайбе сообщили скорость υ в горизонтальном направленииперпендикулярно стержню (см.
рис. 7.6). Шайба абсолютно упругосоударяется со стержнем в точке B на расстоянии l от его центра(точка O). Определить это расстояние в трех случаях:Глава 7. Законы сохранения момента импульса и механической энергии2431) сразу после соударения шайбаYостанавливается,A2) шайба передает стержню максимальный импульс,3) скорость конца стержня (точкаA на рис.
7.6) после соударения равнаOXнулю.υРешениеBI. Задачу решаем относительно лабораторной инерциальной системы отсчета. Поскольку соударение шайбы соРис. 7.6стержнем является абсолютно упругим, ана систему тел «стержень + шайба» не действуют внешние силывдоль горизонтальной поверхности, то выполняются все три законасохранения: закон сохранения импульса, закон сохранения моментаимпульса и закон сохранения механической энергии. Выберем систему координат так, как показано на рис.
7.6. Ось, относительнокоторой будем рассматривать вращение, удобно взять проходящейчерез центр стержня перпендикулярно горизонтальной поверхности и направленной из плоскости чертежа.II. Запишем три закона сохранения для выбранной системытел для интервала времени до соударения – сразу после соударения.Закон сохранения проекции импульса на ось X выбраннойсистемы координат:mυ = mυ ′ + Mυ ′′ .(7.34)Закон сохранения момента импульса относительно выбранной оси:mυl = mυ ′l + J 0ω .(7.35)Закон сохранения механической энергии:mυ 2 mυ ′2 Mυ ′′2 J 0ω 2=++.(7.36)2222Здесь υ ′ , υ ′′ – проекции скоростей шайбы и центра стержня на осьX сразу после соударения (проекции скоростей на ось Y в этот момент времени равны нулю), ω – угловая скорость вращения стержня в тот же момент времени.МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧ244Момент инерции стержня относительно оси, проходящей через его центр масс, равен (6.43):1(7.37)J 0 = ML 2 .12В соответствии с принципом суперпозиции движений (см.(1.26) в Главе 1) скорость υ A точки А стержня складывается изскорости центра масс и скорости вращательного движения этойточки вокруг оси, проходящей через центр масс:Lυ A = υ ′′ − ω .(7.38)2III.
Решение системы уравнений (7.34) – (7.38) относительноискомых величин имеет вид:(m − M ) J 0 + Mml 2υ′ = υ,(7.39)(m + M ) J 0 + Mml 2m2 MJ 0υ ′′ = υ ⋅,(7.40)M (m + M ) J 0 + Mml 2ml2 MJ 0ω =υ ⋅,(7.41)J 0 (m + M ) J 0 + Mml 2⎛ 12mMJ 0lL ⎞⎜ −⎟.(7.42)2 ⎜(m + M ) J 0 + Mml ⎝ M 2 J 0 ⎟⎠Расстояние l от точки соударения до начала координат, прикотором шайба остановится после удара, найдем из (7.39) приυ ′ = 0 с учетом (7.37):M −m.(7.43)l=L12mКак следует из (7.40), максимальное значение скорости центра стержня достигается при l = 0.
При этом условии шайба передаст стержню максимальный импульс.Значение l, при котором скорость точки A сразу после ударабудет равна нулю, находим из (7.42) с учетом (7.37):1l = L.(7.44)6После попадания шайбы в точку с такими координатамистержень сразу после удара будет совершать только вращательноеυA =Глава 7. Законы сохранения момента импульса и механической энергии245движение вокруг мгновенной оси вращения, проходящей черезточку A.Ответ:M −m1) шайба остановится сразу после удара, если l = L;12m2) шайба передаст стержню максимальный импульс, если онапопадет в центр масс стержня (l = 0);3) скорость точки A сразу после удара будет равна нулю при1условии l = L .6Задача 7.3Два одинаковых однородных вращающихся тела сферической формы массой m и радиусом r движутся навстречу друг другус одинаковыми по модулю скоростями υ 0 .
Угловые скорости вращения тел, ω1 и ω2 , составляют угол α и равны по модулюω1 = ω2 = ω0 . В результате лобового абсолютно неупругого соударения образуется одно тело той же плотности, форму которогоможно также считать сферической. Определить угловую скоростьω вращения образовавшегося тела и изменение кинетическойэнергии системы ΔE k .РешениеI.
Система двух тел в данной задаче предполагается изолированной. Следовательно, суммарный импульс системы и суммарныймомент импульса в лабораторной инерциальной системе отсчетасохраняются. Направим ось X лабораторной системы отсчета вдольлинии, соединяющей центры масс двух тел до соударения.II. Запишем закон сохранения проекции импульса рассматриваемой системы тел на ось X для интервала времени, включающегомомент их соударения:mυ0 − mυ0 = 2mυ ,(7.45)где υ – проекция на ось X скорости поступательного движенияобразовавшегося после соударения тела массой 2m.
Как видим,υ = 0 , следовательно, движение образовавшегося тела являетсячисто вращательным.246МЕХАНИКА. МЕТОДИКА РЕШЕНИЯ ЗАДАЧЗапишем закон сохранения момента импульса рассматриваемой системы тел относительно их общего центра масс на интервалевремени, включающем момент их соударения:L1 + L2 = L ,(7.46)где L1 и L2 – моменты импульса первого и второго тел до соударения, L – момент импульса образовавшегося тела после соударения. Поскольку скорости тел до соударения направлены вдоль линии, на которой находится центр масс системы, то в соответствии сформулой (6.27) Главы 6 момент импульса каждого из рассматриваемых тел относительно центра масс системы тел равен моментуимпульса тела относительно его центра масс.Моменты импульса каждого из сферически симметричныхтел относительно их собственных центров масс в соответствии сформулой (6.32) Главы 6 равны:L1 = J 0 ω1 ,(7.47)L2 = J 0ω2 ,(7.48)L = Jω ,(7.49)где J 0 и J – моменты инерции каждого из соударяющихся тел иобразовавшегося тела относительно их собственных осей вращения.
В соответствии с (6.45):2J 0 = mr 2 ,(7.50)52J = ( 2m ) R 2 .(7.51)5Радиус R образовавшегося тела находим из условия сохранения плотности (а, следовательно, и объема):442 πr 3 = πR 3 .(7.52)33Согласно условию задачи модули угловых скоростей вращения тел до их соударения равны:ω1 = ω2 = ω0 .(7.53)Изменение кинетической энергии рассматриваемой системытел ΔE k в результате их абсолютно неупругого соударения в соответствии с (7.6) равно:Глава 7.
Законы сохранения момента импульса и механической энергии247⎛ mυ0 2 J 0ω0 2 ⎞Jω 2⎟.− 2⎜⎜+(7.54)22 ⎟⎠⎝ 2III. Решая систему уравнений (7.46) – (7.53), получаем модуль угловой скорости вращения образовавшегося в результате соударения тела:3αα2Jω = 2ω0 0 cos = ω0cos .(7.55)222JПоскольку в соответствии с (7.46) – (7.49)Jω = 0 (ω1 + ω2 ) ,(7.56)Jа модули угловых скоростей вращения тел до их соударения равны(7.53), то угловая скорость вращения образовавшегося тела ω направлена по биссектрисе угла α, образованного векторами угловыхскоростей ω1 и ω2 .Искомое изменение кинетической энергии рассматриваемойсистемы тел в результате соударения получим, подставляя (7.55) в(7.54) с учетом (7.50) – (7.52):⎞⎛J2ΔE k = J 0ω02 ⎜ 0 (1 + cos α ) − 1⎟ − mυ0 =⎠⎝ JΔE k ==⎞2 2 2⎛ 3 2(1 + cos α ) − 1⎟⎟ − mυ 0 2 .mr ω0 ⎜⎜5⎠⎝ 4(7.57)Задача 7.4Две одинаковые гантели массой m в виде шариков, соединенных стержнем, скользят по гладкойDгоризонтальной поверхности навстречуυ2друг другу со скоростями υ1 и υ2 так, какCизображено на рис.
Задача 2.1.
Жесткий стержень длиной l=1 м и массой M=1 кг свободно висит на горизонтальной идеально гладкой оси вращения О, как показано на рис. 1.
Рисунок 1
Ось вращения перпендикулярна плоскости рисунка. Малый шарик массой m=0,1кг, летящий горизонтально со скоростью , движется в плоскости рисунка и ударяет в стержень. При этом взаимодействие шарика со стержнем может происходить в виде:
-
абсолютно упругого удара (АУУ);
-
неупругого удара (НУУ);
-
абсолютно неупругого удара (АНУУ).
Сразу после удара стержень вращается с угловой скоростью w0, а шарик приобретает скорость и продолжает двигаться в плоскости рисунка. Другие обозначения:
DE – потеря энергии при ударе;
– минимальная начальная скорость шарика, при которой стержень после удара совершает полный оборот;
wK – угловая скорость стержня при прохождении им крайней верхней точки;
jm – максимальный угол отклонения стержня от положения равновесия.
Другие исходные данные и искомые величины для каждого варианта задания представлены в таблице:
|
№ Вар |
|
|
2 |
2V0m |
– |
– |
– |
+ |
+ |
– |
+ |
+ |
Расчет следует начинать с определения характерной скорости шарика
Решение:
Определим момент инерции стержня относительно оси O, проходящей так, как показано на рисунке 1. Момент инерции стержня относительно оси, перпендикулярной ему и проходящей через центр масс стержня, равняется:
(1)
По теореме Штерна определим момент инерции стержня относительно оси O на рисунке 1. Расстояние от оси, проходящей через центр масс стержня, до оси O равняется , поэтому момент инерции относительно оси O равняется:
(2)
До соударения момент импульса системы равнялся , после абсолютно неупругого соударения момент импульса системы:
. Так как момент импульса системы сохраняется, то имеем:
(3)
(4)
Подставим в выражение (4) значение момента импульса стержня (2) и получим:
(5)
Откуда:
(6)
Выберем нулевой уровень потенциальной энергии проходящим через центр масс свободно висящего стержня, так как показано на рисунке 2:
Рисунок 2
В этом случае сразу после соударения потенциальная энергия стержня равняется нулю, то есть . Кинетическая энергия стержня сразу после соударения равняется:
(7)
Учитывая, что момент инерции стержня определяется выражением (2), а его угловая скорость сразу после соударения определяется выражением (6), получим:
![z21-19.jpg [image]](http://www.sanish1.narod.ru/mechanics/z21/z21-19.jpg)
В верхнем положении потенциальная энергия стержня равняется . Из рисунка 2 видно, что
, таким образом, получим:
(9)
Кинетическая энергия в верхнем положении равняется:
(10)
По закону сохранения полной механической энергии для стержня получим:
(11)
Учитывая (8), (9), (10), получим:
(12)
Минимальную начальную скорость шарика , при которой стержень совершает полный оборот, найдём из условия, что в верхнем положении кинетическая энергия стержня равняется нулю
. В этом случае выражение (12) имеет вид:
(13)
Отсюда равняется:
(14)
По условию задачи , поэтому начальная скорость шарика равняется:
(15)
Подставим в выражение (12) и получим:
![z21-33.jpg [image]](http://www.sanish1.narod.ru/mechanics/z21/z21-33.jpg)
(17)
Найдём потерю энергии при ударе. При соударении потенциальная энергия системы не изменяется. Кинетическая энергия системы до соударения равняется кинетической энергии шарика:
![z21-37.jpg [image]](http://www.sanish1.narod.ru/mechanics/z21/z21-37.jpg)
Угловая скорость стержня сразу после соударения определяется выражением (6) и в нашем случае равняется:
(19)
Сразу после соударения стержень и шарик движутся вместе, поэтому кинетическая энергия системы равняется:
![z21-39.jpg [image]](http://www.sanish1.narod.ru/mechanics/z21/z21-39.jpg)
Из закона сохранения энергии следует, что потеря энергии при ударе равняется:
![z21-40.jpg [image]](http://www.sanish1.narod.ru/mechanics/z21/z21-40.jpg)
Таким образом, мы получили:
Подставляя числовые значения, получим:
Ответ:
,
,
,
,
.
Сайт управляется системой uCoz

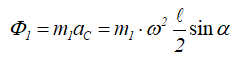
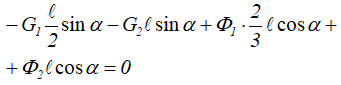
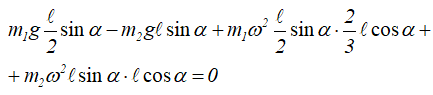
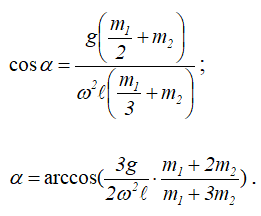
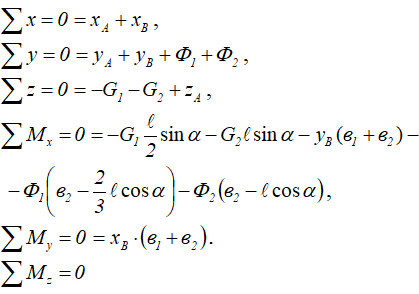

![z21-1.jpg [image]](http://www.sanish1.narod.ru/mechanics/z21/z21-1.jpg)
![z21-16.jpg [image]](http://www.sanish1.narod.ru/mechanics/z21/z21-16.jpg)
