Как найти максимум функции аналитически

Если целевая
функция является аналитической и
дифференцируема, то ее экстремальное
значение может быть найдено методами
дифференциального исчисления.

Если y
= F(х),
т. е. независимая переменная одна, то
рассматриваются первая производная
функции F(х)

и вторая производная

.

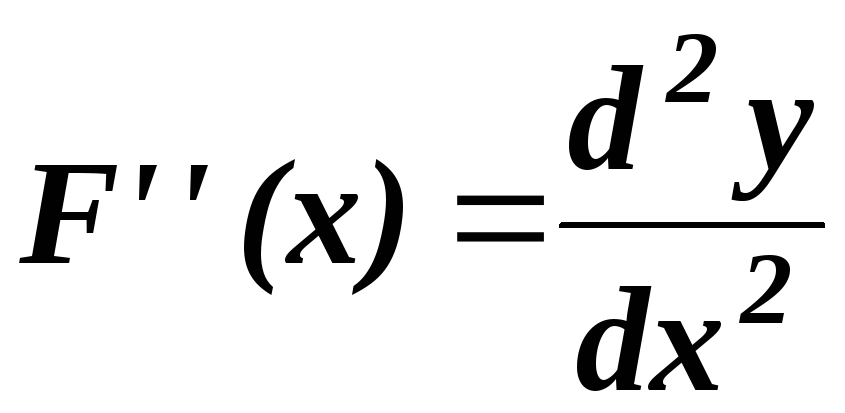
Экстремум находят,
приравнивая первую производную нулю и
определяя знак второй производной. При
этом, если
,
то имеется минимум, если
,
то имеется максимум целевой функции.

Рис.
9.2

Если F(x)
= 0, то
нужно провести дополнительный анализ.
Обычно берут высшие производные и, если
они не равны 0,
то нет ни максимума, ни минимума.

В качестве примера
можно рассмотреть кубическую параболу:

что
не равно 0.

Следовательно,
у кубической параболы нет ни максимума,
ни минимума.

Если переменных
несколько, т.е.
,
то рассматриваются частные производные:

.

Классический
метод поиска экстремума заключается в
решении системы нормальных уравнений:

Типичная задача
– расчет коэффициентов регрессионной
модели методом наименьших квадратов.
В ней критерий оптимальности – сумма
квадратов отклонений, а оптимизирующие
факторы – значения рассчитываемых
коэффициентов регрессии.

Чтобы убедится
в том, что полученные в результате
решения системы уравнений значения
факторов оптимальны, т.е. их совокупность
определяет оптимальное решение задачи,
необходимо выяснить следующие
обстоятельства:

• действительно
  ли решение определяет экстремум (а не
  седловую точку или точку перегиба);

• получается ли
  экстремум того знака (максимум или
  минимум), который нас интересует;

• если система
  имеет несколько решений, то какое из
  них отвечает глобальному оптимуму, а
  какое – локальным; глобальным будет
  тот, который выше или ниже всех остальных,
  а остальные – локальные.

• все ли ограничения
  соблюдаются в точке оптимума.

9.4 Численные методы поиска оптимума

Численные методы
применяют в случаях, когда:

• в точке экстремума
  отсутствуют производные целевой
  функции;

• целевая функция
  задана таким образом, что продифференцировать
  ее в общем виде не удается;

• для решения
  системы уравнений нужны настолько
  громоздкие вычисления, что численные
  методы оказываются проще и их применение
  эффективнее.

9.4.1 Оптимизация перебором

Если число
возможных вариантов значений факторов
целевой функции конечно, достаточно
рассчитать целевую функцию для всех
этих вариантов и выбрать её максимальное
(или минимальное) значение.

Например, можно
рассчитать параметр оптимизации для
случаев протекания процессов в аппаратах
всех стандартных размеров и выбрать
лучший вариант.

Перебор
целесообразно осуществлять на ЭВМ. При
этом все варианты могут быть записаны
в памяти машины, что имеет место при
создании систем автоматического
проектирования – САПР. Применение
перебора иногда позволяет найти и такие
варианты, до которых без ЭВМ дойти
практически было бы невозможно.

9.4.2 Сканирование

Метод сканирования
близок к методу перебора, но применяется
к непрерывным функциям.

Рассмотрим поиск
максимума или минимума функции от одного
фактора при пределах его изменения в
интервале от a
до b,
где a
и b
– ограничения.

Интервал [a,
b],
на котором требуется отыскать экстремум
целевой функции, – это интервал
неопределенности. Необходимо сузить
этот интервал в области оптимума.

Выбирают целое
число q
значений целевой функции, которое
придется рассчитывать. Определяют
ширину частного интервала
.
Концы каждого частного интервала на
отрезке [a,
b]
называются узлами. В каждом узле
рассчитывают значение F(x).
За максимум выбирают наибольшее значение,
за минимум – наименьшее значение.
Истинный экстремум может находиться
либо справа, либо слева от наилучшего
значения и таким образом интервал
неопределенности, равный
,
содержит оптимальное значение функции
y
= F(х).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #

  12.02.20162.61 Mб28.doc

• #
• #
• #
• #
• #
• #
• #
• #
• #

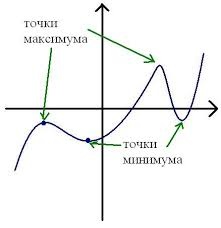
Как найти максимальное значение функции

Пусть дана некоторая функция, заданная аналитически, то есть выражением вида f(x). Требуется исследовать функцию и вычислить максимальное значение, которое она принимает на заданном отрезке [a, b].

Инструкция

Прежде всего нужно установить, определена ли заданная функция на всем отрезке [a, b] и если у нее есть точки разрыва, то какого рода эти разрывы. Например, функция f(x) = 1/x вовсе не имеет ни максимального, ни минимального значения на отрезке [-1, 1], поскольку в точке x = 0 стремится к плюс бесконечности справа и к минус бесконечности слева.

Если заданная функция — линейная, то есть задана уравнением вида y = kx + b, где k ≠ 0, то она на всей своей области определения монотонно возрастает, если k > 0; и монотонно убывает, если k 0; и f(a), если k

Следующий шаг — исследование функции на экстремумы. Даже если установлено, что f(a) > f(b) (или наоборот), функция может достигать больших значений в точке максимума.

Чтобы найти точку максимума, необходимо прибегнуть к помощи производной. Известно, что если в точке x0 функция f(x) имеет экстремум (то есть максимум, минимум или стационарную точку), то ее производная f′(x) в этой точке обращается в ноль: f′(x0) = 0.

Для определения, какой из трех видов экстремума находится в обнаруженной точке, нужно исследовать поведение производной в ее окрестностях. Если она меняет знак с плюса на минус, то есть монотонно убывает, то в найденной точке исходная функция имеет максимум. Если производная меняет знак с минуса на плюс, то есть монотонно возрастает, то в найденной точке исходная функция имеет минимум. Если же, наконец, производная не меняет знака, то x0 — это стационарная точка для исходной функции.

В тех случаях, когда вычислить знаки производной в окрестностях найденной точки сложно, можно воспользоваться второй производной f′′(x) и определить знак этой функции в точке x0:

– если f′′(x0) > 0, то найдена точка минимума;
– если f′′(x0)

Для окончательного решения задачи необходимо выбрать максимальное из значений функции f(x) на концах отрезка и во всех найденных точках максимума.

Следующий шаг — исследование функции на экстремумы. Даже если установлено, что f(a) > f(b) (или наоборот), функция может достигать больших значений в точке максимума.

Чтобы найти точку максимума, необходимо прибегнуть к помощи производной. Известно, что если в точке x0 функция f(x) имеет экстремум (то есть максимум, минимум или стационарную точку), то ее производная f′(x) в этой точке обращается в ноль: f′(x0) = 0.

Для определения, какой из трех видов экстремума находится в обнаруженной точке, нужно исследовать поведение производной в ее окрестностях. Если она меняет знак с плюса на минус, то есть монотонно убывает, то в найденной точке исходная функция имеет максимум. Если производная меняет знак с минуса на плюс, то есть монотонно возрастает, то в найденной точке исходная функция имеет минимум. Если же, наконец, производная не меняет знака, то x0 — это стационарная точка для исходной функции.

В тех случаях, когда вычислить знаки производной в окрестностях найденной точки сложно, можно воспользоваться второй производной f′′(x) и определить знак этой функции в точке x0:

– если f′′(x0) > 0, то найдена точка минимума;
– если f′′(x0)

Для окончательного решения задачи необходимо выбрать максимальное из значений функции f(x) на концах отрезка и во всех найденных точках максимума.

Для окончательного решения задачи необходимо выбрать максимальное из значений функции f(x) на концах отрезка и во всех найденных точках максимума.

Источники:

• найти максимальную скорость точки
• Найти минимальное значение функции

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

План урока:

Исследование функций на монотонность

Экстремумы функции

Выпуклость и вогнутость функций

Исследование функций и построение их графиков

Исследование функций на монотонность

Говоря о смысле производной, мы замечали, что у возрастающих функций она принимает положительные значения, а у убывающих – отрицательные. Убедиться в этом можно с помощью графиков. Действительно, если провести касательную к возрастающей ф-кции, то она образует с осью Ох острый угол, а потому тангенс этого угла (а он как раз равен произ-ной) окажется положительным числом:

Если же ф-кция убывает, то касательная образует с осью Ох тупой угол, чей тангенс будет отрицательным:

Рассмотрим более сложный случай, когда ф-кция на каких-то промежутках убывает, а на каких-то возрастает. В качестве примера приведем зависимость у = х². Она является убывающей на промежутке (– ∞; 0] и возрастающей на промежутке [0; + ∞). Можно заметить, что любая касательная, проведенная на первом из этих промежутков, будет образовывать тупой угол с Ох. И наоборот, любая касательная на втором промежутке имеет острый угол:

Это означает, что произ-ная ф-кции на первом промежутке должна быть отрицательной, а на втором – положительной (сразу отметим, что граничная точка х = 0 стоит особняком, так как входит в оба промежутка). Попробуем найти произ-ную аналитически. Мы рассматриваем ф-кцию у = х², её произ-ная равна

Действительно, произ-ная у′ = 2х принимает отрицательные значения при х∈ (– ∞;0) и оказывается положительной при х∈(0; + ∞). Заметим, что в граничной точке произ-ная равна нулю.

Это наблюдение подсказывает нам, что по знаку произ-ной можно определить, возрастает или убывает ф-кция. Однако сначала надо разобраться с тем случаем, когда произ-ная оказывается равной нулю. Рассмотрим ф-кцию у = х³. Очевидно, что она возрастает на всей числовой прямой. Значит ли это, что её произ-ная на этой прямой строго положительна? Нет, не значит. Запишем у′:

Произ-ная положительна во всех точках, кроме х = 0. При х = 0 у′ также оказывается равной нулю. Однако мы можем сказать, что у′ неотрицательна на всей числовой прямой.

Можно привести пример ф-кции

ее произ-ная равна

Сама ф-кция убывает на всей числовой прямой, а её произ-ная неположительна на ней.

Рассмотрим особый случай, когда у ф-кции произ-ная одновременно и неположительна, и неотрицательна на отрезке. Как ни сложно догадаться, это означает, что производная равна нулю. Мы помним, что нулю равна произ-ная константы:

В качестве примера приведем ф-кцию у = 2. Её произ-ная на всей числовой прямой равна нулю:

При этом ф-кция и не убывает, и не возрастает на числовой прямой:

Рассматривая все эти примеры, можно сделать вывод, что для возрастания ф-кции на промежутке достаточно, чтобы её произ-ная принимала на этом отрезке только положительные отрезки:

Аналогично можно сформулировать и достаточный признак убывания ф-кции:

Сформулированные признаки не охватывают тех ситуаций, когда произ-ная в отдельных точках промежутка обращается в ноль. Если произ-ная равна нулю на всём промежутке, то ф-кция на нем остается неизменной (как в случае с функцией у = 2). Если же производная обращается в ноль только в отдельных точках (случай у = х³ и у = х²), то эти точки оказываются граничными для промежутков возрастания и промежутков убывания функции. В этих случаях эти граничные точки добавляют в соответствующие промежутки.

Задание. Докажите, что функция

возрастает при любом значении аргумента.

Решение. Найдем произ-ную у′:

Найдем, при каких значениях х произ-ная у′ оказывается положительной. Для этого запишем неравенство:

Множитель (5х² + 6) при любом х положителен, а потому мы можем поделить обе части неравенства на него и преобразовать его к виду

Его решениями являются промежутки (– ∞; 0) и (0; + ∞), а при х = 0 произ-ная оказывается равной нулю, то есть это граничная точка. Значит, промежутками возрастания функции являются (– ∞; 0] и [0; + ∞). Обратите внимание, что мы добавили в каждый из промежутков граничную точку х = 0. Но объединением этих промежутков является вся числовая прямая:

Получается, что ф-кция возрастает при любом х.

Теперь попытаемся найти промежутки возрастания и убывания функции

Для их нахождения определим, где произ-ная положительна, а где отрицательна. Для этого сначала найдем произ-ную:

Решим неравенство у′ > 0, при этом мы используем метод интервалов:

Отмечаем нули на координатной прямой и расставляем знаки промежутков:

Напомним, что для определения знаков промежутков можно просто выбрать на каждом из них одну точку и подставить её в неравенство. Например, на интервале х∈(– ∞; – 1) возьмем число – 2:

Итак, произ-ная положительна на промежутках (– ∞; – 1) и (0; + ∞). При х = 0 и х = 1 произ-ная обращается в ноль – это граничные точки, которые надо добавить в промежутки возрастания. То есть ф-кция возрастает на промежутках (– ∞; – 1] и [0; + ∞).

Рассматривая аналогичное неравенство у′ < 0, получаем, что произ-ная отрицательна при х∈(– 1; 0). Тогда промежутком убывания ф-кции является [– 1; 0].

Для наглядности построим график рассматриваемой нами ф-кции:

Проведенное нами действие (поиск промежутков возрастания и убывания ф-кции) называется исследованием функции на монотонность. Для его проведения необходимо вычислить производную ф-кцию у′, а потом найти, на каких промежутках она положительна или отрицательна. Если в граничных точках полученных промежутков произво-дная обращается в ноль, то эти точки следует включить в промежутки.

Экстремумы функции

Еще раз посмотрим на график рассмотренной нами ф-кции

На нем есть две особые точки: (– 1; 0) и (0; – 1). Они являются границами для промежутков возрастания и убывания. При этом значение произ-ной в этих точках оказалось равным нулю. Если мы проведем касательные к графику в этих точках, то окажется, что они являются горизонтальными линиями, то есть их угол наклона равен нулю:

Действительно, если произ-ная в точке равна нулю, то тангенс угла наклона должен быть также равен нулю. А это значит, что и сам угол равен нулю, ведь tg 0 = 0. Геометрически это означает, что касательная будет выглядеть как горизонтальная линия, которая либо параллельна оси Ох, либо совпадает с ней.

Ещё одна особенность точек (– 1; 0) и (0; – 1). Первая из них в некоторой, достаточно малой локальной области является точкой максимума функции. Действительно, если взять промежуток [– 1,5; – 0,5], то на нем именно в точке х = –1 ф-кция принимает наибольшее значение:

Аналогичную окрестность можно указать и для точки х = 0, только на ней точка (0; – 1) окажется точкой минимума функции, а не максимума:

Ни для какой другой точки на графике такую окрестность указать не удастся. Дадим более точное определение таким понятиям, как точка минимума и точка максимума функции:

Ещё раз заметим, что в таких точках ф-кция достигает наибольшего или наименьшего значения только в определенной локальной области. Поэтому часто их называют локальными максимумами или минимумами. Пусть ф-кция задана следующим графиком:

На графике можно отметить 5 минимумов функции и 5 максимумов, причем только один максимум и минимум будут соответствовать наибольшему или наименьшему значению на всей области определения (их ещё называют глобальными максимумами и минимумами):

Грубо говоря, точки максимума соответствуют вершинам графика, а точки минимума – впадинам графика.

Для обозначения этих точек используют специальный термин – точки экстремума функции.

Довольно очевидно, что точки экстремума находятся на границе промежутков возрастания и убывания ф-кции, то есть в тех самых граничных точках. Напомним, что в этих точках произ-ная равна нулю. Однако возможен ещё один случай появления экстремума. Он связан с так называемыми негладкими ф-кциями, пример одной из которых приведен на рисунке:

На графике явно видно два экстремума функции. Однако в этих точках ф-кция меняет свое поведение резко, а не плавно. Из-за этого график кажется «зазубренным». Обратите внимание, что построить единственную касательную к графику в экстремумах не получается:

С точки зрения математического анализа это означает, что произ-ная в таких точках не существует. Заметим, что все элементарные ф-кции, а также сложные ф-кции, получаемые из нескольких элементарных, являются гладкими. Поэтому на практике в школьном курсе такие случаи почти не встречаются.

Итак, можно сформулировать признак существования экстремума:

Задание. Докажите, что у функции вида

где a, b, c, d – постоянные числа, есть не более двух экстремумов.

Решение. Чтобы найти экстремумы функции, сначала просто продифференцируем её:

Заметим, что производная является квадратичной функцией

Эта ф-кция определена при любом значении х. Это значит, что не существует таких экстремумов, в которых произ-ная не существует. Если приравнять произ-ную к нулю, то получим квадратное уравнение:

Напомним, что квадратное уравнение может иметь не более 2 различных корней. То есть у ф-кции есть не более 2 точек, в которых произ-ная обращается в ноль. Следовательно, и экстремумов у ф-кции не более двух.

Точки, в которых произ-ная обращается в ноль или не существует, называют критическими точками функции.

Заметим, что не каждая критическая точка обязательно оказывается экстремумом. Можно снова привести пример ф-кции у = х³. Она возрастает на всей области числовой прямой, то есть не имеет экстремумов. Однако ее произ-ная имеет вид у′ = 3х², и она обращается в ноль при х = 0. В связи с этим встает вопрос – есть ли какой-то метод, позволяющий достоверно определить наличие экстремума у ф-кции? Оказывается, есть. Надо лишь проанализировать поведение производной вблизи критической точки. Если произ-ная в точке меняет знак, то она является экстремумом, а если не меняет – то не является.

Более того, можно определить, является ли экстремум точкой минимума или точкой максимума. Если произ-ная меняет знак с плюса на минус, то это точка максимума, а если с минуса на плюс – то это точка минимума.

Для примера рассмотрим ф-кцию

Попытаемся найти ее экстремумы. Для этого вычислим производную:

Найдем нули произ-ной:

Теперь отметим на координатной прямой нули ф-кции. Они разобьют числовую прямую на три промежутка. Расставим знаки производной на этих промежутках:

Знаки на промежутках можно определить, просто подставив в произ-ную одно из чисел из промежутка:

Получается, что в точке х = 0 произ-ная меняет знак с «+» на (–), а в точке х = 2 знак произ-ной не меняется. Это значит, что точка х = 0 является точкой минимума, а х = 2 – это вообще не экстремум ф-кции:

В общем случае для определения экстремумов ф-кции можно руководствоваться следующей схемой:

До этого мы рассматривали случаи, когда ф-кция была определена при любом значении аргумента. Теперь изучим ф-кцию

Ее особенностью является то, что она не определена при х = 0, так как при таком значении аргумента получается деление на ноль. Вычислим у′:

Теперь найдем нули произ-ной:

Выражение х² + 4 при любом х не равно нулю, а потому на него можно поделить уравнение:

Теперь на числовой прямой мы должны отметить две найденные критические точки. Но также на ней следует отметить число х = 0, так как в этой точке ф-кция не определена:

Обратите внимание, что точка х = 0 НЕ является экстремумом, хотя кажется, что в ней ф-кция меняет свой знак. Дело в том, ф-кция не существует при таком значении аргумента. Это значит, что х = 0 – это асимптота графика. График ф-кции будет выглядеть примерно так:

Выпуклость и вогнутость функций

Нарисуем две немного отличающиеся друг от друга возрастающие ф-кции:

Видно, что эти графики будто выгнуты в разные стороны. Оказывается, в математике есть специальное свойство ф-кций, которое указывает на направление, в котором выгнуты их графики. Левая ф-кция является вогнутой функцией, а правая – выпуклой функцией.

Определить, выпукла или вогнута ф-кция, очень просто. Достаточно провести к графику касательную. Если она проходит выше графика, то это указывает на вогнутость функции, а если ниже, то она выпукла:

Естественно, встречаются ф-кции, которые на одном промежутке выпуклые, а на другом – вогнутые. Классическим примером является кубическая парабола у = х³. На промежутке (– ∞; 0] она вогнутая, а на промежутке [0; + ∞) она становится выпуклой. При этом в точке х = 0 она меняет свой характер. Такая точка называется точкой перегиба функции:

Ранее мы уже заметили, что точка х = 0 для ф-кции у = х³ – этой пример критической точки, которая не является экстремумом. Действительно, произ-ная ф-кции у = х³ имеет вид

и она обращается в ноль при х = 0, однако в этой точке ф-кция возрастает. Это подсказывает нам, что критические точки, в которых ф-кция НЕ меняет своего знака, являются точками перегиба. И это действительно так.

Заметим, однако, что в общем случае точка перегиба может и вовсе не являться критической точкой ф-кции. В рамках школьного курса мы не будем детально изучать выпуклость функций и точки перегиба. Отметим лишь, что для их поиска необходимо вычислять уже не только первую, но и вторую произ-ную функции.

Исследование функций и построение их графиков

Ранее мы строили графики ф-кций в основном «по точкам». То есть мы просто вычисляли значение ф-кции при различных значениях х, отмечали получившиеся точки на координатной плоскости, а потом соединяли их плавной кривой. Однако при этом можно упустить некоторые важные особенности ф-кций – наличие у них минимумов и максимумов, точки их пересечения с осями координат и т.п. Поэтому в математике используют особый алгоритм для построения графиков ф-кции, который называют «исследованием функции».

Последовательность алгоритма следующая:

1. Находят область определения ф-кции. Здесь нужно учесть такие простые правила, согласно которым нельзя делить на ноль, под знаком квадратного корня не может стоять отрицательное число и т.п.
2. Выясняют, является ли ф-кция четной или нечетной, периодической или непериодической.
3. Находят производную ф-кции.
4. Приравнивая произ-ную к нулю, находят критические точки ф-кции, промежутки ее возрастания и убывания (то есть проводят исследование на монотонность).
5. Находят точку пересечения графика с осью Оу, для чего подставляют в ф-кцию х = 0. Конечно, это действие совершается только в том случае, если точка х = 0 входит в область определения ф-кции.
6. Находят точку пересечения графика с горизонтальной осью Ох. Для этого надо составить уравнение у(х) = 0 и решить его. Возможна ситуация, когда решить уравнение точно не получается, тогда этот этап можно пропустить.
7. Находят промежутки знакопостоянства ф-кции.
8. Изучают поведение ф-кции вблизи ее особых точек. Обычно это подразумевает поиск пределов ф-кции на бесконечности или в точках, где она не определена.
9. Определяют область значений ф-кции.
10. С учетом всех особенностей ф-кции строят ее график.

Заметим, что у ф-кции можно также найти точки перегиба ф-кции, исследовать ее на выпуклость и вогнутость, однако в рамках программы 11 класса это не делается.

Сразу скажем, что исследование ф-кции – это трудоемкая задача. Она не очень сложная, но требует больших затрат времени и бумаги.

Для начала рассмотрим относительно простой пример ф-кции

Область ее определения – это вся числовая прямая. Ф-кция не является ни четной, ни нечетной. Доказать это на примере конкретной точки. Возьмем х = 1:

Однако у нас это условие явно не выполняется, ведь 0 ≠ 4. Если бы ф-кция была нечетной, то выполнялось бы условие

Оно также не выполняется, так как 0 ≠ – 4.

Вычислим произ-ную ф-кции:

Произ-ная также определена на всей числовой прямой. Для поиска критических точек приравняем ее к нулю:

Получили две критические точки. Отметим их на прямой и расставим знаки:

Итак, мы смогли найти точку максимума функции, равно как и ее точку минимума.

Сразу же вычислим значение ф-кции в ее экстремумах:

Для расстановки знаков возьмем по одному значению из каждого промежутка. Например, можно взять числа (– 2), 0 и 2:

Далее находим, где прямая пересекается с осью Оу, для чего подставляем в ф-кцию значение х = 0:

Получили точку (0; 2). Для нахождения точек пересечения графика с горизонтальной остью Ох надо приравнять всю ф-кцию к нулю:

Это кубическое уравнение. Решить его можно методом подбора корней и последующим делением многочлена на многочлен. Не останавливаясь на подробностях решения, укажем, что его корнями являются числа (– 2) и 1, а других корней. Убедиться в этом можно, просто подставив в уравнение эти числа.

Следующий шаг – определение промежутков знакопостоянства. Для этого надо решить неравенство у(х) > 0:

Это неравенство решается методом интервалов. Он сводится к тому, что находятся нули левой части, которые мы уже нашли – это числа (– 2) и 1. Далее они отмечаются на прямой, после чего на образовавшихся промежутках проставляются знаки:

Знаки определяем, выбирая по одной точке из каждого промежутка:

Достаточно очевидно, что при х→∞ сама ф-кция также стремится к бесконечности. Если же х→ – ∞, то и у→ – ∞.

Представим найденную нами информацию в виде таблицы. В верхней строке будем записывать промежутки и отдельные точки, а ниже – особенности ф-кции на этих промежутках (возрастает ф-кция или убывает, положительна она или отрицательна и т.п.):

В итоге график ф-кции будет иметь следующий вид:

Теперь исследуем более сложную ф-кцию

Начнем с области определения. Знаменатель дроби не может равняться нулю, а потому

Итак, аргумент ф-кции может принимать любые значение, кроме 1 и (– 1). Поэтому её область определения (она обычно обозначается как D (x)) можно записать так:

Далее проверяем ф-кцию на четность или нечетность. Напомним, что для этого надо подставить в нее вместо аргумента х аргумент (– х):

Мы получили у(х). Это означает, что ф-кция четная, а ее график симметричен относительно оси Оу.

Следующий шаг – находим произ-ную ф-кции:

Заметим, что область определения произ-ной полностью совпадает с областью определения самой ф-кции. Поэтому у ф-кции нет таких критических точек, в которых произ-ная не существует.

Теперь произ-ную можно приравнять к нулю:

Мы нашли всего одну критическую точку. Отметив ее на координатной прямой, можно выяснить, что она является точкой максимума. При этом стоит также отметить точки х = 1 и х = – 1, в которых ф-кция не определена (их ещё называют точками разрывов):

Для определения знаков произ-ной достаточно вычислить её значение в одной точке на каждом получившемся промежутке. Возьмем значения (– 2), (– 0,5), 0,5 и 2

Найдем точку пересечения графика с осью Оу, для чего подставим в ф-кцию значение х = 0:

Получили точку (0; – 1).

Далее находим точку пересечения графика с осью Ох. Для этого подставим в ф-кцию значение у = 0 и решим получившееся уравнение:

Числитель дроби в правой части при любом значении х положителен, то есть не равен нулю. Это значит, что уравнение не имеет решения. Отсюда вывод – график НЕ пересекается с осью Ох.

Следующий шаг – это определение промежутков знакопостоянства функции. Чтобы найти, при каких значениях аргумента ф-кция положительная, составим неравенство:

Это дробно-рациональное неравенство. Для его решения надо отметить на координатной прямой те значения х, при которых либо знаменатель, либо числитель обращается в ноль. Числитель при любом аргументе положителен, а нулями знаменателя являются точки х = – 1 и х = 1:

Знаки на промежутках определяем, подставляя точки из промежутков в ф-кцию:

Далее следует исследовать поведение ф-кции вблизи при х →∞ и х→ –∞. Для этого преобразуем ф-кцию, выделив целую часть:

При х→∞ число (х² – 1) также стремится к бесконечности, а дробь

будет стремиться к единице. Аналогично можно убедиться, что при х→ – ∞ ф-кция также стремится к единице.

Все полученные данные можно удобно представить в табличном виде:

На основании этих результатов строим график:

Из рисунка видно, что область значений ф-кции имеет вид

Итак, мы узнали, что с помощью производной можно определять промежутки, на которых функция возрастает и убывает, а также находить ее минимумы и максимумы. Эти навыки помогают при решении многих практических задач, когда требуется найти такое значение некоторых параметров, при которых какая-то величина принимает максимальное или минимальное значение. Например, продавцы товара могут назначать такую цену на свою продукцию, которая принесет им максимальный доход (просто назначить как можно большую цену нельзя, так как слишком дорогой товар никто не купит). Более подробно такие задачи мы рассмотрим подобные задачи в следующих уроках.

Максимумы, минимумы и экстремумы функций

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Источник

Найдите точку максимума функции

77419.Найдите точку максимума функции у=х 3 –48х+17

Найдём производную заданной функции:

Найдем нули производной:

Определим знаки производной функции подставляя значения из интервалов в полученную производную, и изобразим на рисунке поведение функции:

Получили, что в точке –4 производная меняет свой знак в положительного на отрицательный. Таким образом, точка х=–4 это искомая точка максимума.

77423. Найдите точку максимума функции у=х 3 –3х 2 +2

Найдём производную заданной функции:

Приравняем производную к нулю и решим уравнение:

Определим знаки производной функции и изобразим на рисунке интервалы возрастания и убывания функции подставляя значения из каждого интервала в выражение производной:

В точке х=0 производная меняет знак с положительного на отрицательный, значит это есть точка максимума.

77427. Найдите точку максимума функции у=х 3 +2х 2 +х+3

Найдём производную заданной функции:

При равняем производную к нулю и решим уравнение:

Определим знаки производной функции и изобразим на рисунке интервалы возрастания и убывания функции подставляя значения из каждого интервала в выражение производной:

В точке х=–1 производная меняет знак с положительного на отрицательный, значит это есть искомая точка максимума.

77431. Найдите точку максимума функции у=х 3 –5х 2 +7х–5

Найдём производную функции:

Найдем нули производной:

Решая квадратное уравнение получим:

*Это точки возможного максимума (минимума) функции.

Построим числовую ось, отметим нули производной. Определим знаки производной, подставляя произвольное значение из каждого интервала в выражение производной функции и схематично изобразим возрастание и убывание на интервалах:

3∙0 2 – 10∙0 + 7 = 7 > 0

3∙2 2 – 10∙2 + 7 = – 1 2 – 10∙3 + 7 = 4 > 0

В точке х = 1 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

77435. Найдите точку максимума функции у=7+12х–х 3

Найдём производную функции:

Найдем нули производной:

Решая квадратное уравнение получим:

*Это точки возможного максимума (минимума) функции.

Построим числовую ось, отметим нули производной. Определим знаки производной, подставляя произвольное значение из каждого интервала в выражение производной функции и схематично изобразим возрастание и убывание на интервалах:

12 – 3∙(–3) 2 = –15 2 = 12 > 0

12 – 3∙3 2 = –15

В точке х = 2 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

*Для этой же функции точкой минимума является точка х = – 2.

77439. Найдите точку максимума функции у=9х 2 –х 3

Найдём производную функции:

Найдем нули производной:

Решая уравнение получим:

*Это точки возможного максимума (минимума) функции.

Построим числовую ось, отметим нули производной. Определим знаки производной, подставляя произвольное значение из каждого интервала в выражение производной функции и схематично изобразим возрастание и убывание на интервалах:

18 (–1) –3 (–1) 2 = –21 2 = 15 > 0

18∙7 –3∙7 2 = –1

В точке х=6 производная меняет свой знак с положительного на отрицательный, значит это есть искомая точка максимума.

*Для этой же функции точкой минимума является точка х = 0.

Источник

Как найти точки минимума и максимума функции

Минимум и максимум функции

Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом:

Точка минимума, минимум функции

Минимум функции — значение функции в точке минимума (x_0)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.

Точка максимума, максимум функции

Максимум функции — значение функции в точке максимума (x_0)

Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.

Точки максимума и минимума на графике:

Исследование функций на экстремумы

Теорема. Если функция f(x) имеет экстремум в точке (x=x_0,) то в ней производная либо равна 0, либо не существует.

Алгоритм нахождения экстремумов с помощью производной:

Найти область определения функции — D(y).

Определить производную — f ‘(x).

Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).

Относительно каждой критической точки определить, является ли она точкой максимума, минимума (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).

Вычислить значения функции в точках экстремума.

Примеры задач

Задача 1

Исследовать на экстремумы функцию (f(x)=x^3-3x^2.)

Решение задачи по алгоритму:

3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:

5) Найдем значение экстремумов функции.

Задача 2

Задача 3

Докажите, что функция (f(x)=x^5+2x^3-4) возрастает на всех числовой прямой.

Источник

Этот раздел содержит задачи ЕГЭ по математике на темы, связанные с исследованием функций и их производных. В частности, речь идёт о поиске максимальных и минимальных значений функций, заданных аналитически, то есть формулой.

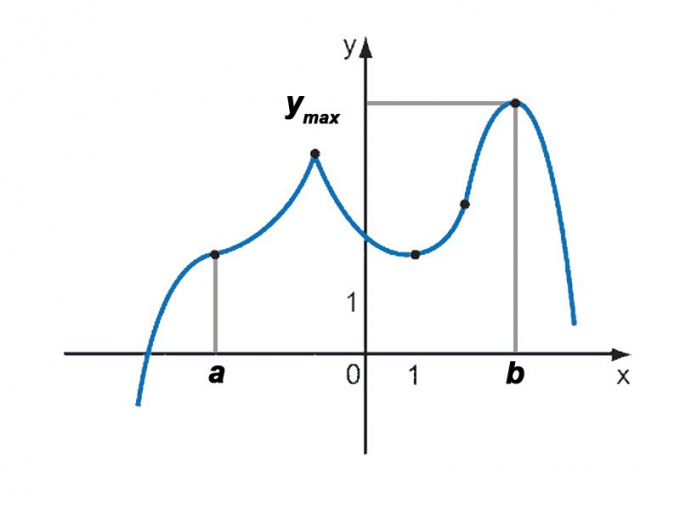
Точкой максимума ( минимума ) функции y = f(x) называется значение аргумента x = a такое, что существует окрестность точки a, в которой f(x) ( f(x) > f(a) ) для x ≠ a.

Максимумом ( минимумом ) функции называется её значение в точке экстремума, т.е. величина f(a).

Что касается наибольших и наименьших значений функции на заданном отрезке, то для непрерывной функции они могут достигаться как внутри отрезка, так и на его концах. Графические иллюстрации к этой теме можно посмотреть здесь.
Если наибольшего (наименьшего) значения функция достигает во внутренней точке отрезка, то эта точка совпадает с точкой соответствующего экстремума. Для ответа на такой вопрос задания следует сравнить значения функции в точках экстремума с её значениями на концах отрезка. (На практике для решения этой задачи не обязательно определять вид экстремума, достаточно вычислить значения функции в критических точках и на концах отрезка и сравнить их между собой.)

В 2022 году это задание имеет номер 11.

Задачи на нахождение точек экстремума функции.

Алгоритм нахождения точек экстремума.

1) Найти область определения функции.
2) Найти её производную f ‘(x).
3) Найти точки, в которых f ‘(x) не существует.
4) Найти точки в которых f ‘(x) = 0.
5) Отметить на числовой прямой область определения функции и все точки, выявленные в п.3 и п.4. Получатся промежутки области определения, на которых производная сохраняет постоянный знак.
6) Определить знак f ‘(x) для каждого промежутка. (Чаще всего это делается подстановкой «удобного» значения x из этого промежутка в полученную в п.2 формулу для производной.)
7) Определить по знакам производной участки возрастания и убывания функции и сделать выводы о наличии или отсутствии экстремума и его характере в каждой из критических точек.

Найдите точку максимума функции y = (x + 7)·e 7 − x .

1) Функция представляет собой произведение линейной и показательной функций, которые определены на всей действительной оси.
D(f) = (−∞;∞).

3) Выражение −e 7 − x ·(x + 6) определено во всех точках действительной оси.
Точек, где y’ не существует, нет.

5) Изображаем «бесконечную» числовую ось, совпадающую в нашем случае с областью определения функции. Отмечаем на ней единственную найденную критическую точку x = −6.

6) Определяем знаки производной на получившихся двух участках оси.
При x 7 − x ·(x + 6) = −e 7 + 10 ·(−10 + 6) = −e 17 ·(−4) = 4e 17 ≈ 4·2,7 17 > 0.
При x > −6, например при x = 7, имеем
y’ = −e 7 − x ·(x + 6) = −e 7 − 7 ·(7 + 6) = −e 0 ·13 = −1·13 = −13 0 и знаком «−», где y’ Внимание: Для усиления обучающего эффекта ответы и решения загружаются отдельно для каждой задачи последовательным нажатием кнопок на желтом фоне. (Когда задач много, кнопки могут появиться с задержкой. Если кнопок не видно совсем, проверьте, разрешен ли в вашем браузере JavaScript.)

Найдите точку минимума функции y = 4x − ln(x + 11) + 12.

По определению логарифма x + 11 > 0, следовательно D(f) = (−11;+∞).

В производной x ≠ −11, но это значение не входит в область определения функции, поэтому критической точкой не является.

Следовательно, x = −10,75 точка минимума функции.

По определению арифметического корня 16 − 4x − x 2 ≥ 0. Полностью решать это неравенство пока не будем. Заметим только, что это квадратное неравенство и ветви соответствующей параболы направлены вниз. Можно сделать вывод, что неотрицательные значения квадратный трёхчлен будет иметь на участке между его корнями. D(f) = [x₁ ; x₂].

y’ не существует в точках, где знаменатель дроби равен нулю, т.е.
при 16 − 4x − x 2 = 0. Эти точки мы уже обозначили x₁ и x₂. Они являются краями области определения функции.

Выбираем значения x для проверки знаков производной на получившихся двух участках. Пусть это будут −3 и 0. Убедимся, что не промахнулись мимо области определения функции, т.е. в том, что для этих точек выполняется неравенство для подкоренного выражения. (Если бы мы сразу дорешали неравенство до конца, то этого делать бы не пришлось. Точки выбирались бы по рисунку.)
16 − 4x − x 2 ≥ 0.
16 − 4·(−3) − (−3) 2 = 19 ≥ 0.
16 − 4·0 − 0 2 = 16 ≥ 0.
Определяем знаки производной в этих точках

y’(−3) = − −3 + 2 _____ √19 __ = 1 ___ √19 __ > 0.

y’(0) = − 0 + 2 ____ √16 __ = − 2 _ 4 = −0,5

Следовательно, x = −2 точка максимума функции.

Замечание: Для кого-то может оказаться легче сразу решить квадратное уравнение и рисовать итоговый чертёж явно. Делайте так.
В данном случае x₁ = −2 − 2 √5 _ ≈ −6,5; x₂ = −2 + 2 √5 _ ≈ 2,5.

Найдите точку минимума функции y = (0,5 − x)cosx + sinx, принадлежащую промежутку (0, π/2).

Точек, где y’ не существует, нет.

Замечание: sin0,45 и sin0,55 положительны, т.к. исследуемый интервал соответствует первой четверти тригонометрического круга.

Задачи на нахождение экстремумов функции.

1) Находим точки экстремумов функции и определяем их характер так же, как в задачах выше.
2) Определяем значения функции в точках максимума или минимума в соответствии с вопросом задачи.
3) Если точек максимума (минимума) на области определения функции несколько, то максимумы (минимумы) называются локальными, а самый большой (самый маленький) называется глобальным максимумом (минимумом) или наибольшим (наименьшим) значением функции. Ещё раз читаем вопрос задачи и выбираем нужный.

Первая часть решения полностью совпадает с решением задачи 3.

y’ не существует в точках −5 и 1.

y’(−3) = 1 __ √8 _ > 0; y’(0) = − 2 __ √5 _ √5 − 4x − x 2 __________
y(−2) = √5 − 4·(−2) − (−2) 2 _______________ = √9 _ = 3.
По стрелкам на рисунке видно, что максимум на всей области определения функции единственный, поэтому полученное значение y(−2) = 3 и будет наибольшим значением функции.

Найдите наименьшее значение функции y = log₃(x 2 − 6x + 10) + 2.

По определению логарифма x 2 − 6x + 10 > 0. Дискриминант этого квадратного трёхчлена D = 36 − 40 коэффициент при x 2 равен 1 > 0, следовательно все его значения положительны. Область определения функции D(f) = (−∞;+∞).

Знаменатель этой дроби > 0 (ln3 > 1, т.к. 3 > e ≈ 2,7), поэтому точек, где y’ не существует, нет.

Найденная точка экстремума единственная на области определения функции, разбивает её на два участка, причем при x 3 y’ > 0, значит это точка глобального минимума.

Находим значение функции в этой точке
y(3) = log₃(x 2 − 6x + 10) + 2 = log₃(3 2 − 6·3 + 10) + 2 = log₃1 + 2 = 0 + 2 = 2.
Это наименьшее значение функции на всей области определения.

Задачи на определение наибольшего (наименьшего) значения функции на отрезке.

Непрерывная на отрезке функция достигает своего наименьшего и наибольшего значений либо во внутренних точках промежутка, либо на его концах. Поэтому для решения задач этого раздела достаточно определить значения функции в точках экстремума и сравнить их с её значениями на концах отрезка. Выявлять тип экстремума необязательно.

Находим значения функции в этих точках и на краях отрезка
y(x) = x 3 + 2x 2 + x + 3;
y(−4) = (−4) 3 + 2(−4) 2 − 4 + 3 = −64 + 2·16 − 4 + 3 = −33;
y(−1/3) = (−1/3) 3 + 2(−1/3) 2 − 1/3 + 3 = −1/27 + 2·1/9 −1/3 + 3 = 2 23 __ 27 ;
y(−1) = (−1) 3 + 2·(−1) 2 − 1 + 3 = −1 + 2 − 1 + 3 = 3.

Выбираем самое большое из получившихся значений y. Это y(−1) = 3.

Найдите наибольшее значение функции y = 36tgx − 36x + 9π + 7 на отрезке [−π/4; π/4].

На отрезке [−π/4; π/4] заданная функция определена и непрерывна (см. график tgx).

y’ = 36· _____ 1 cos 2 x − 36 + 0;

y’ не существует при cosx = 0, x_n = _ π 2 ·n, n Є Z. Ни одна из этих точек не входит в промежуток [−π/4; π/4].

y’ = 0 при cos 2 x = 1, cosx = ±1, x_k = πk, k Є Z. Отрезку [−π/4; π/4] принадлежит только точка x₀ = 0.

Определяем значения функции в этой точке и на концах отрезка.
y(x) = 36tgx − 36x + 9π + 7
y(0) = 36tg0 − 36·0 + 9π + 7 = 0 − 0 + 9π + 7 ≈ 9·3,14 + 7 = 35,26
y(−π/4) = 36tg(−π/4) − 36·(−π/4) + 9π + 7 = 36·(−1) + 9π + 9π + 7 = −29 + 18π ≈ −29 + 18·3,14 = 27,52
y(π/4) = 36tg(π/4) − 36·π/4 + 9π + 7 = 36·1 − 9π + 9π + 7 = 43.
Самым большим из этих чисел является число 43.

Функция определена и непрерывна при всех x > 0, в том числе и на отрезке [ 13 __ 14 ; 15 __ 14 ].

y’ не существует при x = 0. Эта точка не входит в заданный промежуток. Не рассматриваем.

y’ = 0 при 4x 2 − 13x + 9 = 0
Решаем это квадратное уравнение через дискриминант, находим корни x₁ = 1, x₂ = 9/4 = 2,25.

x₁ = 1 является серединой заданного отрезка, x₂ = 2,25 не принадлежит отрезку. Значит нужно определить значения функции y(13/14), y(1) и y(15/14) и сравнить их между собой. Однако в данном случае вычисление значений y(13/14) и y(15/14) может оказаться слишком громоздким и с большой вероятностью привести к ошибкам. Проще вернуться к исследованию поведения производной в окрестности найденной точки экстремума.

Определяем его
y(x) = 2x 2 − 13x + 9lnx + 8
y(1) = 2·1 2 − 13·1 + 9·ln1 + 8 = 2 − 13 + 9·0 + 8 = −3.

Найдите наименьшее значение функции y = x 2 + 25 ______ x на отрезке [1;10].

На отрезке [1;10] функция определена и непрерывна (x = 0 не принадлежит отрезку).

y’ не существует при x = 0. Эта точка не входит в заданный промежуток.

x₁ = −5 не принадлежит отрезку [1;10], x₂ = 5 внутренняя точка отрезка.
Находим значения функции

y(1) = 1 2 + 25 ______ 1 = 26;

y(5) = 5 2 + 25 ______ 5 = 10;

y(10) = 10 2 + 25 _______ 10 = 12,5.

Наименьшее значение y(5) = 10.

Вернуться к списку заданий первой части профильного уровня ЕГЭ по математке.

Нашли опечатку или ошибку? Пожалуйста, сообщите о ней.
E-mail: mathematichka@yandex.ru

Внимание, © mathematichka.
Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.

Источник