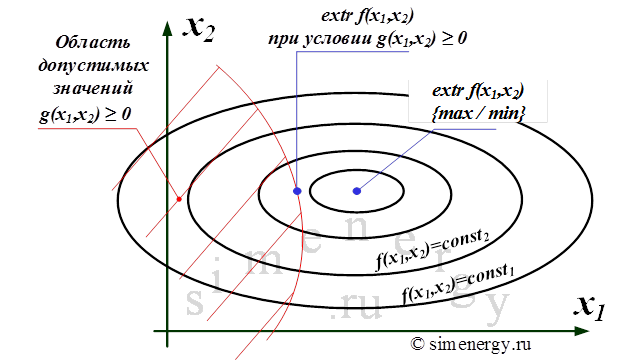
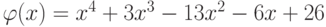Давайте сегодня поговорим об оптимизации с ограничениями. Для начала пусть переменных всего две. Надо найти максимум (или минимум) функции, но так, чтобы выполнялось ограничение вида g(x,y) = 0. Максимум подразумевается локальный. Без ограничения — это поиск вершин холмов; с ограничением — поиск самых высоких положений на тропинке, проложенной по холмистой местности.
Вообще-то, если переменных две, то из ограничения можно выразить одну через другую и переменная окажется всего одна. Но даже в простых случаях выражение будет очень громоздким, да и существует метод получше.
Как мы уже обсуждали, вектор-градиент указывает направление скорейшего роста функции в данной точке. В направлениях под острым углом к градиенту функция тоже растет (хотя бы маленький шажок, но с увеличением высоты над уровнем моря — можно сделать), а под тупым — убывает. В точке условного максимума рост возможен, но только под прямым углом к тропинке. В поиске максимума мы будем идти вверх по тропинке, пока “вверх” не будет строго под прямым углом — тогда уже надо с тропинки сходить, так как по ней далее будет “вниз”.
Разумеется, мы обсуждаем необходимые условия! В точке максимума точно так, но так может быть и не в точке максимума.
Теперь рассмотрим функцию g(x,y). Она должна быть равна нулю, то есть ограничение — наша тропинка — это линия уровня функции. Ее градиент перпендикулярен к линии уровня, потому что на ней функция постоянна — не растет и не убывает. Таким образом, оба градиента лежат на одной прямой в точке максимума:
Можно выразиться иначе, записав функцию Лагранжа L(x,y,λ) = f(x,y) + λg(x,y) и решая задачу о поиске ее максимума без ограничений.
Формально надо добавить еще множитель к f(x,y) и тогда он либо равен единице (нормальный случай), либо нулю — случаи вырожденные, в которых решение от оптимизируемого критерия не зависит.
Можно трактовать множитель λ как ставку величины штрафа за нарушения ограничения. То есть, вместо задачи “найдите самое высокое место на тропинке” мы говорим “найдите самое высокое место; результат будет уменьшен пропорционально расстоянию до тропинки”. При правильно подобранной ставке ограничение нарушено не будет. Помимо решения задачи, мы узнаем еще “цену ограничения” — этот самый множитель λ. Если он близок к нулю, то ограничение маловажно, оно и так не нарушится или нарушится не сильно.
Можно уточнить этот принцип. Пусть ограничение имеет вид G(x,y)-b=0. Это естественно, если нельзя превзойти запас ресурса. То, что он весь будет издержан — ясно, но больше никак нельзя. Величина b — это и есть запас. Решение и оптимальное значение зависят от b. Найдем производную f’=df/db от оптимального значения по b — она и покажет чувствительность оптимума к этой величине, так как выигрыш от изменения запаса на db равен, с точностью до бесконечно малых, f’db.
Получается, что реакция прибыли на вариацию запаса равна множителю Лагранжа с обратным знаком. Если λ<0, то рост запаса повышает прибыль, и мы точно знаем, насколько. В бесконечно-малом, конечно, но дальнейший анализ — уже дело техники.
Для многих переменных все точно так же. Все ограничения добавляются к функции, каждое со своим множителем.
Рассмотрим два примера. Пусть местность описывается уравнением
z=1-x^2-y^2,
а ограничение имеет вид y/x – b = 0. Решая задачу, получаем λ=0. То есть, ограничение роли не играет. Максимум все равно в нуле, в каком направлении не проводи через него тропинки.
Второй пример — классика. Надо отгородить забором данного периметра P прямоугольный участок максимальной площади. Просто огородить, со всех сторон, и у реки — с трех сторон. И между рекой и дорогой — с двух сторон. Площадь равна xy, а половина периметра равна x+y.
Запишем функцию Лагранжа: xy+λ(x+y-P/2) и найдем ее производные по x и y: y+λ=0, x+λ=0. Отсюда следует, что x=y, а λ<0. Первое уравнение решает задачу — искомый участок квадратный, а второе дает ценную информацию: увеличение периметра увеличит и площадь.
Для реки все похоже, только формула для периметра другая и ответ, соответственно: x=L/4, y=L/2: сторона вдоль реки вдвое длиннее.
Третья задача немного коварна. Периметр от y не зависит вообще! Формально получается x=0, но это не максимум и даже не минимум. Максимума вообще нет, потому что два куска забора между рекой и дорогой могут сколь угодно далеко друг от друга располагаться и отгораживать, тем самым, любую площадь.
Поучительно рассмотреть аналогичную задачу о цилиндрической бочке максимального объема при заданной площади поверхности. Бочка с дном и крышкой, бочка без крышки, бочка без дна. Последняя задача не имеет решения: можно делать бочку-блюдце, очень большого радиуса и малой высоты: площадь будет какая задана, а объем — сколь угодно велик.
Последний пример. В заметке про энтропийные распределения мы искали максимум функции с ограничением. Метод Лагранжа показывает, что все переменные равны, причем всегда, если функция есть сумма одинаковых слагаемых для всех переменных.
Можно применить метод и для бесконечного числа переменных, принцип тот же. Там решение “все переменные равны” уже не подходит, ведь сумма бесконечного числа равных величин никак не может равняться единице. Надо добавить еще ограничение, задав матожидание — и получить геометрическое распределение. Множители дают дополнительную информацию, хотя и не очень ценную в данном случае.
Давайте теперь рассмотрим ограничения-неравенства g(x,y)≥0. Их можно свести с неравенствам вида x≥0, если ввести дополнительные переменные h — остатки ресурса — и записать ограничения-равенства g(x,y)-h=0. Переменная h входит только в ограничение и для нее условие на обнуление производной приводит к “условию дополняющей нежесткости” λh=0. Это означает, что либо h=0, то есть ресурс будет исчерпан весь, ограничение насыщенно (обращается в равенство); либо λ=0, то есть условие не существенно, ресурс в избытке, он не будет весь издержан, поэтому небольшие вариации запаса (самого ограничения) не повлияют на решение задачи.
Здесь множители Лагранжа дают очень ценную информацию! По существу, они различают критичные ограничения от менее существенных. Это важно еще и для устойчивости, ведь нехватка критического ресурса испортит сразу все. Впрочем, об устойчивости поговорим в другой раз…
Обзор основных методов математической оптимизации для задач с ограничениями
Время на прочтение
7 мин
Количество просмотров 43K
Я долго готовился и собирал материал, надеюсь в этот раз получилось лучше. Эту статью посвящаю основным методам решения задач математической оптимизации с ограничениями, так что если вы слышали, что симплекс-метод — это какой-то очень важный метод, но до сих пор не знаете, что он делает, то возможно эта статья вам поможет.
P. S. Статья содержит математические формулы, добавленные макросами хабраредактора. Говорят, что они иногда не отображаются. Также есть много анимаций в формате gif.
Преамбула
Задача математической оптимизации — это задача вида «Найти в множестве
элемент
такой, что для всех
из
выполняется
», что в научной литературе скорее будет записано как-то так
Исторически так сложилось, что популярные методы такие как градиентный спуск или метод Ньютона работают только в линейных пространствах (причем желательно простых, например
). На практике же часто встречаются задачи, где нужно найти минимум не в линейном пространстве. Например нужно найти минимум некоторой функции на таких векторах
, для которых
, это может быть обусловлено тем, что
обозначают длины каких-либо объектов. Или же например, если
представляют координаты точки, которая должна быть на расстоянии не больше
от
, т. е.
. Для таких задач градиентный спуск или метод Ньютона уже напрямую не применить. Оказалось, что очень большой класс задач оптимизации удобно покрывается «ограничениям», подобными тем, что я описал выше. Иначе говоря, удобно представлять множество
в виде системы равенств и неравенств
Задачи минимизации над пространством вида
таким образом стали условно называть «задачами без ограничений» (unconstrained problem), а задачи над множествами, заданными наборами равенств и неравенств — «задачами с ограничениями» (constrained problem).
Технически, совершенно любое множество
можно представить в виде одного равенства или неравенство с помощью индикатор-функции, которая определяется как
однако такая функция не обладает разными полезными свойствами (выпуклость, дифференцируемость и т. п.). Тем не менее, часто можно представить
в виде нескольких равенств и неравенств, каждое из которых такими свойствами обладает. Основная теория подведена под случай
где
— выпуклые (но не обязательно дифференцируемые) функции,
— матрица. Для демонстрации работы методов я буду использовать два примера:
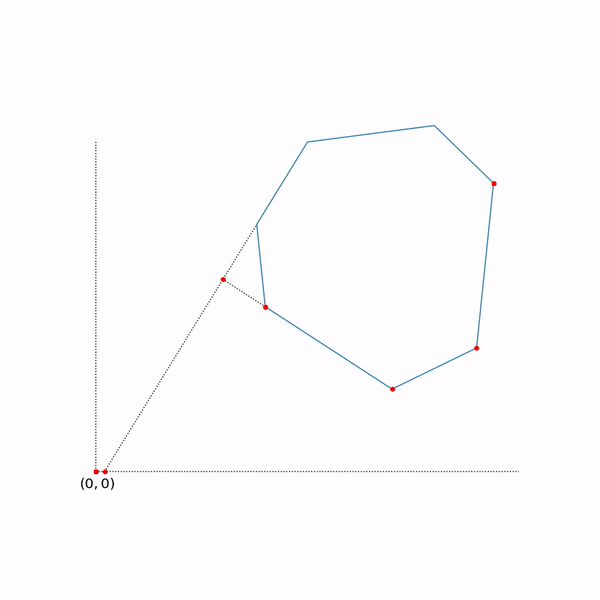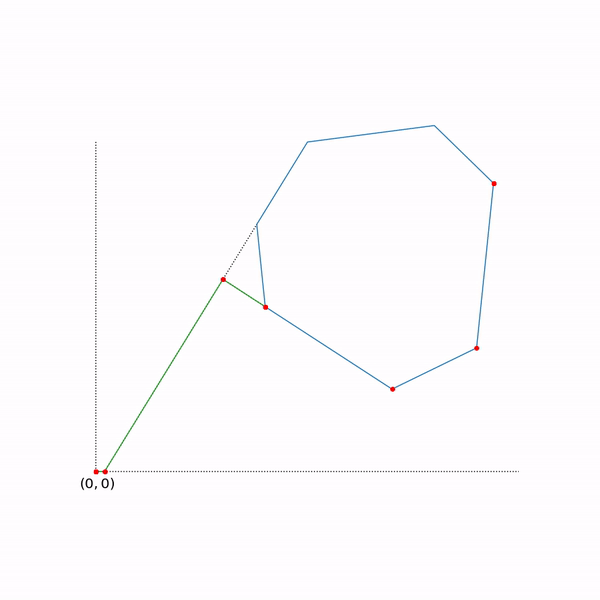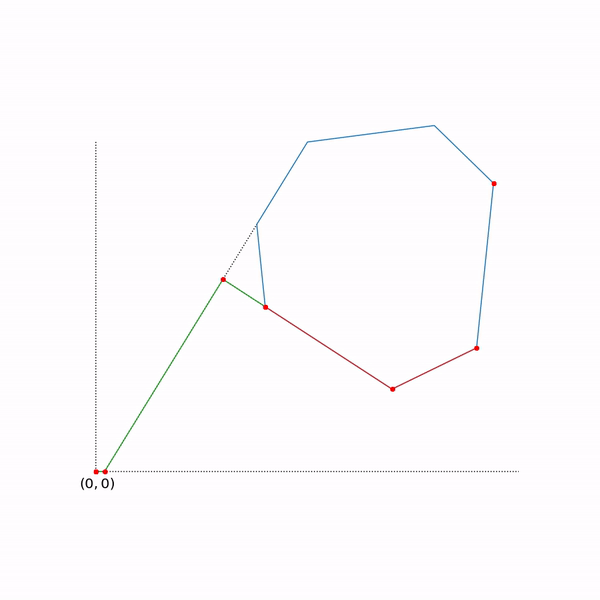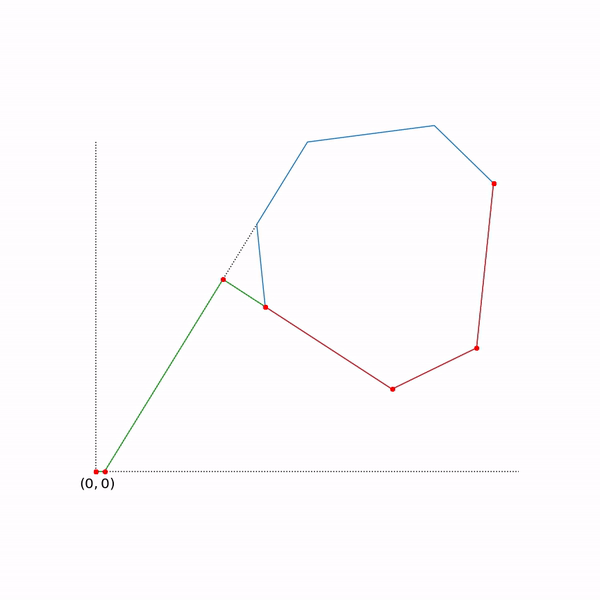
- Задача линейного программирования
По сути эта задача состоит в том, чтобы найти самую дальнюю точку многоугольника в направлении (2, 1), решение задачи — точка (4.7, 3.5) — самая «правая» в многоугольнике). А вот собственно и сам многоугольник
- Минимизация квадратичной функции с одним квадратичным ограничением
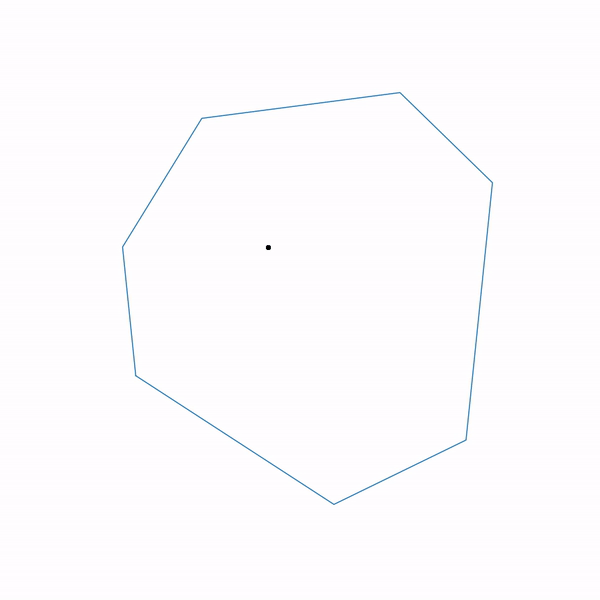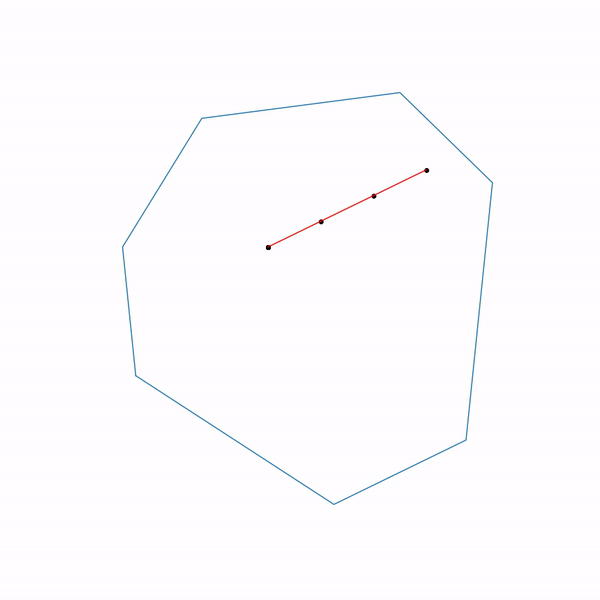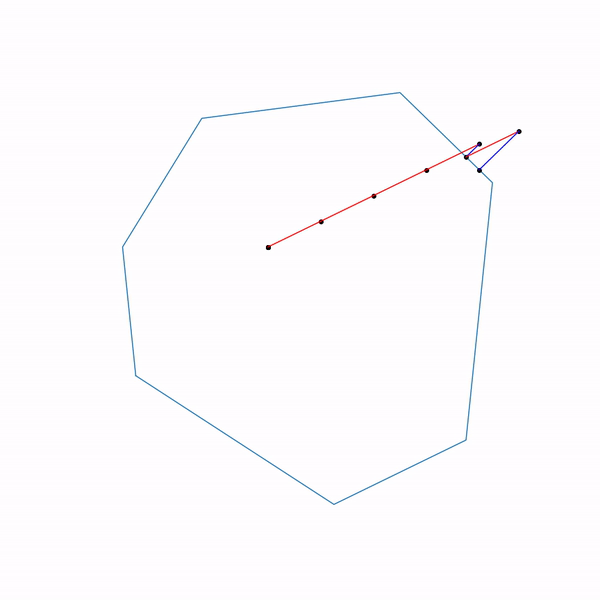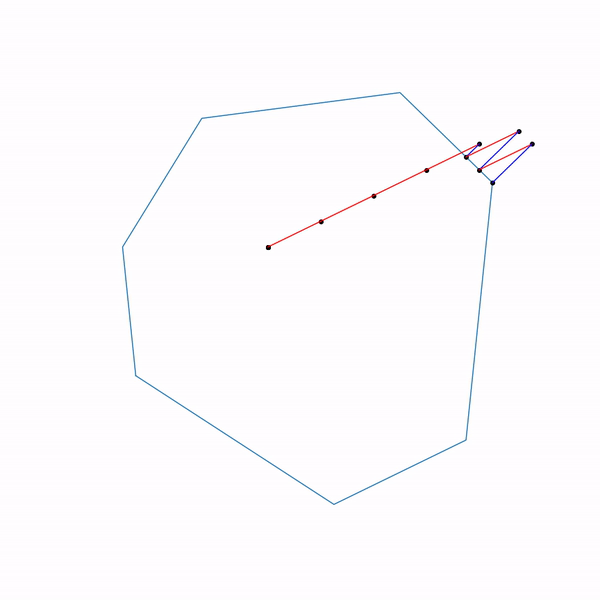
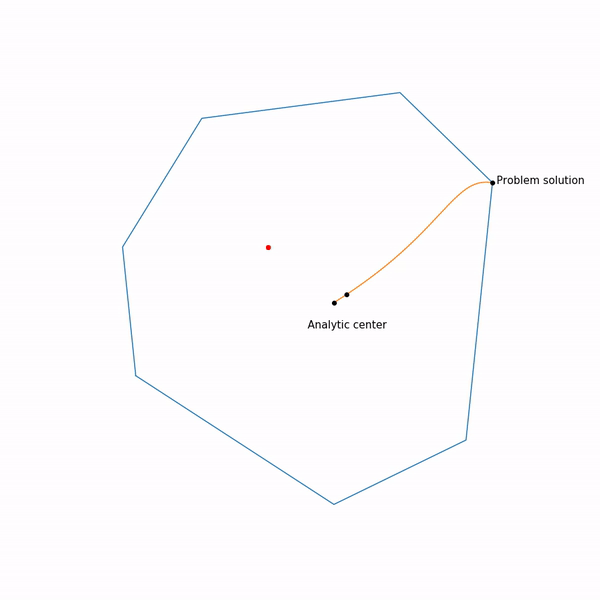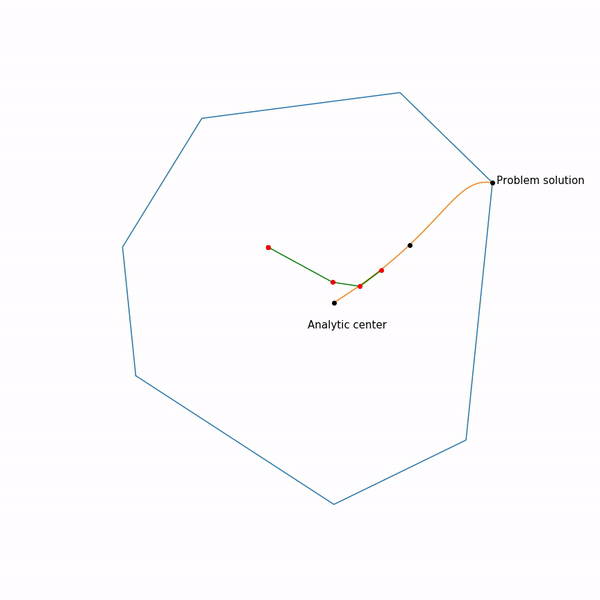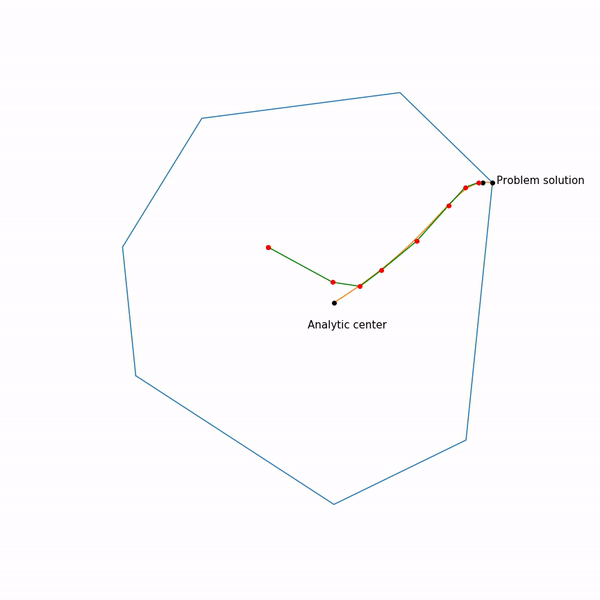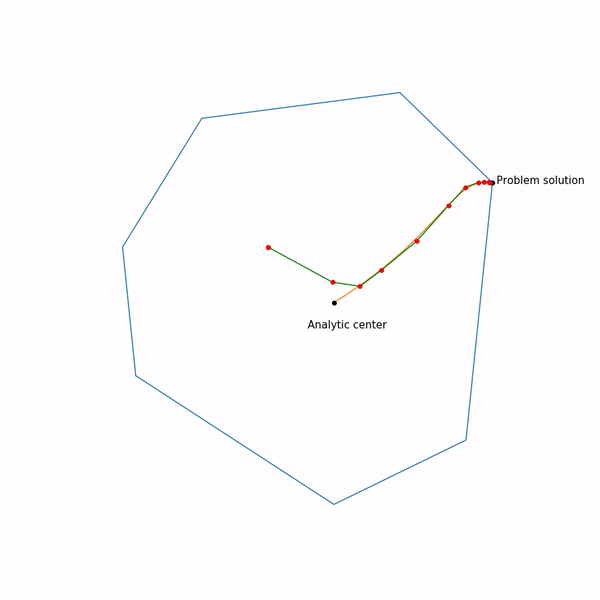
Симплекс-метод
Из всех методов, которые я покрываю этим обзором, симплекс-метод наверно является самым известным. Метод был разработан специально для линейного программирования и единственный из представленных достигает точного решения за конечное число шагов (при условии, что для вычислений используется точная арифметика, на практике это обычно не так, но в теории возможно). Идея симплекс-метода состоит из двух частей:
- Системы линейных неравенств и равенств задают многомерные выпуклые многогранники (политопы). В одномерном случае это точка, луч или отрезок, в двумерном — выпуклый многоугольник, в трехмерном — выпуклый многогранник. Минимизация линейной функции — это по сути нахождение самой «дальней» точки в определенном направлении. Думаю, интуиция должна подсказывать, что этой самой дальней точкой должна быть некая вершина, и это действительно так. В общем случае, для системы из
неравенств в
-мерном пространстве вершина — это точка, удовлетворяющая системе, для которой ровно
из этих неравенств обращаются в равенства (при условии, что среди неравенств нет эквивалентных). Таких точек всегда конечное число, хоть их и может быть очень много.
- Теперь у нас есть конечный набор точек, вообще говоря можно их просто взять и перебрать, то есть сделать что-то такое: для каждого подмножества из
неравенств решить систему линейных уравнений, составленных на выбранных неравенствах, проверить, что решение подходит в исходную систему неравенств и сравнить с другими такими точками. Это довольно простой неэффективный, но рабочий метод. Симплекс-метод вместо перебора двигается от вершины к вершине по ребрам таким образом, чтобы значений целевой функции улучшалось. Оказывается, если у вершины нет «соседей», в которых значений функции лучше, то она оптимальна.
Симплекс-метод является итеративным, то есть он последовательно по чуть-чуть улучшает решение. Для таких методов нужно с чего-то начинать, в общем случае это делается с помощью решения вспомогательной задачи
Если для решения этой задачи
такое, что
, то выполняется
, иначе исходная задача вообще задана на пустом множестве. Чтобы решить вспомогательную задачу, можно также использовать симплекс-метод, начальной же точкой можно взять
с произвольным
. Нахождение начальной точки можно условно назвать первой фазой метода, нахождение решение исходной задачи можно условно назвать второй фазой метода.
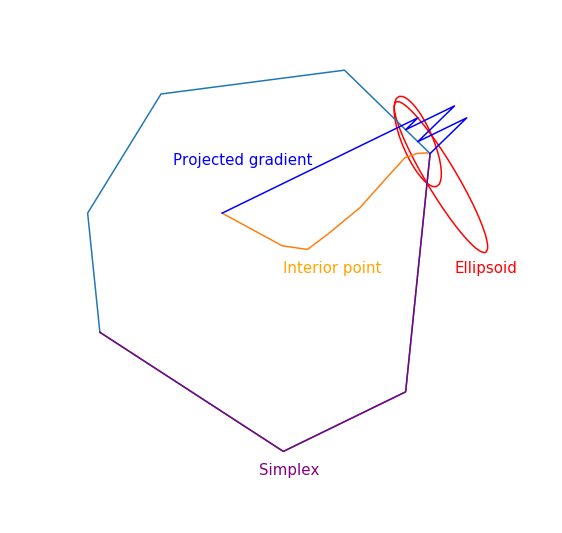
Траектория двухфазового симплекс-метода
Траектория была сгенерирована с помощью scipy.optimize.linprog.
Проективный градиентный спуск
Про градиентный спуск я недавно писал отдельную статью, в которой в том числе кратко описал и этот метод. Сейчас этот метод вполне себе живой, но изучается как часть более общего проксимального градиентного спуска. Сама идея метода совсем банальна: если мы применяем градиентный спуск к выпуклой функции
, то при правильном выборе параметров получаем глобальный минимум
. Если же после каждого шага градиентного спуска корректировать полученную точку, взяв вместо нее её проекцию на замкнутое выпуклое множество
, то в результате мы получим минимум функции
на
. Ну или более формально, проективный градиентный спуск — это алгоритм, который последовательно вычисляет
где
Последнее равенство определяет стандартный оператор проекции на множество, по сути это функция, которая по точке
вычисляет ближайшую к ней точку множества
. Роль расстояния здесь играет
, стоит отметить, что здесь можно использовать любую норму, тем не менее проекции с разными нормами могут отличаться!
На практике проективный градиентный спуск используется только в особых случаях. Основная его проблема состоит в том, что вычисление проекции может быть еще более сложной задачей, чем исходная, а её нужно вычислять много раз. Самый распространенный случай, для которого удобно применять проективный градиентный спуск — это «коробочные ограничения», которые имеют вид
В этом случае проекция вычисляется очень просто, по каждой координате получается
Применение проективного градиентного спуска для задач линейного программирования совершенно бессмысленно, тем не менее если это все-таки сделать, то выглядеть будет как-то так
Траектория проективного градиентного спуска для задачи линейного программирования
А вот как выглядит траектория проективного градиентного спуска для второй задачи, если
выбирать большой размер шага
и если
выбирать небольшой размер шага
Метод эллипсоидов
Этот метод примечателен тем, что является первым полиномиальным алгоритмом для задач линейного программирования, его можно считать многомерным обобщением метода бисекции. Я начну с более общего метода разделяющей гиперплоскости:
- На каждом шаге метода есть некоторое множество, которое содержит решение задачи.
- На каждом шаге строится гиперплоскость, после чего из множества удаляются все точки, лежащие по одну сторону выбранной гиперплоскости, и, возможно, к этому множеству добавятся какие-то новые точки
Для задач оптимизации построение «разделяющей гиперплоскости» основано на следующем неравенстве для выпуклых функций
Если зафиксировать
, то для выпуклой функции
полупространство
содержит только точки со значением не меньше, чем в точке
, а значит их можно отсечь, так как эти точки не лучше, чем та, что мы уже нашли. Для задач с ограничениями можно аналогичным образом избавиться от точек, которые гарантированно нарушают какое-то из ограничений.
Самый простой вариант метода разделяющей гиперплоскости — это просто отсекать полупространства без добавления каких-либо точек. В результате на каждом шаге у нас будет некий многогранник. Проблема этого метода в том, что количество граней многогранника скорее всего будет возрастать от шага к шагу. Более того, оно может расти экспоненциально.
Метод эллипсоидов собственно на каждом шаге хранит эллипсоид. Точнее, после проведения гиперплоскости строится эллипсоид минимального объема, который содержит одну из частей исходного. Этого получается добиться за счет добавления новых точек. Эллипсоид всегда можно задать положительно определенной матрицей и вектором (центром эллипсоида) следующим образом
Построение минимального по объему эллипсоида, содержащего пересечение полупространства и другого эллипсоида, можно осуществить с помощью в меру громоздких формул. К сожалению на практике этот метод оказался все еще на так хорош, как симплекс-метод или метод внутренней точки.
А вот собственно как он работает для
линейного программирования
и для
квадратичного программирования
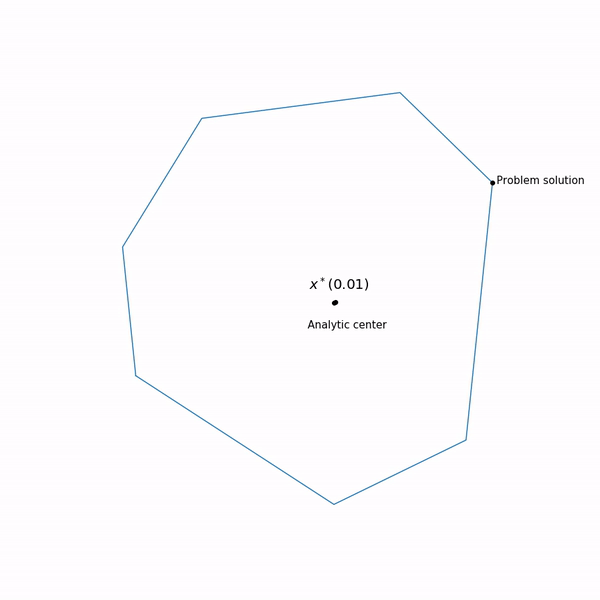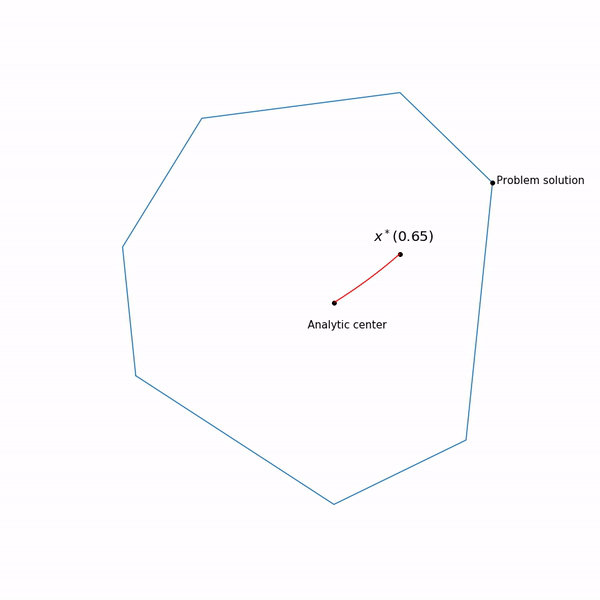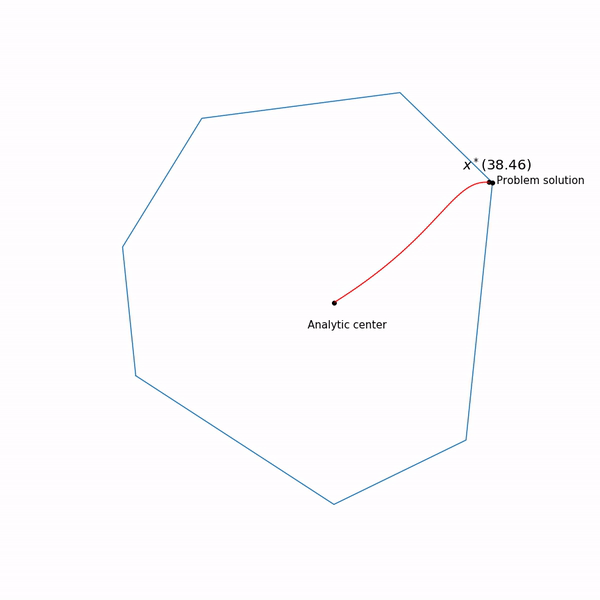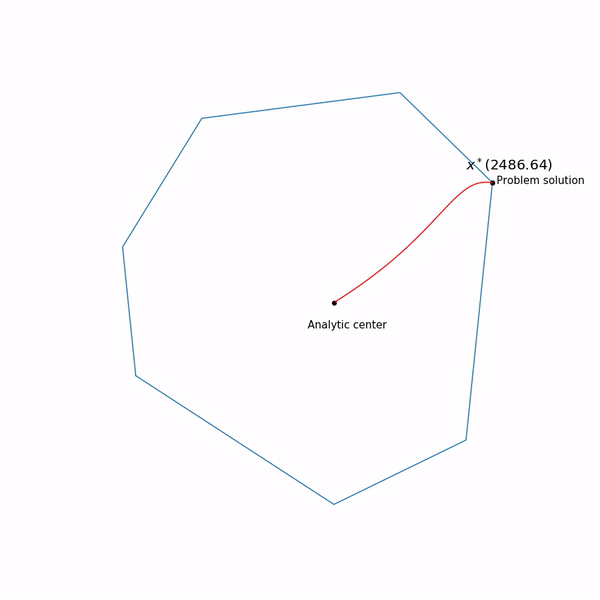
Метод внутренней точки
Этот метод имеет долгую историю развития, одни из первых предпосылок появились примерно в то же время, когда был разработан симплекс-метод. Но в то время он был еще недостаточно эффективен, чтобы использоваться на практике. Позднее в 1984 был разработан вариант метода специально для линейного программирования, который был хорош как в теории, так и на практике. Более того, метод внутренней точки не ограничен только линейным программированием в отличие от симплекс-метода, и сейчас он является основным алгоритмом для задач выпуклой оптимизации с ограничениями.
Базовая идея метода — замена ограничений на штраф в виде так называемой барьерной функции. Функция
называется барьерной функцией для множества
, если
Здесь
— внутренность
,
— граница
. Вместо исходной задачи предлагается решать задачу
и
заданы только на внутренности
(по сути отсюда и название), свойство барьера гарантирует, что у
минимум по
существует. Более того, чем больше
, тем больше влияние
. При достаточно разумных условиях можно добиться того, что если устремить
к бесконечности, то минимум
будет сходиться к решению исходной задачи.
Если множество
задано в виде набора неравенств
, то стандартным выбором барьерной функции является логарифмический барьер
Точки минимума
функции
для разных
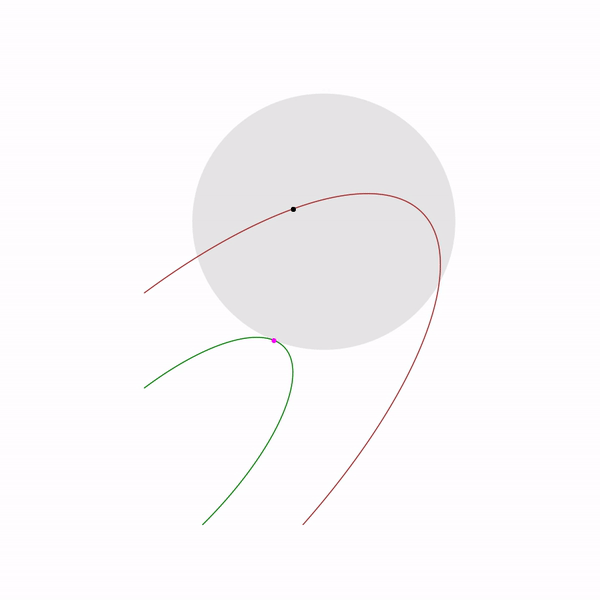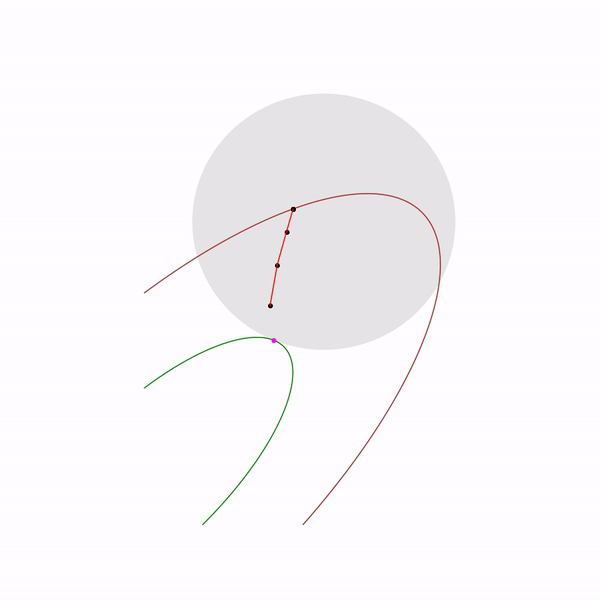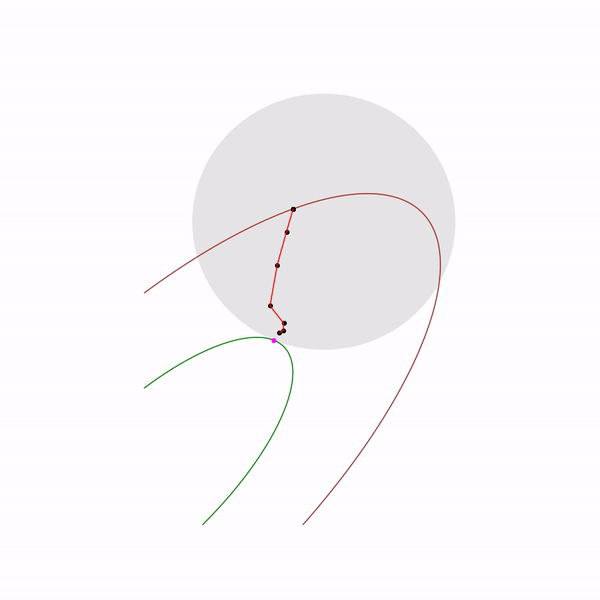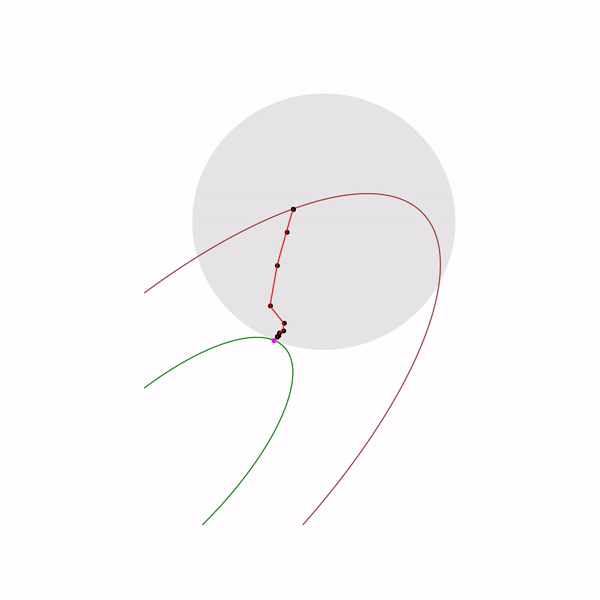
образует кривую, которую обычно называют центральный путь, метод внутренний точки как бы пытается следовать этому пути. Вот так он выглядит для
Примера с линейным программированием
Аналитический центр — это просто
Наконец сам метод внутренней точки имеет следующий вид
- Выбрать начальное приближение
,
- Выбрать новое приближение методом Ньютона
- Увеличить
Использование метода Ньютона здесь очень важно: дело в том, что при правильном выборе барьерной функции шаг метода Ньютона генерирует точку,
которая остается внутри нашего множества
, поэкспериментировали, в таком виде не всегда выдает. Ну и наконец, так выглядит траектория метода внутренней точки
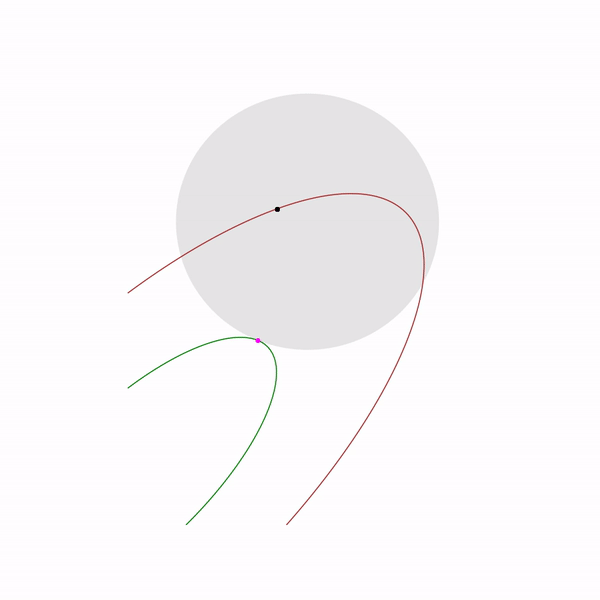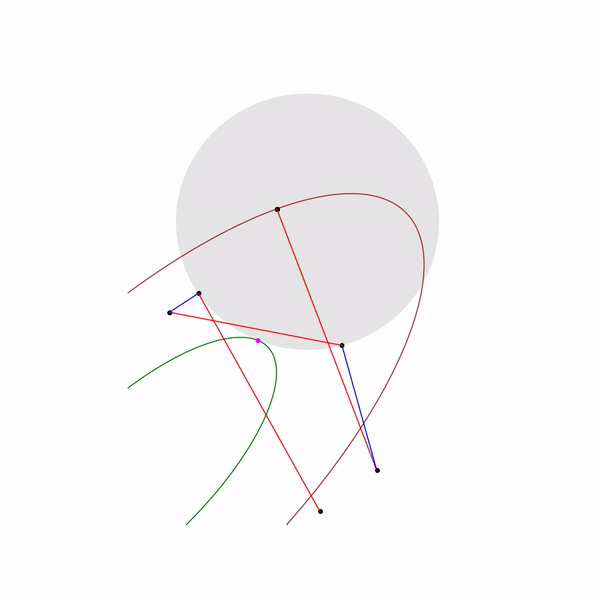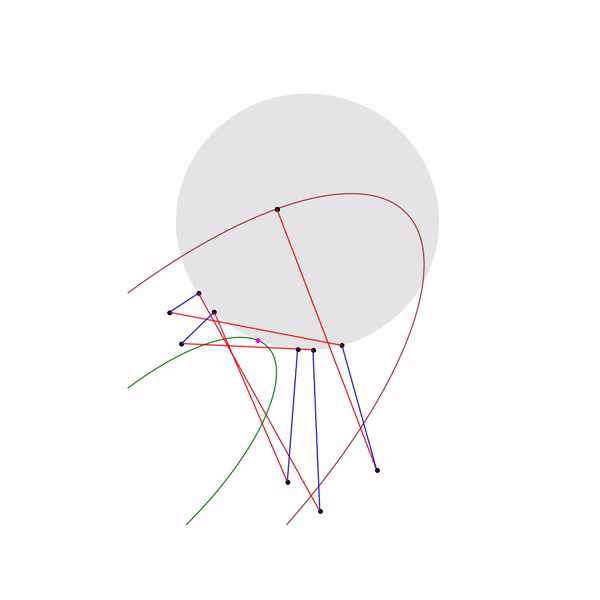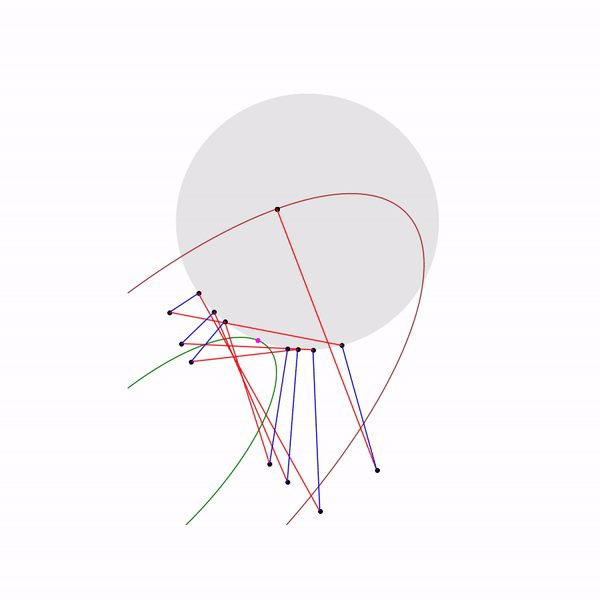
Задача линейного программирования
Прыгающая черная точка — это
, т.е. точка, к которой мы пытаемся приблизиться шагом метода Ньютона на текущем шаге.
Задача квадратичного программирования
Оптимизационная задача – это задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.
Целевая функция представляет собой набор критериев качества, которые должны быть оптимизированы одновременно. В общем случае целевая функция состоит из управляемых и неуправляемых переменных. Условие поиска экстремума целевой функции записывается в следующем виде:
Методы решения оптимизационных задач изучает математическое программирование. Математическое программирование – это математическая дисциплина, изучающая теорию и методы решения задач по определению экстремумов функций на множествах конечномерного векторного пространства, определяемых набором линейных и/или нелинейных ограничений (равенствами и/или неравенствами). Математическое программирование представляет собой, как правило, многократно повторяющуюся вычислительную процедуру, приводящую к искомому оптимальному решению. Выбор метода математического программирования для решения оптимизационной задачи определяется видом зависимостей в математической модели, характером искомых переменных, категорией исходных данных и количеством критериев оптимальности:
- Методы линейного программированияиспользуются в случае, если в математической модели имеются только линейные зависимости между переменными, для решения оптимизационной задачи.
- Методы нелинейного программированияиспользуются в случае, если в математической модели имеются нелинейные зависимости между переменными, для решения оптимизационной задачи.
- Методы целочисленного или дискретного программированияиспользуются в случае, если среди переменных имеются целочисленные или дискретные переменные, соответственно.
- Методы стохастического программирования используются в случае, если исходные данные или их часть являются случайными величинами.
- Математический аппарат теории игриспользуются в случае, если задана недетерминированная (неопределенная) исходная информация.
Решение задачи оптимизации осуществляется с помощью поисковых методов, использующих предшествующую информацию для построения улучшенного решения задачи (итерационные методы расчета). К настоящему времени разработано достаточно много методов локальной оптимизации для решения задач общего вида. Большинство из них используют принцип локального спуска, когда метод последовательно на каждом шаге переходит к точкам с существенно меньшими (большим) значениями целевой функции. Данные методы отличаются один от другого способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, а также критериями окончания поиска. Поиск оптимального значения в таких задачах может быть представлен в виде итерационного соотношения:
где переменная – это приращение вектора управляемых параметров. В зависимости от условия поиска (поиск максимального или минимального значения целевой функции) используется либо знак «+», либо знак «-».
Приращение вектора управляемых параметров в большинстве случаях вычисляется по формуле:
В данном выражении – значение вектора управляемых параметров на k-ом шаге,
– шаг расчета, а
– направление поиска экстремума функции.
В зависимости от числа управляемых параметров различают методы одномерной и многомерной оптимизации (многокритериальная оптимизация). Поиск считается одномерным, в случае если аргументом целевой функции является один управляемый параметр.
Шаг расчета
Итерационная форма методов локальной оптимизации для решения задач поиска экстремума целевой функции требует выбора шага расчета вдоль заданных направлений на каждом шаге итерации. Шаг расчета может быть постоянным или переменным, но оптимальное значение длины шага определяется в результате поиска экстремума целевой функции в выбранном направлении с использованием методов одномерной оптимизации:
Другими словами, величина шага расчета вычисляется при решении следующего выражения:
В результате решения данного уравнение мы получим, что шаг расчета в символьном виде определяется следующим образом:
где – значение аргумента функции на k-ом шаге итерации;
n – количество неизвестных переменных, которые определяются в ходе решения задачи;
L – некоторая константа, которая определяется из определителя следующей матрицы:
В результате для определения оптимального шага расчета требуется выполнить большой объем вычислений целевой функции. Для снижения числа операций на практике используют другой подход: подбирают такие значения шага расчета , чтобы они удовлетворяли любому из представленных ниже условию.
где коэффициент , а шаг расчета
определяется итеративно путем умножения первоначального шага
на коэффициент
до тех пор пока не будет выполняться условие.
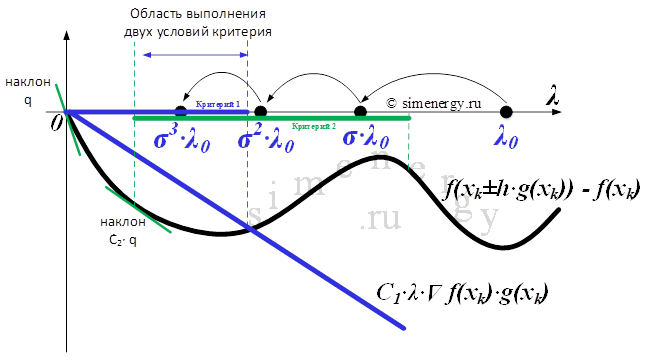
Рис.1. Критерий выбора шага расчета по правилу Армихо
Методика определения шага расчета оптимизационной задачи в соответствии с правилом Армихо заключается в следующем:
1. Задать коэффициент в диапазоне от 0 до 1.
2. Задать начальное значение шага .
Процедура поиска (проверка выполнения условия по правилу Армихо)
3. В случае если условие по правилу Армихо не выполняется, тогда необходимо скорректировать шаг расчета , где переменная
может принимать любое значение от 0 до 1, по умолчанию примем, что переменная
, а
– текущий шаг поиска.
4. В случае если условие по правилу Армихо выполняется, тогда в качестве шага расчета можно принять , а процедура поиска завершается.
Данное правило требует однократного вычисления градиента, после чего небольшое количество итераций затрачивается на подбор подходящего шага. Каждая из таких вложенных итераций, в свою очередь, требует вычисления значения целевой функции без градиента, то есть проводимые испытания относительно легковесны. Следует отметить, что данное условие удовлетворяется для всех достаточно малых . Правило Армихо можно расширить на многокритериальный случай: неравенство 3.19 следует понимать покомпонентно.
- Второе условие(Правило Вольфе-Пауэлла – Wolfe. P) является модифицированным критерием, позволяет выбрать шаг расчета в случае выполнения двух условий:
– функция не должна превышать значения некоторой убывающей линейной функции, равной
в нуле:
– величина скорости изменения функция в заданном направлении была в
раз больше, чем скорость изменения функции в первоначальной точке
Рис.2. Критерий выбора шага расчета по правилу Вольфе-Пауэлла
Методика определения шага расчета оптимизационной задачи в соответствии с правилом Вольфе-Пауэлла заключается в следующем:
1. Задать коэффициент и
в диапазоне от 0 до 1
.
2. Задать начальное значение шага , принять коэффициент
и
Процедура поиска (проверка выполнения условия по правилу Вольфе-Пауэлла)
3. В случае если первое условие по правилу Вольфе-Пауэлла не выполняется, тогда принять коэффициент . Перейти к пункту №5.
4. В случае если второе условие по правилу Вольфе-Пауэлла не выполняется, тогда принять коэффициент :
– в случае если , то перейти к пункту №5;
– в случае если выполнить экстраполяцию, положив
, где r – коэффициент экстраполяции
. Перейти к пункту №3.
5. Выполнить текущий расчет шага по формуле
где – коэффициент интерполяции, который определяется в следующем диапазоне
Перейти к пункту №3.
6. В случае если выполняются оба условия правилу Вольфе-Пауэлла, тогда в качестве шага расчета можно принять , а процедура поиска завершается.
- Третье условие(правило Голдстейна-Армийо) позволяет выбрать шаг расчета, рассматривая следующее неравенство:
Методика определения шага расчета оптимизационной задачи в соответствии с правилом Голдстейна-Армийо заключается в следующем:
1. Задать коэффициент и
в диапазоне от 0 до 1
.
2. Задать начальное значение шага
3. В случае если условие по правилу Голдстейна-Армийо не выполняется, тогда необходимо скорректировать шаг расчета , где переменная
может принимать любое значение от 0 до 1, по умолчанию примем, что переменная
, а
– текущий шаг поиска.
4. В случае если условие по правилу Голдстейна-Армийо выполняется, тогда в качестве шага расчета можно принять , а процедура поиска завершается.
Критерии останова оптимизационного процесса
Поиск оптимального решения завершается в случае, когда на итерационном шаге расчета выполняется один (или несколько) критериев:
– траектория поиска остается в малой окрестности текущей точки поиска:
– приращение целевой функции не меняется:
– градиент целевой функции в точке локального минимума обращается в нуль:
Классификация методов оптимизации.
В настоящее время для решения задач оптимизации разработано огромное количество различных математических методов. Применение того или иного метода определяется постановкой задачи, сложностью вычисления функции и ее производных, поведением функции и т. д.
Задачи оптимизации и методы их решения можно разделить по наличию или отсутствию ограничений (задаётся системой неравенств и равенств или более сложным алгоритмом) в математических моделях на методы условной и безусловной оптимизации. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений.
Методы безусловной оптимизации
Классическая задача безусловной оптимизации формулируется следующим образом: требуется найти вектор переменных , при котором целевая функция принимает экстремальное (максимальное или минимальное значение) значение
Экстремальное значение целевой функции соответствует оптимальному управлению. В графическом виде постановка задачи выглядит следующим образом:
Рис.3. Задача безусловной оптимизации для функции двух переменных
Сущность метода оптимизации в первую очередь определяется способом выбора направления движения к экстремуму. В зависимости от используемого порядка производных целевой функции методы безусловной оптимизации делят на методы нулевого, первого и второго порядков. Если производные не используются, то имеет место метод нулевого порядка, если используются первые или вторые производные, то соответственно метод первого или второго порядка.
- Методы нулевого порядка (методы прямого поиска)для поиска экстремума функции требуют вычисление только значений функции в точках пространства оптимизации. В данном методе информация о производных не используется и, соответственно, не требуют определения аналитического вида производных. В зависимости от количества управляемых параметров различают методы одномерного и многомерного поиска.
Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач нулевого порядка:
Методы одномерного поиска:
– Метод дихотомического деления и метод золотого сечения – это методы одномерной оптимизации, основанные на делении отрезка, на котором ищется экстремум, пополам или в пропорциях золотого сечения (0,382 / 0,618), соответственно.
– Метод полиномиальной аппроксимации (метод квадратичной интерполяции) – это метод одномерной оптимизации, в соответствии с которым целевая функция аппроксимируется квадратичным полиномом.
Методы многомерного поиска:
– Метод покоординатного спуска (Гаусса-Зейделя) – это метод безусловной оптимизации нулевого порядка, в котором направления поиска выбираются поочередно вдоль всех координатных осей, шаг рассчитывается на основе одномерной оптимизации.
– Метод вращающихся координат (Метод Розенброка) – это метод безусловной оптимизации нулевого порядка, в котором реализуется покоординатный спуск, но вдоль координатных осей, поворачиваемых таким образом, чтобы направление одной из осей было близко к направлению, параллельному дну оврага.
– Симплексный метод (метод деформируемого многогранника или метод Нелдера-Мида) – это метод безусловной оптимизации нулевого порядка, основанный на многократно повторяемых операциях построения многогранника с (n+1) вершинами, где n — размерность пространства управляемых параметров, и перемещения наихудшей вершины (с наихудшим значением целевой функции) в направлении центра тяжести многогранника.
- Методы первого порядка (градиентные методы поиска)для поиска экстремума требуют вычисления значений функции в точках пространства оптимизации, а также определение аналитического вида производных первого порядка по управляемым параметрам. Методы первого порядка называют также градиентными, поскольку вектор первых производных функции F(X) по оптимизируемым переменным X есть градиент целевой функции:
Градиент в базовой точке строго ортогонален к поверхности, а его направление показывает направление наискорейшего возрастания функции, а противоположное направление (антиградиента), соответственно, показывает направление наискорейшего убывания функции. Градиентные методы отличаются один от другого способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, а также критериями окончания поиска.
Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач первого порядка:
– Метод градиентного спуска – это метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента с переменным (дробным) шагом, который задается пользователем.
– Метод наискорейшего спуска – это метод нахождения локального минимума (максимума) функции при движении вдоль градиента с оптимальным шагом. Шаг расчета выбирается минимума целевой (минимизируемой) функции в направлении спуска.
– Метод сопряженных градиентов (метод Флетчера-Ривса) – это метод безусловной оптимизации первого порядка, в котором направление поиска на очередном шаге есть градиентное направление, скорректированное с учетом направления поиска на предыдущем шаге.
– Метод переменной метрики (метод Девидона-Флетчера-Пауэлла) – это метод безусловной оптимизации, в котором за основу взято решение системы уравнений, выражающих необходимые условия экстремума.
- Методы второго порядка для поиска экстремума требуют вычисления значений функции в точках пространства оптимизации, а также определение аналитического вида производных первого и второго порядка по управляемым параметрам.
Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач второго порядка:
– Метод Ньютона – это метод безусловной оптимизации, основанный на использовании необходимых условий безусловного экстремума целевой функции: равенству нулю первой производной. В соответствии с данным методом определяют матрицу вторых частных производных целевой функции по управляемым параметрам (матрицу Гессе).
– Метод Марквардта – это метод безусловной оптимизации, направленный на решение задач о наименьших квадратах. Является альтернативой методу Гаусса – Ньютона. Может рассматриваться как комбинация последнего с методом градиентного спуска или как метод доверительных интервалов.
Методы условной оптимизации
Классическая задача условной оптимизации формулируется следующим образом: необходимо найти вектор переменных , при котором целевая функция принимает экстремальное (максимальное или минимальное значение) значение
при заданных условиях (равенствами и/или неравенствами), при этом число ограничений m может быть как больше, так и меньше числа переменных n.
, j=1,2,…,m.
Другими словами, необходимо найти экстремум целевой функции при условии, что значения аргументов функции принадлежат области допустимых значений, которая образуется системой ограничений. Экстремальное значение целевой функции соответствует оптимальному управлению. В графическом виде постановка задачи выглядит следующим образом:
Рис.4. Задача условной оптимизации для функции двух переменных
В зависимости от используемого метода решения методы условной оптимизации можно разделить на методы сведения задачи к безусловной оптимизации и методы непосредственного решения.
- Методы сведения задачи к безусловной оптимизации – это задача условной оптимизации, основанная на преобразование задачи нелинейного программирования в последовательность задач безусловной оптимизации путем построения вспомогательных функций
Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач второго порядка:
– Метод неопределенных множителей Лагранжа – это метод условной оптимизации, ориентированный на поиск экстремума целевой функции при наличии ограничений типа равенств.
– Условия Куна-Таккера – это метод решения оптимизационной задачи математического программирования с заданными ограничениями. Метод является обобщением метода множителей Лагранжа на случай общей задачи нелинейного программирования с ограничениями, как в виде равенств, так и в виде неравенств.
– Метод штрафных функций – это метод или группа методов для решения задач математического программирования, основанные на преобразовании задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции, учитывающей ограничения задачи.
- Методы непосредственного решения задачи условной оптимизации – это задача условной оптимизации, основанная на движении из одной допустимой точки, где выполнены все ограничения, к другой допустимой точке с лучшим значением целевой функции.
Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач второго порядка:
– Метод приведенного градиента – это метод условной оптимизации, ориентированный на решение задач с ограничениями типа равенств. Направление движение в данном методе определяет приведенный градиент функции.
– Метод возможных направлений (метод Зойтендейка) – этот метод решения задач математического программирования основанн на движении из одной допустимой точки к другой с лучшим значением целевой функции.
Численные методы оптимизации реализованы и широко используются в различных математических пакетах. При этом наличие готовых программных средств (математических библиотек и пакетов) не только не снимает необходимость изучения методов, а наоборот, делает подготовку в этом направлении еще более актуальной. Это связано с тем, что при решении реальной задачи от специалиста требуется грамотная математическая постановка задачи, ее формализация, обоснование и выбор наиболее эффективного метода расчета, а также умение производить оценку адекватности и точности полученных результатов.
MathCAD
с помощью встроенных функций решается
только задача поиска локального
экстремума. Чтобы найти глобальный
максимум (или минимум), требуется либо
сначала вычислить все их локальные
значения и потом выбрать из них наибольший
(наименьший), либо предварительно
просканировать
с
некоторым шагом рассматриваемую область,
чтобы выделить из нее подобласть
наибольших (наименьших) значений функции
и осуществить поиск глобального
экстремума, уже находясь в его окрестности.
Второй вариант таит в себе опасность
уйти в окрестность другого локального
экстремума, но часто может быть
предпочтительнее при решении практических
задач.
Для
поиска локальных экстремумов имеются
две встроенные функции, которые могут
применяться как в пределах вычислительного
блока, так и автономно.
-
Minimize
(f, x1, … ,хn)
– вектор значений аргументов, при
которых функция f
достигает минимума; -
Maximize
(f, x1, … ,хn)
– вектор значений аргументов, при
которых функция f
достигает максимума; -
f(x1,
… ,хn)–
заданная целевая функция; -
x1,
… ,хn
– аргументы, по которым производится
минимизация(максимизация).
Всем
аргументам функции f
предварительно следует присвоить
некоторые значения, причем для тех
переменных, по которым производится
минимизация, они будут восприниматься
как начальные приближения.
Пример
7. Поиск локального экстремума в
окрестности заданной точки.
Найти
максимум функции
в
окрестности точки (4;5).
Ответ:
функция имеет максимум, равный 4, в
точке(1;1).
Пример
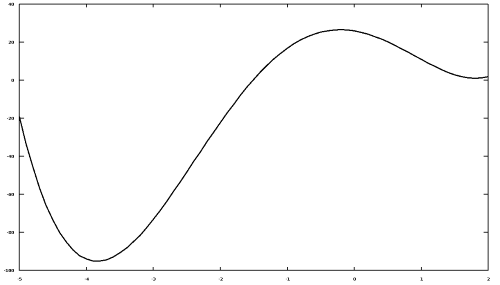
8. Поиск условного экстремума функции.
Найти
минимум функции
при
условиях
Решение.
-
Задаем
целевую функцию, матрицу системы
ограничений и вектор правой части этой
системы -
Задаем
начальное приближение решения.
3.
С помощью вычислительного блока находим
минимальное значение функции и значение
вектора, на котором достигается это
значение.
Ответ:
минимум функции равен 32.155 и достигается
в точке (1,0.623,0.343,1,0.048,1).
Контрольные
вопросы.
-
Что
значит отделить корень
уравнения
?
-
Какие
функции могут быть использованы для
решения нелинейных уравнений? -
Опишите
конструкцию вычислительного блока. -
В
чем состоит градиентный метод? -
В
чем различие между функциями Find
и Minner
для решения систем нелинейных уравнений? -
Где
необходимо расположить ограничительные
условия при решении задачи оптимизации? -
Как
ограничено число ограничительных
условий для решения задачи оптимизации?
Варианты заданий
Вариант
1
-
Решить
уравнение
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
-
Найти
максимум функции.
Вариант
2
-
Решить
уравнение
,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
.
-
Найти
максимум функции
при
ограничении
.
Вариант
3
-
Решить
уравнение
,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
.
-
Найти
максимум функциипри
ограничении.
Вариант
4
-
Решить
уравнение
,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
.
-
Найти
максимум функции
.
Вариант
5
-
Решить
уравнение
,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
.
-
Найти
минимальное и максимальное значения
функции
.
Вариант
6
-
Решить
уравнение
,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
.
-
Найти
максимум функции
при
условиях
,
,
.
Вариант
7
-
Решить
уравнение
,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
.
Выполнить
проверку. -
Найти
минимум функции
при
условиях
,
,
.
Вариант
8
-
Решить
уравнение
,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
.
Выполнить
проверку. -
Найти
минимум функции
при
условиях
,
,
.
Вариант
9
-
Решить
уравнение
,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
.
Выполнить
проверку -
Найти
минимум функции
при
условиях
,
,
.
Вариант
10
-
Решить
уравнение, предварительно оделив корни
7,
,
используя встроенные функции root
и
Find.
Сравнить полученные решения. -
Найти
все корни полинома
.
Проиллюстрировать решение графически. -
Решить
систему нелинейных уравнений:
.
Выполнить проверку.
-
Найти
минимум функции
при
условиях
,
,
.
Тема
4:
Элементы программирования в пакете
инженерных расчетов MathCAD.
Цель
работы:
Изучение возможностей символьного
пакета MathCAD для программирования условных
и циклических выражений. Приобретение
навыков написания простейших
программ.
Используемые
программные средства:
Пакет MathCAD.
Теоретические
сведения.
Д
повышения гибкости Mathcad в системе
предусмотрена возможность написания
небольших программ для решения тех
проблем, которые не могут быть реализованы
стандартными средствами. Обычно прибегать
к программированию приходится в тех
случаях, когда стандартные средства
либо не могут решить задачу, либо
неэффективны. Для написания программ
используется программная палитра,
которая вызывается кнопкой панели
управления. Как видно, всего имеется 10
операторов, из которых и строится
программа. Причём операторы должны
вводиться только из палитры, писать их
“вручную” не рекомендуется.
Практическая
часть
Для
примера приведём простую программу
возвращающую 1, если число чётное, и 0 в
противном случае.
–
начинаем создание программы с кнопки
Add
Line.
Вертикальная линия играет роль операторных
скобок.
–
оператор локального присваивания. В
программе нельзя использовать оператор
присваивания “:=”, вместо него
используется оператор локального
присваивания, отличие которого заключается
в том, что локальная переменная определена
только внутри своего блока и при выходе
из программы теряет своё значение.
Пример:
–
условный
оператор создаёт конструкцию видa:
где
первый операнд выполняется, если
справедливо условие являющееся вторым
операндом. Из всех программных операторов
оператор условия является, пожалуй,
наиболее важным. Его приходится
использовать практически во всех
создаваемых алгоритмах. Как уже показано,
условный оператор if
имеет два маркера. В правый маркер
вводится условие, в левый – операция,
которая должна быть проделана в случае,
если условие выполнится (если же оно не
выполнится, система просчитывает
программу, пропуская данный фрагмент).
В маркер оператора может быть внесено
несколько выражений условий или операций.
В случае задания комплекса условий
будьте предельно внимательны и всегда
помните, чем отличаются формы его
определения через программный блок и
с использованием логического умножения.
Неверное задание формы комплекса условий
– самая распространенная ошибка при
работе с данным оператором.
Пример:
Функция возвращает остаток от деления
на 2:
После
того, как функция определена, она может
использоваться наравне со встроенными
функциями.
С оператором if
возможны более сложные конструкции при
использовании ещё одного оператора
–
реализующего альтернативу. Аналог
традиционной конструкции Если
… То … Иначе … .
Т.е. оператор предназначен для определения
того
действия, которое должно быть выполнено,
если условие оператора if
окажется истинным. Одновременно может
быть использовано несколько условных
операторов if.
Оператор otherwise
в таком случае будет задействован, если
не выполняется условия всех операторов
if.
–
оператор
цикла обеспечивает повторяющиеся
вычисления, если известно количество
шагов.
Первый операнд – переменная
цикла, это интервальная переменная и
её
значения определены во втором операнде.
Третий операнд – тело цикла может
состоять из блока операторов и выполняется
пока не исчерпаются все значения
переменной цикла.
Пример:
Рассмотрим
программу упорядочения чисел по убыванию
в одномерном массиве. Пусть дан массив
чисел: Мы воспользуемся вложенными
циклами и в качестве тела цикла по i
используем ещё один цикл по j.
З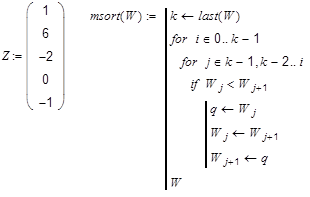
реализован простейший алгоритм
сортировки, так называемый “метод
пузырька”. На самом деле, большие
числа как бы всплывают наверх при каждом
шаге цикла по i, в то время как в цикле
по j на каждом шаге происходит сравнение
пары чисел и замена, если большее число
находится ниже, причём эта замена
осуществляется снизу.
О
что в системе имеется стандартная
функция сортировки sort().
Примечание:
второй цикл мы организовали с отрицательным
шагом от конечного значения к начальному.
Можно использовать программные
возможности Mathcad просто для задания
функций более сложного вида.
–
оператор
break
введён для повышения гибкости
программирования и позволяет закончить
цикл досрочно, не исчерпав всего списка.
Как правило, ввиду того, что цикл бывает
нужным остановить при выполнении
некоторого условия, данный оператор
почти всегда используется с условным
оператором if.
Р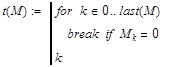
следующую задачу: нам необходимо найти
первое вхождение 0 в числовом массиве
и вернуть его индекс. Мы приводим
работающую программу, где введена
функция last(M)
которая возвращает последний индекс
массива. Возвращаемым значением программы
является последний выполняемый оператор
– k.
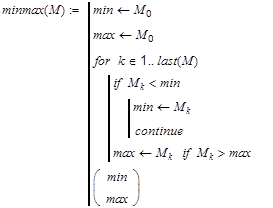
ещё один полезный оператор позволяющий
прервать выполнение текущей итерации
и перейти к следующей.
Рассмотрим
например задачу нахождения максимального
и минимального элемента
массива.
Действительно, если
,
то нет смысла проверять
,
а лучше перейти к следующему шагу цикла.
–
оператор цикла с предусловием используется
в тех случаях, когда заранее неизвестно
количество шагов необходимых для решения
задачи. Условие проверяется перед
началом каждого шага цикла.
Реализуем,
например алгоритм вычисления квадратного
корня a
используя
итерационную формулу
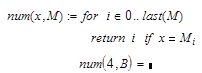
оператор
return
служит для прекращения работы программы
и возврата результата. Обычно данный
оператор используется при описании
действий алгоритма в случае ошибочной
ситуации.
Допустим нам необходимо
вычислить позицию первого вхождения
числа в массив.
Рассмотрим
в качестве ещё одного примера вопрос,
как программным способом построить
скалярное произведение.
В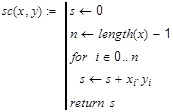
квадрат модуля вектора
Оператор
return
здесь может быть опущен.
В качестве
возвращаемого значения в программе
используется результат последней
операции. Обратите внимание, что в
программах мы не пользуемся оператором
присваивания :=, а вводим оператор
локального присваивания. Переменные,
определённые в программе, теряют значение
при выходе из неё.
–
оператор
on
error
служит для обработки ошибочных ситуаций
типа “деления на нуль”. Данный
оператор по своему синтаксису полностью
соответствует условному оператору if.
В правый его маркер следует внести
величину или выражение, ошибка в
вычислении которого должнв быть
зарегистрирована. В левом маркере
следует прописать условие, которое
должно быть выполнено в случае ошибочной
ситуации.
Например, нам необходимо
описать функцию
,
чтобы не было особенности в 0.
тогда:
Примечание.
Оператор
on
error
может
использоваться в арифметических
выражениях.
Варианты
заданий
Вариант
1
-
Составить
программу которая будет менять местами
2 строки матрицы. -
Используя
оператор on error для предотвращения
появления ошибки “деление на нуль”,
вычислить функцию
.
-
Написать
программу, где функции, возвращающая
–1, 0 или 1 в зависимости от знака аргумента
(соответственно «-», 0, «+»).
Вариант
2
-
Составить
программу, которая будет выводить сумму
геометрической прогрессии, при заданных
значениях
.
-
Написать
программу по выводу матрицы размером
3х3, где на второстепенной диагонали
стояли бы 1. -
Вычислить
значение функции
.
Вариант
3
-
Вычислить
сумму чисел 1+2+3+….+n. -
Для
x изменяющего от -2 до 2 вычислить значение
.
-
Составить
программу по вычислению длины вектора.
Вариант
4
1.Создайте
программу pr(n)
для вычисления произведения
чисел
1*2*3*….*n.
2.Создайте
программу для вычисления и вывода двух
корней квадратного уравнения
.
3.Используя
оператор on error для предотвращения
появления ошибки “деление на нуль”,
вычислить функцию
.
Вариант
5
-
Создайте
программу для вычисления и вывода двух
корней квадратного уравнения
f(x)=ax2+bx+c. -
Дано
натуральное число n, действительное x.
Вычислить
.
-
Написать
программу по выводу на экран знака «+»
(«-»), если значение
.
Вариант
6
-
Написать
программу, которая будет выводить
единичную матрицу. -
Вычислить
значение
,
используя итерационную процедуру
В
качестве приближенного значения корня
квадратного берется такое значение
,
которое удовлетворяет условию
,
где
–
заданная точность вычисления. -
Вычислить
,
где
меняется
от 0 до 10.
Вариант
7
-
Составить
программу, которая будет выводить сумму
арифметической прогрессии при заданных
значениях
.
-
Составим
программу для вычисления переменной
z по формуле
.
-
Написать
программу, которая выводит абсолютное
значение функции
.
Вариант
8
-
Определить
функцию, которая равна 1, если аргумент
размещён между чётным и нечётным числом,
и 0 в противном случае. -
Вычислить
сумму бесконечной геометрической
прогрессии со знаменателем 0,4 и начальным
элементом -8. -
Написать
программу по выводу на экран матрицы,
каждый элемент которой будет вычисляться
по правилу:
,
где
и
–
элементы матриц соответственно
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аннотация: В данной главе рассматриваются решение задач поиска минимума (максимума) в Octave. В первой части на примерах решения практических задач рассматривается функция qp предназначенная для поиска минимума функции одной или нескольких переменных с ограничениями. Вторая часть целиком посвящена задачам линейного программирования.
Изучение оптимизационных задач начнём с обычных задач поиска минимума (максимума) функции одной или нескольких переменных.
10.1 Поиск экстремума функции
Для решения классических оптимизационных задач с ограничениями в Octave можно воспользоваться следующей функцией ![[x, obj, info, iter] = sqp(x_0, phi, g, h, lb, ub, maxiter, tolerance)](https://intuit.ru/sites/default/files/tex_cache/a4a647735091625565821c483eed8c4c.png)
Найти минимум функции 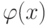
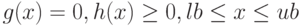
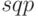
Аргументами функции 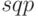
Функция 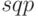
-
— точка, в которой функция, достигает своего минимального значения,
-
— минимальное значение функции,
-
— параметр, характеризующий корректность решения оптимизационной задачи, (если функция sqp возвращает значение info = 101, то задача решена правильно),
-
— реальное количество итераций при решении задачи.
Рассмотрим несколько примеров использования функции 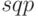
Пример 10.1. Найти минимум функции
При решении задачи оптимизации с помощью функции sqp необходимо иметь точку начального приближения. Построим график функции 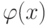
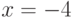
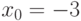
function obj = phi(x) obj = x^4+3*x^3-13*x^2-6*x+26; endfunction [x, obj, info, iter]= sqp(-3, @phi) % Результаты решения x =-3.8407 obj =-95.089 info = 101 iter = 5
Листинг
10.1.
Поиск минимума функции (пример 10.1)
Минимум функции 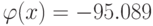
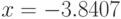
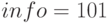
Рис.
10.1.
График функции примера 10.1
Рассмотрим пример поиска минимума функции нескольких переменных.




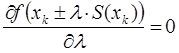
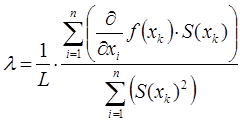
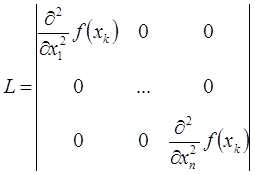

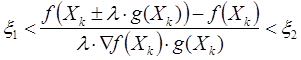

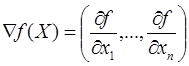
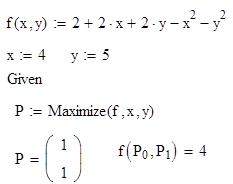
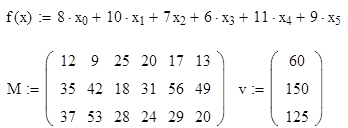
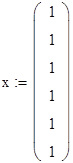
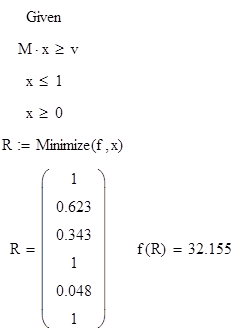
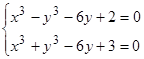 .
.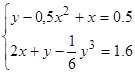 .
.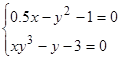 .
.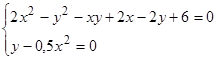 .
.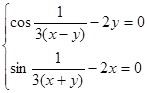 .
.
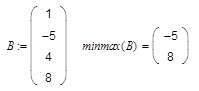
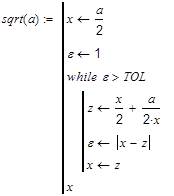
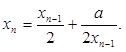
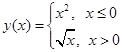 .
. .
.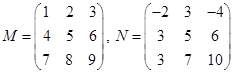
 — точка, в которой функция, достигает своего минимального значения,
— точка, в которой функция, достигает своего минимального значения,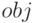 — минимальное значение функции,
— минимальное значение функции, — параметр, характеризующий корректность решения оптимизационной задачи, (если функция sqp возвращает значение info = 101, то задача решена правильно),
— параметр, характеризующий корректность решения оптимизационной задачи, (если функция sqp возвращает значение info = 101, то задача решена правильно), — реальное количество итераций при решении задачи.
— реальное количество итераций при решении задачи.