Как найти максимум функции видео

Сегодня на уроке мы выясним, какая точка называется точкой
максимума функции, а также узнаем, какая точка называется точкой минимума
функции. Сформулируем теорему Ферма. Приведём достаточные условия того, что
стационарная точка является точкой экстремума.

Прежде чем приступить к рассмотрению новой темы, давайте вспомним,
что на нашем прошлом занятии мы исследовали на возрастание и убывание функцию .

Сейчас вы видите график этой функции.

Давайте рассмотрим окрестность точки , то
есть некоторый интервал, содержащий эту точку. Из рисунка видно, что существует
такая окрестность точки , что
наибольшее значение данная функция в этой окрестности принимает в точке .
Например, на интервале  функция
принимает наибольшее значение, равное , в
точке .
Таким образом, точку  называют
точкой максимума функции.

Рассмотрим окрестность точки . Из
рисунка видно, что существует такая окрестность точки , что
наименьшее значение данная функция в этой окрестности принимает в точке .
Например, на интервале  функция
принимает наименьшее значение, равное , в
точке .
Точку  называют
точкой минимума функции.

Сформулируем определение.

Точка  называется
точкой максимума функции , если
существует такая окрестность точки , что
для всех  из
этой окрестности выполняется неравенство .

Так, например, точка  является
точкой максимума функции , так
как  и при
всех значениях  верно
неравенство .

Точка  называется
точкой минимума функции , если
существует такая окрестность точки , что
для всех  из
этой окрестности выполняется неравенство .

Например, точка  является
точкой минимума функции , так
как  и при
всех значениях  верно
неравенство .

Точки минимума и точки максимума называются точками экстремума.

Теперь познакомимся с теоремой Ферма. Пусть функция  определена
в некоторой окрестности точки  и
имеет производную в этой точке. Тогда сформулируем утверждение, которое и
называют теоремой Ферма.

Если  – точка экстремума дифференцируемой
функции , то .

Доказательство этой теоремы приводится в курсе высшей математики.

Геометрический смысл теоремы

Например, рассмотренная выше функция  имеет
максимум в точке . .

Функция  имеет
минимум в точке . , .

Таким образом, мы убедились, что значение производной в точке
экстремума функции равно нулю.

Но отметим, что если , то
этого недостаточно, чтобы утверждать, что  обязательно
является точкой экстремума функции .

Так, например, производная функции  равна
.
Производная равна 0 в точке 0. Однако точка  не
является точкой экстремума, так как данная функция возрастает на всей числовой
оси.

Получается, что не всегда корень уравнения  является
точкой экстремума. Но точки экстремума дифференцируемой функции нужно искать
только среди корней уравнения .

Точки, в которых производная равна нулю, называют стационарными.

Из предыдущих занятий вам известно, что функция  не
имеет производной в точке . При
этом эта точка является точкой минимума данной функции.

Точки, в которых функция имеет производную, равную нулю, или
недифференцируема, называют критическими точками этой функции.

То есть точка  –
критическая точка функции .

Таким образом, чтобы точка  была
точкой экстремума функции ,
необходимо, чтобы эта точка была критической точкой данной функции.

Теперь приведём достаточные условия того, что стационарная
точка является точкой экстремума. Это будут условия, при выполнении которых
стационарная точка является точкой максимума или минимума.

Итак, пусть функция  дифференцируема
на интервале ,  и .
Тогда:

1) если при переходе через стационарную точку  функции
 её
производная меняет знак с «плюса» на «минус», то есть  слева
от точки  и  справа
от точки , то  –
точка максимума функции ;

2) если при переходе через стационарную точку  функции
 её
производная меняет знак с «минуса» на «плюс», то  –
точка минимума функции .

Давайте найдём точки экстремума функции  и значения функции в этих точках.

А сейчас выполним несколько заданий.

Задание первое. Найдите стационарные
точки функций:

а) ; б) .

Решение.

Задание второе. Найдите точки
экстремума функций:

а) ; б) .

Решение.

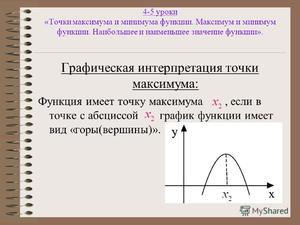Поиск точки максимума и минимума функции – довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом “экстремум” подразумевают наибольшее или наименьшее значение функции. Это не совсем верно. Значение может быть наибольшим или минимальным, но не являться экстремумом.

Глобальный и локальный максимум

Максимум бывает локальным или глобальным. Точка локального максимума – это аргумент, который при подстановке в f(x) даёт значение не меньше, чем в других точках из области около этого аргумента. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум – это локальное экстремальное – минимальное или максимальное – значение.

Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой “найдите точку максимума функции на отрезке”. Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.

Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:

• экстремума, если она попадает в указанный отрезок,
• разрыва,
• ограничивающей заданный отрезок.

Исследование

Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):

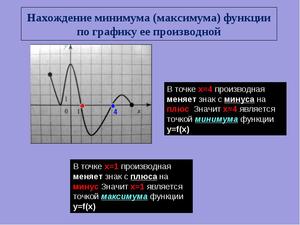1. Найти область допустимых аргументов и пересечения этой области с областью исследования.
2. Выявить асимптоты. Они равны пределу при стремлении аргумента к точкам разрыва.
3. Определить первую производную и вычислить экстремальные точки и выяснить поведение функции в окрестности этих точек.
4. Рассчитать значение f(x) в точках, ограничивающих область исследования.
5. Сравнить экстремум со значением функции в точках разрыва и на концах интервала. Определить среди них наибольшее.

Теперь подробно разберем каждый шаг и рассмотрим некоторые примеры.

Область допустимых аргументов

Область допустимых аргументов – это те x, при подстановке которых в f(x) она не престаёт существовать.Область допустимых аргументов ещё называют областью определения. Например, y = x^2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.

Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения.

Асимптоты

Асимптота – это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность.

Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. А если бы определялся, то аргумент, при котором достигается максимум, совпал бы с точкой пересечения асимптоты и оси аргументов.

Производная и экстремумы

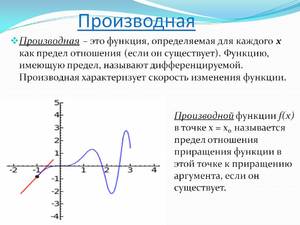Производная – это предел изменения функции при стремящемся к нулю изменении аргумента. Что это значит? Возьмём небольшой участок из области допустимых аргументов и посмотрим как изменится здесь f(x), а потом уменьшим этот участок до бесконечно малого размера, в этом случае f(x) станет изменяться так же, как и некая более простая функция, которая именуется производной.

Значение производной в определенной показывает под каким углом проходит касательная к функции в выбранной точке. Отрицательное значение говорит о том, что функция здесь убывает. Аналогично положительная производная говорит о возрастании f(x). Отсюда появляются два условия.

1) Производная в точке экстремума либо нулевая, либо неопределенная. Это условие необходимое, но недостаточно. Продифференцируем y = x^3, получим уравнение производной: y = 3*x^2. Подставим в последнее уравнение аргумент “0”, и производная обратится в нуль. Однако, это не экстремум для y = x^3. У неё не может быть экстремумов, она убывает на всей оси аргументов.

2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает – производная была положительной, а стала отрицательной.

После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).

Концы интервала и сравнение результатов

При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.

Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.

Для задачи с формулировкой “Найдите точку минимума функции” необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.

Видео