Рассмотрим пример решения задачи линейной оптимизации в Excel
Дана оптимизационная задача в виде таблицы
| Ресурсы | Нормы затрат на изготовление 1 ед. кровати | Нормы затрат на изготовление 1 ед. шкафа | Общее количество ресурсов |
| Сосна | 0,8 | 1,4 | 200 |
| Дуб | 1,2 | 0,6 | 150 |
| Трудоемкость (человеко-часов) | 4 | 5 | 800 |
| Прибыль от продажи одной единицы | 9 | 11 |
По условию задачи составим целевая функция, которая будет иметь вид
Z=9x1+11x2
Ограничения
0,8x1+1,4x2≤200
1,2x1+0,6x2≤150
4x1+5x2≤800
x1,x2≥0
В Excel создаём таблицу с формулами, пример показан ниже
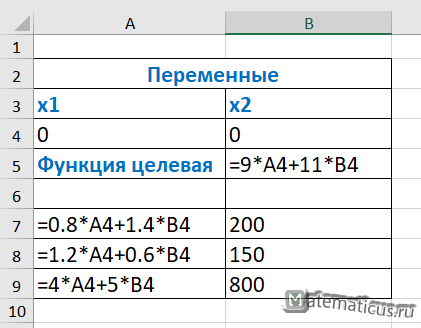
Формулы можно скопировать из этой таблицы
| Переменные | |
| x1 | x2 |
| 0 | 0 |
| Функция целевая | =9*A4+11*B4 |
| =0.8*A4+1.4*B4 | 200 |
| =1.2*A4+0.6*B4 | 150 |
| =4*A4+5*B4 | 800 |
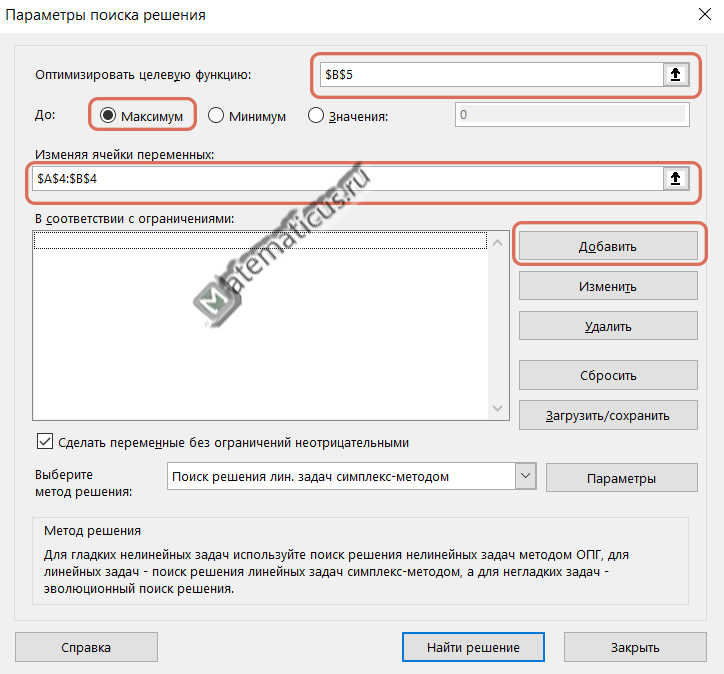
Затем переходим на вкладку Данные -> Поиск решения

Выбираем ячейку, в которой надо оптимизировать целевую функцию, в нашем случае B5. Ставим галочку на максимум, затем выбираем ячейки с изменяемыми переменными это x1 и x2 – A4 и B4 и прописываем ограничения, нажимаем на кнопку добавить.
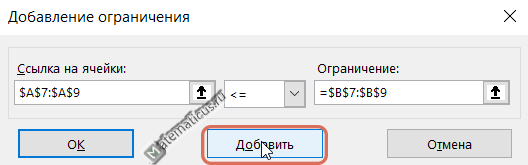
Из условия задачи значения выражений левой части меньше или равно значений правой части. Указываем сразу диапазон значений. Жмём на кнопку добавить ограничения.

И выбираем из списка метод решения – решения линейной задачи симплекс методом.
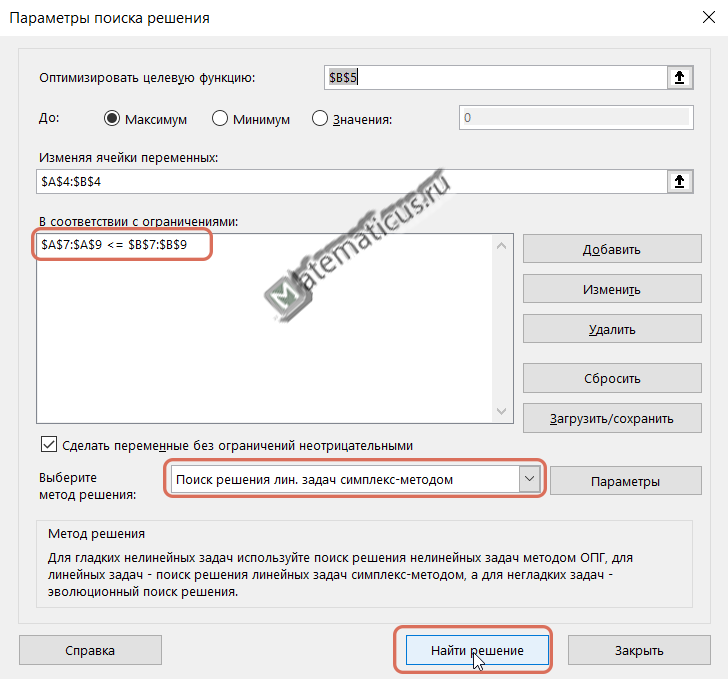
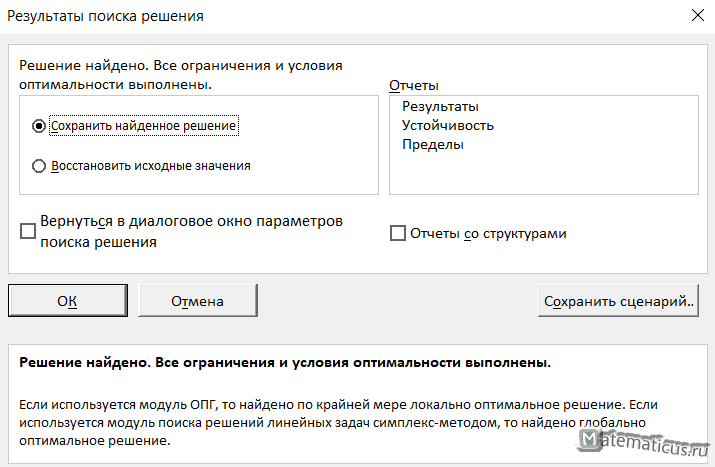
Вылетает информационное окно — результаты поиска решения, жмём Ок.
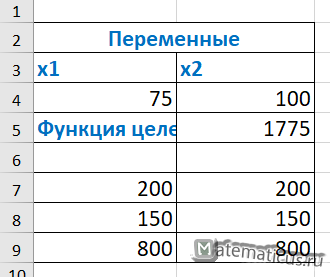
| Переменные | |
| x1 | x2 |
| 75 | 100 |
| Функция целевая | 1775 |
| 200 | 200 |
| 150 | 150 |
| 800 | 800 |
В результате, в исходной таблице появятся значения неизвестных переменных и значение целевой функции. В итоги мы получили оптимизированные значения переменных, на этом задачи оптимизации линейного программирования решена.
![]() 5005
5005
Простейшие задачи
Наипростейшая задача
1-задача.
Найти максимум линейной функции
|
|
(1.1) |
При ограничении
|
|
(1.2) |
Ответ очевиден
??
Простейшая задача
2-задача.
Найти максимум линейной функции
|
|
(1.3) |
При ограничении
|
|
(1.4) |
Ответ очевиден ??
Простенькая задача
3-задача.
Найти максимум линейной функции
|
|
(1.5) |
При ограничениях
|
|
(1.6) |
|
|
(1.7) |
Ответ не очевиден
??
Пользуясь (1.6) получим
|
|
Подставим
![]()
из (1.8) в (1.5) получим
|
|
(1.8) |
|
|
(1.9) |
|
|
(1.10) |
Ответ очевиден ?? см.задачу
1
Простая задача
4-задача.
Найти максимум линейной функции
|
|
(1.11) |
При ограничениях
|
|
(1.12) |
|
|
(1.13) |
Ограничение (1.12) можно рассматривать
как систему из одного уравнения с двумя
неизвестными. По теореме Кронекера-Капелли
одна переменная свободная, другая через
нее выражается (базисная). Пусть
![]()
свободная переменная, тогда
![]()
вычислим по формуле
![]() .
.
Выразим ЦФ через свободную переменную
![]() .
.
|
|
(1.4) |
Т.О имеем задачу, похожую на задачу
1.
|
|
(1.4) |
Вспомним ограничения
|
|
(1.12) |
|
|
(1.13) |
Ответ очевиден ??
-
Ограничения позволяют выразить часть
неизвестных через свободные переменные. -
ЦФ тоже можно выразить через свободные
переменные. -
Свободные переменные выбираем так,
чтобы максимум был очевиден. Для этого
ЦФ должна иметь вид типа
. Точнее

, где

больше нуля (для

больших нуля).
5-задача. Чуть-чуть
сложнее
Найти максимум линейной функции
|
|
(1.14) |
При ограничениях
|
|
(1.15) |
|
|
(1.16) |
Преобразуем (1.15) в равенство, для этого
введем балансовую переменную
![]() .При
.При
этом
![]()
|
|
(1.17) |
|
|
(1.18) |
Ограничение (1.17) можно рассматривать
как систему из одного уравнения с тремя
неизвестными. По теореме Кронекера-Капелли
две переменные свободные, третья через
них выражается (). Пусть
![]()
базисная переменная, тогда она вычисляется
через свободные
![]()
и по формуле
.
|
|
(1.19) |
|
|
ЦФ уже выражена через свободные
переменные
![]()
и
![]()
формула (1.14). Глядя на (1.14), трудно решить
эту задачу. Выберем в качестве базисной
переменной
![]() ,
,
тогда она вычисляется через свободные
![]()
и
![]() по
по
формуле
|
|
(1.20) |
Выразим ЦФ через свободные
![]()
и
![]() по
по
формуле
|
|
(1.21) |
Т.О имеем задачу, похожую на задачу
1 . Все коэффициенты в ЦФ отрицательны
|
|
(1.22) |
Вспомним ограничения
|
|
(1.12) |
|
|
(1.13) |
Ответ очевиден ??
5-задача другое оформление
той же идеи.
|
Свободные |
|||||
|
Базисная переменная |
х1 |
х2 |
х3 |
1 |
|
|
x3 |
1 |
1 |
1 |
10 |
(1.19) |
|
F |
-1 |
-2 |
0 |
110 |
(1.14) |
После вывода
![]()
из базиса и введения в него
![]() ,
,
|
Свободные |
|||||
|
Базисная переменная |
х1 |
х2 |
х3 |
1 |
|
|
X2 |
1 |
1 |
1 |
10 |
(1.20) |
|
F |
1 |
0 |
2 |
130 |
(1.22) |
4
Соседние файлы в папке МОР 1 лекция
- #
- #
- #
В линейном программировании используется графический метод, с помощью которого определяют выпуклые множества (многогранник решений). Если основная задача линейного программирования имеет оптимальный план, то целевая функция принимает значение в одной из вершин многогранника решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Введение в графический метод
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно.
Возможно эта страница вам будет полезна:
Задача линейного программирования в стандартной форме с двумя переменными имеет вид:
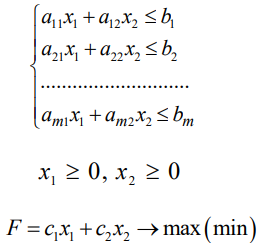
Эти задачи допускают простое геометрическое истолкование.
Рассмотрим вначале геометрическое истолкование системы ограничений задачи. Каждую совокупность значений переменных 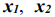 можно изобразить точкой на плоскости, если ввести систему координат и по одной оси откладывать
можно изобразить точкой на плоскости, если ввести систему координат и по одной оси откладывать  , а по другой
, а по другой  . Выясним, что геометрически означает совокупность решений одного отдельно взятого неравенства:
. Выясним, что геометрически означает совокупность решений одного отдельно взятого неравенства:
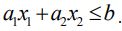
Рассмотрим прямую на плоскости с уравнением:
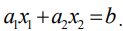
Эта прямая делит плоскость на две полуплоскости, в одной из которых справедливо наше неравенство, а в другой — противоположное. Для того чтобы проверить, какая из полуплоскостей состоит из решений нашего неравенства, следует взять точку из какой-либо полуплоскости и проверить, выполняется ли наше неравенство в этой точке. Множество решений отдельно взятого линейного неравенства представляет собой полуплоскость. Для системы из нескольких таких неравенств точки, координаты которых удовлетворяют всем неравенствам одновременно, должны находиться во всех соответствующих полуплоскостях, т. е. принадлежать теоретико-множественному пересечению этих полуплоскостей. Множество точек на плоскости, удовлетворяющих системе ограничений, составляет, таким образом, некоторую выпуклую многоугольную область (область допустимых решений). Условия неотрицательности переменных 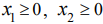 приводят к тому, что эта область находится в первой координатной четверти.
приводят к тому, что эта область находится в первой координатной четверти.
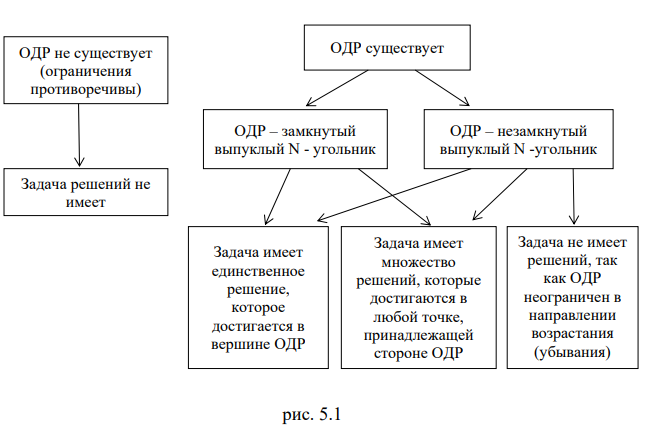
При решении двумерных задач линейного программирования возможны следующие ситуации (ОДР — область допустимых решений):
Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция 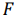 принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня
принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня 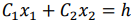 (где
(где 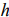 — некоторая постоянная), проходящую через многоугольник решений, и будем передвигать ее в направлении вектора
— некоторая постоянная), проходящую через многоугольник решений, и будем передвигать ее в направлении вектора 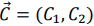 до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи.
до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи.
Отметим, что при нахождении решения задачи (5.1)-(5.3) могут встретиться случаи, изображенные на рис. 5.2- 5.5. Рис.5.2 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке 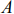 . Из рис. 5.3 видно, что максимальное значение целевая функция принимает в любой точке отрезка
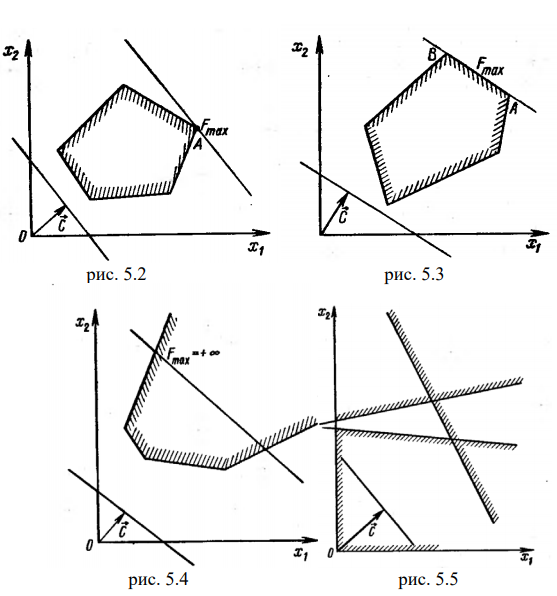
. Из рис. 5.3 видно, что максимальное значение целевая функция принимает в любой точке отрезка 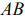 . На рис.5.4 изображен случай, когда целевая функция неограничена сверху на множестве допустимых решений, а на рис.5.5 — случай, когда система ограничений задачи несовместна, т. е. если система неравенств (5.1) при условии (5.2) не имеет решений.
. На рис.5.4 изображен случай, когда целевая функция неограничена сверху на множестве допустимых решений, а на рис.5.5 — случай, когда система ограничений задачи несовместна, т. е. если система неравенств (5.1) при условии (5.2) не имеет решений.
Также отметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня 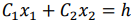 передвигается не в направлении вектора
передвигается не в направлении вектора 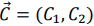 , а в противоположном направлении.
, а в противоположном направлении.
Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.
Алгоритм графического метода решении задач линейного программирования
- Построить область допустимых решений.
- Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, построить нормаль линий уровня
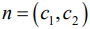 и одну из линий уровня, имеющую общие точки с этой областью.
и одну из линий уровня, имеющую общие точки с этой областью. - Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум — в противоположном направлении.
- Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
- Если задача линейного программирования имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимальных решений вычислить значение целевой функции на этих решениях.
Пример задачи №1
Пусть имеется два станка 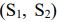 , на каждом из которых можно производить два вида продукции
, на каждом из которых можно производить два вида продукции 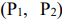 . Станок
. Станок 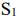 производит единицу продукции
производит единицу продукции  за 1 час, а единицу продукции
за 1 час, а единицу продукции 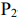 — за 2 часа. Станок
— за 2 часа. Станок 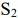 затрачивает на единицу продукции
затрачивает на единицу продукции  — 2 часа, а на единицу продукции
— 2 часа, а на единицу продукции 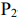 — 1 час. Станок
— 1 час. Станок 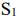 может работать в сутки не более 10 ч., а станок
может работать в сутки не более 10 ч., а станок 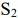 — не более 8 ч. Стоимость единицы продукции
— не более 8 ч. Стоимость единицы продукции  составляет
составляет 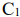 руб., а стоимость единицы продукции
руб., а стоимость единицы продукции 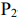 —
— 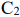 руб. Требуется определить такие объемы выпуска продукции
руб. Требуется определить такие объемы выпуска продукции  и
и 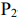 на станок, чтобы выручка от реализации производственной продукции была максимальной.
на станок, чтобы выручка от реализации производственной продукции была максимальной.
Решение:
Для наглядности сведем условие задачи в таблицу 5.1.
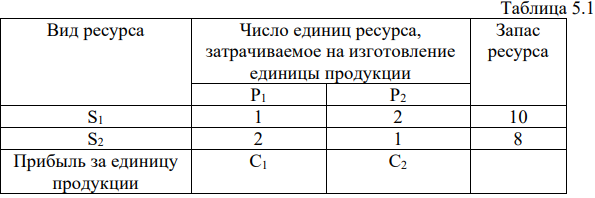
Составим математическую модель задачи. Обозначим через  и
и  количества продукции
количества продукции  и
и 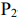 , которые планируется произвести на каждом отдельном станке. Стоимость произведенной продукции
, которые планируется произвести на каждом отдельном станке. Стоимость произведенной продукции 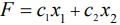 . Мы должны назначить
. Мы должны назначить  и
и  так, чтобы величина
так, чтобы величина 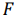 была максимальной.
была максимальной.
Переменные 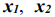 не могут принимать произвольных значений. Их значения ограничены условиями производства, а именно тем, что станки могут работать ограниченное время. На изготовление продукции
не могут принимать произвольных значений. Их значения ограничены условиями производства, а именно тем, что станки могут работать ограниченное время. На изготовление продукции  станок
станок 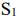 тратит
тратит 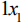 часов, а на изготовление продукции
часов, а на изготовление продукции 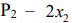 часов. Поскольку время работы станка
часов. Поскольку время работы станка 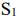 не превосходит 10 ч, то величины
не превосходит 10 ч, то величины  и
и  должны удовлетворять неравенству:
должны удовлетворять неравенству:
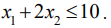
Аналогично можно получить неравенство для станка 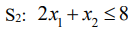 . Кроме того, величины
. Кроме того, величины  и
и  не могут быть отрицательными:
не могут быть отрицательными:
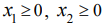
по смыслу задачи. Такие задачи кратко записываются следующим образом:
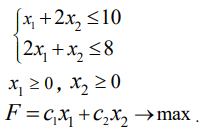
Итак, математическая модель задачи: найти такой план выпуска продукции 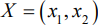 , удовлетворяющий системе (5.4) и условию (5.5), при котором функция (5.6) принимает максимальное значение.
, удовлетворяющий системе (5.4) и условию (5.5), при котором функция (5.6) принимает максимальное значение.
Решения, удовлетворяющие системе ограничений (5.4) и требованиям неотрицательности (5.5), являются допустимыми, а решения, удовлетворяющие одновременно и требованию (5.6) — оптимальными.
Рассмотрим геометрическое истолкование задачи:
Возьмем 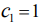 и
и 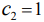 .
.
Математическая модель задачи:
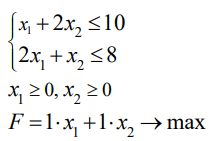
Построение области допустимых решений целевой функции 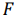 :
:
1.Построим прямоугольную систему координат. Так как,  и
и  неотрицательны, то можно ограничиться рассмотрением первого квадранта.
неотрицательны, то можно ограничиться рассмотрением первого квадранта.
Рассмотрим первое ограничение:
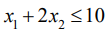
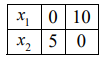
Рассмотрим второе ограничение:
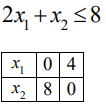
Отложим полученные точки на числовых осях и найдем полуплоскости, которые соответствуют данным ограничениям.
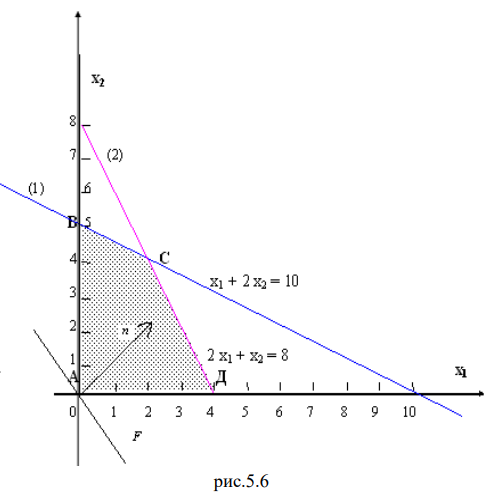
Двумерные задачи линейного программирования решаются графически.
Для случая 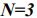 можно рассмотреть трехмерное пространство и целевая функция будет достигать своего оптимального значения в одной из вершин многогранника.
можно рассмотреть трехмерное пространство и целевая функция будет достигать своего оптимального значения в одной из вершин многогранника.
В общем виде, когда в задаче участвуют 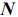 неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в
неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в 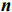 -мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах.
-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах.
Для решения ЗЛП любой размерности существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.
Графический метод решения задач линейного программирования
Множество решений системы ограничений задачи ЛП образует область допустимых решений (ОДР).
Графический метод решения задач ЛП основывается на возможности графического изображения ОДР и нахождении среди них оптимального решения. Этот метод применяется для задач ЛП с одной, двумя или тремя переменными, для которых система ограничений стандартна (состоит из неравенств), и задач со многими переменными, для которых система ограничений содержит 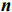 переменных и
переменных и 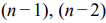 или
или 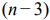 линейно независимых уравнений.
линейно независимых уравнений.
ОДР задачи строится как пересечение областей решений каждого из ограничений и представляет собой выпуклый многогранник (многоугольник, интервал). Область допустимых решений может содержать бесконечное число точек. Для того чтобы найти решение ЗЛП, нужно рассмотреть поведение целевой функции в ОДР.
I. Одномерное пространство переменных
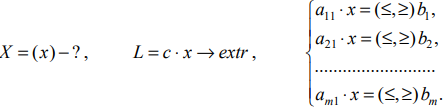
Решение системы ограничений есть пересечение лучей, что определяет интервал решений (ОДР): точку, отрезок, луч или всю числовую прямую.
Значения целевой функции в угловых точках интервала решений определяют наименьшее (наибольшее) значение исследуемой целевой функции, монотонно убывающей (если 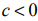 ) или монотонно возрастающей (если
) или монотонно возрастающей (если 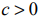 ).
).
В случае неограниченности ОДР задача ЛП может и не иметь оптимума.
II. Двумерное пространство переменных
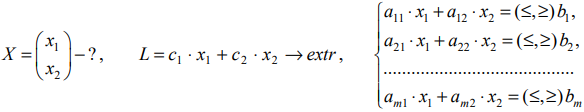
Областью решений линейного неравенства
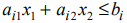
является одна из полуплоскостей, на которые прямая делит всю координатную плоскость. Для того, чтобы определить, какая из двух координатных полуплоскостей является областью допустимых решений неравенства, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку; если же неравенство не удовлетворяется, то областью решений является полуплоскость, не содержащая данную точку.
Решение системы ограничений есть пересечение полуплоскостей с граничными прямыми
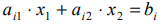
многоугольник решений (ОДР).
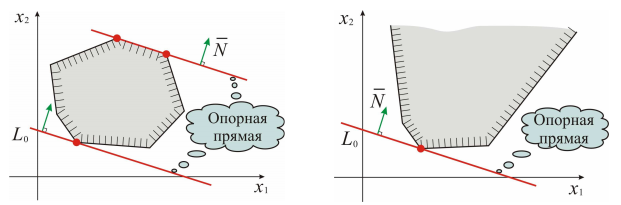
Линией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение
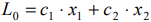
задаёт семейство линий уровня исследуемой целевой функции 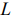 — параллельные прямые с нормальным вектором
— параллельные прямые с нормальным вектором 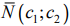 , который определяет направление роста функции
, который определяет направление роста функции 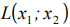 , т. к. является её градиентом.
, т. к. является её градиентом.
Замечание.
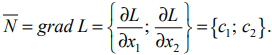
Т. о., если линию уровня  перемещать параллельно самой себе в направлении вектора нормали, то значение целевой функции будет увеличиваться; если линию уровня
перемещать параллельно самой себе в направлении вектора нормали, то значение целевой функции будет увеличиваться; если линию уровня  перемещать параллельно самой себе в направлении противоположном вектору нормали, то значение целевой функции будет уменьшаться. Поскольку требуется найти оптимальное решение, при котором целевая функция стремится к максимуму или минимуму, то необходимо перемещать линию уровня
перемещать параллельно самой себе в направлении противоположном вектору нормали, то значение целевой функции будет уменьшаться. Поскольку требуется найти оптимальное решение, при котором целевая функция стремится к максимуму или минимуму, то необходимо перемещать линию уровня  до положения касания с ОДР (положения опорной прямой).
до положения касания с ОДР (положения опорной прямой).
• Прямая
имеющая с многоугольником решений, расположенным по одну сторону от неё, хотя бы одну общую точку, называется опорной. ОДР любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
Значение 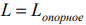 есть экстремальное значение исследуемой целевой функции.
есть экстремальное значение исследуемой целевой функции.
Графически опорная прямая определяет оптимум целевой функции в угловой точке многоугольника решений. Поэтому перебором значений целевой функции во всех угловых точках можно так же выбрать искомый оптимум.
Замечание. Если заданы ограничения неотрицательности переменных, то все построения проводятся в первой четверти.
Особые случаи

Алгоритм графического метода решения задач линейного программирования с двумя переменными
- Находим область допустимых решений из системы ограничений. Если ОДР является пустым множеством, то задача ЛП неразрешима (не имеет решения) в виду несовместности системы ограничений.
- Если область допустимых решений является непустым множеством, строим направляющий вектор
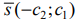 прямой
прямой 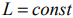 и параллельно ему проводим линию уровня
и параллельно ему проводим линию уровня  .
. - Строим вектор нормали
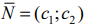 перпендикулярно прямой
перпендикулярно прямой  .
. - Линию уровня
 перемещаем до положения опорной прямой в направлении вектора
перемещаем до положения опорной прямой в направлении вектора 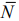 для задач на максимум или в направлении, противоположном
для задач на максимум или в направлении, противоположном 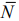 для задач на минимум. Т. е. перемещение проводится до тех пор, пока линия уровня не коснется области допустимых решений. Общая точка (точки) будет точкой экстремума (оптимума) целевой функции в ОДР.
для задач на минимум. Т. е. перемещение проводится до тех пор, пока линия уровня не коснется области допустимых решений. Общая точка (точки) будет точкой экстремума (оптимума) целевой функции в ОДР. - Находим координаты точки экстремума и значение целевой функции в ней, т. е. оптимум задачи ЛП.
Пример задачи №2
Найти 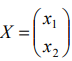 , при котором функция достигает экстремума:
, при котором функция достигает экстремума:
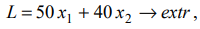
если имеются ограничения:
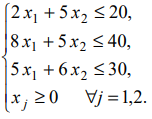
Решение:
Система ограничений определяет граничные прямые:
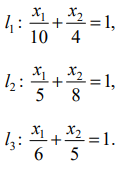
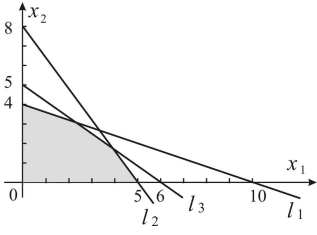
С учётом исходной системы неравенств строим ОДР.
Прямая
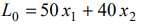
имеет вектор нормали 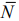 (5;4) и направляющий вектор
(5;4) и направляющий вектор 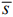 (-4;5). Опорное положение максимума линия уровня функции
(-4;5). Опорное положение максимума линия уровня функции 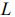 занимает в точке
занимает в точке 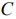 (направление роста вектора нормали); в точке
(направление роста вектора нормали); в точке 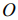 — опорное положение минимального значения линия уровня функции.
— опорное положение минимального значения линия уровня функции.
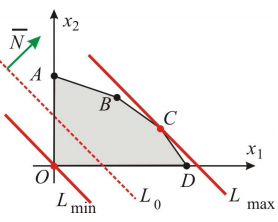
Т. о. имеем:
Тогда
Ответ:
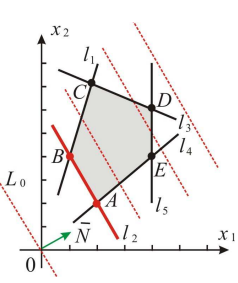
Пример задачи №3
Найти план
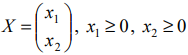
при котором:
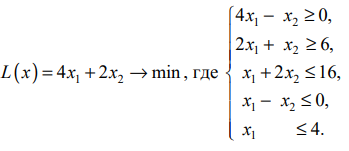
Решение:
Строим ОДР, проводим линии уровня  :
:
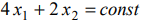
и вектор 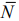 = (4; 2). Т. к. решается задача на отыскание минимума функции, то фиксируем положение опорной прямой в направлении, противоположном вектору
= (4; 2). Т. к. решается задача на отыскание минимума функции, то фиксируем положение опорной прямой в направлении, противоположном вектору 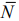 . В результате опорная прямая совпадает с граничной прямой
. В результате опорная прямая совпадает с граничной прямой 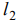 и проходит через две угловые точки
и проходит через две угловые точки 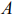 и
и 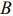 . Задача имеет бесконечно много оптимальных решений, являющихся точками отрезка
. Задача имеет бесконечно много оптимальных решений, являющихся точками отрезка  .
.
Общее решение (выпуклая линейная комбинация точек отрезка  ) имеет вид:
) имеет вид:
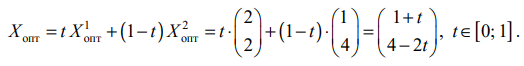
Вычисляем
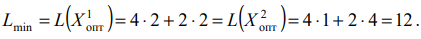
Ответ:
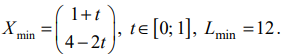
Пример задачи №4
Найти план
при котором
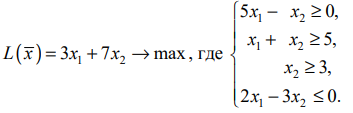
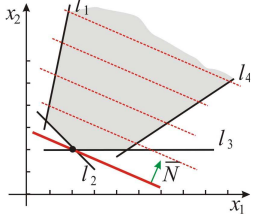
Решение:
Строим ОДР, проводим линию уровня  :
:
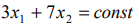
и вектор 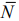 = (3;7). В данной задаче необходимо найти максимум целевой функции, поэтому линию уровня фиксируем в направлении нормального вектора. В виду того, что в направлении вектора нормали ОДР не ограничена, линия уровня уходит в бесконечность, т. е. max
= (3;7). В данной задаче необходимо найти максимум целевой функции, поэтому линию уровня фиксируем в направлении нормального вектора. В виду того, что в направлении вектора нормали ОДР не ограничена, линия уровня уходит в бесконечность, т. е. max 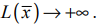
Таким образом, задача ЛП не имеет решения в виду неограниченности целевой функции.
Пример задачи №5
Найти план
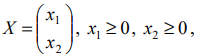
при котором
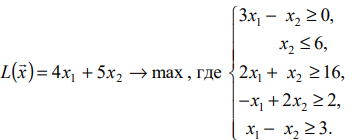
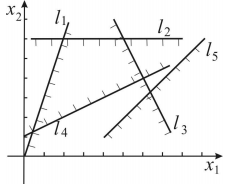
Решение:
Строим прямые линии, соответствующие неравенствам системы ограничений и находим полуплоскости, являющиеся областями решений этих неравенств. Область допустимых решений задачи является пустым множеством. Задача не имеет решения в виду несовместности системы ограничений.
III. Трёхмерное пространство переменных
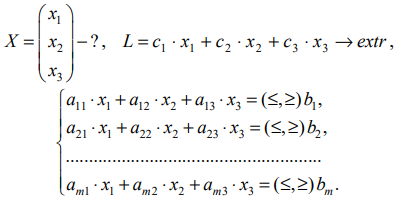
Решение системы ограничений — многогранник решений (ОДР) — пересечение полупространств с граничными плоскостями
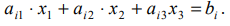
Уравнение
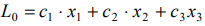
задаёт семейство поверхностей уровня функции 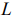 , т.е. параллельных плоскостей с нормальным вектором
, т.е. параллельных плоскостей с нормальным вектором 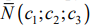 , который определяет направление роста целевой функции
, который определяет направление роста целевой функции 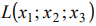 , т. к. является её градиентом.
, т. к. является её градиентом.
Плоскость
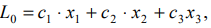
имеющая с многогранником решений, расположенным по одну сторону от нее, хотя бы одну общую точку, называется опорной. Значение 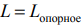 есть экстремальное (оптимальное) значение целевой функции.
есть экстремальное (оптимальное) значение целевой функции.
Графический метод в виду большой размерности реальных практических задач ЛП достаточно редко применяется, однако он позволяет уяснить одно из основных свойств ЛП- если в задаче ЛП существует оптимальное решение, то, по крайней мере, одна из вершин допустимой области определяет собой оптимальное решение.
IV. С помощью графического метода может быть решена основная ЗЛП, система ограничений (уравнений) которой удовлетворяет условию 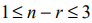 где
где 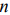 — число неизвестных системы,
— число неизвестных системы, 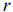 — ранг системы. Если уравнения системы ограничений линейно независимы, то ранг
— ранг системы. Если уравнения системы ограничений линейно независимы, то ранг 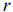 равен числу уравнений системы
равен числу уравнений системы 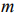 .
.
Основной случай: система ограничений содержит 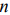 переменных и
переменных и 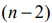 линейно независимых уравнения:
линейно независимых уравнения:
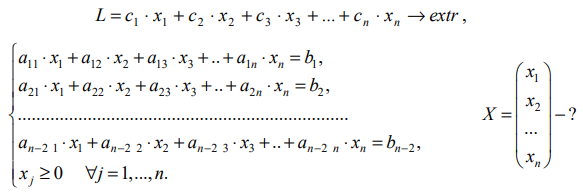
Расширенную матрицу системы с помощью элементарных преобразований строк можно привести к виду:
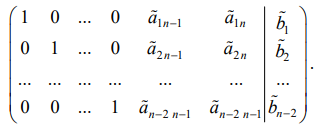
Тогда соответствующая система уравнений примет вид:
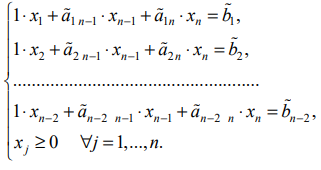
Выражая базисные неизвестные 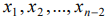 и учитывая их неотрицательность, получим систему неравенств с неизвестными
и учитывая их неотрицательность, получим систему неравенств с неизвестными  :
:
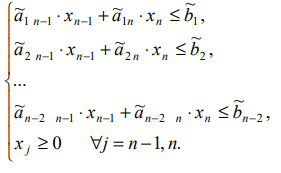
Подставляя полученные выражения для базисных неизвестных в целевую функцию, получим:
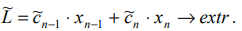
Преобразованная задача ЛП содержит только два неизвестных. Следовательно, возможен графический способ её решения на плоскости.
Найденное решение 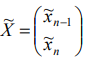 подставляют в систему (*) и получают искомый оптимальный план
подставляют в систему (*) и получают искомый оптимальный план
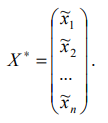
При этом оптимум:
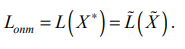
Пример. Решить задачу ЛП:
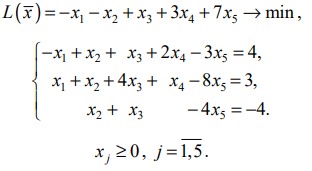
Решение. Метод применим,так как  . Методом Жордана-Гаусса приведём систему уравнений ограничений задачи к равносильной путём выделения базисных и свободных переменных. Одновременно исключим базисные переменные из целевой функции.
. Методом Жордана-Гаусса приведём систему уравнений ограничений задачи к равносильной путём выделения базисных и свободных переменных. Одновременно исключим базисные переменные из целевой функции.
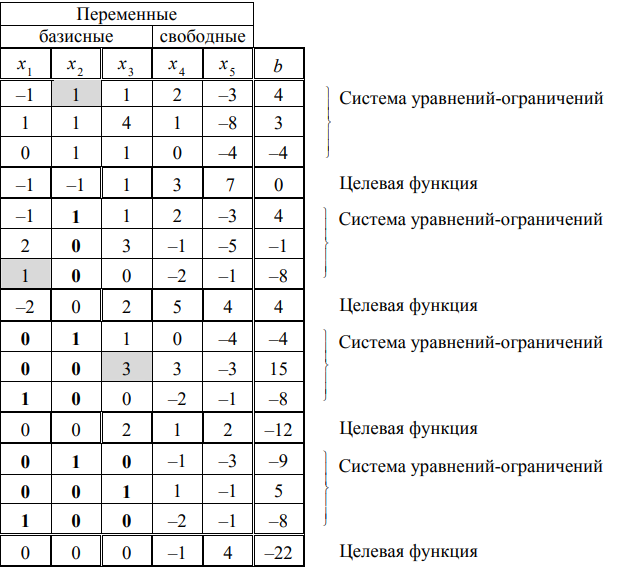
Используя последнюю часть табл., запишем задачу ЛП в преобразованном виде:
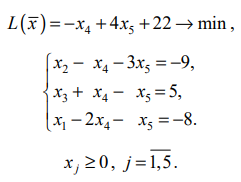
Отбросим в уравнениях-ограничениях неотрицательные базисные переменные 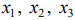 , и заменим знаки равенства знаками неравенства
, и заменим знаки равенства знаками неравенства 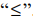 .
.
Получим вспомогательную задачу ЛП с двумя переменными:

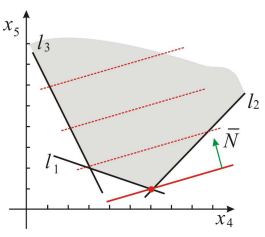
Решаем задачу графическим методом. Свободный член 22 в целевой функции не влияет на отыскание оптимального решения и учитывается только при вычислении значения целевой функции.
Находим оптимальное решение вспомогательной задачи 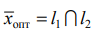 :
:
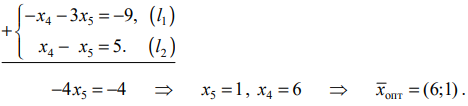
Вычисляем минимальное значение целевой функции
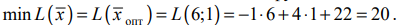
Находим оптимальное решение исходной задачи:
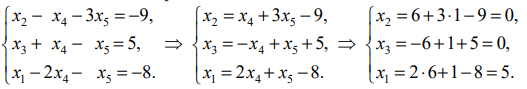
Т. о., получаем:
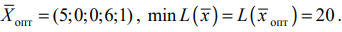
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюЛинейное программирование в ExcelКурсовая работа по линейному программированию

