Как найти максимум множества

Как найти максимум множества

Наименьший
элемент, минимальный элемент

Пусть
на множестве А дан частичный порядок.
Элемент у ∈
А называется
наименьшим
элементом
множества А, если для любого элемента
х
∈
А верно у ≤ х.

Элемент
у ∈
А называется минимальным
относительно
заданного порядка А, если не существует
таких элементов х ∈
А, что х < у.

Вопрос № 21. Наибольший и максимальный элементы множества относительно порядка

Наибольший
элемент, максимальный элемент

Пусть
на множестве А дан частичный порядок.
Элемент у ∈
А называется
наибольшим
элементом
множества А, если для любого элемента
х
∈
А верно у ≥ х.

Элемент
у ∈
А называется максимальным
относительно
заданного порядка А, если не существует
таких элементов х ∈
А, что х > у.

В
диаграмме Хассе вершина а ∈
Vа
соответствует
максимальному элементу, если из нее не
выходит ни одна дуга.

  1. Наибольший
    элемент является и максимальным
    элементом.

  2. Наибольший
    элемент, если он есть, всегда единственный.

  3. Максимальных
    элементов у множества может быть
    несколько.

Вопрос № 22. Вполне упорядоченное множество

Определение:

Частично
упорядоченное множество X
называется вполне упорядоченным, если
любое его непустое подмножество имеет
минимальный элемент.

Теорема:

Всякое
вполне упорядоченное множество является
линейно упорядоченным.

Доказательство:

Пусть
А – вполне упорядоченное множество:

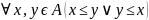
Тогда:


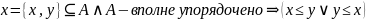
Примеры:

1.
Пустое множество является вполне
упорядоченным.

2. Простейший пример
бесконечного вполне упорядоченного
множества — множество натуральных
чисел с естественным упорядочением.

Вопрос
№23.
Верхняя граница множества Х, syp(X)=?

Пусть
А — частично упорядоченное множество.
Пусть х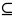

А. х

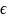
А верхняя граница Х, если

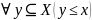
Верхние
и нижние границы не обязаны существовать
для любого множества и если существуют,
то не всегда единственны. Если существует
наименьшая верхняя граница, то она
называется супремумом
и обозначается syp(X).

Вопрос
№24. Нижняя граница множества Х, inf
X=?

Элемент
x∈A
называется нижней границей
множества X,
если для любого y∈X
(x≤y)

Элемент
x∈A
называется наибольшей нижней гранью,
если это наибольшая из нижних границ
множества X
(inf)

Вопрос №25. Определение графа ориентированного, неориентированного, смешанного, пустого

Граф,
неориентированный граф, НГ, ориентированный
граф, оргаф, ОГ, смешанный граф, пустой
граф.

Вопрос №26. Степень вершины, псевдограф, мультиграф

Степенью
вершины
называется число ребер, которым
принадлежит эта вершина. Если это
количество четно, то вершина называется
четной, в противном случае вершина
называется нечетной.

Мультиграф

Определение.
Неориентированный
граф с кратными ребрами без петель
называется мультиграфом. Несколько
ребер, соединяющих одну и ту же пару
вершин, называются кратными.

Для
ориентированного графа имеем два
случая: дуги, имеющие одно направление,
называются кратными, разное направление
– параллельными.

Ориентированный
мультиграф — граф,
соединяющий кратные дуги без петель.

Псевдограф

Определение.
Граф,
содержащий петли и кратные ребра,
называется псевдографом.

Петлей
называется ребро, соединяющее вершину
саму с собой.

При
подсчете степени вершины петля
учитывается дважды.

Для
некоторых авторов, термины псевдограф
и мультиграф являются синонимами. Для
других, псевдограф является мультиграфом,
которому разрешено иметь петли.

Синие
линии – петли

Красные
линии – кратные ребра

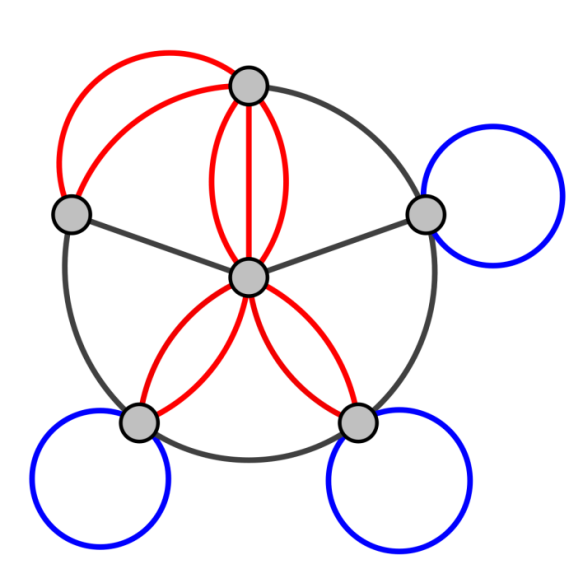
Вопрос
№27.
Изоморфные
графы. Примеры. Гомеоморфизм графов.

Графы
G1
= (V1,
E1)
и G2
= (V2,
E2)
называются изоморфными, если существует
биекция φ
между
множеством вершин V1
и V2,
сохраняющая смежность.

{L1,
L2}
∈
E1
=> {φ(L1),
φ(L2)}
∈
E2.

Для
орграфа:

(L1,
L2)
∈
E1
=> (φ(L1),
φ(L2))
∈
E2.

Для
доказательства того, что графы изоморфны,
достаточно указать отображения,
удовлетворяющие условию, описанному
в определении.

Чтобы
доказать, что графы неизоморфны,
достаточно найти какое-нибудь свойство,
которым обладает один граф и не обладает
другой, и которое у изоморфных графов
должно быть общим.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 30 апреля 2022 года; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Максимум.

Элемент M частично упорядоченного множества A называется максимальным элементом, если

  • {displaystyle forall ain A;(ageqslant MRightarrow a=M).}

Аналогично, элемент {displaystyle min A} называется минимальным, если

  • {displaystyle forall ain A;(aleqslant mRightarrow a=m).}

Записывается как {displaystyle M=max A} (соотв. свойство минимальности записывается как {displaystyle m=min A}). В случае линейно упорядоченного множества (например, в случае подмножества вещественной прямой mathbb {R} с естественным порядком) понятие максимального (соотв. минимального) элемента совпадает с понятием наибольшего (соотв. наименьшего) элемента, но в общем случае эти понятия различаются: наибольший элемент всегда является максимальным, обратное не всегда верно, так как для максимального элемента могут существовать несравнимые с ним элементы.

Не существует максимального элемента подмножества mathbb {R} , если оно не ограничено сверху. Даже если это множество ограничено сверху, максимального элемента также может не существовать (хотя и инфимум, и супремум существуют для любого ограниченного множества). Например, для интервала A=left({a,b}right) не существует ни минимального, ни максимального элемента.

Литература[править | править код]

  • Иванов Г. Е. Лекции по математическому анализу. Часть 1. — М.: МФТИ, 2000. — 359 с. — 800 экз. — ISBN 5-7417-0147-7.

См. также[править | править код]

  • Аргументы максимизации и минимизации
Источник

From Wikipedia, the free encyclopedia

Hasse diagram of the set P of divisors of 60, partially ordered by the relation “x divides y“. The red subset {displaystyle S={1,2,3,4}} has two maximal elements, viz. 3 and 4, and one minimal element, viz. 1, which is also its least element.

In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set (poset) is an element of S that is greater than every other element of S. The term least element is defined dually, that is, it is an element of S that is smaller than every other element of S.

Definitions[edit]

Let {displaystyle (P,leq )} be a preordered set and let {displaystyle Ssubseteq P.}
An element {displaystyle gin P} is said to be a greatest element of S if {displaystyle gin S} and if it also satisfies:

{displaystyle sleq g} for all {displaystyle sin S.}

By using {displaystyle ,geq ,} instead of {displaystyle ,leq ,} in the above definition, the definition of a least element of S is obtained. Explicitly, an element {displaystyle lin P} is said to be a least element of S if lin S and if it also satisfies:

{displaystyle lleq s} for all {displaystyle sin S.}

If {displaystyle (P,leq )} is even a partially ordered set then S can have at most one greatest element and it can have at most one least element. Whenever a greatest element of S exists and is unique then this element is called the greatest element of S. The terminology the least element of S is defined similarly.

If {displaystyle (P,leq )} has a greatest element (resp. a least element) then this element is also called a top (resp. a bottom) of {displaystyle (P,leq ).}

Relationship to upper/lower bounds[edit]

Greatest elements are closely related to upper bounds.

Let {displaystyle (P,leq )} be a preordered set and let {displaystyle Ssubseteq P.}
An upper bound of S in {displaystyle (P,leq )} is an element u such that {displaystyle uin P} and {displaystyle sleq u} for all {displaystyle sin S.} Importantly, an upper bound of S in P is not required to be an element of S.

If {displaystyle gin P} then g is a greatest element of S if and only if g is an upper bound of S in {displaystyle (P,leq )} and {displaystyle gin S.} In particular, any greatest element of S is also an upper bound of S (in P) but an upper bound of S in P is a greatest element of S if and only if it belongs to S.
In the particular case where {displaystyle P=S,} the definition of “u is an upper bound of S in S” becomes: u is an element such that {displaystyle uin S} and {displaystyle sleq u} for all {displaystyle sin S,} which is completely identical to the definition of a greatest element given before.
Thus g is a greatest element of S if and only if g is an upper bound of S in S.

If u is an upper bound of S in P that is not an upper bound of S in S (which can happen if and only if {displaystyle unot in S}) then u can not be a greatest element of S (however, it may be possible that some other element is a greatest element of S).
In particular, it is possible for S to simultaneously not have a greatest element and for there to exist some upper bound of S in P.

Even if a set has some upper bounds, it need not have a greatest element, as shown by the example of the negative real numbers.
This example also demonstrates that the existence of a least upper bound (the number 0 in this case) does not imply the existence of a greatest element either.

Contrast to maximal elements and local/absolute maximums[edit]

A greatest element of a subset of a preordered set should not be confused with a maximal element of the set, which are elements that are not strictly smaller than any other element in the set.

Let {displaystyle (P,leq )} be a preordered set and let {displaystyle Ssubseteq P.}
An element {displaystyle min S} is said to be a maximal element of S if the following condition is satisfied:

whenever sin S satisfies {displaystyle mleq s,} then necessarily {displaystyle sleq m.}

If {displaystyle (P,leq )} is a partially ordered set then {displaystyle min S} is a maximal element of S if and only if there does not exist any sin S such that {displaystyle mleq s} and {displaystyle sneq m.}
A maximal element of {displaystyle (P,leq )} is defined to mean a maximal element of the subset {displaystyle S:=P.}

A set can have several maximal elements without having a greatest element.
Like upper bounds and maximal elements, greatest elements may fail to exist.

In a totally ordered set the maximal element and the greatest element coincide; and it is also called maximum; in the case of function values it is also called the absolute maximum, to avoid confusion with a local maximum.[1]
The dual terms are minimum and absolute minimum.
Together they are called the absolute extrema.
Similar conclusions hold for least elements.

Role of (in)comparability in distinguishing greatest vs. maximal elements

One of the most important differences between a greatest element g and a maximal element m of a preordered set {displaystyle (P,leq )} has to do with what elements they are comparable to.
Two elements {displaystyle x,yin P} are said to be comparable if xleq y or yleq x; they are called incomparable if they are not comparable.
Because preorders are reflexive (which means that {displaystyle xleq x} is true for all elements x), every element x is always comparable to itself.
Consequently, the only pairs of elements that could possibly be incomparable are distinct pairs.
In general, however, preordered sets (and even directed partially ordered sets) may have elements that are incomparable.

By definition, an element {displaystyle gin P} is a greatest element of {displaystyle (P,leq )} if {displaystyle sleq g,} for every {displaystyle sin P}; so by its very definition, a greatest element of {displaystyle (P,leq )} must, in particular, be comparable to every element in P.
This is not required of maximal elements.
Maximal elements of {displaystyle (P,leq )} are not required to be comparable to every element in P.
This is because unlike the definition of “greatest element”, the definition of “maximal element” includes an important if statement.
The defining condition for min P to be a maximal element of {displaystyle (P,leq )} can be reworded as:

For all {displaystyle sin P,} IF {displaystyle mleq s} (so elements that are incomparable to m are ignored) then {displaystyle sleq m.}
Example where all elements are maximal but none are greatest

Suppose that S is a set containing at least two (distinct) elements and define a partial order {displaystyle ,leq ,} on S by declaring that ileq j if and only if {displaystyle i=j.}
If ineq j belong to S then neither ileq j nor jleq i holds, which shows that all pairs of distinct (i.e. non-equal) elements in S are incomparable.
Consequently, {displaystyle (S,leq )} can not possibly have a greatest element (because a greatest element of S would, in particular, have to be comparable to every element of S but S has no such element).
However, every element {displaystyle min S} is a maximal element of {displaystyle (S,leq )} because there is exactly one element in S that is both comparable to m and {displaystyle geq m,} that element being m itself (which of course, is leq m).[note 1]

In contrast, if a preordered set {displaystyle (P,leq )} does happen to have a greatest element g then g will necessarily be a maximal element of {displaystyle (P,leq )} and moreover, as a consequence of the greatest element g being comparable to every element of P, if {displaystyle (P,leq )} is also partially ordered then it is possible to conclude that g is the only maximal element of {displaystyle (P,leq ).}
However, the uniqueness conclusion is no longer guaranteed if the preordered set {displaystyle (P,leq )} is not also partially ordered.
For example, suppose that R is a non-empty set and define a preorder {displaystyle ,leq ,} on R by declaring that ileq j always holds for all {displaystyle i,jin R.} The directed preordered set {displaystyle (R,leq )} is partially ordered if and only if R has exactly one element. All pairs of elements from R are comparable and every element of R is a greatest element (and thus also a maximal element) of {displaystyle (R,leq ).} So in particular, if R has at least two elements then {displaystyle (R,leq )} has multiple distinct greatest elements.

Properties[edit]

Throughout, let {displaystyle (P,leq )} be a partially ordered set and let {displaystyle Ssubseteq P.}

  • A set S can have at most one greatest element.[note 2] Thus if a set has a greatest element then it is necessarily unique.
  • If it exists, then the greatest element of S is an upper bound of S that is also contained in S.
  • If g is the greatest element of S then g is also a maximal element of S[note 3] and moreover, any other maximal element of S will necessarily be equal to g.[note 4]
    • Thus if a set S has several maximal elements then it cannot have a greatest element.
  • If P satisfies the ascending chain condition, a subset S of P has a greatest element if, and only if, it has one maximal element.[note 5]
  • When the restriction of {displaystyle ,leq ,} to S is a total order ({displaystyle S={1,2,4}} in the topmost picture is an example), then the notions of maximal element and greatest element coincide.[note 6]
    • However, this is not a necessary condition for whenever S has a greatest element, the notions coincide, too, as stated above.
  • If the notions of maximal element and greatest element coincide on every two-element subset S of P, then {displaystyle ,leq ,} is a total order on P.[note 7]

Sufficient conditions[edit]

  • A finite chain always has a greatest and a least element.

Top and bottom[edit]

The least and greatest element of the whole partially ordered set play a special role and are also called bottom (⊥) and top (⊤), or zero (0) and unit (1), respectively.
If both exist, the poset is called a bounded poset.
The notation of 0 and 1 is used preferably when the poset is a complemented lattice, and when no confusion is likely, i.e. when one is not talking about partial orders of numbers that already contain elements 0 and 1 different from bottom and top.
The existence of least and greatest elements is a special completeness property of a partial order.

Further introductory information is found in the article on order theory.

Examples[edit]

See also[edit]

  • Essential supremum and essential infimum
  • Initial and terminal objects
  • Maximal and minimal elements
  • Limit superior and limit inferior (infimum limit)
  • Upper and lower bounds

Notes[edit]

  1. ^ Of course, in this particular example, there exists only one element in S that is comparable to m, which is necessarily m itself, so the second condition “and {displaystyle geq m,}” was redundant.
  2. ^ If g_{1} and g_{2} are both greatest, then {displaystyle g_{1}leq g_{2}} and {displaystyle g_{2}leq g_{1},} and hence {displaystyle g_{1}=g_{2}} by antisymmetry.
  3. ^ If g is the greatest element of S and {displaystyle sin S,} then {displaystyle sleq g.} By antisymmetry, this renders ({displaystyle gleq s} and {displaystyle gneq s}) impossible.
  4. ^ If M is a maximal element, then {displaystyle Mleq g} since g is greatest, hence {displaystyle M=g} since M is maximal.
  5. ^ Only if: see above. — If: Assume for contradiction that S has just one maximal element, m, but no greatest element. Since m is not greatest, some {displaystyle s_{1}in S} must exist that is incomparable to m. Hence {displaystyle s_{1}in S} cannot be maximal, that is, {displaystyle s_{1}<s_{2}} must hold for some {displaystyle s_{2}in S.} The latter must be incomparable to m, too, since {displaystyle m<s_{2}} contradicts m‘s maximality while {displaystyle s_{2}leq m} contradicts the incomparability of m and s_{1}. Repeating this argument, an infinite ascending chain {displaystyle s_{1}<s_{2}<cdots <s_{n}<cdots } can be found (such that each s_{i} is incomparable to m and not maximal). This contradicts the ascending chain condition.
  6. ^ Let {displaystyle min S} be a maximal element, for any sin S either {displaystyle sleq m} or {displaystyle mleq s.} In the second case, the definition of maximal element requires that {displaystyle m=s,} so it follows that {displaystyle sleq m.} In other words, m is a greatest element.
  7. ^ If {displaystyle a,bin P} were incomparable, then {displaystyle S={a,b}} would have two maximal, but no greatest element, contradicting the coincidence.

References[edit]

  1. ^ The notion of locality requires the function’s domain to be at least a topological space.
  • Davey, B. A.; Priestley, H. A. (2002). Introduction to Lattices and Order (2nd ed.). Cambridge University Press. ISBN 978-0-521-78451-1.
Источник

Упорядоченные множества

Множество вместе с заданным на нем отношением порядка называют упорядоченным множеством.

Отношение порядка будем, как правило, обозначать leqslant (или значками preccurlyeq,,sqsubseteq и т.п., похожими на leqslant). При этом следует понимать, что даже на некотором множестве S subseteq mathbb{R} рассматриваться может любое отношение порядка, а не только естественный числовой порядок. Множество M с заданным на нем отношением порядка leqslant будем записывать как пару (M,leqslant). Записывая xleqslant y, мы будем говорить, что элемент x не больше элемента y.

Каждому отношению порядка leqslant на множестве M можно сопоставить следующие отношения.

1. Отношение, которое будем обозначать &lt;, получается из исходного отношения порядка leqslant выбрасыванием всех элементов диагонали operatorname{id}M, т.е. x&lt;y для любых x,yin M тогда и только тогда, когда xleqslant y и xne y. Записывая x&lt;y, мы будем говорить, что элемент x строго меньше элемента y. Из определения следует, что отношение &lt; есть иррефлексивное, антисимметричное и транзитивное бинарное отношение на множестве M, т.е. оно является отношением строгого порядка.

Двойственный порядок

2. Двойственный порядок. Это бинарное отношение на множестве M, называемое также и отношением, двойственным к отношению порядка leqslant, определяется как бинарное отношение на множестве M, обратное к отношению leqslant. Его обозначают geqslant. Тогда для любых x,y условие xgeqslant y равносильно тому, что yleqslant x. Можно без труда доказать, что отношение geqslant тоже является отношением порядка.

Записывая xgeqslant y, мы будем говорить, что элемент x не меньше элемента y. Отношение строгого порядка, ассоциированное с geqslant, договоримся обозначать &gt;, говоря при этом, что элемент x строго больше элемента y, если xgeqslant y и xne y.

Отношение доминирования

3. Отношение доминирования. Для двух элементов x и y, по определению, xtriangleleft y тогда и только тогда, когда x строго меньше y и не существует такого элемента z, что x&lt;z&lt;y. Отношение triangleleft называют отношением доминирования (или просто доминированием), ассоциированным с отношением порядка leqslant. Если имеет место xtriangleleft y, то говорят, что элемент y доминирует над элементом x.

Из определения следует, что отношение доминирования иррефлексивно, антисимметрично, но не транзитивно. Оно может быть и пусто. Например, легко видеть, что пустым будет отношение доминирования, если исходный порядок является плотным бинарным отношением на соответствующем множестве.

Пример 1.15. а. Рассмотрим множество действительных чисел с естественным числовым порядком. Пусть a&lt;c. Известно, что для любых a и c найдется такое b, что a&lt;b&lt;c, т.е. это отношение порядка на множестве действительных чисел является плотным. Поэтому отношение доминирования будет пустым.

По той же причине будет пустым отношение доминирования, ассоциированное с естественным числовым порядком на множестве рациональных чисел. Но на множестве целых чисел (опять-таки с естественным числовым порядком) отношение доминирования не пусто. Так, 1triangleleft2, -5triangleleft-4, но, конечно, неверно, что 1triangleleft3, поскольку между единицей и тройкой существует “промежуточный” элемент — двойка.

б. На множестве всех подмножеств трехэлементного множества {a,b,c}, где в качестве отношения порядка взято отношение теоретико-множественного включения subseteq, подмножество {a,b} доминирует над подмножествами {a} и {b}, но не доминирует над пустым множеством. В свою очередь, все множество {a,b,c} доминирует над любым своим двухэлементным подмножеством, но не доминирует над одноэлементным и над пустым.

в. По отношению делимости на множестве натуральных чисел 15 доминирует над 3 и 5, но 20 не доминирует над 5, так как существует „промежуточный” элемент — 10, делитель 20, который делится на 5, но не равен ни 20, ни 5.

Упорядоченное подмножество

Рассмотрим упорядоченное множество (M,leqslant) и его произвольное непустое подмножество Bsubseteq M. Упорядоченное множество (B,leqslantbig|_{B}), где leqslantbig|_{B} — ограничение отношения leqslant на подмножество B, называют упорядоченным подмножеством упорядоченного множества (M,leqslant).

Таким образом, можно переносить отношения порядка на непустые подмножества исходного упорядоченного множества. Как правило, вместо leqslantbig|_{B} будем писать просто leqslant (если ясно, о каком подмножестве B идет речь). Порядок leqslantbig|_{B} на подмножестве B называют также порядком, индуцированным исходным порядком leqslant на всем множестве A. Часто прибегают к такому выражению: “рассмотрим подмножество B упорядоченного множества (M,leqslant) с индуцированным порядком”, понимая под этим порядок leqslantbig|_{B}.

Элементы x и y упорядоченного множества (M,leqslant) называют сравнимыми по отношению порядка leqslant, если xleqslant y или yleqslant x. В противном случае элементы x и y называются несравнимыми.

Упорядоченное множество, все элементы которого попарно сравнимы, называют линейно упорядоченным, а соответствующее отношение — отношением линейного порядка (или просто линейным порядком). Бели индуцированный порядок на подмножестве упорядоченного множества является линейным, то это линейно упорядоченное подмножество называют цепью. Любое подмножество попарно не сравнимых элементов данного упорядоченного множества называют антицепью.

Замечание 1.5. Обратим внимание на то, что термину “упорядоченное множество” (в смысле приведенного определения) отвечает термин “частично упорядоченное множество”, а то, что мы называем линейно упорядоченным множеством, называется просто упорядоченным множеством. Терминология этого выпуска более принята в алгебраической литературе и литературе по дискретной математике. Употребление термина “частично упорядоченное множество” мотивировано желанием подчеркнуть, что в общем случае в упорядоченном множестве существуют не сравнимые элементы.

Пример 1.16. а. Отношение естественного числового порядка на множестве mathbb{R} действительных чисел является отношением линейного порядка, поскольку для любых двух чисел a,b имеет место или неравенство aleqslant b, или неравенство bleqslant a.

б. Отношение делимости (см. пример 1.13.г) на множестве mathbb{N} и отношение включения subseteq на mathcal{B}(A) (см. пример 1.13,д) не являются линейными порядками, за исключением случая, когда A — одноэлементное множество.

Наибольший, наименьший и максимальный, минимальный элементы множества

Пусть (A,leqslant) — упорядоченное множество. Элемент ain A называют наибольшим элементом множества A, если для всех xin A выполняется неравенство xleqslant a.

Элемент b называют максимальным элементом множества A, если для всякого xin A имеет место одно из двух: или xleqslant b, или x и b не сравнимы.

Аналогично определяются наименьший и минимальный элементы упорядоченного множества, а именно: наименьший элемент упорядоченного множества A — это такой его элемент a, что aleqslant x для каждого xin A, а минимальный элемент — это такой элемент bin A, что для любого xin A элементы b и x не сравнимы или bleqslant x.

Покажем, что наибольший (наименьший) элемент множества, если он существует, является единственным. Действительно, полагая, что a и a' — наибольшие элементы A по отношению порядка leqslant, получаем, что для всякого xin A выполняется xleqslant a и xleqslant a'. В частности, a'leqslant a и aleqslant a', откуда ввиду антисимметричности любого отношения порядка следует, что a=a'. Аналогично доказывается единственность наименьшего элемента.

Замечание 1.6. Поскольку на одном и том же множестве могут быть определены разные отношения порядка (например, на множестве натуральных чисел — естественный числовой порядок и отношение делимости), то, когда это необходимо, мы будем говорить о наибольших, наименьших (соответственно максимальных и минимальных) элементах по данному отношению порядка, уточняя тем самым, о каком отношении порядка идет речь.

Следующие примеры показывают, что максимальных (минимальных) элементов может быть сколько угодно. Но заметим, что если у множества есть наибольший (соответственно наименьший) элемент, то он является единственным максимальным (соответственно минимальным) элементом данного множества.

Пример 1.17. Рассмотрим множество точек плоскости с некоторой фиксированной прямоугольной декартовой системой координат. Координаты каждой точки плоскости задаются упорядоченной парой (x,y) действительных чисел. Отношение порядка на множестве точек плоскости определим следующим образом: (a,b)leqslant (c,d), если и только если aleqslant c и bleqslant d. Рассмотрим множество точек треугольника OAB (рис. 1.11, а). Точка с координатами (0;0) является наименьшим элементом этого множества. Максимальными элементами являются все точки, лежащие на стороне AB. Наибольшего элемента нет.

Множества точек треугольника, прямоугольника и трапеции

Верхняя и нижняя грань множества

Пусть (A,leqslant) — упорядоченное множество и Bsubseteq A. Элемент ain A называется верхней (соответственно нижней) гранью множества B, если для всех элементов xin B имеет место xleqslant a (соответственно xgeqslant a).

Наименьший элемент множества всех верхних граней (соответственно наибольший элемент множества всех нижних граней) множества B называют точной верхней гранью B (соответственно точной нижней гранью B) и обозначают sup B~ (inf B).

Множество всех верхних (нижних) граней множества B называют верхним (нижним) конусом B и обозначают B^{triangle} (соответственно B^{triangledown}).

В отличие от наибольшего и наименьшего элементов множества B элементы sup B и inf B не обязаны принадлежать множеству B. Точная верхняя (нижняя) грань множества существует не всегда.

Пример 1.18. а. Рассмотрим множество D точек прямоугольника OABC (рис. 1.11, б) с заданным в примере 1.17 отношением порядка. Точка O является точной нижней гранью, а точка B— точной верхней гранью этого множества. Обе точки принадлежат множеству.

Если рассмотреть множество F (рис. 1.11, в) с тем же отношением порядка, то увидим, что точная нижняя грань (точка O) и точная верхняя грань (точка E) множества F существуют, но не принадлежат множеству.

б. На числовой прямой с “выколотой” точкой b для полуинтервала [a;b) множество верхних граней есть (b;+infty), но точной верхней грани нет.

Вполне упорядоченные множества

Упорядоченное множество (M,leqslant) называют вполне упорядоченным, если его любое непустое подмножество имеет наименьший элемент.

Множество натуральных чисел с отношением естественного числового порядка вполне упорядоченное. Множество целых чисел не вполне упорядоченное, поскольку оно не имеет наименьшего элемента. Аналогично множества рациональных и действительных чисел не являются вполне упорядоченными.

Можно показать, что справедлив принцип двойственности для упорядоченных множеств. Пусть (M,leqslant) — произвольное упорядоченное множество. Тогда любое утверждение, доказанное для порядка leqslant, останется справедливым для двойственного порядка geqslant, если в нем:

1) порядок leqslant заменить на порядок geqslant и наоборот;
2) наименьший (минимальный) элемент заменить наибольшим (максимальным) элементом и наоборот;
3) inf заменить на sup и наоборот.

Например, если для некоторого ain M и для Bsubseteq M мы доказали, что a=sup B при заданном отношении порядка, то для двойственного порядка a=inf B.

Говорят также и о взаимно двойственных определениях: если в любом определении, связанном с упорядоченным множеством, произвести взаимные замены согласно принципу двойственности, то получится новое определение, называемое двойственным к исходному. Так, определение наибольшего (максимального) элемента множества двойственно к определению наименьшего (минимального) элемента, и наоборот. Часто употребляют оборот речи: “двойственным образом…” (или “двойственно…”), понимая под этим переход к утверждению или определению, которое двойственно к исходному.

Способы наглядного представления упорядоченных множеств

Рассмотрим теперь некоторые способы наглядного представления упорядоченных множеств.

Конечное упорядоченное множество можно графически изобразить в виде так называемой диаграммы Хассе. На этой Диаграмме элементы множества изображаются кружочками. При этом если элемент b доминирует над элементом a, то кружочек, изображающий элемент b, располагается выше кружочка, изображающего элемент a, и соединяется с ним прямой линией. Иногда для большей наглядности из a в b ведут стрелку. На рис. 1.12 изображены диаграммы Хассе для упорядоченных множеств делителей чисел 2, 6, 30 и 36 по рассмотренному выше отношению делимости (см. пример 1.13,г).

Диаграммы Хассе для упорядоченных множеств делителей чисел 2, 6, 30 и 36

Диаграмма Хассе для упорядоченного множества всех подмножеств трехэлементного множества {a,b,c} по отношению включения

На рис. 1.13 приведена диаграмма Хассе для упорядоченного множества всех подмножеств трехэлементного множества {a,b,c} по отношению включения (см. пример 1.13.д).

Последовательность {x_i}_{iinmathbb{N}} элементов упорядоченного множества называют неубывающей, если для каждого iinmathbb{N} справедливо неравенство x_ileqslant x_{i+1}.

Элемент а упорядоченного множества (M,leqslant) называют точной верхней гранью последовательности {x_i}_{iinmathbb{N}} если он есть точная верхняя грань множества всех членов последовательности. Другими словами, точная верхняя грань последовательности есть точная верхняя грань области ее значений как функции натурального аргумента.

Точная нижняя грань последовательности

Двойственно определяется точная нижняя грань последовательности.

Упорядоченное множество (M,leqslant) называют индуктивным, если:

1) оно содержит наименьший элемент;
2) всякая неубывающая последовательность элементов этого множества имеет точную верхнюю грань.

Например, множество всех подмножеств некоторого множества по отношению включения будет индуктивным. Наименьший элемент — пустое множество, а точной верхней гранью произвольной неубывающей последовательности множеств будет объединение всех членов этой последовательности (наименьшее по включению множество, содержащее в качестве подмножества любой член последовательности).

Определение 1.5. Пусть (M_1,leqslant) и (M_2,preccurlyeq) — индуктивные упорядоченные множества. Отображение fcolon M_1to M_2 одного индуктивного упорядоченного множества в другое называют непрерывным, если для любой неубывающей последовательности a_1,ldots,a_n,ldots элементов множества M_1 образ ее точной верхней грани равен точной верхней грани последовательности образов f(a_1),ldots,f(a_n),ldots, т.е. справедливо равенство

f(sup a_n)=sup f(a_n).

Определение 1.6. Отображение fcolon M_1to M_2 упорядоченных множеств (M_1,leqslant) и (M_2,preccurlyeq) называют монотонным, если для любых a,bin M_1 из aleqslant b следует f(a)preccurlyeq f(b).

Теорема 1.6. Всякое непрерывное отображение одного индуктивного упорядоченного множества в другое монотонно.

Пусть f — непрерывное отображение индуктивного упорядоченного множества (M_1,leqslant) в индуктивное упорядоченное множество (M_2, preccurlyeq). Пусть a,bin M_1 и aleqslant b. Образуем последовательность {x_i}_{ninmathbb{N}}, где x_1=a, а x_n=b,~ ngeqslant2. Эта последовательность неубывающая. Для нее sup x_n=sup{a,b}=b. В силу непрерывности отображения f

f(b)=f(sup x_n)= f(sup{a,b})= sup{f(a),f(b)}.

откуда следует, что f(a)preccurlyeq f(b).

Заметим, что функция fcolon mathbb{R}to mathbb{R}, непрерывная в смысле определений математического анализа, не обязана быть монотонным отображением упорядоченных множеств mathbb{R} с естественным числовым порядком, т.е. приведенное выше определение 1.5 непрерывности не вполне аналогично определению непрерывности в анализе . Например, рассмотрим непрерывное в смысле определений математического анализа отображение y=-x числовой прямой с естественным числовым порядком на себя. Это отображение не является монотонным в смысле данного выше определения 1.6, поскольку, например, 0leqslant1, однако неравенство f(0)=0leqslant f(1)=-1 не выполняется.

В общем случае монотонное в смысле определения 1.6 отображение не является непрерывным в смысле определения 1.5. Приведем пример, показывающий, что утверждение, обратное теореме 1.6, неверно.

Пример 1.19. Рассмотрим множество всех точек отрезка [0;1] числовой прямой с порядком, индуцированным естественным числовым порядком. Это множество индуктивно: его наименьший элемент — 0, а любая неубывающая последовательность элементов ограничена сверху и по признаку Вейерштрасса имеет предел, который и будет ее точной верхней гранью. Любая кусочно-непрерывная (но не непрерывная!) и монотонная в смысле обычных определений из курса математического анализа функция, отображающая этот отрезок на любой отрезок с порядком, индуцированным естественным числовым порядком, дает пример монотонного в смысле определения 1.6, но не непрерывного в смысле определения 1.5 отображения между индуктивными частично упорядоченными множествами. Например, пусть функция f имеет вид

f=begin{cases}0,!5x,&text{if}quad 0 leqslant x&lt;0,!5,;\ 0,!5+0,!5x,&text{if}quad 0,!5leqslant xleqslant1.end{cases}

Это отображение монотонно. Для последовательности {x_n}= left{ frac{n}{2n+ 1}right}, точная верхняя грань равна 0,!5. Точная верхняя грань последовательности {f(x_n)} равна 0,!25, a f(sup x_n)=f(0,!5)=0,!75. Следовательно, отображение не является непрерывным в смысле определения 1.5.

Не следует путать отображение, монотонное в смысле определения 1.6, с монотонными функциями из курса математического анализа. Функция fcolonmathbb{R}tomathbb{R} будет монотонной в смысле определения 1.6 тогда и только тогда, когда она является неубывающей.

Для приложений особенно важны непрерывные отображения индуктивного упорядоченного множества в себя.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

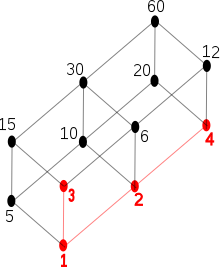
Диаграмма Хассе множества P делителей из 60, частично упорядоченных отношением «x делит y». Красное подмножество S = {1,2,3,4} имеет два максимальных элемента, а именно. 3 и 4, и один минимальный элемент, а именно. 1, который также является его наименьшим элементом.

В математике, особенно в теории порядка, максимальный элемент из подмножества S некоторого частично упорядоченного множества (poset) является элементом S, который не меньше любого другого элемента в S. Минимальный элемент подмножества S некоторого частично упорядоченного множества – это определяется двойственно как элемент S, который не больше любого другого элемента в S.

Понятия максимального и минимального элементов слабее, чем у наибольшего элемента и наименьшего элемента, которые также известны как максимум и минимум, соответственно. Максимум подмножества S частично упорядоченного набора – это элемент S, который больше или равен любому другому элементу S, а минимум S снова определяется двойственно. В то время как частично упорядоченный набор может иметь не более одного каждого максимума и минимума, он может иметь несколько максимальных и минимальных элементов. Для полностью упорядоченных множеств понятия максимального элемента и максимума совпадают, а понятия минимального элемента и минимума совпадают.

Например, в коллекции

S = {{d, o}, {d, o, g}, {g, o, a, d}, {o, a, f} }

упорядочено по включению, элемент {d, o} минимален, так как он не содержит наборов в коллекции, элемент {g, o, a, d} максимален, поскольку нет наборов в коллекции, которая его содержит, элемент {d, o, g} не является ни тем, ни другим, а элемент {o, a, f} минимальным и максимальным. В отличие от этого, ни максимума, ни минимума не существует для S.

Лемма Цорна утверждает, что каждое частично упорядоченное множество, для которого каждое полностью упорядоченное подмножество имеет верхнюю границу, содержит по крайней мере один максимальный элемент. Эта лемма эквивалентна теореме об упорядочении и аксиоме выбора и дает важные результаты в других математических областях, таких как теорема Хана – Банаха, теорема Кирсбрауна, теорема Тихонова, существование базиса Гамеля для каждого векторного пространства и существование алгебраического замыкания для каждого поле.

Содержание

  • 1 Определение
  • 2 Существование и уникальность
  • 3 Наибольшие элементы
  • 4 Направленные множества
  • 5 Свойства
  • 6 Примеры
    • 6.1 Теория потребления
  • 7 Связанные понятия
  • 8 См. Также
  • 9 Примечания
  • 10 Ссылки

Определение

Пусть (P, ≤) { displaystyle (P, leq)}(P, leq) быть частично упорядоченным набором и S ⊆ P { displaystyle S substeq P}{ displaystyle S substeq P} . Тогда m ∈ S { displaystyle m in S}m in S является максимальным элементом S { displaystyle S}S , если S { displaystyle S }S не содержит элементов больше, чем m { displaystyle m}m, формально: если нет s ∈ S { displaystyle s in S}s in S таким образом, что и m ≤ s { displaystyle m leq s}m leq s , и m ≠ s. { displaystyle m neq s.}{ displaystyle m neq s.}

Определение минимальных элементов получается при использовании ≥ вместо ≤.

Существование и уникальность

A ограждение состоит только из минимального и максимального элементов (Пример 3).

Максимальные элементы не должны существовать.

Пример 1: Пусть S = [1, ∞) ⊂ ℝ, для всех m∈S имеем s = m + 1∈S, но m
Пример 2: Пусть S = {s∈ ℚ : 1≤s≤2} ⊂ ℚ и напомним, что 2 { displaystyle { sqrt {2}}}{ sqrt {2}} ∉ℚ.

В общем ≤ является лишь частичным порядком на S. Если m – максимальный элемент и s∈S, остается возможность, что ни s≤m, ни m≤s. Это оставляет открытой возможность того, что существует много максимальных элементов.

Пример 3: В заборе a1< b1>a2< b2>a3< b3>… все a i минимальны, а все b i максимальны, см. рисунок.
Пример 4: Пусть A будет набором по крайней мере из двух элементов и пусть S = {{a}: a∈A} будет подмножеством набора мощности P ( A) состоящий из синглтонов, частично упорядоченных ⊂. Это дискретный ч.у. – никакие два элемента не сравнимы – и, следовательно, каждый элемент {a} ∈S максимален (и минимален), и для любого отличного a ′, a ″ ни {a ′} ⊂ {a ″}, ни {a ″ } ⊂ {a ′}.

Наибольшие элементы

Для частично упорядоченного множества (P, ≤) иррефлексивное ядро ​​ элемента ≤ обозначается как < and is defined by x < y if x ≤ y and x ≠ y. For arbitrary members x, y ∈ P, exactly one of the following cases applies:

  1. x < y,
  2. x = y,
  3. y < x,
  4. x и y несравнимы.

Для подмножества S ⊆ P и некоторого x ∈ S,

  • если случай 1 никогда не применяется ни к одному y ∈ S, то x является максимальным элементом S, как определено выше ;
  • если случаи 1 и 4 никогда не применимы ни к одному y ∈ S, то x называется наибольшим элементом из S.

Таким образом, определение наибольшего элемента сильнее, чем это максимального элемента.

Эквивалентно, наибольший элемент подмножества S может быть определен как элемент S, который больше любого другого элемента S. Подмножество может иметь не более одного наибольшего элемента.

наибольший элемент S, если он существует, также является максимальным элементом S, и единственным. Согласно противопоставлению, если S имеет несколько максимальных элементов, у него не может быть самого большого элемента; см. пример 3. Если P удовлетворяет условию возрастающей цепочки, подмножество S из P имеет наибольший элемент тогда и только тогда, когда имеет один максимальный элемент.

Когда ограничение ≤ на S является общим порядком (S = {1, 2, 4} на самом верхнем рисунке является примером), тогда понятия максимального элемента и наибольшего элемента совпадают. Это не является обязательным условием: всякий раз, когда S имеет наибольший элемент, понятия также совпадают, как указано выше. Если понятия максимального элемента и наибольшего элемента совпадают на каждом двухэлементном подмножестве S из P, то ≤ – это общий порядок на P.

Направленные множества

В полностью упорядоченном При установке термины «максимальный элемент» и «максимальный элемент» совпадают, поэтому оба термина используются взаимозаменяемо в таких полях, как анализ, где учитываются только общие заказы. Это наблюдение применимо не только к полностью упорядоченным подмножествам любого ч.у., но также и к их теоретико-порядковому обобщению с помощью направленных множеств. В ориентированном наборе каждая пара элементов (особенно пары несравнимых элементов) имеет общую верхнюю границу внутри набора. Если направленное множество имеет максимальный элемент, это также его наибольший элемент и, следовательно, его единственный максимальный элемент. Для ориентированного набора без максимальных или наибольших элементов см. Примеры 1 и 2 выше.

Аналогичные выводы верны для минимальных элементов.

Дополнительная вводная информация находится в статье о теории порядка.

Свойства

  • Каждое конечное непустое подмножество S имеет как максимальные, так и минимальные элементы. Бесконечная подстановка не обязательно должна иметь какие-либо из них, например ℤ с обычным порядком.
  • Множество максимальных элементов подмножества S всегда является антицепью, то есть нет двух разных максимальных элементов S сопоставимы. То же самое относится и к минимальным элементам.

Примеры

  • В КПД Парето Оптимум Парето является максимальным элементом по отношению к частичному порядку улучшения Парето, а множество максимальных элементов называется границей Парето.
  • В теории принятия решений допустимое правило принятия решений является максимальным элементом по отношению к частичной порядок доминирующего правила принятия решений.
  • В современной теории портфелей набор максимальных элементов в отношении порядка продукта по риску и доходности называется эффективная граница.
  • В теории множеств набор является конечным тогда и только тогда, когда каждое непустое семейство из подмножеств имеет минимальный элемент, когда упорядочен отношением включения .
  • В абстрактной алгебре концепция максимального общего делителя необходима для обобщения наибольших общих делителей к системам счисления, в которых общие делители набора элементов m могут иметь более одного максимального элемента.
  • В вычислительной геометрии максимумы набора точек максимальны относительно частичного порядка покоординатного доминирования.

Теория потребителей

В экономике можно ослабить аксиому антисимметрии, используя предварительные заказы (обычно общие предварительные заказы ) вместо частичных заказов; понятие, аналогичное максимальному элементу, очень похоже, но используется другая терминология, как подробно описано ниже.

В теории потребителей пространство потребления – это некоторый набор X { displaystyle X}X , обычно положительный ортант некоторого векторного пространства, так что каждое x ∈ X { displaystyle x in X}x in X представляет количество потребления, указанное для каждого существующего товара в экономике. Предпочтения потребителя обычно представлены общим предварительным заказом ⪯ { displaystyle prevq} prevq , так что x, y ∈ X { displaystyle x, y in X}x, y in X и x ⪯ y { displaystyle x prevq y}x prevq y читается так: x { displaystyle x}x является не более предпочтительным, чем y { displaystyle y}y . Когда x ⪯ y { displaystyle x prevq y}x prevq y и y ⪯ x { displaystyle y prevq x}y prevq x , считается, что потребитель безразличен. между x { displaystyle x}x и y { displaystyle y}y , но нет оснований заключать, что x = y { displaystyle x = y}x = y , отношения предпочтений никогда не считаются антисимметричными. В этом контексте для любого B ⊂ X { displaystyle B subset X}B subset X мы называем x ∈ B { displaystyle x in B}x in B a максимальным элементом если

y ∈ B { displaystyle y in B}y in B подразумевает y ⪯ x { displaystyle y prevq x}y prevq x

и интерпретируется как потребительский набор, не преобладает какой-либо другой набор в том смысле, что x ≺ y { displaystyle x prec y}x prec y , то есть x ⪯ y { displaystyle x prevq y}x prevq y , а не y ⪯ x { displaystyle y prevq x}y prevq x .

Следует отметить, что формальное определение очень похоже на определение наибольшего элемента для упорядоченного множества. Однако, когда ⪯ { displaystyle prevq} prevq является только предварительным заказом, элемент x { displaystyle x}x с указанным выше свойством ведет себя очень похоже на максимальный элемент в заказе. Например, максимальный элемент x ∈ B { displaystyle x in B}x in B не является уникальным для y ⪯ x { displaystyle y prevq x}y prevq x не исключает возможности того, что x ⪯ y { displaystyle x prevq y}x prevq y (в то время как y ⪯ x { displaystyle y prevq x}y prevq x и x ⪯ y { displaystyle x prevq y}x prevq y не подразумевают x = y { displaystyle x = y}x = y , а просто безразличие x ∼ y { displaystyle x sim y}x sim y ). Понятие наибольшего элемента для предварительного заказа предпочтения было бы понятием наиболее предпочтительного выбора . То есть некоторый x ∈ B { displaystyle x in B}x in B с

y ∈ B { displaystyle y in B}y in B подразумевает y ≺ х. { displaystyle y prec x.}y prec x.

Очевидное применение – определение соответствия спроса. Пусть P { displaystyle P}P будет классом функционалов на X { displaystyle X}X . Элемент p ∈ P { displaystyle p in P}p in P называется функционалом цены или ценовой системой и отображает каждую группу потребления x ∈ X { displaystyle x in X}x in X в его рыночную стоимость p (x) ∈ R + { displaystyle p (x) in mathbb {R} _ {+}}{ displaystyle p (x) in mathbb {R} _ {+}} . бюджетное соответствие – это соответствие Γ: P × R + → X { displaystyle Gamma двоеточие P times mathbb {R} _ {+} rightarrow X}{ displaystyle Gamma двоеточие P times mathbb {R} _ {+} rightarrow X} отображение любой системы цен и любого уровня дохода в подмножество

Γ (p, m) = {x ∈ X ∣ p (x) ≤ m}. { displaystyle Gamma (p, m) = {x in X mid p (x) leq m }.} Gamma (p, m) = {x in X mid p (x) leq m }.

соответствие спроса отображает любую цену p { displaystyle p}p и любой уровень дохода m { displaystyle m}mв набор ⪯ { displaystyle prevq} prevq -максимальные элементы Γ (p, m) { displaystyle Gamma (p, m)} Gamma (p, m) .

D (p, m) = {x ∈ X ∣ x { displaystyle D (p, m) = { big {} x in X mid x}D (p, m) = big {x in X mid x – максимальный элемент Γ (p, m)} { displaystyle Gamma (p, m) { big } }} Gamma (p, m) большой } .

Это называется соответствием спроса, потому что теория предсказывает, что для p { displaystyle p}p и m { displaystyle m}mс учетом рациональный выбор потребителя x ∗ { displaystyle x ^ {*}}x ^ {*} будет некоторым элементом x ∗ ∈ D (p, m) { displaystyle x ^ {*} in D (p, m)}x ^ * in D (p, m) .

Связанные понятия

Подмножество Q { displaystyle Q}Q частично упорядоченного набора P { displaystyle P}P называется cofinal, если для каждого x ∈ P { dis playstyle x in P}x in P существует y ∈ Q { displaystyle y in Q}y in Q такой, что x ≤ y { displaystyle x leq y }x leq y . Каждое конфинальное подмножество частично упорядоченного множества с максимальными элементами должно содержать все максимальные элементы.

Подмножество L { displaystyle L}L частично упорядоченного набора P { displaystyle P}P называется нижний набор из P { displaystyle P}P , если он закрыт вниз: if y ∈ L { displaystyle y in L}y in L и x ≤ y { displaystyle x leq y}x leq y , тогда x ∈ L { displaystyle x in L}x in L . Каждый нижний набор L { displaystyle L}L конечного упорядоченного набора P { displaystyle P}P равен наименьшему нижнему набору, содержащему все максимальные элементы L { displaystyle L}L .

См. Также

  • Наибольший элемент и наименьший элемент
  • Инфимум и супремум
  • Верхняя и нижняя границы

Примечания

Ссылки

  • значок Математика портал

Источник

Добавить комментарий