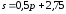Пусть
q
– количество
реализованного товара,
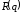 –
–
функция дохода (выручки), – издержки производства, связанные с
– издержки производства, связанные с
выпускомq
единиц продукции. Рассмотрим задачу
выбора оптимального объема производства
фирмой. Функция прибыли от реализации
произведенного товара может быть
смоделирована зависимостью
 . (13.5.1)
. (13.5.1)
В
микроэкономике известно утверждение:
для того чтобы прибыль была максимальной,
необходимо,
чтобы предельный доход и предельные
издержки были равны, так что этот принцип
можно записать в виде
 . (13.5.2)
. (13.5.2)
Действительно,
из необходимого условия экстремума для
функции (13.5.1) следует, что
 ,
,
откуда и получается основной принцип.
Найдем
связь между предельным доходом и
эластичностью спроса по цене:

Рассмотрим
примеры.
Пример
13.4. Найти
максимум прибыли, если текущая рыночная
цена товара равна $20, а функция суммарных
издержек имеет вид
 .
.
Решение.
Суммарная выручка равна произведению
 ,
,
и так как ,
,
тосуммарная
прибыль
 .
.
Предельная
прибыль
принимает вид:
 .
.
Приравнивая
производную прибыли к нулю, получаем
уравнение
 .
.
Корни этого уравнения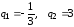 .
.
Проверка показывает, что максимальная
прибыль достигается при :
: .
.
Пример
13.5. В
соответствии с прогнозами прибыль
предприятия описывается функцией
 ,
,
гдеq
– величина, характеризующая объем
производства (в млн. руб.). Найти оптимальный
объем выпуска продукции, производимой
фирмой.
Решение.
Предельная прибыль фирмы
 .
.
Приравниваем производную нулю .
.
Является ли объем выпуска, равный
четырем, оптимальным для фирмы? Исследуем
характер изменения знака производной.
При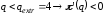 и прибыль убывает. При
и прибыль убывает. При и прибыль возрастает.
и прибыль возрастает.
Следовательно,
в точке экстремума
 прибыль принимает минимальное значение,
прибыль принимает минимальное значение,
и таким образом этот объем производства
не является оптимальным для фирмы.
Каким
же будет оптимальный объем выпуска для
фирмы? Ответ на этот вопрос зависит от
дополнительного исследования
производственных мощностей фирмы. Если
фирма не может производить за
рассматриваемый период больше 8 единиц
продукции
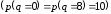 ,
,
то оптимальным решением для фирмы будет
вообще ничего не производить, а получать
доход от сдачи в аренду помещений и/или
оборудования. Если же фирма способна
производить за рассматриваемый период
больше 8 единиц продукции, то оптимальным
решением для фирмы будет выпуск на
пределе своих производственных мощностей.
Пример
13.6. На
начальном этапе производства фирма
минимизирует средние издержки, причем
функция издержек имеет вид  .
.
В дальнейшем цена на единицу товара
устанавливается равной
усл. ед. На
сколько единиц товара фирме следует
увеличить выпуск? На сколько при этом
изменятся средние издержки?
Решение.
Средние
издержки
 .
.
Предельные
средние издержки равны
 .
.
Для того чтобы средние издержки были
минимальными,необходимо,
чтобы производная
 .
.
Решая уравнение ,
,
находим .
.
Минимальное значение средних издержек
при
 равно:
равно:
 .
.
Предельные издержки .При установившейся
.При установившейся
цене
 оптимальное значение прибыли:
оптимальное значение прибыли: .
.
Для того чтобы прибыль была максимальной,необходимо,
чтобы предельный доход и предельные
издержки были равны (13.5.2):
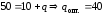 .
.
Таким
образом, выпуск продукции следует
увеличить на 20 единиц, при этом средние
издержки увеличатся:
 .
.
Пример
13.6. Прибыль
фирмы и объем поступления налогов
государству при данной налоговой ставке.
Пусть цена
на продукцию
 ,
,
а издержки ,
,
где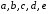 – положительные константы. Пусть налог
– положительные константы. Пусть налог
является акцизом со ставкойt,
т.е. с каждой проданной единицы товара
платится налог t,
и вся налоговая сумма равна
 .
.
Итак, фирма получает прибыль .
.
Желая ее максимизировать, фирма ищет
оптимальный объем производства.
Необходимое условие максимума прибыли ;
;
отсюда получаем значение ,
,
при этом ,
,
т.е. действительно точка максимума. Так как
действительно точка максимума. Так как ,
,
то, очевидно, что такая налоговая система
приводит к снижению оптимального выпуска
продукции.
Вычислим
суммарный налоговый доход правительства
(государства) при объеме производства
 :
: .
.
Возникает вопрос: каким должен быть
налогt,
чтобы величина суммарного налога T
со всей продукции была наибольшей?
Кривая доходов правительства представляет
параболу, ветви которой направлены
вниз. Ясно, что максимум достигается
при
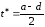 и равен
и равен ,
,
а оптимальный выпуск продукции при этом
значении равен
равен ,
,
и прибыль фирмы равна .
.
Прибыль же фирмы при налоговой ставкеt
равна

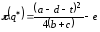 ,
,
откуда следует, что с ростомt
прибыль уменьшается
 .
.
Хотя доходы правительства при указанныхt
положительны,
существует область значений налоговой
ставки (а именно, при
 ),
),
при которой прибыль фирмы отрицательна.
При происходит резкое сокращение деловой
происходит резкое сокращение деловой
активности предприятий. Понятно, почему
производители прикладывают столько
усилий, чтобы снизить ставку налога.
Упражнения
-
Объем
реализации
 продукции зависит от цены
продукции зависит от цены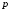 :
: .
.
При этом издержки определяются формулой .
.
Найти оптимальный объем производства
и соответствующие ему значения прибыли
и издержек. -
Зависимость
между доходом фермерского хозяйства
(ден. ед./день) и количеством его работников
 имеет вид:
имеет вид: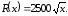 Найти оптимальный размер фермерского
Найти оптимальный размер фермерского
хозяйства и его прибыль, если дневная
зарплата рабочего равна 360 (ден. ед.), а
прочие расходы хозяйства составляют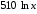 (ден. ед.).
(ден. ед.). -
У
фермера имеется стадо в 100 коров, каждая
массой в 200 кг. Содержание одной коровы
обходится в 92 цента в день. Корова
прибавляет 2 кг в день. Рыночная цена
коров составляет 10 долларов за 1 кг и
падает на 1 цент в день. Как долго фермер
должен откладывать продажу, чтобы
получить наибольший доход? Сколько он
выиграет по сравнению с немедленной
продажей? -
Бизнесмен
Вася купил две автомашины по 20 тыс.
долларов и перепродал их. При перепродаже
первой автомашины прибыль составила
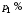 ,
,
второй – ,
,
причем .
.
О второй сделке Вася не сообщил в
налоговую инспекцию, и с него взяли
штраф, составляющий прибыли, полученной от продажи второго
прибыли, полученной от продажи второго
автомобиля. Выгодной ли оказалась
сделка Васи? Каковы его максимально
возможные потери? -
Приведите
анализ прибыли фирмы и ее налоговой
политики, если издержки фирмы
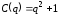 ,
,
доход ,
,
налог является акцизом со ставкойt.
Функции
спроса и предложения
1.
Дана функция предложения
 ,
,
где –
–
цена товара. Если равновесный объем
спроса-предложения равен 8, то функция
спроса может иметь вид
может иметь вид
1)

2)

3)
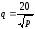
4)

Решение:
Вычислим
равновесную цену спроса-предложения
из условия
 :
: .
.
Решив это уравнение, получим .
.
Тогда в качестве функции спроса можно
взятьубывающую
функцию, которая проходит через точку
с координатами
 .
.
Этим условиям удовлетворяет, например,
функция .
.
(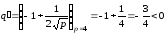 ),
),
точка

удовлетворяет
уравнению
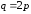 ,
,
однако
 ,
,
т. е. функция
 не может быть функцией спроса, т. к. она
не может быть функцией спроса, т. к. она
возрастает.
2.
Функции спроса
 и предложения
и предложения от цены
от цены выражаются соответственно уравнениями:
выражаются соответственно уравнениями: Соответствие эластичности и равновесной
Соответствие эластичности и равновесной
цены их значениям:
|
Эластичность |
|
|
Эластичность |
0,64 |
|
Равновесная |
64 |
|
Эластичность |
|
Решение:
Равновесная
цена находится
из уравнения
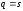 :
:
 .
.
Сделаем замену
 .
.
Корнями уравнения
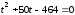 являются числа
являются числа .
.
Поэтому равновесная цена .
.
Вычислим
эластичность
спроса при
равновесной
цене для
функции

по формуле
 .
.
Имеем
 .
.
Эластичность
предложения
при равновесной цене
для функции

находим аналогично по формуле
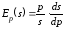 :
:
 .
.
Вычислим
эластичность
дохода при
равновесной цене. Доход, получаемый
фирмой, равен произведению цены единицы
товара на количество проданных единиц
товара:
 .Поэтому
.Поэтому
 .
.
3.
Кривая спроса по цене
 с постоянной эластичностью спроса может
с постоянной эластичностью спроса может
иметь вид
1)

2)

3)
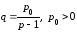
4)

Решение:
Вычислим
коэффициенты эластичности спроса по
цене для данных функций по
формуле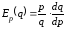 .
.
Тогда
для функции

 ;
;
для
функции

 ;
;
для
функции

 ;
;
для
функции

 .
.
Следовательно,
правильным будет ответ
 .
.
4.
Функция спроса по цене
 характеризуется неэластичным спросом.
характеризуется неэластичным спросом.
Тогда значение параметра может быть равно …
может быть равно …
1)

2)

3)

4)

Решение:
Значения
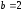
и

не могут
быть ответами, так как при них функция
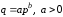 возрастает и
возрастает и
не является
функцией спроса.
Найдем
эластичность функции
 :
:
 .
.
Если
 ,
,
то спроснеэластичный.
Поэтому правильный ответ
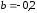 .
.
5.
Даны функция спроса
 и предложения
и предложения ,
,
гдеq
и s
– количество товара, соответственно
покупаемого и предлагаемого на продажу
в единицу времени, р
– цена единицы товара. Тогда
равновесная цена спроса-предложения
равна…
1)

2)

3)
1,96
4)
2
6.
Дана функция спроса по цене
 .
.
Тогда спрос будет эластичным при …
1)

2)
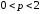
3)
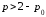
4)

Решение:
Найдем
эластичность функции
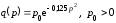 :
:
 .
.
Если
 ,
,
то спросэластичный,
т. е.
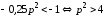 .
.
Поэтому правильный ответ .
.
7.
Дана функция спроса по цене на товар
 .
.
Коэффициент эластичности спроса при
цене 6 ден. ед. составит…
1)

2)

3)
1
4)

8.
Дана функция спроса по цене
 .
.
Эластичность спроса по цене составит ,
,
если цена равна…
равна…
1)
80
2)
160
3)
40
4)
20
9.
Спрос
 на некоторые товары народного потребления
на некоторые товары народного потребления
зависит от их стоимости следующим образом:
следующим образом: Спрос будет нейтральным (с единичной
Спрос будет нейтральным (с единичной
эластичностью) при …
1)

2)

3)
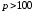
4)

Решение:
Найдем
эластичность функции
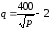 :
:
 .
.
Тогда:
 .
.
10.
Функции спроса
 и предложения
и предложения на некоторые фрукты от их цены
на некоторые фрукты от их цены имеют соответственно вид
имеют соответственно вид Эластичность спроса в точке равновесной
Эластичность спроса в точке равновесной
цены равна…
1)

2)

3)

4)
1
11.
Функция потребления некоторой страны
имеет вид:
 ,
,
гдех
– совокупный национальный доход. Если
национальный доход составляет 256 единиц,
то эластичность потребления по доходу
 равна…
равна…
1)

2)

3)

4)
1
12.
Функция потребления некоторой страны
имеет вид:
 ,
,
гдех
– совокупный национальный доход. Если
национальный доход составляет 32 единицы,
то эластичность потребления по доходу
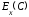 равна…
равна…
1)

2)

3)

4)
1
13.
Если зависимость между объемом выпуска
готовой продукции
 (млн руб.) и объемом производственных
(млн руб.) и объемом производственных
фондов (млн руб.) выражается уравнением
(млн руб.) выражается уравнением ,
,
то эластичность выпуска продукции для
предприятия, имеющего фонды в размере
36 млн руб. равна…
1)

2)
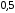
3)

4)
1
14.
Зависимость между спросом
 и ценой
и ценой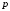 за единицу продукции дается соотношением
за единицу продукции дается соотношением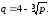 Спрос будет нейтральным (с единичной
Спрос будет нейтральным (с единичной
эластичностью) при …
1)

2)
216
3)

4)
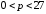
15.
Зависимость
между себестоимостью продукции C и
объемом производства Q выражается как
 .
.
Коэффициент эластичности себестоимости
при объеме производства равен
равен .
.
Тогда значение параметра равно …
равно …
1)
180
2)

3)

4)
300
Решение:
Найдем
эластичность функции
 :
:
 .
.
При объеме производства
 имеем
имеем .
.
16.
Дана функция спроса по цене
 .
.
Тогда спрос будет неэластичным при …
1)
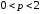
2)

3)
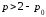
4)

Решение:
Найдем
эластичность функции
 :
:
 .
.
Если
 ,
,
то спроснеэластичный.
Поэтому
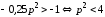 .
.
Этому условию удовлетворяет ответ .
.
17.
Дана функция спроса по цене
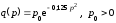 .
.
Тогда спрос будет нейтральным при …
1)

2)

3)

4)

18.
Функция совокупной полезности

товара
 для потребителя имеет вид:
для потребителя имеет вид: ,
,
где – количество потребленного в единицу
– количество потребленного в единицу
времени товара. Точка, при которой
совокупная полезность является
максимальной и потребитель достигает
насыщения, равна…
1)
26
2)
0
3)
52
4)
2,5
19.
Пусть функция полезности

задана
уравнением:
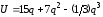 .
.
Тогда объем потребления ( ),
),
при котором начинает действовать закон
убывания предельной полезности, равен…
1)
7
2)
0
3)
15
4)

20.
Дана функция спроса
 ,
,
где –
–
цена товара. Если равновесный объем
спроса-предложения равен 3,75, то функция
предложения может
может
иметь вид …
-
Зависимость
между себестоимостью продукции C
и объемом производства Q
выражается
как
 . Коэффициент эластичности себестоимости
. Коэффициент эластичности себестоимости
при объеме производства равен
равен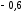 .
.
Тогда значение параметра равно …
равно …
-
Дана
функция спроса по цене
 .
.
Тогда спрос будет неэластичным при …
-
Дана
функция спроса по цене
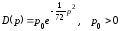 .
.
Тогда спрос будет эластичным при …///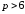
-
Дана
функция спроса по цене
 .
.
Тогда спрос будет эластичным при …
-
Зависимость
между себестоимостью продукции C
и объемом производства Q
выражается
как
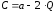 . Коэффициент эластичности себестоимости
. Коэффициент эластичности себестоимости
при объеме производства равен
равен .
.
Тогда значение параметра равно …90
равно …90
-
Дана
функция спроса по цене
 .
.
Тогда спрос будет нейтральным при … *
* -
Дана
функция спроса по цене
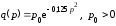 .
.
Тогда спрос будет нейтральным при … *
*
-
Дана
функция предложения
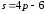 ,
,
где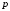 –
–
цена товара. Если равновесный объем
спроса-предложения равен 10, то функция
спроса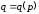 может иметь вид …
может иметь вид …
1)
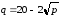 ;
;
2) ;
;
3) ;
;
4) *
*
-
Пусть
 есть функция спроса на товар. Тогда
есть функция спроса на товар. Тогда
обратная к ней функция определения
цены в зависимости от спроса имеет вид…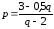 *
*
-
Дана
функция спроса
 и предложения
и предложения ,
,
где –
–
цена товара. Если равновесный объем
спроса-предложения равен ,
,
то значение параметра равно
равно
…0,5 -
Даны
функция спроса
 и предложения
и предложения ,
,
гдеq
и s
– количество товара, соответственно
покупаемого и предлагаемого на продажу
в единицу времени, р
– цена единицы товара. Тогда
равновесная цена спроса-предложения
равна…4 -
Функция
совокупной полезности

товара
 для потребителя имеет вид:
для потребителя имеет вид: ,
,
где – количество потребленного в единицу
– количество потребленного в единицу
времени товара. Точка, при которой
совокупная полезность является
максимальной и потребитель достигает
насыщения, равна…12
-
Замков
О.О., Толстопятенко А.В., Черемных Ю.Н.
Математические
методы в экономике. – М.: Издательство
“ДИС”, 1997. – 368 с. -
Колесников
А.Н. Краткий
курс математики для экономистов. – М.:
ИНФРА-М, 1997. – 208 с. -
Красс
М.С., Чупрынов Б.П. Основы
математики и ее приложения в экономическом
образовании. – М.: Дело, 2001. – 688 с. -
Кремер
Н.Ш. и др. Высшая
математика для экономистов. – М.: ЮНИТИ,
1998. – 472 с. -
Малыхин
В.И. Математика
в экономике. – М.: ИНФРА-М, 2001. – 356 с. -
Томпсон
Артур, Формби Джон.
Экономика фирмы / Пер. с англ. – М.: ЗАО
«Издательство
БИНОМ», 1998. – 544 с.
61
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Даны функция спроса на продукцию монополиста
Q = 26 – 0,5 × P
и функция общих затрат
ТС = 120 – 8 × Q + Q2.
Найти максимальную прибыль и соответствующую цену.
Решение:
Запишем обратную функцию спроса:
P = 52 – 2 × Q.
Общий доход найдём по формуле:
TR = Р × Q = (52 – 2 × Q) × Q = 52 × Q – 2 × Q2.
Найдём предельный доход как производную от функции общего дохода:
MR = TR’ = (52 × Q – 2 × Q2)’ = 52 – 4 × Q.
Определим функцию предельных затрат, взяв производную от функции общих затрат:
MC = TC’ = (120 – 8 × Q + Q2)’ = – 8 + 2 × Q.
Условие максимизации прибыли на рынке несовершенной конкуренции имеет вид:
MC = MR
– 8 + 2 × Q = 52 – 4 × Q
Q = 10 – оптимальный объём производства, при котором прибыль максимальна.
Цена на продукцию монополии будет соответственно равна
P = 52 – 2 × 10 = 32.
Прибыль вычислим по формуле:
П = TR – TC = P × Q – 120 + 8 × Q – Q2 = 32 × 10 – 120 + 8 × 10 – 102 = 180.
Пусть Q — количество реализованного товара, R(Q) — Функция дохода; C(Q) — функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организации инфраструктуры и т. п. Прибыль от реализации произведенного товара дается формулой
![]()
В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны. Оба упомянутых предельных показателя определяются по аналогии с (5.14а), так что этот принцип можно записать в виде R‘(Q) = C‘(Q). Действительно, из необходимого условия экстремума для функции (5.16) следует, что П'(Q) = 0, откуда и получается основной принцип.
Пример 4. Найти максимум прибыли, если доход и издержки определяются следующими формулами:

Решение. Согласно (5.16), прибыль П(Q) = – Q3 + 36Q2 – 69Q — 4000. Приравнивая производную функции прибыли к нулю, получаем уравнение
![]()
Корни этого уравнения Q1 = 1, Q2 = 23. Проверка показывает, что максимальная прибыль достигается при Q = 23: Пmах = 1290.
| < Предыдущая | Следующая > |
|---|

Математические приложения в математике Часть 2 Максимальные прибыли

Пусть – количество реализованного товара, функция дохода, – функция затрат на производство товара. В реальности вид этих функций зависит в первую очередь от способа производства, организации инфраструктуры в т. п. Прибыль от реализации произведённого товара дается формулой (1)

В макроэкономике известно утверждение: для тот чтобы прибыль была максимальной, необходимо, чтобы предельный доход в предельные издержки были равны. Тогда производные предельного дохода и предельных издержек также равны. Действительно, из необходимого условия экстремума для функции (1) следует, что , откуда и получается основной принцип.

Пример Найдите максимум прибыли, если доход и издержки определяются следующими формулами: Решение: Согласно (1), прибыль Приравнивая производную функции прибыли к нулю, получаем уравнение .

Пример Решение: Согласно (1), прибыль Приравнивая производную функции прибыли к нулю, получаем уравнение Корни этого уравнения Проверка показывает, что максимальная прибыль достигает при