Как найти максимум света

• Радиус k–ой.зоны Френеля:

для сферической волны

,

где а —расстояние диафрагмы с
круглым отверстием от точечного источника
света;b —расстояние
диафрагмы от экрана, на котором ведется
наблюдение дифракционной картины;k
—номер зоны Фре­неля; λ —длина
волны;

для плоской волны

.

• Дифракция света на одной щели при
нормальном падении лучей. Условие
минимумов интенсивности света

,k=1,2,3,…,

где а —ширина щели; φ— угол дифракции;k —номер минимума;

λ —длина волны.

Условие максимумов интенсивности света

,
k=l,
2, 3,…,

где φ’ — приближенное значение угла
дифракции.

• Дифракция света на дифракционной
решетке при нормальном падении лучей.
Условие главных максимумов интенсивности

d sinφ=±kλ,
k=0,1,2,3,…,

где d— период (постоянная) решетки;k —номер главного макси­мума; φ
—угол между нормалью к поверхности
решетки и нап­равлением дифрагированных
волн.

• Разрешающая сила дифракционной
решетки

,

где Δλ— наименьшая
разность длин волн двух соседних
спектраль­ных линий (λ и λ+Δλ), при
которой эти линии могут быть видны
раздельно в спектре, полученном
посредством данной решетки;N —число штрихов решетки;k —порядковый
номер дифракцион­ного максимума.

• Угловая дисперсия дифракционной
решетки

,

линейная дисперсия дифракционной
решетки

.

Для малых углов дифракции

,

где f— главное фокусное
расстояние линзы, собирающей на экра­не
дифрагирующие волны.

• Разрешающая сила объектива телескопа

,

где β — наименьшее угловое расстояние
между двумя светлыми точками, при котором
изображения этих точек в фокальной
плос­кости объектива могут быть видны
раздельно; D —диаметр объек­тива;
λ —длина волны.

• формула Вульфа — Брэгга

2d
sin
=kλ,

где d —расстояние
между атомными плоскостями кристалла;— угол скольжения (угол между направлением
пучка параллель­ных лучей, падающих
на кристалл, и гранью кристалла),
опре­деляющий направление, в котором
имеет место зеркальное отраже­ние
лучей (дифракционный максимум).

Примеры решения задач

Пример 1.На диафрагму с круглым
отверстием радиусомr=1
мм падает нормально параллельный пучок
света длиной волны λ=0,05 мкм. На пути
лучей, прошедших через отверстие,
помещают экран. Определить максимальное
расстояниеb_maxот центра от­верстия до экрана, при
котором в центре дифракционной картины
еще будет наблюдаться темное пят­но.

Решение.Расстояние, при котором
будет видно темное пят­но, определяется
числом зон Фре­неля, укладывающихся
в отвер­стии. Если число зон четное,
то в центре дифракционной картины бу­дет
темное пятно.

Число зон Френеля, помещаю­щихся в
отверстии, убывает по мере удаления
экрана от отверстия. Наименьшее четное
число зон равно двум. Следовательно,
максимальное расстояние, при котором
еще будет наблюдаться темное пятно в
центре экрана, определяется условием,
согласно которому в отверстии должны
поместиться две зоны Френеля.

Из рис. 31.1 следует, что расстояние от
точки наблюдения Oна
экране до края отверстия на 2(λ/2)больше, чем расстояниеb_max.

По теореме Пифагора получим

.

Учтя, что λ<<b_mахи что членом, содержащим λ², можно
пренеб­речь, последнее равенство
перепишем в виде

r²=2λb_max.
откудаb_max=r²/(2λ).
Произведя вычисления по последней
формуле, найдем

b_max=1
м.

Пример 2.На щель ширинойа=0,1 мм
нормально падает параллельный пучок
света от монохроматического источника
(λ==0,6 мкм). Определить ширинуlцентрального максимума в дифракционной
картине, проецируемой с помощью линзы,
нахо­дящейся непосредственно за
щелью, на экран, отстоящий от лин­зы
на расстоянииL=lм.

Решение.
Центральный максимум интенсивности
света за­нимает область между ближайшими
от него справа и слева миниму­мами
интенсивности. Поэтому ширину центрального
максимума интенсивности примем равной
расстоянию между этими двумя минимумами
интенсивности (рис. 31.2).

Минимумы интенсивности света при
дифракции от одной щели наблюдаются
под углами φ, определяемыми
условием

a sin
φ=±kλ, (1)

где k —порядок
минимума; в нашем случае равен единице.

Расстояние между двумя минимумами на
экране определим не­посредственно
по чертежу: l=2Ltgφ. Заметив, что при малых
уг­лахtgφsinφ, перепишем эту формулу в виде

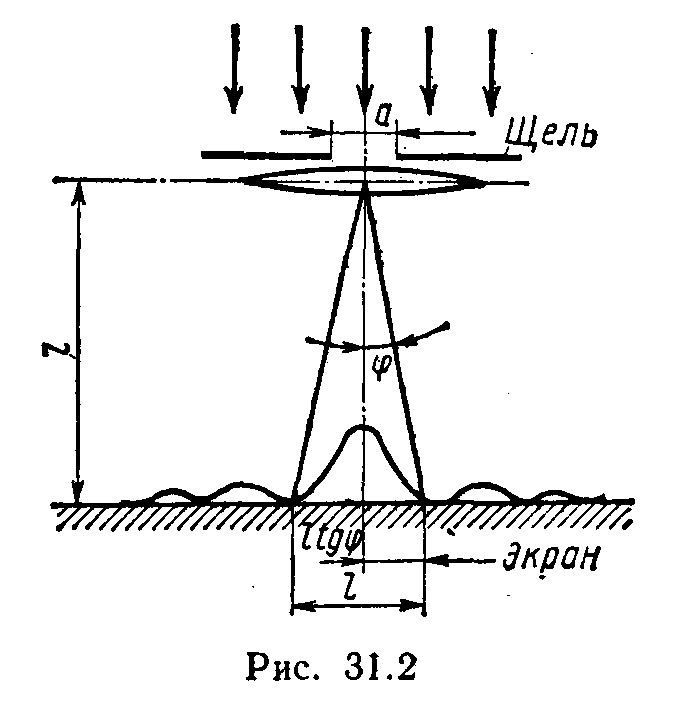
/=2L sin φ. (2)

Выразим sinφ из формулы
(1) и подставим его в равенство (2):

l=2Lkλ/a. (3)

Произведя вычисления по фор­муле (3),
получим l=1,2 см.

Пример 3.На дифракционную решетку
нормально к ее поверх­ности падает
параллельный пучок света с длиной волны
λ=0,5мкм. Помещенная вблизи решетки лин­за
проецирует дифракционную картину на
плоский экран, удаленный от линзы наL=lм.
Расстоя­ниеlмежду
двумя максимумами интенсивности первого
порядка, наблюдаемыми на экране, равно
20,2 см (рис. 31.3). Определить: 1) постояннуюdдифракционной
решетки; 2) числоnштрихов на 1 см; 3) число максимумов,
которое при этом дает дифракционная
решетка; 4) максимальный угол φ_mахотклонения лучей, соот­ветствующих
последнему дифракционному максимуму.

Решение 1. Постоянная dдифракционной
решетки, длина волныλи угол φ
отклоне­ния лучей, соответствую­щийk-му дифракционному
максимуму, связаны соот­ношением

dsin φ=kλ,
(1)

где k— порядок спектра,
или в случае монохрома­тического
света порядок максимума.

В данном случае k=1,
sinφ=tgφ
(ввиду того, чтоl/2<<L),tgφ=(l/2)L(следует из рис. 31.3). С учетом последних
трех равенств соотношение (1) примет вид

,

откуда постоянная решетки

d=2Lλ/l.

Подставляя данные, получим

d=4,95 мкм.

2. Число штрихов на 1 см найдем из формулы

п=1/d.

После подстановки числовых значений
получим n=2,02-10³см^-1.

3. Для определения числа максимумов,
даваемых дифракцион­ной решеткой,
вычислим сначала максимальное значение
k_maxисходя из того, что максимальный угол
отклонения лучей решеткой не может
превышать 90°.

Из формулы (1) запишем

. (2)

Подставляя сюда значения величин,
получим

K_max=9,9.

Число kобязательно
должно быть целым. В то же время оно не
может принять значение, равное 10, так
как при этом значенииsinφ должен быть больше единицы, что
невозможно. Следователь­но,k_mах=9.

Определим общее число максимумов
дифракционной картины, полученной
посредством дифракционной решетки.
Влево и вправо от центрального максимума
будет наблюдаться по одинаковому числу
максимумов, равному k_mах,т. е. всего 2k_mах.
Если учесть также центральный нулевой
максимум, получим общее число мак­симумов

N=2k_max+l.

Подставляя значение k_mахнайдем

N=2*9+1=19.

4. Для определения максимального угла
отклонения лучей, соответствующего
последнему дифракционному максимуму,
выра­зим из соотношения (2) синус этого
угла:

sinφ_max=k_maxλ/d.

Отсюда

φ_max=arcsin(k_maxλ/d).

Подставив сюда значения величин λ, d,k_mахи произведя вычис­ления, получим

φ_mах=65,4°.

Задачи

Зоны
Френеля

31.1.Зная формулу радиусаk–й.зоны Френеля для сферической волны
(ρ_k=),
вывести соответствующую формулу для
плоской волны.

31.2.Вычислить радиус ρ₅пятой
зоны Френеля для плоского волнового
фронта (λ=0,5 мкм), если построение делается
для точки наблюдения, находящейся на
расстоянииb=1 м от
фронта волны.

31.3.Радиус ρ₄четвертой зоны
Френеля для плоского волнового фронта
равен 3 мм. Определить радиусρ₆шестой зоны Френеля.

31.4.На диафрагму с круглым отверстием
диаметромd=4 мм падает
нормально параллельный пучок лучей
монохроматического света (λ=0,5 мкм).
Точка наблюдения находится на оси
отверстия на расстоянииb=1
м от него. Сколько зон Френеля укладывается
в отверстии? Темное или светлое пятно
получится в центре дифрак­ционной
картины, если в месте наблюдений поместить
экран?

31.5.Плоская световая волна (λ=0,5 мкм)
падает нормально на диафрагму с круглым
отверстием диаметромd=lсм. На каком рас­стоянииbот отверстия должна находиться точка
наблюдения, что­бы отверстие открывало:
1) одну зону Френеля? 2) две зоны Френеля?

31.6.Плоская световая волна падает
нормально на диафрагму с круглым
отверстием. В результате дифракции в
некоторых точках оси отверстия,
находящихся на расстоянияхb_i,от его центра, наблю­даются максимумы
интенсивности. 1. Получить вид функцииb=f(r,
λ, п),гдеr— радиус
отверстия; λ — длина волны;п —чис­ло зон Френеля, открываемых для
данной точки оси отверстием. 2. Сделать
то же самое для точек оси отверстия, в
кото­рых наблюдаются минимумы
интенсивности.

31.7.Плоская световая волна (λ=0,7
мкм) падает нор­мально на диафрагму
с круг­лым отверстием радиусомr=1,4
мм. Определить рас­стоянияb₁,b₂,b₃от диафраг­мы до трех наиболее
удален­ных от нее точек, в которых
наблюдаются минимумы интенсив­ности.

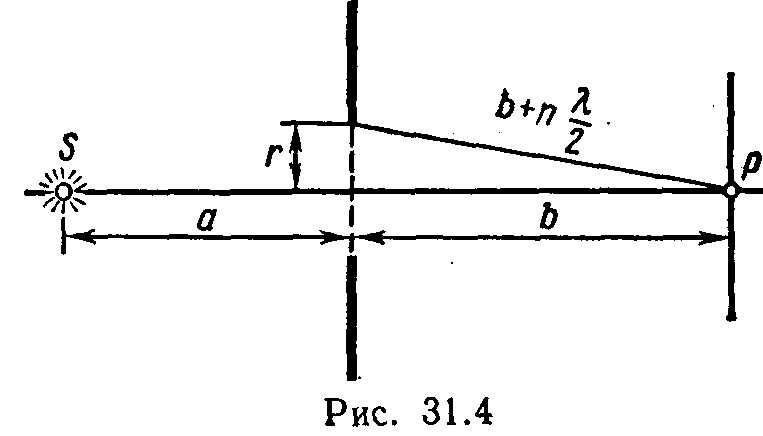
31.8.Точечный источникSсвета (λ=0,5 мкм), плоская диафрагма с
круглым отверстием радиусомr=1
мм и экран расположены, как это указано
на рис. 31.4 (а=1 м). Определить расстояниеbот экра­на до
диафрагмы, при котором отверстие
открывало бы для точкиР три зоны
Френеля.

31.9.Как изменится интенсивность в
точкеР(см. задачу 31.8), если убрать
диафрагму?

Соседние файлы в папке Чертов Задачи_6. Оптика

• #
• #
• #
• #
• #
• #

В рамках геометрической оптики, распространение луча в оптически однородной среде — прямолинейное, однако в природе существует ряд явлений, где можно наблюдать отклонение от этого условия.

Дифракция – явление огибания световыми волнами встреченных препятствий. В школьной физике изучаются две дифракционные системы (системы, при прохождении луча в которых наблюдается дифракция):

• дифракция на щели (прямоугольном отверстии)
• дифракция на решётке (набор равноотстоящих друг от друга щелей)

Дифракция на щели — дифракция на прямоугольном отверстии (рис. 1).

Пусть дана плоскость со щелью, шириной , на которую под прямым углом падает пучок света А. Большинство света проходит на экран, однако часть лучей дифрагирует на краях щели (т.е. отклоняется от своего первоначального направления). Далее эти лучи интерферируют друг с другом с образованием дифракционной картины на экране (чередование ярких и тёмных областей). Рассмотрение законов интерференции достаточно сложно, поэтому ограничимся основными выводами.

Полученная дифракционная картина на экране состоит из чередующихся областей с дифракционными максимумами (максимально светлыми областями) и дифракционными минимумами (максимально тёмными областями). Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:

• для дифракционных максимумов

(1)

• где

Нулевым максимумом дифракции называется центральная точка на экране под щелью (рис. 1).

• для дифракционных минимумов

(2)

• где

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (1) или (2).

Дифракция на дифракционной решётке. 

Дифракционной решёткой называется система, состоящая из чередующихся щелей, равноотстоящих друг от друга (рис. 2).

Так же, как и для  щели, на экране после дифракционной решётки будет наблюдаться дифракционная картина: чередование светлых и тёмных областей. Вся картина есть результат интерференции световых лучей друг с другом, однако на картину от одной щели будет воздействовать лучи от других щелей. Тогда дифракционная картина должна зависеть от количества щелей, их размеров и близкорасположенности.

Введём новое понятие — постоянная дифракционной решётки:

(3)

Тогда положения максимумов и минимумов дифракции:

• для главных дифракционных максимумов (рис. 3)

(4)

• где

• для дифракционных минимумов

(5)

• где

Отдельным вопросом задач на дифракцию является вопрос о наибольшем количестве максимумов, которые можно наблюдать в текущей системе. Наибольший угол, под которым можно наблюдать максимум — , тогда, исходя из (4):

(6)

Главное помнить, что число максимумов — число, т.е. от полученного ответа необходимо брать только целую часть.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (4) или (5).

Общий вывод: задачи на дифракцию должны содержать в себе словосочетания, связанные с «дифракцией». Далее разбираемся с объектом: щель или дифракционная решётка и используем соответствующие соотношения для минимума или максимума.

Содержание:

Волновая оптика – раздел оптики, объясняющий оптические явления на основе волновой природы света. Световые волны рассматриваются по своей природе как электромагнитные волны, обладающие всеми их свойствами. Волновая оптика описывает такие оптические явления, как интерференция, дифракция, поляризация и дисперсия.

Природа света

Первые научные взгляды на природу света были высказаны в XVII в. В одной из них предполагалось, что свет – это вещество, которое представляет собой поток корпускул; в другой, что свет – это волна.

И. Ньютон, основываясь на свойствах механических волн огибать препятствия и распространяться в упругой среде, остановился на вещественной теории света. Согласно его теории, созданной в 1672 г., свет состоит из малых частичек, испускаемых светящимся телом. Подобно макроскопическим телам частицы света движутся прямолинейно и не огибают препятствий, за ними образуются тени. Частицы света не нуждаются в упругой среде.

Х. Гюйгенс разработал волновую теорию света. Он считал, что световые волны не способны огибать препятствия аналогично тому, как короткие волны, ударяясь о борт корабля, не могут обогнуть его. Он предположил, что существует упругая среда − эфир, заполняющая все пространство и проникающая внутрь всех тел. Впервые процессы распространения, отражения и преломления света с точки зрения волновой теории Х. Гюйгенс изложил в сочинении «Трактат о свете», опубликованном в 1690 г.

Христиан Гюйгенс (1629–1695)  – голландский математик, физик и  астроном. В  «Трактате о  свете» изложил волновую теорию света. Известны его работы прикладного характера: он усовершенствовал линзовый телескоп, изобрел микрометр для измерения малых углов. С  помощью сконструированного им телескопа в  1655 г. обнаружил кольцо у Сатурна и его спутник Титан, определил период обращения Титана вокруг планеты.

Корпускулярная и волновая теории существовали параллельно длительное время. На основе корпускулярной теории сложно было объяснить, почему частицы света, пересекаясь в пространстве, не рассеиваются, тогда как волновая теория это легко объясняла. На основе волновой теории в начале XIX в. были объяснены такие явления, как: интерференция, дифракции, дисперсия и поляризация света.

Во второй половине XIX в. Дж. Максвелл создал теорию электромагнитных волн. Совпадение скорости световой волны

Свет обладает корпускулярно-волновым дуализмом, то есть проявляет как корпускулярные, так и волновые свойства.

Астрономический метод определения скорости света

В XVII веке в связи с бурным развитием мореплавания появилась идея использовать периодичность восхода и захода открытых Г. Галилеем спутников Юпитера: Ио, Европы, Ганимеда, Каллисто в качестве точного хронометра. В 1672 г. астроном Джованни Кассини обнаружил нарушения в периодичности выхода из тени Юпитера его спутника Ио. Причем с удалением Земли от Юпитера промежутки времени между восходами увеличивались, а с приближением – уменьшались.

В 1676 г., исследуя это явление, Олаф Ремер предположил, что скорость распространения света конечна. Когда Земля в своем движении вокруг Солнца удаляется от Юпитера от точки 1 к точке 2 (рис. 122), то промежутки времени между моментами выхода Ио из тени Юпитера увеличиваются, поскольку свету нужно дополнительное время, чтобы догнать отдаляющуюся Землю. При сближении Земли с Юпитером промежутки времени между восходами Ио уменьшаются. Разница во времени между моментами восхода Ио в самой дальней и самой ближней к Юпитеру точках орбиты Земли по измерениям О. Ремера составила около 22 минут. По известному расстоянию от Солнца до Земли О. Ремер смог вычислить скорость света: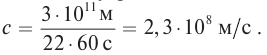

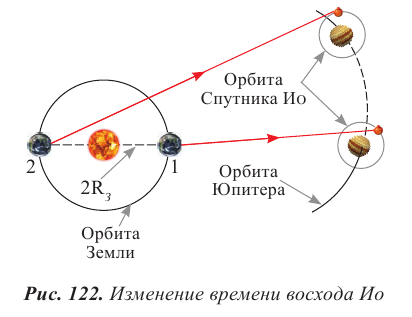
Из измерений О. Ремера следовало, что скорость света имеет гигантское значение по сравнению со скоростью всех остальных процессов, наблюдавшихся на Земле.

Лабораторные методы определения скорости света И. Физо и А. Майкельсона

Впервые скорость света лабораторным методом удалось измерить французскому физику И. Физо в 1849 г. Свет от источника, пройдя через линзу, падал на полупрозрачное зеркало (рис. 123). После отражения от зеркала сфокусированный узкий пучок направлялся на зубцы быстро вращающегося колеса. Пройдя между зубцами, свет достигал плоского отражающего зеркала, находившегося на расстоянии 8,633 км от колеса. Отразившись от зеркала, свет, прежде чем попасть в глаз наблюдателя, должен был пройти опять между зубцами вращающегося колеса.

Когда диск вращался медленно, свет, отраженный от зеркала, был виден. При увеличении скорости вращения он постепенно исчезал. Пока свет, прошедший между двумя зубцами, шел до зеркала и обратно, диск успевал повернуться так, что на место прорези вставал зубец, и свет переставал быть видимым. При дальнейшем увеличении скорости вращения свет вновь становился видимым. Очевидно, что за время распространения света до зеркала и обратно диск проворачивался так, что на место прежней прорези встала следующая. При известном значении этого промежутка времени и расстояния между диском и зеркалом можно определить скорость света:

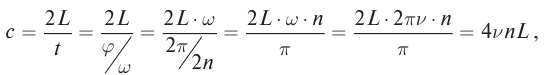
где L – расстояние от зеркала до вращающегося диска, t – промежуток времени, за которое свет проходит расстояние – угол поворота вращающегося диска, угловая скорость диска, n – число зубцов на диске, 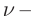частота вращения диска.

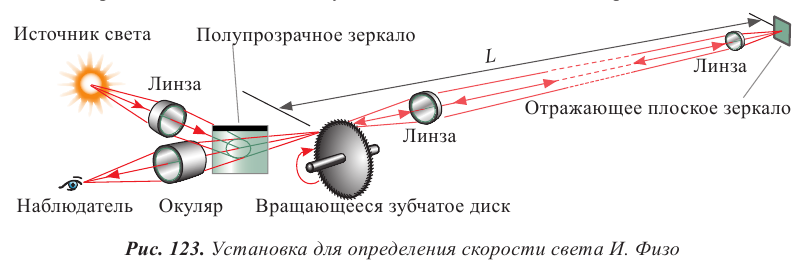
В своем опыте Физо получил следующий результат:

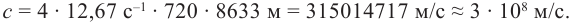
В 1924–1927 г. г. американский физик А. Майкельсон разработал схему опыта, в котором луч света был направлен с вершины горы Вильсон на вершину горы Сан-Антонио на расстояние порядка 35 км (рис. 124). Вместо диска было использовано восьмигранное вращающееся зеркало, приводимое в движение высокоскоростным ротором. Изменяя частоту вращения ротора, наблюдатель добивался возникновения в окуляре устойчивого изображения источника света. Знание расстояния между установками и частоты вращения зеркала позволяли вычислить скорость света. Значение скорости света, полученное Майкельсоном, было самым точным для того времени 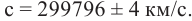По современным данным, скорость света в вакууме равна 299792458 м/с с точностью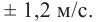

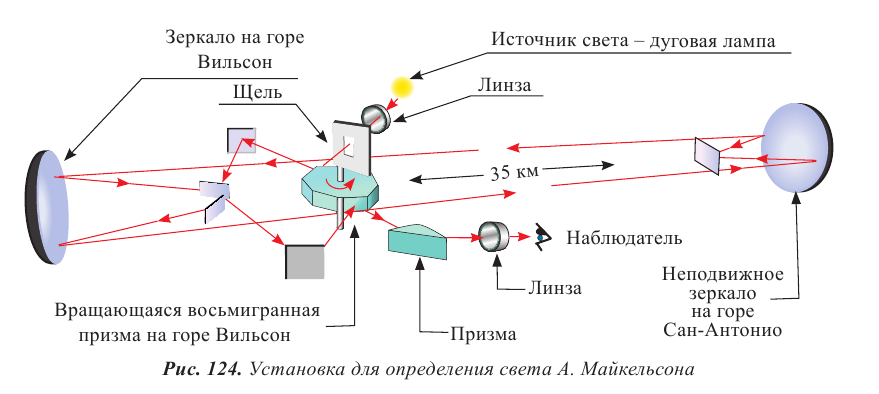
Дисперсия света

Первые экспериментальные наблюдения дисперсии света были проведены в 1672 г. И. Ньютоном. Через маленькое отверстие в ставне окна затемненной комнаты он направил луч солнечного света на стеклянную призму. Луч света, дважды преломившись в трехгранной призме, отклонился от своего первоначального направления и разложился на семь основных цветов спектра: красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый (рис. 125). И. Ньютон назвал изображение с радужным чередованием цветов спектром, а само явление дисперсией (от лат. «dispergo» − разброс). Наблюдая радужный дисперсионный спектр, он пришел к выводу, что от цвета луча зависит показатель преломления стекла. Меньше всего отклоняется свет красного цвета, больше – фиолетового, следовательно, стекло имеет для света более высокой частоты наибольший показатель преломления, а для более низкой − наименьший.

Зависимость показателя преломления вещества от частоты света называют дисперсией.

Дисперсия является следствием различной скорости распространения волн разной частоты в одной и той же среде. Чем больше частота световой волны, тем меньше ее длина и скорость в среде, тем больше для нее показатель преломления.

Вспомните! Показатель преломления определяет во сколько раз уменьшается скорость распространения электромагнитной волны в данной среде: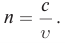

Сложный и первичный свет. Дополнительный цвет

В наблюдаемом спектре различают семь цветов. В действительности белый свет состоит из трех основных цветов: красного, зеленого и синего. Эти цвета называют первичными, потому что они не могут быть получены комбинациями света других цветов.

Свет, состоящий из света первичных цветов, называют сложным.

Другие цвета радужного спектра являются соединением первичных цветов. Зеленый и красный образуют желтый, зеленый и синий – голубой, синий и красный – фиолетовый рис. 126). В телевидении используют три основных цвета для получения всевозможных оттенков цветного изображения.

Цвета излучений, которые при смешении дают белый цвет, называются дополнительными цветами.

Дополнительными цветами являются желтый и синий, голубой и красный, фиолетовый и зеленый.

Цвета тел

Цвета окружающих тел определяются отраженным светом. Если предмет, например, лист бумаги, отражает все падающие на него лучи различных цветов, то он будет казаться белым. Покрывая бумагу слоем красной краски, мы не создаем при этом света нового цвета, но задерживаем на листе некоторый диапазон частот света отражателя. В данном случае отражаться будут только красные лучи, остальные поглотятся слоем краски. Трава и листья деревьев кажутся нам зелеными потому, что из всех падающих на них солнечных лучей они отражают только зеленые, поглощая остальные. Если посмотреть на траву через красное стекло, пропускающее только красные лучи, то она будет казаться почти черной.

Цвет непрозрачных предметов определяют отраженные лучи, прозрачных – отраженные и проходящие лучи.

Возьмите на заметку:

Используемые для освещения источники излучают не когерентные волны, в них присутствуют волны различной частоты и разности фаз. Источник света излучает видимые волны в диапазоне от 400 нм до 750 нм с частотами от 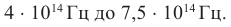Излучение атома представляет собой «обрывок» волны, который называют цугом. Переход атома из возбужденного в невозбужденное состояние происходит за малый промежуток времени, порядка 10 нс спонтанно, следовательно, длина цуга достигает около 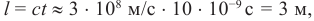а разность фаз между цугами может иметь произвольное значение.

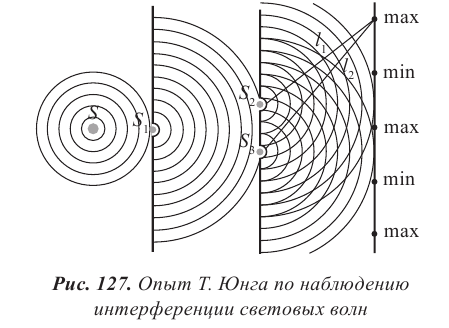
Опыт Т. Юнга по наблюдению интерференции световых волн

Английский физик Т. Юнг в 1802 г. наблюдал интерференцию света от одного монохроматического источника методом деления фронта волны, он использовал две преграды с одним и двумя небольшими отверстиями (рис. 127). На экране Т. Юнг увидел чередование светлых и темных полос, они определялись разностью хода лучей. Усиление света происходило в том случае, если к данной точке экрана обе волны достигали с синфазными колебаниями. В этом случае гребень одной волны накладывается на гребень другой. 

Томас Юнг (1773–1829) – английский физик, механик, врач, астроном и  востоковед, один из  создателей волновой теории света. Он описал первые опыты по  определению длин волн света. Высказал гипотезу о поперечности световых волн, разработал теорию цветного зрения.

Условия максимума и минимума освещенности

Запишем уравнение бегущей волны от двух отверстий:

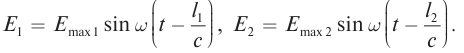
Разность фаз колебаний в точке падения луча равна:

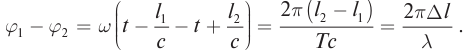
Колебания синфазны, если разность фаз кратна 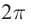 − цикличности синусоиды:

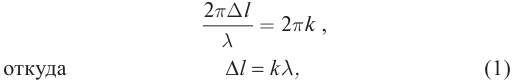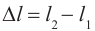где − разность хода лучей, 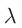− длина волны,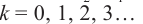

Максимум освещенности наблюдается в том случае, если разность хода когерентных лучей в однородной среде кратна целому числу длин волн.

Если колебания происходят в противофазе, то гребень одной волны накладывается на впадину другой, происходит ослабление волны. Разность фаз таких колебаний составляет 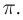 Учитывая периодичность синусоиды, запишем: 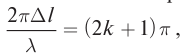для разности хода лучей получим

Минимум освещенности наблюдается, если разность хода когерентных лучей в однородной среде кратна нечетному числу полудлин волн.

Условия максимума интерференции на тонких пленках

Различные цвета тонких пленок – это результат наложения отраженных или преломленных лучей от двух поверхностей пленки (рис. 128, 129). Цвет пленки определяется условием максимума. Если в разность хода лучей 1 и 2 монохроматического источника света помещается целое число длин волн, то пленка окрашивается в цвет источника. Если разность хода равна нечетному числу длин полуволн, пленка становится темной. Разность хода лучей OB + BC (рис. 128, 129) зависит от толщины пленки и угла преломления луча:

Оптическая разность хода 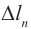превышает разность хода лучей 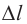в n раз:

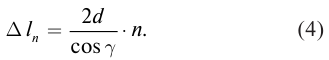
Исследования показали, что при отражении от оптически более плотной среды фаза волны меняется на 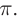Поэтому оптическая разность хода лучей 1 и 2 в отраженном свете (рис. 128) уменьшается на 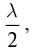следовательно, условие максимума (1) в отраженных лучах примет вид:

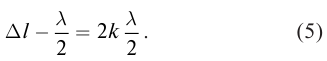
Подставив (4) в (5), получим условие максимума в отраженном свете:

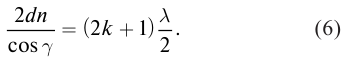
В проходящем свете отражение луча 2 происходит от менее плотной среды (рис. 129), следовательно, условие максимума останется таким же, как для волн, распространяющихся в однородной среде:

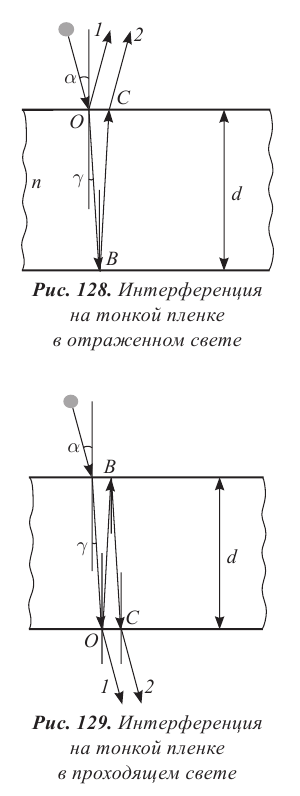
Дифракция света

Согласно геометрической оптике на экране в результате прохождения световых лучей через отверстие диаметром d появляется изображение в виде яркого круглого пятна большего диаметра D (рис. 131).

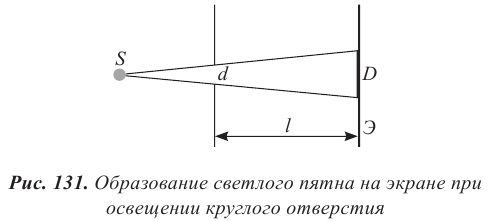
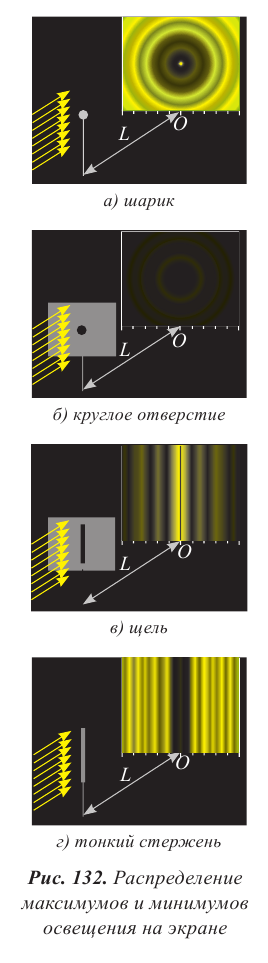
При уменьшении диаметра отверстия d и увеличении расстояния до экрана l изображение меняется. Оно представляет собой чередующиеся темные и светлые кольца, в центре которых может быть как светлое, так и темное пятно. При освещении малых по размеру тел наблюдается такая же картина (рис. 132 а, б).

Дифракция света – это явление огибания светом препятствий малых размеров и попадание его в область геометрической тени.

Различают два случая дифракции света: дифракцию Френеля в сходящихся лучах и дифракцию Фраунгофера в параллельных лучах.

Объяснение дифракционной картины на основе зон Френеля

Рассмотрим прохождение света через круглое отверстие и выясним условия максимума и минимума освещенности центральной части пятна на экране. Волновая поверхность в малом отверстии согласно принципу Гюйгенса – Френеля представляет собой часть сферы. Разобьем ее на зоны таким образом, чтобы расстояния от края каждой последующей зоны BO, CO, DO (рис. 133) отличались от предыдущей на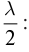

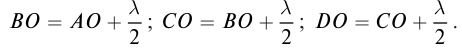
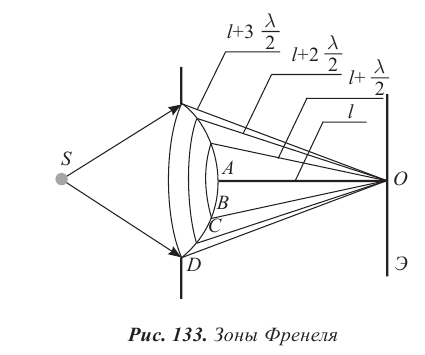
Поскольку разность хода волн от выделенных зон отличается на 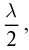то при четном их количестве в точке O на экране произойдет ослабление света. Волны от двух соседних зон создадут в точке O колебания противоположной фазы, в результате в центре изображения на экране будет темное пятно, окруженное светлыми и темными кольцами. Если на волновой поверхности размещается нечетное число зон, то центральная часть изображения на экране будет светлой.

Интересно знать! Впервые изображение чередующихся колец в тени круглого диска наблюдал итальянский физик Франческо Гримальди и  описал его в своем сочинении «Физическое учение о  свете, цветах и радуге». Ф. Гримальди объяснил наблюдаемое явление огибанием световыми волнами препятствий подобно волнам на  воде и  назвал его дифракцией (от лат. diffractus − огибание, разбиение).

Дифракция Фраунгофера на одной щели

Немецкий физик И. Фраунгофер рассмотрел дифракцию света в параллельных лучах. Для осуществления такого вида дифракции необходимо точечный источник света S поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием (рис. 134).

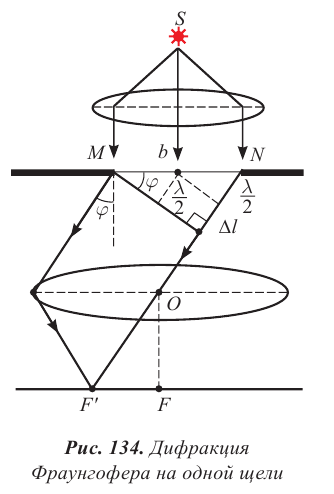
Пусть монохроматическая волна падает перпендикулярно плоскости бесконечно длинной узкой щели шириной b. Разность хода между крайними лучами, которые отклонились от прямолинейного направления на угол 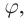равна:

Разобьем волновую поверхность на участке щели МN на зоны Френеля. Они будут иметь вид полос, параллельных краю щели МN, так как фронт волны для параллельных лучей является плоскостью. Ширина каждой полосы выбирается так, чтобы разность хода лучей на границе этих зон была равна 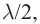тогда на ширине щели поместится всего 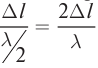зон.

Если число зон Френеля четное 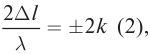то в точке 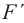будет наблюдаться дифракционный минимум. Запишем условие минимума:

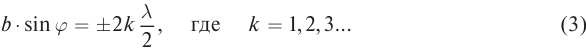
Если число зон Френеля нечетное:

то в точке F´ будет наблюдаться дифракционный максимум. Условие максимума для дифракции на одной щели:

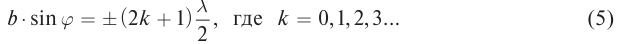
При 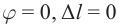в щели укладывается одна зона Френеля, следовательно, в точке F наблюдается главный или центральный максимум нулевого порядка. Основная часть световой энергии сосредоточена в главном максимуме.

Дифракционная решетка

Дифракция Фраунгофера лежит в основе принципа действия дифракционной решетки. Одномерная дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей в экране, разделенных также одинаковыми по ширине непрозрачными промежутками (рис. 135).

Специальная делительная машина наносит на стеклянную пластину равноудаленные параллельные непрозрачные штрихи, число которых в современных решетках достигает порядка 3600 на 1 мм. Качество прибора характеризуется постоянной решетки d, которая равна сумме ширины прозрачной щели a и ширины нанесенного штриха b:

Постоянную или период дифракционной решетки d при известном значении ширины стеклянной пластины L и нанесенном количестве полос N определяют по формуле:

В отражательных дифракционных решетках полосы наносятся резцом на отшлифованной металлической пластине.

Дифракционная решетка представляет собой совокупность большого числа узких щелей, разделенных непрозрачными промежутками.

Условие максимума для дифракционной решетки

В дифракционной решетке осуществляется многолучевая интерференция параллельных когерентных пучков света, идущих от всех щелей.

Рассмотрим ход лучей через дифракционную решетку ДР в проходящем свете. Пусть на решетку падает плоская монохроматическая волна (рис. 136 а). Согласно принципу Гюйгенса вторичные источники в щелях решетки создают сферические волновые поверхности, огибающие препятствия и распространяющиеся по всем направлениям. Если за решеткой поставить собирающую линзу Л, то параллельные лучи от всех щелей соберутся в фокальной плоскости линзы в одну полосу. Определим разность хода лучей от двух соседних щелей из (рис. 136 б):

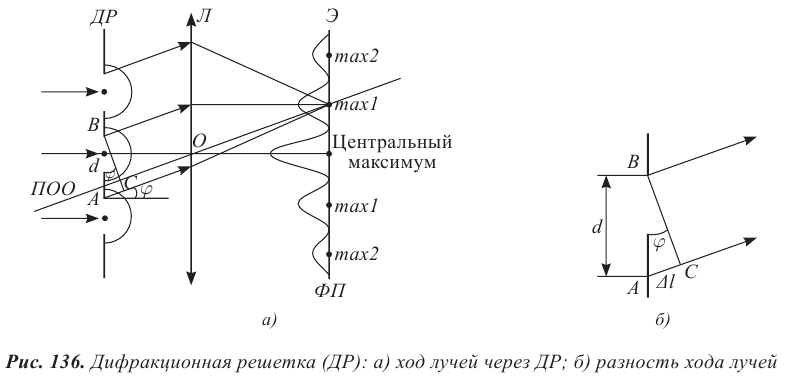
где 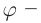угол отклонения световых лучей от перпендикуляра к плоскости решетки. Если разность хода лучей кратна целому числу длин волн, то на экране наблюдается максимум освещенности, выполняется соотношение:

где k − порядок дифракционного максимума.

Из полученного уравнения следует, что для различных длин волн условие максимума выполняется при определенном значении угла дифракции. Чем больше длина волны, тем больше угол отклонения (рис. 137). При освещении дифракционной решетки белым светом максимумы освещения на экране окрашиваются в радужные цвета от фиолетового до красного, центральный максимум остается белым. Интенсивность света с увеличением порядка спектра ослабевает.

Поперечность электромагнитных волн. Поляризация волн

Колебания зарядов в передающей антенне происходит вдоль антенны, поэтому в электромагнитной волне вектор напряженности расположен в той же плоскости, что и антенна. Вынужденные электрические колебания в приемной антенне совершаются свободными электронами под действием электрического поля волны. Это свидетельствует как о поперечности электромагнитной волны, так и о ее поляризации. Плоскость, проходящую через вектор напряженности электромагнитной волны, и направление ее распространения, называют плоскостью поляризации (рис. 138).

Электромагнитную волну, вектор напряженности в которой колеблется только в одной плоскости, называют плоско-поляризованной.

Вспомните! Для приема электромагнитной волны антенну необходимо установить параллельно передающей. При повороте приемной антенны вокруг горизонтальной оси на 90° прием сигнала прекращается.

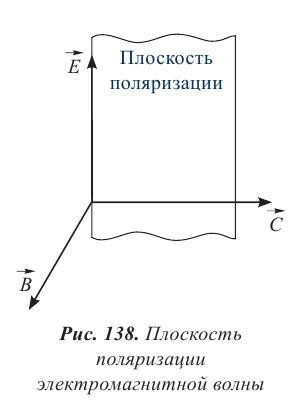
Поляризация света

Явление поляризации впервые было обнаружено при прохождении пучка световых лучей сквозь пластины турмалина. Турмалин – это прозрачный кристалл красного, синего или зеленого цвета с сильно выраженной одноосной оптической анизотропией. Грани пластин в проведенном опыте параллельны этой оси. Вращение одной пластины в плоскости, перпендикулярной направлению распространения света, не влияет на его интенсивность (рис. 140). При вращении двух пластин турмалина в той же плоскости относительно друг друга интенсивность световых лучей уменьшается, в момент перпендикулярного расположения осей пластин свет полностью гасится. Обыкновенный луч света полностью поглощается пластиной турмалина толщиной около 1 мм.

Возьмите на заметку:

Т. Юнг и О. Френель долгое время считали световые волны продольными, которые подобно звуковым волнам распространяются в упругом эфире, пронизывающем окружающие нас пространство и тела.

Явление поляризации можно объяснить, предположив, что свет является поперечной волной.

При прохождении естественного света через кристалл из всех направлений колебаний выделяется только одно, параллельное оси кристалла, происходит поляризация света. Кристалл турмалина в этом случае называют поляризатором. Если при прохождении второй пластины колебания происходят вдоль оси кристалла, то амплитуда и интенсивность колебаний поляризованного света не меняются. При повороте второй пластины относительно первой на угол 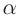амплитуда колебаний напряженности уменьшится до значения:

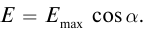
При повороте на угол 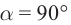напряженность световой волны станет равной нулю E = 0, такие поляризатор и анализатор называются скрещенными. Вторая пластина турмалина позволяет отличить поляризованный свет от естественного, поэтому она названа анализатором.

Опыт с турмалином показал, что световая волна является поперечной и симметричной относительно направления распространения, поскольку ее интенсивность не зависит от вращения пластины турмалина.

Поляризаторы и поляроиды

Поляризатор – это устройство для получения полностью или частично поляризованного света. Свойством поляризации обладают полимерные пленки с длинными молекулами, ориентированными в одном направлении, призмы и пластинки, обладающие оптической анизотропией из кристаллов турмалина, исландского шпата, кварца. Тонкую поляризационную пленку, вклеенную между двумя прозрачными пленками для защиты от влаги и механических повреждений, называют поляроидом. Явление поляризации света имеет большое практическое применение. Поляроид широко используется для разнообразных целей, например: для устранения бликов при фотографировании, для создания 3D-изображения, для изготовления жидкокристаллических экранов, для устранения ослепляющего действия света на водителей автомобилей от фар встречных машин. Используя явление поляризации, можно плавно регулировать интенсивность светового излучения. Два поляризатора позволяют плавно изменять интенсивность освещения в 100 000 раз.кварца. Тонкую поляризационную пленку, вклеенную между двумя прозрачными пленками для защиты от влаги и механических повреждений, называют поляроидом.

Явление поляризации света имеет большое практическое применение. Поляроид широко используется для разнообразных целей, например: для устранения бликов при фотографировании, для создания 3D-изображения, для изготовления жидкокристаллических экранов, для устранения ослепляющего действия света на водителей автомобилей от фар встречных машин. Используя явление поляризации, можно плавно регулировать интенсивность светового излучения. Два поляризатора позволяют плавно изменять интенсивность освещения в 100 000 раз.

Применение поляризаторов

Поляризованный свет используют для гашения света, зеркально отраженного от гладких поверхностей. На этом принципе устроены, например, поляроидные солнечные очки. Когда естественный неполяризованный свет падает на поверхность водоема, часть его зеркально отражается и при этом поляризуется. Отраженный свет мешает видеть предметы, расположенные под водой. Если смотреть на воду через ориентированный соответствующим образом поляризатор, то большая часть зеркально отраженного света будет поглощаться, и видимость подводных объектов значительно улучшится. Этот принцип используется при фотосъемке. Поляризационные фильтры для фото- и видеосъемки (рис. 141) удаляют блики и отражения с отражающих поверхностей за исключением металлических. В солнечный день он также может «притемнить» небо, делая его более фактурным (рис. 142)

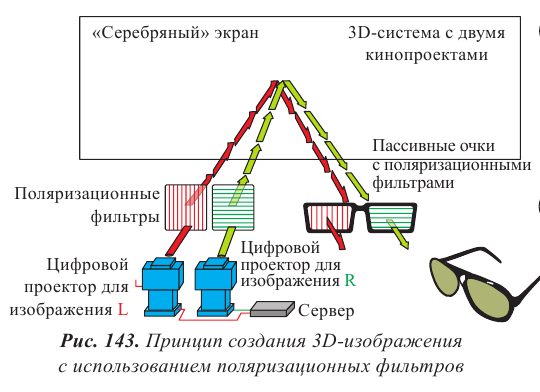
Поляризационные очки используют в стереокино 3D, дающем иллюзию объемности. В основе иллюзии лежит создание стереопары: двух изображений, снятых под разными углами, соответствующими углам зрения правого и левого глаза. Их рассматривают так, чтобы каждый глаз видел только предназначенный для него снимок. Изображение для левого глаза проецируют на экран через поляроид с вертикальной осью пропускания, а для правого − с горизонтальной осью и точно совмещают их на экране (рис. 143). Для стереоскопического телевидения применяется способ быстрого попеременного затемнения стекол очков, синхронизированного со сменой изображений на экране. За счет инерции зрения возникает объемное изображение, предметы выстраиваются в перспективе от зрителя в глубину экрана в зависимости от их взаимного расположения. Без очков такое изображение выглядит двоящимся и размытым.

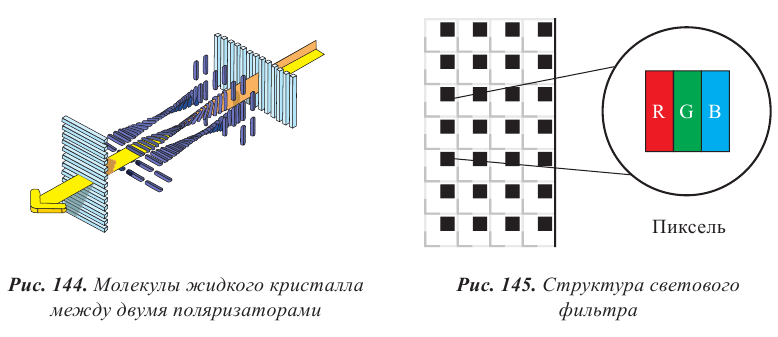
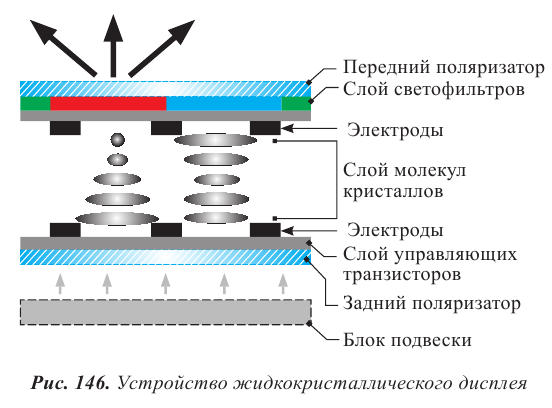
В жидкокристаллическом экране два поляризатора располагают взаимно перпендикулярно, так, чтобы свет через них не проходил. Между поляризаторами размещают жидкий кристалл (рис. 144). Молекулы в жидких кристаллах не закреплены кристаллической решеткой и могут вращаться под действием электрического поля. При этом молекулы кристалла организованы в четкую структуру, они располагаются слоями, каждый слой закручивается по отношению к предыдущему. Закрученные слои молекул меняют направление поляризации проходящего света. В ЖК-дисплеях используют структуру, закрученную на 90°. Молекулы меняют направление поляризации света на 90°, и он полностью проходит через второй поляризационный фильтр. На электроды, расположенных с двух сторон от поляризаторов, подается напряжение, под действием которого меняется расположение молекул жидкого кристалла. Поляризованный свет падает на световой фильтр, состоящий из трехцветных ячеек – пикселей (рис. 145). В зависимости от напряжения, каждый цвет в отдельности может менять свою прозрачность, от сочетания яркости синего, красного и зеленого цвета, на экране получают цветное изображение.

Физика в нашей жизни

Интерферометр – это измерительный прибор, действие которого основано на явлении интерференции (рис. 147). Применяется для точного измерения длины с высокой точностью, соизмеримой с длиной волны; для оценки качества оптических приборов. Интерферометры, которые позволяют определять малые изменения показателя преломления прозрачных веществ (твердых, жидких, газообразных), связанные с изменением давления, температуры, введением примесей и т.д. называют интерференционными рефрактометрами. Точность измерения прибора достигает 0,000001.

Принцип действия интерферометра заключается в том, что луч света разделяется на два или большее количество когерентных лучей, каждый из которых проходит различные оптические пути и направляется на экран. По интерференционной картине устанавливается разность фаз и хода интерферирующих лучей.

Итоги:

Законы и принципы

Принцип Х. Гюйгенса:

Каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Огибающая фронты вторичных волн является фронтом результирующей волны.

Принцип О. Френеля:

При наложении вторичных когерентных волн происходит интерференция, в результате которой амплитуда колебаний в различных точках пространства становится разной: по направлению распространения волны усиливается, в обратном направлении – уменьшается.

Глоссарий

Дисперсия – зависимость показателя преломления вещества от частоты света.

Дифракция – явление огибания светом препятствий малых размеров и попадание его в область геометрической тени.

Интерференция света – усиление или ослабление света при наложении световых волн.

Когерентные волны – волны одной частоты с постоянным сдвигом фаз.

Цвета первичные – цвета света, которые не могут быть получены комбинациями из других цветов.

Цвета дополнительные − цвета света, которые при смешении дают белый цвет.

Электромагнитная природа света

Оптика — раздел физики, в котором изучают свойства света, его физическую природу и взаимодействие с веществом. Поэтому световые явления часто называют оптическими. Большинство сведений о природе и происходящих явлениях человек получал и получает с помощью зрительных ощущений, возникающих под действием света. Само слово оптика произошло от греческого слова 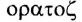— видимый, зримый.

Зрение по количеству и качеству получаемой с его помощью информации намного превосходит слух. Это имеет простое физическое обоснование, связанное, прежде всего, с существенным различием длин волн видимого света и слышимого звука (меньше 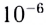м для света и больше 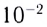м для звука).

Известно, что минимальные размеры изображения, создаваемого с помощью данного волнового процесса, не могут быть меньше соответствующей длины волны. Поэтому в человеческих глазах могут возникать оптические изображения, содержащие до 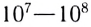независимых элементов изображения с различной интенсивностью световых сигналов, которые передают большое количество информации об окружающих нас объектах.

Конкурентность слуха со зрением несколько повышается благодаря тому, что диапазон частот слышимых звуков (более 8 октав) примерно в 10 раз больше диапазона частот видимого света (менее 1 октавы). Напомним, что октава — это интервал частот между ближайшими одноименными звуками различной высоты. Диапазон электромагнитных волн, доступный для современной техники (от 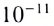м для 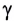-лучей при ядерных реакциях до 100 км для радиоволн), несоизмеримо шире диапазона звуков (от 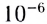м для ультразвука до 1 км для инфразвука).

Под светом в оптике понимают электромагнитные волны с частотами от 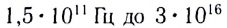Гц (длины волн находятся в диапазоне, соответствующем инфракрасному, видимому и ультрафиолетовому излучениям).
Современная оптика базируется на электромагнитной теории света.

Впервые гипотезу о том, что свет представляет собой быстро распространяющиеся поперечные волны, высказал английский ученый Роберт Гук в 1672 г. в докладе английскому Королевскому обществу. Теорию продольных световых волн разработал Христиан Гюйгенс в 1690 г. в «Трактате о свете». Гюйгенс, исходя из аналогии между акустическими и оптическими явлениями, полагал, что свет, как упругие волны, распространяется в особой среде — эфире, заполняющем все пространство как внутри материальных тел, так и между ними. В трактате с позиций волновой природы света объяснялось отражение и преломление света.

Во второй половине XIX в. шотландский физик Джеймс Максвелл неопровержимо доказал существование электромагнитных волн, которые, в отличие от упругих волн, распространяются и в вакууме. Их скорость распространения в вакууме совпадает со скоростью света. Максвеллом был сделан вывод, что световые явления тесно связаны с электромагнитными и что свет представляет собой один из видов электромагнитных волн.
К концу XIX в. после экспериментального подтверждения немецким физиком Генрихом Герцем теории Максвелла у физиков не оставалось сомнений, что свет — это электромагнитная волна.

Наблюдая за салютом, можно отметить, что световые волны в воздухе рас– пространяются гораздо быстрее звуковых, так как сначала мы видим вспышку и только через некоторое время слышим звук разрыва.
Первые попытки измерения скорости света на расстоянии нескольких километров. предпринятые Галилеем в 1607 г., не увенчались успехом в силу недостаточной точности хронометрирования (измерения времени).

Единственный вывод, который сделал Галилей, это что свет распространяется чрезвычайно быстро — почти мгновенно. Декарт впервые обратил внимание на то, что если скорость света очень большая, то для ее измерения необходимо использовать огромные (астрономические) расстояния.
Датский астроном Олаф Рёмер наблюдал в 1676 г. затмения спутника Юпитера Ио.

Он заметил, что промежуток времени между затмениями Ио в ноябре (положение II на рис. 228) увеличился на 16 мин по сравнению с маем того же года (положение 1 на рис. 228).

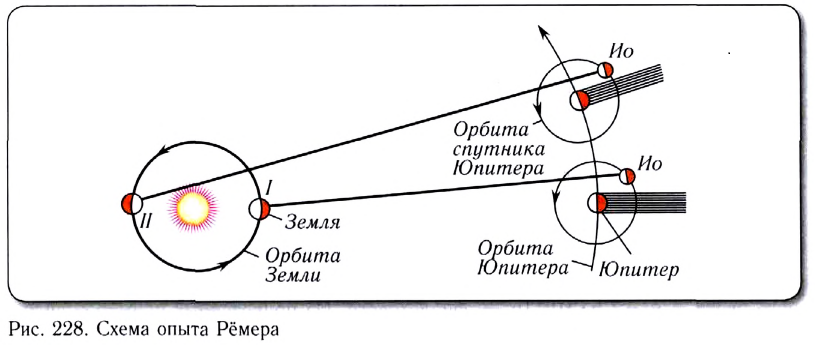
Рёмер объяснил это различие конечностью скорости распространения света.
На основании имевшихся в то время данных о диаметрах орбит Земли и Юпитера он получил для скорости света значение

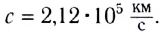
Описание опытов Рёмера выполнил Гюйгенс в своем «Трактате о свете».
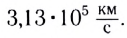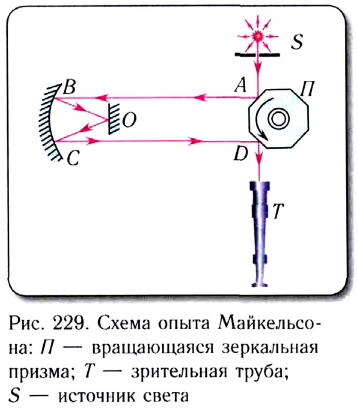
Значение скорости света, полученное Рёмером, уточнил в 1849 г. лабораторным методом французский физик Арман Ипполит Луи Физо. Измеренное им значение скорости света — Американский физик Альберт Абрахам Майкельсон в 1926 г. для более точного измерения скорости света использовал метод вращающихся зеркал.

Этот метод основывался на том, что луч света от источника S сможет попасть в зрительную трубу Т только в том случае, если за время его распространения по
пути ABOCD зеркальная призма повернется так, как показано на рисунке 229.
Майкельсон получил значение скорости света в вакууме, близкое к современным данным. 

Согласно современным измерениям скорость света в вакууме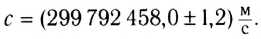

В 1983 г. на заседании Генеральной ассамблеи мер и весов было принято новое определение метра, из которого следовало, что скорость света в вакууме точно равна 299 792 458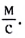

При решении задач используют приближенное значение

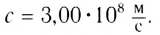
Таким образом, скорость света в вакууме является хотя и очень большой, но конечной величиной. Кроме того, она является предельной скоростью для материальных объектов.

Как показывает опыт, световое ощущение у человека вызывают лишь электромагнитные волны с частотами, лежащими в интервале от 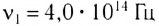до 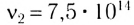Гц. Этим частотам соответствуют длины волн от 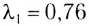мкм до 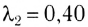мкм. Каждой частоте (длине волны) соответствует свое цветовое ощущение. Так, например, свет частотой 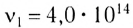Гц вызывает ощущение красного цвета, a 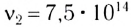Гц — фиолетового. Из приведенных примеров видно, что свойства электромагнитных волн сильно зависят от их частоты.

Измерения скорости света в различных прозрачных веществах показали, что она в них всегда меньше, чем в вакууме. Например, в воде скорость света уменьшается в 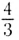раза. Отношение скорости света с в вакууме к скорости света v в веществе  

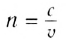
характеризует оптические свойства вещества и называется абсолютным показателем преломления. Он показывает, во сколько раз скорость света в данной среде меньше скорости света в вакууме.

Одним из основных параметров, характеризующих волну, является длина волны 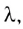связанная с периодом колебаний Т соотношением

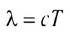
и с частотой v соотношением

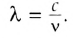
Подчеркнем, что абсолютный показатель преломления вещества n зависит от частоты v волны. Зависимость показателя преломления вещества, а также скорости света от его частоты называется дисперсией света и проявляется при распространении света в веществе. Белый свет представляет собой совокупность волн всевозможных частот. Волна определенной частоты называется монохроматической. Цвет зависит от частоты световой волны, подобно тому как различным высотам звука соответствуют различные частоты звуковых волн.

Дисперсия света называется нормальной в случае, если показатель преломления монотонно возрастает с увеличением частоты (или убывает с увеличением длины волны). Если показатель преломления монотонно убывает с увеличением частоты, дисперсия света называется аномальной.

Отметим, что длина световой волны 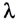при переходе из одного вещества в другое изменяется, так как она зависит не только от частоты (или периода колебаний), но и от скорости распространения волны в веществе. А, как известно, скорость волны определяется показателем преломления данного вещества.

Длина световой волны 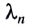в веществе с показателем преломления n определяется соотношением  

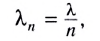
где 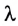— длина световой волны в вакууме.

Следует помнить, что при переходе электромагнитной волны из вакуума в вещество или из одного вещества в другое частота колебаний векторов 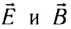в ней не изменяется, т. е.

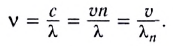
Поскольку цвет волн, воспринимаемых глазом, определяется только частотой световой волны, то цвет при переходе из одного вещества в другое не изменяется.
 

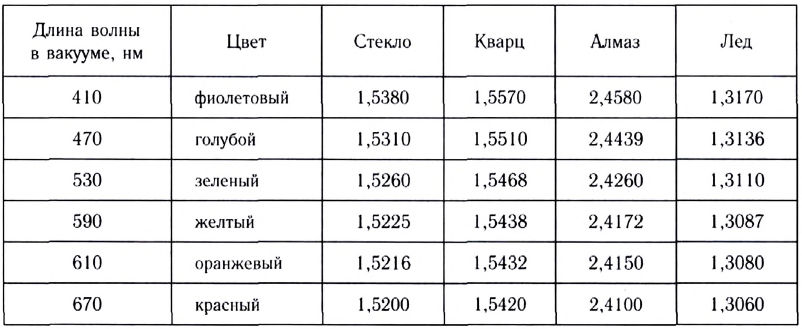
Таблица 10
Показатели преломления некоторых прозрачных веществ

Принцип Гюйгенса. Законы отражения и преломления

Геометрическое место точек в пространстве, до которых дошло волновое возмущение в данный момент времени, называется волновым фронтом (поверхностью). Все точки фронта имеют одинаковую фазу, т. е. колеблются синфазно.

Углом падения 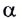называется угол между падающим лучом света и перпендикуляром к границе раздела двух сред, восстановленным в точке падения.

Углом отражения называется угол между отраженным лучом и перпендикуляром к отражающей поверхности, восстановленным в точке падения.

Углом преломления называется угол между преломленным лучом и перпендикуляром к границе раздела двух сред, проведенным через точку падения.

Для изучения свойств электромагнитных волн необходимо знать как закономерности их распространения в однородной среде, так и отражения и преломления на границе раздела двух сред.

Рассмотрим распространение волн в изотропной среде. В этом случае скорость волн v по всем направлениям одинакова, и если источник излучения S точечный, то фронт волны имеет вид сферической поверхности (рис. 230).

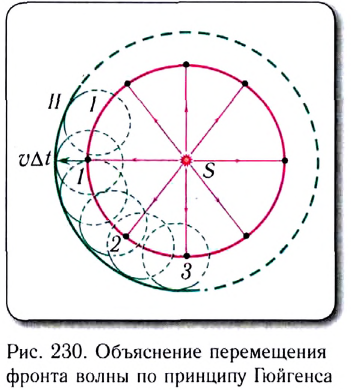
Фронт волны в момент времени t занимает положение I. Через промежуток времени фронт займет положение II, точки которого будут удалены от начального фронта волны на расстояние 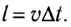 Для определения положения волнового фронта в любой последующий момент времени по его положению в данный момент времени применяют принцип Гюйгенса, сформулированный в 1690 г. в «Трактате о свете»:

• каждый элемент волнового фронта, которого достигла в данный момент волна, является источником вторичных сферических волн. Огибающая вторичных волн в следующий момент времени совпадает с новым положением волнового фронта.

Для нахождения положения волнового фронта согласно принципу Гюйгенса проведем окружности радиусом представляющие собой фронты вторичных волн, с центром на фронте в положении I. Огибающая вторичных волн (1, 2, 3 и т.д.) определяет новое положение волнового фронта — положение II.
Напомним, что огибающей называется поверхность, касательная ко всем вторичным волнам. Линия, перпендикулярная волновому фронту, называется лучом. Световой луч, вдоль которого происходит распространение волны, определяет также направление переноса энергии волной.

На очень больших расстояниях от точечного источника волны, излучаемые им, можно считать плоскими. Например, световые лучи в приходящем на Землю солнечном излучении считаются параллельными друг другу.

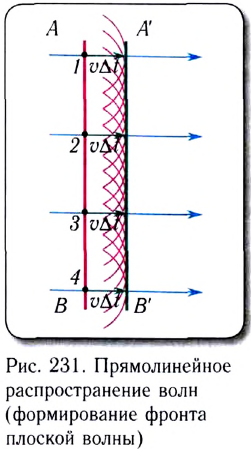
Принцип Гюйгенса объясняет прямолинейное распространение волн. Как видно из рисунка 231, волновой фронт АВ плоской волны с течением времени перемещается (А’В’) в одном и том же направлении, оставаясь параллельным своему начальному положению АВ.

Рассмотрим процессы, происходящие при падении плоской волны на плоскую поверхность раздела однородных изотропных и прозрачных сред, при условии, что размеры поверхности раздела намного больше длины волны падающего излучения.

Пусть на плоскую поверхность LM раздела двух сред падает плоская волна, фронт которой АВ (рис. 232).

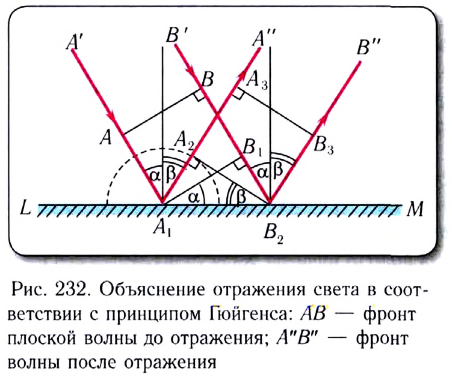
Если угол падения 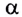 отличен от нуля, то различные точки фронта АВ волны достигнут границы раздела LM неодновременно.

Согласно принципу Гюйгенса точка 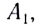 которой фронт волны достигнет раньше всего (см. рис. 232), станет источником вторичных волн. Вторичные волны будут распространяться со скоростью v и за промежуток времени 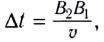за который точка фронта 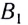достигнет границы раздела двух сред (точки 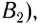вторичные волны из точки 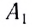пройдут расстояние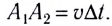

Падающая и возникающие вторичные волны распространяются в одной и той же среде, поэтому их скорости одинаковы, и они пройдут одинаковые расстояния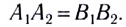

Касательная, проведенная из точки к полуокружности радиусом 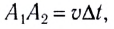является огибающей вторичных волн и дает положение фронта волны через промежуток времени Затем он перемещается в направлении 
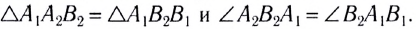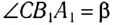Из построения следует, что С учетом определений угла падения и угла отражения находим, что и как углы со взаимно перпендикулярными сторонами.

Следовательно, угол отражения равен углу падения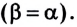 

Кроме того, как показывает опыт, луч падающий, луч отраженный и перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (см. рис. 232).

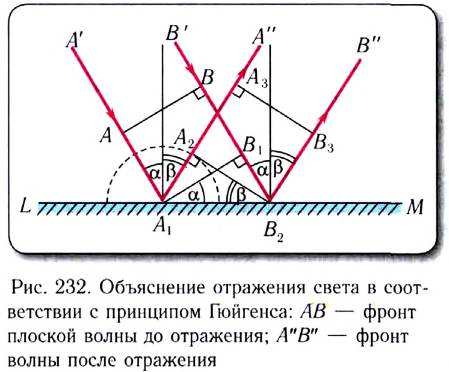
Таким образом, исходя из волновой теории света, на основании принципа Гюйгенса получен закон отражения света.

Рассмотрим теперь, что будет происходить во второй среде, если скорость 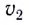распространения волн в ней меньше, чем в первой 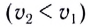(рис. 233).

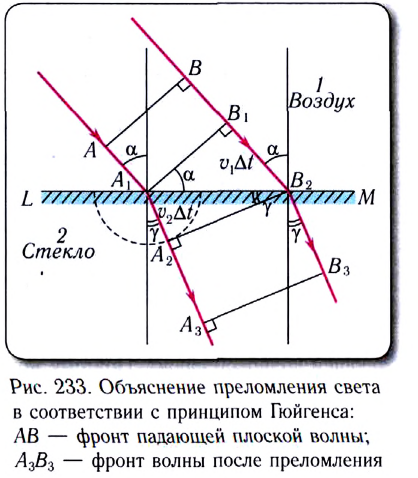
Фронт падающей волны АВ будет перемещаться со скоростью 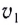по направлению  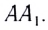К моменту времени  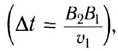 когда точка В фронта достигнет границы раздела двух сред (точка 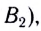вторичная волна из точки 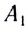(согласно принципу Гюйгенса) пройдет расстояние 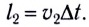Фронт волны, распространяющейся во второй среде, можно получить, проводя прямую линию, касательную к полусфере с центром в точке

С учетом определения угла преломления из построения видно, что как углы со взаимно перпендикулярными сторонами.
Из находим 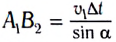 и из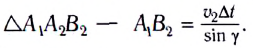
Откуда получаем соотношение

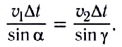
Из него следует закон преломления:

Вспомним, что абсолютным показателем преломления называется отношение скоростей распространения электромагнитной волны в вакууме сив данной среде v: 

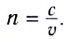
С учетом соотношения (1) закон преломления принимает вид:

Таким образом, исходя из волновой теории света, получен закон преломления электромагнитных волн:

• отношение синуса угла падения 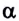к синусу угла преломления есть величина постоянная для двух данных сред;
• лучи падающий и преломленный лежат в одной плоскости с перпендикуляром, проведенным в точке падения луча к плоскости границы раздела двух сред.

Перепишем закон преломления в следующем виде:

Это выражение, сохраняющее свое значение, называется оптическим инвариантом. При такой записи закона преломления не надо запоминать, показатель преломления какой среды стоит в числителе, а какой — в знаменателе. Необходимо всегда умножать абсолютный показатель преломления на синус угла, который образует в среде луч с нормалью.

Отметим, что причиной преломления волн, т. е. изменения направления распространения волн на границе раздела двух сред, является изменение скорости распространения электромагнитных волн при переходе излучения из одной среды в другую.

Из рисунка 233 видно, что гребень (пик) волны соответствует линии, изображающей волновой фронт. Поэтому можно записать:

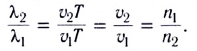
Если обозначить длину волны в вакууме 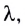то длина волны в среде с показателем преломления n будет определяться соотношением

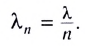
Отметим, что этот результат согласуется с постоянством частоты при переходе волны из одной среды в другую. Так как длина волны в вакууме 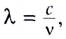в среде  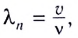получаем

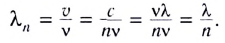
Когерентность. Интерференция света

Если в некоторую точку пространства Р приходят две монохроматические волны с одинаковой частотой от разных источников то они возбуждают в ней гармонические колебания той же частоты (рис. 234).

Начальные фазы этих колебаний могут различаться, но разность фаз при этом остается постоянной.

Волны, разность фаз которых в данной точке пространства не изменяется с течением времени, называются когерентными (когерентность от латинского слова cohaerens — связанный, сцепленный), а явление согласованного протекания в пространстве и во времени нескольких колебательных или волновых процессов — когерентностью.

Эксперименты показывают, что амплитуда результирующего колебания в точке Р не равна алгебраической сумме амплитуд исходных колебаний. Это означает, что волны интерферируют друг с другом.
 

Интерференция (от латинских слов inter — взаимно, между собой и ferio — ударяю, поражаю) — явление сложения двух или более когерентных воли, приводящее к образованию в пространстве устойчивой картины чередующихся максимумов и минимумов амплитуд результирующего колебания (рис. 235).

Устойчивое во времени распределение амплитуд колебаний в пространстве при интерференции называется интерференционной картиной.

Рассмотрим простейший случай интерференции — сложение двух гармонических волн одинаковой частоты 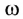при совпадении направления колебаний в них.

Пусть в точку Р (cм. рис. 234) пришли две волны одинаковой частоты, прошедшие различные расстояния от одинаковых когерентных источников. Амплитуда результирующего колебания согласно принципу суперпозиции в любой момент времени равна векторной сумме амплитуд каждой волны в отдельности. Тогда эти волны будут иметь в точке Р одинаковую амплитуду, но разные фазы:

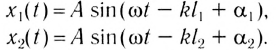
Результирующее колебание представляет собой их сумму:

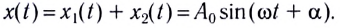
Амплитуду 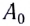результирующего колебания в точке Р можно найти по теореме косинусов (рис. 236, а):

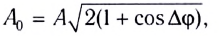
где 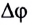— разность фаз колебаний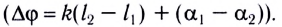

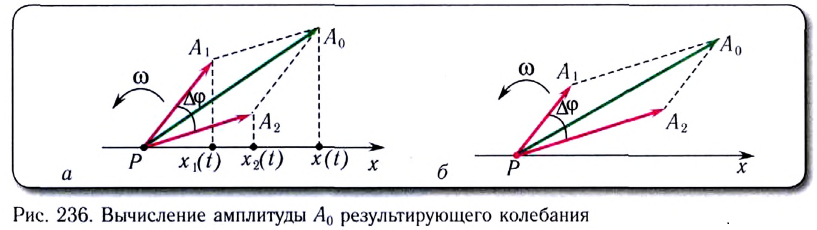
В случае, когда амплитуды складывающихся волн различны (например,квадрат амплитуды результирующего колебания в точке Р можно найти также, используя теорему косинусов (рис. 236, б):

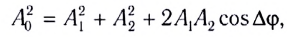
где 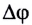— разность фаз колебаний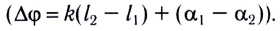
Амплитуда результирующего колебания зависит от величины 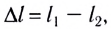называемой разностью хода волн от источников до точки наблюдения. При распространении волн в средах с различными показателями преломления 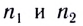необходимо учитывать оптическую разность хода волн:

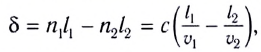
т. е. разность расстояний, пройденных волнами с учетом их различных скоростей 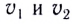распространения в этих средах.
Если оптическая разность хода равна целому числу длин волн
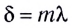(условие максимума),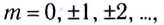
то волны приходят в точку Р (см. рис. 234) синфазно — разность фаз кратна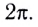

Действительно,

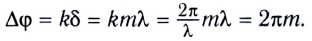
Складываясь, волны усиливают друг друга и дают колебание с удвоенной амплитудой: 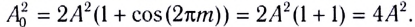Откуда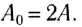

В случае, когда разность хода равна нечетному числу полуволн
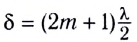(условие минимума),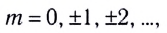
волны приходят в точку Р в противофазе, разность фаз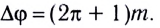

В этом случае волны гасят друг друга и дают колебание с нулевой амплитудой: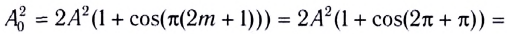  

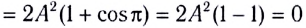
Колебания в каждой точке среды, в которой происходит сложение когерентных колебаний (интерференция волн), характеризуются определенным, не изменяющимся с течением времени значением амплитуды. Вследствие того что энергия волны пропорциональна квадрату амплитуды, энергия результирующего колебания не равна в общем случае сумме энергий складываемых колебаний, так как 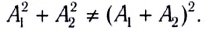Например, результирующая амплитуда колебаний в точках максимума возрастет в два раза, а энергия, соответственно, в четыре. Отметим, что если бы в точке Р складывались две некогерентные волны с одинаковыми амплитудами, то энергия результирующего колебания была бы равна сумме энергий отдельных волн, независимо от положения точки Р относительно источника. Это означало бы просто удвоение энергии, принесенной одной из волн в данную точку.
Наиболее распространенные бытовые источники света (лампы накаливает ния, лампы дневного света, свечи и т. д.) не являются когерентными, т. е. не позволяют наблюдать явление интерференции.

Изобретение и распространение когерентных источников излучения — лазеров — сделало демонстрацию явления интерференции достаточно простой.
Для наблюдения интерференционной картины при отсутствии когерентных источников (лазеров) пользуются методом разделения волны, излучаемой одним источником А, на две. В качестве источника света используется щель А, выделяющая из волнового фронта падающего излучения небольшой участок постоянной амплитуды и фазы. В классической интерференционной схеме (схеме Юнга) пучок света разделяется на два когерентных пучка с помощью отверстий В и С в ширме (рис. 237).

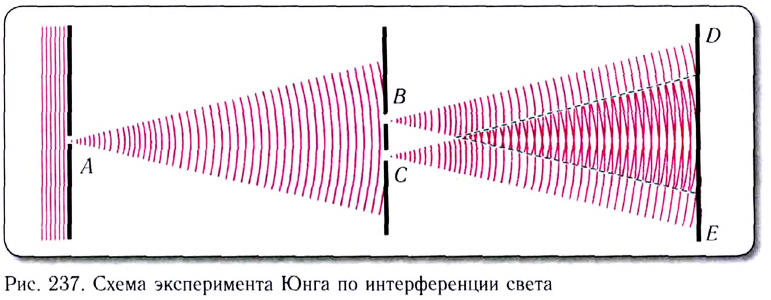
Эти пучки, созданные одним и тем же источником, являются когерентными. На экране в области DE наблюдается интерференционная картина.
Свой знаменитый эксперимент Томас Юнг провел в 1801 г. Он убедительно  подтвердил волновую природу света и измерил длину световой волны.

Отметим еще один распространенный случай интерференции — сложение плоских волн одинаковой частоты, распространяющихся в противоположных направлениях (например, падающей и отраженной волн), приводящее к образованию в пространстве устойчивой картины чередования максимумов амплитуды колебаний (пучностей) и минимумов (узлов). Волна, возникающая в результате сложения двух волн одинаковой частоты, распространяющихся в противоположных направлениях, называется стоячей волной (рис. 238).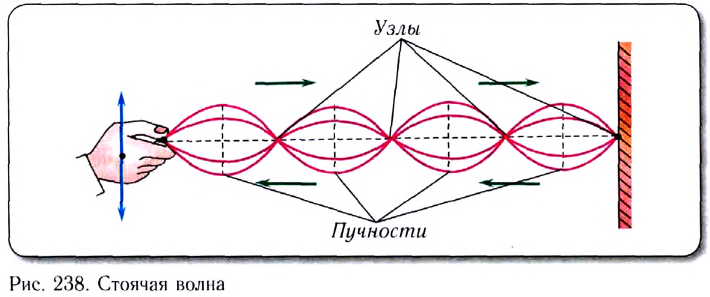

Явление интерференции не противоречит закону сохранения энергии, так как энергия колебаний в среднем остается равной сумме энергий интерферирующих волн и лишь перераспределяется в пространстве.

Применение интерференции

Наиболее известное проявление интерференции, с которым мы часто встречаемся в повседневной жизни, — радужное окрашивание мыльных пузырей или тонких пленок бензина (нефти) на воде или асфальте. Радужные цвета возникают вследствие интерференции света, отраженного двумя поверхностями пленки.

Рассмотрим падение монохроматической световой волны длиной 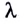под углом 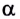на тонкую пленку толщиной d (рис. 240).

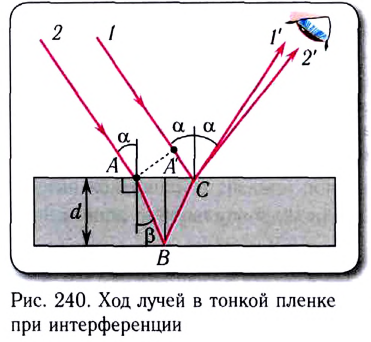
Она частично отражается (волна 1) от верхней поверхности пленки, частично проходит в пленку и частично отражается (волна 2) от нижней поверхности пленки. В результате волна, отраженная от нижней поверхности, проходит дополнительное расстояние (АВС — А’С) по сравнению с волной, отраженной от верхней поверхности пленки. Между отраженными от пленки волнами (1′ и 2′) возникает оптическая разность хода 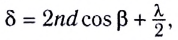которая зависит от угла преломления 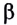волны, толщины пленки, показателя преломления и длины волны. Слагаемое  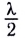учитывает изменение фазы на 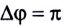при отражении волны от одной из поверхностей пленки. Если оптическая разность хода 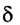равна целому числу длин волн, то будет наблюдаться интерференционный максимум, если нечетному числу полуволн, — минимум.

При падении белого света (400—800 нм) под некоторым углом на пленку максимум интерференционной картины будет только для определенной длины волны 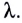При других углах падения максимумы будут наблюдаться для других длин волн. Таким образом, при падении на пленку белого света в отраженном свете мы увидим яркие разноцветные полосы, расположенные друг за другом.
Между длиной волны 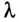интерферирующих волн, их оптической разностью хода 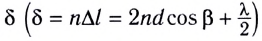и расположением максимумов и минимумов существует определенная связь. Это позволяет, с одной стороны, по расположению максимумов и минимумов интерференционной картины определять длину волны или измерять показатель преломления вещества. С другой стороны, зная положение максимумов и минимумов, можно определять разность хода интерферирующих волн и таким образом очень точно измерять расстояния.

Интерференция света находит широкое применение в различных областях науки и техники, так как позволяет значительно повысить точность измерений. Приборы, принцип действия которых основан на явлении интерференции, называются интерферометрами. Оптические интерферометры применяются для измерения показателей преломления прозрачных сред, длин волн, угловых размеров звезд.

Явление интерференции в тонких пленках используется для создания зеркал, фильтров, просветляющих покрытий, контроля качества шлифовки поверхностей.

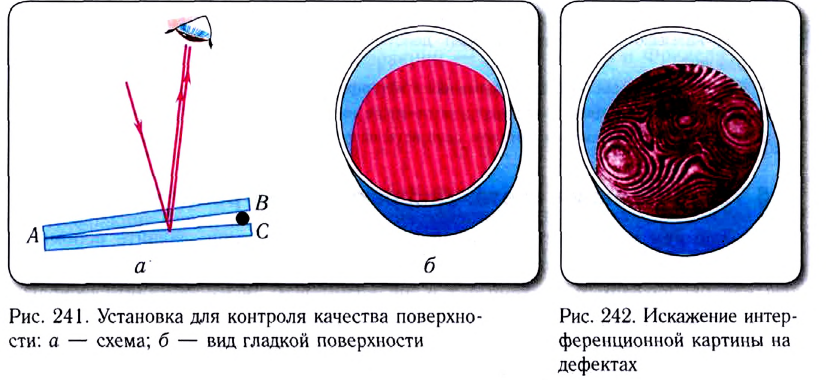
Для проверки качества обработки поверхности между ней и эталонной гладкой пластинкой создают тонкую клиновидную прослойку ВАС воздуха (рис. 241, а). Волны, отражаясь от верхней (контролируемой) и нижней (эталонной) поверхностей, образуют интерференционную картину — светлые и темные полосы. Причем полосы будут ровными только тогда, когда поверхности идеально гладкие (рис. 241,6). Если на контролируемой поверхности имеется какой-либо дефект, например вмятина или царапина, то это приведет к искажению интерференционных полос (рис. 242). По форме полос и их ширине можно судить о характере дефектов и их глубине (высоте). Применение интерференционных методов позволяет измерять отклонение от плоскости с погрешностью порядка 0,01 мкм. При нормальном падении монохроматического света на образец повышается точность измерений, так как увеличивается резкость интерференционных полос.

Интерференционный метод — очень чувствительный метод проверки гладкости поверхностей, так как позволяет оценить качество обработки с точностью порядка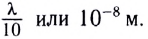

Дифракция света и дифракционная решетка

Прежде чем переходить к изучению явления дифракции, давайте вспомним простой пример: стоя за углом дома, мы хорошо слышим, что едет автомобиль, хотя как бы находимся в «тени», т. е. не видим его. Таким образом, звуковые волны достигают нашего уха, «заворачивая за угол»!
Явление огибания волнами препятствий и проникновение их в «область тени» получило название дифракции (рис. 243, а, б, в).

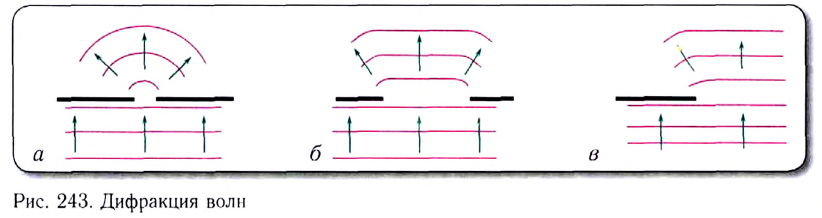
Оно является одним из подтверждений волновой природы света.
Для проявления дифракции размеры препятствий (отверстий) должны быть меньше или сравнимы с длиной волны, вот почему в рассмотренном примере звук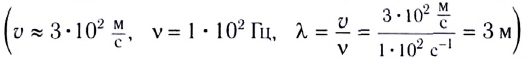 смог «завернуть за угол», а свет, отраженный от автомобиля — нет.

Французский физик Огюстен Жан Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн, которые являются когерентными.

Принцип Гюйгенса — Френеля позволил охарактеризовать явление дифракции количественно:

• все вторичные источники, расположенные на волновом фронте, когерентны между собой. Огибающая волна, получающаяся в результате интерференции вторичных волн, совпадает с волной, наблюдаемой как исходная от источника.

Согласно Френелю дифракция объясняется интерференцией вторичных волн.
В оптике различают два типа дифракции — Фраунгофера и Френеля.
Дифракция Фраунгофера наблюдается при падении плоских волн (параллельных лучей) длиной волны 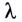на щель размером D, причем экран расположен очень далеко от препятствия  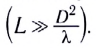  За щелью находится линза, направляющая на экран пучок параллельных лучей.
Дифракция Френеля наблюдается при падении сферических или плоских волн на препятствие при расположении экрана вблизи щели 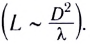Линзы для фокусировки лучей не применяются.

Рассмотрим дифракцию света на одной щели в непрозрачном экране. Предположим, что на щель шириной b падает плоская волна, длина которой 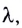и на экране, расположенном в фокальной плоскости линзы, получается дифракционная картина. Из принципа Гюйгенса следует, что волны, дифрагировавшие на щели, распространяются за ней по всем направлениям. Рассмотрим интерференцию волн, проходящих различные участки щели.

Если экран расположен достаточно далеко от щели, то волны, попадающие на любую из его точек, по существу, параллельны.

При нормальном падении волн (угол падения на щель (рис. 244, а), все вторичные волны имеют одинаковую фазу, так как плоскость щели совпадает с фронтом волны. В центре экрана возникает светлое пятно, или центральный максимум освещенности (точка А на рисунке 244, г), так как направление наблюдения и первоначальное направление распространения волны совпадают, а вторичные волны не приобретают никакой разности фаз.
Рассмотрим вторичные волны, идущие после прохождения щели под углом 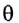(рис. 244, б). Если разность их хода от верхнего и нижнего краев щели равна длине волны то разность хода волн, распространяющихся от верхнего края щели и от ее центра, составит 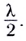 Следовательно, эти волны, интерферируя, будут гасить друг друга.

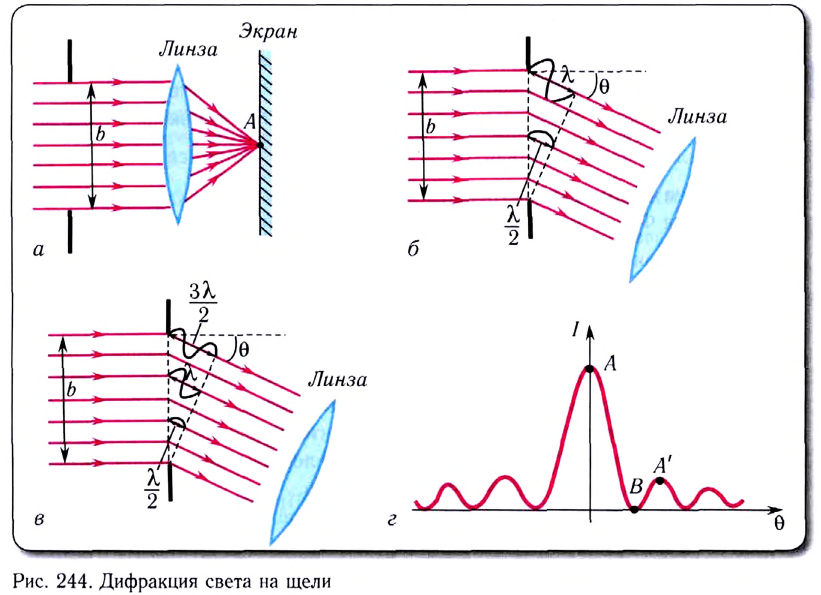
Аналогично будут попарно гасить друг друга волны, смещенные на одно и то же небольшое расстояние к нижнему краю щели относительно верхнего края щели и ее центра. Таким образом, волны, идущие от верхней половины щели, будут находиться в противофазе с волнами, идущими от ее нижней половины.

Интерферируя, такие волны гасят друг друга. В результате на экране будет темное пятно (минимум) в точке В (см. рис. 244, г), соответствующее углу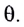

Аналогично будут гаситься попарно все вторичные волны, соответствующие
углу Минимумы будут располагаться симметрично относительно центра щели. Угол, соответствующий минимуму, удовлетворяет соотношению (см. рис. 244, б):

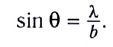
Если разность хода волн от верхнего и нижнего краев щели равна нечетному числу полуволн, например 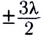(рис. 244, в), то волны из нижней трети щели гасят волны из средней трети, так как, попарно интерферируя, оказываются в противофазе.

Когда свет из верхней трети щели достигает экрана, в этом месте возникает светлое пятно — максимум (точка А’ на рис. 244, г), правда, не такой яркий, как центральный.

Таким образом, максимумы освещенности экрана наблюдаются под углами удовлетворяющими условию 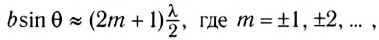а минимумы — условию .

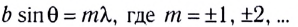Эффект перераспределения энергии плоской волны в пространстве можно значительно усилить, если использовать специальные устройства, содержащие много однотипных щелей. Это устройство получило название дифракционной решетки.

Дифракционной решеткой называют оптический прибор, предназначенный для очень точного измерения длин волн и разложения света в спектр. Дифракционная решетка состоит из большого числа равноотстоящих параллельных штрихов, нанесенных на стеклянной или металлической поверхности. Длины решеток составляют 10—15 см. Решетки содержат 10 000—20 000 штрихов на 1 см. Наблюдения проводятся как в отраженном свете (на металлических решетках), так и в проходящем (на стеклянных).
Простейшая дифракционная решетка представляет собой систему из N одинаковых равноотстоящих параллельных щелей в плоском непрозрачном экране (рис. 245). Если ширина каждой щели b, ширина непрозрачной части между щелями а, то величина d = a + b называется постоянной решетки или ее периодом. Условия главных дифракционных максимумов, наблюдаемых под углами имеют вид

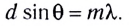
Здесь 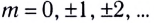— порядок максимума, или порядок спектра, 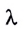— длина волны падающего излучения.

Полученное условие определяет направления распространения света в пространстве, по которым на отрезке 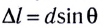укладывается целое число длин волн 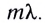В этом случае вторичные волны от всех щелей решетки приходят в
точку наблюдения с фазами, отличающимися на число, кратное

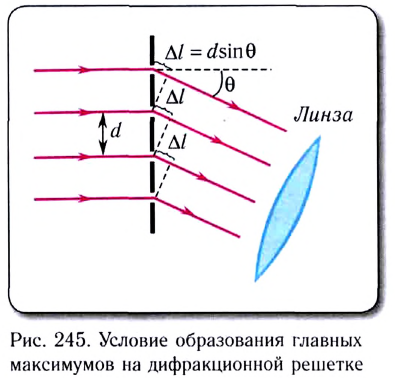
При помощи собирающей линзы (см. рис. 245) вторичные волны (параллельные лучи), идущие от всех щелей, фокусируются в точку на экране, расположенном в фокальной плоскости линзы, и интерферируют, усиливая или ослабляя друг друга.

Таким образом, дифракционная картина на экране состоит из чередующихся максимумов и минимумов освещенности различных участков экрана. Дифракционные максимумы, соответствующие m = 1, образуют спектр первого порядка, m=2 — спектр второго порядка и т. д. (рис. 246).

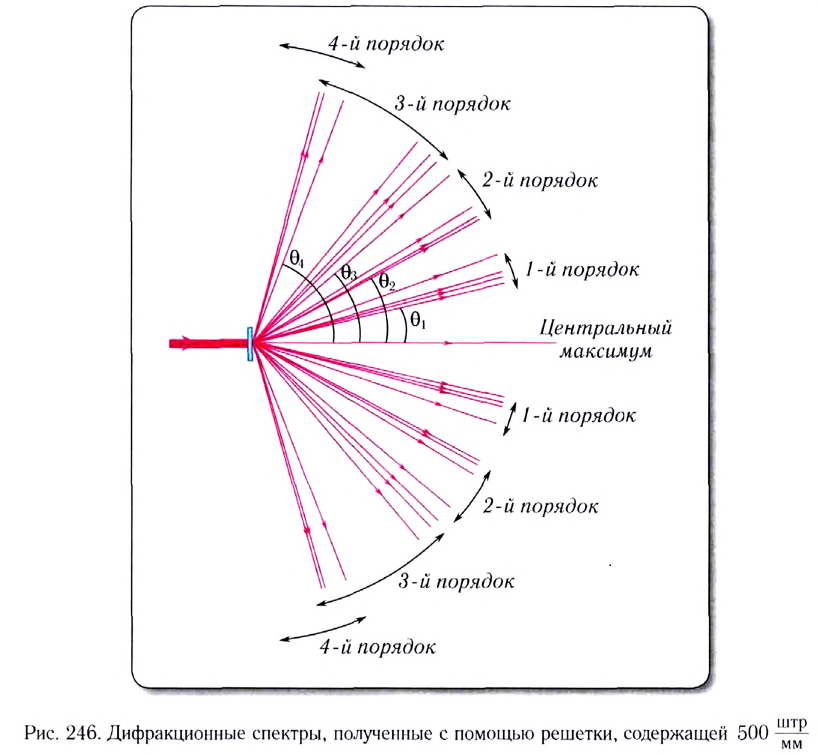
Между максимумами расположены минимумы, так как при изменении угла 9 на отрезке (см. рис. 245) уже не будет укладываться целое число длин волн.
По мере увеличения числа щелей дифракционной решетки максимумы па экране становятся более узкими, а расстояния между ними более широкими (рис. 247). При этом происходит перераспределение энергии падающего излучения, большая часть которой приходится на максимумы.

При палении на решетку белого света спектральные максимумы любого порядка (кроме нулевого) содержат все цвета радуги (рис. 248, а).

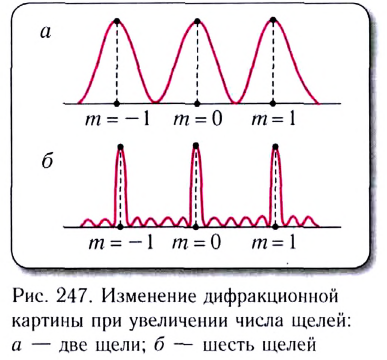
Кроме того, в дифракционном спектре больше всего отклоняются от начального направления распространения красные лучи (рис. 248, 6), меньше всего — сине-фиолетовые (рис. 248, в), что и следует из формулы для определения максимумов дифракционной решетки.

Отметим, что направления, в которых наблюдались минимумы интенсивности от одной щели, так и остаются минимумами для дифракции света на решетке. К ним добавляются минимумы, связанные с интерференцией излучения, идущего от каждой из щелей (см. рис. 247).

Эти минимумы легко определить из условия, что разность хода света от соседних щелей в данном направлении должна быть кратна нечетному числу полуволн. 

• Заказать решение задач по физике

Голография

Голография — метод получения объемных изображений предметов, основанный на использовании явления интерференции.

Голография (от греческого — весь, полный и — пишу) — способ записи и восстановления волнового фронта. Он основан на регистрации интерференционной картины, которая образована волной, отраженной объектом, освещенным источником света (предметная волна), и когерентной с ней волной, идущей непосредственно от источника (опорная волна).

Голография — процесс, состоящий из двух этапов.

На первом этапе (этапе записи) регистрируется предметная волна, распространяющаяся от освещенного объекта и несущая информацию о нем. Эта информация записывается на фотопластинку в виде интерференционной картины от опорной и предметной волн. Образующаяся интерференционная картина представляет голограмму. Этот термин был впервые введен ее изобретателем — венгерским физиком Денисом Габором.

На втором этапе (этапе восстановления) с помощью этой голограммы восстанавливается отраженная предметом волна и получается видимое оптическое изображение. Этот этап называется процессом восстановления изображения. Для полного восстановления информации, закодированной в голограмме, ее необходимо освещать тем же когерентным светом, что и при записи голограммы. Чем сложнее объект, чем больше деталей он содержит, тем сложнее микроузор на фотопластинке.

Три основных отличия голограммы от обычной фотографии:

1. Голограмма не является подобным изображением объекта.
2. Для освещения объекта используется когерентный свет.
3. Для отражения части падающего на пластину пучка когерентного света используется зеркало (рис. 249).

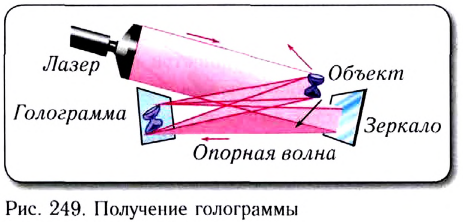
Фотопластинка регистрирует интерференционную картину, создаваемую волнами, отраженными зеркалом и объектом.

Основными характеристиками волны являются амплитуда и фаза, или интенсивность и частота. На обычной фотографии регистрируется лишь распределение амплитуды падающей на нее волны посредством соответствующего ему почернения фотоэмульсии. На голограмме, кроме распределения амплитуды, регистрируется еще и распределение фазы предметной волны относительно фазы опорной волны (разность фаз двух волн).
Информация об амплитуде предметной волны записана на голограмме в виде контраста интерференционной картины, а информация о фазе — в виде формы и частоты интерференционных полос (рис. 250).

Волна, восстановленная в голограмме, распространяется в обе стороны от нее (рис. 251).

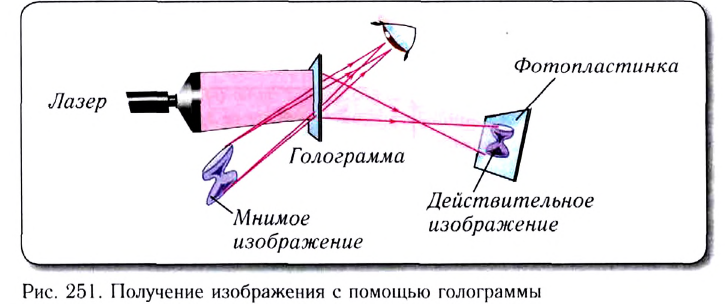
Расходящаяся волна образует мнимое изображение, а сходящаяся — действительное. Мнимое изображение, образованное дифракционным спектром первого порядка, можно увидеть, смотря сквозь голограмму как через окно. Можно без труда заглянуть за объект и увидеть ранее скрытый вид. Более того, можно перевести взгляд для того, чтобы рассмотреть дальний объект.

Каждая часть голограммы, как бы мала она ни была, может полностью представить все изображение. Поэтому каждый ее кусочек дает возможность представить полное трехмерное изображение объекта, но чем меньше этот кусочек, тем меньше четкость изображения и ощущение объемности.
На одну пластинку можно наложить несколько изображений путем последовательных экспозиций, причем каждое из них можно легко восстановить без всяких помех со стороны других. Это достигается либо записью различных изображений волнами с другими частотами, либо изменением направления опорной волны.

Емкость голограмм огромна: на пластине площадью 100 может быть записана информация, соответствующая 1 • 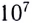книжных страниц. Голографическая запись обеспечивает высокую помехоустойчивость и надежность ее хранения вследствие нечувствительности голограмм к царапинам, пыли и т. п.

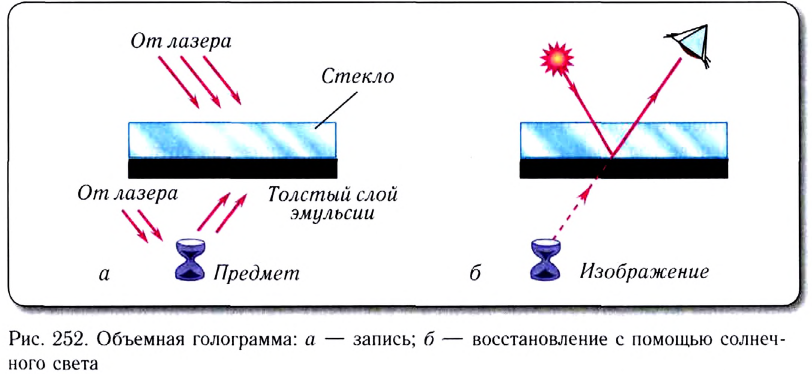
Для получения цветного изображения в процессе восстановления изображения используются три монохроматические волны, относящиеся к трем основным цветам — красному, зеленому, синему.

Если фотослой тонкий, то голограмму называют двухмерной.
Для получения трехмерных (объемных) голограмм советский физик Юрий Николаевич Денисюк предложил использовать прозрачный фотослой толщиной 15—20 мкм. Такой фотослой позволяет освещать объект через пластину (рис. 252). Из нее выходят неослабленными только волны с разностью хода 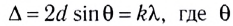— угол скольжения (дополнительный к углу падения), k — целое число. Все остальные волны ослабляются, так как не удовлетворяют этому условию.

Для восстановления волны, рассеянной объектом, можно пользоваться обычным источником света и из широкого спектра голограмма сама выделит свет только определенного направления длиной волны с высокой степенью монохроматичности.

Монохроматичность источника необходима потому, что интерференционная  картина зависит от длины волны падающего излучения.

Свет должен выходить из точечного источника, так как если источник большой, то каждый его элемент будет порождать свои интерференционные полосы, смещенные относительно полос других элементов. В результате сумма всех этих полос усреднится почти до равномерного освещения. Вследствие этого широкое применение голографии началось только с появлением лазеров — источников, обладающих пространственной и временной когерентностью.
Оптическая голография применяется для исследования механических деформаций, для обработки и хранения информации, для контроля качества поверхностей различных деталей. Голограмма может быть рассчитана и на компьютере, и такая цифровая голограмма используется для получения объемных изображений несуществующих объектов.

На основе голограмм создается современная безлинзовая оптика, позволяющая фокусировать очень широкие пучки света — до 10 м в диаметре.

Для получения голограмм могут использоваться волны не только световые, но и звуковые. Для восстановления акустической голограммы в воспринимаемый зрительный образ используется лазер. Так как звуковые и ультразвуковые волны могут проникать через непрозрачные предметы, то этот метод нашел широкое применение во многих областях техники и медицины. Акустическая голография используется в геофизике для исследования строения земной коры, поиска полезных ископаемых, получения изображений морского дна. В медицине она применяется для получения изображений внутренних органов, сосудов и новообразований.

Поляризация света

В продольной волне колебания происходят вдоль направления распространения волны.

В поперечной волне колебания происходят в направлении, перпендикулярном направлению распространения.

Рассмотрим еще одно важное свойство света, которое состоит в том, что свет может быть поляризован. Слово поляризация происходит от латинского polus — конец оси, полюс. Применительно к свету термин «поляризация» ввел в 1704—1706 гг. Ньютон.

Для того чтобы лучше разобраться в этом явлении, рассмотрим пример волны, бегущей по веревке. С помощью веревки можно создать поперечные волны, колебания в которых могут происходить как в вертикальной, так и в горизонтальной плоскости (рис. 253, а, б).

Если в направлении распространения таких волн поставить два ящика со щелями, параллельными направлениям колебаний в волнах, то волны пройдут через оба из них (рис. 254, а). Если же один из ящиков повернуть на 90°, так чтобы щели были взаимно перпендикулярны, то ни одна из волн не пройдет через второй ящик (рис. 254, б).

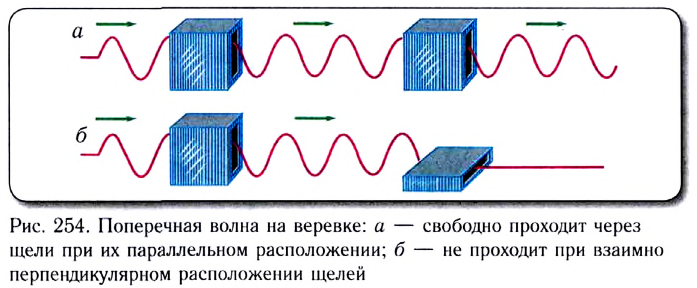
Таким образом можно «погасить» поперечные волны. Продольные волны, в которых колебания совершаются вдоль направления распространения, так «погасить» невозможно, поскольку они будут проходить через щели ящиков при их произвольной взаимной ориентации.

Если представить теперь поперечную волну, колебания в которой происходят вдоль любых прямых линий в плоскости, перпендикулярной ее направлению распространения, то погасить такую волну можно, если пропустить ее через два
ящика со скрещенными щелями. При пропускании такой волны че
рез один ящик в ней будут оставаться колебания, параллельные его щели.
Поперечная волна называется плоско-поляризованной, если колебания во всех ее точках происходят только в одной плоскости.

Прибор, превращающий неполяризованную волну в поляризованную, называется поляризатором. Прибор, позволяющий установить, поляризована или нет проходящая через него волна, называется анализатором.
Заметим, что анализатор по своей конструкции ничем не отличается от поляризатора. У этих устройств различные назначения: поляризатор выделяет поляризованное излучение из неполяризованного, а анализатор определяет направление поляризации.

Явление поляризации света можно обнаружить, пропуская его через две одинаковые пластины 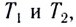вырезанные из кристаллов турмалина (рис. 255).

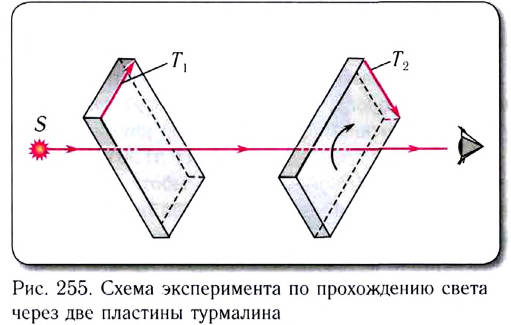
Свет попадает в глаз наблюдателя, если пластины расположены одинаково. Если поворачивать одну из пластин в плоскости, перпендикулярной направлению распространения света, то попадающий в глаз наблюдателя свет будет постепенно ослабляться до тех пор, пока пластины не будут скрещены. В этот момент свет вообще не будет проходить через систему пластинок. Дальнейшее вращение пластины приведет к усилению пропускаемого света. Максимальное пропускание будет при одинаковой ориентации пластин

Рассмотренный эксперимент является доказательством поперечное™ электромагнитных волн.

В качестве направления поляризации электромагнитных волн принято выбирать направление колебаний вектора напряженности электрического поля

Плоскость поляризации определяется как плоскость, содержащая вектор и вектор скорости волны. Если вектор колеблется только в этой плоскости, то свет называется плоско поляризованным или линейно поляризованным (рис. 256).

Если же конец вектора 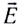при колебаниях описывает окружность, то свет называется поляризованным по кругу, а если эллипс, то — эллиптически поляризованным (рис. 257).

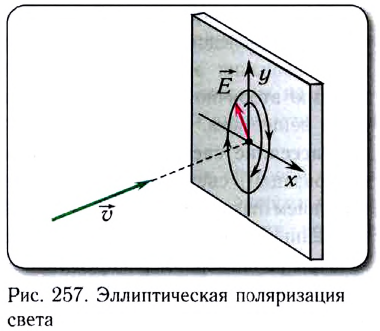
Круговая поляризация является частным случаем эллиптической поляризации.

Свет также может быть неполяризованным, или естественно поляризованным. В этом случае колебания вектора 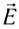происходят неупорядоченно по всевозможным направлениям, но остаются все время перпендикулярными к направлению распространения.

Неполяризованный свет излучается большинством окружающих нас источников, к которым относятся Солнце, другие звезды, лампы накаливания и т. д.

Поляризованный свет дают экраны калькуляторов, мобильных телефонов и жидкокристаллические мониторы компьютеров. В этом легко убедиться с помощью поляроидных очков, вращая, например, экран мобильного телефона в
плоскости, нормальной лучу зрения (см. рис. 255). При некотором положении телефона его экран практически полностью затемнится.

Рассеяние и поглощение света

Наше восприятие оптических явлений в окружающем мире определяется взаимодействием света с веществом.

Свет, падающий на тело, частично отражается, частично пропускается и частично поглощается. Доля каждого из этих процессов определяется коэффициентами отражения, пропускания и поглощения. Эти коэффициенты зависят от длины волны падающего излучения. Именно поэтому при освещении тел возникают разнообразные эффекты.

Оптически однородной называется среда, показатель преломления которой не зависит от координат и является постоянным по всему объему.

Оптически неоднородной называется среда, показатель преломления которой изменяется от точки к точке среды. Оптическими неоднородностями являются границы сред, включения инородных частиц. Примерами оптически неоднородных сред являются мутные среды — туманы, дымы, эмульсии, коллоидные растворы.

При распространении световой волны в среде происходит уменьшение энергии волны вследствие рассеяния (отражения) волны на неоднородностях среды, преобразования энергии волны во внутреннюю энергию вещества среды или энергию вторичного излучения. Последние два явления связаны с поглощением света веществом.

Рассеяние света — это изменение характеристик (интенсивности, частоты, поляризации) светового излучения при его взаимодействии с веществом. Под действием падающего света электроны атомов и молекул среды совершают вынужденные колебания и излучают вторичные волны.

При равномерном распределении молекул по объему среды рассеяние света отсутствует, так как по всем направлениям, кроме направления падающей волны, излучаемые когерентные вторичные волны взаимно «гасятся» в результате интерференции.

Если в объеме среды молекулы распределены неравномерно или имеются инородные частицы, то возбуждаемые вторичные волны имеют некогерентные составляющие. В результате наблюдается рассеяние света. Поэтому энергия распространяющейся волны убывает, и в начальном направлении распространения обнаруживается ослабление света.

Последовательное описание рассеяния света возможно только в рамках квантовых представлений о строении вещества. Но во многих случаях оказывается достаточным описание рассеяния в рамках волновой теории излучения.

Рассеяние света мелкими частицами, размеры которых намного меньше его длины волны обусловливает явления, которые можно описать на основе теории дифракции света на частицах. Рассеяние света большими частицами рассматривают на основе законов геометрической оптики с учетом интерференции волн, отраженных и преломленных на поверхностях частиц. Именно рассеяние на крупных частицах обусловливает ареолы, радуги, гало, явления, происходящие в туманах и аэрозолях.

Рассеяние света земной атмосферой зависит от его длины волны. Частицы,
размеры которых намного меньше длины световой волны (например, молекулы кислорода и азота), слабее рассеивают длинные волны и сильнее короткие. С увеличением длины волны рассеяние ослабевает пропорционально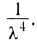

Следовательно, красный и оранжевый свет рассеивается гораздо слабее, фиолетовый и голубой, и поэтому небо выглядит голубым.

Па закате солнечные лучи проходят максимальный слой атмосферы, и значительная часть голубого излучения рассеивается. Поэтому свет, достигающий поверхности Земли, кажется красноватым, так как он лишается голубой составляющей.

Облака содержат капельки воды и кристаллы льда, размеры которых значительно превышают Они рассеивают свет практически равномерно на всех частотах. Именно поэтому облака кажутся белыми.

Многие методы определения размеров и формы частиц основаны на рассеянии света. Это особенно важно при измерении атмосферной видимости и при исследовании полимерных растворов.

Поглощением света называют явление уменьшения энергии световой волны при ее распространении в веществе, вследствие преобразования энергии волны во внутреннюю энергию вещества или энергию вторичного излучения, которое имеет иной спектральный состав и иные направления распространения.

Под действием падающего излучения электроны атомов и молекул среды совершают вынужденные колебания с частотой, равной частоте падающего излучения. Энергия падающей волны переходит во внутреннюю энергию частиц вещества, и оно нагревается. Если частота световой волны приближается к частоте собственных колебаний атомов и молекул, то возникает явление резонанса. Частицы становятся источниками вторичных световых волн. В веществе под действием поглощенной энергии могут происходить также различные реакции, например химические.

При падении на поверхность непрозрачного тела часть света проникает внутрь вещества и поглощается в нем. Мы воспринимаем отраженную часть света, т. е. видим предмет в отраженном свете. Доля отраженного света зависит от длины волны. Тела, для которых поглощение для всех длин волн велико, будут черными непрозрачными телами. Если же на поверхность тела падает белый свет, а отраженный содержит больше синего света, чем красного, то воспринимаемый цвет будет представлять оттенок синего или даже зеленого цвета. Этим объясняется, например, зеленый цвет листьев растений.

Поверхности более темных цветов поглощают свет сильнее, чем поверхности более светлых цветов. Именно поэтому в светлой одежде Вам летом прохладнее, чем в темной. Белая поверхность отражает большую часть падающего солнечного света.

Инфракрасное и ультрафиолетовое излучения

Распределение энергии какого-либо излучения по длинам волн или частотам колебаний называется спектром этого излучения. Оптическая область спектра включает инфракрасный, видимый и ультрафиолетовый диапазоны.

К инфракрасной области относят излучение с длиной волны от нескольких миллиметров до 0,75 мкм. Видимая область занимает участок спектра примерно от 0,75 мкм до 0,4 мкм. Электромагнитное излучение, соответствующее этой области, воспринимается глазом человека как видимый свет различных цветов в зависимости от частоты волны. Ультрафиолетовая область спектра примыкает непосредственно к фиолетовому участку видимой области и продолжается вплоть до рентгеновских лучей.

Ультрафиолетовую область, в свою очередь, разделяют на три участка: ближний и средний (0,4 — 0,23 мкм), дальний (0,23 — 0,185 мкм) и вакуумный (0,185 — 0,05 мкм) ультрафиолет.

Инфракрасные лучи были обнаружены в 1800 г. Их испускают все тела в природе. Этот вид излучения связан с тепловым движением молекул и атомов. Его часто еще называют тепловым излучением. При повышении температуры тела энергия инфракрасного излучения быстро возрастает.

Инфракрасное излучение способствует выравниванию температур различных тел на Земле. Тело с более высокой температурой теряет энергии больше, чем получает, и в результате охлаждается. Так, например, инфракрасное излучение Земли уносит энергию в мировое пространство, что способствует охлаждению поверхности планеты. И наоборот, более холодные тела, поглощая инфракрасное излучение, получают больше энергии, чем отдают, т. е. нагреваются.

Наиболее распространенным методом обнаружения и измерения инфракрасного излучения является тепловой, применяемый для любой длины волны. При этом используются очень чувствительные термометры (электрические, например термопары), позволяющие определять изменение температуры на миллионную долю градуса.

В технике инфракрасное излучение используют для сушки материалов, пищевых продуктов, для фотографирования в темноте, в приборах ночного видения. Специальные приборы — тепловизоры — широко применяются в медицинской диагностике, ветеринарии (рис. 258), энергетике, строительстве (помогают определять, например, качество теплоизоляции строений). В военной технике инфракрасные лучи используются для наведения ракет на цель, излучающую тепловые волны, для обнаружения замаскированного противника.

В научных исследованиях инфракрасное излучение применяется для изучения строения молекул излучающего вещества.

Ультрафиолетовые лучи были открыты в 1801 г. немецким ученым И. В. Риттером и независимо от него английским ученым У. Волластоном. Естественными источниками ультрафиолетового излучения являются Солнце, другие звезды, туманности. Однако лишь длинноволновая часть этого излучения достигает поверхности Земли, остальное излучение поглощается ее атмосферой на высотах от 30 до 200 км. Все тела, температура которых достигает нескольких тысяч градусов, излучают в ультрафиолетовой области спектра. Источниками ультрафиолетового излучения являются ртутные, ксеноновые и другие газоразрядные лампы. Интенсивное ультрафиолетовое излучение испускают электроны в ускорителях.
Исследование ультрафиолетового излучения проводят с помощью фотоэлектрических приемников.

Ультрафиолетовые лучи обладают ярко выраженным химическим действием и широко используются в фотографии. Их биологическое действие применяется в медицине. Малые дозы ультрафиолетового излучения способствуют образованию витаминов группы D, улучшают иммунобиологические свойства организмов. Загар объясняется образованием под действием ультрафиолетового излучения пигмента, придающего коже коричневый цвет.

Большие дозы этого излучения могут вызвать повреждение глаз и ожог кожи.
В научных исследованиях спектры ультрафиолетового излучения используются для изучения внешних электронных оболочек атомов различных химических элементов.

За ультрафиолетовым диапазоном следует рентгеновский, в котором излучение и поглощение связаны с изменением внутреннего строения атомов и ядер.

Существенная особенность рентгеновских лучей — их высокая проникающая способность во многие вещества, непрозрачные для видимого света. Рентгеновские лучи принято различать по их жесткости. Чем короче длина волны рентгеновского излучения, тем они считаются более жесткими. Чем жестче рентгеновские лучи, тем слабее они поглощаются и тем выше их проникающая способность.

Рентгеновское излучение широко используется в медицине для диагностики и лечения различных заболеваний, обнаружения в теле инородных предметов.
За рентгеновской расположена область -лучей, испускаемых веществом при различных ядерных превращениях.

Спектры испускания и поглощения. Спектральные приборы

Источником оптического излучения принято называть физическое тело, преобразующее любой вид энергии в энергию электромагнитных излучений оптического диапазона спектра. Любой источник света характеризуется полной энергией, которую он излучает в единицу времени. Эта энергия распределяется неравномерно между волнами различной длины. В общем случае произвольный электромагнитный сигнал состоит из набора различных электромагнитных волн, длины волн (или частоты) которых можно установить. Подобную процедуру называют спектральным анализом сигнала, а совокупность полученных «простейших» электромагнитных волн — спектром. Таким образом, спектр — распределение энергии, излучаемой или поглощаемой веществом, но частотам или длинам волн.

Направим луч белого света на стеклянную призму, за которой установлен экран. Вследствие явления дисперсии призма различным образом преломляет лучи
разных цветов. На экране увидим разноцветную полоску, которую Исаак Ньютон назвал спектром (рис. 259).

Спектры, полученные от самосветящихся тел, называются спектрами испускания. Они бывают трех типов: линейчатые, полосатые и сплошные.
Линейчатые спектры имеют все вещества в газообразном атомарном состоянии. Эти спектры состоят из отдельных узких линий различного цвета, разделенных темными промежутками (рис. 260).

Изучение линейчатых спектров показало, что каждый химический элемент обладает своим строго индивидуальным спектром. Такие спектры отличаются друг от друга цветом, положением и числом отдельных светящихся линий.
 

Полосатые спектры имеют газы, состоящие из слабо связанных друг с другом молекул. Эти спектры состоят из ряда цветных полос, разделенных темными промежутками (рис. 261).

 

Непрерывные (сплошные) спектры имеют нагретые тела, находящиеся в твердом и жидком состояниях, а также газы при высоком давлении и плазма. Вследствие интенсивного взаимодействия между молекулами индивидуальные черты, присущие отдельным частицам, в таких спектрах неразличимы. В них представлены все длины волн, нет темных промежутков и на экране видна сплошная разноцветная полоса (рис. 262).

Прозрачные вещества поглощают часть падающего на них излучения, и в спектре, полученном после прохождения белого света через такие вещества, появляются темные линии, или полосы поглощения. Такой спектр называется спектром поглощения (рис. 263).

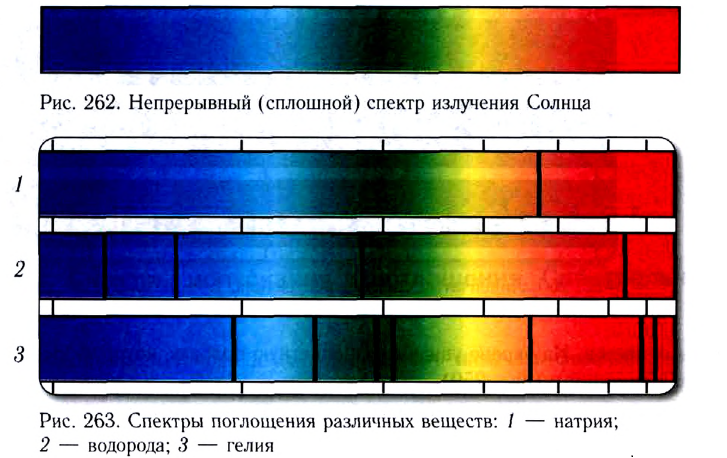
Так, вещество в газообразном состоянии поглощает наиболее сильно свет тех длин волн, которые оно испускает в нагретом состоянии. Это означает, что темные линии в спектре поглощения будут находиться как раз в тех местах, где находятся светящиеся линии в спектре испускания данного химического элемента. Эти строго установленные закономерности в линейчатых спектрах дают возможность обнаружить те или иные элементы в данном веществе.

Наиболее изученным спектром поглощения является спектр Солнца. Его сплошной спектр содержит значительное количество черных линий. Эти линии являются линиями поглощения, возникающими при прохождении света через газовую оболочку Солнца и атмосферу Земли. Они получили название фраунгоферовых линий, так как Фраунгофер впервые наблюдал спектр Солнца и установил, что закономерность их расположения не случайна и линии поглощения (темные линии) появляются всегда на строго определенных местах. Их принято обозначать латинскими буквами от А до К.

Для определения качественного и количественного состава вещества применяется метод, основанный на получении и исследовании его спектров. Этот метод называется спектральным анализом. Это самый быстрый и простой способ определения состава различных химических соединений.
Основатели спектрального анализа немецкие физики Роберт Бунзен и Густав Кирхгоф, исследуя спектр паров соединений щелочных металлов лития, натрия и калия, обнаружили новые элементы — рубидий и цезий, названные так по цвету наиболее ярких линий в их спектрах. У рубидия — красная, у цезия — синяя линия.

Спектральный анализ базируется на двух основных положениях:

1. каждый химический элемент или химическое соединение характеризуется определенным спектром;
2. интенсивность линий и полос в спектре зависит от концентрации того или иного элемента в веществе.

К достоинствам спектрального анализа можно отнести:

По спектрам определяют, из каких химических элементов состоит вещество
и их количество.

Приборы для визуального наблюдения спектров называются спектроскопами, приборы с фотографической регистрацией спектров — спектрографами (применяются в различных областях спектра с соответствующей чувствительностью фотоматериалов), приборы с фотоэлектрическими и тепловыми приемниками излучения — спектрометрами, или спектрофотометрами (рис. 264).

Спектральные приборы в зависимости от способа спектрального разложения подразделяются на призменные, интерференционные, дифракционные.
Электромагнитные волны переносят энергию. Именно благодаря этому энергия излучения Солнца достигает Земли и поддерживает жизнь на нашей планете. Известно, что свет нагревает тела, на которые падает. Нагревание означает сообщение этому телу энергии. Следовательно, распространение света сопровождается переносом энергии и передачей ее от светящегося тела к освещенному. Энергия электромагнитной волны складывается из энергий электрического и магнитного полей, составляющих ее. Объемная плотность энергии электрического поля в электромагнитной волне равна объемной плотности энергии магнитного поля 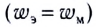в каждой точке пространства и в любой момент времени. Плотность энергии электромагнитного поля, распространяющегося в вакууме, пропорциональна квадрату напряженности электрического поля

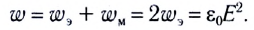
Переносимая волнами энергия характеризуется также поверхностной плотностью потока излучения I, которая равна отношению энергии W, переносимой волной за промежуток времени 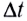через перпендикулярную лучам поверхность площадью S, к произведению площади и промежутка времени :

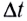Эту величину называют интенсивностью волны.

Можно показать, что поверхностная плотность потока излучения равна произведению объемной плотности электромагнитной энергии и скорости ее распространения:

где с — скорость распространения света в вакууме, 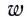— объемная плотность электромагнитной энергии волны, равная сумме объемных плотностей энергий электрического и магнитного полей. Энергия электромагнитного поля, заключенного в объеме 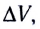может быть вычислена по формуле

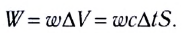
Формулы для волновой оптики

Скорость света в вакууме:

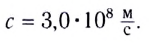
Скорость света в веществе:

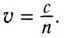
Абсолютный показатель преломления вещества:

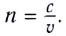
Длина волны света в веществе:

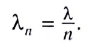
Монохроматическое колебание:

Результирующая амплитуда колебаний двух когерентных волн:

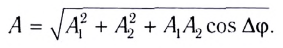
 Закон отражения света:

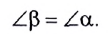
Закон преломления света:

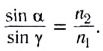
Дифракционная решетка (условие максимумов):
 

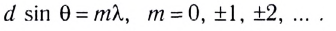
Свет как электромагнитная волна. Развитие представлений о природе света

Представления о природе света как одного из основных источников восприятия человеком окружающего мира развивались на протяжении многих веков. В древнейшие времена они были наивными, вроде того, что наши глаза обладают невидимыми «щупальцами», благодаря которым возникают зрительные образы наблюдаемых предметов. По пятно, что такой примитивный взгляд был не в состоянии объяснить истинную природу светя. Значительно позже она была раскрыта как с точки зрения волновой теории гнета, так и на основе квантовой физики.

В классической физике существовало два взгляда на природу свата – волновая и корпускулярная теории света.

Между этими двумя теориями происходила длительная дискуссия, у истоков которой стояли известные ученые: И. Ньютон (1613-1727), который считал свет потоком частиц, названных им корпускулами, и X. Гюйгенс (1629-1695), по убеждению которого свет – это волны, заполняющие собой окружающее пространство и проникающие внутрь тел. Обе теории благодаря авторитету этих ученых и способности объяснить простейшие световые явления длительное время существовали параллельно. Например, И. Ньютон, опираясь на закон инерции, сумел на основании корпускулярных представлений объяснить прямолинейное распространение света и дисперсию. X. Гюйгенс, исходя из волновых представлений, обосновал законы отражения и преломления света.

Однако со временем преимущество стали отдавать волновой теории света, поскольку были открыты световые явления, которые можно было объяснить лишь с позиций распространения света как волнового движения. В частности, в начале XIX в. английский физик Т. Юнг (1773 1829) наблюдал так называемую интерференцию света (усиление и ослабление световых пучков, исходящих от одного источника света, при их наложении) и дифракцию (огибание световым лучом преград), которые нельзя было объяснить с позиций корпускулярной гипотезы света И. Ньютона. Позже О.Ж. Френель (1788-1827), повторяя опыты Т. Юнга, убедился, что в данном случае проявляется волновая природа света. В этой связи 162 он сформулировал принцип распространения света как волны (принцип Гюйгенса-Френеля), благодаря которому стало возможным объяснение всех известных в то время световых явлений. Таким образом, волновая теория стала доминирующей в толковании природы света. Триумф ноя ноной теории света подтвердил Дж. Максвелл (1831-1879), теоретически доказав, что свет это распространение в пространстве электромагнитных волн определенной частоты (длины волны).

Учитывая, что основными характеристиками электромагнитного излучения являются частота v и длина волны λ, установлено, что они находятся в обратно пропорциональной зависимости между собой и связаны со скоростью света соотношением: .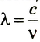

В первой половине XX в., когда начала стремительно развиваться квантовая теория, представления о природе света также претерпели изменения. Когда А. Эйнштейн (1879-1955) высказал предположение о квантовых свойствах света, это было воспринято неоднозначно. Он утверждал, что свет является потоком микрочастиц, названных им фотонами, которые несут наименьшую порцию световой энергии. Со временем выяснилось, что корпускулярная теория света, в равной степени как и волновая, также имеет право па существование, особенно при толковании явлений излучения и поглощения света.

Фотон – это корпускула света, которая обладает минимальной порцией световой энергии, названной квантом света. 

Ограниченный характер волновой теории подтвердили опыты по фотоэффекту, проведенные А.Г. Столетовым (1839-1896). Их результаты указывали на то, что свет проявляет себя подобно потоку частиц, которые обладают определенной энергией и импульсом и подчиняются законам квантовой физики.

Таким образом, многочисленные исследования световых явлений продемонстрировали неоднозначность проявления свойств света: в одних случаях (интерференция, дифракция) они подтверждают волновую природу света, в иных (излучение и поглощение) – отчетливее проявляется его корпускулярная природа. Поэтому можно утверждать, что свету присущ корпускулярно-волновой дуализм он обладает как непрерывными, волновыми свойствами, так и дискретными, корпускулярными.

Гипотезу о двойственной природе света – так называемом корпускулярно-волновом дуализме – впервые высказал А. Эйнштейн.

Как известно, свет излучают различные тела Солнце, звезды, свеча, вольфрамовая спираль электрической лампочки, молния, раскаленные предметы и т. д. Все они являются источниками видимого света, потому что излучают электромагнитные волны, воспринимаемые глазом. Человеческий глаз является самым совершенным приемником электромагнитного излучения оптического диапазона. Видимый свет, который он в состоянии воспринимать, имеет длину волны от 380 нм (фиолетовый цвет) до 760 нм (красный цвет), Наибольшую чувствительность глаз имеет в диапазоне зеленого света (около 550 пм), па который приходится максимум спектра солнечного излучения. Кроме того, приемниками светового излучения могут быть фотометры, фотоэлементы и другие приборы, способные фиксировать энергию светового ∣κrι,oκa. Кроме видимого света к оптическому диапазону относятся инфракрасное и ультрафиолетовое излучения (см. форзац).

Для того чтобы тело стало источником светя, ему необходимо сообщить определенную энергию, благодаря которой атомы начнут излучать свет. Самым простым и распространенным способом является нагревание тел. Например, солнечный свет -это излучение, возникшее вследствие разогрева поверхности Солнца (так называемой фотосферы) до температуры свыше 6000 К в результате термоядерных реакций, происходящих внутри Солнца. Свет от электрической лампы накаливания образуется в результате нагревания вольфрамовой нити до высокой температуры (около 3000 К). Чем сильнее нагрето тело, тем больше частота излучения, на которую приходится максимум. При определенной температуре тепловое излучение становится видимым сначала в красном диапазоне волн, а с повышением температуры начинает смещаться к желтому и далее.

Источники света делят на естественные и искусственные, т. е. те, которые создает человек для своих жизненных потребностей.

Свет могут излучать газы при электрическом разряде. Примером такого источника света является молния. В результате некоторых химических реакций, которые проходят с выделением энергии, часть ее может идти на излучение света. Ото так называемое холодное свечение. Его можно наблюдать у некоторых живых организмов (светлячков, бактерий). Существуют и другие способы возбуждения атомов, которые излучают свет, избавляясь таким образом от излишней энергии.

В зависимости от характера распространения световых лучей различают точечные источники смета и источники направленного излучения. Точечными называют такие источники света, размерами которых можно пренебречь по сравнению с расстояниями, проходимыми светом. От них свет равномерно распространяется во всех направлениях, однако в расчетах освещенности поверхности следует учитывать направление падающего луча. У источников направленного излучения световые лучи считаются параллельными, поэтому освещенность поверхности от такого источника света будет одинаковой на всей площади, куда падает свет. Данное условие выполнимо, если точечный источник света бесконечно удален от освещаемой поверхности. Классическим примером такого источника является Солнце.

Естественный солнечный свет неполяризован. Однако  отраженные световые лучи всегда частично или полностью поляризованы.

Свету как электромагнитному излучению в определенных условиях свойственна поляризация, т. е. ориентация колебаний векторов напряженности электрического поля или индукции магнитного поля в определенном направлении. Впервые это явление наблюдал в 1669 г. датский ученый Э. Бартолин во время двойного преломления луча света в кристалле исландского шпата. При прохождении света сквозь кристалл образуется два луча, один из которых имеет особые свойства.

Человеческий глаз не отличает поляризованный свет от обычного. Однако некоторые насекомые, например пчелы, обладают такой способностью.

Выяснилось, что существуют кристаллические вещества,  имеющие оптическую анизотропию — неоднородность оптических свойств в зависимости от направления распространения света. Когда свет проходит сквозь такие кристаллы, он поляризуется, т. е. векторы и электромагнитного поля длительное время остаются в одной плоскости. Например, кристалл турмалина имеет разные значения показателя пpeломления в зависимости от направления ориентации граней кристаллической решетки. Поэтому он является естественным поляризатором света.

Для того чтобы определить, поляризовал ли свет, применяют устройства, называемые анализаторами. Это те же поляризаторы, которые имеют иную плоскость поляризации и поэтому  влияют на интенсивность проходящего сквозь них спета; существенное ее уменьшение указывает на наличие поляризации света. Нa данном принципе, в частности, основывается действие сахарометров — приборов, с помощью которых определяют концентрацию сахара в сахарном растворе, например в патоке.

Поглощение и рассеивание света. Отражение света

Распространение светового излучения в оптической среде, как правило, сопровождается поглощением, рассеиванием или отражением света. Все эти процессы происходят вследствие взаимодействия электромагнитного излучения с веществом, в результате которого часть световой энергии преобразуется в другие виды энергии. Например, нам известно, что благодаря солнечному излучению, которое поглощается земной поверхностью, Земля нагревается, т. е. световая энергия преобразуется в тепловую.

C точки зрения квантовых представлений поглощение света – это процесс захвата фотонов атомами вещества, в котором распространяется свет, вследствие чего они отдают им свою энергию.

Поглощательную способность оптической среды характеризует коэффициент поглощения, который определяет, как изменяется интенсивность излучения с глубиной проникновения света в вещество.

Прохождение света сквозь среду сопровождается также рассеиванием светового потока на частичках вещества или иных микрообъектах, размеры которых меньше длины волны света. Оно может происходить без изменения частоты излучения (так называемое релеевское рассеивание) либо комбинационным способом, когда в спектре света при прохождении сквозь среду возникают спектральные линии, частота которых отличается от первоначального (возбуждающего) света. Частота и положение дополнительных спектральных линий зависят от молекулярного строения вещества. Поэтому комбинационное рассеивание широко используется в спектральном анализе для исследования особенностей молекулярной структуры вещества.

На границе двух сред может происходить также отражение светового излучения, т. е. достигая границы раздела, оно может изменить направление и вернуться в среду, откуда вышло. Отражение бывает зеркальным, для которого справедлив закон отражения света, и рассеивающим (диффузным), когда световые лучи, отражаясь от неровностей поверхности, на которую они падают, расходятся в разные стороны. Это происходит при условии, когда размер таких неровностей соразмерен с длиной волны света. Поэтому поверхность, которая является зеркальной для ультрафиолетового излучения, может не быть таковой для инфракрасного излучения, поскольку длина его волны больше и может быть близкой по размерам к неровностям отражающей поверхности.

Рассеивающее (диффузное) отражение света происходит при падении света на шероховатые матовые поверхности.

При зеркальном отражении света выполняется закон, известный нам из курса физики 7-го класса: падающий и отраженный лучи лежат в одной плоскости с перпендикуляром к отражающей поверхности в точке падения светового луча; перпендикуляр делит угол между падающим и отраженным лучами на. две равные части.

Данный закон получил обоснование как с точки зрения корпускулярной, так и со стороны волновой теории света. Первая в своем толковании опиралась на законы механики при упругом соударении корпускул света (фотонов) с отражающей поверхностью. В основу объяснения закона отражения света волновой теорией положены принципы Ферма и Гюйгенса-Френеля.

Согласно принципу Ферма свет, распространяется из начальной в конечную точку таким образом, чтобы, время прохождения световой, волны было минимальным. Принцип Гюйгенса-Френеля определяет, что каждая точка пространства, в которую приходит фронт световой волны, становится источником вторичных световых волн.

Объясним теперь закон отражения света на основе представлений о волновой природе света. Первая часть закона указывает на то, что направление отраженного светового луча не может быть произвольным. Как известно, через две прямые, отрезками которых являются падающий АО и отраженный OB лучи (рис. 4.1), можно провести только одну плоскость N, перпендикулярную к плоскости отражающей поверхности М.

Пусть па поверхность МN падает световая волна, фронт которой распространяется вдоль прямой AB (рис. 4.2). Когда световой луч достигает точки А, то согласно принципу Гюйгенса-Френеля данная точка становится источником новой сферической волны. За время, пока фронт падающей волны достигнет точки С, фронт отраженной в точке А волны образует полусферу радиуса r, где где r = AD. За это время такие же волны будут распространяться и от других точек поверхности МN, образуя новый фронт волны CD отраженного света. Чтобы определить направление, в котором он будет перемещаться, рассмотрим треугольники ACD и АВС. Поскольку их стороны AD = BC и AB = CD, a AC общая, то данные треугольники равны.

Как известно, равные треугольники имеют одинаковые углы. Учитывая это, можно утверждать, что углы аир между лучом и перпендикуляром в точке падения, как дополняющие для равных углов, также будут равны: . Нa основании этого можно заключить, что угол отражения светового луча от поверхности равен углу его падения.

Таким образом, на основе волновых представлений о природе света доказана и вторая часть закона отражения света, которую можно подтвердить также экспериментальным путем. Установим на оптическом диске плоское зеркало и направим на него узкий пучок света (рис. 4.3). C помощью меток на диске можно легко убедиться, что угол между падающим лучом и перпендикуляром (угол падения) равен углу между перпендикуляром и отраженным лучом (угол отражения).

Рис. 4.3. Оптический диск

Подводя итоги, можно сделать вывод, что свет взаимодействует с оптической средой, в которой распространяется, в результате чего может происходить его поглощение, рассеивание или отражение. Все эти явления объясняют и волновая, и корпускулярная теории света.

Зеркала и получение изображений при помощи зеркал

Явление отражения света широко используется в технике и повседневной жизни, в частности когда необходимо изменить направление распространения световых пучков на противоположное. C этой целью применяют зеркала, которые в зависимости от формы отражающей поверхности могут быть плоскими, сферическими, параболическими и т. п.

Плоское зеркало – самое распространенное оптическое приспособление, использующее законы отражения света. Возможность видеть изображения предметов в зеркале является результатом совместного действия зеркала и глаза человека. Для подтверждения этого построим изображение точки, полуценное при помощи плоского зеркала (рис. 4.4).

Pиc. 4.4. Построение изображения точки, полученного при помощи зеркала

Пусть на плоское зеркало MN падает пучок световых лучей из точки S. Изобразим два луча, падающих на зеркало под разными углами α₁ и α₂ . Согласно закону отражения углы β₁и β₂ отраженных световых лучей будут равны соответствующим углам падения. Вследствие этого от зеркала будет распространяться расходящийся пучок света. Если продлить отраженные лучи за плоскость зеркала, то они пересекутся в точке S’. Соединив прямой точки S и S’, получим дна равных треугольника △SAO и△S’AO. Из условия равенства данных треугольников следует, что отрезки SO и S’O также равны.

Следовательно, можно сделать вывод, что предмет и изображение, полученное в плоском зеркале, симметричны относительно плоскости зеркала; оно всегда мнимое, поскольку находится на пересечении продленных отрезков расходящихся лучей.

Рассуждениями относительно построения изображения точки, полученного при помощи зеркала, можно воспользоваться и для построения изображения предмета, представляя его как совокупность точек.

Чтобы построить изображение предмета, полученное в плоском зеркале, можно воспользоваться простыми правилами:

• от точечного источника света следует опустить перпендикуляр па поверхность зеркала и продлить его за его плоскость;
• измерить расстояние от источника света до зеркала и отложить его на продолжении перпендикуляра за зеркалом;
• метка на данном отрезке определяет положение мнимого изображения точечного источника света, полученного при помощи зеркала.

Построение изображений, полученных при помощи сферических зеркал, основывается на тех же законах отражения света, что и для плоского зеркала. Однако сферическая поверхность таких зеркал не только изменяет направление распространения света, но и влияет на конфигурацию пучков света.

Например, параллельный пучок света, падая на вогнутую зеркальную поверхность, может собираться в одной точке F, которая называется фокусом сферического зеркала (рис. 4.5). И наоборот, если источник света поместить в фокусе сферического зеркала, то получим параллельный пучок света. Данное свойство используется в отражателях света (рефлекторах) фонарей и мощных прожекторов, имеющих сферическую или параболическую форму.

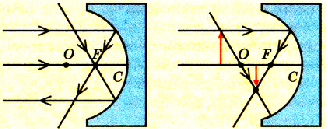
Pиc. 4.5. Отражение света в сферическом зеркале

Построение изображений, полученных при помощи сферических зеркал, подчиняется формуле сферического зеркала:

где F  – фокусное расстояние сферического зеркала; d  – расстояние от зеркала до предмета; f – расстояние от зеркала до изображения.

Установлено, что фокусное расстояние сферического зеркала равно половине радиуса сферической поверхности, образующей данное зеркало: . У вогнутых зеркал оно имеет положительное значение, а в выпуклых — отрицательное, что следует учитывать при решении задач по формуле сферического зеркала.

Преломление света и законы преломления света

Как известно, на границе двух сред свет может как отражаться, так и преломляться, если вторая среда оптически прозрачна. Проведем такой опыт. Нальем в стеклянный сосуд воду, подкрашенную специальным веществом, светящимся под действием света. Над поверхностью воды создадим легкую дымовую завесу, которая также даст нам возможность наблюдать за ходом световых лучей. Если теперь направить узкий пучок света на поверхность воды под некоторым углом, то можно увидеть, что на ее поверхности он разделится на два пучка (рис. 4.6). Один из них будет отраженным от поверхности воды в соответствии с законом отражения света, а другой проникнет в воду, отклонившись при этом от прямолинейной траектории, т. е. произойдет его преломление.

Puc. 4.6. Отражение и преломление света на границе двух сред

Такую особенность прохождения луча в оптической среде можно объяснить лишь тем, что скорость распространения света в различных средах неодинакова и отличается от скорости снега в вакууме. Их соотношение характеризует показатель преломления вещества n, определяющий, во сколько раз скорость света с вакууме с больше скорости распространения световых волн 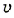в данной среде:

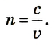
В XVII в. голландский физик В. Снелл открыл закон преломления света: падающий, и преломленный лучи лежат в одной плоскости с перпендикуляром, опущенным на границу двух сред в точке падения луча: угол падения а светового луча на поверхность раздела двух сред связан с углом преломления γ соотношением (рис. 4.7):

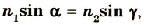
или 

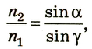
где n₁ – показатель преломления среды, из которой идет луч; n₂ — показатель преломления среды, в которой свет распространяется после прохождения границы раздела.

Часто отношение 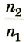 навивают относительным показателем преломления второй среды относительно первой и обозначают n_2l. Если учесть формулу показателя преломления 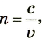то и
можно сделать вывод, что относительный показатель преломления характеризует отношение скоростей света в средах, в которых он распространяется:

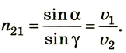
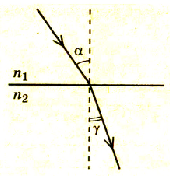
Pиc. 4.7. Закон преломления света

Таким образом, закон преломления света позволяет найти значение угла преломления, который зависит от соотношения скоростей света в каждой из сред. Отсюда следует, что не всегда угол преломления меньше угла падения. К примеру, если световой луч выходит из среды с большим по значению показателем преломления и попадает в среду с меньшим показателем преломления (например, из воды в воздух), то угол преломления будет больше угла падения (рис. 4.8).

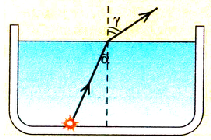
Pиc. 4.8. Xog светового луча из воды в воздух

Показатель преломления света относительно вакуума называется абсолютным показателем преломления. Как правило, в таблицах приводят именно его, а относительные показатели преломления находят экспериментальным путем или вычисляют по формуле 

Абсолютные показатели преломления веществ

Вещество	Показатель преломления	Вещество	Показатель преломления
Воздух	1,0003	Полиэтилен	1,52
Вода	1,33	Алмаз	2,42
Стекло (разное)	1,52-1,89	Кварц	1,46

Построение изображений, получаемых при помощи линз

Преломление света на границе двух сред нашло широкое практическое применение в оптических устройствах, называемых линзами. Основная их особенность состоит с том, что они способны изменять конфигурацию световых пучков и направление их распространения, в частности собирать их в точку (собирающие линзы) либо делать их расходящимися (рассеивающие линзы). Благодаря этому их свойству можно получать увеличенные или уменьшенные изображения предметов на экране либо па сетчатке глаза.

Для построения изображений при помощи линз учитывают характерные точки и линии этих оптических устройств, а также особенности прохождения в них световых лучей. Вспомним их из курса физики 7 го класса.

Прямая, соединяющая центры сферических поверхностей, образующих линзу, называется главной оптической осью линзы. На ней находится фокус линзы, т. е. точка, в которой сходятся все световые лучи, идущие параллельно главной оптической оси, либо продолжения таких лучей, если линза образуй’!1 расходящиеся пучки (рис. 4.9). В последнем случае говорят, что фокус мнимый (им обладают все рассеивающие линзы). Поэтому при помощи рассеивающих линз нельзя получить изображение предмета на экране. Мы его видим лишь благодаря действию хрусталика глаза, который вместе с рассеивающей линзой образует своеобразную оптическую систему, собирающую расходящиеся лучи на сетчатке глаза. Для простоты изложения материала в дальнейшем будем рассматривать только собирающие линзы.

Рис. 4.9. Характерные точки и линии линз

Для построения изображения предмета, как правило, пользуются двумя-тремя лучами, которые выходят из произвольной точки предмета и имеют направления, характерные для линз. Один из таких лучей направлен параллельно главной оптической оси; после преломления он пересекает ось в фокусе линзы (рис. 4.10). Второй луч, который проходит через фокус, после преломления в линзе направлен параллельно главной оптической оси. Третьим может быть луч, проходящий через оптический центр линзы, поскольку он не преломляется. Все они пересекутся в точке S^/ которая является изображением выбранной точки предмета.
 

Рис. 4.10. Xog лучей в собирающей линзе

Существуют правила построения изображений, получаемых при помощи линзы, когда предмет расположен в определенных точках относительно нее. Рассмотрим их на примере собирающей линзы.

1.    Предмет находится между фокусом и двойным фокусом линзы (рис. 4.11). Направим два характерных луча (один -параллельно главной оптической оси, второй через фокус), при помощи которых получим изображение предмета, находящееся справа от линзы за двойным фокусом. Оно будет действительным, перевернутым и увеличенным.

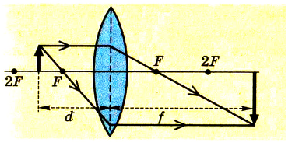
Рис. 4.11. Построение изображения, если F < d < 2F

2.    Предмет находится в двойном фокусе линзы (рис. 4.12). Направим те же два характерных луча — параллельный главной оптической оси и через фокус и получим справа от линзы симметричное относительно нее изображение предмета, расположенное в точке двойного фокуса. Оно будет действительным, перевернутым и по размеру равным предмету.

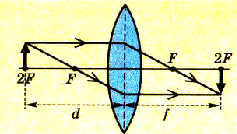
Рис. 4.12. Построение изображения, если d = 2F

3.    Предмет находится за двойным фокусом линзы (рис. 4.13). Направим на линзу те же два характерных луча, которые теперь пересекутся в точке, находящейся справа от линзы между фокусом и двойным фокусом. Изображение предмета будет действительным, перевернутым и уменьшенным.

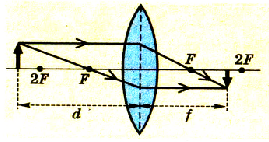
Puc. 4.13. Построение изображения, если d > 2F

4.    Предмет находится перед фокусом линзы (рис. 4.14). Направим на линзу два характерных луча — параллельный главной оптической оси и через оптический центр линзы. После преломления в ней лучи становятся расходящимися. Чтобы получить изображение, продлим их до пересечения в точке, расположенной с той же стороны от .линзы, что и предмет, слева. В данном случае изображение будет действительным, прямым и увеличенным.

Рис. 4.14. Построение изображения, если d < F

Чтоб найти положение изображения предмета относительно линзы, применяют формулу линзы, которая связывает между собой фокусное расстояние линзы F, расположение предмета и его изображения относительно нее:

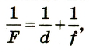
где d — расстояние от предмета до линзы; f – расстояние от линзы до изображения.

Припомним также, что величину, обратную фокусному расстоянию линзы, называют оптической силой линзы: .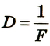
Ее измеряют в диоптриях (дптр).

 1 диоптрия – это оптическая сила такой линзы, фокусное расстояние которой равно 1 м. 

Пример решения задачи

Найти положение изображения предмета, которое дает собирающая линза с фокусным расстоянием 5 см, если предмет расположен на расстоянии 3 см от линзы.

Дано: F = 5 см, d = 3 см	Решение Для решения задачи воспользуемся формулой линзы: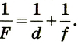
f – ?

Отсюда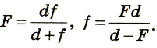 

 Знак «-» означает, что изображение является мнимым, оно находится с той же стороны, что и предмет.

Интерференция света

Как известно, если направить пучок на любую поверхность, то ее освещенность увеличится. Иную картину можно наблюдать, когда на поверхность надают дна пучка света от одного источника, накладываясь один на другой (рис. 4.15). В случае попадания их на один и тот же участок поверхности наблюдается чередование максимумов и минимумов освещенности. Такую картину от двух щелей впервые наблюдал в 1801 г. английский ученый Т. Юнг, давший впоследствии объяснение данному явлению на основании волновой теории света.

Pиc. 4.15. Интерферениионные картины света от двух щелей разного размера

Явление перераспределения интенсивности падающего света он назвал интерференцией (от лат. – наложение}. Оно является результатом взаимного усиления или ослабления амплитуды электромагнитных волн, которые исходят от одного источника.  Интерференционную картину, полученную вследствие наложения световых волн, можно наблюдать лишь при соблюден ни определенных условий: электромагнитные волны должны быть когерентными, т. с. иметь одинаковую частоту и разность фаз. Практически это достигается путем расщепления светового пучка от одного источника света на два и более. Рассмотрим данное явление детальнее (рис. 4.16).

Pиc. 4.16. Интерференция света от двух щелей 

Согласно принципу Гюйгенса-Френеля всякий световой пучок от щели представляет собой самостоятельную электромагнитную волну, которая, попадая на экран, взаимодействует с другой, когерентной ей волной. Если в некоторую точку экрана приходят две волны одной частоты и фазы, то в результате их наложения освещенность экрана в данной точке возрастает (максимумы интерференционной картины). Если же они приходят в данную точку в противофазе, то в результате наложения их интенсивности взаимно компенсируются (минимумы интерференционной картины).

Положения максимумов (светлых полос) и минимумов (темных полос) в интерференционной картине можно определить, воспользовавшись формулами условий максимума и минимума. Пусть в произвольную точку А на экране попадает свет от когерентных источников S₁ и S₂ с некоторым смещением фаз, учитывая разные расстояния, проходимые фронтами этих волн (рис. 4.17).

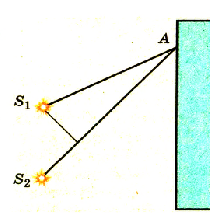
Рис. 4.17. Разность хода световых лучей

На рисунке видно, что S₁A < S₂A. Следовательно, в данном случае говорят, что существует разность хода световых лучей, равная △l = S₂A – S₁A. Если в эту разность хода вкладывается четное число полуволн, тогда в данной точке пространства наблюдается максимум освещенности:

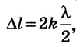
где λ – длина волны; k = 1, 2, 3,… n.

Если же разность хода равна нечетному числу полуволн, то в данной точке наблюдается минимум освещенности:

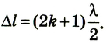
Явление интерференции широко используется в науке и технике, н частности для проведения точных измерений расстояний при помощи интерферометров (погрешность измерений мопсе 100 нм).

Например, американский физик А. Майкельсон при помощи сконструированного им интерферометра с высокой точностью измерил скорость света в вакууме, а в 1892-1893 гг. произвел сравнение эталонного метра с длиной волны видимого света.

Метод просветления оптики впервые был предложен украинским физиком А.Т. Смакулой (1900-1983).

Явление интерференции нашло практическую реализацию в оптических приборах, когда необходимо было уменьшить в несколько раз интенсивность прохождения света (так называемое просветление оптики, используемое, например, н очках). C этой целью поверхность линз покрывают тонкой прозрачной пленкой. Проходя сквозь нее, свет дважды испытывает отражение: сначала от верхней поверхности пленки, повторно – от нижней. Отраженные пучки света когерентны и имеют определенную разность хода, на значение которой влияет толщина пленки и материал, из которого она произведена. Наложение этих двух пучков света приводит к интерференции. Когда разность их хода равна нечетному числу полуволн, происходит уменьшение интенсивности отраженного света. Полное «погашение» отраженного света для определенного значения длины волны зависит от толщины пленки. Поэтому ее рассчитывают, как правило, для зеленого света, поскольку человеческий глаз к нему наиболее чувствителен.

Дифракция света

Как известно, прямолинейность распространения света является одним из основных положений геометрической оптики. Оно является основополагающим при построении изображений в оптических системах, объяснении образования тени и полутени, солнечного и лунного затмений. Доказано, что если на пути пучка света поместить непрозрачный предмет, то на экране за ним образуется четкая тень; если пучок света проходит сквозь отверстие, то на экране наблюдается четкое светлое пятно, т. е. прямолинейность распространения света подтверждена многочисленными экспериментами и нашим собственным жизненным опытом.

Если на пути снега встречаются небольшие по размерам предметы или отверстия, четкость изображения тени или снегового пятна теряется, их края становятся размытыми. Когда преграда будет соразмерна длине волны падающего света (десятые доли миллиметра и меньше), то на экране наблюдается совсем иная картина: свет будет проникать в область тени, нарушая тем самым основы геометрической оптики. Т. е. там, где должна быть темная тень, будут появляться светлые полосы, а в центре светлого пятна может появиться темная область (рис. 4.20).

Pиc. 4.20. Дифракция света (λ = 650 нм) от отверстия диаметра 0,2 мм

Явление попадания света в область геометрической тени, словно свет огибает преграду, называется дифракцией.

Впервые дифракцию света наблюдал Т. Юнг. Объяснил же данное явление на основе волновой теории света Ж.О. Френель.

Пусть на щель падает сферическая волна, исходящая от точечного источника света. Согласно принципу Гюйгенса-Френеля ее края станут источниками новых волн, которые могут попасть и в область геометрической тени (рис. 4.21). Данные волны когерентны, поэтому вследствие наложения образуют интерференционную картину с максимума и минимумами освещенности. Ее называют дифракционной картиной, поскольку она отображает явление дифракции света.

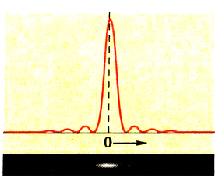
Рис. 4.21. Объяснение дифракции света на основе принципа Гюйгенса-Френеля

Явление дифракции присуще всем волновым процессам, поэтому оно происходит во всем диапазоне длин волн электромагнитного излучения. Кроме того, дифракция наблюдается у электронов при их рассеивании во время прохождения сквозь кристаллические тела. Этим фактически подтверждается, что микрочастицы обладают также волновыми свойствами, т. е. им также присущ корпускулярно-волновой дуализм. Для микрочастиц он проявляется в существовании так называемых волн де Бройля (см. § 61).

Дисперсия света и спектроскоп

Наблюдая в 1672 г. прохождение солнечного света сквозь призму, И. Ньютон обнаружил, что свет разлагается на цвета (рис. 4.22). Данное явление было названо дисперсией света. Сущность ее состоит в том, что скорость распространения световых волн различной частоты в прозрачной оптической среде, за исключением вакуума, неодинакова: в оптической среде она тем больше, чем меньше частота световой волны (больше длина волны). т. е. в одной и той же среде у красного света (λ = 620÷760 нм) скорость выше, нежели у фиолетово го (λ = 88O÷45O нм).

Pиc. 422. Дисперсия света (опыт И. Ньютона)

Соответственно, учитывая формулу показателя преломления среды с 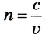, можно сделать вывод, что его значение зависит от скорости света в данной среде, следовательно, от длины световой волны: как правило, он больше у свеч’я с меньшей длиной волны. Таким образом, дисперсия – это фактически зависимость абсолютного показателя преломления оптической среды от длины волны света: n = f(λ).

Поэтому при прохождении солнечного света сквозь призму мы наблюдаем спектр, в котором лучи фиолетового цвета, имеющие наименьшую скорость, отклоняются больше всех, а красного цвета меньше. В лабораторных условиях это можно наблюдать, если сквозь призму поочередно пропускать лучи, например, красного и фиолетового цветов.

Графическая зависимость показателя преломления от длины волны для некоторых веществ приведена на рисунке 4.23. Как видно из графика, она имеет нелинейный характер.

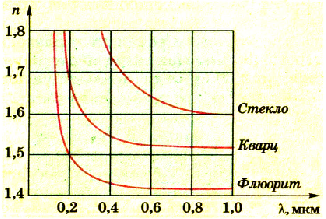
Рис. 4.23. Зависимость показателя преломления вещества от длины волны

Например, у одного из видов стекла показатель прелом линия для лучей фиолетового цвета равен 1,532, для зеленого 1,519, а для красного – 1,513. Следовательно, при прохождении сквозь призму солнечного света, в составе которого лущи разной длины волны, из-за дисперсии они преломляются по-разному, образуя разноцветный непрерывный спектр. В таком спектре присутствуют все цвета от красного до фиолетового, плавно переходя от одного к другому. В природе его можно наблюдать в виде радуги.

Установлено, что в зависимости от состава спектра можно судить о свойствах вещества и на этом основании различать их, поскольку каждое вещество имеет особый, присущий лишь ему спектр. C целью исследования свойств веществ применяют спектроскопы и спектрометры, при помощи которых изучают спектры различных веществ. Основной деталью такого оптического прибора является дисперсионная призма (рис. 4.24), разлагающая узкий пучок света от исследуемого образца в спектр. Его фиксируют визуально либо на фотопленку (у снектроскопов) или современными детекторами излучения (у спектрометров).

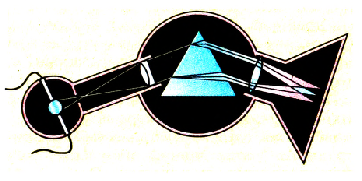
Pиc. 4.24. Устройство спектроскопа

Сравнивая полученный спектр исследуемого тела со спектрами других веществ, можно выяснить его химический состав либо сделать иные выводы о его химическом составе. В частности, современные спектрометры (рис, 4.25) применяют в изучении химического состава различных образцов, для исследования астрономических объектов, в экологических экспертизах с целью выявления загрязнения пищевых продуктов и грунтов, во время контроля качества сырья в металлургии и на химическом производстве, для анализа художественных произведений на их соответствие оригиналу и т. д.

Pиc. 4.25. Современный спектрометр

Инфракрасное и ультрафиолетовое излучения

Спектр видимого света с одной стороны ограничен фиолетовым светом, а с другой – красным. За их пределами глаз не видит никакого излучения. Вместе с тем при помощи специальных приборов, чувствительных к определенному диапазону волн, выявлены другие виды электромагнитного излучения. К примеру, если в темную часть экрана за красным участком спектра поместить термодатчик, то он зафиксирует нагревание. Это свидетельствует о том, что на данном участке спектра существует энергия электромагнитного излучения, которое человеческий глаз не воспринимает. Измерения показывают, что длина волны данного излучения больше длины волны красного света видимого спектра. Поэтому оно получило название инфракрасного. Диапазон инфракрасных волн довольно широкий: от 760 пм до 0,1 мм.

Пределы диапазона инфракрасных волн от 760 нм до I 0,1 мм.

Открыл инфракрасное излучение известный английский астроном и оптик В. Гершель в 1800 г.

Инфракрасные волны излучают нее тела, независимо от их температуры. При этом следует учитывать, что длина волны, на которую приходится максимальная энергия излучения, уменьшается с повышением температуры тела. Данный вид излучения часто называют тепловым, поскольку благодаря инфракрасному излучению осуществляется один из видов теплообмена. Например, таким образом передается на Землю тепловая составляющая солнечной энергии.

Распространением инфракрасных лучей, как и любым другим излучением, можно управлять, используя их взаимодействие с веществом. C этой целью отбирают такие материалы, которые слабо поглотают инфракрасные лучи. К ним относятся кухонная соль и эбонит. Например, в технической сфере применяют различные устройства, действие которых основывается на использовании энергии инфракрасного излучения. Это различные сушилки, применяемые во время покраски автомобилей, обезвоживание влажной древесины и т. п.

Инфракрасное излучение незначительно поглощается воздухом, при этом хорошо отражается от поверхности твердых тел. Это его свойство положено в основу систем так называемого ночного видения, широко применяемых в военном деле и научных исследованиях. В таких системах приемник фиксирует волны, которые излучает каждое тело в инфракрасном диапазоне, либо отраженное от предметов излучение, испускаемое инфракрасными прожекторами. Сложные электронные системы преобразуют полученную информацию в видимое глазом изображение на мониторе.

C противоположного края видимого света, прилегающего к диапазону фиолетовых волн, находится так называемое ультра-фиолетовое излучение, также имеющее особые свойства.

Например, многие вещества излучают видимый свет, когда на них попадает ультрафиолетовое излучение. Данное свойство положено в основу методов выявления ультрафиолетового излучения, а также неразрушающего анализа различных веществ. В частности, по цвету свечения продуктов питания, на которые направлено ультрафиолетовое излучение, можно определить их пищевое качество; по цветовой гамме свечения некоторых минералов геологи выясняют их химический состав. Известен также метод обнаружения фальшивых денежных банкнот, применяемый в банковских учреждениях и магазинах.

Ультрафиолетовое излучение обладает сильным бактерицидным действием. Под его воздействием гибнет большинство болезнетворных бактерий. Поэтому во всех операционных комнатах больниц имеются специальные ультрафиолетовые лампы, применяемые для дезинфекции помещений. Таким же образом ультрафиолетовое излучение используют для стерилизации различных медицинских материалов и инструментов, дезинфекции питьевой воды.

Под действием ультрафиолетового излучения в человеческом организме вырабатываются вещества (например, витамин D), благоприятствующие укреплению здоровья человека. Поэтому малые дозы такого излучения используют для оздоровления людей в медицинских учреждениях и санаториях, в частности во время процедур загорания под солнечными лучами, которые содержат значительную долю ультрафиолетового излучения.

В то же время ультрафиолетовое излучение (особенно в коротковолновом диапазоне) может навредить здоровью человека. Оно способно оказать отрицательное влияние на сетчатку при  прямом попадании в глаз, вызвать ожоги кожи, привести к необратимым процессам в организме.

Различные вещества по-разному взаимодействуют с ультрафиолетовым излучением, пропуская или поглощая его. Например, обычное оконное стекло поглощает почти все волны ультрафиолетового диапазона, а кварцевое стекло пропускает их практически без изменений.

Ультрафиолетовое излучение можно получить при помощи искусственных источников – так называемых ламп черного света, специальных лазерных установок.

Как определить количество максимумов дифракционной решетки?

Петрович Г.И. О порядке главных максимумов от дифракционной решётки в ЦТ

Петрович Г. И. О порядке главных максимумов от дифракционной решётки в решениях задач централизованного тестирования // Фiзiка: праблемы выкладання. – 2009. – № 3. – С. 34-40.

При перпендикулярном (нормальном) падении параллельного пучка монохроматического света на дифракционную решётку на экране в фокальной плоскости собирающей линзы, расположенной параллельно дифракционной решётке, наблюдается неоднородная картина распределения освещённости разных участков экрана (дифракционная картина).

Главные максимумы этой дифракционной картины удовлетворяют следующим условиям:

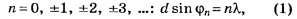
где n — порядок главного дифракционного максимума, d — постоянная (период) дифракционной решётки, λ— длина волны монохроматического света, φ_n — угол между нормалью к дифракционной решётке и направлением на главный дифракционный максимум n-го порядка.

Постоянная (период) дифракционной решётки длиной l

где N — количество щелей (штрихов), приходящихся на участок дифракционной решётки длиной I.

Наряду с длиной волны 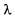часто используется частота v волны.

Для электромагнитных волн (света) в вакууме

где с = 3 *10 8 м/с — скорость распространения света в вакууме.

Выделим из формулы (1) наиболее трудно математически определяемые формулы для порядка главных дифракционных максимумов:

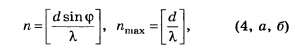
где 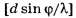обозначает целую часть числа d*sin(φ/λ).

Недоопределённые аналоги формул (4, а,б) без символа [. ] в правых частях содержат в себе потенциальную опасность подмены физически обоснованной операции выделения целой части числа 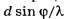операцией округления числа d*sin(φ/λ) до целочисленного значения по формальным математическим правилам.

Подсознательная тенденция (ложный след) подмены операции выделения целой части числа d*sin(φ/λ) операцией округления

этого числа до целочисленного значения по математическим правилам ещё более усиливается, когда речь идёт о тестовых заданиях типа В на определение порядка главных дифракционных максимумов.

В любых тестовых заданиях типа В численные значения искомых физических величин по договорённости округляются до целочисленных значений. Однако в математической литературе нет единых(го) правил(а) округления чисел.

В справочной книге В. А. Гусева, А. Г. Мордковича по математике для учащихся [1] и белорусском учебном пособии Л. А. Латотина, В. Я. Чеботаревского по математике для IV класса [2] приводятся по существу одни и те же два правила округления чисел. В [1] они сформулированы так: «При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяются нулями, а если стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра больше или равна пяти, то последнюю оставшуюся цифру увеличивают на 1. Если же первая следующая за этим разрядом цифра меньше 5, то последнюю оставшуюся цифру не изменяют».

В справочнике М. Я. Выгодского по элементарной математике [3], выдержавшем двадцать семь (!) изданий, написано (с. 74): «Правило 3. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится до ближайшего чётного числа, т.е. последняя сохраняемая цифра остаётся неизменной, если она чётная, и усиливается (увеличивается на 1), если она нечётная».

Ввиду существования различных правил округления чисел следовало бы правила округления десятичных чисел явно сформулировать в «Инструкции для учащихся», прилагаемой к заданиям централизованного тестирования по физике. Это предложение приобретает дополнительную актуальность, так как в белорусские вузы поступают и проходят обязательное тестирование не только граждане Беларуси и России, но и других стран, и заведомо неизвестно, какими правилами округления чисел они пользовались при обучении в своих странах.

Во всех случаях округление десятичных чисел будем производить по правилам, приведённым в [1], [2].

После вынужденного отступления, возвратимся к обсуждению рассматриваемых физических вопросов.

С учётом нулевого (n = 0) главного максимума и симметричного расположения остальных главных максимумов относительно него общее количество наблюдаемых главных максимумов от дифракционной решётки подсчитывается по формулам:

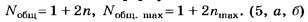
Если расстояние от дифракционной решётки до экрана, на котором наблюдается дифракционная картина, обозначить через Н, то координата главного дифракционного максимума n-го порядка при отсчёте от нулевого максимума равна

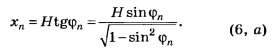
Если то 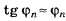(радиан) 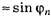и

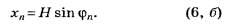
Задачи на рассматриваемую тему часто предлагают на тестированиях по физике.

Начнём обзор с рассмотрения российских тестов, использовавшихся белорусскими вузами на начальном этапе, когда тестирование в Беларуси было необязательным и проводилось отдельными учебными заведениями на свой страх и риск как альтернатива обычной индивидуальной письменно-устной форме проведения вступительных экзаменов.

А32. Наибольший порядок спектра, который можно наблюдать при дифракции света с длиной волны λ на дифракционной решётке с периодом d=3,5λ равен

1) 4; 2) 7; 3) 2; 4) 8; 5) 3.

При освещении дифракционной решётки монохроматическим светом ни о каких спектрах не может быть и речи. В условии задачи речь должна идти о главном дифракционном максимуме наибольшего порядка при перпендикулярном падении монохроматического света на дифракционную решётку.

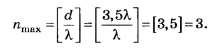
Из недоопределённого условия

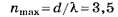
на множестве целых чисел, после округления получаем n_mах =4.

Только благодаря несовпадению целой части числа d/λ с его округлённым целочисленным значением правильное решение ( n_mах =3) отличается от неправильного ( n_max =4) на тестовом уровне.

Изумительная миниатюра, несмотря на огрехи формулировки, с филигранно выверенным по всем трём версиям округления чисел ложным следом!

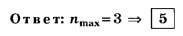
А18. Если постоянная дифракционной решётки d= 2 мкм, то для нормально падающего на решётку белого света 400 нм <λ < 700 нм наибольший полностью наблюдаемый порядок спектра равен

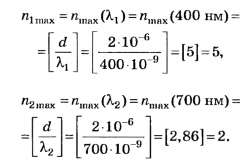
Округляя числа d/λ до целочисленных значений по правилам [1] — [3], получаем:

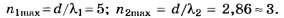
Благодаря тому, что целая часть числа d/λ₂ отличается от его округлённого целочисленного значения, данное задание позволяет на тестовом уровне объективно отличить правильное решение (n_сп= 2) от неправильного (n_сп=3). Прекрасная задача с одним ложным следом!

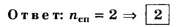
ЦТ 2002 г. Тест № 3 [5]

В5. Найдите наибольший порядок спектра для жёлтой линии Na ( λ = 589 нм), если постоянная дифракционной решётки d = 2 мкм.

Задание сформулировано научно некорректно. Во-первых, при освещении дифракционной решётки монохроматическим светом, как уже отмечалось выше, не может быть и речи о спектре (спектрах). В условии задачи речь должна идти о наибольшем порядке главного дифракционного максимума.

Во-вторых, в условии задания должно быть указано, что свет падает нормально (перпендикулярно) на дифракционную решётку, ибо только этот частный случай рассматривается в курсе физики средних общеобразовательных учреждений. Считать это ограничение подразумевающимся по умолчанию нельзя: в тестах все ограничения должны быть указаны явно! Тестовые задания должны представлять собою самодостаточные, научно корректные задания.

С учётом вышеприведённых уточнений

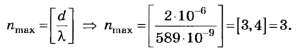
Число 3,4, округлённое до целочисленного значения по правилам арифметики [1] — [3], также даёт 3. Именно поэтому данное задание следует признать простым и, по большому счёту, неудачным, так как на тестовом уровне оно не позволяет объективно различить правильное решение, определяемое по целой части числа 3,4, от неправильного решения, определяемого по округлённому целочисленному значению числа 3,4. Различие обнаруживается только при подробном описании хода решения, что и сделано в данной статье.

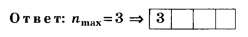
Дополнение 1. Решите вышеприведённую задачу, заменив в её условии d=2 мкм на d= 1,6 мкм. Ответ: n_max = 2.

ЦТ 2002 г. Тест 4 [5]

В5. На дифракционную решётку направляется свет от газоразрядной лампы. На экране получаются дифракционные спектры излучения лампы. Линия с длиной волны λ ₁= 510 нм в спектре четвёртого порядка совпадает с линией длины волны λ₂ в спектре третьего порядка. Чему равна λ₂ (в [нм])?

В данной задаче основной интерес представляет не решение задачи, а формулировка её условия.

При освещении дифракционной решётки немонохроматическим светом( λ₁ , λ₂ ) вполне естественно говорить (писать) о дифракционных спектрах, которых в принципе нет при освещении дифракционной решётки монохроматическим светом.

В условии задания следовало бы указать, что свет от газоразрядной лампы падает нормально на дифракционную решётку.

Кроме того, следовало бы изменить филологический стиль третьего предложения в условии задания. Режет слух оборот «линия с длиной волны λ » , его можно было бы заменить на «линия, соответствующая излучению длиной волны λ » или на более краткий — «линия, соответствующая длине волны λ » .

Формулировки тестов должны быть научно корректными и литературно безупречными. Тесты формулируют совсем не так, как исследовательские и олимпиадные задачи! В тестах всё должно быть точно, конкретно, однозначно.

С учётом приведённого уточнения условия задания имеем:

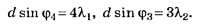
Так как по условию задания 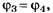то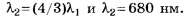

ЦТ 2002 г. Тест № 5 [5]

В5. Найдите наибольший порядок дифракционного максимума для жёлтой линии натрия с длиной волны 5,89·10 -7 м, если период дифракционной решётки равен 5 мкм.

Решение

По сравнению с заданием В5 из теста № 3 ЦТ 2002 г. данное задание сформулировано точнее, тем не менее в условии задания речь следовало бы вести не о «дифракционном максимуме», а о «главном дифракционном максимуме«.

Наряду с главными дифракционными максимумами всегда имеются ещё и вторичные дифракционные максимумы [6, с. 617, 618]. Не объясняя этого нюанса в школьном курсе физики, тем более надо строго соблюдать сложившуюся научную терминологию и вести речь только о главных дифракционных максимумах.

Кроме того, следовало бы указать, что свет падает нормально на дифракционную решётку.

С учётом вышеприведённых уточнений

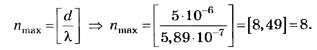
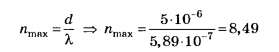
по правилам математического округления числа 8,49 до целочисленного значения опять же получаем 8. Поэтому данное задание, как и предыдущее, следует признать неудачным.

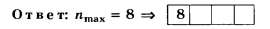
Дополнение 2. Решите вышеприведённое задание, заменив в его условии d =5 мкм на (1=А мкм. Ответ: n_max =6.)

Пособие РИКЗ 2003 г. Тест № 6 [7]

В5. Если второй дифракционный максимум находится на расстоянии 5 см от центра экрана, то при увеличении расстояния от дифракционной решётки до экрана на 20% этот дифракционный максимум будет находиться на расстоянии . см.

Условие задания сформулировано неудовлетворительно: вместо «дифракционный максимум» надо «главный дифракционный максимум», вместо «от центра экрана» — «от нулевого главного дифракционного максимума».

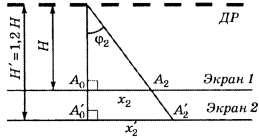
Как видно из приведённого рисунка,

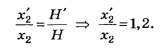
Отсюда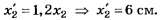

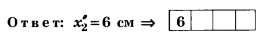
Пособие РИКЗ 2003 г. Тест № 7 [7]

В5. Определите наибольший порядок спектра в дифракционной решётке, имеющей 500 штрихов на 1 мм, при освещении её светом с длиной волны 720 нм.

Условие задания сформулировано крайне неудачно в научном отношении (см. уточнения заданий № 3 и 5 из ЦТ 2002 г.).

Есть претензии и к филологическому стилю формулировки задания. Вместо словосочетания «в дифракционной решётке» надо было бы использовать словосочетание «от дифракционной решётки», а вместо «свет с длиной волны» — «светом, длина волны которого». Длина волны — не нагрузка к волне, а её основная характеристика.

С учётом уточнений

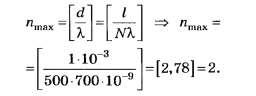
По всем трём вышеприведённым правилам округления чисел округление числа 2,78 до целочисленного значения даёт 3.

Последний факт даже при всех недостатках формулировки условия задания делает его интересным, так как позволяет на тестовом уровне различить правильное ( n_max =2) и неправильное ( n_max =3) решения.

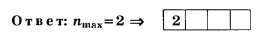
Много заданий на рассматриваемую тему содержится в ЦТ 2005 г. [8].

В условиях всех этих заданий (В1) надо добавить ключевое слово «главный» перед словосочетанием «дифракционный максимум» (см. комментарии к заданию В5 ЦТ 2002 г. Тест № 5).

К сожалению, во всех вариантах тестов В1 ЦТ 2005 г. численные значения d (l,N) и λ подобраны неудачно и всегда дают в дробях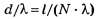

число «десятых» меньше 5, что не позволяет на тестовом уровне отличить операцию выделения целой части дроби (правильное решение) от операции округления дроби до целочисленного значения (ложный след). Это обстоятельство ставит под сомнение целесообразность использования этих заданий для объективной проверки знаний абитуриентов по рассматриваемой теме.

Похоже на то, что составители тестов увлеклись, образно говоря, приготовлением различных «гарниров к блюду», не думая об улучшении качества основной компоненты «блюда» — подборе численных значений d (l,N) и λ с целью увеличения числа «десятых» в дробях d/ λ=l/(N* λ).

ЦТ 2005 г. Вариант 4 [8]

В1. На дифракционную решётку, период которой d₁ =1,2 мкм, падает нормально параллельный пучок монохроматического света с длиной волны λ =500 нм. Если её заменить на решётку, период которой d₂ =2,2 мкм, то число максимумов увеличится на . .

Решение

Вместо «свет с длиной волны λ» надо «свет длиной волны λ » . Стиль, стиль и ещё раз стиль!

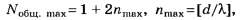
то с учётом того, что X — const, a d₂>di,

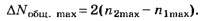
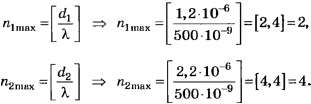
При округлении чисел 2,4 и 4,4 до целочисленных значений тоже получаем соответственно 2 и 4. По этой причине данное задание следует признать простым и даже неудачным.

Дополнение 3. Решите вышеприведённую задачу, заменив в её условии λ =500 нм на λ =433 нм (синяя линия в спектре водорода).

ЦТ 2005 г. Вариант 6

В1. На дифракционную решётку с периодом d= 2 мкм падает нормально параллельный пучок монохроматического света с длиной волны λ = 750 нм. Количество максимумов, которые можно наблюдать в пределах угла а=60°, биссектриса которого перпендикулярна плоскости решётки, равно . .

Решение

Словосочетание «света с длиной волны λ » уже обсуждалось выше в ЦТ 2005 г., вариант 4.

Второе предложение в условии данного задания можно было бы упростить и записать так: «Количество наблюдаемых главных максимумов в пределах угла а = 60°» и далее по тексту исходного задания.

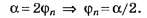
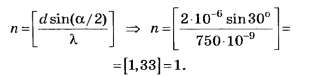
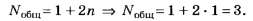
Это задание, как и предыдущее, не позволяет на тестовом уровне объективно определить уровень понимания обсуждаемой темы абитуриентами.

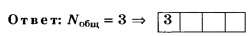
Дополнение 4. Выполните вышеприведённое задание, заменив в его условии λ =750 нм на λ = 589 нм (жёлтая линия в спектре натрия). Ответ: N_o6щ=3.

ЦТ 2005 г. Вариант 7

В1. На дифракционную решётку, имеющую N₁ — 400 штрихов на l=1 мм длины, падает параллельный пучок монохроматического света с длиной волны λ =400 нм. Если её заменить решёткой, имеющей N₂ =800 штрихов на l=1 мм длины, то количество дифракционных максимумов уменьшится на . .

Опустим обсуждение неточностей формулировки задания, так как они те же, что и в предыдущих заданиях.

Из формул (4, б), (5, б) следует, что

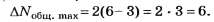
Комментарии о качестве данного задания опустим, «рука. колоть устала»!

Дополнение 5. Решите вышеприведённую задачу, заменив в её условии λ =400 нм на λ =461 нм (голубая линия в спектре стронция). Ответ: ∆ N =6.

ЦТ 2005 г. Вариант 8

В1. На дифракционную решётку с d =1 мкм падает нормально параллельный пучок монохроматического света. Если длина волны света λ =400 нм, то число максимумов, которые образует эта решётка, равно . .

Злополучное «с» уже перекочевало от «света с длиной волны» к «решётке с d=1 мкм». Появилось и новое жаргонное выражение — «число максимумов, которые образует эта решётка». Сама по себе «решётка» не образует дифракционной картины, поэтому следовало бы написать «количество главных максимумов, образованных освещённой решёткой, равно. «.

По формулам (5, б), (4, б)

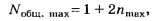
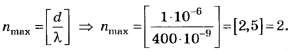
По версии округления чисел [1], [2] целочисленное значение числа 2,5 равно 3, а по версии М. Я. Выгодского [3] — 2.

В сравнении с российским заданием А32 из № 7 Тестов по физике [4], которое рассмотрено выше, данный белорусский тест является ущербным, но на фоне белорусских тестов ЦТ 2005 г. на рассматриваемую в данной статье тему он является лучшим, несмотря на неточности его формулировки.

Итак, N_{общ. max} =1+2*2=5 а по версии округления чисел [1], [2] N_{общ. max} = 1+2*3 =7 (ложный след).

Благодаря этому ложному следу, данное задание в рамках версии округления чисел [1], [2] позволяет на тестовом уровне отличить правильное решение ( N_{общ. max}= 5) от неправильного ( N_{общ. ma x} =7).

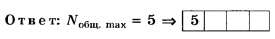
ЦТ 2008 г. Вариант 1 [9]

В12. На дифракционную решётку нормально падает параллельный пучок монохроматического света длиной волны λ =720 нм. Если период решётки d = 5 мкм, то максимальный порядок k_max дифракционного спектра . .

Решение

Задание сформулировано научно некорректно (см. условия предыдущих заданий), но численные значения величин d и λ подобраны удачно и на тестовом уровне правильное решение, определяемое по целой части числа, отличается от неправильного решения, определяемого по округлённому целочисленному значению числа d/λ

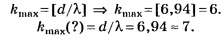
Задания В12 из других вариантов тестов ЦТ 2008 г. предлагаю читателям рассмотреть самостоятельно.

За многие годы проведения централизованных тестирований по физике так и не созданы качественные задания на определение порядка главных дифракционных максимумов при перпендикулярном освещении дифракционной решётки монохроматическим светом: то ли условия заданий были сформулированы некорректно, то ли численные значения величин d(l, N) и X были подобраны неудачно и не позволяли на тестовом уровне отличить правильное решение от неправильного.

Список использованной литературы

1. Математика: справочные материалы: кн. для учащихся / В. А. Гусев, А. Г. Мордкович. — Москва : Просвещение, 1988.

2. Математика: учеб. пособие для 4-го класса общеобр. школы с рус. яз. обуч. / Л. А. Лату-тин, В. Д. Чеботаревский; пер. с бел. яз. Т. В. Водневой. — 2-е изд. — Минск : Нар. асвета, 2002.

3. Справочник по элементарной математике. — 27-е изд., испр. / М. Я. Выгодский. — Москва : Наука, 1986.

4. Тесты по физике. 11 кл. / Центр тестирования Министерства образования России. — Москва : Просвещение, 2001.

5. Тесты. Физика. Русский язык: варианты и ответы централизованного тестирования: пособие для подготовки к тестированию / Респ. ин-т контроля знаний. — Минск : Асар, 2003.

6. Справочник по физике для инженеров и студентов вузов. — 6-е изд., испр. / Б. М. Яворский, А. А. Детлаф. — Москва : Наука, 1974.

7. Тесты: Физика. Материалы для подготовки к централизованному тестированию / Респ. ин-т контроля знаний. — Мозырь : Белый Ветер, 2003.

8. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Юнипресс, 2005.

9. Централизованное тестирование. Физика: сб. тестов / Респ. ин-т контроля знаний Мин-ва образования Респ. Беларусь. — Минск : Аверсэв, 2008.

Как найти количество максимумов дифракционной решетки

Физика

Электродинамика

Магнитное поле

Механические колебания

Электромагнитные колебания

Механические волны

Электромагнитные волны

Оптика

Геометрическая оптика

Задачи на сферическое зеркало

Линза

Волновая оптика

Основы теории относительности

Основы квантовой физики

Излучения и спектры

Световые кванты

Атомная физика

Ядерная физика

Физика элементарных частиц

Открытие позитрона. Античастицы

Современная физическая картина мира

Современная физическая картина мира

Строение Вселенной

Строение Вселенной

Звёзды и источники их энергии. Современные представления о происхождении и эволюции Солнца и звёзд

Дифракционная решетка

Рассмотрим дифракцию на одномерной дифракционной решетке, так как этот случай дифракций находит широкое применение во многих экспериментальных методах спектрального анализа.

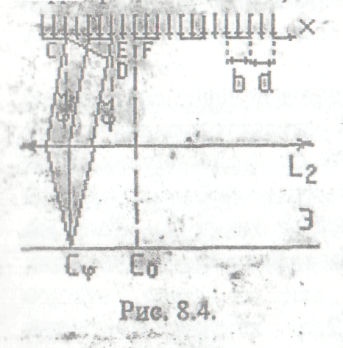Дифракционная решетка представляет собой систему большого числа одинаковых по ширине и параллельных друг другу щелей лежащих в одной плоскости и разделённых непрозрачными промежутками, равными по ширине. Дифракционная решетка изготавливается путём нанесения параллельных штрихов на поверхность стекла с помощью делительных машин. Места, прочерченные делительной машиной, рассеивают свет во все стороны и являются, таким образом, практически непрозрачными промежутками между неповрежденными частями пластинки, которые играют роль щелей. Число штрихов на 1 мм определяется областью спектра исследуемого излучения — от 300 1/мм (в инфракрасной области) до 1200 1/мм (в ультрафиолетовой).

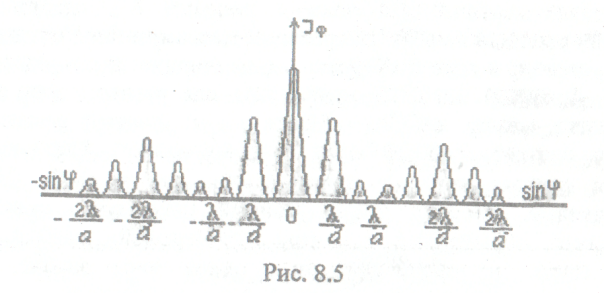Итак, имеется система из N параллельных щелей с шириной каждой щели а ирасстоянием между соседними щелями b (рис.8.4).Сумма а + b=d называется периодом или постоянной дифракционной решетки. На решетку нормально падает плоская монохроматическая волна. Требуется исследовать интенсивность света, распространяющегося в направлении, составляющем угол φ с нормалью к плоскости решетки. Кроме распределения интенсивности вследствие дифракции на каждой щели, нужно учесть интерференцию между N пучками(перераспределение световой энергии за счет интерференции волн от N щелей когерентных источников). Очевидно, что минимумы будут находиться на прежних местах, ибо условие минимума дифракции для всех щелей (рис.8.5) одинаково. Эти минимумы называются главными. Условие главных минимумов asinφ=±kλ совпадает с условием (8.8).

Положение главных минимумов sinφ=±λ/a, 2λ/a,… показано на рис. 8.5. Однако в случае многих щелей к главным минимумам, создаваемым каждой щелью в отдельности, добавляются минимумы возникающие в результате интерференции света, прошедшего через различные щели. Появляются добавочные минимумы в областях дифракционных максимумов. Внешне это проявляется в том, что широкие полосы, даваемые одной узкой щелью, покрываются рядом более тонких полос вызванных интерференцией лучей,исходящих от разных щелей: первой и второй, первой и третьей и т.д. Чем больше щелей, тем больше добавочных минимумов может возникнуть. Так как общий световой поток остается неизменным, происходит усиление световых потоков около направлений,удовлетворяющих условиям усиления при интерференции от разных щелей, за счет уменьшения световой энергии в других направлениях. На рис. 8.5 для, примера показано распределение интенсивности и расположение максимумов и минимумов в случае двух щелей с периодом d и шириной щели а.

В одном и том же направлении все щели излучают совершенно одинаково. Амплитуды колебаний одинаковы. И результат интерференции зависит от разности фаз Колебаний, исходящих от сходственных точек соседних щелей (например C и E,B и F),илиотоптической разности хода EDот сходственных точек двух соседних щелей до точки С_φ. Для всех сходственных точек эта разность хода одинакова. Если ЕD=±kλ или, так как ED =dsinφ,

колебания соседних щелей взаимно усиливают друг друга, и в точке С_φ фокальной плоскости линзы наблюдается максимум дифракции. Амплитуда суммарного колебания в этих точках экрана максимальна:

где А_φ— амплитуда колебания, посылаемого одной щелью под углом; φ интенсивность

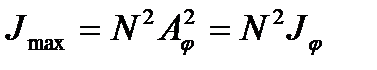(8.9)

Поэтому формула (8.9) определяет положение главных максимумов интенсивности. Число kдает порядок главного максимума.

Положение главных максимумов (8.9) определяется соотношением

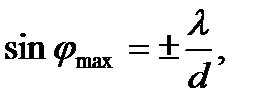
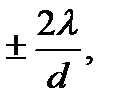
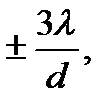… (8.10)

Максимум нулевого порядка один и расположен в точке С₀, максимумов первого, второго и т.д. порядков по два, и расположены они симметрично относительно С₀, на что указывает знак ±. На рис.8.5 показано положение главных максимумов.

Кроме главных максимумов, имеется большое число более слабых побочных максимумов, разделенных добавочными минимумами. Побочные максимумы значительно слабее главных. Расчет показывает, что интенсивность побочных максимумов не превышает 1/23 интенсивности ближайшего главного максимума.

В главных максимумах амплитуда в N раз, а интенсивность в N 2 раз больше, чем дает в соответствующем, месте одна щель. Это увеличение максимумов происходит за счет того, что отдельные яркие главные максимумы разделены темными областями добавочных минимумов и очень слабых побочных максимумов (пропорционально 1/N, которые становятся более узкими (тонкими и яркими). Такие яркие линии, четко локализованные в пространстве, легко обнаруживаются и могут быть использованы в целях спектроскопических исследований.

По мере удаления от центра экрана, интенсивность дифракционных максимумов убывает (увеличивается расстояние от источников). Поэтому не удается наблюдать все возможные дифракционные максимумы. Заметим, что количество дифракционных максимумов, даваемых решеткой по одну сторону экрана, определяется условием |sinφ| ≤ 1 (φ=π/2 —максимальный угол дифракций), откуда с учетом (8.7)

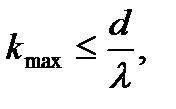(8.11)

При этом не следует забывать, что k — целое число.

Положение главных максимумов зависит от длины волны λ. Поэтому при освещении дифракционной решетки белым светом все максимумы, кроме центрального (k=0), разложатся в спектр, обращенный фиолетовым концом к центру дифракционной картины. Таким образом, дифракционная решетка может служить для исследования спектрального состава света, т.е. для определения частот (или длин волн) и интенсивности всех его монохроматических компонент. Применяемые для этого приборы называются дифракционными спектрографами, если исследуемый спектр регистрируется с помощью фотопластинки, и дифракционными спектроскопами, если спектр наблюдается визуально.