Какой алгоритм для поиска максимума в случайном массиве использовать? В статье собрано 5 эффективных must-have алгоритмов.
Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:
- углубишься в решение практических задач;
- узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.
Ты также будешь на связи с преподавателем и другими студентами.
В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂
Интересно, хочу попробовать
Самый быстрый и простейший алгоритм
Следует пояснить, что под “быстротой” алгоритма будет подразумеваться его асимптотическая сложность, а не физическое время выполнения.
В действительности, единственный способ точно найти самое большое число в случайном массиве будет перебор каждого числа в поисках максимума. Поэтому сложность такого алгоритма – O(N). Они называются линейными.
Простейшая реализация алгоритма на С:
#include <stdio.h>
int main()
{
int array[100];
int maximum, size, index = 0;
printf("Введите длину массива (не больше 100)n");
scanf("%d", &size);
printf("Введите %d целых чисел массиваn", size);
for (int i = 0; i < size; i++)
scanf("%d", &array[i]);
maximum = array[0]; // За изначальный максимум берем первый элемент массива
for (int i = 1; i < size; i++)
{
if (array[i] > maximum)
{
maximum = array[i];
index = i;
}
}
printf("Максимум находится в позиции %d и его значение %d.n", index, maximum);
return 0;
}
А как насчет распараллеливания?
После прочтения абзаца выше многие могут предложить поиск максимума с помощью параллельных вычислений, потому что он будет быстрее. И это так, если мы говорим о физическом времени. Но несмотря на то, сколько у вас есть процессов, вам всё равно придется просмотреть каждый элемент массива. Сложность алгоритма остается такой же, O(N).
Рассмотрим ситуацию на примере. Есть 200 карточек, на каждой из которых случайное число. Ваша задача найти карточку с самым большим числом. Допустим, друг согласился помочь, забрав половину карточек. Теперь каждый из вас ищет максимум из 100 карточек, вместо 200. Как только вы оба закончите, останется сравнить максимумы обеих половин. Время сократилось вдвое, но просмотреть пришлось все 200 карточек.
Сама по себе задача является так называемой чрезвычайно параллельной задачей, что ещё раз подтверждает возможность её решения именно распараллеливанием, без ущерба для конечного результата.
Задача о разборчивой невесте
Есть ещё один вариант нахождения максимума в случайном массиве.
Идем по первой половине всех значений в массиве. Запоминаем самое большое. Назовём его Х. Далее проходим по второй половине. Когда (и если) находим значение, которое больше Х, останавливаемся. Обозначим его Y. Какова вероятность того, что Y – максимум в массиве?
Чтобы это утверждение было истинным, Y должно находиться во второй половине массива. А так как значения в массиве случайны, шанс такого = 50%. Тогда если второй максимум присутствует в первой половине, это гарантирует, что найден правильный максимум.
Вероятность, что второй максимум в первой половине также = 50%. Посему вероятность, что и второй максимум в первой половине, и первый максимум во второй половине, равна 25%.
В итоге, такой алгоритм гарантирует точность 25% в нахождении максимума в массиве случайных чисел. Можно улучшить алгоритм, если искать второй максимум не в первой половине (1/2), а в 1/e (основание натурального логарифма) части массива. Этот способ впервые был предложен для решения задачи о разборчивой невесте или задачи секретаря (The Secretary Problem).
Аналоговый алгоритм
Спагетти-сортировка – прекрасный аналоговый алгоритм для решения задачи нахождения максимума в массиве.
Представим, что в массиве только N целых чисел. Возьмите N не приготовленных палочек спагетти, длина каждой сопоставляется с единственным значением в массиве.
Соберите спагетти в руку. Аккуратно, чтобы не сломать, поставьте горсть на ровную поверхность. В результате выше всех будет видна самая длинная (максимум) соломинка.
Асимптотическая сложность такого алгоритма – O(1). Но в цифровом мире он не применим.
Квантовый алгоритм
Алгоритм Гровера (или схема Гровера) используется в квантовых вычислениях для решения задач перебора. С его помощью сложность поиска максимума уменьшается до O(sqrt(N)) (большая О от корня N).
Данный способ решения может быть применен только на квантовом компьютере, что сильно умаляет его полезность в современном мире, но его нельзя не упомянуть.
Источник
Хотите дополнить? Ждём ваши предложения в комментариях 😉
13.1. Поиск максимального (минимального) элемента в массиве
|
Очень часто для решения задачи требуется находить не заданный элемент массива, а максимальный (наибольший) или минимальный (наименьший) элемент. Рассмотрим задачу нахождения максимального элемента. Если в массиве один-единственный элемент, то он и есть максимальный. Если элементов больше одного, то максимальным в массиве из i элементов является максимум из a[i] и максимального среди первых i – 1 элементов. Находить максимум будем последовательно, сравнивая текущий элемент с максимумом, найденным на предыдущем шаге. Если текущий элемент больше, то значение максимума, найденное на предыдущем шаге, нужно обновить (пример 13.1). Данный алгоритм находит значение максимального элемента, но не позволяет определить, на каком месте в массиве расположен этот максимальный элемент. Будем использовать переменную n_max для хранения индекса максимального элемента. Значение переменной n_max будет изменятся тогда, когда изменяется значение максимального элемента (пример 13.2). Если в массиве несколько элементов имеют максимальное значение, то значением переменной n_max будет индекс первого из них. Если использовать условие a[i] >= max, то переменная n_max будет хранить индекс последнего из максимальных элементов. Если известен индекс i элемента массива, то значение этого элемента можно получить, обратившись к элементу по индексу: a[i]. Поэтому при поиске максимального элемента достаточно хранить только его индекс n_max. Значение максимального элемента — a[n_max] (пример 13.3). Поиск минимального элемента осуществляется аналогично. В программе достаточно заменить знак > в условии оператора ветвления на знак < (пример 13.4). Имя переменной для хранения номера минимального элемента — n_min. |
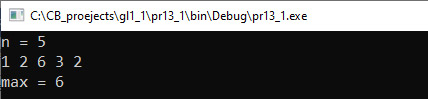
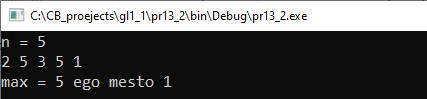
Пример 13.1. V. Программа: #include <iostream> #include <vector> using namespace std; int main() { int n; cout << “n = “; cin >> n; vector <int> a(n); for (int i = 0; i < n; i++) cin >> a[i]; //поиск максимального элемента int Max = a[0]; for (int i = 1; i < n; i++) if (a[i] > Max) Max = a[i]; cout << “max = “ << Max; cout << endl; return 0; } VI. Тестирование. Пример 13.2. V. Программа: #include <iostream> #include <vector> using namespace std; int main() { int n; cout << “n = “; cin >> n; vector <int> a(n); for (int i = 0; i < n; i++) cin >> a[i]; //поиск максимального элемента int Max = a[0], n_max = 0; for (int i = 1; i < n; i++) if (a[i] > Max){ Max = a[i]; n_max = i; } cout << “max = “ << Max; cout << ” ego mesto “ << n_max; cout << endl; return 0; } VI. Тестирование. Пример 13.3. Фрагмент программы: int n_max = 0; for (int i = 1; i < n; i++) if (a[i] > a[n_max]) n_max = i; cout << “max = “ << a[n_max]; cout << ” ego mesto “ << n_max; Пример 13.4. Фрагмент программы: int n_min = 0; for (int i = 1; i < n; i++) if (a[i] < a[n_min]) n_min = i; |
13.2. Решение задач с использованием алгоритма поиска максимального (минимального) элементов
|
Пример 13.5. В массиве хранится информация о результатах спортсменов, участвовавших в лыжной гонке. Определить результат победителя и его номер. Данные прочитать из текстового файла. Этапы выполнения задания I. Исходные данные: массив a — числа, являющиеся временем прохождения трассы, количество спортсменов — n. II. Результат: a[n_min] — минимальное время, n_min — номер победителя. III. Алгоритм решения задачи. 1. Ввод исходных данных. IV. Описание переменных: n, n_min – int, а – vector <double>. Пример 13.6. Определить, сколько раз в линейном массиве встречается элемент, равный минимальному. Этапы выполнения задания I. Исходные данные: массив а, количество чисел n. II. Результат: a[n_min] — минимальный элемент, k — количество минимальных. III. Алгоритм решения задачи. 1. Ввод исходных данных. IV. Описание переменных: n, n_min, k — int, а – vector <int>. Пример 13.7. Задан массив из слов. Найти в нем самое длинное и самое короткое слово. Этапы выполнения задания I. Исходные данные: массив а, количество cлов n. II. Результат: a[n_min] — короткое слово, a[n_max] — длинное слово. III. Алгоритм решения задачи. 1. Ввод исходных данных. IV. Описание переменных: n, n_min, n_max – int, а – vector <string>. [1] Сравнение строк осуществляется лексикографически: s1 < s2, если для первого несовпадающего символа с номером i верно, что s1[i] < s2[i], или все символы строк совпадают, но s1 короче s2. |
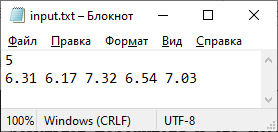
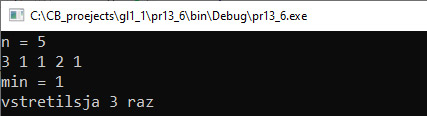
Пример 13.5. V. Программа: #include <iostream> #include <fstream> #include <vector> using namespace std; int main() { setlocale(0,“”); ifstream fin(“input.txt”); int n; fin >> n; vector <double> a(n); for (int i = 0; i < n; i++) fin >> a[i]; //поиск минимального элемента int n_min = 0; for (int i = 1; i < n; i++) if (a[i] < a[n_min]) n_min = i; cout << “победитель — лыжник №”; cout << n_min + 1 << endl; cout << “его время – “<< a[n_min]; cout << endl; return 0; } IV. Тестирование. Пример 13.6. V. Программа: #include <iostream> #include <vector> using namespace std; int main() { int n; cout << “n = “; cin >> n; vector <int> a(n); for (int i = 0; i < n; i++) cin >> a[i]; //поиск минимального элемента int n_min = 0; for (int i = 1; i < n; i++) if (a[i] < a[n_min]) n_min = i; //подсчет количества int k = 0; for (int i = 0; i < n; i++) if (a[i] == a[n_min]) k++; cout << “min = “<< a[n_min]; cout << endl << “vstretilsja “; cout << k << ” raz” << endl; return 0; } VI. Тестирование. Пример 13.7. V. Программа: #include <iostream> #include <vector> #include <string> using namespace std; using namespace std::__cxx11; int main() { int n; cout << “n = “; cin >> n; vector <string> a(n); for (int i = 0; i < n; i++) cin >> a[i]; //поиск минимального слова int n_min = 0; for (int i = 1; i < n; i++) if (a[i].length() < a[n_min].length()) n_min = i; //поиск максимального слова int n_max = 0; for (int i = 1; i < n; i++) if (a[i].length() > a[n_max].length()) n_max = i; cout << “min – “<< a[n_min]; cout << “, max – “<< a[n_max]; cout << endl; return 0; } VI. Тестирование. |
Вопросы к параграфу
 |
1. Какой элемент массива является максимальным? Какой минимальным? 2. Как найти максимальный элемент в массиве? 3. Как найти минимальный элемент? 4. Каким образом определить номер первого элемента, равного максимальному? 5. Как определить номер последнего элемента, равного минимальному? |
Упражнения


1. Измените программы из примеров 13.1 и 13.2 так, чтобы находился минимальный элемент в массиве.
2. Для примера 13.5 выполните перечисленные задания.
1. Найдите номер спортсмена, пришедшего на финиш последним.
2. Определите, был ли победитель единственным или есть еще лыжник, прошедший трассу с таким же результатом (см. пример 13.6).
3. Добавьте еще один массив и введите в него фамилии спортсменов. Реализуйте пункты 1 и 2 так, чтобы выводилась фамилия, а не номер (см. пример 12.9).
3. Напишите программу, которая заменит в массиве нулями все элементы, равные минимальному.
4. Напишите программу, которая заменит в массиве нулями все элементы, стоящие перед максимальным. Предполагается, что в массиве единственный максимальный элемент.
5. Напишите программу, которая заменит нулями все элементы в массиве, стоящие после минимального. Если минимальных элементов несколько, то заменять нужно элементы, стоящие после последнего минимального.
6. Напишите программу, которая определит, какой из элементов — минимальный или максимальный — встречается в массиве раньше (имеет меньший индекс).
7. Напишите программу, которая определит, какой из элементов — минимальный или максимальный — встречается в массиве чаще.
8. Напишите программу, которая запишет в новый массив те элементы из исходного, которые расположены между минимальным или максимальным (по индексам).
9. В массиве хранится информация о стоимости автомобилей. Определите стоимость самого дорогого автомобиля и его номер в массиве. Если есть несколько таких автомобилей, то выведите все номера.
10. В массиве хранится информация о среднесуточной температуре декабря. Определите, сколько в декабре было дней с самой низкой и с самой высокой температурой.
11. Размеры n прямоугольников хранятся в двух массивах (длина и ширина). Найдите прямоугольник с минимальным периметром. (Вывести номер прямоугольника и значение периметра.)
12. Известны данные о массе (в кг) и объеме (в см3) n предметов, изготовленных из различных материалов. Найдите предметы с минимальной и максимальной плотностями. Вывести номер предмета и значение плотности.
13. Задан массив из слов. Найдите в нем самое длинное слово, заканчивающееся буквой «а».
14. Задан массив из слов. Найдите в нем самое короткое слово, начинающееся с заглавной буквы.
15. Задан массив из слов. Найдите в нем слово, в котором максимальное количество гласных букв. Если таких слов несколько, выведите все.
16. Задан массив из слов. Найдите в нем слово, в котором минимальное количество согласных букв. Если таких слов несколько, то выведите самое длинное из них.
Без сортировки задача может быть решена, например, так. Создаем рабочий массив длины m и заполняем его начальными значениями. В общем случае можно в качестве такого значения выбрать минимальное значение int/integer для соответствующей среды программирования. А если известна нижняя граница значений исходного массива, то можно взять любое число, меньшее этой границы.
Итак рабочий массив заполнен одинаковыми значениями. Теперь берем элемент за элементом исходного массива и вставляем его в нужное место рабочего массива. При этом длину рабочего массива сохраняем равной m (после вставки последний элемент пропадает). Если очередной элемент меньше последнего значения рабочего массива, то он просто пропускается. Этот процесс имеет вычислительную сложность O(nm). Тогда как сортировка в лучшем случае описывается асимптотикой O(n*og(n)). Асимптотики показывают, как ведет себя функция (в данном случае – время сортировки) при стремлении параметров к бесконечности. Можно сказать, что время описанного алгоритма при стремлении n к бесконечности задается формулой t1=k1*O(n), а время сортировки t2=k2*O(n*log(n)). Здесь k1 и k2 – некие константы, зависящие от процессора, языка программирования, операционной системы и других факторов.
Я построил три системы тестов (для Питона, Java и VBA). Все тесты устроены по сути одинаково: строились массивы возрастающих размеров, заполнялись случайными числами задаваемого диапазона, сортировались с фиксацией времени и прогонялись через описанный выше алгоритм тоже с фиксацией времени. Каждый тест повторялся 10 раз и время усреднялось. В Питоне и Java использовалась встроенная сортировка, в VBA – реализация QuickSort.
Питон
Ниже показан код питоновских тестов.
import time
from random import randint
def max_n_1(arr,n):
return sorted(arr,reverse=True)[0:n]
def max_n_2(arr,n):
res=[-1 for _ in range(n)]
for x in arr:
if x > res[n-1]:
i=n-1
j=i-1
while(j>=0 and res[j]<x):
res[i]=res[j]
i=i-1
j=j-1
res[i]=x
return res
def start():
k=10
n=10000
print("k=",k)
while(n<=500000):
print("n=",n,end=' ')
t1=0.0
for i in range(10):
arr=[randint(1,2000) for _ in range(n)]
start_time = time.time()
z1=max_n_1(arr,k)
fin_time = time.time()
t1=t1+(fin_time-start_time)
print(t1/10.0,end=' ')
t2=0.0
for i in range(10):
arr=[randint(1,2000) for _ in range(n)]
start_time = time.time()
z2=max_n_2(arr,k)
fin_time = time.time()
t2=t2+(fin_time-start_time)
print(t2/10.0)
n+=10000
start()
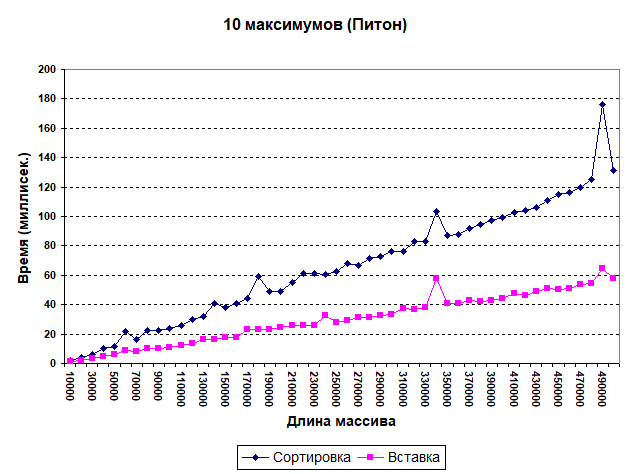
Размеры массива менялись от 10 до 500 тыс. элементов с шагом 10 тыс. Было выполнено два прогона: определение пяти и десяти максимумов. Результат для 10 максимумов показан ниже.
Время здесь приведено в миллисекундах. Что видим? Сортировка отстает (на краю интервала – вдвое). Для пяти максимумов картина аналогична. И надо заметить, что хотя питоновская сортировка очень эффективна, простой алгоритм оказывается быстрее. Заметны резкие провалы в производительности (зубцы на графиках). Они, вероятно, объясняются влиянием внутренних процессов (типа сборки мусора). Это же замечание относится и к другим графикам.
Java
Код тестов выглядел так:
import java.util.*;
class Start
{
public static void main(String [] args)
{
Random random = new Random();
Scanner inp = new Scanner(System.in);
long startTime,endTime,tot1,tot2;
int i,a,b,n,m,x,ii,jj,u;
a=1;
b=3000; // диапазон случайных чисел [a,b]
m=10;
System.out.println(a+" "+b+" "+m);
for (n=50000; n<=5000000; n+=50000)
{
int arr[] = new int[n];
int ma[] = new int[m];
tot1=0;
for (u=0; u<10; u++)
{
for (i=0; i<n; i++)
{
arr[i]=a+random.nextInt(b-a+1);
}
startTime = System.currentTimeMillis();
Arrays.sort(arr);
endTime = System.currentTimeMillis();
tot1=tot1+(endTime-startTime);
}
tot2=0;
for (u=0; u<10; u++)
{
for (i=0; i<n; i++)
{
arr[i]=a+random.nextInt(b-a+1);
}
startTime = System.currentTimeMillis();
for (i=0; i<m; i++) ma[i]=-999999;
for (i=0; i<n; i++)
{
x=arr[i];
if (x >= ma[m-1])
{
ii=m-1;
jj=ii-1;
while(jj>=0 && ma[jj]<x)
{
ma[ii]=ma[jj];
ii--;
jj--;
}
ma[ii]=x;
}
}
endTime = System.currentTimeMillis();
tot2=tot2+(endTime-startTime);
}
System.out.println(n+" "+tot1+" "+tot2);
}
}
}Здесь размер массива тоже менялся от 10 тыс. до 500 тыс. элементов. Время – в миллисекундах. Результат оказался весьма похожим на питоновский (только сортировка Javа, увы, медленнее).
VBA
В этом языке нет универсальной встроенной сортировки (можно, правда, сортировать ячейки листа, но в этом случае будут велики накладные расходы, связанные с загрузкой и выгрузкой данных). Поэтому пришлось реализовать QuickSort вручную. Все это выглядит так:
Private Declare Function GetTickCount Lib "kernel32" () As Long
'::: Собственно сортировка
Sub QSort(A() As Long, Optional b As Long = 1, Optional e As Long = 0)
If b > e Then Exit Sub
i& = b
j& = e
w& = A((i& + j&) / 2)
Do While (True)
Do While (A(i&) < w&)
i& = i& + 1
Loop
Do While (A(j&) > w&)
j& = j& - 1
Loop
If i& <= j& Then
Tmp& = A(i&)
A(i&) = A(j&)
A(j&) = Tmp&
i& = i& + 1
j& = j& - 1
End If
If i& > j& Then Exit Do
Loop
If j& > b Then QSort A, b, j&
If i& < e Then QSort A, i&, e
End Sub
'::: Проверка успешности сортировки
Function check(X() As Long) As Boolean
n& = UBound(X)
For i& = 1 To n& - 1
If X(i& + 1) < X(i&) Then
Debug.Print "Err! i=" + CStr(i&)
check = False
Exit Function
End If
Next i&
check = True
End Function
'::: Вставка в упорядоченный массив
Sub ins_in_arr(X As Long, A() As Long, n As Integer)
If X < A(n) Then Exit Sub
For i% = 1 To n
If X > A(i%) Then
For j% = n To i% + 1 Step -1
A(j%) = A(j% - 1)
Next j%
A(i%) = X
Exit Sub
End If
Next i%
End Sub
'::: Собственно тест
Sub test()
Const sz = 500
Dim X() As Long
Dim Ma(1 To sz) As Long
Randomize
ooo& = 1
For n& = 10000 To 500000 Step 10000
t1# = 0
For nc% = 1 To 10
ReDim X(1 To n&) As Long
For i& = 1 To n&
X(i&) = Rnd() * 5000
Next i&
s1& = GetTickCount
For i& = 1 To sz
Ma(i&) = -2147483647
Next i&
For i& = 1 To n&
ins_in_arr X(i&), Ma, 10
Next i&
s2& = GetTickCount
t1# = t1# + s2& - s1&
Next nc%
Cells(ooo&, 1).Value = n&
Cells(ooo&, 2).Value = t1# / 10
t2# = 0
For nc% = 1 To 10
ReDim X(1 To n&) As Long
For i& = 1 To n&
X(i&) = Rnd() * 5000
Next i&
s1& = GetTickCount
QSort X, 1, n&
s2& = GetTickCount
If Not check(X) Then
MsgBox "Ошибка при сортировке!"
Exit Sub
End If
t2# = t2# + s2& - s1&
Next nc%
Cells(ooo&, 3).Value = t2# / 10
ooo& = ooo& + 1
Next n&
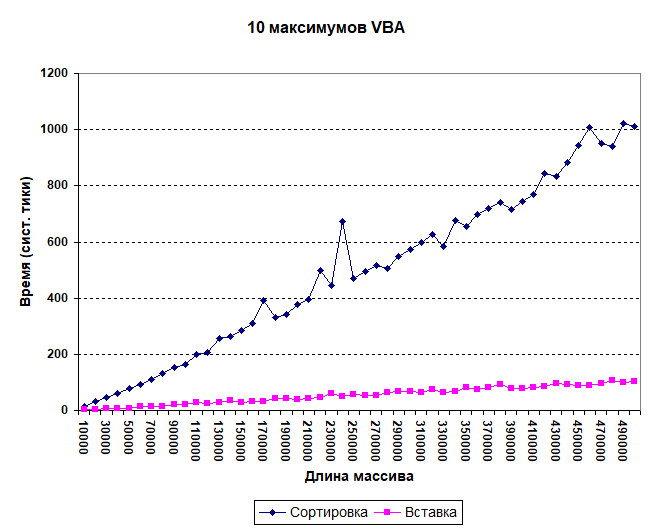
End SubНа каждом витке цикла корректность сортировки проверяется. Время проверки, естественно, не включается в общий хронометраж. Набор исходных данных тот же – от 10 до 500 тыс. целых чисел. Получает, в общем, похожая картина:
Представляет некоторый интерес изучить зависимость времени от количества искомых максимумов (при фиксированном размере массива). Здесь, очевидно, сортировка будет тем выгоднее, чем больше максимумов требуется найти. А вставка в упорядоченный массив будет тем медленнее, чем массив больше.
Самым невыгодным случаем будет являться, как ни странно, входной массив, уже упорядоченный по возрастанию. В этом случае количество сравнений при вставке достигнет максимума и будет равно n*m. Массив, упорядоченный по убыванию, напротив, весьма выгоден. Число сравнений здесь будет ~ m+n.
Описанный в самом начале статьи алгоритм, можно ускорить, если вместо простого упорядоченного массива использовать древовидную или пирамидальную структуру. Именно так и реализована в Питоне в модуле heapq функция nsmallest.
Для небольших массивов (несколько тысяч элементов и менее) разница в подходах представляется несущественной. И если нужно быстро написать код, то сортировка – вполне приемлемое решение. Для больших массивов выгоднее от сортировки отказаться.
Вот и все, что я хотел рассказать об этой задаче. Спасибо, что дочитали до конца. С наступившим 2021-м годом!
В информатике алгоритм выбора — это алгоритм для нахождения k-го по величине элемента в массиве (такой элемент называется k-й порядковой статистикой). Частными случаями этого алгоритма являются нахождение минимального элемента, максимального элемента и медианы. Существует алгоритм, который гарантированно решает задачу выбора k-го по величине элемента за O(n).
Выбор с помощью сортировки[править | править код]
Задачу выбора можно свести к сортировке. В самом деле, можно упорядочить массив, а затем взять нужный по счету элемент. Это эффективно в том случае, когда выбор нужно делать многократно: тогда можно отсортировать массив за O(n log n) и затем выбирать из него элементы. Однако если выбор нужно произвести однократно, данный алгоритм может оказаться неоправданно долгим.
Линейный алгоритм для нахождения минимума (максимума)[править | править код]
Очевидно, как за линейное время найти минимум (максимум) в данном массиве:
Линейный в среднем алгоритм для нахождения k-й порядковой статистики[править | править код]
Существует алгоритм для нахождения k-й порядковой статистики, основанный на алгоритме быстрой сортировки и работающий за O(n) в среднем.
Идея алгоритма заключается в том, что массив разбивается на две части относительно случайно (равновероятно) выбранного элемента — в одну часть попадают элементы, меньшие, чем выбранный, в другую — остальные (эта операция выполняется за 







Алгоритм BFPRT (линейный детерминированный)[править | править код]
BFPRT-Алгоритм позволяет найти k-ю порядковую статистику гарантированно за O(n). Назван в честь своих изобретателей: Manual Blum, Robert W. Floyd, Vaughan R. Pratt, Ronald L. Rivest и Robert Endre Tarjan. Используется при достаточно длинном списке элементов, свыше 800 элементов.
Принцип действия[править | править код]
Ввод: число 

- Список делится на подмножества элементов, по 5 элементов в каждом (кроме последнего подмножества). Число элементов в подмножествах может превышать 5 и должно быть в любом случае нечётным. Однако если делить список на подмножества из 3 элементов, время работы не будет линейным.
- Каждое подмножество сортируется с помощью подходящего алгоритма сортировки.
- Пусть
— множество медиан, образовавшихся в подмножествах после сортировки. Рекурсивно находится медиана в
— медиана медиан. Назовем её
.
- Результирующая после 3 шага структура, имеет следующую особенность:
- Теперь список разбивается относительно медианы s на 2 подмножества
и
. При этом нужно сравнить с s только половину всех элементов, так как две четверти элементов уже отсортированы относительно s. В результате каждое из подмножеств
и
содержит максимально 3/4 всех элементов (минимально — 1/4 всех элементов).
- Если:
Гарантированное время работы[править | править код]
При каждом рекурсивном вызове, алгоритм позволяет отбросить минимум четверть всех элементов. Это обеспечивает верхнюю оценку на гарантированное линейное время работы для детерминированного алгоритма, так как оно выражается рекуррентным соотношением 


Литература[править | править код]
- Volker Heun. Основные Алгоритмы = Grundlegende Algorithmen. — 1-е изд. — Мюнхен: Vieweg Verlag, 2000. — С. 86. — ISBN 3-528-03140-9.
- Time Bounds for Selection by Manual Blum, Robert W. Floyd, Vaughan Pratt, Ronald L. Rivest, and Robert E. Tarjan. Journal of Computer and System Sciences 7,4 August 1973, 448—460 (англ.)
The theoretical answers from everyone else are all neat, but let’s be pragmatic. ActionScript provides the tools you need so that you don’t even have to write a loop in this case!
First, note that Math.min() and Math.max() can take any number of arguments. Also, it’s important to understand the apply() method available to Function objects. It allows you to pass arguments to the function using an Array. Let’s take advantage of both:
var myArray:Array = [2,3,3,4,2,2,5,6,7,2];
var maxValue:Number = Math.max.apply(null, myArray);
var minValue:Number = Math.min.apply(null, myArray);
Here’s the best part: the “loop” is actually run using native code (inside Flash Player), so it’s faster than searching for the minimum or maximum value using a pure ActionScript loop.
answered Jan 8, 2009 at 23:51
Josh TynjalaJosh Tynjala
5,2253 gold badges23 silver badges25 bronze badges
4
There isn’t any reliable way to get the minimum/maximum without testing every value. You don’t want to try a sort or anything like that, walking through the array is O(n), which is better than any sort algorithm can do in the general case.
answered Jan 8, 2009 at 16:00
Adam BellaireAdam Bellaire
107k19 gold badges148 silver badges163 bronze badges
If
- The array is not sorted
- Finding the min and max is done simultaneously
Then there is an algorithm that finds the min and max in 3n/2 number of comparisons. What one needs to do is process the elements of the array in pairs. The larger of the pair should be compared with the current max and the smaller of the pair should be compared with the current min. Also, one needs take special care if the array contains odd number of elements.
In c++ code (borrowing some code from Mehrdad).
struct MinMax{
int Min,Max;
}
MinMax FindMinMax(int[] array, int start, int end) {
MinMax min_max;
int index;
int n = end - start + 1;//n: the number of elements to be sorted, assuming n>0
if ( n%2 != 0 ){// if n is odd
min_max.Min = array[start];
min_max.Max = array[start];
index = start + 1;
}
else{// n is even
if ( array[start] < array[start+1] ){
min_max.Min = array[start];
min_max.Max = array[start+1];
}
else{
min_max.Min = array[start+1];
min_max.Max = array[start];
}
index = start + 2;
}
int big, small;
for ( int i = index; i < n-1; i = i+2 ){
if ( array[i] < array[i+1] ){ //one comparison
small = array[i];
big = array[i+1];
}
else{
small = array[i+1];
big = array[i];
}
if ( min_max.Min > small ){ //one comparison
min_max.Min = small;
}
if ( min_max.Max < big ){ //one comparison
min_max.Max = big;
}
}
return min_max;
}
It’s very easy to see that the number of comparisons it takes is 3n/2. The loop runs n/2 times and in each iteration 3 comparisons are performed. This is probably the optimum one can achieve. At this moment, I cannot point to a definite source of that. (But, I think I have seen a proof of that somewhere.)
The recursive solution given by Mehrdad above, probably also achieves this minimal number of comparisons (the last line needs to be changed). But with the same number of comparisons an iterative solution will always beat a recursive solution due to overhead in the function call as he mentioned. However, if one only cares about finding min and max of a few numbers (as Eric Belair does), no one will notice any difference in todays computer with any of the approaches above. For a large array, the difference could be significant.
Though this solution and the solution given by Matthew Brubaker has O(n) complexity, in practice one should carefully asses the hidden constants involved. The number of comparisons in his solution is 2n. The speedup gained with the solution with 3n/2 comparisons as opposed to 2n comparisons would be noticeable.
answered Jul 26, 2009 at 7:41
2
Unless the array is sorted, that’s the best you’re going to get. If it is sorted, just take the first and last elements.
Of course, if it’s not sorted, then sorting first and grabbing the first and last is guaranteed to be less efficient than just looping through once. Even the best sorting algorithms have to look at each element more than once (an average of O(log N) times for each element. That’s O(N*Log N) total. A simple scan once through is only O(N).
If you are wanting quick access to the largest element in a data structure, take a look at heaps for an efficient way to keep objects in some sort of order.
answered Jan 8, 2009 at 16:10
EclipseEclipse
44.6k20 gold badges112 silver badges170 bronze badges
9
You have to loop through the array, no other way to check all elements. Just one correction for the code – if all elements are negative, maxValue will be 0 at the end. You should initialize it with the minimum possible value for integer.
And if you are going to search the array many times it’s a good idea to sort it first, than searching is faster (binary search) and minimum and maximum elements are just the first and the last.
answered Jan 8, 2009 at 16:03
1
Depends on what you call “best.” From a theoretical point of view, you cannot solve the problem in less than O(n) in a deterministic Turing machine.
The naive algorithm is too loop and update min, max. However, a recursive solution will require less comparisons than naive algorithm, if you want to get min, max simultaneously (it isn’t necessarily faster due to function call overhead).
struct MinMax{
public int Min,Max;
}
MinMax FindMinMax(int[] array, int start, int end) {
if (start == end)
return new MinMax { Min = array[start], Max = array[start] };
if (start == end - 1)
return new MinMax { Min = Math.Min(array[start], array[end]), Max = Math.Max(array[start], array[end]) } ;
MinMax res1 = FindMinMax(array, start, (start + end)/2);
MinMax res2 = FindMinMax(array, (start+end)/2+1, end);
return new MinMax { Min = Math.Min(res1.Min, res2.Min), Max = Math.Max(res1.Max, res2.Max) } ;
}
The simplest solution would be to sort and get the first and last item, though it’s obviously not the fastest 😉
The best solution, performance-wise, to find the minimum or maximum is the naive algorithm you written (with a single loop).
answered Jan 8, 2009 at 16:06
Mehrdad AfshariMehrdad Afshari
413k90 gold badges850 silver badges788 bronze badges
9
Math.max() is actually as3 code compiled to AVM2 opcodes, and as such is not more “native” than any other as3 code. As a consequence, it is not necessarily the fastest implementation.
Actually, given that it works on Array type, it is slower than carefully written code usign Vector:
I did a quick benchmark comparison of several naive Vector and Array implementations of Math.max, using gskinner’s PerformanceTest (Vector and Array being filled with identical random Numbers).
The fastest Vector implementation appeared to be more than 3x faster than Math.max with recent AIR SDK/release player (flash player WIN 14,0,0,122 RELEASE, compiled with AIR SDK 14):
average 3.5 ms for 1,000,000 values, compared to Math.max() average of 11ms :
function max(values:Vector.<Number>):Number
{
var max:Number = Number.MIN_VALUE;
var length:uint = values.length;
for (var i:uint = 0; i < length ; ++i)
if (values[i] > max)
max = values[i];
return max;
}
Conclusion is that if you are concerned by performance, you should use Vector over Array anywhere you can in the first place, and not always rely on default implementations, especially when they force the use of Array
PS:same implementation with a for each() loop is 12x slower …!
answered Aug 27, 2014 at 13:47
jaubouxjauboux
8886 silver badges12 bronze badges
This depends on real world application requirements.
If your question is merely hypothetical, then the basics have already been explained. It is a typical search vs. sort problem. It has already been mentioned that algorithmically you are not going to achieve better than O(n) for that case.
However, if you are looking at practical use, things get more interesting. You would then need to consider how large the array is, and the processes involved in adding and removing from the data set. In these cases, it can be best to take the computational ‘hit’ at insertion / removal time by sorting on the fly. Insertions into a pre-sorted array are not that expensive.
The quickest query response to the Min Max request will always be from a sorted array, because as others have mentioned, you simply take the first or last element – giving you an O(1) cost.
For a bit more of a technical explanation on the computational costs involved, and Big O notation, check out the Wikipedia article here.
Nick.
answered Jan 8, 2009 at 16:18
NickNick
2,2852 gold badges14 silver badges26 bronze badges
If you are building the array once and want to find the maximum just once, iterating is the best you can do.
When you want to modify the array and occasionally want to know the maximum element, you should use a Priority Queue. One of the best data structures for that is a Fibonacci Heap, if this is too complicated use a Binary Heap which is slower but still good.
To find minimum and maximum, just build two heaps and change the sign of the numbers in one of them.
answered Jan 8, 2009 at 16:12
martinusmartinus
17.7k15 gold badges72 silver badges92 bronze badges
Please take into account that sorting the array will only be faster that looping up to certain size of the array. If your array is small (and it will be like that any time) then your solution is perfectly fine. But if it might get too large you should use a conditional to use the sort approach when the array is small, and the normal iteration when it is too large
answered Jan 28, 2009 at 21:21
If you want to find both the min and max at the same time, the loop can be modified as follows:
int min = int.maxValue;
int max = int.minValue;
foreach num in someArray {
if(num < min)
min = num;
if(num > max)
max = num;
}
This should get achieve O(n) timing.
answered Jan 8, 2009 at 16:29
Matthew BrubakerMatthew Brubaker
3,0971 gold badge21 silver badges18 bronze badges
Shortest way :
Math.min.apply(null,array); //this will return min value from array
Math.max.apply(null,array); //this will return max value from array
otherway of getting min & max value from array
function maxVal(givenArray):Number
{
var max = givenArray[0];
for (var ma:int = 0; ma<givenArray.length; ma++)
{
if (givenArray[ma] > max)
{
max = givenArray[ma];
}
}
return max;
}
function minVal(givenArray):Number
{
var min = givenArray[0];
for (var mi:int = 0; mi<givenArray.length; mi++)
{
if (givenArray[mi] < min)
{
min = givenArray[mi];
}
}
return min;
}
As you can see, the code in both of these functions is very similar. The function sets a variable – max (or min) and then runs through the array with a loop, checking each next element. If the next element is higher than the current, set it to max (or min). In the end, return the number.
answered Feb 6, 2014 at 3:39
sajansajan
1,3451 gold badge14 silver badges18 bronze badges
Below is Solution with o(n):-
public static void findMaxAndMinValue(int A[]){
int min =0, max = 0;
if(A[0] > A[1] ){
min = A[1];
max = A[0];
}else{
max = A[1];
min = A[0];
}
for(int i = 2;i<A.length ;i++){
if(A[i] > max){
max = A[i];
}
if(min > A[i]){
min = A[i];
}
}
System.out.println("Maxinum Value is "+min+" & Minimum Value is "+max);
}
answered Jun 17, 2015 at 18:06
Ajay KumarAjay Kumar
4,6481 gold badge38 silver badges42 bronze badges
Amazed no-one mentioned parallelism here.
If you got really a huge array, you can use parallel-for, on sub ranges.
In the end compare all sub-ranges.
But parallelism comes width some penalty too, so this would not optimize on small arrays. However if you got huge datasets it starts to make sense, and you get a time division reduction nearing the amount of threads performing the test.
answered Mar 21, 2018 at 9:26
PeterPeter
2,0071 gold badge20 silver badges45 bronze badges
Find max values from a array
Let’s see how to obtain min, max values by using a single funtion
public void findMaxValue(){
int[] my_array = {1,2,,6,5,8,3,9,0,23};
int max = my_array[0];
for(int i=1; i<my_array.length; i++)
{
if(my_array[i] > max)
max = my_array[i];
}
return max;
}
same thing can do for find min value
answered Oct 24, 2018 at 16:00
After reading everyone’s comments (thank you for your interest), I found that the “best” way (least amount of code, best performing) to do this was to simply sort the Array, and then grab the first value in the Array:
var myArray:Array /* of Number */ = [2,3,3,4,2,2,5,6,7,2];
myArray.sort(Array.NUMERIC);
var minValue:int = myArray[0];
This also works for an Array of Objects – you simply use the Array.sortOn() function and specify a property:
// Sample data
var myArray:Array /* of XML */ =
[
<item level="2" name="a" />
<item level="3" name="b" />
<item level="3" name="c" />
<item level="2" name="d" />
<item level="5" name="e" />
]
// Perform a descending sort on the specified attribute in Array to get the maximum value
myArray.sortOn("@level", Array.DESCENDING | Array.NUMERIC);
var lowestLevel:int = myArray[0].@level;
I hope this helps someone else someday!
answered Jan 23, 2009 at 22:34
Eric BelairEric Belair
10.6k13 gold badges75 silver badges116 bronze badges