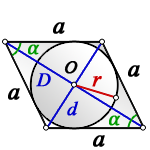
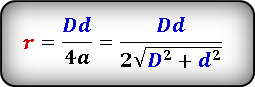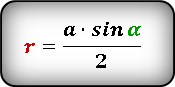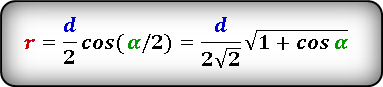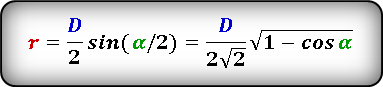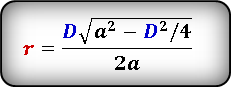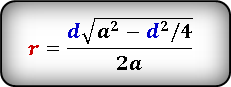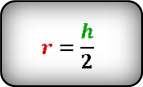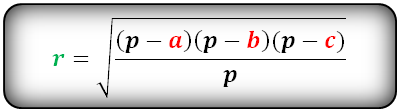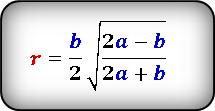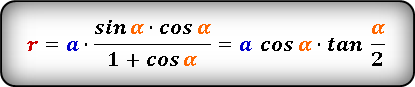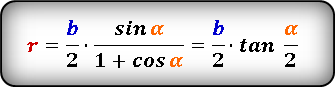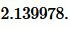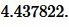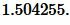1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
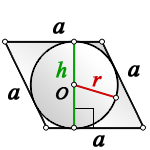
a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
a – сторона ромба
h – высота
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :
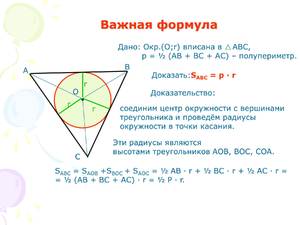
Нахождение радиуса описанной вокруг треугольника окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
Формула радиуса окружности, вписанной в треугольник
Если окружность располагается внутри угла и касается его сторон, её называют вписанной в этот угол. Центр такой вписанной окружности располагается на биссектрисе этого угла.
Если же она лежит внутри выпуклого многоугольника и соприкасается со всеми его сторонами, она называется вписанной в выпуклый многоугольник.
Окружность, вписанная в треугольник
Окружность, вписанная в треугольник, соприкасается с каждой стороной этой фигуры лишь в одной точке. В один треугольник возможно вписать лишь одну окружность.
Радиус такой окружности будет зависеть от следующих параметров треугольника:
- Длин сторон треугольника.
- Его площади.
- Его периметра.
- Величины углов треугольника.
Для того чтобы вычислить радиус вписанной окружности в треугольник, не всегда обязательно знать все перечисленные выше параметры, поскольку они взаимосвязаны между собой через тригонометрические функции.
Вычисление с помощью полупериметра
Чтобы рассчитать величину радиуса вписанной окружности в треугольник, необходимо учитывать следующие параметры:
- Если известны длины всех сторон геометрической фигуры (обозначим их буквами a, b и c), то вычислять радиус придётся путём извлечения квадратного корня.
- Приступая к вычислениям, необходимо добавить к исходным данным ещё одну переменную — полупериметр (р). Его можно рассчитать, сложив все длины и полученную сумму разделив на 2. p = (a+b+c)/2. Таким образом можно существенно упростить формулу нахождения радиуса.
- В целом формула должна включать в себя знак радикала, под который помещается дробь, знаменателем этой дроби будет величина полупериметра р.
- Числителем данной дроби будет представлять собой произведение разностей (p-a)*(p-b)*(p-c)
- Таким образом, полный вид формулы будет представлен следующим образом: r = √(p-a)*(p-b)*(p-c)/p).
Вычисление с учётом площади треугольника
Если нам известна площадь треугольника и длины всех его сторон, это позволит найти радиус интересующей нас окружности, не прибегая к извлечению корней.
- Для начала нужно удвоить величину площади.
- Результат делится на сумму длин всех сторон. Тогда формула будет выглядеть следующим образом: r = 2*S/(a+b+c).
- Если воспользоваться величиной полупериметра, можно получить совсем простую формулу: r = S/p.
Расчёт с помощью тригонометрических функций
Если в условии задачи присутствует длина одной из сторон, величина противоположного угла и периметр, можно воспользоваться тригонометрической функцией — тангенсом. В этом случае формула расчёта будет иметь следующий вид:
r = (P /2- a)* tg (α/2), где r — искомый радиус, Р — периметр, а — значение длины одной из сторон, α — величина противоположного стороне, а угла.
Радиус окружности, которую необходимо будет вписывать в правильный треугольник, можно найти по формуле r = a*√3/6.
Окружность, вписанная в прямоугольный треугольник
В прямоугольный треугольник можно вписать только одну окружность. Центр такой окружности одновременно служит точкой пересечения всех биссектрис. Эта геометрическая фигура имеет некоторые отличительные черты, которые необходимо учесть, вычисляя радиус вписанной окружности.
- Для начала необходимо выстроить прямоугольный треугольник с заданными параметрами. Построить такую фигуру можно по размеру её одной стороны и величинам двух углов или же по двум сторонам и углу между этими сторонами. Все эти параметры должны быть указаны в условии задачи. Треугольник обозначается как АВС, причём С — это вершина прямого угла. Катеты при этом обозначаются переменными, а и b, а гипотенуза — переменной с.
- Для построения классической формулы и вычисления радиуса окружности необходимо найти размеры всех сторон описанной в условии задачи фигуры и по ним вычислить полупериметр. Если в условиях даются размеры двух катетов, по ним можно вычислить величину гипотенузы, исходя из теоремы Пифагора.
- Если в условии дан размер одного катета и одного угла, необходимо понять, прилежащий этот угол или противолежащий. В первом случае гипотенуза находится с помощью теоремы синусов: с=a/sinСАВ, во втором случае применяют теорему косинусов с=a/cosCBA.
- Когда все расчёты выполнены и величины всех сторон известны, находят полупериметр по формуле, описанной выше.
- Зная величину полупериметра, можно найти радиус. Формула представляет собой дробь. Её числителем является произведение разностей полупериметра и каждой из сторон, а знаменателем —величина полупериметра.
Следует заметить, что числитель данной формулы является показателем площади. В этом случае формула нахождения радиуса гораздо упрощается — достаточно разделить площадь на полупериметр.
Определить площадь геометрической фигуры можно и в том случае, если известны оба катета. По сумме квадратов этих катетов находится гипотенуза, далее вычисляется полупериметр. Вычислить площадь можно, умножив друг на друга величины катетов и разделив полученное на 2.
Если в условиях даны длины и катетов и гипотенузы, определить радиус можно по очень простой формуле: для этого складываются длины катетов, из полученного числа вычитается длина гипотенузы. Результат необходимо разделить пополам.
Видео
Из этого видео вы узнаете, как находить радиус вписанной в треугольник окружности.
Все формулы для радиуса вписанной окружности
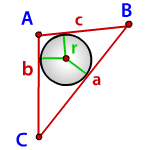
Радиус вписанной окружности в треугольник
a , b , c – стороны треугольника
p – полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
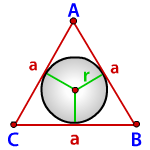
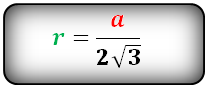
Радиус вписанной окружности в равносторонний треугольник
a – сторона треугольника
r – радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
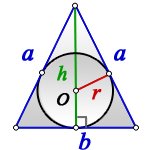
Радиус вписанной окружности равнобедренный треугольник
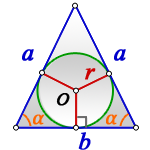
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a – равные стороны равнобедренного треугольника
b – сторона ( основание)
α – угол при основании
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a – равные стороны равнобедренного треугольника
b – сторона ( основание)
h – высота
О – центр вписанной окружности
r – радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/formula-radiusa-okruzhnosti-vpisannoj-v-treugolnik
http://www-formula.ru/2011-09-24-00-40-48
[/spoiler]
Радиус вписанной окружности в прямоугольный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Содержание
- Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
- Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
- Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
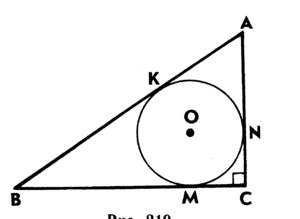
1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
где
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
где c вычисляется из теоремы Пифагора:
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на ( small a+b-c ):
Учитывая (5), формулу (6) можно переписать так:
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
Подставим значения ( small a=17, ; b=5; c=17.720045 ) в (7):
Ответ:
2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
Из теоремы синусов имеем:
Учитывая, что ( small alpha=90°-beta ) и ( small sin (90°-beta)=cos beta ), получим:
Тогда из (8) получим:
Далее, из теоремы синусов:
Откуда:
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения ( small b ) и ( small c ) из (9) и (10) в (7):
или
Пример 2. Известны катет ( small a=21 ) и прилежащий к нему угол ( small beta=30° ) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения ( small a=21 ) ( small beta=30° ) в (11):
Ответ:
3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Пусть известны катет a прямоугольного треугольника и противолежащий угол ( small alpha; ) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
или
Пример 3. Известны катет ( small a=6 ) прямоугольного треугольника и противолежащий угол ( small alpha=53°. ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение ( small a=6, ; alpha=53° ) в (12):
Ответ:
Смотрите также:
- Радиус описанной окружности около треугольника онлайн
- Радиус вписанной в треугольник окружности онлайн
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- Радиус вписанной окружности в равносторонний треугольник онлайн
Утверждение.
Радиус вписанной в прямоугольный треугольник окружности равен
где a и b — катеты, c — гипотенуза.
Доказательство:
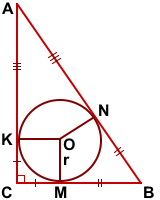
Проведём радиусы OK, OM, ON к сторонам треугольника.
(как радиусы, проведённые в точку касания).
(как отрезки касательных, проведённых из одной точки).
Отсюда следует, что четырёхугольник CKOM — квадрат, стороны которого равны радиусу вписанной в треугольник ABC окружности: CK=CM=OM=OK=r.
Следовательно,
то есть
Таким образом, формула радиуса вписанной в прямоугольный треугольник окружности
Что и требовалось доказать.
ВИДЕОУРОК
Вписанная окружность
прямоугольного треугольника.
Радиус окружности,
вписанной в прямоугольный треугольник,
можно найти по формуле:
где r –
искомый радиус, а и b – катеты,
с – гипотенуза треугольника.
Радиус вписанной в
прямоугольный треугольник окружности
равен произведению катетов, делённому на сумму
катетов и гипотенузы,
где r –
искомый радиус, а и b – катеты,
с – гипотенуза треугольника.
Радиус вписанной в
прямоугольный треугольник окружности равен площади этого треугольника, делённой
на полупериметр:
где р – полупериметр
ЗАДАЧА:
Точка касания окружности, вписанной в прямоугольный треугольник,
делит один из катетов на отрезки 2 см и 8 см,
отсчитывая от вершины прямого угла. Найдите периметр треугольника.
РЕШЕНИЕ:
Начертим чертёж:
ВМ
= ВN = х.
(2 + х)2 + (2 + 8)2 = (8
+ х)2,
х2 + 4х + 4
+ 100 =
= х2 + 16х + 64,
12х = 40,
х =
10/3 (см).
Р = (2 + 8) + (8 + 10/3) + (10/3 + 2) = 262/3 (см).
ЗАДАЧА:
Вписанная окружность прямоугольного треугольника АВС касается гипотенузы АВ в точке
К. Найдите радиус
вписанной окружности, если АК = 4 см, ВК
= 6 см.
РЕШЕНИЕ:
За свойством касательных имеем:
АК = АМ = 4 см,
ВК = ВN = 6 см.
Обозначим радиус вписанной окружности
через х:
СN = СM = NО = МО = х.
Тогда
АС =
(4 + х) см.
ВС = (6 + х) см,
АВ =
4 см +
6 см =
10 см.
По теореме Пифагора для треугольника АВС
можно записать соотношение:
(4 + х)2 + (6 + х)2 = 102.
Решим это квадратное уравнение:
16 + 8x + x2
+ 36 + 12x + x2 = 100,
2x2 + 20x + 52 – 100 = 0,
2x2 + 20x – 48 = 0,
x2 + 10x – 24 = 0,
x1 = 2, x2 = –10.
x2 не
удовлетворяет условию задачи.
ОТВЕТ: 2 см.
ЗАДАЧА:
Точка касания окружности, вписанной в прямоугольный треугольник,
делить гипотенузу на отрезки 8 см и 12
см. Найдите периметр треугольника.
РЕШЕНИЕ:
Начертим чертёж:
(8 + 12)2
= (8 + х)2 + (12 + х)2,
400 = 64 + 16x + x2
+ x2 + 24x + 144,
2x2 + 40x – 192 = 0,
x2 + 20x – 96 = 0,
x1 = 4, x2 = –24.
x2 не
подходит.
Р
= 8 + 12 + 12 + 4 + 4 + 8 = 48 (см).
ОТВЕТ: 48 см.
Описанная окружность
прямоугольного треугольника.
Центром окружности, описанной
вокруг прямоугольного треугольника, будет середина его гипотенузы.
Диаметр окружности,
описанной вокруг прямоугольного треугольника, равен его гипотенузе.
Медиана прямоугольного
треугольника, проведённая к его гипотенузе, равна половине гипотенузы и
является радиусом окружности, описанной около этого треугольника.
ОА = ОВ = ОС = R
Радиус описанной окружности равен половине
гипотенузы:
ЗАДАЧА:
Отрезок ВС – диаметр окружности, изображённой на рисунку.
Угол АВС = 55°.
Найдите
величину
угла АСВ
?
РЕШЕНИЕ:
ВС – диаметр,
поэтому ∠ ВАС = 90°,
∠ АСВ = 180° – (90° + 55°) = 35°.
ЗАДАЧА:
Перпендикуляр,
опущенный из точки окружности на его диаметр, делит диаметр на отрезки, разность
между которыми равна 5 см. Найдите радиус окружности, если длина перпендикуляра равна 6 см.
РЕШЕНИЕ:
Пусть АВ – диаметр окружности с
центром в точке О, СD ⊥ АВ,
где С – точка окружности,
СD = 6 см, АD = х см,
ВD – АD = 5 см.
Тогда
DВ = (х + 5) см.
Треугольник АСВ – прямоугольный (угол С прямой, так как
он вписанный и опирается на диаметр).
СD – перпендикуляр, проведений из вершины прямого угла на
гипотенузу. Тогда:
АD ∙ DВ = СD2,
х(х + 5) = 62,
х2
+ 5х – 36 = 0,
x1 = –9, x2 = 4.
x1 не подходит.
Поэтому, АD = 4 см,
DВ = 4 + 5 = 9 (см).
АВ
= АD
+ DВ
=
=
4
+ 9 = 13 (см).
Тогда
r = АВ :
2 = 13 : 2 = 6,5 (см).
ОТВЕТ: 6,5 см
ЗАДАЧА:
Из точки на окружности проведены две перпендикулярные
хорды, разность между которыми равна 4 см. Найдите эти хорды, если радиус окружности равен 10
см.
РЕШЕНИЕ:
Пусть задана окружность радиуса R,
в
которой
проведены
хорды АВ и
АС (АВ ⊥ АС),
R = АО = ВО = СО =
10 см,
АС – АВ =
4
см.
Пусть АВ = х см, тогда
АС = (4
+ х) см.
Так как ∠ А = 90°, то треугольник
ВАС –
прямоугольный,
в
котором
ВС = 2ОВ= 2 ∙ 10 = 20 см.
Из
прямоугольного треугольника ВАС имеем:
АВ2 + АС2
= ВС2,
х2 + (4 + х)2
= 202,
х2 + 16 + 8х
+ х2 = 400,
х2 + 4х –
192 = 0,
х1 = 12,
х2
= –16 – не подходит.
Поэтому,
АВ = 12 см,
АС
= 4 + 12 = 16 (см).
ОТВЕТ: 12
см, 16 см
ЗАДАЧА:
Угол между биссектрисой и
медианой прямоугольного треугольника, проведёнными из вершины прямого угла,
равен 14°.
Найдите меньший угол этого треугольника.
РЕШЕНИЕ:
Начертим чертёж.
Так как треугольник
прямоугольный и медиана ВМ иcходит
из прямого угла В, то точка М является центром
описанной окружности вокруг треугольника
АВС.
Следовательно,
АМ
= МС = МВ = R,
где R –
радиус описанной окружности.
Найдём сначала угол МВС.
Учитывая, что BD – биссектриса, то
∠ DВС = 90/2 = 45°. Тогда
∠ МВС = ∠ МВD + ∠ DВС,
∠ МВС = 14° + 45° = 59°.
Рассмотрим
равнобедренный треугольник МВС со сторонами
МВ = МС,
в
котором углы при основании ВС равны, то есть
∠ С = ∠ МВС
= 59°.
Так
как сумма острых углов в прямоугольном треугольнике равна 90°, то
∠ А + ∠ С = 90°,
∠ А = 90° – ∠ С =
= 90° – 59° = 31°.
ЗАДАЧА:
Периметр
прямоугольного треугольника равен 72 м, а радиус вписанной в него окружности – 6 м. Найдите диаметр описанной окружности.
РЕШЕНИЕ:
DO = OF = OE = r = 6 м.
Поэтому AD =
AF =
6 м.
FC = EC, BD = BE (отрезки касательных, проведённых из
одной точки)
Пусть
BD = BE = x,
FC = EC = y,
Тогда
AB
= x + 6, AC = y + 6,
BC = x + y.
AB + AC + BC =
= x + 6 + y + 6
+ x + y = 72.
2x + 2y + 12 = 72,
2x + 2y = 60,
x + y = 30.
(x + y) – гипотенуза, или диаметр описанной окружности.
ОТВЕТ: 30 м.
ЗАДАЧА:
В окружности на расстоянии 6
см от его центра проведена хорда длинной 16
см. Найдите радиус окружности.
РЕШЕНИЕ:
Начертим чертёж:
Пользуясь теоремой
Пифагора, находим радиус.
ЗАДАЧА:
Две окружности, радиусы которых равны 4 см и 9 см, имеют внешнее касание. Найдите расстояние между
точками касания данных окружностей с их общей внешней касательной.
РЕШЕНИЕ:
ВК ⊥ АD, АК = 9 – 4 = 5 см.
Из ∆ ВКА: