|
|
Макеты страниц
О единицах количества теплоты. Единицу количества теплоты — «малую» калорию — мы определили выше как количество теплоты, которое требуется для повышения температуры  воды на 1 К при атмосферном давлении. Но так как теплоемкость воды при разных температурах различна, необходимо условиться о той температуре, при которой выбирается этот одноградусный интервал.
воды на 1 К при атмосферном давлении. Но так как теплоемкость воды при разных температурах различна, необходимо условиться о той температуре, при которой выбирается этот одноградусный интервал.
В СССР принята так называемая двадцатиградусная калория, для которой принят интервал от 19,5 до 20,5°С. В некоторых странах применяется пятнадцатиградусная калория (интервал  Первая из них равна
Первая из них равна  Дж, вторая –
Дж, вторая –  Дж. Иногда применяется средняя калория, равная одной сотой количества тепла, необходимого для нагревания
Дж. Иногда применяется средняя калория, равная одной сотой количества тепла, необходимого для нагревания  воды от
воды от  до
до 
Измерение количества теплоты. Для непосредственного измерения количества теплоты, отданного или полученного телом, служат специальные приборы — калориметры.
В наиболее простой своей форме калориметр представляет собой сосуд, заполненный веществом, теплоемкость которого хорошо известна, например водой (удельная теплоемкость 
Измеряемое количество теплоты тем или иным путем передается калориметру, в результате чего изменяется его температура. Измерив это изменение температуры  мы получим теплоту
мы получим теплоту 

где с — удельная теплоемкость вещества, заполняющего калориметр,  его масса.
его масса.
Необходимо учитывать, что теплота передается не только веществу калориметра, но и сосуду и различным устройствам, которые могут в нем помещаться. Поэтому перед измерением нужно определить так называемый тепловой эквивалент калориметра — количество теплоты, нагревающее «пустой» калориметр на один градус. Иногда эту поправку вводят добавлением к массе воды  добавочной массы
добавочной массы  теплоемкость которой равна теплоемкости сосуда и других частей калориметра. Тогда можно считать, что тепло передается массе воды, равной
теплоемкость которой равна теплоемкости сосуда и других частей калориметра. Тогда можно считать, что тепло передается массе воды, равной  Величина
Величина  называется водяным эквивалентом калориметра.
называется водяным эквивалентом калориметра.
Измерение теплоемкости. Калориметр служит также для измерения теплоемкости. В этом случае необходимо точно знать количество подведенного (или отведенного) тепла  Если
Если  известно, то удельная теплоемкость вычисляется из равенства
известно, то удельная теплоемкость вычисляется из равенства

где  масса исследуемого тела, а
масса исследуемого тела, а  изменение его температуры, вызванное теплотой
изменение его температуры, вызванное теплотой 
Тепло к телу подводится в калориметре, который должен быть устроен так, чтобы подводимое тепло передавалось только исследуемому телу (и, конечно, калориметру), но не терялось в окружающем пространстве. Между тем такие потери тепла в какой-то мере всегда происходят, и их учет является главной заботой при калориметрических измерениях.
Измерение теплоемкости газов затруднено тем, что из-за малой их плотности теплоемкость той массы газа, которая может быть помещена в калориметр, мала. При обычных температурах она может оказаться сравнимой с теплоемкостью пустого калориметра, что неизбежно понижает точность измерений. Это особенно относится к измерению теплоемкости при постоянном объеме  При определении
При определении  эту трудность можно обойти, если исследуемый газ заставить протекать (при постоянном давлении) через калориметр (см. ниже).
эту трудность можно обойти, если исследуемый газ заставить протекать (при постоянном давлении) через калориметр (см. ниже).

Рис. 41.
Измерение  Едва ли не единственным методом непосредственного измерения теплоемкости газа при постоянном объеме является метод, предложенный Жоли (1889 г.). Схема этого метода представлена на рис. 41.
Едва ли не единственным методом непосредственного измерения теплоемкости газа при постоянном объеме является метод, предложенный Жоли (1889 г.). Схема этого метода представлена на рис. 41.
Калориметр состоит из камеры К, в которой на концах коромысла точных весов  подвешены два одинаковых полых медных шара
подвешены два одинаковых полых медных шара  снабженных тарелками снизу и отражателями сверху. Один из шаров откачивается, другой наполняется исследуемым газом. Для того чтобы газ имел заметную теплоемкость, его вводят под значительным давлением
снабженных тарелками снизу и отражателями сверху. Один из шаров откачивается, другой наполняется исследуемым газом. Для того чтобы газ имел заметную теплоемкость, его вводят под значительным давлением  Массу
Массу  введенного газа определяют с помощью весов, восстанавливая гирями нарушенное введением газа равновесие.
введенного газа определяют с помощью весов, восстанавливая гирями нарушенное введением газа равновесие.
После того как между шарами и камерой установится тепловое равновесие, в камеру впускают водяной пар (трубки для входа и выхода пара расположены на передней и задней стенках камеры и на рис. 41 не показаны). Пар конденсируется на обоих шарах, нагревая их, и стекает в тарелки. Но на сфере, заполненной газом, конденсируется больше жидкости, так как ее теплоемкость больше. Из-за избытка конденсата на одном из шаров равновесие шаров снова нарушится. Уравновесив весы, мы узнаем ту избыточную массу жидкости, которая сконденсировалась благодаря присутствию газа в шаре. Если эта избыточная масса воды равна  то, умножив ее на теплоту конденсации воды
то, умножив ее на теплоту конденсации воды  найдем количество теплоты, которое пошло на нагревание газа от начальной температуры
найдем количество теплоты, которое пошло на нагревание газа от начальной температуры  до температуры водяного пара
до температуры водяного пара  Измерив эту разность термометром, получим:
Измерив эту разность термометром, получим:

где  удельная теплоемкость – газа. Зная удельную теплоемкость
удельная теплоемкость – газа. Зная удельную теплоемкость  мы найдем, что молярная теплоемкость
мы найдем, что молярная теплоемкость 
Измерение  Мы уже упоминали, что для измерения теплоемкости при постоянном давлении исследуемый газ заставляют протекать через калориметр. Только таким путем можно обеспечить постоянство давления газа, несмотря на подвод тепла и нагревание, без которого нельзя измерять теплоемкость. В качестве примера такого метода приведем здесь описание классического опыта Реньо (
Мы уже упоминали, что для измерения теплоемкости при постоянном давлении исследуемый газ заставляют протекать через калориметр. Только таким путем можно обеспечить постоянство давления газа, несмотря на подвод тепла и нагревание, без которого нельзя измерять теплоемкость. В качестве примера такого метода приведем здесь описание классического опыта Реньо ( Схема аппарата представлена на рис. 42.
Схема аппарата представлена на рис. 42.

Рис. 42.
Исследуемый газ из резервуара А через кран  пропускают через змеевик, помещенный в сосуде с маслом В, нагреваемым каким-нибудь источником тепла. Давление газа регулируется краном
пропускают через змеевик, помещенный в сосуде с маслом В, нагреваемым каким-нибудь источником тепла. Давление газа регулируется краном  а его постоянство контролируется манометром
а его постоянство контролируется манометром  Проходя длинный путь в змеевике, газ принимает температуру масла, которая измеряется термометром
Проходя длинный путь в змеевике, газ принимает температуру масла, которая измеряется термометром 
Нагретый в змеевике газ проходит затем через водяной калориметр, охлаждаясь в нем до некоторой температуры  измеряемой термометром
измеряемой термометром  и выходит наружу. Измерив давление газа в резервуаре А в начале и в конце опыта (для этого служит манометр
и выходит наружу. Измерив давление газа в резервуаре А в начале и в конце опыта (для этого служит манометр  мы узнаем массу
мы узнаем массу  прошедшего через аппарат газа.
прошедшего через аппарат газа.
Количество теплоты  отданное газом калориметру, равно произведению водяного эквивалента
отданное газом калориметру, равно произведению водяного эквивалента  калориметра на изменение его температуры
калориметра на изменение его температуры  где
где  начальная температура калориметра:
начальная температура калориметра:

С другой стороны, тепло, отданное газом, равно произведению его массы на удельную теплоемкость и на изменение температуры газа от начального значения  до той температуры, которую он принимает в калориметре. Но температура калориметра изменяется от
до той температуры, которую он принимает в калориметре. Но температура калориметра изменяется от  до
до  Поэтому средняя температура газа в калориметре равна
Поэтому средняя температура газа в калориметре равна
 Следовательно, изменение температуры газа равно
Следовательно, изменение температуры газа равно  а отданное им тепло
а отданное им тепло

Таким образом,

откуда для удельной теплоемкости получается равенство

а молярная теплоемкость 
Измерение отношения  было показано, что отношение теплоемкостей газов
было показано, что отношение теплоемкостей газов  играет важную роль в теории идеальных газов, так как оно определяет число степеней свободы молекул. Кроме того, эта величина входит в уравнение адиабаты. Роль этой величины заключается еще и в том, что, зная ее, можно не прибегать к измерениям
играет важную роль в теории идеальных газов, так как оно определяет число степеней свободы молекул. Кроме того, эта величина входит в уравнение адиабаты. Роль этой величины заключается еще и в том, что, зная ее, можно не прибегать к измерениям  которые всегда трудны. Значение
которые всегда трудны. Значение  можно получить из измеренных значений
можно получить из измеренных значений  Часто именно так и поступают.
Часто именно так и поступают.
Существует несколько способов измерения  Наиболее удобным и точным из них следует считать метод, основанный на измерении скорости звука. Дело в том, что скорость звука и в газе определяется формулой
Наиболее удобным и точным из них следует считать метод, основанный на измерении скорости звука. Дело в том, что скорость звука и в газе определяется формулой

где  давление газа,
давление газа,  его плотность. Если
его плотность. Если  известны, то, измерив скорость звука, мы получаем и значение величины
известны, то, измерив скорость звука, мы получаем и значение величины  Метод этот удобен тем, что, используя его, нет надобности измерять ни количество теплоты, ни температуру. Со способами измерения скорости звука читатель познакомится в других курсах.
Метод этот удобен тем, что, используя его, нет надобности измерять ни количество теплоты, ни температуру. Со способами измерения скорости звука читатель познакомится в других курсах.
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава I. КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ
- § 1. Идеальный газ
- § 2. Давление газа
- § 3. Температура
- § 4. Уравнение состояния идеального газа
- § 5. Законы идеального газа
- § 6. Скорости газовых молекул
- § 7. Броуновское движение
- § 8. Барометрическая формула
- § 9. Закон Больцмана
- § 10. Понятие о вероятности
- § 11. Понятие о распределении. Функция распределения
- § 12. Распределение молекул по компонентам скорости
- § 13. Распределение молекул по скоростям
- § 14. Средние скорости молекул
- § 15. Наивероятнейшая скорость молекул
- § 16. Формула Максвелла для относительных скоростей
- § 17. Закон распределения молекул по скоростям и атмосферы планет
- § 18. Экспериментальная проверка закона распределения
- § 19. Измерение параметров состояния
- Глава II. КИНЕТИЧЕСКАЯ ТЕОРИЯ ТЕПЛОТЫ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
- § 20. Внутренняя энергия идеального газа
- § 21. Количество теплоты
- § 22. Механический эквивалент теплоты
- § 23. Первое начало термодинамики
- § 24. Теплоемкость идеальных газов
- § 25. Теплоемкость одноатомных газов
- § 26. Теплоемкость газов и число степеней свободы молекул
- § 27. Теплоемкость двухатомных и многоатомных газов
- § 28. Изменение состояния при изменении объема газа
- § 29. Работа при изотермическом изменении объема идеального газа
- § 30. Адиабатное изменение объема идеального газа
- § 31. Работа при адиабатном изменении объема газа
- § 32. Политропический процесс
- § 33. Расширение газа в пустоту
- § 34. Измерение количества теплоты и теплоемкости
- Глава III. СТОЛКНОВЕНИЯ МОЛЕКУЛ И ЯВЛЕНИЯ ПЕРЕНОСА
- § 35. Молекулярные движения и явления переноса
- § 36. Среднее число столкновений в единицу времени и средняя длина свободного пробега молекул
- § 37. Эффективное поперечное сечение частицы и вероятность
- § 38. Рассеяние молекулярного пучка в газе
- § 39. Экспериментальное определение длины свободного пробега
- § 40. Диффузия в газах
- § 41. Нестационарная диффузия
- § 42. Стационарная диффузия. Вычисление коэффициента диффузии
- § 43. Коэффициент взаимной диффузии
- § 44. Термическая диффузия
- § 45. Теплопроводность газов
- § 46. Нестационарная теплопроводность
- § 47. Стационарная теплопроводность. Вычисление коэффициента теплопроводности
- § 48. Вязкость газов (внутреннее трение)
- § 49. Измерение коэффициента вязкости (вискозиметрия)
- § 50. Соотношения между коэффициентами переноса
- Глава IV. ФИЗИЧЕСКИЕ ЯВЛЕНИЯ В РАЗРЕЖЕННЫХ ГАЗАХ (ВАКУУМЕ)
- § 51. Теплопередача в газах при малых давлениях
- § 52. Течение газов при малых давлениях (молекулярное течение)
- § 53. Молекулярное течение газа в цилиндрической трубе
- § 54. Молекулярное течение смеси газов. Разделение газовых смесей
- § 55. Диффузия газов в вакууме
- § 56. Разность давлений между различно нагретыми частями газа (тепловая транспирация)
- § 57. Элементы вакуумной техники
- § 58. Измерение малых давлений
- § 59. Вакуумная установка
- Глава V. НЕИДЕАЛЬНЫЕ (РЕАЛЬНЫЕ) ГАЗЫ. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА
- § 60. Отклонения свойств газов от идеальности
- § 61. Сжижение газов (конденсация)
- § 62. Фазовый переход
- § 63. Фазовые диаграммы
- § 64. Методы определения критических параметров
- § 65. Уравнение Ван-дер-Ваальса
- § 66. Изотермы Ван-дер-Ваальса
- § 67. Критическая температура и критическое состояние
- § 68. Экспериментальное определение констант уравнения Ван-дер-Ваальса
- § 69. Сравнение уравнения Ван-дер-Ваальса с данными опыта
- § 70. Приведенное уравнение Ван-дер-Ваальса. Закон соответственных состояний
- § 71. Межмолекулярные силы взаимодействия в реальном газе
- § 72. Теплоемкость неидеальных газов
- Глава VI. ЭЛЕМЕНТЫ ТЕРМОДИНАМИКИ
- § 73. Равновесные состояния
- § 74. Обратимые и необратимые процессы
- § 75. Квазистатические процессы
- § 76. Необратимость и вервятность
- § 77. Взаимные превращения механической и тепловой энергии
- § 78. Первое начало термодинамики
- § 79. Преобразование теплоты в механическую работу
- § 80. Цикл Карно
- § 81. Холодильная машина
- § 82. Доказательство теорем Карно
- § 83. Свободная энергия
- § 84. Энтропия
- § 85. Некоторые термодинамические соотношения
- § 86. Энтропия при обратимых процессах в замкнутой системе
- § 87. Энтропия при необратимых процессах в замкнутой системе, акон возрастания энтропии
- § 88. Второе начало термодинамики и превращение теплоты в работу
- § 89. Физический смысл энтропии. Энтропия и вероятность
- § 90. Энтропия и беспорядок
- § 91. «Демон» Максвелла
- § 92. Термодинамическая шкала температур
- § 93. Третье начало термодинамики
- § 94. Отрицательные температуры
- Глава VII. СВОЙСТВА ЖИДКОСТЕЙ
- § 95. Объемные свойства жидкостей
- § 96. Теплоемкость жидкостей
- § 97. Явления переноса в жидкостях
- § 98. Явления на границе жидкости
- § 99. Условия равновесия на границе двух сред. Краевой угол
- § 100. Силы, возникающие на кривой поверхности жидкости
- § 101. Капиллярные явления
- § 102. Некоторые методы измерения коэффициента поверхностного натяжения
- § 103. Зависимость коэффициента поверхностного натяжения от температуры
- § 104. Испарение и кипение жидкостей
- § 105. Температурная зависимость упругости насыщенных паров
- § 106. Упругость насыщенного пара над кривой поверхностью жидкости
- § 107. Кипение жидкостей
- § 108. Жидкие растворы
- § 109. Осмотическое давление
- Глава VIII. НИЗКИЕ ТЕМПЕРАТУРЫ
- § 110. Сжижение газов
- § 111. Эффект Джоуля-Томсона
- § 112. Адиабатное расширение газа с совершением внешней работы
- § 113. Сжижение газов с использованием эффекта Джоуля — Томсона (метод Линде)
- § 114. Сжижение газов методом адиабатного расширения в детандерах (метод Клода)
- § 115. Некоторые свойства сжиженных газов
- § 116. Сверхнизкие температуры
- § 117. Свойства вещества при низких температурах
- § 118. Жидкий гелий
- Глава IX. ТВЕРДОЕ ТЕЛО
- § 120. Кристаллическая решетка
- § 121. Дефекты в кристаллах
- § 122. Механические свойства твердых тел. Деформации
- § 123. Деформация растяжения и сжатия. Сдвиг
- § 124. Связь между модулями упругости
- § 125. Упругая деформация и тепловое расширение
- § 126. Зависимость деформации от напряжения
- § 127. Механизм пластической деформации
- § 128. Дислокации в кристаллах
- § 129. Переход в твердое состояние
- § 130. Диаграмма состояния. Тройная точка
- § 131. Фазовые переходы первого и второго рода
- § 132. Твердый гелий
- § 133. Растворение и кристаллизация из раствора
- § 134. Сплавы. Диаграммы плавкости
- § 135. Зонная очистка металлов
- § 136. Опытное определение температуры плавления
- § 137. Тепловые свойства твердых тел
- § 138. Измерение теплоемкости
- § 139. Тепловое расширение твердых тел
- § 140. Теплопроводность
- § 141. Диффузия в твердых телах
ОГЭ 2021 по физике ›

1. Изменение внутренней энергии путём совершения работы характеризуется величиной работы, т.е. работа является мерой изменения внутренней энергии в данном процессе. Изменение внутренней энергии тела при теплопередаче характеризуется величиной, называемой количеством теплоты.
Количеством теплоты называется изменение внутренней энергии тела в процессе теплопередачи без совершения работы.
Количество теплоты обозначают буквой ( Q ). Так как количество теплоты является мерой изменения внутренней энергии, то его единицей является джоуль (1 Дж).
При передаче телу некоторого количества теплоты без совершения работы его внутренняя энергия увеличивается, если тело отдаёт какое-то количество теплоты, то его внутренняя энергия уменьшается.
2. Если в два одинаковых сосуда налить в один 100 г воды, а в другой 400 г при одной и той же температуре и поставить их на одинаковые горелки, то раньше закипит вода в первом сосуде. Таким образом, чем больше масса тела, тем большее количество теплоты требуется ему для нагревания. То же самое и с охлаждением: тело большей массы при охлаждении отдаёт большее количество теплоты. Эти тела сделаны из одного и того же вещества и нагреваются они или охлаждаются на одно и то же число градусов.
[ Qsim m ]
3. Если теперь нагревать 100 г воды от 30 до 60 °С, т.е. на 30 °С, а затем до 100 °С, т.е. на 70 °С, то в первом случае на нагревание уйдёт меньше времени, чем во втором, и, соответственно, на нагревание воды на 30 °С, будет затрачено меньшее количество теплоты, чем на нагревание воды на 70 °С. Таким образом, количество теплоты прямо пропорционально разности конечной ( (t_2,^circ C) ) и начальной ( (t_1,^circ C) ) температур: ( Qsim(t_2-t_1) ).
4. Если теперь в один сосуд налить 100 г воды, а в другой такой же сосуд налить немного воды и положить в неё такое металлическое тело, чтобы его масса и масса воды составляли 100 г, и нагревать сосуды на одинаковых плитках, то можно заметить, что в сосуде, в котором находится только вода, температура будет ниже, чем в том, в котором находятся вода и металлическое тело. Следовательно, чтобы температура содержимого в обоих сосудах была одинаковой нужно воде передать большее количество теплоты, чем воде и металлическому телу. Таким образом, количество теплоты, необходимое для нагревания тела зависит от рода вещества, из которого это тело сделано.
5. Зависимость количества теплоты, необходимого для нагревания тела, от рода вещества характеризуется физической величиной, называемой удельной теплоёмкостью вещества.
Физическая величина, равная количеству теплоты, которое необходимо сообщить 1 кг вещества для нагревания его на 1 °С (или на 1 К), называется удельной теплоёмкостью вещества.
Такое же количество теплоты 1 кг вещества отдаёт при охлаждении на 1 °С.
Удельная теплоёмкость обозначается буквой ( c ). Единицей удельной теплоёмкости является 1 Дж/кг °С или 1 Дж/кг К.
Значения удельной теплоёмкости веществ определяют экспериментально. Жидкости имеют большую удельную теплоёмкость, чем металлы; самую большую удельную теплоёмкость имеет вода, очень маленькую удельную теплоёмкость имеет золото.
Удельная теплоёмкость свинца 140 Дж/кг °С. Это значит, что для нагревания 1 кг свинца на 1 °С необходимо затратить количество теплоты 140 Дж. Такое же количество теплоты выделится при остывании 1 кг воды на 1 °С.
Поскольку количество теплоты равно изменению внутренней энергии тела, то можно сказать, что удельная теплоёмкость показывает, на сколько изменяется внутренняя энергия 1 кг вещества при изменении его температуры на 1 °С. В частности, внутренняя энергия 1 кг свинца при его нагревании на 1 °С увеличивается на 140 Дж, а при охлаждении уменьшается на 140 Дж.
Количество теплоты ( Q ), необходимое для нагревания тела массой ( m ) от температуры ( (t_1,^circ C) ) до температуры ( (t_2,^circ C) ), равно произведению удельной теплоёмкости вещества, массы тела и разности конечной и начальной температур, т.е.
[ Q=cm(t_2{}^circ-t_1{}^circ) ]
По этой же формуле вычисляется и количество теплоты, которое тело отдаёт при охлаждении. Только в этом случае от начальной температуры следует отнять конечную, т.е. от большего значения температуры отнять меньшее.
6. Пример решения задачи. В стакан, содержащий 200 г воды при температуре 80 °С, налили 100 г воды при температуре 20 °С. После чего в сосуде установилась температура 60 °С. Какое количество теплоты получила холодная вода и отдала горячая вода?
При решении задачи необходимо выполнять следующую последовательность действий:
- записать кратко условие задачи;
- перевести значения величин в СИ;
- проанализировать задачу, установить, какие тела участвуют в теплообмене, какие тела отдают энергию, а какие получают;
- решить задачу в общем виде;
- выполнить вычисления;
- проанализировать полученный ответ.
1. Условие задачи.
Дано: ( m_1 ) = 200 г ( m_2 ) = 100 г ( t_1 ) = 80 °С ( t_2 ) = 20 °С ( t ) = 60 °С ______________
( Q_1 ) — ? ( Q_2 ) — ? ( c_1 ) = 4200 Дж/кг · °С
2. СИ: ( m_1 ) = 0,2 кг; ( m_2 ) = 0,1 кг.
3. Анализ задачи. В задаче описан процесс теплообмена между горячей и холодной водой. Горячая вода отдаёт количество теплоты ( Q_1 ) и охлаждается от температуры ( t_1 ) до температуры ( t ). Холодная вода получает количество теплоты ( Q_2 ) и нагревается от температуры ( t_2 ) до температуры ( t ).
4. Решение задачи в общем виде. Количество теплоты, отданное горячей водой, вычисляется по формуле: ( Q_1=c_1m_1(t_1-t) ).
Количество теплоты, полученное холодной водой, вычисляется по формуле: ( Q_2=c_2m_2(t-t_2) ).
5. Вычисления. ( Q_1 ) = 4200 Дж/кг · °С · 0,2 кг · 20 °С = 16800 Дж ( Q_2 ) = 4200 Дж/кг · °С · 0,1 кг · 40 °С = 16800 Дж
6. В ответе получено, что количество теплоты, отданное горячей водой, равно количеству теплоты, полученному холодной водой. При этом рассматривалась идеализированная ситуация и не учитывалось, что некоторое количество теплоты пошло на нагревание стакана, в котором находилась вода, и окружающего воздуха. В действительности же количество теплоты, отданное горячей водой, больше, чем количество теплоты, полученное холодной водой.
Понятие количества теплоты.
Мы знаем, что внутреннюю энергию тела можно изменить двумя способами. Путем совершения работы и путём теплообмена. При осуществлении 2 способа изменение внутренней энергии равно количеству переданной теплоты. Количество теплоты может быть, как положительным, так и отрицательным.
Если внутренняя энергия тела увеличивается в процессе теплообмена, то количество теплоты больше нуля. Если внутренняя энергия тела уменьшается в процессе теплообмена, то количество теплоты меньше нуля. То есть тело отдает количество теплоты. Отсюда можно сделать вывод:
Количеством теплоты называют ту часть внутренней энергии, которую тело теряет или получает при теплопередаче.
Как рассчитать количество теплоты для нагревания тела
Например, необходимо рассчитать количество теплоты, которое нужно потратить для того, чтобы нагреть 3 кг воды с температуры 15 0С до температуры 85 0С. Нам известна удельная теплоемкость воды, то есть количество энергии, которое нужно для того, чтобы нагреть 1 кг воды на 1 градус. То есть для того, чтобы узнать количество теплоты в нашем случае, нужно умножить удельную теплоемкость воды на 3 и на то количество градусов, на которое нужно увеличить температуры воды. Итак, это 4200*3*(85-15) = 882 000.
В скобках мы рассчитываем точное количество градусов, отнимая от конечного необходимого результата начальное
Итак, для того, чтобы нагреть 3 кг воды с 15 до 85 0С, нам потребуется 882 000 Дж количества теплоты.
Количество теплоты обозначается буквой Q, формула для его расчета выглядит следующим образом:
Q=c*m*(t2-t1).
Отчего зависит Q
Опыт № 1: Возьмём два одинаковых сосуда. Нальем в один из них воду массой 400 г, а в другой растительное масло массой 400 г. Начнём их нагревать с помощью одинаковых горелок. Наблюдая за показаниями термометров. Мы видим, что масло нагревается быстрее. Значит количество теплоты зависит от температуры. Опыт 2: Возьмём 1 кг воды и 1 кг подсолнечного масла. Нагреем оба сосуда на 1 градус. На нагревание воды было потрачено 4.200 Дж. А для нагревания масла потрачено 1700 Дж. Отсюда можно сделать вывод: Количество теплоты зависит от рода вещества.
Физическая величина, показывающая, какое количество теплоты требуется для нагревания 1 кг вещества на 1 градус называется удельной теплоемкостью вещества.
Обозначается буквой С. Измеряется в Дж, поделить на кг, умножить на градус по Цельсию.
Опыт 3: Возьмём в одном сосуде 400 г воды, а в другом сосуде 200 г воды. Нагреем оба сосуда на одинаковое количество градусов. Для нагревания 1 сосуда потребовалось потратить большее количество теплоты. Вывод: количество теплоты зависит от массы.
Удельная теплоемкость вещества
Это физическая величина, выражающая количество тепла, необходимое веществу на единицу массы для повышения температуры на одну единицу.

Таким образом, удельная теплоёмкость является свойством вещества, поскольку его значение является репрезентативным для каждого вещества, каждое из которых, в свою очередь, имеет различные значения в зависимости от того, в каком состоянии оно находится (жидкое, твердое или газообразное).
Удельная теплоёмкость обозначается маленькой буквой c и измеряется в Дж/кг∗°С, представляет собой коэффициент повышения температуры в одной единице всей системы или всей массы вещества.
Кроме того, удельная теплоёмкость меняется в зависимости от физического состояния вещества, особенно в случае твердых частиц и газов, поскольку его молекулярная структура влияет на теплопередачу в системе частиц. То же самое относится и к условиям атмосферного давления: чем выше давление, тем ниже удельное тепло.
Основной состав удельной теплоты вещества должен быть с = С/m, т. е. удельная теплота равна соотношению калорийности и массы.
Однако когда это применяется к данному изменению температуры, говорят о средней удельной теплоемкости, которая рассчитывается на основе следующей формулы:
где:
Q — передача тепловой энергии между системой и средой (Дж);
m — масса системы (кг);
Δt или (t2 — t1) — повышение температуры, которой она подвергается (°C).
Формула для нахождения количества теплоты Q:
Q = c∗m(t2
— t1)
Чем выше удельная теплоёмкость вещества, тем больше тепловой энергии потребуется, чтобы его температура повысилась. Например, для нагрева воды (своды = 4200 Дж/кг∗°С) потребуется больше тепловой энергии, чем для нагрева свинца (ссвинца = 140 Дж/кг∗°С).
Уравнение теплового баланса:
Q отданное + Q полученное = 0.
Ниже представлена таблица значений удельной теплоёмкости некоторых веществ:

Q требуется
При нагревании
Формула: Q = cm (t2 -t1)
При плавлении вещества
Плавлением называют переход вещества из твердого состояния в жидкое состояние.
Формула: Q = m * λ
.
Физический смысл удельной теплоты плавления: лямбда показывает, какое количество теплоты необходимо для того, чтобы расплавить 1 кг вещества при температуре плавления.
Единица измерения: Дж/кг.
В чем измеряется количество теплоты
За единицу количества теплоты принято считать 1 Джоуль. До появления единицы измерения энергии ученые считали количество теплоты калориями. Сокращенно эту единицу измерения принято писать — “Дж”
Калория — это количество теплоты, которое необходимо для того, чтобы нагреть 1 грамм воды на 1 градус Цельсия. Сокращенно единицу измерения калории принято писать — “кал”.
1 кал = 4,19 Дж.
Обратите внимание, что в этих единицах энергии принято отмечать пищевую ценность продуктов питания кДж и ккал.
1 ккал = 1000 кал.
1 кДж = 1000 Дж
1 ккал = 4190 Дж = 4,19 кДж
Количество теплоты выделяется
- При горении топлива.
- При охлаждении вещества.
- При кристаллизации жидкости.
- При конденсации пара.
Для нагревания тел часто используют энергию, выделяющуюся при сгорании топлива.
Различают виды топлива: уголь, нефть, бензин, керосин, торф, спирт, природный газ и так далее.
Энергия, выделяющееся при полном сгорании топлива, называют теплотой сгорания топлива.
Формула: Q = m * q
где q называется удельной теплотой сгорания топлива.
Физический смысл: q показывает какое количество теплоты выделится при горении 1 кг топлива.
Единицы: Дж / кг.
При охлаждении веществ: (Так же как и при нагревании вещества).
Формула Q = cm (t2 — t1)
При кристаллизации веществ: (Так же как и при плавлении вещества).
Формула Q = m * λ
Как связаны и чем отличаются количество теплоты и удельная теплоемкость
Будем рассматривать такие процессы, как нагревание и охлаждение.
- нагревание — тело получает тепловую энергию (количество теплоты).
- охлаждение – тело отдает тепловую энергию в окружающее пространство.
Благодаря процессам нагревания и охлаждения мы можем обогреваться зимой с помощью русской печи. Сначала печь получит количество теплоты (тепловую энергию) от сгорающего топлива — дров. А затем, будет остывать и отдавать это количество теплоты всем телам, находящимся в помещении.
Отличия удельной теплоемкости от количества теплоты
Запомнить, что такое количество теплоты, и чем оно отличается от удельной теплоемкости, можно так (рис. ):

- Количество теплоты – это энергия нагревания (охлаждения) нескольких килограммов на несколько градусов.
- Удельная теплоемкость – это энергия нагревания 1-го килограмма на 1 градус.
Связь количества теплоты и удельной теплоемкости — формула
Если известны:
- удельная теплоемкость вещества;
- количество килограммов вещества;
- количество градусов, на которое нужно нагреть вещество,
то легко посчитать общую тепловую энергию – т. е. количество теплоты.
Для этого используем формулу:
[large boxed{ Q = c cdot m cdot (t_{text{конеч}} — t_{text{нач}}) }]
(large Q left( text{Дж} right) ) – количество теплоты, т. е. общая тепловая энергия;
(large c left( frac{text{Дж}}{text{кг} cdot text{град}} right) ) – удельная теплоемкость;
(large m left( text{кг} right) ) – масса вещества;
(large t_{text{конеч}} left( text{град} right) ) – температура после нагревания;
(large t_{text{нач}} left( text{град} right) ) – температура до нагревания;
Гордюнин С.А. Закон сохранения энергии в электростатике // Квант
Закон сохранения энергии определяет в самом общем виде энергетический баланс при всевозможных изменениях в любой системе. Запишем его следующим образом:
(1)
где Aвнеш — работа, совершенная над рассматриваемой системой внешними силами, ΔW — изменение энергии системы, Q — количество теплоты, выделяемое в системе. Договоримся, что если Aвнеш > 0, то над системой совершают положительную работу, а если Aвнеш < 0, положительную работу совершает система; если ΔW > 0, то энергия системы увеличивается, а если ΔW < 0, энергия уменьшается; наконец, если Q > 0, то в системе выделяется тепло, а если Q < 0, тепло системой поглощается.
В этой статье мы рассмотрим, как закон сохранения энергии «работает» в электростатике. В общем случае электростатическая система содержит взаимодействующие между собой заряды, находящиеся в электрическом поле.
Рассмотрим каждое слагаемое в уравнении (1) по отдельности.
Начнем с энергии. Энергия взаимодействия зарядов выражается через характеристики электрического поля этой системы зарядов. Так, например, энергия заряженного конденсатора емкостью C задается известным выражением
(2)
где q — заряд обкладок, U — напряжение между ними. Напомним, что конденсатор — это система двух проводников (обкладок, пластин), обладающая следующим свойством: если с одной обкладки на другую перенести заряд q (т. е. одну обкладку зарядить зарядом +q, а другую –q), то все силовые линии созданного таким образом поля будут начинаться на одной (положительно заряженной) обкладке и заканчиваться на другой. Поле конденсатора существует только внутри него.
Энергию заряженного конденсатора можно представить также как энергию поля, локализованного в пространстве между пластинами с плотностью энергии где E — напряженность поля. В сущности, именно этот факт дает основание говорить о поле как об объекте, реально существующем, — у этого объекта есть плотность энергии. Но надо помнить, что это просто эквивалентный способ определения энергии взаимодействия зарядов (которую теперь мы называем энергией электрического поля). Таким образом, мы можем считать энергию конденсатора как по формулам (2), так и по формуле
(3)
где V — объем конденсатора. Последней формулой легко пользоваться, конечно, только в случае однородного поля, но представление энергии в такой форме очень наглядно, а потому удобно.
Конечно, кроме энергии взаимодействия зарядов (энергии электрического поля) в энергию системы может входить и кинетическая энергия заряженных тел, и их потенциальная энергия в поле тяжести, и энергия пружин, прикрепленных к телам, и т. п.
Теперь о работе внешних сил. Помимо обычной механической работы Aмех (например, по раздвиганию пластин конденсатора), для электрической системы можно говорить о работе внешнего электрического поля. Например, о работе батареи, заряжающей или перезаряжающей конденсатор. Задача батареи — создать фиксированную, присущую данному источнику разность потенциалов между теми телами, к которым она присоединена. Делает она это единственно возможным способом — забирает заряд от одного тела и передает его другому. Источник никогда не создает заряды, а только перемещает их. Общий заряд системы при этом сохраняется — это один из краеугольных законов природы.
В источниках разных конструкций электрическое поле, необходимое для перемещения зарядов, создают различные «механизмы». В батареях и аккумуляторах — это электрохимические реакции, в динамомашинах — электромагнитная индукция. Существенно, что для выбранной системы зарядов (заряженных тел) это поле — внешнее, стороннее. Когда через источник с ЭДС от отрицательного полюса к положительному протекает заряд Δq, сторонние силы совершают работу
(4)
При этом если Δq > 0, то Aбат > 0 — батарея разряжается; если же Δq < 0, то Aбат < 0 — батарея заряжается и в ней накапливается химическая (или магнитная) энергия.
Наконец, о выделении тепла. Заметим только, что это джоулево тепло, т.е. тепло, связанное с протеканием тока через сопротивление.
Теперь обсудим несколько конкретных задач.
Задача 1. Два одинаковых плоских конденсатора емкостью C каждый присоединены к двум одинаковым батареям с ЭДС . В какой-то момент один конденсатор отключают от батареи, а другой оставляют присоединенным. Затем медленно разводят пластины обоих конденсаторов, уменьшая емкость каждого в n раз. Какая механическая работа совершается в каждом случае?
Если процесс изменения заряда на конденсаторе осуществляется все время медленно, тепло выделяться не будет. Действительно, если через резистор сопротивлением R протек заряд Δq за время t, то на резисторе за это время выделится количество теплоты
При достаточно больших t количество теплоты Q может оказаться сколь угодно малым.
В первом случае фиксирован заряд на пластинах (батарея отключена), равный Механическая работа определяется изменением энергии конденсатора:
Во втором случае фиксирована разность потенциалов на конденсаторе и работает батарея, поэтому
Через батарею протекает заряд
Этот заряд меньше нуля, значит, батарея заряжается и ее работа
Энергия поля в конденсаторе уменьшается:
Таким образом,
Зарядка батареи происходит за счет работы по раздвиганию пластин и за счет энергии конденсатора.
Заметим, что слова про раздвигание пластин существенной роли не играют. Такой же результат будет при любых других изменениях, приводящих к уменьшению емкости в n раз.
Задача 2. В схеме, изображенной на рисунке, найдите количество теплоты, выделившееся в каждом резисторе после замыкания ключа. Конденсатор емкостью C1 заряжен до напряжения U1, а конденсатор емкостью C2 — до напряжения U2. Сопротивления резисторов R1 и R2.
Рис. 1
Закон сохранения энергии (1) для данной системы имеет вид
т. е.
Начальная энергия конденсаторов равна
Для определения энергии в конечном состоянии воспользуемся тем, что суммарный заряд конденсаторов не может измениться. Он равен (для случаев, когда конденсаторы были соединены одноименно или разноименно заряженными пластинами соответственно). После замыкания ключа этим зарядом оказывается заряжен конденсатор емкостью C1 + C2 (конденсаторы емкостями C1 и C2 соединены параллельно). Таким образом,
и
Как и должно быть, в обоих случаях выделяется тепло — есть джоулевы потери. Замечательно, что выделившееся количество теплоты не зависит от сопротивления цепи — при малых сопротивлениях текут большие токи и наоборот.
Теперь найдем, как количество теплоты Q распределяется между резисторами. Через сопротивления R1 и R2 в каждый момент процесса перезарядки текут одинаковые токи, значит, в каждый момент мощности, выделяемые на сопротивлениях, равны
и
Следовательно,
Кроме того, . Поэтому окончательно
Задача 3. В схеме на рисунке 2 конденсатор емкостью C заряжен до напряжения U. Какое количество химической энергии запасется в аккумуляторе с ЭДС после замыкания ключа? Какое количество теплоты выделится в резисторе?
Рис. 2
Первоначальный заряд на конденсаторе . После окончания перезарядки заряд на конденсаторе станет равным . Протекший через батарею заряд в случае, когда к минусу батареи подключена отрицательно заряженная обкладка конденсатора, будет равен
В противном случае и при этом аккумулятор будет разряжаться (Δq > 0). А в первом случае при аккумулятор заряжается (Δq < 0), и количество химической энергии, запасенной в аккумуляторе после замыкания ключа, равно работе батареи:
Теперь запишем закон сохранения энергии (1) –
– и найдем выделившееся количество теплоты:
Задача 4. Плоский конденсатор находится во внешнем однородном поле с напряженностью , перпендикулярной пластинам. На пластинах площадью S распределены заряды +q и –q. Расстояние между пластинами d. Какую минимальную работу надо совершить, чтобы поменять пластины местами? Расположить параллельно полю? Вынуть из поля?
Работа будет минимальной, когда процесс проводится очень медленно — при этом не выделяется тепло. Тогда, согласно закону сохранения энергии,
Чтобы найти ΔW, воспользуемся формулой (3). Поле между пластинами представляет собой суперпозицию поля данного плоского конденсатора –
– и внешнего поля .
При перемене пластин местами поле меняется на –, а поле снаружи не меняется, т. е. изменение энергии системы связано с изменением ее плотности между пластинами конденсатора:
Если направления векторов и были одинаковы, то плотность энергии между пластинами уменьшилась после перемены пластин местами, а если направления были противоположны, то плотность энергии увеличилась. Таким образом, в первом случае — конденсатор хочет сам развернуться и его надо удерживать (A < 0), а во втором случае
Когда пластины конденсатора расположены параллельно полю и перпендикулярны друг другу. Энергия поля внутри конденсатора в этом случае равна . Тогда
Когда конденсатор вынули из поля, в том месте, где он был, поле стало , а в нем самом теперь поле , т.е. ΔW и Amin оказываются такими же, как и в предыдущем случае.
Задача 5. Конденсатор емкостью С без диэлектрика заряжен зарядом q. Какое количество теплоты выделится в конденсаторе, если его заполнить веществом с диэлектрической проницаемостью ε? То же, но конденсатор присоединен к батарее с ЭДС .
При заливании диэлектрика емкость конденсатора увеличилась в ε раз.
В первом случае фиксирован заряд на пластинах, внешних сил нет, и закон сохранения энергии (1) имеет вид
Отсюда
Тепло выделяется за счет уменьшения энергии взаимодействия зарядов.
Во втором случае есть работа батареи и фиксировано напряжение на конденсаторе:
Тогда из уравнения (1) следует
Задача 6. Две соединенные проводником пластины площадью S каждая находятся на расстоянии d друг от друга (это расстояние мало по сравнению с размерами пластин) во внешнем однородном поле с напряженностью , перпендикулярной пластинам (рис. 3). Какую работу надо совершить, чтобы сблизить их до расстояния d/2?
Рис. 3
Пластины эквипотенциальны, и между ними поля нет. Результатом работы по сближению является создание поля с напряженностью Е в объеме . Тогда, в соответствии с уравнениями (1) и (3),
Упражнения
1. Два одинаковых плоских конденсатора емкостью С каждый соединены параллельно и заряжены до напряжения U. Пластины одного из конденсаторов медленно разводят на большое расстояние. Какая при этом совершается работа?
2. Два конденсатора, каждый емкостью С, заряжены до напряжения U и соединены через резистор (рис. 4). Пластины одного из конденсаторов быстро раздвигают, так что расстояние между ними увеличивается вдвое, а заряд на пластинах за время их перемещения не изменяется. Какое количество теплоты выделится в резисторе?
Рис. 4
3. Плоский воздушный конденсатор присоединен к батарее с ЭДС . Площадь пластин S, расстояние между ними d. В конденсаторе находится металлическая плита толщиной d1, параллельная пластинам (рис. 5). Какую минимальную работу нужно затратить, чтобы удалить плиту из конденсатора?
Рис. 5
4. Большая тонкая проводящая пластина площадью S и толщиной d помещена в однородное электрическое поле с напряженностью , перпендикулярной поверхности пластины. Какое количество теплоты выделится в пластине, если поле мгновенно выключить? Какую минимальную работу надо совершить, чтобы удалить пластину из поля?
5. Одна из пластин плоского конденсатора подвешена на пружине (рис. 6). Площадь каждой пластины S, расстояние между ними в начальный момент d. Конденсатор на короткое время подключили к батарее, и он зарядился до напряжения U. Какой должна быть минимальная жесткость пружины, чтобы не произошло касание пластин? Смещением пластин за время зарядки пренебречь.
Рис. 6
Ответы.
1. (весь заряд оказывается на конденсаторе, пластины которого не раздвигали).
2. (в первый момент после разведения пластин замкнутыми друг на друга оказываются конденсатор емкостью С с напряжением U и конденсатор емкостью С/2 с напряжением 2U).
3. (минимальная работа по удалению плиты равна разности изменения энергии конденсатора и работы батареи).
4. (сразу после выключения внешнего поля в пластине есть поле поляризационных зарядов, напряженность которого равна Е удаление пластины из поля эквивалентно созданию поля с напряженностью Е в объеме пластины).
5. (результат получается из закона сохранения энергии и из условия равновесия пластины ).
| Теплоёмкость | |
|---|---|
 |
|
| Размерность | L2MT −2Θ−1 |
| Единицы измерения | |
| СИ | Дж/К |
| СГС | эрг/К |
| Примечания | |
| Скалярная величина |
Теплоёмкость — количество теплоты, поглощаемой (выделяемой) телом в процессе нагревания (остывания) на 1 кельвин. Более точно, теплоёмкость — физическая величина, определяемая как отношение количества теплоты 


Малое количество теплоты обозначается 


Удельная, молярная и объёмная теплоёмкости[править | править код]
Очевидно, что чем больше масса тела, тем больше требуется теплоты для его нагревания, и теплоёмкость тела пропорциональна количеству вещества, содержащегося в нём. Количество вещества может характеризоваться массой или количеством молей. Поэтому удобно пользоваться понятиями удельной теплоёмкости (теплоёмкости единицы массы тела):
и молярной теплоёмкости (теплоёмкости одного моля вещества):
где 



Объёмная теплоёмкость (теплоёмкость единицы объёма тела):
Теплоёмкость для различных процессов и состояний вещества[править | править код]
Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа).
Теплоёмкость идеального газа[править | править код]
Теплоёмкость системы невзаимодействующих частиц (например, идеального газа) определяется числом степеней свободы частиц.
Молярная теплоёмкость при постоянном объёме:
где 

Молярная теплоёмкость при постоянном давлении связана с 
Теплоёмкость кристаллов[править | править код]

Сравнение моделей Дебая и Эйнштейна для теплоёмкости твёрдого тела
Существует несколько теорий теплоёмкости твёрдого тела:
- Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определённой точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).
- Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.
- Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.
Температурная зависимость[править | править код]
С ростом температуры теплоёмкость растёт у кристаллов, практически не меняется у жидкостей и газов.
При фазовом переходе происходит скачок теплоёмкости. Теплоёмкость вблизи самого фазового перехода стремится к бесконечности, поскольку температура фазового перехода остаётся постоянной при изменении теплоты.

Удельная теплоёмкость воды при различных давлениях
Примечания[править | править код]
- ↑ Теплоёмкость. БРЭ, 2016.
- ↑ Булидорова Г. В. и др., Физическая химия, кн. 1, 2016, с. 41.
- ↑ Артемов А. В., Физическая химия, 2013, с. 14.
- ↑ Ипполитов Е. Г. и др., Физическая химия, 2005, с. 20.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2006, с. 65.
- ↑ Сивухин Д. В., Термодинамика и молекулярная физика, 2006, с. 66.
- ↑ 1 2 Лифшиц Е. М., Теплоёмкость, 1992.
- ↑ Белов Г. В., Термодинамика, ч. 1, 2017, с. 94.
- ↑ Лифшиц Е. М., Теплоёмкость, 1976.
- ↑ Базаров И. П., Термодинамика, 2010, с. 39.
- ↑ Борщевский А. Я., Физическая химия, т. 1, 2017, с. 115.
- ↑ Кубо Р., Термодинамика, 1970, с. 22.
- ↑ Беляев Н. М., Термодинамика, 1987, с. 5.
- ↑ 1 2 Никеров. В. А. Физика: учебник и практикум для академического бакалавриата. — Юрайт, 2015. — С. 127—129. — 415 с. — ISBN 978-5-9916-4820-2.
- ↑ 1 2 Ильин В. А. Физика: учебник и практикум для прикладного бакалавриата. — Юрайт, 2016. — С. 142—143. — 399 с. — ISBN 978-5-9916-6343-4.
Литература[править | править код]
- Артемов А. В. Физическая химия. — М.: Академия, 2013. — 288 с. — (Бакалавриат). — ISBN 978-5-7695-9550-9.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
- Белов Г. В. Термодинамика. Часть 1. — 2-е изд., испр. и доп. — М.: Юрайт, 2017. — 265 с. — (Бакалавр. Академический курс). — ISBN 978-5-534-02731-0.
- Беляев Н. М. Термодинамика. — Киев: Вища школа, 1987. — 344 с.
- Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — (Высшее образование: Бакалавриат). — ISBN 978-5-16-104227-4.
- Булидорова Г. В., Галяметдинов Ю. Г., Ярошевская Х. М., Барабанов В.П. Физическая химия. Книга 1. Основы химической термодинамики. Фазовые равновесия. — М.: КДУ; Университетская книга, 2016. — 516 с. — ISBN 978-5-91304-600-0.
- Ипполитов Е. Г., Артемов А. В., Батраков В.В. Физическая химия / Под ред. Е. Г. Ипполитова. — М.: Академия, 2005. — 448 с. — (Высшее профессиональное образование). — ISBN 978-5-7695-1456-6.
- Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
- Лифшиц Е. М. Теплоёмкость // Физическая энциклопедия / Ред. А. М. Прохоров. — М.: Большая Советская Энциклопедия, 1992. — Т. 5. — С. 77–78.
- Лифшиц Е. М. Теплоёмкость // Большая советская энциклопедия / Ред. А. М. Прохоров. — 3-е издание. — М.: Большая Советская Энциклопедия, 1976. — Т. 25. — С. 451.
- Сивухин Д. В. Общий курс физики. — Издание 5-е, исправленное. — М.: Физматлит, 2006. — Т. II. Термодинамика и молекулярная физика. — 544 с. — ISBN 5-9221-0601-5.
- Теплоемкость // Большая российская энциклопедия. — М.: Большая российская энциклопедия, 2016. — Т. 32. — С. 54.
Потребность в расчетах количества
теплоты в научной и инженерной практике
появилась задолго до «рождения»
термодинамики. Эта потребность
стимулировала появление специальной
науки – калориметрии, в которой
центральным понятием является понятие
теплоемкости. Исторически термин
«емкость теплоты» перешел в «теплоемкость»,
которая различается по многим
характеристикам.
Определение. Истинной теплоемкостью
вещества называется отношение бесконечно
малого количества теплоты к бесконечно
малому изменению температуры:
![]()
Дж/К (2.9)
Смысл слова «истинная» состоит в том,
что бесконечно малое приращение
температуры dT берется от
какой-то температуры Т. Поэтому истинная
теплоемкость является функцией от самой
температуры (параметр, влияющий на
свойства вещества).
Наверное, понятно, что при одном и том
же изменении температуры dT элементарное
количество теплоты dQ и,
следовательно, теплоемкость при таком
изменении зависят от количественной
меры вещества. В химической технологии
– это число молей (кмоль), в технике и
быту количество вещества определяют
или массой m (кг), или
объемом V0 при нормальных условиях
(нм3)(в химии р0 = 760 мм. рт. ст,
Т0 = 298К). Поэтому истинную теплоемкость
относят (уделяют) на одну из этих
мер. Соответственно, получается удельная
истинная теплоемкость массовая, мольная
и объемная. Их обозначения (не
стандартизованы) и размерность следующие:
[c] = Дж/кгК, [μc] = Дж/кмольК,
[c΄] = Дж/нм3К.
Определение. Средней теплоемкостью
называется

, ΔT = t2
– t1 (2.10)
Индекс «m» внизу у значка теплоемкости
присвоен для обозначения слова «средний»
(от английского слова middle или немецкого
mittel). По существу, средняя теплоемкость
– это средне интегральная величина
истинной теплоемкости.
Иными словами, средняя теплоемкость
вещества в каком-то интервале температуры
– это количество теплоты, которое
надо подвести (отвести) к (от) рабочему
телу, чтобы изменить его температуру
на 1 градус.
Так как удельное (полное) количество
теплоты q (Q) является функцией процесса,
то в калориметрии пришлось отдельно
рассматривать теплоемкости по процессам:
изохорную (v = const) и изобарную (p = const), так
как эти процессы наиболее часто
применяются на практике (емкости, трубы,
аппараты и т.д.) Обозначение этих
теплоемкостей (калорических величин)
следующее: ср, сv
или
![]()
,
![]()
для истинных и средних теплоемкостей
соответственно.
В итоге выстраивается обширная
классификация теплоемкостей: по
интервалам температур на истинные и
средние, по количествам вещества на
массовые, мольные и объемные; по свойствам
самих веществ; и, наконец, по множеству
видов процессов, среди которых чаще
всего встречаются изохорный и изобарный.
Это численное и содержательное обилие
теплоемкостей требует внимательного
отношения к символам и размерностям
рассмотренной калорической величины.
Мы рекомендуем студентам в своей учебной
работе всякий раз четко понимать и
обозначать, о какой же теплоемкости
в их расчетах идет речь (а их оказалось
7 видов без учета свойств веществ, а с
ними и номенклатуры теплоемкостей). При
любых расчетах всегда надо
указывать размерность и номенклатуру
(т.е. название) используемой теплоемкости.
Тогда удельное количество теплоты
находится как:
q =
![]()
ΔT,
Дж/кг, q = μ![]()
ΔT, Дж/кмоль, и q
=
![]()
ΔT,
Дж/нм3.
А полное количество теплоты находится
как:
Q = mq = m
ΔT, Q = nq
= n μ
ΔT,
Q = V0q
= V0
ΔT
, Дж.
Соотношение теплоемкостей, отнесенных
к разным количествам вещества следующее:
μс = μ∙с = с΄∙22,4 кДж/кмольК. (2.11)
Примечание: конкретное освоение и
расчет теплоемкостей рассматривается
на лабораторной работе №2 «Определение
объемной теплоемкости воздуха при
постоянном давлении».
. Существуют многочисленные табличные
данные в справочной литературе по этим
величинам теплоемкостей. Но для
прикидочных расчетов, в которых нет
особых требований к точности результата,
полезно пользоваться постоянными
величинами теплоемкостей, которые
приводятся в таблице ниже.
Таблица приближенных значений мольных
теплоемкостей газов при невысоких
температурах.
-
Газ
μcv,
кДж/кмоль КОдноатомный
12,6
Двухатомный
20,9
Трех и более атомный
29,1
Окончательно: теплоемкость, как
калорическая (тепловая) величина, не
относится к категории функций состояния
и тем более к параметрам состояния.
Строго говоря, понятие теплоемкости
чуждо термодинамике, так как количество
термического воздействия внешней среды
на систему можно рассчитать и без
теплоемкости как dq = Tds. Тем не менее
обилие справочного материала по
теплоемкости для большого числа веществ
и привычка к этой калорической
характеристике сделали ее широко
употребительной в термодинамических
и других физико-химических расчетах.
Теперь с помощью простых физических
соображений покажем, что изобарная
теплоемкость любого вещества всегда
больше изохорной (ср > cv).
Сначала проведем мысленный эксперимент,
как бы используя экспериментальную
установку на рис.2.5.
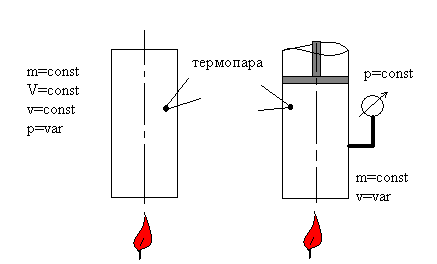
Рис.2.5. Схема двух экспериментов.
Измеряемые величины: температура Т с
помощью термопар,
давление р с помощью манометра, количество
теплоты q.
В первом случае (слева) просто нагреваем
баллон с газом, во втором – нагреваем
и поддерживаем постоянное давление в
сосуде, позволяя газу расширяться.
Зададимся вопросом: «В каком случае
необходимо подвести больше теплоты,
если начальная температура Т и ее
изменение ΔТ в обоих случаях одинаковы?».
Или иначе: «Какая теплоемкость больше:
ср или сv?».
Ответ основывается на принципиальном
различии экспериментов: слева
термодинамическая система деформационно
изолирована от внешней среды, т.е. не
может совершить работу dw = pdv, а справа
– может. И газ по-прежнему нагревается
на ΔТ от подведенной теплоты qv
= cvΔT,
а во втором случае qp
= qv(ΔT)
+ q(w) ≡ cpΔT.
Поэтому ответ на поставленный вопрос:
ср > сv.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет количества теплоты при нагревании и охлаждении:
Вы уже знаете, что изменить внутреннюю энергию тела можно передачей ему количества теплоты. Как связано изменение внутренней энергии тела, т. е. количество теплоты, с характеристиками самого тела?
Внутренняя энергия тела есть суммарная энергия всех его частиц. Значит, если массу данного тела увеличить в два или три раза, то и количество теплоты, необходимое для его нагревания на одно и то же число градусов, увеличится в два или три раза. Например, на нагревание двух килограммов воды от 20 °C до 80 °C потребуется в два раза больше теплоты, чем на нагревание одного килограмма воды (рис. 40, а).
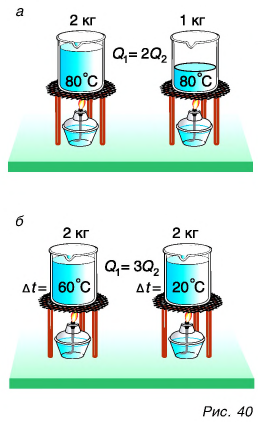
Очевидно также, что для нагревания воды на 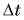
Из этих рассуждений следует подтвержденный опытами вывод. Количество теплоты, необходимое для нагревания тела, прямо пропорционально его массе и изменению температуры.
А зависит ли количество теплоты, идущее на нагревание, от рода вещества, которое нагревается?
Для ответа на этот вопрос проведем опыт. В два одинаковых стакана нальем по 150 г подсолнечного масла и воды. Поместим в них термометры и поставим на нагреватель (рис. 41).
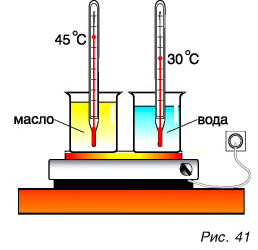
Получив за одинаковое время от нагревателя равное с водой количество теплоты, масло нагрелось больше, чем вода. Значит, для изменения температуры масла на одну и ту же величину требуется меньше теплоты, чем для изменения температуры такой же массы воды.
Поэтому для всех веществ вводят специальную величину — удельную теплоемкость вещества. Эту величину обозначают буквой с (от лат. capacite — емкость, вместимость). Теперь мы можем записать строгую формулу для количества теплоты, необходимого для нагревания:
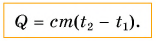
Выразим из этой формулы с: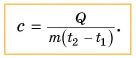
Удельная теплоемкость есть физическая величина, численно равная количеству теплоты, которое необходимо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C. Удельная теплоемкость измеряется в джоулях на килограмм-градус Цельсия 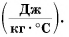
Для любознательных:
Часто формулу 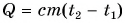 записывают в виде
записывают в виде 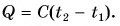 Здесь величина
Здесь величина 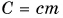 называется теплоемкостью тела (обратите внимание — не вещества). Она численно равна количеству теплоты, необходимому для нагревания всей массы тела на 1 °C. Измеряется теплоемкость тела в джоулях на градус Цельсия
называется теплоемкостью тела (обратите внимание — не вещества). Она численно равна количеству теплоты, необходимому для нагревания всей массы тела на 1 °C. Измеряется теплоемкость тела в джоулях на градус Цельсия 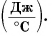
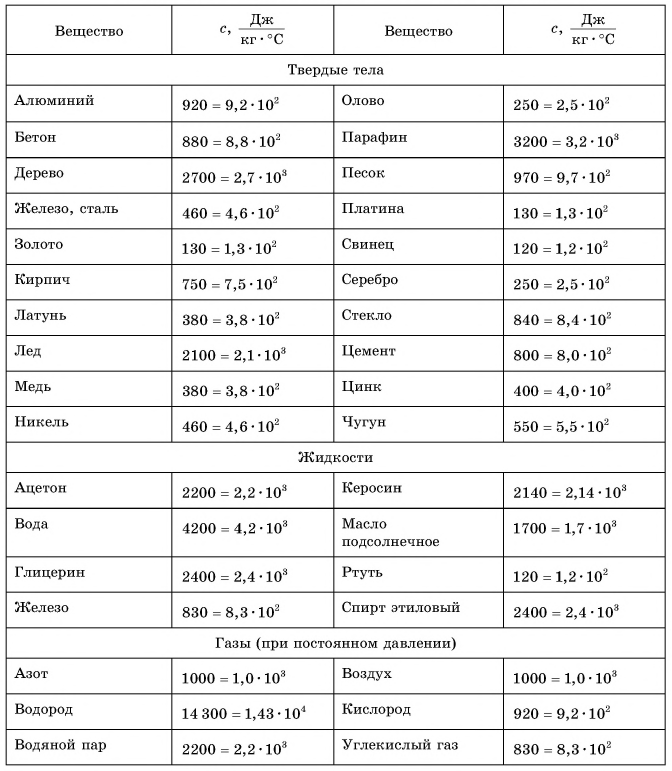
В таблице 1 представлены значения удельной теплоемкости различных веществ (в различных состояниях). Как следует из этой таблицы, среди жидкостей максимальное значение удельной теплоемкости имеет вода: для нагревания 1 кг воды на 1 °C требуется 4200 Дж теплоты — это почти в 2,5 раза больше, чем для нагревания 1 кг подсолнечного масла, и в 35 раз больше, чем для нагревания 1 кг ртути.
Формула 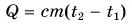 дает возможность найти и выделяемую при охлаждении тела теплоту. Так как конечная температура
дает возможность найти и выделяемую при охлаждении тела теплоту. Так как конечная температура 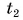 остывшего тела меньше начальной
остывшего тела меньше начальной 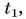 то изменение температуры оказывается отрицательным числом. Значит, и выделяемое телом количество теплоты выражается отрицательным числом, что обозначает не рост, а убыль внутренней энергии тела.
то изменение температуры оказывается отрицательным числом. Значит, и выделяемое телом количество теплоты выражается отрицательным числом, что обозначает не рост, а убыль внутренней энергии тела.
В заключение заметим, что при теплообмене двух или нескольких тел абсолютное значение количества теплоты, которое отдано более нагретым телом (телами), равно количеству теплоты, которое получено более холодным телом (телами):
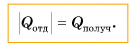
Это равенство называется уравнением теплового баланса и выражает, по сути, закон сохранения энергии. Оно справедливо при отсутствии потерь теплоты.
Таблица 1. Удельная теплоемкость некоторых веществ
Главные выводы:
- Количество теплоты, необходимое для нагревания тела (выделившееся при охлаждении), прямо пропорционально его массе, изменению температуры тела и зависит от вещества тела.
- Удельная теплоемкость вещества численно равна количеству теплоты, которое надо передать 1 кг данного вещества, чтобы изменить его температуру на 1 °C.
- При теплообмене количество теплоты, отданное более горячим телом, равно по модулю количеству теплоты, полученному более холодным телом, если нет потерь теплоты.
- Заказать решение задач по физике
Пример решения задачи:
Для купания ребенка в ванночку влили холодную воду массой 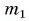 = 20 кг при температуре
= 20 кг при температуре 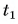 = 12 °C. Какую массу горячей воды при температуре
= 12 °C. Какую массу горячей воды при температуре 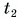 = 80 °C нужно добавить в ванночку, чтобы окончательная температура воды стала
= 80 °C нужно добавить в ванночку, чтобы окончательная температура воды стала 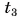 = 37 °C? Удельная теплоемкость воды с = 4200
= 37 °C? Удельная теплоемкость воды с = 4200 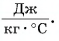
Дано:
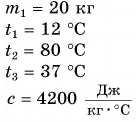
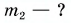
Решение
По закону сохранения энергии 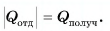
Отдавала теплоту горячая вода, изменяя свою температуру от 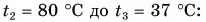
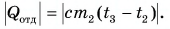
Холодная вода получила эту теплоту и нагрелась от 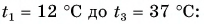
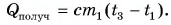
Так как нас интересует только модуль 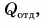 то можно записать:
то можно записать:
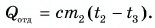
Тогда 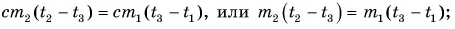
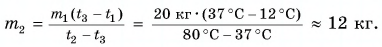
При решении мы пренебрегали потерями теплоты на нагревание ванночки, окружающего воздуха и т. д.
Возможен и другой вариант решения.
Рассчитаем сначала количество теплоты, которое было получено холодной водой:
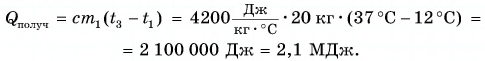
Полагая, что эта теплота отдана горячей водой, запишем: 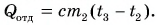 Выразим искомую массу:
Выразим искомую массу:
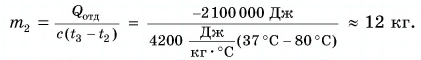
Ответ: 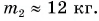
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
- Поверхностное натяжение жидкости
- Излучение тепла в физике
- Виды излучений в физике
- Инфракрасные излучения
- Количество теплоты в физике







