Как найти малую ось цилиндра

Соседние файлы в папке ЭС – Инженерная графика

• #
• #
• #
• #

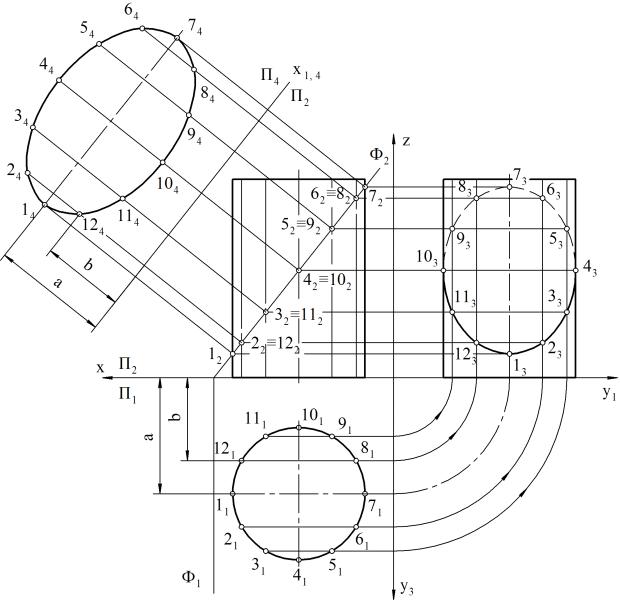
Сечение цилиндра плоскостью

Построение сечения прямого кругового цилиндра аналогично построению сечения призмы, так как прямой круговой цилиндр можно рассматривать как прямую призму с бесчисленным количеством ребер — образующих цилиндра.

Выполнение чертежа начинают с построения трех проекций прямого кругового цилиндра. На поверхности цилиндра проводят несколько равномерно расположенных образующих, в данном примере двенадцать. Для этого горизонтальную проекцию основания делят на 12 равных частей. С помощью линий связи проводят фронтальные проекции образующих цилиндра (рисунок 186).

Из комплексного чертежа видно, что плоскость а” пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под углом к оси цилиндра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса (рисунок 186).

Фронтальная проекция фигуры сечения совпадает с фронтальным следом /₀” плоскости а”. Горизонтальная проекция этой фигуры совпадает с горизонтальной проекцией основания цилиндра.

Профильная проекция фигуры сечения представляет собой проекцию части эллипса и может быть построена по нескольким точкам, которые строятся с помощью линий связи по горизонтальной и фронтальной проекциям фигуры сечения. Полученные таким образом профильные проекции точек фигуры сечения соединяют кривой по лекалу.

Действительный вид фигуры сечения получен на рисунке 186 способом перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой. Новая ось проекций 7г₂/тг₄ может быть проведена параллельно следу /₀” на произвольном расстоянии, но для упрощения построений она выполнена совпадающей с /₀“. От оси л:₂/л:₄ откладывают отрезки 5″5 1У = 5’5_Х, 6″ 6 ,у = 6’6_Х, т. е. отрезки тип и т. д., так как расстояние от новой проекции этой точки до новой оси проекций равно расстоянию от прежней проекции этой точки до прежней оси проекций.

Развертка боковой поверхности усеченного цилиндра с основанием и фигурой сечения показана на рисунке 187.

Для построения развертки на горизонтальной прямой откладывают длину окружности основания, равную nd, и делят ее на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку nd, на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости а’, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки 7₀. 9₀, соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой 1₀9₀ (сегмент), а фигуру нижнего основания цилиндра (окружность) соединяют с нижней частью развертки.

Изометрическую проекцию усеченного цилиндра строят следующим образом (рисунок 188).

Сначала строят изометрию нижнего основания (эллипс) и части верхнего основания — сегмента (часть эллипса). На диаметре окружности нижнего основания от центра откладывают отрезки а, бит. д., взятые с горизонтальной проекции основания (рисунок 186). Затем из намеченных точек проводят прямые, параллельные оси цилиндра до пересечения с осью эллипса.

Через полученные точки проводят прямые, параллельные оси у, и на них откладывают отрезки, взятые с действительного вида сечения. Полученные точки соединяют по лекалу. Заканчивают построение проведением очерковых образующих, касательных к основаниям эллипса.

Сечение геометрических тел плоскостями и развертки их поверхностей с примерами и образцами выполнения

Содержание:

Разверткой (выкройкой) поверхности тела называется плоская фигура, полученная путем совмещения всех точек данной поверхности с плоскостью без разрывов и складок. Построение разверток выполняется обычно графическими приемами, с применением способов, предлагаемых начертательной геометрией.

Понятие о сечениях геометрических тел

Детали машин и приборов очень часто имеют формы, представляющие собой различные геомет­рические поверхности, рассеченные плоскостями (рис. 175). Кроме того, иногда необходимо выпо­лнить развертки поверхности полых деталей, усе­ченных плоскостью. Это применяется в раскрое листового материала, из которого изготовляются полые детали. Такие детали обычно представляют собой части всевозможных трубопроводов, венти­ляционных устройств, кожухов для закрытия механизмов, ограждения станков и т.п. (рис. 176)

Построения прямоугольных и аксонометричес­ких проекций усеченных тел, а также определе­ние истинного вида сечений и разверток повер­хностей геометрических тел часто используются на практике.

Рассекая геометрическое тело плоскостью, по­лучают сечение — ограниченную замкнутую линию. все точки которой принадлежат как секущей плоскости, так и поверхности тела.

При пересечении плоскостью многогранника (например, призмы, пирамиды) в сечении получа­ется многоугольник с вершинами, расположенны­ми на ребрах многогранника. При пересечении плоскостью тел вращения (например, цилиндра, конуса) фигура сечения часто ограничена кривой линией. Точки этой кривой находят с помощью вспомогательных линий — прямых или окружнос­тей, взятых на поверхности тела. Точки пересечения этих линий с секущей плоскостью будут искомыми точками контура криволинейного сече­ния.

Пример сечения плоскостью Р геометрического тела — куба, лежащего на горизонтальной плос­кости проекции Н, показан на рис. 177.

В первом случае (рис 177, а) куб усечен фронтально-проецирующей плоскостью Р. Фигурой сечения является прямоугольник.

При построении двух проекций такого сечения (рис. 177, б) следует иметь в виду, что фронталь­ная проекция фигуры сечения совпадает с фрон­тальным следом секущей плоскости Р_V.

Горизонтальная проекция фигуры сечения — прямоугольник.

Во втором случае (рис. 177, в) куб усечен горизонтально-проецирующей плоскостью Р. Фигура сечения — прямоугольник.

На рис. 177, г приведено построение проекции этого сечения. Горизонтальная проекция фигуры сечения совпадает с горизонтальным следом Р_Н секущей плоскости. Фронтальной проекцией сече­ния будет прямоугольник, одной стороной которо­го является линия пересечения плоскости Р с плоскостью передней грани куба.

Если куб пересечен плоскостью общего положе­ния (рис. 177, д, е), то полученная фигура сече­ния в данном случае (треугольник) проецируется на плоскости проекции V и H с искажением.

Сечение призмы плоскостью

Фигура сечения прямой пятиугольной приз­мы фронтально -проецирующей плоскостью Р (рис. 178, а) представляет собой плоский пяти­угольник 12345.

Для построения проекций фигуры сечения на­ходят проекции точек пересечения плоскости Р с ребрами призмы и соединяют их прямыми линия­ми. Фронтальные проекции этих точек получают­ся при пересечении фронтальных проекций ребер призмы с фронтальным следом P_V секущей плос­кости Р (точки 1’. 5′).

Горизонтальные проекции точек пересечения 1. 5 совпадают с горизонтальными проекциями ребер. Имея две проекции этих точек, с помощью линий связи находят профильные проекции 1”…5”. Полученные точки 1”…5” соединяют пря­мыми линиями и получают профильную проекцию фигуры сечения.

Действительный вид фигуры сечения можно определить любым из способов: вращения, совме­щения или перемены плоскостей проекций (см. гл. 15).

В данном примере (рис. 178, а) применен способ перемены плоскостей проекций. Гори­зонтальная плоскость проекций заменена но­вой Н₁, причем ось х₁ (для упрощения по­строений) совпадает с фронтальным следом плоскости Р.

Для нахождения новой горизонтальной проек­ции какой-либо точки фигуры сечения (например, точки 1) необходимо выполнить следующие по­строения. Из точки 1’ восставляют перпендику­ляр к новой оси х₁ и откладывают на нем расстоя­ние от прежней оси х до прежней горизонтальней проекции точки 1, т.е. отрезок п. В результате получают точку 1₍₎. Так же находят и новые гори­зонтальные проекции точек 2. 5. Соединив пря­мыми линиями новые горизонтальные проекции 1_()….5_о , получают действительный вил фигуры се­чения.

Разверткой называется плоская фигура, полу­ченная при совмещении поверхности геометричес­кого тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).

Развертку боковой поверхности (рис. 178, б) с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на кото­рой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпен­дикуляры, на которых откладывают действитель­ные длины ребер усеченной призмы, беря их с фронтальной или профильной проекции (рис. 178, а), получают развертку боковой повер­хности призмы.

К развертке боковой поверхности пристраивают фигуру нижнего основания — пятиугольник и фигуру сечения. При этом используют метод три­ангуляции (см. рис. 50, б) или метод координат, известный из геометрического черчения. На рис. 178, а показано построение вершины 5 метолом триангуляции. Линии сгиба по ГОСТ 2.303-68 показывают на развертке штрихпунктирной линией с двумя точками.

Для наглядности выполним построение усечен­ного тела в аксонометрической проекции. На рис. 178, в построена изометрическая проекция усеченной призмы. Порядок построения изометри­ческой проекции следующий. Строят изометричес­кую проекцию основания призмы; проводят в вертикальном направлении линии ребер, на кото­рых от основания откладывают их действительные длины, взятые с фронтальной или профильной проекции призмы. Полученные точки сое­диняют прямыми линиями.

Сечение цилиндра плоскостью

Построение сечения прямого кругового цилин­дра аналогично построению сечения призмы, так как прямой круговой цилиндр можно рассматри­вать как прямую призму с бесчисленным множес­твом ребер — образующих цилиндра (рис. 179, а).

Выполнение чертежа начинают с построения трех проекций прямого кругового цилиндра. На поверхности цилиндра проводят несколько равно­мерно расположенных образующих, в данном примере двенадцать. Для этого горизонтальную проекцию основания делят па 12 равных частей. С помощью линий связи проводят фронтальные проекции образующих цилиндра (рис. 179, а).

Из комплексного чертежа видно, что плоскость Р пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под углом к оси цилин­дра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса (рис. 179, в).

Фронтальная проекция фигуры сечения совпа­дает с фронтальным сладом Р_V плоскости Р. Гори­зонтальная проекция этой фигуры совпадает с горизонтальной проекцией основания цилиндра.

Профильная проекция фигуры сечения пред­ставляет собой проекцию части эллипса и может быть построена по нескольким точкам, которые строятся с помощью линий связи по горизонталь­ной и фронтальной проекциям фигуры сечения. Полученные таким образом профильные проекции точек фигуры сечения соединяют кривой по лекалу.

Действительный вид фигуры сечения получен на рис. 179, а способом перемены плоскостей про­екций. Горизонтальная плоскость проекций заме­нена новой. Новая ось проекций x₁ может быть проведена параллельно следу Р_V на произвольном расстоянии, но для упрощения построений она выполнена совпадающей с Р_V (аналогично рис 178). От оси x₁ откладывают отрезки 5’5₀ = 55_x, 4’4₀ = 44_x, т.е. отрезки т, п и т.д., так как расстояние от новой проекции этой точки до но­вой оси проекций равно расстоянию от прежней проекции этой точки до прежней оси проекции.

Развертка боковой поверхности усеченного цилиндра с основанием и фигурой сечения пока­зана на рис. 179, б.

Для построения развертки боковой поверхности на горизонтальной прямой откладывают длину окружности основания, равную πD и делят ее на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку πD, на них откладыва­ют действительные длины образующих цилиндра от основания до секущей плоскости Р, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки 1₁—9₁ соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой l₁9₁ (сегмент), а фигуру нижнего основания цилиндра (окружность) соеди­няют с нижней частью развертки.

Изометрическую проекцию усеченного цилин­дра строят следующим образом (рис. 179, в). Сна­чала строят изометрию нижнего основания (овал) и части верхнего основания — сегмента (часть овала). На диаметре окружности нижнего основа­ния от центра О’ откладывают отрезки а, b и т.д., взятые с горизонтальной проекции основания. Затем из намеченных точек проводят прямые, параллельные оси цилиндра до пересечения с осью эллипса.

Через полученные точки проводят прямые, параллельные оси у, и на них откладывают отрез­ки, взятые с действительного вида сечения. Полу­ченные точки соединяют но лекалу. Заканчивают построение проведением очерковых образующих, касательных к основаниям — овалам.

Пылесборник машины для очистки литых дета­лей (рис. 179, г) представляет собой усеченный цилиндр. Форма крышки А трубы пылесборника является фигурой сечения прямого кругового ци­линдра и представляет собой эллипс.

Сечение пирамиды плоскостью

Правильная шестиугольная пирамида, пересе­ченная фронтально-проецирующей плоскостью Р, показана на рис 180.

Как и в предыдущих примерах, фронтальная проекция сечения совпадает с фронтальным сле­дом Р_V плоскости. Горизонтальную и профильную проекции фигуры сечения строят по точкам, кото­рые являются точками пересечения плоскости Р с ребрами пирамиды.

Действительный вид фигуры сечения в этом примере определяется способом совмещения.

Развертка боковой поверхности усеченной пи­рамиды с фигурой сечения и фигурой основания приведена на рис. 180, б.

Сначала строят развертку неусеченной пирами­ды, все грани которой, имеющие форму треуголь­ника. одинаковы. На плоскости намечают точку s₁ (вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки s”e” или s”b”, так как зги ребра парал­лельны плоскости W и изображаются на ней дей­ствительной длиной. Далее по дуге окружности от любой точки, например а₁, откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника — основания пира­миды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab).Точки а₁… f₁ соединяют прямыми с вершиной s₁. Затем от вершины а₁ на этих пря­мых откладывают действительные длины отрезков ребер до секущей плоскости.

На профильной проекции усеченной пирамиды имеются действительные длины только двух отрезков — s”5 и s”2. Действительные длины ос­тальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к плоскости Н и проходящей через вершину s. Например, повер­нув отрезок s”6“ около оси до положения, парал­лельного плоскости W, получим на этой плоскости его действительную длину. Для этого достаточно через точку 6″ провести горизонтальную прямую до пересечения с действительной длиной ребра SE или SB. Отрезок s”6“ ₀ (см. рис. 180).

Полученные точки 1₁, 2₁, 3₁ и т.д. соединяют прямыми и пристраивают фигуры основания и сечения, пользуясь методом триангуляции. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.

Построение изометрической проекции усечен­ной пирамиды начинают с построения изометри­ческой проекции основания пирамиды по разме­рам, взятым с горизонтальной проекции комплек­сного чертежа. Затем на плоскости основания по координатам точек 1. 6 строят горизонтальную проекцию сечения (см. тонкие синие линии на рис. 180, а, в). Из вершин полученного шести­угольника проводят вертикальные прямые, на которых откладывают координаты, взятые с фронтальной или профильной проекций призмы, на­пример, отрезки К₁ К₂, К₃ И т.д. Полученные точки I. 6 соединяем, получаем фигуру сечения. Соединив точки 1. 6 с вершинами шестиугольни­ка, основания пирамиды, получим изометричес­кую проекцию усеченной пирамиды. Невидимые ребра изображают штриховыми линиями.

Пример сечения треугольной неправильной пирамиды фронтально-проецируемой плоскостью показан на рис. 181.

Все ребра на трех плоскостях проекций изображены с искажением. Горизонтальная проекция основания представляет собой его действительный вид, так как основание пирамиды расположено на плоскости Н.

Действительный вид 1₀, 2₀, 3₀ фигуры сечения получен способом перемены плоскостей проекций. В данном примере горизонтальная плоскость про­екций Н заменена новой плоскостью, которая параллельна плоскости Р новая ось х₁ совмещена со следом (рис. 181, а).

Развертку поверхности пирамиды строят следу­ющим образом. Способом вращения находят дей­ствительную длину ребер пирамиды и их отрезков от основания до секущей плоскости Р.

Например, действительные длины ребра SC и его отрезка СЗ равна соответственно длине фрон­тальной проекции s’с’ ребра и отрезка с’₁ 3₁ после поворота.

Затем строят развертку треугольной неправиль­ной пирамиды (рис. 181, в). Для этого из произвольной точки S проводят прямую, на которой откладывают действительную длину ребра SA. Из точки s делают засечку радиусом R₁ равным действительной длине ребра SB ,а из точки А — засечку радиусом R₂, равным стороне основания пирамиды AB, в результате чего получают точку b₁ и грань s₁b₁а₁ пирамиды. Затем из точек s и b₁, как из центров, делают засечки радиусами, равными действительной длине ребра SC и его стороне ВС, и получают грань s₁b₁c₁ пирамиды. Также строится грань s₁с₁а_1.

Для построения изометрической проекции усе­ченной пирамиды (рис. 181. б) проводят изомет­рическую ось х. По координатам т и п строят основание пирамиды АВС. Сторона основания АС параллельна оси х или совпадает с осью х. Как и в предыдущем примере, строят изометрическую проекцию горизонтальной проекции фигуры сече­ния 1₂2₂3₂ (используя точки I, III и IV). Из этих точек проводят вертикальные прямые, на которых откладывают отрезки, взятые с фронтальной или профильной проекции призмы К₁, К₂ и К₃. Полу­ченные точки 1, 2. 3 соединяют прямыми между собой и с вершинами основания.

Сечение прямого кругового конуса плоскостью

В зависимости от расположения секцией плос­кости Р относительно оси прямого кругового кону­са получаются различные фигуры сечения, ограниченные кривыми линиями.

Сечение прямого кругового конуса фронтально-проецирующей плоскостью Р рассматривается на рис. 182. Основание конуса расположено на плос­кости Н. Фигура сечения в данном случае будет ограничена эллипсом.

Фронтальная проекция фигуры сечения распо­ложена на фронтальном следе плоскости Р (рис. 182. а).

Для построения горизонтальной проекции кон­тура фигуры сечения горизонтальную проекцию основания конуса (окружности) делят, например, на 12 равных частей. Через точки деления на горизонтальной и фронтальной проекциях прово­дят вспомогательные образующие. Сначала нахо­дят фронтальные проекции точек сечения 1‘. 12’, лежащих на плоскости Р₁. Затем с по­мощью линии связи находят их горизонтальные проекции. Например, горизонтальная проекция точки 2, расположенной на образующей s2, прое­цируется на горизонтальную проекцию этой же образующей в точку 2.

Найденные горизонтальные проекции точек контура сечения соединяют по лекалу. Действи­тельный вид фигуры сечения в данном примере найден способом перемены плоскости проекции. Плоскость H заменяется новой плоскостью проек­ции H₁.

На фронтальной плоскости проекции V фигура сечения — эллипс изображается в виде прямой 1’7′, совпадающей с фронтальной проекцией секущей плоскости Р. Эта прямая 1’7’ является большой осью эллипса. Малая ось эллипса а’Ь’ перпендикулярна к большой оси 1’7′ и проходит через ее середину. Чтобы найти малую ось сече­ния, через середину большой оси 1’7′ эллипса проводят горизонтальную плоскость N, которая рассечет конус по окружности, диаметр которой будет равняться малой оси эллипса (a₀b₀).

Построение развертки поверхности конуса (рис. 182, б) начинают с проведения дуги окружности радиусом, равным длине образующей кону­са из точки s₀. Длина дуги определяется углом α:

где d — диаметр окружности основания конуса; l — длина образующей конуса .

Дугу делят на 12 частей и полученные точки соединяют с вершиной s₀. От вершины откладывают действительные длины отрезков образующих от вершины конуса до секущей плоскости Р.

Действительные длины этих отрезков находят, как и в примере с пирамидой, способом вращения около вертикальной оси, проводящей через вер­шину конуса. Так, например, чтобы получить действительную длину отрезка S2, надо из 2‘ про­вести горизонтальную прямую до пересечения в точке Ь’ с контурной образующей конуса, являю­щейся действительной ее длиной.

К развертке конической поверхности пристраивают фигуры сечения и основания конуса.

Построение изометрической проекции усечен­ного конуса (рис. 182, в) начинают с построения основания—эллипса. Изометрическую проекцию любой точки кривой сечения находят с помощью трех координат, как показано на рис. 182, в.

На оси х откладывают точки I…VII, взятые с горизонтальной проекции конуса. Из полученных точек проводят вертикальные прямые, на которых откладывают координаты z, взятые с фронтальной проекции. Через полученные на наклонной оси эллипса точки проводят прямые, параллельные оси у, и на них откладывают отрезки 6₀8₀ и 4₀10_0, взятые на действительном виде сечения.

Найденные точки соединяют по лекалу. Край­ние очерковые образующие проводят по каса­тельной к контуру основания конуса и эллипса.

Пример сечения прямого кругового конуса при­веден на рис. 182, г. Колпак сепаратора представ­ляет собой сварную конструкцию из тонкой лис­товой стали и состоит из двух конусов.

Развертка сферической поверхности

Горизонтальную проекцию сферической поверхности делим горизонтально-проецирующими плоскостями на несколько равных частей (клинь­ев), например на 12 (рис. 183, а). Фронтальную проекцию сферы поверхности тоже делят на не­сколько равных частей (желательно на 12).

Через полученные точки деления II. VI прово­дят фронтально- проецирующие плоскости Р_V1… Р_V5 (рис. 183, а).

Для построения развертки сферической повер­хности на горизонтальной прямой откладывают длину окружности диаметра D, равную πD (рис. 183, б). Полученный отрезок делят на 12 равных частей.

Через середину каждого деления проводят пер­пендикуляр и откладывают на нем отрезок I—VII, равный 0.5 длине окружности диаметра D. Отрезок I—VII делят на 6 равных частей, через полу­ченные точки деления проводят горизонтальные прямые, на которых откладывают отрезки, равные 1/12 части окружности соответствующего радиуса, например, отрезок с₁с₂ соответствует 1/12 длине окружности радиуса I—II, взятого с горизонталь­ной проекции. Полученные точки соединяют по лекалу. Развертки остальных одиннадцати клинь­ев строят аналогично.

На рис. 184 и 185 приведены примеры исполь­зования развертки сферической поверхности.

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Развертки поверхностей в начертательной геометрии с примерами

Содержание:

Развертки поверхностей:

Развертыванием поверхности называется такое преобразование, в результате которого поверхность всеми точками совмещается с плоскостью. Полученная при этом плоская фигура называется разверткой.

Поверхности делятся на развертываемые и неразвертываемые.

Разветываемые поверхности совмещаются с плоскостью без разрывов и складок. Признаком развертываемости является пересечение соседних образующих или их параллельность. К развертываемым поверхностям относятся многогранные, цилиндрические, конические, торсовые. Развертки многогранников строятся точно, учитываются лишь погрешности инструмента и графических построений. Развертки цилиндрических, конических и торсовых поверхностей получаются приближенно, так как эти поверхности заменяются вписанными в них или описанными около них многогранными поверхностями, которые и развертываются.

Неразвертываемые поверхности с плоскостью не совмещаются, т.е. теоретически они разверток не имеют, так как образующие их скрещиваются. К неразвертываемым относятся поверхности с плоскостью параллелизма (цилиндроид, коноид, косая плоскость), криволинейные (сфера, тор и т.п.) и графические.

В инженерной практике строятся условные развертки неразверты-ваемых поверхностей. Для этого неразвертываемая поверхность делится на части (доли), которые заменяются развертываемыми поверхностями.

Если рассматривать поверхность и ее развертку как множество точек, то между этими множествами устанавливается взаимооднозначное соответствие, т.е. каждой точке на поверхности соответствует единственная точка на развертке и наоборот.

Свойства развертки

1. Прямая на поверхности переходит в прямую на развертке.

2. Параллельные прямые на поверхности будут параллельными прямыми на развертке.

3. На развертке сохраняются:

• – длина линии, лежащей на поверхности;
• – величина угла между линиями поверхности;
• – величина площади фигуры на поверхности.

Развертки прямых круговых цилиндра и конуса

Развертка боковой поверхности прямого кругового цилиндра представляет собой прямоугольник, высота которого равна высоте цилиндра, а длина – длине окружности основания

Развертка боковой поверхности прямого кругового конуса (рис. 241) представляет собой круговой сектор. Длина дуги

Отложив центральный угол и проведя дугу из центра радиусом строят точную развертку прямого кругового конуса, не считая графических погрешностей.

Развертки линейчатых поверхностей

Способ триангуляции

Способ триангуляции (треугольников) универсален, его можно применять для построения разверток любых поверхностей, в том числе и криволинейных (например, подвесные сферические своды). Однако способ триангуляции не всегда является рациональным. Для каждой группы поверхностей рекомендуется соответствующий графический способ построения разверток. Все линейчатые поверхности, включая и неразвертываемые (цилиндроид, коноид, косая плоскость), можно развернуть способом триангуляции.

Сущность способа заключается в следующем:

1. Криволинейная поверхность заменяется вписанной в нее многогранной поверхностью. Так, на рис. 242 в наклонный эллиптический конус (нормальное сечение – эллипс) с круговым основанием вписана двенадцатигранная пирамида. Для этого основание конуса разбивается па 12 равных частей.

Исследование точности построения разверток показало, что оптимально деление окружности на 12 частей. При делении на 8 и менее частей длина кривой на развертке получается значительно короче длины окружности основания. При делении более чем на 12 частей, увеличивается величина графических неточностей. Полученные после деления окружности дуги заменяются стягивающими хордами. Затем проводятся образующие которые являются ребрами вписанной пирамиды.

2. Определяются натуральные величины сторон каждого треугольника У данной поверхности образующие являются фронталями, их фронтальные проекции равны натуральной величине и Все остальные образующие – прямые общего положения. Их натуральные величины удобно определять вращением вокруг оси проходящей через вершину конуса перпендикулярно горизонтальной плоскости проекции. Натуральные величины образующих равны соответственно отрезкам и т.д.

Третьей стороной у каждого треугольника являются хорды, которые на горизонтальную плоскость проекций проецируются без искажения. Натуральные величины хорд

3. Развертка выполняется последовательным построением всех треугольников. Каждый треугольник строят по трем сторонам, натуральные величины которых известны. Если отсек поверхности симметричен, то развертку следует выполнять также симметричной и построение начинать с оси симметрии. Допускается строить половину развертки, которая с одной стороны должна быть ограничена осевой линией. Рекомендуется поверхность разрезать по самой короткой образующей, чтобы длина соединительных “швов” была наименьшей.

Осевая линия располагается на чертеже вертикально или горизонтально. На ней откладывается отрезок Из точки 1 проводится дуга радиусом а из точки – вторая дуга радиусом до пересечения с первой в точке 2: соединив тонкими линиями точки 1 и 2, и 2, получаем Аналогично пристраивается и т.д. Точки 1, 2, 3 соединяются плавной кривой. Контур развертки обводится основной линией до оси симметрии (см. рис. 242).

На развертках часто приходится строить линии, расположенные на поверхностях. К ним относятся линии пересечения двух поверхностей и сечения поверхности плоскостью.

Для построения на развертке точки выполняют следующее:

1. через данную точку проводят линию, лежащую на поверхности и удобную для построения (чаще всего это прямая или окружность). На рис. 242 точка принадлежит образующей
2. определяют натуральную величину этой линии и на нее переносят рассматриваемую точку. На рис. 242 – натуральная величина образующей и точка
3. на развертке строят соответствующую линию. Образующая располагается между образующими и Отрезок равен хорде, а расстояние берется равным натуральной величине –

Способ нормального сечения

Способ применяется для построения разверток призматических и цилиндрических поверхностей.

При построении развертки призматической поверхности необходимо все ее грани последовательно совместить с плоскостью. В общем случае (наклонная призма с непараллельными основаниями) боковые грани призмы – трапеции. Чтобы построить натуральные величины этих граней, необходимо определить натуральные величины ребер призмы, которые являются основаниями трапеций – отрезки и (рис. 243). Кроме того, нужно знать или расстояние между ребрами – высоты трапеций, или натуральные величины сторон основания призмы и – боковые стороны трапеций.

В зависимости от того, высота или боковые стороны применяются при построении разверток, различают два способа: нормального сечения и раскатки. В первом способе расстояние между образующими определяется при помощи нормального сечения. В способе раскатки используются натуральные величины сторон основания призмы.

Развертка призматической поверхности строится точно, не считая графических погрешностей. При построении развертки цилиндрической поверхности необходимо сначала вписать в нее призматическую поверхность, которую затем развернуть. Следовательно, развертка цилиндрической поверхности является приближенной.

На рис. 244 показано построение развертки наклонной призмы способом нормального сечения. При помощи нормального сечения, перпендикулярного к образующим, определяют расстояния между ними. Способ целесообразно применять в тех случаях, когда основания призмы или цилиндра заданы в общем положении.

1) определяются натуральные величины образующих, если они заданы в общем положении (см. рис. 244). Натуральные величины ребер определяются проецированием на дополнительную плоскость проекций параллельную ребрам: Тогда -натуральные величины ребер;

2) строится нормальное сечение перпендикулярно ребрам призмы. Так как ребра параллельны плоскости то сечение вырождается в прямую линию – прямая) и является проецирующим относительно Относительно плоскостей и это сечение занимает общее положение;

3) определяется натуральная величина нормального сечения любым способом. В данном примере она определена проецированием на плоскость Проекция – натуральная величина;

4) строится развертка следующим образом:

а) периметр нормального сечения “развертывается” в прямую линию, на которой то есть эти отрезки равны расстояниям между образующими (ребрами):

б) через точки 1, 2, 3 проводятся образующие, перпендикулярные развертке нормального сечения;

в) на этих линиях откладываются натуральные величины образующих: и т.д.;

г) полученные точки соединяются ломаной линией.

На рис. 244 показано построение на развертке точки принадлежащей поверхности призмы. Точка принадлежит образующей, параллельной ребрам.

Развертки криволинейных поверхностей вращения

Криволинейные поверхности вращения (сфера, тор и др.) относятся к неразвертываемым, их нельзя совместить с плоскостью без разрывов и складок, поэтому при выполнении их из листового материала строятся условные развертки.

1. поверхность разрезается по меридианам или параллелям на ряд частей;
2. каждая такая часть заменяется вписанной или описанной развертываемой поверхностью (цилиндрической или конической);
3. строятся развертки отдельных частей, из которых затем собирается заданная поверхность.

При разрезании по меридианам каждая доля заменяется описанной цилиндрической поверхностью. Такой прием называется способом вспомогательных цилиндров.

При разрезании по параллелям поверхность разбивается на ряд поясов, которые заменяются вписанными коническими поверхностями. Этот прием называется способом вспомогательных конусов.

Способ вспомогательных цилиндров

Построение развертки сферы способом вспомогательных цилиндров показано на рис. 245:

1. поверхность сферы меридиональными плоскостями и разрезают на равные части (доли). Рекомендуется разбивать ее не менее чем на 12 частей. В примере принято 6 долей для того, чтобы отрезки были крупнее и чертеж более четким;
2. каждую такую долю заменяют описанной цилиндрической поверхностью, касающейся ее по линии симметрии доли.

Цилиндрическая поверхность касается доли I по главному меридиану. Разделив его на 6 равных частей, через точки 2, 3, 4, 5, 6 проводят параллели – окружности. Затем строят образующие цилиндра, касающиеся параллелей в точках 2, 3, 6. Образующие являются фронтально-проецирующими. Таким образом, цилиндрическая поверхность, касательная к доле I, является фронтально-проецирующей и фронтальная проекция ее совпадает с главным меридианом

3) строят развертку каждого описанного цилиндра способом нормального сечения:

а) нормальным сечением доли 1 является главный меридиан, который развертывается в отрезок вертикальной прямой. На ней откладывают отрезки, равные фронтальным проекциям хорд: и т.д.;

б) через полученные точки 2, 3, 4, 5, 6 проводят образующие цилиндра перпендикулярно ”развертке” нормального сечения. Размеры образующих берут с горизонтальной проекции Через полученные точки и проводят плавную кривую. Развертка каждой доли имеет вертикальную и горизонтальную оси симметрии, поэтому, построив 1/4 часть развертки, аналогично строят остальные 3/4. Полная развертка сферы будет состоять из шести (двенадцати) таких долей. На практике подобные развертки удобно делать по шаблону. На рис. 245 такой шаблон заштрихован.

Местоположение точки на развертке, как и любой точки на плоскости, определяется двумя координатами – вертикальной и горизонтальной. Вертикальная координата – расстояние от точки соседней параллели, горизонтальная – от оси симметрии. Вертикальная координата берется с фронтальной проекции, горизонтальная – c горизонтальной плоскости проекций.

Способ вспомогательных конусов

Построение развертки сферы этим способом показано на рис. 246:

1) поверхность сферы разрезается по параллелям горизонтальными плоскостями на ряд поясов и два сегмента;

2) в полученные шаровые пояса и сегменты вписываются поверхности вращения, оси которых совпадают с осью сферы, а основания – с соответствующими параллелями.

В шаровой сегмент IV вписывается полный конус вращения, вершина которого совпадает с точкой пересечения оси вращения с главным меридианом сферы.

В шаровые пояса III и II вписываются усеченные конусы вращения. Образующие конусов совпадают с хордами и Вершины конусов и получаются на пересечении этих образующих с осью вращения.

В экваториальный пояс I вписывается цилиндр вращения;

3) строятся развертки вписанных поверхностей.

Разверткой конуса является сектор, радиус которого равен образующей конуса. Для пояса II – образующая для III – для IV – Центры секторов рекомендуется размещать на одной линии, принимаемой за ось симметрии разверток. Длины дуг секторов равны длинам параллелей окружностей соответствующих поясов. Их размеры берутся с горизонтальной плоскости проекций, для этого окружности делятся на 12 частей. Так, длина дуги на развертке равна длине горизонтальной проекции параллели

Построенные части I и II соединяются между собой по линиям II и III – по линиям III и IV – по линиям

Примеры построения разверток некоторых поверхностей

Задача 1 (рис. 247). Дано: поверхность цилиндроида, плоскостью параллелизма которой является плоскость проекций

Требуется: построить развертку способом триангуляции.

1. В заданную поверхность вписывается многогранная поверхность. Окружность нижнего основания разбивается на 12 равных частей. Окружность верхнего основания лежит в профильной плоскости уровня, поэтому дополнительно строится полуокружность, соответствующая его профильной проекции. Полуокружность разбивается на 6 равных частей. Полученные дуги заменяются стягивающими хордами, точки деления переносят на фронтальную и горизонтальную проекции верхнего основания. Затем проводятся образующие и диагонали

В результате получается многогранная поверхность, ограниченная треугольниками

2. Определяются натуральные величины диагоналей (способом плоскопараллельного перемещения). У образующих натуральными величинами являются их фронтальные проекции, т.к. все они параллельны – плоскости параллелизма данного цилиндроида.

3. Строится развертка. Заданная поверхность имеет плоскость симметрии, поэтому развертка будет симметричной и достаточно построить ее половину.

Поверхность разрезается по наименьшей образующей тогда образующая совпадает с осью симметрии развертки, которая на чертеже занимает вертикальное положение. К ней пристраивается треугольник со сторонами: – фронтальная проекция образующей, – натуральная величина диагонали, — профильная проекция хорды, стягивающей 1/12 часть окружности верхнего основания.

На стороне строится второй треугольник у которого – натуральная величина образующей, – горизонтальная проекция хорды, стягивающей 1/12 часть нижнего основания.

Аналогично продолжается построение следующих треугольников. Полученные точки нижнего основания (1, 2, 3. 7) и верхнего основания соединяются по лекалу плавной линией.

Задача 2 (рис. 248). Дано: отвод под углом 90° (1/4 часть тора).

Требуется: построить развертку поверхности тора способом описанных цилиндров.

1. Поверхность тора проецирующими меридиональными плоскостями делится на четыре части. Деление надо произвести так, чтобы у крайних звеньев с торца получались окружности, к которым присоединяются трубопроводы круглого сечения. С этой целью торцевые звенья делаются равными половине средних. Торцевые звенья равняются 1/6 части отвода и их центральный угол равен 15°, а средние равны 2/6 частям каждый, центральный угол которых 30°.

2. Все звенья кругового кольца заменяются описанными цилиндрами. Нормальным сечением этих цилиндров является окружность /, образующая тор. Эта окружность делится на 8 (или 12) частей. Через точки деления 2, 3. 8 проводятся параллели (на фронтальной проекции это четверти окружностей радиусами Затем строятся образующие цилиндров, касательные к параллелям. У крайних звеньев точки касания расположены на торцевых окружностях, а у средних – на линии симметрии.

3. Строятся развертки описанных цилиндров способом нормального сечения. Нормальное сечение каждой части (сечение, перпендикулярное образующим цилиндров) есть окружность заданного диаметра которая разворачивается в прямую линию. На рис. 248 ”развертка” нормального сечения изображается отрезком 1, 2, 3, 8, 1 горизонтальной прямой. Перпендикулярно к этой линии через точки 1, 2, 3 и т.д. проводятся образующие цилиндров, размеры которых берут с фронтальной проекции. Для торцевых звеньев образующие Полученные точки и соединяют плавной кривой линией. Развертка звена симметрична относительно образующей На практике обычно строится шаблон половины развертки торцевого звена (на рис. 248 заштрихованная часть). Повернув его вокруг образующей очерчивается вторая половина развертки. На развертке среднего звена укладываются 4 таких шаблона.

Весь тор можно раскроить из единого листа без обрезков. Для этого развертки звеньев надо разместить на листе так, как показано на рис. 248. Из чертежа видно, что звенья разрезаются попеременно, то по образующей то по образующей Таким образом, при сборке тора швы на звеньях получаются прерывистыми.

В практике при раскрое даются припуски на швы в соответствии с типом соединения.

Развертка поверхностей

Разверткой поверхности называется плоская фигура, полученная путем совмещения элементов поверхности с плоскостью.

Если для поверхности можно построить её развертку точно без складок и разрывов, то поверхность называется развертываемой, в противном случае – неразвертываемой.

К развертываемым поверхностям относятся все гранные, а из линейчатых только -цилиндрические, конические и поверхности е ребром возврата.

Построение разверток развертываемых поверхностей

Существуют следующие способы построения разверток развертываемых поверхностей:

1. Способ триангуляции (треугольников);
2. Способ раскатки;
3. Способ нормального сечения.

Способ триангуляции (треугольников) применяется для построения разверток пирамидальных и конических поверхностей. Они выполняются по одному принципу. Каждая грань пирамиды представляет треугольник и для построения развертки необходимо определить натуральные величины всех сторон треугольника. По найденным натуральным величинам сторон вычерчиваются последовательно треугольные грани. Коническая поверхность, заменяется вписанной в нее, пирамидальной и решение задачи ведется аналогично пирамиде.

Рассмотрим пример, построения развертки, конической поверхности (рисунок 10.1)

Для построения развертки в конус вписываем двенадцатигранную пирамиду. Т.к. по условию конус расположен симметрично относительно оси, построим половину развертки.

Образующие конуса имеют разную длину, поэтому натуральную величину определяем вращением до положения параллельного фронтальной плоскости проекций. Только образующие проецируются в натуральную величину. По полученным натуральным величинам образующих и размерам хорд окружности основания, между образующими, строим половину развертки, состоящую из шести треугольников вписанной в конус пирамиды. Точки основания соединяем плавной кривой линией.

Способ раскатки применяется для построения разверток призматической и цилиндрической поверхности. И если поверхность цилиндрическая, то в нее вписывается призматическая поверхность. Поэтому принцип построения этих разверток одинаков.

Рассмотрим пример построения развертки наклонной треугольной призмы

Развертку можно выполнять только в том случае, если боковые ребра призмы параллельны плоскости проекций, как на рисунке 10.2. В противном случае, сначала выполняется преобразование (методом замены строится новая проекция на плоскость параллельную ребрам). При выполнении развертки методом раскатки точки перемещаются по перпендикулярам к боковым ребрам призмы. А натуральные величины отрезков берутся из горизонтальной проекции, т.к. основание призмы параллельно плоскости Боковые ребра остаются на развертке параллельными, т.к. каждая грань призмы является параллелограммом.

Способ нормального сечения используется также для построения разверток призматической и цилиндрической поверхностей.

Рассмотрим построение развертки призмы изображенной на рисунке 10.3а. Для этого построим нормальное сечение – сечение перпендикулярное боковым ребрам призмы Определим натуральную величину этого сечения, расположив его параллельно плоскости проекций Для построения развертки боковой поверхности призмы, строим периметр треугольника нормального сечения (рисунок 10.36). Через точки сечения 1,2,3,1 проводим боковые ребра перпендикулярно сечению и откладываем на них натуральную величину, которая берется из фронтальной проекции рисунка 10.3а.

Соединив построенные точки, получим развертку боковой поверхности данной призмы (рисунок 10.36).

Построение приближенной развертки неразвёртываемых поверхностей

Когда надо развернуть неразвертывающуюся поверхность ее заменяют развертывающейся (цилиндрической, конической, одной или несколькими), имеющей общие линии е данной.

Такая замена называется аппроксимацией, а полученная развертка – условной или приближенной.

Рассмотрим построение такой развертки на примере полусферы (рисунок 10.4).

Полусферическую поверхность разделим меридиональными плоскостями на дольки (на 12 частей). По высоте сферу делим на несколько частей параллелями. Возьмем одну дольку, ось которой параллельна фронтальной проекции и развернем ее в плоскую фигуру, ось которой будет равна длины окружности (рисунок 10.5).

Через точки 1,2,3,4 проводим перпендикуляры к оси дольки и на них откладываем от оси в обе стороны половину ширины каждой дольки измеренную на горизонтальной проекции. Полная развертка составит двенадцать таких долек.

Если развертывающаяся долька начинается с экватора, то на развертке линия экватора изобразится прямой (рисунок 10.5). Если же долька начинается какой-то параллелью, то на развертке эта параллель изобразится окружностью. Например, параллель, проходящая через точку 3. Для нахождения радиуса этой окружности на фронтальной проекции необходимо провести касательную прямую в точке 5, к окружности до пересечения с осью сферы . И при построении дольки через точку 3 проводим дугу радиуса (рисунок 10.6).

Решение задач

Задача 1. Построить развертку усеченного прямого кругового цилиндра (рисунок

Развертка боковой поверхности цилиндра строится фактически методом нормального сечения, т.к. основание цилиндра перпендикулярно оси. Окружность основания развертывается в прямую линию равную длине окружности Можно ее построить, отложив размер хорд, соединяющих точки основания. Конечно, длина будет тем точнее, чем на большее число частей разбита окружность. Кривая сечения на развертке изобразится синусоидой (рисунок 10.7,б) Для построения полной развертки необходимо к развертке боковой поверхности добавить основание и натуральную величину сечения.

Задача 2. Построить развертку усеченного прямого кругового конуса (рисунок

Так как в прямом круговом конусе все образующие одинаковой длины, развертка представляет собой сектор окружности с радиусом равным длине образующей конуса а длина дуги равная длине окружности основания конуса (рисунок 10.86). Поэтому, разделив окружность основания на 12 частей и затем, отложив на дуге сектора таких же 12 частей, получим развертку.

Угол а также можно определить по формуле:

где d – диаметр основания.

Что такое развертка поверхности

Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).

Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью.

Если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой.

Свойства развёртки

Длины двух соответствующих линий поверхности и ее развертки равны между собой;

Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;

Прямой на поверхности соответствует также прямая на развертке;

Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;

Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.

Способы построения развёртки

Существует три способа построения развертки многогранных поверхностей:

1. Способ треугольника
2. Способ нормального сечения
3. Способ раскатки

К развертывающим поверхностям относятся все поверхности гранные, то есть поверхности, состоящие из отсеков плоскостей. Из кривых поверхностей к ним относятся только те линейчатые поверхности. У которых касательная плоскость касается поверхности о всех точках ее прямолинейной образующей. Этому условию удовлетворяют три типа линейчатых поверхностей: цилиндрическая, коническая, торсовая [1].

Все остальные поверхности относятся к неразвёртывающимся или косым.

Развертки могут быть точными. Это развертки прямого кругового цилиндра и конуса. Если пренебречь графическими ошибками, то к точным развёрткам можно отнести развертки многогранников.

Развертки всех других поверхностей как развертывающихся, так и неразвёртывающихся, которые, как правило, строятся графически, являются приближенными.

Любая конструкция рассматривается как комбинация простейших геометрических поверхностей.

Рассмотрим наиболее простую гранную поверхность.

Развертки гранных поверхностей

Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.

Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины истинных размеров и формы отдельных граней поверхности – плоских многоугольников и вычерчиванию их в том порядке, в каком они следуют друг за другом на самой поверхности.

Рассмотрим на примере решение задачи

Развертка поверхности прямой призмы

Представим, что поверхности призмы разрезана по ребру АА1.

Развернем ее боковую поверхность и совместим се грани с плоскостью чертежа (рис.10.1) [1].

Так как призма прямая, то ее основание развернется в прямую линию. Поэтому на свободном поле чертежа проведем прямую линию, на которой произвольно выберем точку А. От этой точки развернем основание призмы. Поскольку основание данной призмы проецируется на горизонтальную плоскость проекций в натуральную величину, на прямой от точки А последовательно отложим отрезки, равные соответствующим сторонам основания.

Рисунок 10.1- Развертка поверхности прямой призмы

Учитывая, что призма прямая и ее ребра проецируются на фронтальную плоскость проекций в натуральную величину, к прямой – развёртке основания в точках – проведем перпендикуляры, на которых отложим величину ребра. Соединив точки , получим развертку боковой поверхности призмы.

Полная развертка призмы состоит из развертки ее боковой поверхности и двух оснований – верхнего и нижнего.

Так как призма прямая, и ее основание проецируется на горизонтальную плоскость проекций в натуральную величину, к боковой развертке в любом месте пристраиваем два четырехугольника , перенося их адекватно с горизонтальной проекции призмы.

Развертка поверхности наклонной призмы

Построение развёртки может быть выполнено способом нормального (перпендикулярного) сечения. Способом раскатки и способом треугольников (триангуляция). Рассмотрим каждый способ в раздельности [1].

Построение развертки способом нормального сечения (рис.10.2).

Рисунок 10.2 – Построение развертки призмы способом нормального сечения

Если разрезать боковую поверхность наклонной призмы по любому ребру и совместить с плоскостью чертежа, то очевидно, что основание такой призмы развернется не в прямую, а в ломаную линию.

Если же призму пересечь плоскостью, перпендикулярной рёбрам, то полученное при этом сечение при развертывании даст прямую линию. Поэтому для решения задачи необходимо:

1. Пересечь призму плоскостью, перпендикулярной ее ребрам;
2. Найти проекции сечения вспомогательной плоскости с призмой;
3. Определить истинную величину нормального сечения;
4. Развернуть полученный четырехугольник сечения прямую линию;
5. Отложить вверх и вниз от этой линии истинные величины отрезков ребер относительно сечения призмы.

Проведем плоскость Р, перпендикулярную ребрам призмы (рис.10.2 а).

Эта плоскость Р – фронтально проецирующая и следы ее будут перпенди-кулярны соответствующим проекциям ребер.

Найдем проекции сечения призмы плоскостью Р. Фронтальные проекции точек пересечения ребер с плоскостью лежат на ее фронтальном следе , горизонтальные проекции определяются по линиям связи. Соединив проекции точек прямыми, получим проекции сечения.

Истинную величину фигуры (четырёхугольника) сечения определяем любым способом, например. Способом замены плоскостей проекций.

На свободном поле чертежа (рис.10.2 б) проведём горизонтальную прямую, на которой последовательно отложим от точки истинные величины сторон четырехугольного сечения. Через точки проведем перпендикуляры к прямой, на которых откладываем истинные величины отрезков боковых ребер вверх и вниз от прямой , перенося соответствующие отрезки с фронтальной проекции призмы (так как ребра призмы параллельны плоскости проекций V). Соединив концы сложенных отрезков, получим развертку боковой поверхности призмы.

Развертка призмы способом раскатки

Так как основание призмы на горизонтальной плоскости проекций изображается в натуральную величину, ее развертку можно построить более удобным способом, чем способ нормального сечения.

Построения развертки призмы способом раскатки показано на рис 10.3.

Поскольку ребра призмы параллельны фронтальной плоскости проек-ций, то каждую грань можно повернуть вокруг бокового ребра (как вокруг фронтали) до положения, при котором грань будет параллельна плоскости V и спроецируется на эту плоскость без искажения. Разворачивая таким образом одну грань за другой по порядку, получим развертку боковой поверхности.

Практически такое построение выполняется следующим образом [1] .

Так как при повороте грани вокруг ребра точка В будет перемещаться по окружности, фронтальная проекция которой изображается прямой, перпендикулярной , через точку проведем прямую, перпен-дикулярную Радиусом равным истинной величине стороны основания призмы из точки делаем засечку на перпендикуляре.

Таким образом, находим точку развертки. Через точку проведем прямую, параллельную на которой откладываем истинную величину ребра призмы, т.е. величину его фронтальной проекции, получим точку

Рисунок 10.3 – Построение развертки призмы способом раскатки

Из точки проведем перпендикуляр к Сделав в нем засечку радиусом из точки найдем точку развертки. Через проведем прямую, параллельную и отложим на ней величину ребра призмы. Получим точку Аналогичным способом определяются точки Соединив их прямыми, соответствующими сторонам оснований, получим развертку боковой поверхности призмы.

Следует отметить, что если ребра призмы не параллельны плоскости проекций, а развертку необходимо выполнить раскаткой, то предварительно меняют плоскости проекций новой системой, в которой ребра окажутся параллельными одной из плоскостей проекций.

Построение развертки пирамиды (способ треугольника)

Так как боковые грани наклонной призмы являются парраллелограммами, для построение их истиной величины недостаточно иметь только истинные значения ребер и сторон основания призмы. Для этого необходима еще одна величина – диагонали, что и положено в основу построения развертки боковой поверхности призмы способом треугольника [1].

При построении развертки следует:

1. Разбить каждую из граней призмы диагоналями на треугольники;
2. Определить длину неизвестных сторон треугольника (например, методом плоскопараллельного перемещения);
3. Построить треугольники в плоскости чертежа в той последователь-ности, в которой они расположены в многограннике.

Задача. Построить развертку поверхности пирамиды SABC (рис.10.4).

Развернутая поверхность пирамиды состоит из треугольника – ее боковых граней, расположенных в определенной последовательности, и основания.

Для построения боковых граней – треугольника развертки, необходимо определить истинные длины боковых ребер с учетом того, что основание пирамиды на горизонтальной проекции изображается в натуральную величину. Используем наиболее простой способ – способ вращения. Выберем ось вращения I, перпендикулярную плоскости H и проходящую через вершину пирамиды S. Поворачивая вокруг оси горизонтальные проекции ребер до положения, параллельного оси X, получим на фронтальной проекции отрезки представляющие собой истинные длины ребер пирамиды.

Каждая боковая грань строится как треугольник по трем известным сторонам, и развертка получается в виде примыкающих друг к другу в соответствующем порядке треугольников с общей вершиной S.

Рисунок 10.4 – Построение развертки пирамиды

Развертывание поверхностей вращения

Как было упомянуто ранее, развертки кривых поверхностей, как правило, строятся приближенные. Даже для таких развертывающихся поверхностей как цилиндрическая и коническая, которые имеют теоретические точные развертки, на практике строят их приближенными, заменяя (аппроксимируя) эти поверхности гранными, вписывая или описывая их вокруг заданной поверхности.

Надо иметь в виду, что если развертываемый элемент имеет плоскость симметрии, то линию разреза поверхности лучше выбирать так, чтобы развертка получалась в виде симметричной фигуры. При этом предпочтительнее выбирать наиболее короткую линию разреза.

Развёртка цилиндрической поверхности

Развертка цилиндрической поверхности выполняется аналогично развертке призмы. Предварительно в заданный цилиндр вписывают n-угольную призму. Чем больше углов в призме, тем точнее развертка ( при n → ∞ призма преобразуется в цилиндр).

На рис. 10.6. приведено построение полной развёртки усечённого цилиндра (см. условия задания рис. 8.2) стр. 61.

Для построения развертки боковой поверхности на горизонтальной прямой откладывают длину окружности основания πd и делят ее на 12 равных частей (с определенной степенью точности вместо 1/12 длины окружности можно откладывать длину соответствующей хорды) [5]. Из точек деления проводят перпендикуляры к отрезку πd и на них откладывают длины образующих от основания до секущих плоскостей α , β, χ. Для построения точек А, В, С, D на развертке использовано расположение этих точек на горизонтальной проекции цилиндра (от точек деления откладывают длины дуг 2А и 12В) Точки 1, А, С и 1, В, D соединены прямыми линиями.

Точки С, 3. 11, D соединяют плавной линией.

Рисунок 10.6 – Полная развёртка поверхности усечённого цилиндра.

К прямой линии πd (развертка нижнего основания цилиндра) присоединяют окружность основания, а к верхней части боковой развертки натуральные фигуры сечения плоскостями (часть эллипса, прямоугольник, сегмент окружности).

Развертка поверхности конуса

Развертка боковой поверхности прямого кругового конуса с радиусом снованием r представляет собой круговой сектор, радиус которого равен длине образующей конуса L, а центральный угол φ=Пr/L.

Чтобы избежать вычислений, связанных с определением длины дуги сектора или угла, вначале в основанием конуса вписывают правильный 12-угольник. Затем на свободном поле чертежа из точки S проводят дугу радиусом l. От произвольно выбранной начальной точки по дуге последо-вательно засекают 12 дуг, хорды которых равны стороне 12-угольника.

Таким образом, построение развертки боковой поверхности конуса заменяют построением развертки, вписанной в него правильной 12-гранной пирамиды [1] (рис. 10.7).

Рисунок 10.7 – Построение развертки боковой поверхности конуса

На рисунке 10.7 построена развертка боковой поверхности конуса и нанесена ней линия сечения плоскостью P.

В конус впишем правильную 12-гранную пирамиду. Для этого основание конуса разбиваем на 12 равных частей (рис. 7 а). На фронтальной плоскости проекций получим фронтальные проекции (на оси X) точек деления 1″, 2″ ,3″ и т.д. и соединим их с точкой S′ (1″s″, 2″s″, 3″s″, 4″s″ и т.д. – фронтальные проекции образующих конуса, т.е. ребер вписанной пирамиды).

На свободном поле чертежа из произвольно выбранной точки S, проведем угу радиусом L и отложим на ней 12 дуг, хорды которых равны сторонам основания пирамиды (рис. 10.7). Полученные точки соединим с вершиной S, в результате чего образуется развертка боковой поверхности конуса.

Затем на ней строим линию сечения. Для этого найдем истинные величины отрезков образующих, или ребер пирамиды, от вершины до плоскости сечения. Истинные величины можно найти любым способом. Найденные отрезки отложим на соответствующих образующих на развертке. Полученные точки соединим плавной кривой. Последняя и будет линией сечения.

Развертка наклонных тел вращения

Развертки наклонных тел вращения строятся аналогично предыдущим задачам, т.е. поверхность вращения аппроксимируется гранной ( пирамидой или призмой) соответственно с максимально возможным числом граней, а затем используются все те же методы решения, что и при развертке гранных поверхностей.

На рис.10.8 приведено построение полной равертки наклонного конуса [1].

Рисунок 10.8 – Построение полной развертки наклонного конуса

Построение условной развертки сферы

На рисунке 10.9 показано построение условной развертки сферы [5].

Так как сферическая поверхность принадлежит к числу не развертывающихся, то возможна лишь ее приближенная (условная) развертка. Способ построения состоит в том, что сферу разбивают с помощью меридианов на узкие равные между собой доли (клинья). Каждую такую долю заменяют описанной цилиндрической поверхностью, которая касается сферы по среднему меридиану доли. Этот средний меридиан будет нормальным сечением цилиндрической поверхности. Границами цилиндрической поверхности будут плоскости меридианов, ограничивающих рассматриваемую долю.

Рисунок 10.9 – Построение условной развертки сферы.

Горизонтальную проекцию n’ экватора n разбиваем на 12 равных частей и через полученные точки проводим горизонтальные проекции меридианов ( рис. 10.9 а).

Рассмотрим построение приближенной развертки 1/12 части (доли) сферы, средним меридианом которой является меридиан

Заменим часть сферы цилиндрической поверхностью. Описанной около нее. Образующие этой поверхности будут фронтально-проецирующими прямыми. Для построения развертки элемента цилиндрической поверхности половину фронтального меридиана разбиваем на 6 равных частей (отмечены точками 1, 2, 3, 4 только половина симметричной части). На горизонтальной прямой (рис. 8.14,б) откладываем отрезок равный 1/12 окружности диаметра D. Через середину проводим перпендикуляр и откладываем на нем отрезки равные длине дуг меридиана m. Через полученные точки проводим горизонтальные прямые, на которых откладываем отрезки соответственно равные длине образующим цилиндрической поверхности C-D, E-F. Отрезки A-B, C-D, E-F представляют собой спрямленные дуги соответствующих параллелей сферической доли. Соединив найденные точки лекальной кривой. Получим плоскую фигуру, являющейся приближенной разверткой 1/12 части сферы.

Для придания каждой доли развертки сферической поверхности кроме изгибания проводят растяжение и сжатие материала.

Положение произвольной точки К принадлежащей поверхности сферы, может быть определено на развертке с помощью двух «координат» – длин дуг Дуга определяет смещение точки Л от одной из параллелей по меридиану, а дуга – смещение ее от одного из меридианов по параллели сферы.

Построение развёрток поверхностей

Развёрткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга.)

Развертка усеченной призмы

Развертку боковой поверхности с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпендикуляры, на которых откладывают действительные длины ребер усеченной призмы, беря их с фронтальной или профильной проекции, получают развертку боковой поверхности призмы.

К развертке боковой поверхности пристраивают фигуру нижнего основания — пятиугольник и фигуру сечения. При этом используют метод триангуляции (метод засечек). На рисунке показано построение вершины 5 методом триангуляции. Линии сгиба по ГОСТ 2.303—68 показывают на развертке штрих-пунктирной линией с двумя точками.

Развертка усеченного цилиндра

Для построения развертки на горизонтальной прямой откладывают длину окружности основания, равную и делят ее на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку , на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости Р, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой (сегмент), а фигуру нижнего основания цилиндра (окружность) соединяют с нижней частью развертки.

Развертка усеченной пирамиды

Сначала строят развертку неусеченной пирамиды, все грани которой, имеющие форму треугольника, одинаковы. На плоскости намечают точку (вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки s”e” или s”b’, так как эти ребра параллельны плоскости W и изображаются на ней действительной длиной. Далее по дуге окружности от любой точки, например откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника — основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab). Точки соединяют прямыми с вершиной ..Затем от вершины на этих прямых откладывают действительные длины отрезков ребер до секущей плоскости.

На профильной проекции усеченной пирамиды имеются действительные длины только двух отрезков — Действительные длины остальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к плоскости Н и проходящей через вершину Например, повернув отрезок s”6″ около оси до положения, параллельного плоскости W, получим на этой плоскости его действительную длину. Для этого достаточно через точку 6” провести горизонтальную прямую до пересечения с действительной длиной ребра SE (или SB). Отрезок представляет собой действительную длину отрезка S6 .

Полученные точки и т. д. соединяют прямыми и пристраивают фигуры основания и сечения, пользуясь методом триангуляции. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.

Развертка усеченного конуса

Построение развертки поверхности конуса начинают с проведения дуги окружности радиусом, равным длине образующей конуса из точки л». Длина дуги определяется углом а:

где d — диаметр окружности основания конуса в мм;

l — длина образующей конуса в мм.

Дугу делят на 12 частей и полученные точки соединяют с вершиной л>. От вершины откладывают действительные длины отрезков образующих от вершины конуса до секущей плоскости Р.

Действительные длины этих отрезков находят, как и в примере с пирамидой, способом вращения около вертикальной оси, проходящей через вершину конуса. Так, например, чтобы получить действительную длину отрезка S2, надо из 2′ провести горизонтальную прямую до пересечения в точке с контурной образующей конуса, являющейся действительной ее длиной.

К развертке конической поверхности пристраивают фигуры сечения и основания конуса.

Развертки поверхностей

Фигура, получающаяся при совмещении всех точек поверхности с плоскостью (без складок и разрывов), получила название развертки. Поверхности же, допускающие такую операцию, называют развертывающимися.

Построение разверток является важной практической задачей, что связано с изготовлением множества изделий из листового материала (резервуары и трубы, изделия швейной и кожевенной промышленности и т.п.).

Из физической модели процесса развертывания поверхности на плоскость следует, что площадь отсека поверхности должна быть равна площади отсека плоскости на развертке.

Свойство сохранения площади влечет за собой справедливость следующих двух утверждений: длины соответственных линий поверхности и ее развертки равны, углы, образованные линиями поверхности, равны углам, составленным их образами на развертке. Углом между двумя линиями поверхности в их точке пересечения называют угол, составленный касательными, проведенными к кривым в точке.

Это в свою очередь приводит к следующему: прямая поверхности отображается на прямую развертки; параллельные прямые поверхности, отображаются на параллельные прямые развертки.

На этих свойствах и базируются графические и машинные алгоритмы построения разверток.

Из дифференциальной геометрии известно, что к развертывающимся поверхностям относятся только поверхности нулевой кривизны (состоящие только из параболических точек). У этих (линейчатых) поверхностей касательные плоскости, проведенные во всех точках одной образующей, совпадают.

Изо всего множества линейчатых поверхностей развернуты на плоскость могут быть только цилиндрические, конические и торсовые. Развертки для них строятся приближенно. В процессе построения развертки эти поверхности аппроксимируются (заменяются) многогранными поверхностями. Последнее вызвано тем, что спрямление кривых линий базируется на замене их ломаными. Точные развертки аппроксимирующих многогранных поверхностей принимают за приближенные развертки развертываемых поверхностей.

Развертки гранных поверхностен

Процесс получения развертки гранной поверхности сводится к совмещению с плоскостью ее граней. Для гранной поверхности всегда можно построить развертку.

К наиболее распространенным многогранным поверхностям следует отнести призмы и пирамиды.

Развертка поверхности призмы строится в основном двумя способами, с помощью треугольников (триангуляции) и нормальных сечений.

первом способе каждая грань призмы разбивается на два треугольника, для которых определяются натуральные длины сторон. Затем на плоскости последовательно строят треугольники в натуральную величину. Способ основан на свойстве «жесткости» треугольника — три отрезка определяют единственный треугольник.

По способу нормальных сечений призма пересекается плоскостью перпендикулярной ее боковым ребрам. Затем определяются длины сторон ломаной линии (сечения), и она (ломаная) развертывается в отрезок прямой.

Через точки, соответствующие положению вершин, проводятся прямые, перпендикулярные к развертке ломаной. На построенных перпендикулярах откладываются натуральные длины соответствующих отрезков ребер. Концы ребер последовательно соединяются отрезками прямых.

При необходимости к построенной развертке боковой поверхности призмы пристраиваются натуральные фигуры оснований призмы.

Способ нормальных сечений эффективен, если ребра призмы являются линиями уровня. Если же при этом основания призмы расположены в плоскостях уровня, то реализуется частный случай этого способа — способ раскатки (рисунок 10.4).

Построение развертки поверхности пирамиды сводится к отысканию истинных величин граней этой пирамиды и последующему совмещению их с плоскостью. Для нахождения истинных величин граней необходимо (каким-либо способом) найти натуральные длины всех ребер пирамиды (рисунок 11.33).

Приближенное построение разверток

Выше было отмечено, что для всех поверхностей строятся приближенные развертки. Однако для таких поверхностей, как цилиндрическая и коническая поверхности вращения, могут быть вычислены все параметры необходимые для точной развертки.

Отсек цилиндра вращения радиуса R и высоты h развертывается в прямоугольник Развертка усеченного цилиндра представлена на рисунке 11.31.

Отсек конуса вращения с высотой h и радиусом основания R развертывается в круговой сектор, радиус которого равен длине образующей отсека конической поверхности ,а его центральный угол a—

Построение разверток поверхностей начинается с аппроксимации их многогранными поверхностями, базирующейся на линейной аппроксимации направляющих. Как правило, кривая заменяется вписанной ломаной. Проиллюстрируем все выше сказанное примерами.

Развертка боковой поверхности усеченного конуса вращения представлена на рисунке 10.3.

Развертывание боковой поверхности усеченного конуса, в общем случае, производится по схеме развертывания поверхности пирамиды.

Коническая поверхность заменяется вписанной в нее поверхностью пирамиды. Построение развертки будет тем точнее, чем больше граней имеет пирамида, заменяющая коническую поверхность.

Истинные величины отрезков образующих определятся на очерковой образующей конуса.

Развертка боковой поверхности наклонного кругового цилиндра показана на рисунке 10.4.

На первом этапе в цилиндрическую поверхность вписывается призма, основанием которой служит многоугольник с n сторонами. Достаточная точность аппроксимации может быть получена при длине стороны равной четверти радиуса окружности. В силу того, что рассматриваемая поверхность симметрична относительно фронтальной плоскости уровня, достаточно построить развертку лишь одной ее половинки.

Развертка вписанной призмы выполняется по способу раскатки. Некоторая фронтальная плоскость совмещается с ребром Затем с ней совмещаются боковые грани призмы последовательным вращением их вокруг соответствующих ребер.

Вращением вокруг ребра грань совмещается с плоскостью. Построение совмещенного положения ребра ВВ’ базируется на том, что точки В и В’ вращаются в плоскостях перпендикулярных ребру и равно отстоят от точек Для построения точек В и В ‘ на развертке через их фронтальные проекции проводятся следы фронтально-проецирующих плоскостей и на которых фиксируется положение точек В. Далее, аналогичным образом строится грань и т. д.

Условные развертки поверхностей

Для неразвертывающихся поверхностей строят условные развертки. Для этого, исходя из требуемой точности развертки, исходную поверхность разрезают на несколько равных частей. Затем полученные отсеки аппроксимируются отсеками развертывающихся поверхностей, для которых (по рассмотренной выше методике) и выполняют развертки. Последние и принимают за условную развертку исходной поверхности.

Рассмотрим построение разверток поверхностей вращения по описанной выше методике на примерах, приведенных на рисунках 10.5 и 10.6.

Условные развертки поверхностей вращения выполняют в основном двумя способами: способом цилиндров и способом конусов.

При построении условной развертки способом цилиндров исходная поверхность разрезается плоскостями, проходящими через ее ось вращения (рисунок 10.5).

Каждый выделенный отсек заменяется отсеком цилиндрической поверхности, которая касается исходной поверхности по ее среднему меридиану. Образующие отсека цилиндра ограничены плоскостями меридианов, ограничивающих отсек исходной поверхности.

При этом дуги параллелей исходной поверхности аппроксимируются отрезками образующих соответствующих цилиндров.

Для построения развертки поверхности вращения способом конусов исходная поверхность разрезается плоскостями перпендикулярными ее оси вращения, на несколько частей — «поясов». Каждый из поясов аппроксимируется отсеком конуса вращения.

Таким образом, задача сводится к построению разверток отсеков аппроксимирующих конусов.

Выбор способа построения условной развертки поверхности вращения, в реальном проектировании, во многом зависит от конкретных размеров поверхности и технологии изготовления изделия.

Развертки поверхностей

Разверткой называется плоская фигура, в которую преобразуется поверхность предмета при ее совмещении с плоскостью. При этом подразумевается, что поверхность – это гибкая, но нерастяжимая и несжимаемая пленка и при ее развертке не происходит разрывов и образования складок.

Поверхности, которые допускают такое преобразование, называются развертывающимися.

К развертывающимся поверхностям относятся многогранники и некоторые линейчатые поверхности – цилиндрические, конические и поверхности с ребром возврата (торсы – развертка торсов не рассматривается).

Развертки можно построить точные и приближенные.

Точные развертки можно строить для гранных поверхностей призмы и пирамиды (не считая графических погрешностей построения), для круговых цилиндров (развертка – прямоугольник с размерами (π·d)×H) и круговых конусов (круговой сектор с углом φ = R·360 o /L, где R – радиус основания конуса; L – длина его образующей).

Развертки, которые можно построить графически, заменяя (аппроксимируя) заданные поверхности участками развертывающихся призматических, пирамидальных или цилиндрических поверхностей, называются приближенными. К поверхностям, развертку которых можно построить приближенно, относятся круговые наклонные конуса, эллиптические цилиндры с круговыми сечениями, сферические, торовые, а также комбинированные поверхности, участки которых состоят из развертывающихся поверхностей.

Каждой точке на поверхности соответствует единственная точка на развертке, т. е. между поверхностью и ее разверткой существует взаимно однозначное соответствие, которое обладает следующими основными свойствами:

• а) длины соответствующих линий на поверхности и на развертке равны;
• б) линии, параллельные на поверхности, сохраняют параллельность на развертке;
• в) углы между соответствующими пересекающимися линиями на поверхности и на развертке равны;
• г) площади соответствующих фигур на поверхности и на развертке, ограниченные замкнутыми линиями, равны.

Развертки многогранников

Построение развертки многогранников сводится к определению натуральных величин боковых граней или ребер этих поверхностей. Натуральные величины граней (плоскостей) или ребер (прямых) могут быть определены любым из рассмотренных выше способов преобразования чертежа (см. тему «Преобразование чертежа»).

Развертка поверхности призмы

Построение развертки поверхности призмы можно выполнить несколькими способами:

1. Способ нормального сечения.
2. Способ раскатки.
3. Способ треугольников (триангуляции) – здесь не рассматривается.

Рассмотрим на примерах построение развертки поверхности призмы первыми двумя способами.

1-й способ. Способ нормального сечения (нормальное сечение перпендикулярно ребрам призмы).

Этот способ развертки боковой поверхности призмы можно применить, если на чертеже:

• – ребра призмы являются прямыми уровня, то есть имеют на одной из заданных проекций натуральную величину,
• – на проекциях нет натуральных величин оснований призмы.

. Если на чертеже ребра призмы являются прямыми общего положения, то следует изменить положение призмы относительно плоскостей проекций, преобразовав ребра в прямые уровня, например, способом замены плоскостей проекций.

Построение развертки боковой поверхности призмы способом нормального сечения выполняется по следующему графическому алгоритму:

1-е действие. Провести на проекции призмы, на которую ребра призмы проецируются в натуральную величину, плоскость нормального сечения, перпендикулярную ее ребрам (в произвольном месте по длине ребер).

2-е действие. Построить натуральную величину многоугольника нормального сечения (например, способом замены плоскостей проекций).

3-е действие. Развернуть на свободном поле чертежа натуральный многоугольник сечения в прямую и через точки его вершин провести перпендикулярные прямые

4-е действие. Отложить на направлениях ребер в обе стороны от линии нормального сечения натуральные отрезки соответствующих ребер.

5-е действие. Соединить построенные конечные точки ребер отрезками прямых и достроить плоскую фигуру развертки боковой поверхности призмы.

6-е действие. Оформить чертеж развертки, проведя линии сгиба в местах расположения ребер тонкими штрихпунктирными линиями с двумя короткими пунктирами.

На рис. 9.1 показан пример построения развертки поверхности треугольной призмы способом нормального сечения, так как на чертеже призмы ее ребра являются горизонтальными прямыми уровня, а основания являются плоскостями общего положения, т. е. не имеют натуральной величины.

Поверхность призмы «разрезана» по ребру А и развернута по часовой стрелке.

Для построения развертки выполнены графические действия предложенного алгоритма.

1-е действие. Провести горизонтально-проецирующую плоскость нормального сечения α(α_h) перпендикулярно горизонтальным проекциям ребер призмы (произвольно по длине ребер).

2-е действие. Способом замены плоскостей проекций построить натуральную величину нормального сечения

• – треугольник 1₁“-2₁“-3₁“, стороны которого определяют ширину каждой грани призмы.

3-е действие. На свободном поле чертежа треугольник 1₁“-2₁“-3₁” нормального сечения развернуть в горизонтальную линию и отметить натуральные величины его сторон; из отмеченных на линии сечения точек 1, 2, 3 и 1 провести перпендикулярные прямые – направления ребер.

4-е действие. Отложить на проведенных направлениях ребер вверх и вниз отрезки натуральных величин ребер (см. ребро B’-B’₁), взятых с заданной горизонтальной проекции призмы, где ребра имеют натуральную величину.

5-е действие. Соединить отрезками прямых построенные конечные точки ребер и достроить плоскую фигуру развертки.

6-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам призмы тонкими штрихпунктирными линиями с двумя короткими штрихами.

На этом же рис. 9.1 показано также построение на развертке точки Е(Е”,Е’), лежащей на грани АВ призмы.

2-й способ. Способ раскатки

Этот способ развертки применяется, если на чертеже:

• – ребра призмы являются прямыми уровня;
• – основания призмы (или одно из оснований) лежат в плоскости уровня, т. е. имеют на чертеже натуральную величину.

Суть способа в том, что, «разрезав» поверхность призмы по одному из ее ребер, вращением призмы (раскаткой) вокруг этого ребра ближайшая грань призмы совмещается с плоскостью развертки (за плоскость развертки принимается плоскость проекций, которой параллельны ребра призмы). Затем последовательным вращением призмы вокруг следующих ребер с плоскостью развертки совмещаются все прочие грани призмы, т. е. выполняется полная раскатка ее боковой поверхности.

На рис. 9.2 показан пример построения развертки способом раскатки, так как на чертеже ребра призмы являются фронтальными прямыми, а оба основания лежат в горизонтальных плоскостях уровня и на горизонтальной проекции призмы имеют натуральную величину. За плоскость развертки принята фронтальная плоскость проекций, так как ребра призмы фронтальные прямые.

Построение развертки способом раскатки выполняется по следующему графическому алгоритму:

1-е действие. «Разрезать» поверхность призмы по очерковому ребру A-A₁(A”-A₁“) и повернуть вокруг этого ребра грань АВ призмы до совмещения с плоскостью развертки, построив ребро В-B₁; чтобы построить на развертке это ребро, нужно провести из вершин оснований В(B”) и B₁(B₁“) перпендикуляры к ребру A-A₁(A”-A₁“) и на пересечении этих перпендикуляров с дугой-засечкой, равной стороне основания AВ(A’B’), построить точки B и B₁, определяющие положение ребра В-B₁ на развертке (ребро В-B₁ параллельно ребру А-A₁).

2-е действие. Повторить последовательное вращение каждой грани вокруг следующего ребра и совместить каждую грань с плоскостью развертки, построив конечные точки каждого ребра с помощью дуг-засечек, равных следующим сторонам основания BC(B’C’) и CА(C’А’).

3-е действие. Соединить построенные конечные точки ребер отрезками прямых и достроить плоскую фигуру развертки (достроено также одно основание призмы).

4-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам тонкими штрихпунктирными линиями с двумя короткими пунктирами.

На этом же рисунке показано построение на развертке точки E, лежащей на грани BC призмы.

Развертка поверхности пирамиды

Построение развертки боковой поверхности пирамиды по натуральным величинам ее ребер выполняется по следующему графическому алгоритму.

1-е действие. Построить на заданных проекциях пирамиды натуральные величины всех ее боковых ребер (например, способом вращения вокруг проецирующей прямой) и натуральные величины сторон многоугольника основания пирамиды (если основание лежит в плоскости уровня, то натуральные величины даны на одной из проекций).

2-е действие. Построить на свободном поле чертежа последовательно грани пирамиды по натуральным величинам ребер и натуральным величинам сторон основания (с помощью дуг-засечек) так, чтобы они имели общую вершину S и примыкали друг к другу.

3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями.

На рис. 9.3 показан пример построения развертки поверхности правильной треугольной пирамиды, основание которой треугольник АВС на горизонтальной проекции имеет натуральные величины сторон, так как лежит в горизонтальной плоскости уровня.

Для построения развертки выполнены графические действия предложенного алгоритма.

1-е действие. Построить на заданной фронтальной проекции натуральные величины ребер пирамиды способом вращения вокруг горизонтально-проецирующей оси i(i’), проходящей через вершину пирамиды точку S (S’) и совпадающую с ее высотой. Напоминаем графические действия этого способа преобразования:

1.1. Повернуть горизонтальные проекции ребер S’А’, S’В’ и S’С’ вокруг оси i(i’) так, чтобы они расположились параллельно фронтальной плоскости проекций V (все ребра правильной пирамиды равны по длине), и получить совмещенные проекции точек A_o‘≡B_o‘≡C_o‘.

1.2. На фронтальной проекции пирамиды конечные точки А”, В” и С” ребер перемещаются по горизонтальной линии, перпендикулярной оси i(i”), и на пересечении с линией связи от точек A_o‘(B_o‘≡C_o‘) построить точки A_o“(B_o“≡C_o“).

1.3. Соединить вершину пирамиды S(S”) с совпадающими точками A_o“(B_o≡C_o“)

– полученный отрезок S”A”(S”B”≡S”C”) и есть натуральная величина всех ребер пирамиды.

2-е действие. На свободном поле чертежа построить последовательно (например, против часовой стрелки) от ребра SA, по которому «разрезается» поверхность, треугольники граней пирамиды с общей вершиной S следующим образом:

2.1. Провести дугу радиусом R равным натуральной величине ребер S”A_o” пирамиды из произвольной точки S плоскости чертежа.

2.2. На дуге отметить (произвольно) вершину основания точку A, то есть построить ребро SA пирамиды.

2.3. На проведенной дуге засечками, равными длине сторон основания пирамиды A’В’=В’C’=C’A’ отметить следующие точки вершин основания

2.4. Построить треугольники граней пирамиды, соединив вершину S с вершинами основания и достроить основание пирамиды к стороне, например, ВС грани SBC.

3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями с двумя короткими пунктирами.

Геодезическая линия

Геодезическая линия – это линия кратчайшего расстояния между двумя точками на поверхности. На развертке этой линии соответствует прямая. Геодезическая линия строится на развертке по двум ее конечным точкам, заданным на проекциях предмета, а затем достраивается на заданных проекциях по дополнительным промежуточным точкам, взятым на построенной развертке.

На рис. 9.3 показано построение проекций геодезической линии на поверхности пирамиды по двум заданным на проекциях конечным точкам D(D”,D’-?) и E(E’,E”-?). Порядок графических действий для построения геодезической линии:

1-е действие. Построить полную развертку поверхности (в данном примере развертка пирамиды уже построена).

2-е действие. Построить на развертке геодезическую линию.

2.1. Построить на развертке заданные точки D(D”,D’) и E(E’,E”):

– точка D определяется на развертке на пересечении вспомогательной линии m, проведенной параллельно стороне АВ основания на расстоянии А-2_o, равным отрезку A_o“-2_o“, взятому на построенной натуральной величине ребер и отложенному по ребру SA развертки, и линии, проведенной через точку S и точку 1, построенную на стороне АВ развертки по отрезку A’-1′, взятому на горизонтальной проекции А’В’ стороны основания;

• – точка E определяется на пересечении аналогично построенных линий 4_o-Е и S-3;

2.2. Соединить построенные на развертке точки геодезической линией D-E, которая пересекает ребро SB в точке F.

3-е действие. Достроить фронтальную и горизонтальную проекции геодезической линии D-F-E на проекциях пирамиды по промежуточной точке F с учетом видимости линии на поверхности (на проекциях пирамиды проекции геодезической линии – ломаные линии):

3.1. Отрезок B-F, взятый на развертке (отмечен скобкой), отложить на натуральной величине ребер, построенных на фронтальной проекции, и определить положение точки F_о“.

3.2. Провести через точку F_о” линию, параллельную основанию пирамиды, и на пересечении с проекцией ребра SB(S”B”) построить фронтальную проекцию точки F(F”) геодезической линии.

3.3. Достроить горизонтальную проекцию точки F(F’) по вспомогательной точке 5(5′), лежащей на ребре SC.

3.4. Соединить на проекциях пирамиды заданные проекции точек D и E с построенной точкой F, определив видимость участков ломаной геодезической линии.

На рис. 9.4 показан пример построения развертки неправильной треугольной пирамиды SABC и геодезической линии D-E-F на развертке и на проекциях пирамиды по заданным конечным точкам D и E. Основание пирамиды лежит в горизонтальной плоскости и на горизонтальной проекции пирамиды стороны основания имеют натуральную величину.

Построение развертки поверхности пирамиды выполнено по приведенному выше алгоритму с дополнительными графическими действиями по построению геодезической линии:

1-е действие. Построить на фронтальной проекции пирамиды способом вращения вокруг горизонтально-проецирующей оси i(i’), проходящей через вершину пирамиды S(S’), натуральные величины всех ребер пира-миды и вспомогательной линий S-1, проведенной на грани пирамиды SAC через заданную точку D, и определить проекцию D_о” точки D на натуральной величине S”-1_o” вспомогательной линии S-1: вспомогательная линия S-2, проведенная через точку E(E’,E”), является фронтальной (//V), и проекция S”-2″ есть ее натуральная величина, которую можно использовать для построения точки E на развертке.

2-е действие. Построить на свободном поле чертежа последовательно от ребра SA по часовой стрелке треугольники граней пирамиды с общей вершиной S по натуральным величинам ее ребер и сторон основания дугами-засечками соответствующей величины и достроить основание пирамиды к стороне АВ.

3-е действие. Оформить чертеж развертки, проведя линии сгиба.

4-е действие. Построить геодезическую линию на развертке и заданных проекциях пирамиды.

4.1. Построить на развертке конечные точки D и E на вспомогательных линиях S-1 и S-2 по натуральным величинам отрезков 1-D(1_o“-D_о“) и 2-E(2″-E”) и соединить эти точки прямой геодезической линией D-E, которая пересекает ребро SC в точке F.

4.2. Достроить фронтальную и горизонтальную проекции ломаной геодезической линии D-F-E на проекциях пирамиды с учетом ее видимости, определив проекции точки F(F’,F”) на ребре SC(S’C’,S”C”) по ее положению на развертке (по отрезку C-F).

Приближенные развертки цилиндрических и конических поверхностей

Развертки цилиндрических и конических поверхностей выполняются аналогично разверткам призматических и пирамидальных поверхностей. При этом цилиндрическая поверхность заменяется (аппроксимируется) вписанной многоугольной призматической поверхностью (обычно 12-угольной), а коническая поверхность заменяется вписанной многоугольной пирамидальной поверхностью, т. е. строятся приближенные развертки.

Развертка кругового цилиндра

Развертку поверхности прямого кругового цилиндра можно выполнять следующими способами:

• – способом нормального сечения на свободном поле чертежа, если образующие являются прямыми уровня, а основания не перпендикулярны образующим;
• – способом раскатки при тех же условиях (развертка является при этом продолжением проекции).

Развертка эллиптического цилиндра (нормальное сечение – эллипс) выполняется способом раскатки, если образующие являются прямыми уровня, и на проекциях есть круговое основание (не рассматривается).

Графические алгоритмы для построения разверток поверхности цилиндра этими способами аналогичны вышеприведенным графическим алгоритмам для построения разверток призмы такими же способами.

На рис. 9.5 показан пример построения развертки боковой поверхности прямого кругового цилиндра, наклоненного относительно горизонтальной плоскости проекций H и срезанного по одному торцу профильной плоскостью.

Поскольку по условию задачи образующие являются фронтальными прямыми уровня, а нормальным сечением кругового цилиндра является окружность, то здесь для построения развертки можно объединить и способы построения, и графические действия алгоритмов.

Развертка выполняется по предлагаемому графическому алгоритму.

1-е действие. Провести на фронтальной проекции цилиндра фронтально-проецирующую плоскость нормального сечения α(α_V) перпендикулярно фронтальным проекциям образующих (в произвольном месте по длине образующих) и построить окружность нормального сечения, повернув плоскость этой окружности вокруг линии сечения.

1.1. Окружность нормального сечения разделить на двенадцать частей и точки деления пронумеровать от точки O на очерковой образующей А”-A₁“, то есть цилиндр заменить (аппроксимировать) двенадцатиугольной вписанной призмой; из точек деления окружности сечения провести на фронтальной проекции образующие до их пересечения с проекциями оснований.

2-е действие. На продолжении линии нормального сечения отметить двенадцать отрезков – сторон двенадцатиугольника (хорды окружности), которым заменяется окружность сечения, и провести направления ребер (образующих), перпендикулярно линии сечения (линии пронумеровать), то есть выполнить от ребра А”-A₁” последовательную раскатку граней призмы, заменившей цилиндр.

3-е действие. Построить конечные точки каждой образующей (ребра) на пересечении образующих с линиями, проведенными перпендикулярно образующим из одноименных точек нижнего основания.

4-е действие. Оформить чертеж развертки боковой поверхности цилиндра, соединив построенные конечные точки образующих плавными кривыми линиями (в примере развертка оборвана из-за недостатка места). Для построения более точной развертки следует по формуле (1) (рис. 9.5, где L – диаметр цилиндра) вычислить длину развертки и разделив эту длину на 12 равных частей, провести образующие и далее выполнить 3 и 4 действия алгоритма.

Развертка кругового конуса

На рис. 9.6 показан пример построения развертки боковой поверхности прямого кругового конуса со срезом фронтально-проецирующей плоскостью α(α_V), которая пересекает его поверхность по эллипсу.

Построение развертки боковой поверхности конуса выполняется по алгоритму, приведенному выше для построения развертки пирамиды, с некоторыми дополнениями.

Развертка выполняется по предлагаемому алгоритму.

1-е действие. Заменить прямой круговой конус вписанной правильной 12-угольной пирамидой с ребрами-образующими.

2-е действие. Построить развертку боковой поверхности пирамиды по натуральным величинам ребер (образующих) и сторон основания, выполнив следующие графические действия:

2.1. Отметить на свободном поле чертежа точку S и провести дугу радиусом L, равным натуральной величине всех образующих конуса (ребер пирамиды).

2.2. Отметить на дуге точку O на вертикальной линии симметрии развертки и построить вправо и влево на дуге засечками, равными сторонам-хордам 12-угольника, точки, соответствующие вершинам этого многоугольника; пронумеровать эти точки и соединить их с вершиной развертки, построив таким образом вспомогательные ребра-образующие (грани пирамиды).

3-е действие. Достроить на развертке линию среза конуса фронтально-проецирующей плоскостью α(α_V), выполнив следующие графические действия:

3.1. На фронтальной проекции конуса перенести горизонтально на натуральную величину образующей S”-6″ точки сечения, отмеченные на вспомогательных образующих, то есть вращением вокруг оси i(i”,i’) построить натуральные величины отрезков образующих-ребер сечения.

3.2. Отложить на соответствующих образующих развертки натуральные величины отрезков образующих-ребер до точек сечения (отмечены на фронтальной проекции и на развертке фигурными скобками отрезки O”-O_o” образующей для точки O_o и 2″-2_o” образующей для точки 2_o) и соединить построенные точки сечения на развертке плавной кривой линией.

4-е действие. Оформить чертеж развертки, проведя сплошными толстыми линиями контур построенной развертки.

Для построения более точной развертки следует вычислить по формуле (2) (рис. 9.6, где R – радиус основания конуса; L – длина образующей конуса) угол развертки и разделить дугу развертки на 12 равных частей, провести образующие и далее выполнить 3 и 4 действия алгоритма.

На рис. 9.7, а дан чертеж поверхностей кругового цилиндра и кругового конуса, описанных вокруг сферы, и построена линия пересечения этих поверхностей по теореме Г. Монжа.

На рис. 9.7, б построена развертка конической части этой конструкции по следующему графическому алгоритму:

1-е действие. Провести произвольное сечение, перпендикулярное оси конуса, и повернуть половину окружности сечения в очерковую плоскость конуса.

2-е действие. Разделить окружность сечения на 6 частей и перенести точки 1-6 параллельно оси конуса на линию сечения (проекцию окружности), то есть построить точки 1_o-6_o.

3-е действие. Через вершину конуса S(S”) и точки 1_o-6_o провести образующие конуса до пересечения с проекцией линии пересечения с проекцией линии пересечения цилиндра и конуса О₁“-6”.

4-е действие. Вращением построенных образующих вокруг оси конуса перенести точки 1_o“-5_o” на очерковую образующую S”-6″, имеющую на чертеже натуральную величину.

5-е действие. На свободном поле чертежа провести радиусом R=S”O_o дугу и отложить на этой дуге шесть отрезков-хорд, на которые было поделено сечение конуса.

6-е действие. Через точку S на развертке и построенные точки O_o-6 провести семейство образующих.

7-е действие. Отложить от точек O_o-6 на каждой образующей развертки соответствующие натуральные величины образующих, взятые с чертежа, то есть отрезки 6_o-1_o, 6_o-2_o и т. д.

8-е действие. Построенные на концах семейства образующих точки соединить плавной кривой и оформить чертеж развертки (построена половина развертки).

На рис. 9.8 показано построение развертки боковой поверхности боковой поверхности усеченного конуса (если вершину конуса на чертеже достроить нельзя) с основаниями, равными d и D.

Предварительно на чертеже усеченного конуса строится вспомогательный неусеченный конус подобный заданному так, чтобы отношение диаметра D исходного конуса к диаметру вспомогательного конуса d, было целым число, то есть K = D/d₁ – целое число, где K – коэффициент кратности оснований конусов.

Примем K = 3 и впишем в заданный конус вспомогательный конус с вершиной S”.

Достроим горизонтальную проекцию вспомогательного конуса и разделим половину окружности основания d₁ на 6 частей (1-6).

Далее приступаем к построению развертки половины усеченного конуса по следующему графическому алгоритму:

1-е действие. На свободном поле чертежа построить развертку вспомогательного конуса с вершиной S (см. рис. 9.8), то есть построить точки 0-2-4-6 на дуге развертки.

2-е действие. На оси симметрии развертки (биссектриса полной развертки) выбрать произвольную точку К и провести семейство лучей, соединяющих соответственно произвольную точку К с точками 0-2-4-6 развертки вспомогательного конуса.

3-е действие. Отложить на проведенных лучах отрезки, величины которых определяются произведениями:

где К – принятый коэффициент пропорциональности, а величины KO, K2, K4 и K6 следует измерить на строящейся развертке. На концах лучей определяются точки O_o, 2_o, 4_o и 6_o.

4-е действие. Через построенные точки на концах лучей провести прямые n₀-n₆, каждая из которых должна быть соответственно параллельна образующим вспомогательного конуса на его развертке.

5-е действие. На проведенных прямых n₀-n₆ отложить натуральную величину длин образующих заданного усеченного конуса L.

6-е действие. Оформить чертеж развертки, соединив построенные точки развертки лекальными прямыми.

Условные развертки поверхностей

Условные развертки можно выполнить для некоторых неразвертывающихся поверхностей.

Рассмотрим построение условных разверток неразвертывающихся поверхностей сферы и открытого тора (кругового кольца).

Развертка сферической поверхности

На рис. 9.9 показано построение условной развертки сферической поверхности.

Поверхность сферы условно разрезают на какое-то количество частей (6, 12 и более) и каждую часть заменяют (аппроксимируют) цилиндрической описанной поверхностью, фронтальная проекция которой совпадает с фронтальным очерком сферы – окружностью.

Далее выполнятся развертка одной доли поверхности сферы как сектора цилиндрической поверхности по следующему графическому алгоритму:

1-е действие. На горизонтальной проекции разрезать поверхность сферы на 6 частей и рассмотреть эту 1/6 часть (сектор) как фронтально-проецирующий цилиндр, описанный вокруг сферы.

2-е действие. Разделить дугу очерковой окружности A₀B₀ сферы, которая совпадает с окружностью описанного цилиндра, на 12 частей (поскольку есть симметрия, рассматриваем дугу A₀С₀) и заменить участки хордами (то есть вписать 12-угольную призму) – A₀“-1″, 1″-2” и т. д.

3-е действие. Спроецировать точки 1″-6″ на стороны взятого сектора его горизонтальной проекции.

4-е действие. Свободном поле чертежа провести вертикальную линию и отложить от точки C₀ вверх и вниз по 6 отрезков, равных величине хорд (точки пронумеровать).

5-е действие. Через каждую построенную точку А-6 провести горизонтальные линии и на каждой отложить величину соответствующей образующей: 1₀-1₀, 2₀-2₀ и т. д.

6-е действие. Конечные точки соединить лекальной кривой.

Таким образом построена 1/6 доля условной поверхности сферы, а 6 таких долей составят развертку всей поверхности.

С увеличением количества долей (1/12, 1/24 и т. д.) точность развертки увеличивается.

Развертка поверхности открытого тора

На рис. 9.10 показана условная развертка поверхности открытого тора.

Поверхность кольца разрезают на какое-то количество долей (6, 12 и более) плоскостями, проходящими через его ось i”, и заменяют каждую долю (сектор) поверхности описанной цилиндрической поверхностью.

Далее выполняют развертку одной доли поверхности по графическому алгоритму, приведенному для построения развертки одной доли поверхности сферы.

На рис. 9.11 приведен чертеж построения части (правой) развертки комбинированной геометрической поверхности, состоящей из трех полых цилиндров, сообщенных двумя коническими рукавами, в котором подытоживается изученный материал данной темы. Показано, что развертка каждой части комбинированной поверхности строится отдельно.

Структуризация материала девятой лекции в рассмотренном объеме схематически представлена на рис. 9.12 (лист 1). На последующих листах 2–5 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 9.13–9.16).

Развертки поверхностей:

Развертка – плоская фигура, в которую преобразовывается поверхность при ее совмещении с плоскостью без разрывов и складок.

Геодезическая линия – кратчайшее расстояние между двумя точками на поверхности. На развертке этой линии соответствует прямая.

Развертка гранных поверхностей

а. Способ нормального сечения (применяется, если на чертеже ребра призмы являются прямыми уровня)

1. Построить натуральную величину нормального сечения, перпендикулярного к ребрам призмы.

2. Развернуть стороны сечения в линию и из вершин, провести направления ребер перпендикулярно к линии развертки.

3. Отложить вверх и вниз от точек вершин натуральные отрезки ребер и соединить построенные вершины; провести линии сгиба на месте ребер тонкими штрихпунктирными линиями с двумя штрихами.

б. Способ раскатки (применяется, если на чертеже ребра являются прямыми уровня и есть натуральная величина основания) Графический алгоритм построения на чертеже геодезической линии:

1. Построить развертку поверхности призмы.

2. Построить на развертке заданные на поверхности точки (M и N) и соединить прямой геодезической линией, которая пересекает ребро A в т.K.

3. Вернуть построенную т.K на проекции призмы и соединить с заданными точками M и N ломаной линией с учетом ее видимости на поверхности.

Развертка поверхности пирамиды.

Графический алгоритм построения развертки поверхности пирамиды:

1. Построить натуральные величины всех ребер пирамиды (способом вращения вокруг проецирующей оси).

2. Выполнить развертку поверхности, построив по натуральным величинам ребер треугольники граней и основание.

3. Соединить отрезками построенные на развертке вершины и оформить линии сгиба.

Развертка цилиндрических поверхностей

1. Способ нормального сечения

2. Способ раскатки

Рекомендую подробно изучить предметы:

Инженерная графика Начертательная геометрия Компас Автокад Черчение Проекционное черчение Аксонометрическое черчение Строительное черчение Техническое черчение Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

• Способы преобразования проекций
• Взаимное положение прямой и плоскости
• Решение метрических задач
• Тени в ортогональных проекциях
• Преобразование чертежа
• Кривые линии
• Образование и задание поверхности на чертеже
• Пересечение поверхности плоскостью и прямой

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

[spoiler title=”источники:”]

http://natalibrilenova.ru/sechenie-geometricheskih-tel-ploskostyami-i-razvertki-ih-poverhnostej-s-primerami-i-obraztsami-vyipolneniya/

http://www.evkova.org/razvertki-poverhnostej

[/spoiler]

Для построения кривой линии, получаемой при пересечении
цилиндрической поверхности плоскостью, следует в общем случае находить
точки пересечения образующих с секущей плоскостью, как было сказано на
с. 170 в отношении линейчатых поверхностей вообще. Но это не исключает
возможности применять и вспомогательные плоскости, пересекающие каждый
раз поверхность и плоскость.

Прежде всего отметим, что любая цилиндрическая поверхность
пересекается плоскостью, расположенной параллельно образующей этой
поверхности, по прямым линиям (образующим). На рис. 360 показано
пересечение цилиндрической поверхности плоскостью. В данном случае эта
поверхность является вспомогательным элементом при построении точки
пересечения кривой линии с плоскостью: через заданную кривую (см. рис.
360, слева) DMNE проведена цилиндрическая поверхность, проецирующая
кривую на пл. π₁. Далее, плоскость (на рис. 360 — треугольник) пересекает цилиндрическую поверхность по плоской кривой М₁ … N₁. Искомая точка пересечения кривой с плоскостью — точка К — получается в пересечении кривых — заданной и построенной.

Такая схема решения задачи на пересечение кривой линии с плоскостью
совпадает со схемой решения задач на пересечение прямой линии с
плоскостью (см. §§ 23

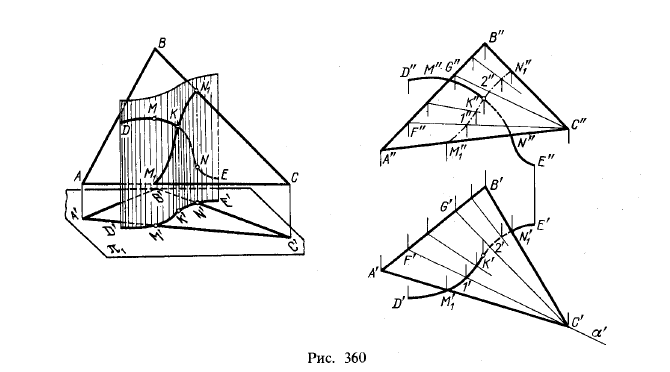
и 25); в обоих случаях через линию проводят вспомогательную поверхность, которая для прямой линии является плоскостью.

Горизонтальная проекция кривой M₁…N₁, по
которой цилиндрическая поверхность пересекается с плоскостью, совпадает с
горизонтальной проекцией кривой D … Е, так как эта кривая является
направляющей для цилиндрической поверхности при перпендикулярных к пл.
π₁, ее образующих. Поэтому по точке М’₁ на проекции А’С’ мы можем найти проекцию М”₁ на А”С” и по точке N’₁ — проекцию N”₁. Далее, на рис. 360 справа показана вспомогательная пл. α, пересекающая ABC по прямой CF, а цилиндрическую поверхность — по ее образующей с горизонтальной проекцией
в точке 1′. В пересечении этой образующей с прямой CF получается точка с
проекциями 1′ и 1″, принадлежащая кривой М₁ … N₁
Очевидно, можно не указывать следа плоскости, а просто провести прямую в
треугольнике, как это показано в отношении прямой CG, на которой
получена точка с проекциями 2′ и 2″.

В рассмотренных далее примерах будут показаны развертки.
Развертывание цилиндрической поверхности в общем случае может
производиться по схеме развертывания поверхности призмы. Цилиндрическая
поверхность как бы заменяется вписанной в нее или описанной
призматической, ребра которой соответствуют образующим цилиндрической поверхности. Само развертывание, подобно показанному на рис. 283, производится при помощи нормального сечения. Но вместо ломаной линии проводится плавная кривая.

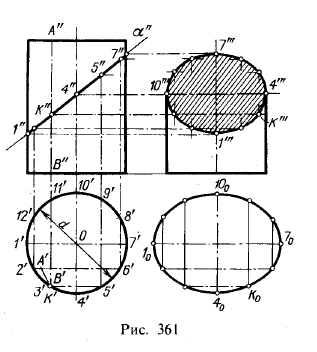
На рис. 361 показано пересечение прямого кругового цилиндра
фронтально-проецирующей плоскостью. Фигура сечения представляет собой
эллипс, малая ось которого равна диаметру основания цилиндра; величина
большой оси зависит от угла между секущей плоскостью и осью цилиндра.

Так как ось цилиндра перпендикулярна к пл. π₁ то горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией цилиндра.

Обычно для построения точек контура сечения проводят равномерно
расположенные образующие, т. е. такие, проекции которых на пл. π₁
являются точками, равноотстоящими друг от друга. Этой «разметкой» удобно
пользоваться не только для построения проекций сечения, но и развертки
боковой поверхности цилиндра, как это будет показано ниже.

Проекция фигуры сечения на пл. π₃ — эллипс, большая ось
которого в данном случае равна диаметру цилиндра, а малая представляет
собой проекцию отрезка 1″7″. На рис. 361 на пл. π₃ изображение построено так, как будто верхняя часть цилиндра снята после пересечения его плоскостью.

Если бы на рис. 361 плоскость α составляла с осью цилиндра угол 45°, то проекцией эллипса на π₃ была бы окружность. При этом отрезки 1″‘7″‘ и 4″’10″‘ оказались бы равными.

Если тот же цилиндр пересекать плоскостью общего положения, также
составляющей с осью цилиндра угол 45°, то проекцию фигуры сечения
(эллипса) в виде окружности можно получить на дополнительной плоскости
проекций, параллельной оси цилиндра и горизонталям секущей плоскости.

Очевидно, при увеличении угла наклона секущей плоскости к оси отрезок
1″‘7″‘ уменьшается; если же этот угол будет меньше 45°, отрезок 1′”7′”
увеличивается и становится большой осью эллипса на пл. π₃, малой же осью этого эллипса становится отрезок 4″’10″‘.

Натуральный вид сечения представляет собой, как уже сказано выше, эллипс. Его оси получаются на чертеже: большая — отрезок 1₀7₀ = 1″7″, малая — отрезок 4₀10₀, равный диаметру цилиндра. Эллипс может быть построен по этим осям.

На рис. 362 показана полная развертка нижней части цилиндра.

Развернутая окружность основания цилиндра разделена на равные между
собой части соответственно делениям на рис. 361; отрезки образующих
отложены на перпендикулярах, проведенных в точках деления развернутой
окружности основания цилиндра. Концы этих отрезков соответствуют точкам
эллипса. Поэтому, проведя через них кривую линию, получаем развернутый
эллипс (эта линия представляет собой синусоиду) — верхнюю кромку
развертки боковой поверхности цилиндра.

К развертке боковой поверхности на рис. 362 присоединены круг
основания и эллипс — натуральный вид сечения, что дает возможность
сделать модель усеченного цилиндра.

На рис. 363 изображен эллиптический цилиндр с круговым основанием; его ось параллельна пл. π₂. Для определения нормального сечения этого цилиндра его надо рассечь
плоскостью, перпендикулярной к образующим, в данном случае
фронтально-проецирующей плоскостью. Фигура нормального сечения
представляет собой эллипс с большой осью, равной отрезку 3₀7₀, и с малой, равной 1₀5₀ = 1″5″.

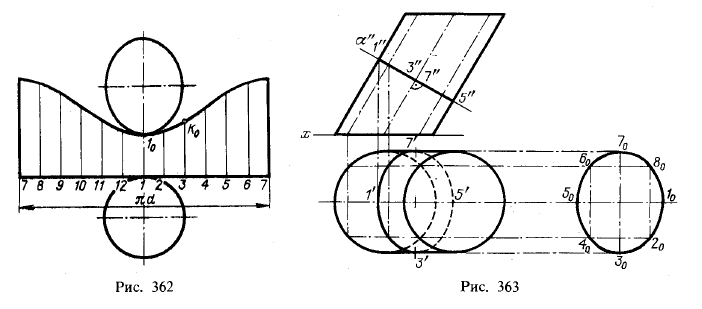
Если надо будет развернуть боковую поверхность данного цилиндра, то,
имея нормальное сечение, развертывают ограничивающую его кривую в прямую
линию и в соответствующих точках этой прямой, перпендикулярно к ней,
откладывают отрезки образующих, беря их с фронтальной проекции. Для
разметки образующих делят окружность основания на равные части. При этом
и эллипс (нормальное сечение) разделится на такое же число частей, но
не все эти части получаются равной

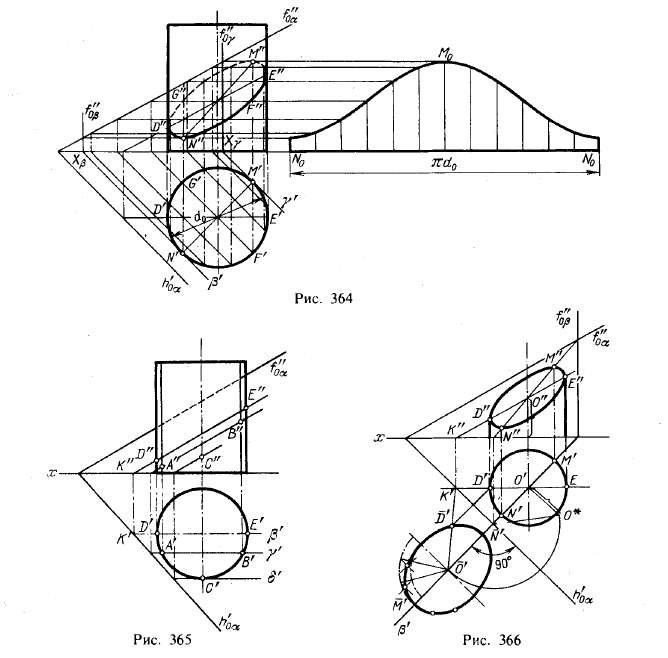
длины. Развертывание эллипса в прямую можно произвести путем
последовательного откладывания на прямой достаточно малых частей
эллипса.

На рис. 364 показан прямой круговой цилиндр, пересеченный плоскостью
общего положения. В сечении получается эллипс: секущая плоскость
составляет с осью конуса некоторый острый угол.

Подобно тому, как это было на рис. 361, горизонтальная проекция
сечения совпадает с горизонтальной проекцией цилиндра. Поэтому положение
горизонтальной проекции точки пересечения любой из образующих цилиндра с
пл. α известно (например, точка А’ на рис. 365). Для нахождения
соответствующей фронтальной проекции можно ировести в пл. α горизонталь
или фронталь, на которой должна находиться искомая точка. На рис. 365
проведена фронталь; в том месте, где фронтальная проекция фронтали
пересекает фронтальную проекцию соответствующей образующей, лежит
проекция А”. Одна и та же фронталь определяет две точки кривой, А и В
(рис. 365). Если же построить фронталь, соответствующую точке С, то

эта линия определит лишь одну точку кривой пересечения. Фронталь, построенная по точкам D и Е, определяет крайние точки D” и Е”.

Продолжая аналогичные построения, можно найти достаточно точек для вычерчивания фронтальной проекции линии пересечения.

На рис. 366 верхняя часть цилиндра как бы срезана. Если же
фронтальную проекцию показывают полностью, то линию пересечения
вычерчивают так, как показано на рис. 364.

На рис. 365 показаны вспомогательные фронтальные плоскости β, γ, δ
пересекающие цилиндр по образующим, а пл. α по фронталям. Это
соответствует тому, что было сказано в начале параграфа. Вспомогательная
пл. δ лишь касается цилиндра, что дает возможность определить только
одну точку для кривой.

При построении фронтальной проекции линии пересечения, помимо точек
D” и Е” (рис. 365), следует найти еще две крайние точки, а именно М” и
N” — наивысшую и наинизшую точки проекции сечения на пл. π₂.
Для их построения надо выбрать вспомогательную плоскость,
перпендикулярную к следу h’_0α и проходящую через ось цилиндра (рис. 366).
Эта плоскость является общей плоскостью симметрии данных цилиндра и
секущей пл. а. Найдя линию пересечения плоскостей α и β, отметим точки
М” и N”, построив их на фронтальной проекции по точкам М’ и N’.

Иной способ нахождения точек М” и N” заключается в проведении двух
плоскостей, касательных к цилиндру, горизонтальные следы которых
параллельны следу h’_0α. Эти плоскости пересекутся с пл. α по горизонталям последней (рис. 364, вспомогательные плоскости β и γ); отметив точки М’ и N’ построим точки М” и N” на фронтальных проекциях горизонталей.

Отрезок MN представляет собой большую ось эллипса — фигуры сечения
данного цилиндра пл. α. Это видно и на рис. 366, где построен в
совмещении с пл. π₁ эллипс — натуральный вид сечения. Но отрезок M”N” на
том же рисунке отнюдь не является большой осью эллипса — фронтальной
проекции фигуры сечения. Эту большую ось можно найти по сопряженным
диаметрам M”N” и F”G” (рис. 364) построением, указанным в § 21, или
специальным построением, приведенным в § 76.

Натуральный вид сечения может быть найден совмещением секущей плоскости с одной из плоскостей проекций, π₁ или π₂.

На рис. 366 эллипс в совмещенном положении построен по большой и малой осям (там же точка D’ получена совмещением фронтали).

Развертка боковой поверхности показана на рис. 364. Обратите внимание
на то, что разметка точек — горизонтальных проекций образующих — на
окружности основания производилась от точки N’. Этим построение
упрощалось, так как с помощью одной и той же горизонтали получаются две
точки на фронтальной проек

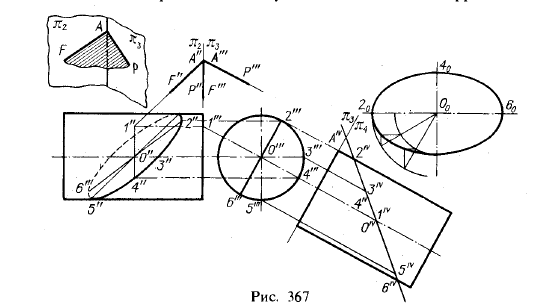
ции эллипса. Кроме того, фигура развертки имеет ось симметрии. Но при
этом точки D’ и Е’ не попали в число точек, размеченных на окружности.

Еще один пример построения фигуры сечения цилиндра вращения
плоскостью дан на рис. 367. Это построение выполнено при помощи способа
перемены плоскостей проекций. Секущая плоскость задана пересекающимися
прямыми — фронталью (AF) и профильной прямой (АР). Так как профильная
проекция фронтали и фронтальная проекция профильной прямой лежат на
одной прямой А”≡A'”, A”‘F”‘ = А”Р”, то эти прямые лежат соответственно
в плоскостях π₂ и π₃, (см. рис. 367, слева вверху). Ось π₂/π₃ проходит через A'”F'”(A”P”).

Вводим новую пл. π₄ так, что π₄⊥π₃, и π₄⊥АР. Секущая плоскость оказывается перпендикулярной к π₄, и проекция на π₄ фигуры сечения получается в виде отрезка прямой 2 ^IV6^IV, равного большой оси эллипса — фигуры сечения. Положение прямой A^IV6^IV определяется построением проекций точек А и 1 на пл. π₄.

Проследим построение некоторых точек. Чтобы избежать излишних
построений, проекция 1″‘ была взята на продолжении перпендикуляра,
проведенного из О'” на π₃/ π₄. По точке 1″‘ была получена проекция 1″; отрезок 1″1″‘, отложенный от оси π₃/π₄, определил точку ^IV и совпадающую с ней точку О¹ — проекцию центра эллипса. Зная проекции 0^IV и О'”, можно получить О” — центр эллипса — искомой фронтальной проекции фигуры сечения.

По точкам 2^IV и 2″‘ найдена точка 2″, наименее удаленная от π₃, а по точкам 6^IV и 6′” – точка 6″, наиболее удаленная от π₃.

По точке 5″‘ взяга точка 5^IV, и теперь по точкам 5^IV
и 5″‘ найдена точка 5″— одна из точек, определяющих разделение эллипса на фронтальной проекции цилиндра на «видимую» и «невидимую» части. Вторая точка расположена симметрично точке 5″ по отношению к О”.

Остальное ясно из чертежа. Натуральный вид фигуры сечения (эллипс на рис. 367, справа) построен по осям — большой, равной 2^IV6^IV, и малой, равной диаметру цилиндра.

Вопросы к §§ 55 -56

1. Как строится кривая линия при пересечении кривой поверхности плоскостью?
2. По каким линиям пересекается цилиндрическая поверхность плоскостью, проведенной параллельно образующей этой поверхности?
3. Каким приемом пользуются в общем случае для нахождения точки пересечения кривой линии с плоскостью?
4. Какие линии получаются при пересечении цилиндра вращения плоскостями?
5. В каком случае эллипс, получаемый при пересечении цилиндра вращения, ось которого перпендикулярна к пл. π₁, фронтально-проецирующей плоскостью, спроецируется на пл. π₃ в виде окружности?
6. Как следует расположить дополнительную плоскость проекций, чтобы эллипс, получаемый при пересечении цилиндра вращения, ось которого перпендикулярна к пл. π₁, плоскостью общего положения, составляющей с осью цилиндра угол 45°, спроецировался на эту плоскость проекций в виде окружности?

Научимся изображать в перспективе сложные геометрические объемы на основе концентрических окружностей разного размера.

Изобразите на листе пять одинаковых по высоте цилиндров, поставленных друг на друга.

Приступая к выполнению задания, рассмотрите ортогональные проекции (рис. 3.116) и представьте тот объем, который должен появиться на листе (рис. 3.117).

В целом конструкция напоминает ступенчатый конус. Пять невысоких цилиндров имеют общую вертикальную ось, диаметры цилиндров постепенно уменьшаются от нижнего цилиндра к верхнему. Для лучшего понимания пространственной структуры представьте вписанный в этот объем конус, что также поможет вам в дальнейшем построении.

Для выполнения этого задания сначала научитесь рисовать концентрические окружности в перспективе. Рассмотрите схему на рис. 3.118. На плане (вверху) две окружности имеют общий центр и образуют кольцо определенной ширины. Чтобы изобразить эти окружности в перспективе (внизу), сначала нарисуйте внешний эллипс. Для изображения внутреннего эллипса необходимо найти крайние точки (габариты эллипса) и его оси. Определите, в каком отношении находится ширина кольца к диаметру внешней окружности (в нашем примере 1:2). Разделив на перспективном рисунке радиусы (вертикальный и горизонтальный) внешней окружности в том же отношении, вы получите габариты внутреннего эллипса. Теперь необходимо определить его оси. Малая ось внутреннего эллипса лежит на той же прямой, что и малая ось внешнего. Разделив малую ось внутреннего эллипса ровно пополам, найдите его центр.

На рисунке эта точка расположена между точкой центра окружностей и центром внешнего эллипса. Таким образом центр внутреннего эллипса смещен относительно центра внешнего эллипса дальше от зрителя. Проведите большую ось внутреннего эллипса горизонтально через его центр. По двум осям и четырем крайним точкам изобразите в перспективе внутреннюю окружность. Вы, конечно, заметили, что на вашем рисунке точки центров эллипсов расположены на столь малом расстоянии, что проведенные через них большие оси эллипсов, скорее всего, сольются в одну линию. Поэтому в дальнейшем, изображая концентрические окружности, сосредоточьте ваше внимание на том, чтобы внутренний эллипс был смещен относительно внешнего эллипса, а ширина кольца, образованного окружностями на рисунке, менялась в соответствии с перспективными сокращениями. Нарисуйте несколько таких концентрических окружностей разного раскрытия в перспективе (рис. 3.119).

Теперь переходите к выполнению основного задания. Расположите лист вертикально. В центре листа проведите вертикальную ось и отметьте на ней общую высоту всех цилиндров. Разделите эту высоту короткими засечками на пять равных отрезков, а затем проведите через эти засечки горизонтальные линии — большие оси эллипсов оснований цилиндров.

Наметьте на листе легкими линиями вписанный конус. Две образующие конуса определяют на горизонтальных прямых размеры больших осей эллипсов нижних оснований всех пяти цилиндров. Нарисуйте эллипсы нижних оснований цилиндров, определив их раскрытие при помощи вертикального сечения (рис. 3.120). Наметьте образующие цилиндров и постройте эллипсы верхних оснований. Их раскрытие также определите при помощи вертикальных сечений (рис. 3.121). В своей работе опирайтесь на знания, полученные в рисунке концентрических окружностей. Все изображенные эллипсы должны быть подчинены единой системе: их раскрытие должно постепенно уменьшаться от нижних цилиндров к верхним, а раскрытия эллипсов, лежащих в одной плоскости, должны быть примерно равны (рис. 3.122). Завершите рисунок, усилив линии первого плана.