Как найти малую площадь - Сайт, где вы сможете решить свои вопросы

Наименьшая площадь

Профи

(776),
закрыт

13 лет назад

Дополнен 13 лет назад

извините, описался, y=0.25x^2-x+8

ValKo

Высший разум

(112944)

13 лет назад

Здесь все гораздо проще.
Если точка А является точкой пересечения прямой ОВ с заданной параболой (а они пересекаются!) , то площадь треугольника АОВ, будет минимальной (равной нулю)!

Viktor

Просветленный

(49792)

13 лет назад

Я не согласен с предыдущими ответчиками. В условии сказано – ” площадь треугольника с вершинами АОВ”. Если площадь (наименьшая) предлагается равна 0, то треугольника не будет существовать. Задачу нужно, по-моему, решать из условия существования треугольника. Поэтому задача будет иметь два решения, которые нужно проверять. Первое: если точка А максимально будет приближаться к прямой ОВ в первом квадранте и второе – в третьем квадранте. Судя по графикам линий – это будет третий квадрант. Нужно найти точку пересечения параболы с прямой ОВ и найти площадь по длине трех сторон: ОВ, ОА и АВ. И не стоит забывать, что точка А лежит на параболе.

Источник

Рассмотрим фигуру ниже:

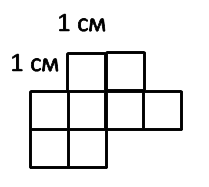
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.

Площадь одного такого квадрата называют квадратным сантиметром и записывают:
1 см².

Площадь всей фигуры 8 см².

Запомните!

Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.

В математике для нахождения площади геометрических фигур используют специальные формулы,
в которых площадь обозначается заглавной латинской буквой «S».

Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.

Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата,
равна 1 м, то его площадь равна 1
квадратному метру (1 м²); если длина
его стороны равна 1 см, то его площадь
равна 1 квадратному сантиметру
(1 см²).

Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.

Как перевести квадратные единицы

Рассмотрим квадрат со стороной 1 см.

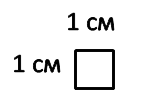
Его площадь равна:

S = 1 см · 1 см = 1см²

Рассмотрим квадрат со стороной 1 м.

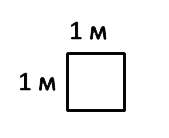
Его площадь равна:

S = 1 м · 1 м = 1 м²

Известно, что: 1 м = 100 см

1 м² = 1 м · 1 м = 100 см · 100 см = 10 000 см²

Увеличим сторону квадрата равную 1 м в
10 раз. Получим квадрат со
стороной 10 м.

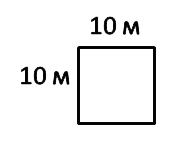
Площадь такого квадрата называют ар или сотка.

S = 10 м · 10 м = 100 м²

В одном аре — сто квадратных метров.

Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».

1 ар (сотка) = 100 м²

Чтобы выразить ар в cм², вспомним, что 1 м² = 10 000 см².

Значит: 1 ар (сотка) = 100 м² = 100 · 10 000 см² = 1 000 000 см²

Увеличим сторону квадрата равную 10 м в 10 раз.
Получим квадрат со
стороной 100 м.

Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование
проговаривается полностью.

Выразим гектар в квадратных метрах.

1 га = 100 м · 100 м = 10 000 м²

Теперь определим, сколько в одном гектаре аров.

1 ар = 100 м²

Значит: 10 000 м² : 100 м² = 100 (ар)

1 га = 100 ар

Для измерения больших площадей, например, территорий государств, материков используют квадратный километр.
То есть квадрат со стороной 1 км и
площадью 1 км².

1 км = 1000 м

1 км² = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м²

Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.

Таблица переводов квадратных единиц

Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.

	га	ар	м²	cм²
1 км²	100 га	10 000 ар	1 000 000 м²	1 000 000 000 cм²
1 га	1 га	100 ар	10 000 м²	100 000 000 cм²
1 ар	0,01 га	1 ар	100 м²	1 000 000cм²
1 м²	0,000 1 га	0,01 ар	1 м²	10 000 cм²

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

12 сентября 2018 в 20:57

Дмитрий Мозговой
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Дмитрий Мозговой
Профиль
Благодарили: 0

Сообщений: 1

Внутри большего квадрата расположен меньший квадрат площади 73. Известно, что длины отрезков, на которые сторона большего квадрата делится вершинами меньшего квадрата, — натуральные числа. Чему равна площадь большего квадрата?

0
Спасибо thanks
Ответить

14 октября 2018 в 20:45
Ответ для Дмитрий Мозговой

Дарья Тихая
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Дарья Тихая
Профиль
Благодарили: 0

Сообщений: 1

146

0
Спасибо thanks
Ответить

21 октября 2018 в 15:44
Ответ для Дмитрий Мозговой

Владимир Шварцман
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Владимир Шварцман
Профиль
Благодарили: 0

Сообщений: 1

Пусть отрезки большего квадрата a и в. Тогда а² ₊_в² =73 Сумма двух чисел нечётна если одно чёт., а второе нечёт. Это 1,9,25,49 и 4, 16,36.64 Легко видеть, что это числа 9 и 64.Т.е. а=3 и в=8 Пл. большого квадрата=11² =121

0
Спасибо thanks
Ответить

12 ноября 2018 в 3:31
Ответ для Дмитрий Мозговой

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

Неверно.

0
Спасибо thanks
Ответить

22 июня 2016 в 20:17

Клара Чукаева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Клара Чукаева
Профиль
Благодарили: 0

Сообщений: 1

д вечер. у меня вопрос: как найти площадь таблички размером 50 см на 75 см? если перемножить, как нам предлагает школьная программа, то получается 3750 см2, разве это возможно? я ошибаюсь? напишите формулу для расчета пожалуйста?

0
Спасибо thanks
Ответить

24 июня 2016 в 12:18
Ответ для Клара Чукаева

Павел Асафов
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Павел Асафов
Профиль
Благодарили: 0

Сообщений: 2

Здравствуйте! Все верно.
Формула площади прямоугольника S=a · b
(a)50 · (b)75=3750 см²Может вы спутали с периметром? Периметр будет равен 250 см
a ·2+b · 2

0
Спасибо thanks
Ответить

16 января 2016 в 18:29

Надюша Бисерова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Надюша Бисерова
Профиль
Благодарили: 0

Сообщений: 1

ширина прамоугольника 23 см. на сколько увеличиться площадь прамоугольника, если его длину увеличить на 3 см?
подскажите решение пожалуйста

0
Спасибо thanks
Ответить

21 января 2016 в 16:17
Ответ для Надюша Бисерова

Сергей Фадеев
(^-^)
Профиль
Благодарили: 0

Сообщений: 6

(^-^)
Сергей Фадеев
Профиль
Благодарили: 0

Сообщений: 6

на 3 см квадратных
если я не ошибаюсь взависимости от длины

0
Спасибо thanks
Ответить

24 января 2016 в 13:50
Ответ для Надюша Бисерова

Инна Шабрашина
(^-^)
Профиль
Благодарили: 0

Сообщений: 5

(^-^)
Инна Шабрашина
Профиль
Благодарили: 0

Сообщений: 5

увеличится на 69

0
Спасибо thanks
Ответить

12 октября 2015 в 17:22

Мося Мося
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Мося Мося
Профиль
Благодарили: 0

Сообщений: 1

найди площадь квадрата периметр которого 280см

0
Спасибо thanks
Ответить

1 июля 2016 в 14:20
Ответ для Мося Мося

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Для нахождения площади квадрата в данном случае нам понадобятся две формулу, а именно:
1) Формула периметра квадрата P=4a. Подробно про периметр читаем здесь http://math-prosto.ru/?page=pages/perimeter/perimeter.php
2) Формула площади квадрата S=a². Подробно читать здесь http://math-prosto.ru/?page=pages/area/area_figures.php

Приступим к решению. Выразим сторону квадрата из формулы периметра:
P=4a
a=P: 4
a= 280: 4 = 70 (см)
Теперь воспользуемся формулой площади квадрата:
S=a²S=70²=4900 (см²)
Ответ: площадь квадрата равна 4900 см²

0
Спасибо thanks
Ответить

4 сентября 2015 в 15:44

Игорь Винников
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Игорь Винников
Профиль
Благодарили: 0

Сообщений: 2

Площадь прямоугольника64мс², одна из сторон 16см. Надо найти соседнюю сторону

0
Спасибо thanks
Ответить

1 сентября 2016 в 10:18
Ответ для Игорь Винников

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Площадь прямоугольника рассчитывается по формуле S=a · b. Подставим значения в формулу и вычислим вторую сторону:
64=16 · b
b=64/16=4
вторая сторона равна 4.
проверка: 16 · 4 = 64.

Ответ: Соседняя сторона прямоугольника равна 4 см.

0
Спасибо thanks
Ответить

6 июля 2015 в 17:48

Дмитрий Рыжков
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Дмитрий Рыжков
Профиль
Благодарили: 0

Сообщений: 2

Посмотрите, у вас не первый раз перепутаны буквы в примерах.Например посмотрите нм тему: площадь сложных фигур.там же треугольник обозначен одними буквами, а написано в примере другими совершенно. Никто не ответил по предыдущей теме.спасибо.

0
Спасибо thanks
Ответить

12 июля 2015 в 13:31
Ответ для Дмитрий Рыжков

Борис Гуров
(^-^)
Профиль
Благодарили: 1

Сообщений: 27

(^-^)
Борис Гуров
Профиль
Благодарили: 1

Сообщений: 27

Здравствуйте, Дмитрий.

Благодарим Вас за указанное замечание.

Пожалуйста, укажите, более конкретно место ошибки.

В уроке «Площадь сложных фигур» мы не нашли ошибку, о которой Вы написали.

0
Спасибо thanks
Ответить

17 мая 2015 в 10:59

Соня Кизилова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Соня Кизилова
Профиль
Благодарили: 0

Сообщений: 1

Самостоятельная работа.
Задание 3.
На сколько частей разбивают плоскость 4 прямые, пересекающиеся в одное точке?
Задание 2.
Начертите угол MON. Отметьте точку K, лежащую внутри этого угла, и точку L, лежащую на отрезке NK.
Задание 4.
Постройте треугольник ABC со стороной AB= 6см,?ABC= 45градусов, ?BAC= 75 градусов.Помогите пожалуйста cry …

0
Спасибо thanks
Ответить

17 мая 2015 в 12:57
Ответ для Соня Кизилова

Ярослава Фесенко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Ярослава Фесенко
Профиль
Благодарили: 0

Сообщений: 3

1.8 частей

0
Спасибо thanks
Ответить

Источник

Содержание:

Определения
Формулы площади основных геометрических фигур

Определения

Площадь является одним из основных математических понятий. Она характеризует как плоские, так и поверхностные геометрические объекты.

Определение

Площадью плоской замкнутой фигуры называется величина части плоскости, которая находится внутри указанной фигуры.

Единицей измерения площади плоской фигуры является квадрат со стороной, равной единице. Число, соответствующее
площади некоторой фигуры, состоящей из частей, равно сумме чисел, соответствующих площадям этих частей. Измерение
площадей треугольников и многоугольников основано на возможности построения равновеликих им прямоугольников.

Площадь произвольной ограниченной плоской фигуры определяется как общий предел площадей описанных и
вписанных в нее многоугольников, наибольшие стороны которых по длине стремятся к нулю.

Если фигура имеет площадь, то она называется квадрируемой.

Формулы площади основных геометрических фигур

Площадь треугольника

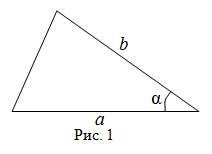
Чтобы найти площадь треугольника, надо найти полупроизведение двух его сторон на синус угла между ними.
То есть если известны длины двух сторон треугольника $ABC$, которые равны
$a$ и $b$, а также угол
$alpha$ между этими сторонами, то искомая площадь:

$$mathrm{S}_{Delta A B C}=frac{1}{2} a b sin alpha$$

Читать дальше: формулы площади треугольника и примеры решений →

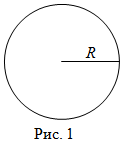
Площадь круга

Чтобы найти площадь круга, надо найти произведение числа
$pi$ на квадрат радиуса этого круга, то есть

$$mathrm{S}_{kappa p}=pi R^{2}$$

Читать дальше: формула площади круга и примеры решений →

Площадь квадрата

Чтобы найти площадь квадрата, надо длину его стороны возвести в квадрат, то есть

Читать дальше: формула площади квадрата и примеры решений →

Площадь прямоугольника

Чтобы найти площадь прямоугольника, надо его длину умножить на ширину, то есть

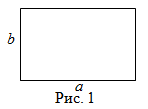
Читать дальше: формула площади прямоугольника и примеры решений →

Площадь параллелограмма

Чтобы найти площадь параллелограмма, нужно найти произведение стороны
$a$ параллелограмма на высоту
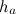, проведенную к этой стороне, то есть

Читать дальше: формулы площади параллелограмма и примеры решений →

Площадь трапеции

Чтобы найти площадь трапеции, нужно длину средней линии
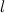умножить на длину высоты
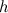, опущенной к основанию:

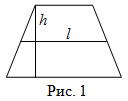
Читать дальше: формулы площади трапеции и примеры решений →

Площадь ромба

Чтобы найти площадь ромба, надо длину стороны умножить на длину высоты, проведенной к этой стороне:

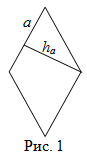
Читать дальше: формулы площади ромба и примеры решений →

Площадь эллипса

Чтобы найти площадь эллипса, нужно найти произведение длин большой и малой полуосей этого эллипса на число
$pi$, то есть

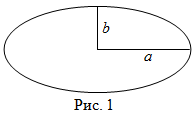
Читать дальше: формула площади эллипса и примеры решений →

Как найти площадь треугольника
Как найти площадь ромба
Как найти площадь эллипса
Как найти площадь прямоугольного треугольника
Как найти площадь равнобедренного треугольника
Как найти площадь равностороннего треугольника
Как найти площадь круга
Как найти площадь квадрата
Как найти площадь прямоугольника
Как найти площадь параллелограмма
Как найти площадь трапеции

Источник

Площадь – это величина пространства, которое ограниченное замкнутым контуром (периметром фигуры).

Площадь прямоугольника находится по формуле: длину умножить на ширину фигуры (S = a*b)

Плошадь квадрата можно найти по двум формулам:

через известное значение одной из сторон: одну из сторон квадрата поднести к квадрату или умножить саму на себя (S = a*a)
через диагональ квадрата: диагональ квадрата поднести к квадрату и умножить на одну/вторую (или получившееся значение разделить на два) (S = 1/2* c*c) (S = c*c : 2)

Площадь треугольника можно найти через основание и высоту фигуры: основание треугольника умножить на высоту и разделить на два (умножить на одну/вторую) (S = a*h :2) (S = a*h *1/2)

Площадь круга можно найти, зная радиус или диаметр фигуры:

число “пи” умножить на радиус круга, поднесенный к квадрату (S = π * r*r)
число “пи”, разделенное на четыре, умножить на диаметр, поднесенный к квадрату: (S = π/4 * D*D)

система выбрала этот ответ лучшим

Hamster1337
[28.6K]

2 года назад

Площадь – это величина поверхности какой либо фигуры (квадрата, треугольника и т.д). Например, квадрат 2 на 2 (см) имеет площадь 4 см (по формуле a^2). Более подробно узнать о формулах вычисления площадей простейших фигур, вписанных и описанных в круг фигур и т. д. можно здесь.

Михаил 33
[36.4K]

5 лет назад

Нам постоянно приходится слышать о площади геометрических фигур, и можно полноценно сказать, что это одна из наиважнейших составляющих всей геометрии, как научной дисциплины.

Немаловажным фактором является то, что необходимость определить величину площади чего-либо возникает в нашей жизни очень часто.

Для примера возьмём обычный ремонт квартиры или дома.

Сколько раз приходится вычислить площадь комнаты, потолка, стен, пола и т.д.

И любые ошибки при данных вычислениях приводят лишь к одному, к нашим избыточным денежным затратам, так как закупка стройматериалов полностью зависит от площади, для которой предназначаются те или иные стройматериалы.

Примеров того, что понятие площади необходимо знать всем, сотни, но речь не об этом.

И так, что такое площадь?

Площадью называется часть плоскости, заключённой внутри какой либо геометрической фигуры. Соответственно и нахождение её будет зависеть именно от того, в какой именно фигуре заключена данная часть плоскости.

Как находится площадь отдельных геометрических фигур:

AlexSEO
[85.9K]

3 года назад

Площадь (ранее принятое название – квадратура), и это следует сразу же отметить, относится к фигуре (геометрической) плоской (возможно – искривленной), где есть два измерения (при вводе третьего измерения получается объем), например – длина/ширина. По сути – это не что иное, как размер той или иной фигуры или совокупность (сложение) всех точек, входящих в нее.

Если фигуры стандартные (круг/квадрат/прямоугольник/трапеция/треугольник), то найти их площадь просто – есть соответствующие формулы, нужно лишь знать размеры, например, зная сторону такой фигуры, как квадрат, легко найти площадь, просто умножив ее (или возведя в квадрат) на саму себя. Другие формулы:

Если фигура сложная, то тут применяют интегралы (для теоретических вычислений) или же специальные приспособления, например, планиметр или палетку (для практических измерений).

Alex2837
[113K]

более года назад

Понятие площади фигуры изучается на уроках математики в средних классах. Очень часто ученики путают эту меру с периметром геометрической фигуры.

Если не обращаться к научной литературе, то понятие площади простыми словами можно обозначить, как часть плоскости, которая ограничивается сторонами фигуры.

Например, площадь треугольника ограничивается его тремя сторонами, площадь прямоугольника или квадрата ограничивается четырьмя сторонами.

Для вычисления площади используются специальные формулы. Для каждой геометрической фигуры имеется своя отдельная формула. Например, для определения площади прямоугольника, достаточно просто умножить его длину на ширину.

Мудрый Датч
[75.1K]

2 года назад

Площадь является мерой того, сколько на плоской поверхности имеется пространства.

В математике вычисляются разными путями площади фигур. Если мы возьмём, к примеру, прямоугольник, то его площадь следует определять как произведение его высоты и ширины, а площадь квадрата, где сторона обозначается буквой “а”, будет равняться

=а*а (“а” в квадрате). Но и будет несправедиво не упомянуть площадь такой фигуры как треугольник, а равна площадь треугольника произведению половины его основания на высоту. Ниже привожу небольшую подсказку в определении площади фигур.

Domino-12
[201]

4 недели назад

В математике площадью называют величину, характеризующую протяженность двумерной геометрической фигуры (прямоугольника, треугольника и т.д.) или области на плоскости.

Площадь обозначается буквой S.

Для каждой геометрической фигуры существуют формулы площади, выбор формулы зависит от того, что дано в условии задачи.

Вот, например, несколько формул для нахождения площади треугольника:

Если известны все 3 стороны, то можно воспользоваться 2 формулой (она называется формулой Герона) – в ней a, b, c являются сторонами, а p – полупериметром (нужно сложить числовые значения всех сторон и разделить на 2).

А если мы знаем, чему равна высота и основание треугольника, то площадь можно посчитать по 1 формуле – половина произведения основания на высоту.

Отдельный случай – это нахождение площади произвольного многоугольника.

Здесь тоже имеются формулы, но в некоторых случаях можно сделать и так: разбить многоугольник на несколько стандартных фигур и найти их площадь, площадь многоугольника будет равна сумме площадей этих фигур.

То есть:

S = S1 + S2 + S3 = …

А в некоторых случаях проще достроить многоугольник до прямоугольника или квадрата, найти площадь полученной фигуры, а затем вычесть из неё площади лишних областей.

ЕкатеринаКрест
[34]

5 лет назад

Площадь-часть плоскости, заключённая внутри замкнутой геометрической фигуры. Как всем известно,фигуры есть самые разнообразные,но самое элементарное-нахождение площади(S) прямоугольника,треугольника. Чтобы найти S прямоугольника,нужно умножить ее ширину на длину,то есть а*в. Квадрат-тот же самый прямоугольник,но с равными сторонами,следовательно S квадрата=а*а или “а” в квадрате. И,чтобы найти S треугольника нужно умножить половину его основания(а) на высоту(h)(S=12a*h)

Виталий Чер
[5.8K]

5 лет назад

Площадь это поверхность какого либо предмета, к примеру площадь прямоугольника находится по следующей формуле: a*b-где a,b -стороны (длина и ширина), квадрата a^2, круга ПR^2-где П-3,14 а R-радиус, конуса ПR(l+R)-где l-длина конуса и т.д.