Как найти малую полуось орбиты планеты - Сайт, где вы сможете решить свои вопросы

СБ, 11/20/2010 – 10:57 — mav

Все относительно: и бред, и знанье.
Срок жизни истины-
Двадцать-тридцать лет,-
Предельный возраст водовозной клячи.
Мы ищем лишь удобства вычислений,
А в сущности не знаем ничего:
Ни емкости, ни смысла тяготенья,
Ни масс планет, ни формы их орбит,
На вызвездившемся небе мы не можем
Различить глазом “ завтра ” и “вчера”…
М. Волошин

Урок 3/9

презентация

Тема: Законы движения планет – законы Кеплера.

Цель: Ввести понятие эллипса, познакомится с законами Кеплера и закрепить их на решении задач.

Задачи:
1. Обучающая: Продолжить формирование понятия «эллипс» (определение, фокусы, центр, эксцентриситет, радиусы-векторы, большая и малая полуоси, способ построения). Ввести новые понятия: орбита планеты, афелий (апогей), перигелий (перигей) сидерический (звездный) период обращения, астрономическая единица, возмущение, небесная механика. Изучить законы Кеплера. Использовать решение задач для продолжения формирования расчетных навыков.
2. Воспитывающая: Показать, что открытие законов Кеплера и их уточнение Ньютоном – пример познаваемости мира и его закономерностей. Акцентировать внимание учащихся на том, что законы использует не только для более глубокого познания природы (например, для определения масс небесных тел), но и для решения практических задач (космонавтика, астродинамика).
3. Развивающая: доказать учащимся, что открытие законов Кеплера представляет собой не только следующий (после открытия гелиоцентрической системы) шаг познания Солнечной системы (эллиптичность орбит, неравномерное движение планет вокруг Солнца, строгая математическая зависимость между расстояниями и периодами обращений планет), но и новый шаг в познании Вселенной (законы Кеплера, как и закон всемирного тяготения, действуют за пределами Солнечной системы).

Знать:
1-й уровень (стандарт)– понятие эллипса и его характерных точек, понятие и значение астрономической единицы, формулировки трех законов Кеплера.
2-й уровень – понятие эллипса и его характерных точек, понятие и значение астрономической единицы, формулировки трех законов Кеплера.

Уметь:
1-й уровень (стандарт)– вычислять для эллипса его определяющих характеристик, производить расчеты по третьему закону периодов и полуосей.
2-й уровень – объяснить принцип вывода эллиптической орбиты Кеплером, вычислять для эллипса его определяющих характеристик, производить расчеты по третьему закону периодов и полуосей.

Оборудование: Таблица “Солнечная система”, д/ф “Борьба за становление научного мировоззрения в астрономии”. CD- “Red Shift 5.1” (нахождение небесного объекта в заданный момент времени).
Межпредметная связь: Планеты (природоведение, 5 кл.). Движение по окружности с постоянной по модулю скоростью, период и частота. Движение ИСЗ. Эллипс как проекция окружности, построение овала черчение, 7 кл.). Длина окружности, площадь круга (математика, 6 кл). Движение под действием силы тяжести. Движение ИСЗ (физика, 9 кл).

Ход урока:

Новый материал (20мин).

Гелиоцентрическая система Н. Коперника

1. Планеты движутся по круговым орбитам (считалось с древнейших времен – по окружности).
2. Планеты движутся равномерно

Но между предвычисленным и наблюдаемым положением планет существовало различие – это выявил австрийский астроном – основоположник теоретической астрономии ИОГАН КЕПЛЕР (27.12.1571 – 15.11.1630). Он впервые решился пересмотреть причины движения планет вокруг Солнца, Луны вокруг Земли. Он ошибался в оценке природы притягивающей силы, но догадывался, что Солнце искажает притяжением пути планет, которые стремятся двигаться по прямой.
Работая в Праге учеником у Тихо Браге (1546-1601, Дания) он унаследовал результатов кропотливых и многолетних наблюдений Тихо Браге за планетой Марс – подробные таблицы наблюдения движения Марса и на их основе (этих данных) вывел законы движения планет (но не объяснил их т.к. не был открыт И. Ньютоном закон всемирного тяготения), преодолев предрассудки о равномерном движении по “самой совершенной” кривой – окружности. Открытие этих законов явилось важнейшим этапом в развитии гелиоцентризма. Позднее, после открытия Ньютоном закона всемирного тяготения, законы Кеплера были выведены как точное решение задачи двух тел.
Открытые законы носят имя Кеплера.
Для построения орбиты планет (на примере Марса) Кеплер перейдя от экваториальной системы координат к системе координат, указывающих его положение в плоскости орбиты принял в приближении орбиту Земли окружностью. Для построения орбиты применил способ показанный на рисунке, отсчитывая прямое восхождение от точки весеннего равноденствия на положение нескольких противостояний Марса. Проведя по полученным точкам плавную кривую получил эллипс и нашел формулу описывающую орбиту планеты X=е*sin (а)+M.
CD- “Red Shift 5.1” – нахождение сегодняшнего положения Марса и его характеристика по выведенным таблицам.

1^ый закон Кеплера. [открыт в 1605 году, напечатан в 1609г в книге “Новая астрономия ….”= вместе с 2-м законом].
Определение: Орбита каждой планеты есть эллипс, в одном из фокусов которого находится Солнце.

Эллипс– замкнутая кривая, у которой сумма расстояний от любой точки до фокусов постоянна (const).
Если расстояние F₁F₂ обозначить 2с, а длину веревки считать 2а, то в системе координат, где ось ОХ совпадает с линией F₁F₂, а начало совпадает с серединой отрезка F₁F₂, эллипс задается уравнением х² : а² + у² : в² = 1. Числа а и в задают размеры полуосей эллипса. Если а = в, то эллипс превращается в окружность. е=с=0 эллипс превращается в окружность, а при е=1 в отрезок. Приложение IХ.
Форма эллипса (степень отличая от окружности – “сплюснутость”) характеризуется эксцентриситетом: е=с/а (форм.14), где а большая полуось орбиты, а с=OF расстояние от центра эллипса до его фокуса. При

планета	а	е	планета	а	е	карликовая планета	а	е
Меркурий	0,39	0,206	Юпитер	5,20	0,048	Плутон	39,52	0,253
Венера	0,72	0,007	Сатурн	9,54	0,054	Эрида	67,67	0,442
Земля	1,00	0,017	Уран	19,19	0,046	Седна	486,0	0,850
Марс	1,52	0,093	Нептун	30,07	0,008	Церера	2,80	0,089

Большая полуось орбиты Земли (среднее расстояние Земли от Солнца) – расстояние, принятое за астрономическую единицу. 1а.е.=149 597 868 ± 0,7 км ≈ 149,6 млн. км.

Для эллиптической орбиты планеты характерны относительно Солнца точки: Перигелий (греч. пери – возле, около) ближайшая к Солнцу точка орбиты планеты (для Земли 1-5 января). В перигелии южное полушарие Земли получает солнечной энергии на 6% больше, чем северное полушарие.
Афелий (греч. апо – вдали) наиболее удаленная от Солнца точка орбиты планеты (для Земли 1-6 июля). Учитывая греческие названия планет, характерные точки эллиптической орбиты ее спутников будут иметь собственные названия. Так Луна – Селена (переселений, апоселений), Земля – Гея (перигей, апогей).

2^ый закон Кеплера [открыт в 1601 году, напечатан в 1609г в книге “Новая астрономия ….”= вместе с 1-м законом]. Определение: Радиус-вектор планеты за равные промежутки времени описывает равные площади.

    Называют законом площадей. Заштрихованные площади фигур равны за равные промежутки времени. Из чертежа дуги разные, отсюда υ_п>υ_а, т.е в перигелии υ_max, а в афелииυ_min.
    По закону сохранения энергии полная механическая энергия замкнутой системы, между которыми действует сила тяготения, остается неизменной при любых движениях тел этой системы. Поэтому сумма кинетической и потенциальной энергии планеты неизменна во всех точках орбиты. По мере приближения к Солнцу кинетическая энергия планеты возрастает а ее потенциальная энергии уменьшается.
     В соответствии со вторым законом Кеплера, орбитальная скорость обратно пропорциональна радиус-вектору. Поэтому скорость движения Земли по орбите также не постоянна, а изменяется от 29,5 км/с в афелии (июль) до 30,3 км/с в перигелии (январь). Соответственно, и расстояние от осеннего до весеннего равноденствия на орбите Земля проходит быстрее, чем противоположную, летнюю часть, а весна и лето в Северном полушарии на 6 суток продолжительнее осени и зимы. Например, Земля проходила точку перигелия, ближайшую к Солнцу, в 1998 году 04 января в 21 часов 15 минут 1 секунду всемирного времени UT. При этом ее расстояние от Солнца составляло 147099552 км. Противоположную точку орбиты, афелий, Земля проходила 3 июля 1998 года в 23 часа 50 минут 11 секунд всемирного времени UT. При этом Земля была от Солнца на расстоянии 152095605 км, т.е. на 5 миллионов километров больше. Это изменение расстояния до Солнца также хорошо заметно по изменению его видимого углового размера, который от 32´34″ в январе уменьшается до 31´30″ в июле.
Поток энергии от Солнца, падающий на Землю, изменяется обратно пропорционально квадрату расстояния. Поэтому зимы в северном полушарии менее суровые, чем в южном, а лето в северном полушарии более прохладное.

3^ый закон Кеплера. (Гармонический закон) [открыт в 1618 году, напечатан в 1619г в книге “Гармония мира”].

	Определение: Квадраты звездных (сидерических) периодов обращения планет относятся между собой как кубы больших полуосей их орбит.
Законы Кеплера применимы не только для планет, но и к движению их естественных и искусственных спутников.

II. Закрепление материала (18мин)

Пример №4 (стр.42) просмотреть и записать решение.
Задача Противостояние некоторой планеты повторяется через 2 года. Чему равна большая полуось ее орбиты? [1/S=1/Т_з – 1/Т, отсюда T=(1^.2)/(2-1)=2 года, по третьему закону Кеплера получим а=[(Т^2.а_з)/Т_з³]^1/3 =[2^2.1)/1]^1/3=4^1/3, а=1.59а.е.]
Задача Отношение квадратов периодов обращения двух планет равно 8. Чему равно отношение больших полуосей этих планет? (желательно показать решение в общем виде, а₁/а₂=2)
Задача С помощью CD- “Red Shift 5.1” определите в этом году время нахождения Земли в перигее и апогее.

Задача “Спутник-1”, запущенный 4 октября 1957г на орбиту Земли имел перигей 228 км и апогей 947 км при периоде обращения 96,2 мин. Определите большую полуось и эксцентриситет орбиты.
Решение:Из рисунка полуось а=(а_п+R+R+а_а)/2= (228+ 6371+6371+947)/2=6958,5 км

е=с/а [c= (а_а – а_п)/2- почему эта формула получилась?, так как с=а-а_п=(а_а + а_п)/2-а_п=а_а – а_п], получим е=0,052.

Итог:
1) Какие законы движения мы изучили?
2) На чем основывался Кеплер, открывая свои законы?
3) Что такое перигелий, афелий?
4) Когда Земля обладает наибольшей кинетической энергией, наименьшей?
5) Как найти эксцентриситет?
6) О каких периодах вращения синодических или сидерических идет речь в третьем законе Кеплера?
7) У некоторой малой планеты большая полуось орбиты равна 2,8 а.е., а эксцентриситет равен нулю. Чему равна малая полуось ее орбиты?
8) Оценки

Домашнее задание: §9, вопросы стр. 42, ПР№3, Сообщение ученика = Книга “Астрономия в ее развитии” = Рождение великого закона (стр. 38).

Урок оформил член кружка “Интернет-технологии” – Прытков Денис (10кл)

Изменен 28.10.2009 года

«Планетарий» 410,05 мб	Ресурс позволяет установить на компьютер учителя или учащегося полную версию инновационного учебно-методического комплекса “Планетарий”. “Планетарий” – подборка тематических статей – предназначены для использования учителями и учащимися на уроках физики, астрономии или естествознания в 10-11 классах. При установке комплекса рекомендуется использовать только английские буквы в именах папок.
Демонстрационные материалы 13,08 мб	Ресурс представляет собой демонстрационные материалы инновационного учебно-методического комплекса “Планетарий”.
Планетарий 2,67 мб	Данный ресурс представляет собой интерактивную модель “Планетарий”, которая позволяет изучать звездное небо посредством работы с данной моделью. Для полноценного использования ресурса необходимо установить Java Plug-in
Урок	Тема урока	Разработки уроков в коллекции ЦОР	Статистическая графика из ЦОР
Урок 9	Законы Кеплера		Важнейшие точки и линии эллипса 144 кб Построение эллипса 134,6 кб Второй закон Кеплера 143,5 кб Третий закон Кеплера 149,6 кб

Источник

Большая полуось (a) и малая полуось (b) эллипса

В геометрии большая ось эллипса – это его самый длинный диаметр : отрезок линии, который проходит через центр и оба фокусы с концами в самых широких точках периметра .

Большая полуось составляет половину большой оси и, таким образом, проходит от центра через фокус и по периметру. Малая полуось эллипса или гиперболы – это отрезок прямой, который находится под прямым углом с большой полуосью и имеет один конец в центре конического участка. В частном случае окружности длины обеих полуосей равны радиусу окружности.

Длина большой полуоси a эллипса связана с длиной малой полуоси b через эксцентриситет e и прямую полуось ℓ { displaystyle ell} ell следующим образом:

b = a 1 – e 2, ℓ = a (1 – e 2), a ℓ = b 2. { displaystyle { begin {align} b = a { sqrt {1-e ^ {2}}}, \ ell = a left (1-e ^ {2} right), , a ell = b ^ {2}. end {align}}}

${ displaystyle { begin {align} b = a { sqrt {1-e ^ {2}}}, \ ell = a left (1-e ^ {2} right), , \ a ell = b ^ {2}. End {выравнивается}}}$

Большая полуось гиперболы , в зависимости от соглашения, составляет плюс или минус половина расстояние между двумя ветвями. Таким образом, это расстояние от центра до любой вершины гиперболы.

A парабола может быть получена как предел последовательности эллипсов, в которой один фокус фиксируется, а другой может перемещаться произвольно далеко в одном направлении, сохраняя ℓ { displaystyle ell} ell исправлено. Таким образом, a и b стремятся к бесконечности, а быстрее, чем b.

Большая и малая оси – это оси симметрии кривой: в эллипсе малая ось является более короткой; в гиперболе это тот, который не пересекает гиперболу.

Содержание

1 Эллипс
2 Гипербола
3 Астрономия
- 3,1 Период обращения
- 3,2 Среднее расстояние
- 3,3 Энергия; вычисление большой полуоси из векторов состояния
- 3.4 Большая и малая полуоси планет
4 См. также
5 Ссылки
6 Внешние ссылки

Эллипс

Уравнение эллипса:

(x – h) 2 a 2 + (y – k) 2 b 2 = 1. { displaystyle { frac { left (xh right) ^ {2}} {a ^ {2}}} + { frac { left (yk right) ^ {2}} {b ^ {2}}} = 1.}

${ displaystyle { frac { left (xh right) ^ {2}} {a ^ {2}}} + { frac { left ( yk right) ^ {2}} {b ^ {2}}} = 1.}$

где (h, k) – центр эллипс в декартовых координатах, в котором произвольная точка задается как (x, y).

Большая полуось – это среднее значение максимального и минимального расстояний r max { displaystyle r _ { max}} ${ displaystyle r _ { max}}$ и r min { displaystyle r _ { min}} ${ displaystyle r _ { min}}$ эллипса от фокуса – то есть расстояний от фокуса до конечных точек большой оси. В астрономии эти крайние точки называются апсидами.

a = r max + r min 2. { displaystyle a = { frac {r _ { max} + r _ { min}} {2}}.}

${ displaystyle a = { frac {r _ { max} + r _ { min}} {2}}.}$

Малая полуось эллипса – это среднее геометрическое этих расстояния:

b = r max r min. { displaystyle b = { sqrt {r _ { max} r _ { min}}}.}

${ displaystyle b = { sqrt { r _ { max} r _ { min}}}.}$

эксцентриситет эллипса определяется как

e = 1 – b 2 a 2 { displaystyle e = { sqrt {1 – { frac {b ^ {2}} {a ^ {2}}}}}}

${ displaystyle e = { sqrt {1- { frac {b ^ {2}} {a ^ {2}}}}}}$ поэтому

r min = a (1 – e), r max = a (1 + e) { displaystyle r _ { min} = a (1-e), r _ { max} = a (1 + e)}

${ displaystyle r _ { min} = a (1-e), r _ { max} = а (1 + е)}$ .

Теперь рассмотрим уравнение в полярные координаты, с одним фокусом в начале координат, а другой в направлении (θ = π) – { displaystyle ( theta = pi) -},

г (1 + е соз ⁡ θ) = ℓ. { displaystyle r (1 + e cos theta) = ell. ,}

Среднее значение r = ℓ / (1 – e) { displaystyle r = ell / (1- e)}и r = ℓ / (1 + e) { displaystyle r = ell / (1 + e)}для θ = π { displaystyle theta = pi}и θ = 0 { displaystyle theta = 0}равно

a = ℓ 1 – e 2. { displaystyle a = { ell over 1-e ^ {2}}. ,}

$a = { ell over 1-e ^ {2}}. ,$

В эллипсе большая полуось – это среднее геометрическое расстояния от центра для фокусировки и расстояния от центра до любой директрисы.

Малая полуось эллипса проходит от центра эллипса (точка на полпути между фокусами и на линии между ними) до края эллипса. Малая полуось – это половина малой оси. Малая ось – это самый длинный отрезок прямой, перпендикулярный большой оси, который соединяет две точки на краю эллипса.

Малая полуось b связана с большой полуосью a через эксцентриситет e и прямую полуось ℓ { displaystyle ell} ell следующим образом:

b = a 1 – e 2 a ℓ = b 2. { displaystyle { begin {align} b = a { sqrt {1-e ^ {2}}} , ! \ a ell = b ^ {2}. , ! end {выровнено }}}

${ displaystyle { begin {align} b = a { sqrt {1 -e ^ {2}}} , ! \ a ell = b ^ {2}. , ! end {align}}}$

Длину малой полуоси можно также найти с помощью следующей формулы:

2 b = (p + q) 2 – f 2 { displaystyle 2b = { sqrt {(p + q) ^ {2} -f ^ {2}}}}

$2b = { sqrt {(p + q) ^ {2} -f ^ {2}} }$

где f – расстояние между фокусами, p и q – расстояния от каждого фокуса до любой точки эллипса.

Гипербола

Большая полуось гиперболы находится, в зависимости от соглашения, плюс или минус половина расстояния между двумя ветвями; если это a в направлении x, уравнение будет следующим:

(x – h) 2 a 2 – (y – k) 2 b 2 = 1. { displaystyle { frac { left (xh right) ^ {2}} {a ^ {2}}} – { frac { left (yk right) ^ {2}} {b ^ {2}}} = 1.}

${ frac { left (xh right) ^ {2}} {a ^ {2}}} - { frac { left (yk right) ^ {2}} { b ^ {2}}} = 1.$

В терминах полу -latus rectum и эксцентриситет мы имеем

a = ℓ e 2 – 1. { displaystyle a = { ell over e ^ {2} -1}.}

${ displaystyle a = { ell over e ^ {2} -1}.}$

Поперечная ось гиперболы совпадает с большой осью.

В гиперболе – сопряженная ось или малая ось Ось длины 2 b { displaystyle 2b}, соответствующая малой оси эллипса, может быть проведена перпендикулярно поперечной оси или большой оси, последняя соединяет две вершины (точки поворота) гиперболы, причем две оси пересекаются в центре гиперболы. Конечные точки (0, ± b) { displaystyle (0, pm b)}малой оси лежат на высоте асимптот над / под вершинами гиперболы. Любая половина малой оси называется малой полуосью длиной b. Обозначая длину большой полуоси (расстояние от центра до вершины) как a, длины малой и большой полуосей появляются в уравнении гиперболы относительно этих осей следующим образом:

x 2 a 2 – y 2 b 2 = 1. { displaystyle { frac {x ^ {2}} {a ^ {2}}} – { frac {y ^ {2}} {b ^ {2}}} = 1.}

${ frac {x ^ {2}} {a ^ { 2}}} - { frac {y ^ {2}} {b ^ {2}}} = 1.$

Малая полуось – это также расстояние от одного из фокусов гиперболы до асимптоты. Часто называемый параметром удара, он важен в физике и астрономии и позволяет измерить расстояние, на которое частица не попадет в фокус, если ее путешествие не будет нарушено телом в фокусе.

Малая полуось и большая полуось связаны через эксцентриситет следующим образом:

b = ae 2 – 1. { displaystyle b = a { sqrt {e ^ {2} -1}}.}

$b = a { sqrt {e ^ {2} -1}}.$

Обратите внимание, что в гиперболе b может быть больше a.

Астрономия

Орбитальная период

В астродинамике период обращения T малого тела, вращающегося вокруг центрального тела по круговой или эллиптической орбите, равен:

T = 2 π a 3 μ { displaystyle T = 2 pi { sqrt {a ^ {3} over mu}}}

$T = 2 pi { sqrt {a ^ {3} over mu}}$

где:

a – длина большой полуоси орбиты

μ { displaystyle mu}

– это стандартный гравитационный параметр центрального тела

. Обратите внимание, что для всех эллипсов с данной большой полуосью период обращения то же самое, несмотря на их эксцентричность.

удельный угловой момент h небольшого тела, вращающегося вокруг центрального тела по круговой или эллиптической орбите:

h = a μ (1 – e 2) { displaystyle h = { sqrt {a mu left (1-e ^ {2} right)}}}

${ displaystyle h = { sqrt {a mu left (1-е ^ {2} right)}}}$

где:

a и

μ { displaystyle mu}

определены выше e – эксцентриситет орбиты

В астрономии большая полуось является одной из наиболее важных орбитальных элементы орбиты вместе с его периодом обращения. Для объектов Солнечной системы большая полуось связана с периодом орбиты третьим законом Кеплера (первоначально эмпирически получено),

T 2 ∝ a 3 { displaystyle T ^ {2} propto a ^ {3} ,}

$T ^ {2 } propto a ^ {3} ,$

где T – период, а a – большая полуось. Эта форма оказывается упрощением общей формы для задачи двух тел, как определено Ньютоном :

T 2 = 4 π 2 G (M + m) a 3 { displaystyle T ^ {2} = { frac {4 pi ^ {2}} {G (M + m)}} a ^ {3} ,}

${ displaystyle T ^ {2} = { frac {4 pi ^ { 2}} {G (M + m)}} a ^ {3} ,}$

где G – гравитационная постоянная, M – масса центрального тела, а m – масса движущегося по орбите тела. Обычно масса центрального тела настолько больше, чем масса вращающегося тела, что m можно не принимать во внимание. Это предположение и использование типичных астрономических единиц приводит к более простой форме, которую открыл Кеплер.

Путь движущегося по орбите тела вокруг барицентра и его путь относительно его первичного элемента являются эллипсами. Большая полуось иногда используется в астрономии как расстояние между первичными и вторичными объектами, когда отношение масс первичного элемента к вторичному значительно велико (M ≫ m { displaystyle M gg m} M gg m ); таким образом, параметры орбит планет даны в гелиоцентрических терминах. Разницу между примоцентрическими и «абсолютными» орбитами лучше всего можно проиллюстрировать, взглянув на систему Земля – Луна. Соотношение масс в данном случае составляет 81,30059. Характерное расстояние Земля – Луна, большая полуось геоцентрической лунной орбиты, составляет 384 400 км. (Учитывая эксцентриситет лунной орбиты e = 0,0549, ее малая полуось составляет 383 800 км. Таким образом, орбита Луны почти круговая.) Барицентрическая лунная орбита, с другой стороны, имеет большую полуось 379 730 км, земную. встречная орбита, принимающая разницу, 4670 км. Средняя барицентрическая орбитальная скорость Луны составляет 1,010 км / с, а у Земли – 0,012 км / с. Сумма этих скоростей дает геоцентрическую среднюю орбитальную скорость Луны 1,022 км / с; такое же значение можно получить, рассматривая только значение большой геоцентрической полуоси.

Среднее расстояние

Часто говорят, что большая полуось – это «среднее» расстояние между основными фокус эллипса и вращающееся тело. Это не совсем точно, потому что это зависит от того, какое среднее значение берется за основу.

Усредненное по времени значение обратной величины радиуса, r – 1 { displaystyle r ^ {- 1}} ${ displaystyle r ^ {- 1}}$ , это a – 1 { displaystyle a ^ {- 1}} $a ^ {- 1}$ .

Энергия; вычисление большой полуоси из векторов состояния

В астродинамике большая полуось a может быть вычислена из векторов орбитального состояния :

a = – μ 2 ε { displaystyle a = – { mu over {2 varepsilon}} ,}

для эллиптической орбиты и, в зависимости от соглашения, то же самое или

a = μ 2 ε { displaystyle a = { mu over {2 varepsilon}} ,}

для гиперболической траектории и

ε = v 2 2 – μ | г | { displaystyle varepsilon = {v ^ {2} over {2}} – { mu over left | mathbf {r} right |}}

$varepsilon = {v ^ {2} over {2}} - { mu over left | mathbf {r} right |}$

(удельная орбитальная энергия ) и

μ = GM { displaystyle mu = GM ,}

(стандартный гравитационный параметр ), где:

v – орбитальная скорость от вектора скорости движущегося по орбите объекта,
rявляется декартовым вектором положения орбитального объекта в координатах системы отсчета, относительно которой должны быть вычислены элементы орбиты (например, геоцентрическая экваториальная для орбиты вокруг Земли или гелиоцентрическая эклиптика для орбиты вокруг Солнца),
G – гравитационная постоянная,,
M – масса гравитирующего тела, и
ε { displaystyle varepsilon}– это удельная энергия движущегося по орбите тела.

Обратите внимание, что для данного количества общей массы удельная энергия и большая полуось всегда одинаковы, независимо от эксцентриситета. или соотношение масс. И наоборот, для данной общей массы и большой полуоси общая удельная орбитальная энергия всегда одинакова. Это утверждение всегда будет верным при любых данных условиях.

Большая и полу-малая оси планет

Орбиты планет всегда приводятся в качестве ярких примеров эллипсов (первый пример Кеплера закон ). Однако минимальная разница между большой и малой полуосями показывает, что они практически круглые по внешнему виду. Эта разница (или соотношение) основывается на эксцентриситете и рассчитывается как ab = 1 1 – e 2 { displaystyle {{a} over {b}} = {1 over { sqrt {1-e ^ {2}}}}} ${ displaystyle {{a} over { b}} = {1 over { sqrt {1-e ^ {2}}}}}$ что для типичных эксцентриситетов планет дает очень маленькие результаты.

Причина предположения о выдающихся эллиптических орбитах, вероятно, кроется в гораздо большей разнице между афелием и перигелием. Эта разница (или соотношение) также зависит от эксцентриситета и рассчитывается как rarp = 1 + e 1 – e { displaystyle {{r _ { text {a}}} over {r _ { text {p }}}} = {{1 + e} over {1-e}}} ${ displaystyle {{ r _ { text {a}}} over {r _ { текст {p}}}} = {{1 + e} over {1-e}}}$ . Из-за большой разницы между афелием и перигелием второй закон Кеплера легко визуализируется.

Имя	Эксцентриситет	Большая полуось a (AU )	Малая полуось b (AU )	разница (%)	Перигелий (AU )	Афелий (AU )	разница (%)
Меркурий	0,206	0,38700	0,37870	2,2	0,307	0,467	52
Венера	0,007	0,72300	0,72298	0,002	0,718	0,728	1,4
Земля	0,017	1,00000	0,99986	0,014	0,983	1,017	3,5
Марс	0,093	1,52400	1,51740	0,44	1,382	1,666	21
Юпитер	0,049	5,20440	5,19820	0,12	4,950	5,459	10
Сатурн	0,057	9,58260	9,56730	0,16	9,041	10,124	12
Уран	0,046	19,21840	19,19770	0,11	18,330	20,110	9,7
Нептун	0,010	30.11000	30.10870	0.004	29.820	30.400	1.9

См. Также

Ссылки

Внешние ссылки

Источник

Сегодня речь пойдет о конфигурации планет.

Конфигурация — характерное взаимное положение Солнца, планет, других небесных тел Солнечной системы на небесной сфере.

Будем называть планеты нижними, если они расположены ближе к Солнцу, чем Земля. Остальные планеты будут верхними – они расположены дальше нашей планеты от Солнца.

Планета может расположиться так, что Земля, Солнце и указанная планета находятся на одной линии. При этом может оказаться, что Солнце расположилось между Землей и рассматриваемой планетой. Такое расположение будем называть верхним соединением. Если же планета оказалась между Землей и Солнцем – то это уже нижнее соединение. Также может быть, что Земля находится между верхней планетой и Солнцем – тогда речь пойдет о противостоянии, или оппозиции.

Элонгация — одна из конфигураций планет, такое положение планеты, при котором её угловое расстояние от Солнца максимально для земного наблюдателя. Различают восточную и западную элонгацию (планета находится, соответственно, к востоку и к западу от Солнца). Об элонгации имеет смысл говорить только для Венеры и Меркурия; наилучшие условия для наблюдения этих планет наступают именно вблизи элонгаций. Из-за того, что орбиты планет не вполне круговые, угловое расстояние от Солнца в момент элонгации может быть разным, для Меркурия — от до , для Венеры — около .

Квадратура — в астрономии такая конфигурация Луны или верхней планеты (то есть планеты, более удалённой от Солнца, чем Земля) относительно Земли и Солнца, когда угол планета-Земля-Солнце равен . Если светило при этом находится к востоку от Солнца, конфигурация называется восточной квадратурой, к западу — западной квадратурой.

Сидерический период – это время совершения полного оборота какого-либо тела (планеты, кометы, астероида или искусственного спутника) вокруг главного тела (Солнца или др. планеты для спутника планеты) относительно неподвижных звёзд. Сидерический период также называют годом. Например, Меркурианский год, Юпитерианский год, и т. п.

Синодический же период – это время наблюдения с Земли совершения полного оборота планеты вокруг Солнца или Луны (искусственного спутника) вокруг Земли относительно Солнца ; промежуток времени между двумя последовательными соединениями Луны или какой-нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем должны происходить в фиксированном линейном порядке, что существенно для внутренних планет: например, это будут последовательные верхние соединения, когда планета проходит за Солнцем.

Будем помнить также и о том, что орбиты планет не круговые. Это эллипсы, причем Солнце находится в одном из главных фокусов орбиты планеты.

Перигелий — ближайшая к Солнцу точка орбиты планеты или иного небесного тела Солнечной системы.

Антонимом перигелия является афелий (апогелий) — наиболее удалённая от Солнца точка орбиты. Воображаемую линию между афелием и перигелием называют линией апсид.

Названия апоцентров меняются: эти точки получают конкретные наименования но названию центрального тела, и некоторые из них приведены в нижеследующей таблице:

Задача 9.

Центральное тело	Греческое название	Наименование перицентра	Наименование апоцентра
Солнце	Гелиос	перигелий	афелий
Земля	Гея	перигей	апогей
Венера	Геспер	перигесперий	апогесперий
Марс	Арес	периарий	апоарий
Сатурн	Кронос	перикроний	апокроний
Луна	Селена	периселений	апоселений

Теперь обратимся к математике и разберемся, что же такое эксцентрисистет. Будем говорить об эксцентриситете эллипса, поскольку нас пока больше интересуют орбиты планет.

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси; обозначив эксцентриситет буквой , получаем:

Так как , то , т. е. эксцентриситет каждого эллипса меньше единицы. Заметим, что , поэтому

Или

Следовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к единице, тем меньше , тем меньше, следовательно, отношение ; значит, чем больше эксцентриситет, тем более эллипс вытянут. В случае окружности и .

Радиус перигелия рассчитывается по формуле:

где:

— большая полуось;

— эксцентриситет орбиты.

Скорость в перигелии рассчитывается по формуле:

где:

— гравитационная постоянная;

— масса Солнца;

— большая полуось;

— эксцентриситет орбиты.

Афелийное расстояние рассчитывается по формуле

Следовательно, большая полуось орбиты планеты является средним ее расстоянием от Солнца

Cидерические периоды обращения и двух планет связаны с их средними расстояниями и от Солнца третьим законом Кеплера

Если дается в годах и — в астрономических единицах, то, принимая для Земли год и а. е., получим для любой планеты

Средняя орбитальная, или круговая, скорость планеты

всегда выражается в км/с. Так как обычно задается в астрономических единицах (1 а. е.= км) и T— в годах (1 год= с), то

Подставляя , получим:

Где скорость планеты теперь выражена в км/с.

Средняя продолжительность синодического периода обращения планеты связана с сидерическим периодом уравнением синодического движения: для верхних планет

для нижних планет

где — сидерический период обращения Земли, равный 1 звездному году.

Задача 1.

Найти перигельное и афелийное расстояния, сидерический и синодический периоды обращения, а также круговую скорость малой планеты Поэзии, если большая полуось и эксцентриситет ее орбиты равны 3,12 а. е. и 0,144.

Перигельное расстояние, а.е.

афелийное расстояние, а.е.

Сидерический период обращения

а так как а. е., то планета верхняя и поэтому ее синодический период обращения вычисляется по формуле

при году:

Круговая скорость, км/с:

Задача 2.

Вычислить перигельное и афелийное расстояния планет Сатурна и Нептуна, если их средние расстояния от Солнца равны 9,54 а. е. и 30,07 а. е., а эксцентриситеты орбит— 0,054 и 0,008.

Перигельное расстояние Сатурна, а.е.

афелийное расстояние Сатурна, а.е.

Перигельное расстояние Нептуна, а.е.

афелийное расстояние Нептуна, а.е.

Ответ: а.е., а.е., а.е., а.е.

Задача 3.

Какая из двух планет — Нептун (а = 30,07 а.е., ) или Плутон (а = 39,52 а. е., ) — подходит ближе к Солнцу? В скобках даны большая полуось и эксцентриситет орбиты планеты.

Нужно сравнить перигельные расстояния, причем для Нептуна мы его уже вычислили: а.е. Вычислим для Плутона:

Таким образом, Плутон ближе подходит к Солнцу.

Задача 4.

Найти эксцентриситет орбиты и перигельное расстояние планеты Марса и астероида Адониса, если у Марса большая полуось орбиты равна 1,52 а. е. и наибольшее расстояние от Солнца 1,66 а. е., а у Адониса соответственно 1,97 а. е. и 3,50 а. е. Указать, какая из этих двух планет подходит ближе к Солнцу.

Опять определим перигельные расстояния. Наибольшие расстояния от Солнца нам известны – афелийные. Тогда для Марса

Следовательно, перигельное расстояние Марса равно

Для Адониса

Следовательно, перигельное расстояние Адониса равно

Таким образом, Адонис подходит ближе к Солнцу.

Ответ: , а.е. , , а.е.

Задача 5.

На каком среднем и наибольшем гелиоцентрическом расстоянии движутся малые планеты Икар и Симеиза, если у Икара перигельное расстояние и эксцентриситет орбиты равны 0,187 а. е. и 0,827, а у Симеизы — 3,219 а. е. и 0,181? У какой из этих планет радиус-вектор изменяется в больших пределах, абсолютно и относительно?

Так как афелийное расстояние у Симеизы больше, то радиус-вектор ее длиннее (абсолютно). Но, так как , то относительно радиус-вектор Икара больше изменяется.

Задача 6.

Вычислить периоды обращения вокруг Солнца планеты Венеры и астероида Европы, у которых средние гелиоцентрические расстояния соответственно равны 0,723 а. е. и 3,10 а. е.

Сидерический период Венеры равен:

Или 224,5 суток.

Сидерический период астероида Европы равен:

Ответ: сидерический период Венеры равен 0,615 года или 224,5 суток, а у Европы 5,458 года.

Задача 7.

Определить периоды обращения вокруг Солнца малой планеты Аполлона и кометы Икейи, если обе они проходят вблизи Солнца почти на одинаковых расстояниях, равных у Аполлона 0,645 а. е., а у кометы 0,633 а. е., но их орбиты имеют эксцентриситеты 0,566 и 0,9933 соответственно.

Определим большие полуоси орбит Аполлона и кометы Икейи:

Тогда сидерический период Аполлона

Тогда сидерический период Икейи

Ответ: года, лет.

Задача 8.

Первый спутник планеты Юпитера — Ио обращается вокруг нее за 42ч28м на среднем расстоянии в 421 800 км. С какими периодами обращаются вокруг Юпитера его спутники Европа и Ганимед, большие полуоси орбит которых равны 671,1 тыс. км и 1070 тыс. км?

Для спутников справедлив закон Кеплера. Применим его для Европы:

Период 42ч28м= ч.

А теперь то же самое для Ганимеда:

Ответ: Период Европы 85,23 ч, или 3^д 55, период Ганимеда 171,59 ч, или 7^д15

Задача 9.

Найти средние расстояние от Сатурна его спутников Мимаса и Реи, обращающихся вокруг планеты с периодами в 22ч37м и 4^д,518. Самый крупный спутник планеты — Титан, обращается за 15^д,945 по орбите с большой полуосью в 1221 тыс. км.

Переведем периоды в часы: период Мимаса 22,62 ч, период Реи 108,43 ч, период Титана 382, 68 ч.

Применяем закон Кеплера для Титана и Мимаса:

То же для Реи:

Ответ: большая полуось Мимаса 185,27 тыс. км, Реи 526,7 тыс. км.

Источник

Большая полуось — один из основных геометрических параметров объектов, образованных посредством конического сечения.

Эллипс[править | править код]

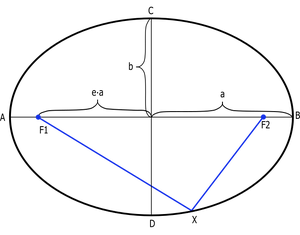
Основные параметры эллипса. Большая полуось обозначена как .

Большой осью эллипса называется его наибольший диаметр — отрезок проходящий через центр и два фокуса. Большая полуось составляет половину этого расстояния и идёт от центра эллипса к его краю через фокус.

Под углом в 90° к большой полуоси располагается малая полуось — минимальное расстояние от центра эллипса до его края. У частного случая эллипса — круга — большая и малая полуоси равны и являются радиусами. Таким образом, можно рассматривать большую и малую полуоси как некоего рода радиусы эллипса.

Длина большой полуоси связана с длиной малой полуоси через эксцентриситет , фокальный параметр и фокальное расстояние (полурасстояние между фокусами) следующим образом:

${displaystyle b=a{sqrt {1-e^{2}}},}$

${displaystyle p=a(1-e^{2}),}$

${displaystyle ap=b^{2}.}$

${displaystyle a^{2}=b^{2}+c^{2}}$

Большая полуось представляет собой среднее арифметическое между расстояниями от любой точки эллипса до его фокусов.

Рассмотрев уравнение в полярных координатах, с точкой в начале координат (полюс) и лучом, начинающейся из этой точки (полярная ось):

Получим средние значения и
и большую полуось ${displaystyle a={p over 1-e^{2}}.}$

Парабола[править | править код]

График построения параболы простейшей функции y = x²

Параболу можно получить как предел последовательности эллипсов, где один фокус остаётся постоянным, а другой отодвигается в бесконечность, сохраняя постоянным. Таким образом и стремятся к бесконечности, причём быстрее, чем .

Гипербола[править | править код]

Большая полуось гиперболы составляет половину минимального расстояния между двумя ветвями гиперболы, на положительной и отрицательной сторонах оси (слева и справа относительно начала координат). Для ветви расположенной на положительной стороне, полуось будет равна:

${frac {left(x-hright)^{2}}{a^{2}}}-{frac {left(y-kright)^{2}}{b^{2}}}=1.$

Если выразить её через коническое сечение и эксцентриситет, тогда выражение примет вид:

${displaystyle a={p over e^{2}-1}}$

Прямая, содержащая большую ось гиперболы, называется поперечной осью гиперболы.^[1]

Астрономия[править | править код]

Орбитальный период[править | править код]

В небесной механике орбитальный период обращения малых тел по эллиптической или круговой орбите вокруг более крупного центрального тела рассчитывается по формуле:

$T=2pi {sqrt {a^{3} over mu }}$

где:

— это размер большой полуоси орбиты

— это стандартный гравитационный параметр (произведение гравитационной постоянной на массу объекта

)

Следует обратить внимание, что в данной формуле для всех эллипсов период обращения определяется значением большой полуоси, независимо от эксцентриситета.

В астрономии большая полуось, наряду с орбитальным периодом, является одним из самых важных орбитальных элементов орбиты космического тела.

Для объектов Солнечной системы большая полуось связана с орбитальным периодом по третьему закону Кеплера.

$frac{T_1^2}{T_2^2} = frac{a_1^3}{a_2^3}$

где:

— орбитальный период в годах;

— большая полуось в астрономических единицах.

Это выражение является частным случаем общего решения задачи двух тел Исаака Ньютона:

${displaystyle T^{2}={frac {4pi ^{2}}{G(M+m)}}a^{3}}$

где:

— гравитационная постоянная

— масса центрального тела

— масса обращающегося вокруг него спутника. Как правило, масса спутника настолько мала по сравнению с массой центрального тела, что ею можно пренебречь. Поэтому, сделав соответствующие упрощения в этой формуле, получим данную формулу в упрощённом виде, который приведён выше.

Орбита движения спутника вокруг общего с центральным телом центра масс (барицентра), представляет собой эллипс. Большая полуось используется в астрономии всегда применительно к среднему расстоянию между планетой и звездой, в результате орбиты планет Солнечной системы приведены к гелиоцентрической системе, а не к системе движения вокруг центра масс. Эту разницу удобнее всего проиллюстрировать на примере системы Земля—Луна. Отношение масс в этом случае составляет 81,30059. Большая полуось геоцентрической орбиты Луны составляет 384 400 км, в то время как расстояние до Луны относительно центра масс системы Земля—Луна составляет 379 730 км — из-за влияния массы Луны центр масс находится не в центре Земли, а на расстоянии 4670 км от него. В итоге средняя орбитальная скорость Луны относительно центра масс составляет 1,010 км/с, а средняя скорость Земли — 0,012 км/с. Сумма этих скоростей даёт орбитальную скорость Луны 1,022 км/с; то же самое значение можно получить, рассматривая движение Луны относительно центра Земли, а не центра масс.

Среднее расстояние[править | править код]

Часто говорят, что большая полуось является средним расстоянием между центральным и орбитальным телом. Это не совсем верно, так как под средним расстоянием можно понимать разные значения — в зависимости от величины, по которой производят усреднение:

усреднение по эксцентрической аномалии. В таком случае среднее расстояние будет точно равно большой полуоси орбиты.
усреднение по истинной аномалии, тогда среднее расстояние будет точно равно малой полуоси орбиты.
усреднение по средней аномалии даст значение среднего расстояния, усреднённое по времени:

${displaystyle aleft(1+{frac {e^{2}}{2}}right).}$

усреднение по радиусу, которое получают из следующего соотношения:

${displaystyle {sqrt {ab}}=a{sqrt[{4}]{1-e^{2}}}.}$

Энергия; расчёт большой полуоси методом векторов состояния[править | править код]

В небесной механике большая полуось может быть рассчитана методом векторов орбитального состояния:

{displaystyle a={-mu over {2varepsilon }}}

для эллиптических орбит

для гиперболической траектории

$varepsilon ={v^{2} over {2}}-{mu over left|{mathbf {r}}right|}$

(удельная орбитальная энергия)

(стандартный гравитационный параметр),
где:

— орбитальная скорость спутника, на основе вектора скорости,

— вектор положения спутника в координатах системы отсчёта, относительно которой должны быть вычислены элементы орбиты (например, геоцентрический в плоскости экватора — на орбите вокруг Земли, или гелиоцентрический в плоскости эклиптики — на орбите вокруг Солнца),

— гравитационная постоянная,

— массы тел.

Большая полуось рассчитывается на основе общей массы и удельной энергии, независимо от значения эксцентриситета орбиты.

Большие и малые полуоси орбит планет[править | править код]

Орбиты планет всегда приводятся в качестве главных примеров эллипсов (первый закон Кеплера). Однако минимальная разница между большой и малой полуосями показывает, что они практически круговые по внешнему виду. Эта разница (или соотношение) основывается на эксцентриситете и вычисляется как ${displaystyle a/b=1/{sqrt {1-e^{2}}}}$ , что для типичных эксцентриситетов планет дает очень малые значения. Причина предположения о значительной эллиптичности орбит, вероятно, кроется в гораздо большей разнице между афелием и перигелием. Эта разница (или соотношение) также основывается на эксцентриситете и рассчитывается как ${displaystyle r_{text{a}}/r_{text{p}}=(1+e)/(1-e)}$ . Из-за большой разницы между афелием и перигелием второй закон Кеплера легко изобразить графически.

	Эксцентриситет	Большая полуось a (а. е.)	Малая полуось b (а. е.)	Разница (%)	Перигелий (а. е.)	Афелий (а. е.)	Разница (%)
Меркурий	0.206	0.38700	0.37870	2.2	0.307	0.467	52
Венера	0.007	0.72300	0.72298	0.002	0.718	0.728	1.4
Земля	0.017	1.00000	0.99986	0.014	0.983	1.017	3.5
Марс	0.093	1.52400	1.51740	0.44	1.382	1.666	21
Юпитер	0.049	5.20440	5.19820	0.12	4.950	5.459	10
Сатурн	0.057	9.58260	9.56730	0.16	9.041	10.124	12
Уран	0.046	19.21840	19.19770	0.11	18.330	20.110	9.7
Нептун	0.010	30.11000	30.10870	0.004	29.820	30.400	1.9

См. также[править | править код]

Элементы орбиты
Кеплеровы элементы орбиты
Эксцентриситет
Апоцентр и перицентр

Примечания[править | править код]

↑ 7.1 Alternative Characterization. Дата обращения: 15 сентября 2010. Архивировано 24 октября 2018 года.

Ссылки[править | править код]

Semi-major and semi-minor axes of an ellipse Архивная копия от 2 апреля 2012 на Wayback Machine With interactive animation

Источник

https://ru.wikipedia.org/wiki/%D0%9A%D0%B5%D0%BF%D0%BB%D0%B5%D1%80%D0%BE%D0%B2%D1%8B_%D1%8D%D0%BB%D0%B5%D0%BC%D0%B5%D0%BD%D1%82%D1%8B_%D0%BE%D1%80%D0%B1%D0%B8%D1%82%D1%8B

Введение

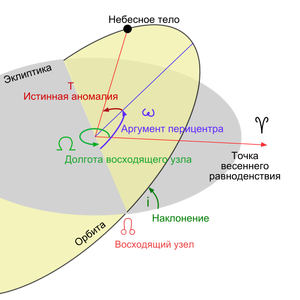
Кеплеровские элементы орбиты, включая аргумент перицентра (рис.1)

Части эллипса (рис.2)

Кеплеровы элементы — шесть элементов орбиты, определяющих положение небесного тела в пространстве в задаче двух тел:

Первые два определяют форму орбиты, третий, четвёртый и пятый — ориентацию по отношению к базовой системе координат, шестой — положение тела на орбите.

Большая полуось

Большая полуось — это половина главной оси эллипса (обозначена на рис.2 как ). В астрономии характеризует среднее расстояние небесного тела от фокуса

Эксцентриситет

Эксцентрисите́т (обозначается «» или «ε») — числовая характеристика конического сечения.
Эксцентриситет инвариантен относительно движений плоскости и преобразований подобия.^[1]
Эксцентриситет характеризует «сжатость» орбиты. Он выражается по формуле:

${displaystyle varepsilon ={sqrt {1-{frac {b^{2}}{a^{2}}}}}}$

, где

— малая полуось (см. рис.2)

Можно разделить внешний вид орбиты на пять групп:

Наклонение

A — Объект
B — Центральный объект
C — Плоскость отсчёта
D — Плоскость орбиты
i — Наклонение

Наклонение орбиты (накло́н орбиты, накло́нность орбиты, наклоне́ние) небесного тела — это угол между плоскостью его орбиты и плоскостью отсчёта (базовой плоскостью).

Обычно обозначается буквой i (от англ. inclination). Наклонение измеряется в угловых градусах, минутах и секундах.

Если

°, то движение небесного тела называется прямым^[2].

Если

°, то движение небесного тела называется обратным.

В применении к Солнечной системе, за плоскость отсчёта обычно выбирают плоскость орбиты Земли (плоскость эклиптики). Орбиты других планет Солнечной системы и Луны отклоняются от орбиты Земли лишь на несколько градусов.
Для искусственных спутников Земли за плоскость отсчёта обычно выбирают плоскость экватора Земли.
Для спутников других планет Солнечной системы за плоскость отсчёта обычно выбирают плоскость экватора соответствующей планеты.
Для экзопланет и двойных звёзд за плоскость отсчёта принимают картинную плоскость.

Аргумент перицентра

Аргуме́нт перице́нтра — определяется как угол между направлениями из притягивающего центра на восходящий узел орбиты и на перицентр (ближайшую к притягивающему центру точку орбиты спутника), или угол между линией узлов и линией апсид. Отсчитывается из притягивающего центра в направлении движения спутника, обычно выбирается в пределах 0° – 360°. Для определения восходящего и нисходящего узла выбирают некоторую (так называемую базовую) плоскость, содержащую притягивающий центр. В качестве базовой обычно используют плоскость эклиптики (движение планет, комет, астероидов вокруг Солнца), плоскость экватора планеты (движение спутников вокруг планеты) и т. д.

При исследовании экзопланет и двойных звёзд в качестве базовой используют картинную плоскость — плоскость, проходящую через звезду и перпендикулярную лучу наблюдения звезды с Земли. Орбита экзопланеты, в общем случае случайным образом ориентированная относительно наблюдателя, пересекает эту плоскость в двух точках. Точка, где планета пересекает картинную плоскость, приближаясь к наблюдателю, считается восходящим узлом орбиты, а точка, где планета пересекает картинную плоскость, удаляясь от наблюдателя, считается нисходящим узлом. В этом случае аргумент перицентра отсчитывается из притягивающего центра против часовой стрелки.

Обозначается ().

Долгота восходящего узла

Долгота́ восходя́щего узла́ — один из основных элементов орбиты, используемых для математического описания формы орбиты и её ориентации в пространстве. Определяет точку, в которой орбита пересекает основную плоскость в направлении с юга на север. Для тел, обращающихся вокруг Солнца, основная плоскость — эклиптика, а нулевая точка — Первая точка Овна (точка весеннего равноденствия).

Обозначается ☊ или Ω.

Средняя аномалия

Аномалии (рис.3)

Средняя аномалия для тела, движущегося по невозмущённой орбите — произведение его среднего движения и интервала времени после прохождения перицентра. Таким образом, средняя аномалия есть угловое расстояние от перицентра гипотетического тела, движущегося с постоянной угловой скоростью, равной среднему движению.

Обозначается буквой (от англ. mean anomaly)

В звёздной динамике средняя аномалия вычисляется по следующим формулам:

${displaystyle M=M_{0}+n(t-t_{0}),!}$

где:

Либо через уравнение Кеплера:

где:

Вычисление кеплеровых элементов

Рассмотрим следующую задачу: пусть имеется невозмущённое движение и известны вектор положения ${displaystyle mathbf {r} _{0}(x_{0},y_{0},z_{0})}$ и вектор скорости ${displaystyle mathbf {dot {r}} ({dot {x}}_{0},{dot {y}}_{0},{dot {z}}_{0})}$ на момент времени . Найдём кеплеровы элементы орбиты.

Прежде всего, вычислим большую полуось:

${displaystyle r_{0}^{2}=x_{0}^{2}+y_{0}^{2}+z_{0}^{2}}$

${displaystyle {dot {r}}_{0}^{2}={dot {x}}_{0}^{2}+{dot {y}}_{0}^{2}+{dot {z}}_{0}^{2}}$

${displaystyle r_{0}cdot {dot {r}}_{0}=x_{0}cdot {dot {x}}_{0}+y_{0}cdot {dot {y}}_{0}+z_{0}cdot {dot {z}}_{0}}$

По интегралу энергии:

(1) ${displaystyle {frac {1}{a}}={frac {2}{r_{0}}}-{frac {v_{0}^{2}}{k^{2}}}}$

, где k — гравитационный параметр равный произведению гравитационной постоянной на массу небесного тела, для Земли K = 3,986005×10⁵ км³/c², для Солнца K = 1,32712438×10¹¹ км³/c².

Следовательно, по формуле (1) находим .

Страница: 0

en: Kepler orbit

de: [1]

Примечания

↑ А. В. Акопян, А. А. Заславский Геометрические свойства кривых второго порядка, — М.: МЦНМО, 2007. — 136 с.
↑ То есть, объект движется вокруг Солнца в том же направлении, что и Земля

См. также

Элементы орбиты

Ссылки

Литература

Википедия Кеплеровы элементы орбиты адрес
Викисловарь — адрес
Викицитатник — адрес
Викиучебник — адрес
Викитека — адрес
Викиновости — адрес
Викиверситет — адрес
Викигид — адрес

Выделить Кеплеровы элементы орбиты и найти в:

Вокруг света элементы орбиты адрес
Академик элементы орбиты/ru/ru/ адрес
Астронет адрес
Элементы элементы орбиты+&search адрес
Научная Россия элементы орбиты&mode=2&sort=2 адрес
Кругосвет элементы орбиты&results_per_page=10 адрес
Научная Сеть
Традиция — адрес
Циклопедия — адрес
Викизнание — элементы орбиты адрес

Google
Bing
Yahoo
Яндекс
Mail.ru
Рамблер
Нигма.РФ
Спутник
Google Scholar
Апорт
Онлайн-переводчик
Архив Интернета
Научно-популярные фильмы на Яндексе
Документальные фильмы

Список ru-вики
Вики-сайты на русском языке
Список крупных русскоязычных википроектов
Каталог wiki-сайтов
Русскоязычные wiki-проекты
Викизнание:Каталог wiki-сайтов
Научно-популярные сайты в Интернете
Лучшие научные сайты на нашем портале
Лучшие научно-популярные сайты
Каталог научно-познавательных сайтов
НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов

Страница 0 – краткая статья
Страница 1 – энциклопедическая статья
Разное – на страницах: 2 , 3 , 4 , 5
Прошу вносить вашу информацию в «Кеплеровы элементы орбиты 1», чтобы сохранить ее

Комментарии читателей:

Для статьи

Источник

Содержание

Эллипс

Гипербола

Астрономия

Орбитальная период

Среднее расстояние

Энергия; вычисление большой полуоси из векторов состояния

Большая и полу-малая оси планет

См. Также

Ссылки

Внешние ссылки

Эллипс[править | править код]

Парабола[править | править код]

Гипербола[править | править код]

Астрономия[править | править код]

Орбитальный период[править | править код]

Среднее расстояние[править | править код]

Энергия; расчёт большой полуоси методом векторов состояния[править | править код]

Большие и малые полуоси орбит планет[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Введение

Большая полуось

Эксцентриситет

Наклонение

Аргумент перицентра

Долгота восходящего узла

Средняя аномалия

Вычисление кеплеровых элементов

Примечания

См. также

Ссылки

Литература

Комментарии читателей:

Для статьи

Вам также может понравиться

Как найти где находится выключенный телефон

Тормозит интернет в телефоне как исправить

Как найти ошибку в магическом квадрате

Добавить комментарий Отменить ответ