Целое число 01012
можно представить в виде 01012 =0*23
+ 1*22 + 0*21 + 1*20
Аналогично можно
записать двоичную дробь:
11.01012 =1*21+
1*20 + 0*2-1 + 1*2-2 + 0*2-3
+ 1*2-4
Заметим, что сдвиг
двоичной точки на n разрядов вправо
(чаще говорят о сдвиге самого числа
влево) эквивалентен умножению числа на
(102)n = 2n. Сдвиг точки
влево (то есть сдвиг самого числа вправо)
– делению на 2n.
Мантисса и порядок числа
Рассмотрим
сначала упрощенную схему хранения чисел
в формате с плавающей точкой (floating
point), несколько отличающуюся от реальной.
Число
x с плавающей
точкой может быть представлено в виде
x=s*m*2p.
Множитель s – знак числа. Второй множитель
m называется мантиссой, а число p
– порядком числа.
Для
простоты рассмотрим 10-битовую ячейку,
состоящую из трёх независимых частей:
знак
порядок мантисса
1
бит 4 бита
5 бит
Первым
идёт знаковый бит. Если он равен 0, число
положительно, если равен 1 – отрицательно.
Набор бит, хранящийся в мантиссе, задает
положительное число m, лежащее в пределах
1≤m<2. Оно получается из нашего двоичного
числа путем переноса двоичной точки на
место после первой значащей цифры числа.
Например, числа 1.01012, 10.1012 и
0.101012 и имеют одну и ту же мантиссу,
равную 1.01012. При этом следующая
за ведущей единицей точка в ячейке,
выделяемой под мантиссу, не хранится
– она подразумевается. То есть мантиссы
приведённых чисел будут храниться в
виде 101012.
Число
сдвигов двоичной точки (с учетом знака)
хранится в части ячейки, выделяемой под
порядок числа. В нашем примере числа
1.01012, 10.1012 и 0.101012 будут
иметь порядки 0, 1 и -1, соответственно.
При перемножении чисел их мантиссы
перемножаются, а порядки складываются.
При делении – мантиссы делятся, а порядки
вычитаются. И умножение, и деление
мантисс происходит по тем же алгоритмам,
что и для целых чисел. Но при выходе за
размеры ячейки отбрасываются не старшие,
а младшие байты. В результате каждая
операция умножения или деления даёт
результат, отличающийся от точного на
несколько значений младшего бита
мантиссы. Аналогичная ситуация с потерей
младших бит возникает при умножениях
и делениях. Ведь если в ячейках для чисел
данного типа хранится k
значащих цифр числа, то при умножении
двух чисел точный результат будет иметь
2k значащих цифр,
последние k из
которых при записи результата в ячейку
будут отброшены даже в том случае, если
они сохранялись при вычислениях. А при
делении в общем случае при точных
вычислениях должна получаться бесконечная
периодическая двоичная дробь, так что
даже теоретически невозможно провести
эти вычисления без округлений. С этим
связана конечная точность вычислений
на компьютерах при использовании формата
с “плавающей точкой”. При этом чем
больше двоичных разрядов выделяется
под мантиссу числа, тем меньше погрешность
в такого рода операциях.
Замечание:
системы символьных вычислений (или, что
то же, – аналитических вычислений, или,
что то же, системы компьютерной алгебры)
позволяют проводить точные численные
расчеты с получением результатов в виде
формул. Однако они выполняют вычисления
на много порядков медленнее, требуют
намного больше ресурсов и не могут
работать без громоздкой среды разработки.
Поэтому для решения большинства
практически важных задач они либо
неприменимы, либо их использование
нецелесообразно.
При
сложении или вычитании сначала происходит
приведение чисел к одному порядку:
мантисса числа с меньшим порядком
делится на 2n, а порядок увеличивается
на n, где n
– разница в порядке чисел. При этом
деление на 2n осуществляется путем
сдвига мантиссы на n
бит вправо, с заполнением освобождающихся
слева бит нулями. Младшие биты мантиссы,
выходящие за пределы отведенной под
нее части ячейки, теряются.
Пример:
сложим
числа 11.0112 и 0.110112 . Для первого
числа мантисса 1.10112, порядок 1, так
как 11.0112=1.10112*(102)1.
Для второго – мантисса 1.10112 ,
порядок -1, так как 0.110112 =1.10112*(102)-1.
Приводим порядок второго числа к значению
1, сдвигая мантиссу на 2 места вправо,
так как разница порядков равна 2:
0.110112
= 0.0110112* (102)1.
Но
при таком сдвиге теряется два последних
значащих бита мантиссы (напомним,
хранится 5 бит), поэтому получаем
приближенное значение 0.01102* (102)1.
Из-за чего в машинной арифметике
получается
1.10112*(102)1
+ 0.0110112*(102)1 = (1.10112
+ 0.0110112)*(102)1 ≈ (1.10112
+ 0.01102)*(102)1 =10.00012*
(102)1 ≈ 1.00002*(102)2
вместо
точного значения 1.00001112*(102)2.
Таким
образом, числа в описанном формате
являются на деле рациональными, а не
вещественными. При этом операции
сложения, вычитания, умножения и деления
выполняются с погрешностями, тем
меньшими, чем больше разрядность
мантиссы. Число двоичных разрядов,
отводимых под порядок числа, влияет
лишь на допустимый диапазон значений
чисел, и не влияет на точность вычислений.
Научная нотация
записи вещественных чисел
При
записи программы в текстовом файле или
выдачи результатов в виде “плоского
текста” (plain text) невозможна запись
выражений типа
![]()
.
В этом случае используется так называемая
научная нотация, когда вместо основания
10 пишется латинская буква E (сокращение
от Exponent – экспонента). Таким образом,
запишется как 1.5E14, а
![]()
как 0.31E-7. Первоначально буква E писалась
заглавной, что не вызывало проблем.
Однако с появлением возможности набора
текста программы в нижнем регистре
стали использовать строчную букву e,
которая в математике используется для
обозначения основания натуральных
логарифмов. Запись вида 3e2
легко воспринять как
![]()
,
а не
![]()
.
Поэтому лучше использовать заглавную
букву.
Литерные константы
для вещественных типов по умолчанию
имеют тип double. Например,
1.5 , -17E2 , 0.0 . Если требуется
ввести литерную константу типа float,
после записи числа добавляют постфикс
f (сокращение от “float”):
1.5f , -17E2f
, 0.0f .
Минимальное
по модулю не равное нулю и максимальное
значение типа float
можно получить с помощью констант
Float.MIN_VALUE
– равна 2-149
Float.MAX_VALUE
– равна (2-2-23)∙2127
Аналогичные
значения для типа double
– с помощью констант
Double.MIN_VALUE
– равна
2-1074
Double.MAX_VALUE
– равна
(2-2-52)∙21023.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что нужно знать про арифметику с плавающей запятой
Время на прочтение
14 мин
Количество просмотров 858K

В далекие времена, для IT-индустрии это 70-е годы прошлого века, ученые-математики (так раньше назывались программисты) сражались как Дон-Кихоты в неравном бою с компьютерами, которые тогда были размером с маленькие ветряные мельницы. Задачи ставились серьезные: поиск вражеских подлодок в океане по снимкам с орбиты, расчет баллистики ракет дальнего действия, и прочее. Для их решения компьютер должен оперировать действительными числами, которых, как известно, континуум, тогда как память конечна. Поэтому приходится отображать этот континуум на конечное множество нулей и единиц. В поисках компромисса между скоростью, размером и точностью представления ученые предложили числа с плавающей запятой (или плавающей точкой, если по-буржуйски).
Арифметика с плавающей запятой почему-то считается экзотической областью компьютерных наук, учитывая, что соответствующие типы данных присутствуют в каждом языке программирования. Я сам, если честно, никогда не придавал особого значения компьютерной арифметике, пока решая одну и ту же задачу на CPU и GPU получил разный результат. Оказалось, что в потайных углах этой области скрываются очень любопытные и странные явления: некоммутативность и неассоциативность арифметических операций, ноль со знаком, разность неравных чисел дает ноль, и прочее. Корни этого айсберга уходят глубоко в математику, а я под катом постараюсь обрисовать лишь то, что лежит на поверхности.
1. Основы
Множество целых чисел бесконечно, но мы всегда можем подобрать такое число бит, чтобы представить любое целое число, возникающее при решении конкретной задачи. Множество действительных чисел не только бесконечно, но еще и непрерывно, поэтому, сколько бы мы не взяли бит, мы неизбежно столкнемся с числами, которые не имеют точного представления. Числа с плавающей запятой — один из возможных способов предсталения действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений.
Число с плавающей запятой состоит из набора отдельных разрядов, условно разделенных на знак,
экспоненту
порядок и мантиссу. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой в следующем виде:

Математически это записывается так:
(-1)s × M × BE, где s — знак, B-основание, E — порядок, а M — мантисса.
Основание определяет систему счисления разрядов. Математически доказано, что числа с плавающей запятой с базой B=2 (двоичное представление) наиболее устойчивы к ошибкам округления, поэтому на практике встречаются только базы 2 и, реже, 10. Для дальнейшего изложения будем всегда полагать B=2, и формула числа с плавающей запятой будет иметь вид:
(-1)s × M × 2E
Что такое мантисса и порядок? Мантисса – это целое число фиксированной длины, которое представляет старшие разряды действительного числа. Допустим наша мантисса состоит из трех бит (|M|=3). Возьмем, например, число «5», которое в двоичной системе будет равно 1012. Старший бит соответствует 22=4, средний (который у нас равен нулю) 21=2, а младший 20=1. Порядок – это степень базы (двойки) старшего разряда. В нашем случае E=2. Такие числа удобно записывать в так называемом
«научном»
стандартном виде, например «1.01e+2». Сразу видно, что мантисса состоит из трех знаков, а порядок равен двум.
Допустим мы хотим получить дробное число, используя те же 3 бита мантиссы. Мы можем это сделать, если возьмем, скажем, E=1. Тогда наше число будет равно
1,01e+1 = 1×21+0×20+1×2-1=2+0,5=2,5
Здесь, поскольку E=1, степень двойки первого разряда (который идет перед запятой), равна «1». Два других разряда, расположенных правее (после запятой), обеспечивают вклад 2E-1 и 2E-2 (20 и 2-1 соответственно). Очевидно, что регулируя E одно и то же число можно представить по-разному. Рассмотрим пример с длиной мантиссы |M|=4. Число «2» можно представить в следующем виде:
2 = 10 (в двоичной системе) = 1.000e+1 = 0.100e+2 = 0.010e+3. (E=1, E=2, E=3 соответственно)
Обратите внимание, что одно и то же число имеет несколько представлений. Это не удобно для оборудования, т.к. нужно учитывать множественность представлния при сравнении чисел и при выполнении над ними арифметических операций. Кроме того, это не экономично, поскольку число представлений — конечное, а повторения уменьшают множество чисел, которые вообще могут быть представлены. Поэтому уже в самых первых машинах начали использовать трюк, делая первый бит мантиссы всегда положительным. Такое предаставление назвали нормализованным.

Это экономит один бит, так как неявную единицу не нужно хранить в памяти, и обеспечивает уникальность представления числа. В нашем примере «2» имеет единственное нормализованное представление («1.000e+1»), а мантисса хранится в памяти как «000», т.к. старшая единица подразумевается неявно. Но в нормализованном представлении чисел возникает новая проблема — в такой форме невозможно представить ноль.
Строго говоря, нормализованное число имеет следующий вид:
(-1)s × 1.M × 2E.
Качество решения задач во многом зависит от выбора представления чисел с плавающей запятой. Мы плавно подошли к проблеме стандартизации такого представления.
2. Немного истории
В 60-е и 70-е годы не было единого стандарта представления чисел с плавающей запятой, способов округления, арифметических операций. В результате программы были крайне не портабельны. Но еще большей проблемой было то, что у разных компьютеров были свои «странности» и их нужно было знать и учитывать в программе. Например, разница двух не равных чисел возвращала ноль. В результате выражения «X=Y» и «X-Y=0» вступали в противоречие. Умельцы обходили эту проблему очень хитрыми трюками, например, делали присваивание «X=(X-X)+X» перед операциями умножения и деления, чтобы избежать проблем.
Инициатива создать единый стандарт для представления чисел с плавающей запятой подозрительно совпала с попытками в 1976 году компанией Intel разработать «лучшую» арифметику для новых сопроцессоров к 8086 и i432. За разработку взялись ученые киты в этой области, проф. Джон Палмер и Уильям Кэхэн. Последний в своем интервью высказал мнение, что серьезность, с которой Intel разрабатывала свою арифметику, заставила другие компании объединиться и начать процесс стандартизации.
Все были настроены серьезно, ведь очень выгодно продвинуть свою архитектуру и сделать ее стандартной. Свои предложения представили компании DEC, National Superconductor, Zilog, Motorola. Производители мейнфреймов Cray и IBM наблюдали со стороны. Компания Intel, разумеется, тоже представила свою новую арифметику. Авторами предложенной спецификации стали Уильям Кэхэн, Джероми Кунен и Гарольд Стоун и их предложение сразу прозвали «K-C-S».
Практически сразу же были отброшены все предложения, кроме двух: VAX от DEC и «K-C-S» от Intel. Спецификация VAX была значительно проще, уже была реализована в компьютерах PDP-11, и было понятно, как на ней получить максимальную производительность. С другой стороны в «K-C-S» содержалось много полезной функциональности, такой как «специальные» и «денормализованные» числа (подробности ниже).
В «K-C-S» все арифметические алгоритмы заданы строго и требуется, чтобы в реализации результат с ними совпадал. Это позволяет выводить строгие выкладки в рамках этой спецификации. Если раньше математик решал задачу численными методами и доказывал свойства решения, не было никакой гарантии, что эти свойства сохранятся в программе. Строгость арифметики «K-C-S» сделала возможным доказательство теорем, опираясь на арифметику с плавающей запятой.
Компания DEC сделала все, чтобы ее спецификацию сделали стандартом. Она даже заручилась поддержкой некоторых авторитетных ученых в том, что арифметика «K-C-S» в принципе не может достигнуть такой же производительности, как у DEC. Ирония в том, что Intel знала, как сделать свою спецификацию такой же производительной, но эти хитрости были коммерческой тайной. Если бы Intel не уступила и не открыла часть секретов, она бы не смогла сдержать натиск DEC.
Подробнее о баталиях при стандартизации смотрите в интервью профессора Кэхэна, а мы рассмотрим, как выглядит представление чисел с плавающей запятой сейчас.
3. Представление чисел с плавающей запятой сегодня
Разработчики «K-C-S» победили и теперь их детище воплотилось в стандарт IEEE754. Числа с плавающей запятой в нем представлены в виде знака (s), мантиссы (M) и порядка (E) следующим образом:
(-1)s × 1.M × 2E
Замечание. В новом стандарте IEE754-2008 кроме чисел с основанием 2 присутствуют числа с основанием 10, так называемые десятичные (decimal) числа с плавающей запятой.
Чтобы не загромождать читателя чрезмерной информацией, которую можно найти в Википедии, рассмотрим только один тип данных, с одинарной точностью (float). Числа с половинной, двойной и расширенной точностью обладают теми же особенностями, но имеют другой диапазон порядка и мантиссы. В числах одинарной точности (float/single) порядок состоит из 8 бит, а мантисса – из 23. Эффективный порядок определяется как E-127. Например, число 0,15625 будет записано в памяти как

Рисунок взят из Википедии
В этом примере:
- Знак s=0 (положительное число)
- Порядок E=011111002-12710 = -3
- Мантисса M = 1.012 (первая единица не явная)
- В результате наше число F = 1.012e-3 = 2-3+2-5 = 0,125 + 0,03125 = 0,15625
Чуть более подробное объяснение
Здесь мы имеем дело с двоичным представлением числа «101» со сдвигом запятой на несколько разрядов влево. 1,01 — это двоичное представление, означающее 1×20 + 0×2-1 + 1×2-2. Сдвинув запятую на три позиции влево получим 1,01e-3 = 1×2-3 + 0×2-4 + 1×2-5 = 1×0,125 + 0×0,0625 + 1×0,03125 = 0,125 + 0,03125 = 0,15625.
3.1 Специальные числа: ноль, бесконечность и неопределенность
В IEEE754 число «0» представляется значением с порядком, равным E=Emin-1 (для single это -127) и нулевой мантиссой. Введение нуля как самостоятельного числа (т.к. в нормализованном представлении нельзя представить ноль) позволило избежать многих странностей в арифметике. И хоть операции с нулем нужно обрабатывать отдельно, обычно они выполняются быстрее, чем с обычными числами.
Также в IEEE754 предусмотрено представление для специальных чисел, работа с которыми вызывает исключение. К таким числам относится бесконечность (±∞) и неопределенность (NaN). Эти числа позволяет вернуть адекватное значение при переполнении. Бесконечности представлены как числа с порядком E=Emax+1 и нулевой мантиссой. Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль. Бесконечность при делении разработчики определили исходя из существования пределов, когда делимое и делитель стремиться к какому-то числу. Соответственно, c/0==±∞ (например, 3/0=+∞, а -3/0=-∞), так как если делимое стремиться к константе, а делитель к нулю, предел равен бесконечности. При 0/0 предел не существует, поэтому результатом будет неопределенность.
Неопределенность или NaN (от not a number) – это представление, придуманное для того, чтобы арифметическая операция могла всегда вернуть какое-то не бессмысленное значение. В IEEE754 NaN представлен как число, в котором E=Emax+1, а мантисса не нулевая. Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.
Как можно получить NaN? Одним из следующих способов:
- ∞+(- ∞)
- 0 × ∞
- 0/0, ∞/∞
- sqrt(x), где x<0
По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.
Зачем нулю знак (или +0 vs -0)
Любознательный читатель вероятно уже
замелил
заметил, что в описанном представлении чисел с плавающей запятой существует два нуля, которые отличаются только знаком. Так, 3·(+0)=+0, а 3·(-0)=-0. Но при сравнении +0=-0. В стандарте знак сохранили умышленно, чтобы выражения, которые в результате переполнения или потери значимости превращаются в бесконечность или в ноль, при умножении и делении все же могли представить максимально корректный результат. Например, если бы у нуля не было знака, выражение 1/(1/x)=x не выполнялось бы верно при x=±∞, так как 1/∞ и 1/-∞ равны 0.
Еще один пример:
(+∞/0) + ∞ = +∞, тогда как (+∞/-0) +∞ = NaN
Чем бесконечность в данном случае лучше, чем NaN? Тем, что если в арифметическом выражении появился NaN, результатом всего выражения всегда будет NaN. Если же в выражении встретилась бесконечность, то результатом может быть ноль, бесконечность или обычное число с плавающей запятой. Например, 1/∞=0.
3.3 Денормализованные числа
Что такое
субнормальные
денормализованные (subnormal) числа рассмотрим на простом примере. Пусть имеем нормализованное представление с длиной мантиссы |M|=2 бита (+ один бит нормализации) и диапазоном значений порядка -1≤E≤2. В этом случае получим 16 чисел:

Крупными штрихами показаны числа с мантиссой, равной 1,00. Видно, что расстояние от нуля до ближайшего числа (0 — 0,5) больше, чем от этого числа к следующему (0,5 — 0,625). Это значит, что разница двух любых чисел от 0,5 до 1 даст 0, даже если эти числа не равны. Что еще хуже, в пропасть между 0,5 и 0 попадает разница чисел, больших 1. Например, «1,5-1,25=0» (см. картинку).
В «околонулевую яму» подпадает не каждая программа. Согласно статистике 70-х годов в среднем каждый компьютер сталкивался с такой проблемой один раз в месяц. Учитывая, что компьютеры приобретали массовость, разработчики «K-C-S» посчитали эту проблему достаточно серьезной, чтобы решать ее на аппаратном уровне. Предложенное ими решение состояло в следующем. Мы знаем, что при E=Emin-1 (для float это «-127») и нулевой мантиссе число считается равным нулю. Если же мантисса не нулевая, то число считается не нулевым, его порядок полагается E=Emin, причем неявный старший бит мантиссы полагается равным нулю. Такие числа называются денормализованными.
Строго говодя, числа с плавающей запятой теперь имеют вид:
(-1)s × 1.M × 2E, если Emin≤E≤Emax (нормализованные числа)
(-1)s × 0.M × 2Emin, если E=Emin-1. (денормализованные числа)
Вернемся к примеру. Наш Emin=-1. Введем новое значение порядка, E=-2, при котором числа являются денормализованными. В результате получаем новое представление чисел:

Интервал от 0 до 0,5 заполняют денормализованные числа, что дает возможность не проваливаться в 0 рассмотренных выше примерах (0,5-0,25 и 1,5-1,25). Это сделало представление более устойчиво к ошибкам округления для чисел, близких к нулю.
Но роскошь использования денормализованного представления чисел в процессоре не дается бесплатно. Из-за того, что такие числа нужно обрабатывать по-другому во всех арифметических операциях, трудно сделать работу в такой арифметике эффективной. Это накладывает дополнительные сложности при реализации АЛУ в процессоре. И хоть денормализованные числа очень полезны, они не являются панацеей и за округлением до нуля все равно нужно следить. Поэтому эта функциональность стала камнем преткновения при разработке стандарта и встретила самое сильное сопротивление.
3.4 Очередность чисел в IEEE754
Одна из удивительных особенностей представления чисел в формате IEEE754 состоит в том, что порядок и мантисса расположены друг за другом таким образом, что вместе образуют последовательность целых чисел {n} для которых выполняется:
n<n+1 ⇒ F(n) < F(n+1), где F(n) – число с плавающей запятой, образованное от целого n, разбиением его битов на порядок и мантиссу.
Поэтому если взять положительное число с плавающей запятой, преобразовать его к целому, прибавить «1», мы получим следующее число, которое представимо в этой арифметике. На Си это можно сделать так:
float a=0.5;
int n = *((int*) &a);
float b = *((float*) &(++n));
printf("После %e следующее число: %e, разница (%e)n", a, b, b-a);
Этот код будет работать только на архитектуре с 32-битным int.
4. Подводные камни в арифметике с плавающей запятой
Теперь – к практике. Рассмотрим особенности арифметики с плавающей запятой, к которым нужно проявить особую осторожность при программировании.
4.1 Округление
С ошибками из-за погрешностей округления в современной арифметике с плавающей запятой встретиться сложно, особенно если использовать двойную точность. Правило округления в стандарте IEEE754 говорит о том, что результат любой арифметической операции должен быть таким, как если бы он был выполнен над точными значениями и округлен до ближайшего числа, представимого в этом формате. Это требует от АЛУ дополнительных усилий и некоторые опции компилятора (такие как «-ffast-math» в gcc) могут отключить такое поведение. Особенности округления в IEEE754:
- Округление до ближайшего в стандарте сделано не так как мы привыкли. Математически показано, что если 0,5 округлять до 1 (в большую сторону), то существует набор операций, при которых ошибка округления будет возрастать до бесконечности. Поэтому в IEEE754 применяется правило округления до четного. Так, 12,5 будет округлено до 12, а 13,5 – до 14.
- Самая опасная операция с точки зрения округления в арифметике с плавающей запятой — это вычитание. При вычитании близких чисел значимые разряды могут потеряться, что
может в разы увеличить относительную погрешность. - Для многих широко распространенных математических формул математики разработали специальную форму, которая позволяет значительно уменьшить погрешность при округлении. Например, расчет формулы «x2-y2» лучше вычислять используя формулу «(x-y)(x+y)».
4.2 Неассоциативность арифметических операций
В арифметике с плавающей запятой правило (a*b)*c = a*(b*c) не выполняется для любых арифметических операций. Например,
(1020+1)-1020=0 ≠ (1020-1020)+1=1
Допустим у нас есть программа суммирования чисел.
double s = 0.0;
for (int i=0; i<n; i++) s = s + t[i];
Некоторые компиляторы по умолчанию могут переписать код для использования нескольких АЛУ одновременно (будем считать, что n делится на 2):
double sa[2], s;
sa[0]=sa[1]=0.0;
for (int i=0; i<n/2; i++) {
sa[0]=sa[0]+t[i*2+0];
sa[1]=sa[1]+t[i*2+1];
}
S=sa[0]+sa[1];
Так как операции суммирования не ассоциативны, эти две программы могут выдать различный результат.
4.3 Числовые константы
Помните, что не все десятичные числа имеют двоичное представление с плавающей запятой. Например, число «0,2» будет представлено как «0,200000003» в одинарной точности. Соответственно, «0,2 + 0,2 ≈ 0,4». Абсолютная погрешность в отдельном
случае может и не высока, но если использовать такую константу в цикле, можем получить накопленную погрешность.
4.4 Выбор минимума из двух значений
Допустим из двух значений нам нужно выбрать минимальное. В Си это можно сделать одним из следующих способов:
- x < y? x: y
- x <= y? x: y
- x > y? y: x
- x >= y? y: x
Часто компилятор считает их эквивалентными и всегда использует первый вариант, так как он выполняется за одну инструкцию процессора. Но если мы учтем ±0 и NaN, эти операции никак не эквивалентны:
| x | y | x < y? x: y | x <= y? x: y | x > y? y: x | x >= y? y: x |
| +0 | -0 | -0 | +0 | +0 | -0 |
| NaN | 1 | 1 | 1 | NaN | NaN |
4.5 Сравнение чисел
Очень распространенная ошибка при работе с float-ами возникает при проверке на равенство. Например,
float fValue = 0.2;
if (fValue == 0.2) DoStuff();
Ошибка здесь, во-первых, в том, что 0,2 не имеет точного двоичного представления, а во-вторых 0,2 – это константа двойной точности, а переменная fValue – одинарной, и никакой гарантии о поведении этого сравнения нет.
Лучший, но все равно ошибочный способ, это сравнивать разницу с допустимой абсолютной погрешностью:
if (fabs(fValue – fExpected) < 0.0001) DoStuff(); // fValue=fExpected?Недостаток такого подхода в том, что погрешность представления числа увеличивается с ростом самого этого числа. Так, если программа ожидает «10000», то приведенное равенство не будет выполняться для ближайшего соседнего числа (10000,000977). Это особенно актуально, если в программе имеется преобразование из одинарной точности в двойную.
Выбрать правильную процедуру сравнения сложно и заинтересованных читателей я отсылаю к статье Брюса Доусона. В ней предлагается сравнивать числа с плавающей запятой преобразованием к целочисленной переменной. Это — лучший, хотя и не портабельный способ:
bool AlmostEqual2sComplement(float A, float B, int maxUlps) {
// maxUlps не должен быть отрицательным и не слишком большим, чтобы
// NaN не был равен ни одному числу
assert(maxUlps > 0 && maxUlps < 4 * 1024 * 1024);
int aInt = *(int*)&A;
// Уберем знак в aInt, если есть, чтобы получить правильно упорядоченную последовательность
if (aInt < 0) aInt = 0x80000000 - aInt;
//aInt &= 0x7fffffff; //(см. комментарий пользователя Vayun)
// Аналогично для bInt
int bInt = *(int*)&B;
if (bInt < 0) bInt = 0x80000000 - bInt;
/*aInt &= 0x7fffffff;*/
unsigned int intDiff = abs(aInt - bInt); /*(см. комментарий пользователя Vayun)*/
if (intDiff <= maxUlps)
return true;
return false;
}В этой программе maxUlps (от Units-In-Last-Place) – это максимальное количество чисел с плавающей запятой, которое может лежать между проверяемым и ожидаемым значением. Другой смысл этой переменной – это количество двоичных разрядов (начиная с младшего) в сравниваемых числах разрешается упустить. Например, maxUlps=16, означает, что младшие 4 бита (log216) могут не совпадать, а числа все равно будут считаться равными. При этом, при сравнении с числом 10000 абсолютная погрешность будет равна 0,0146, а при сравнении с 0.001, погрешность будет менее 0.00000001 (10-8).
5. Проверка полноты поддержки IEE754
Думаете, что если процессоры полностью соответствуют стандарту IEEE754, то любая программа, использующая стандартные типы данных (такие как float/double в Си), будет выдавать один и тот же результат на разных компьютерах? Ошибаетесь. На портабельность и соответствие стандарту влияет компилятор и опции оптимизации. Уильям Кэхэн написал программу на Си (есть версия и для Фортрана), которая позволяет проверить удовлетворяет ли связка «архитектура+компилятор+опции» IEEE754. Называется она «Floating point paranoia» и ее исходные тексты доступны для скачивания. Аналогичная программа доступна для GPU. Так, например, компилятор Intel (icc) по умолчанию использует «расслабленную» модель IEEE754, и в результате не все тесты выполняются. Опция «-fp-model precise» позволяет компилировать программу с точным соответствием стандарту. В компиляторе GCC есть опция «-ffast-math», использование которой приводит к несоответствию IEEE754.
Заключение
Напоследок поучительная история. Когда я работал над тестовым проектом на GPU, у меня была последовательная и параллельная версия одной программы. Сравнив время выполнения, я был очень обрадован, так как получил ускорение в 300 раз. Но позже оказалось, что вычисления на GPU «разваливались» и обращались в NaN, а работа с ними в GPU была быстрее, чем с обычными числами. Интересно было другое — одна и та же программа на эмуляторе GPU (на CPU) выдавала корректный результат, а на самом GPU – нет. Позже оказалось, что проблема была в том, что этот GPU не поддерживал полностью стандарт IEEE754 и прямой подход не сработал.
Сейчас арифметика с плавающей запятой почти совершенна. Практически всегда наивный подход сработает, и программа, не учитывающая все ее особенности, выдаст правильный результат, а описанные подводные камни касаются только экзотических случаев. Но нужно всегда оставаться бдительным: в таком вопросе как компьютерная математика легко наступить на грабли.
P.S. Спасибо пользователю uqlock за важное замечание. Деньги нельзя хранить в виде числа с плавающей запятой, т.к. в этом случае нельзя выделить значимые разряды. Если в языке программирования нет типов данных с фиксированной запятой, можно выйти из положения и хранить деньги в виде целого числа, подразумевая копейки (иногда доли копеек).
P.P.S. Благодарность за найденные опечатки и ошибки пользователям: gribozavr, kurokikaze, Cenness, TheShock, perl_demon, GordTremor, fader44, DraculaDis, icc, f0rbidik, Harkonnen, AlexanderYastrebov, Vayun, EvilsInterrupt!
Литература
- Интервью с Уильамом Кэхэном про становление стандарта IEE754.
- What Every Computer Scientist Should Know About Floating-Point Arithmetic, David Goldberg — книга с математическими выкладками.
- Comparing floating point numbers, Bruce Dowson.
Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.
Число с плавающей запятой состоит из набора отдельных двоичных разрядов, условно разделенных на так называемые знак (англ. sign), порядок (англ. exponent) и мантиссу (англ. mantis). В наиболее распространённом формате (стандарт IEEE 754) число с плавающей запятой представляется в виде набора битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа ( — если число положительное, — если число отрицательное). При этом порядок записывается как целое число в коде со сдвигом, а мантисса — в нормализованном виде, своей дробной частью в двоичной системе счисления. Вот пример такого числа из двоичных разрядов:
| Знак | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 10 | 9 | 0 |
Знак — один бит, указывающий знак всего числа с плавающей точкой. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой в следующем виде:
, где — знак, — основание, — порядок, а — мантисса.
Десятичное число, записываемое как , где — число в полуинтервале , — степень, в которой стоит множитель ; в нормализированной форме модуль будет являться мантиссой, а — порядком, а будет равно тогда и только тогда, когда принимает отрицательное значение.
Например, в числе
Порядок также иногда называют экспонентой или просто показателем степени.
При этом лишь некоторые из вещественных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями.
Более простым вариантом представления вещественных чисел является вариант с фиксированной точкой, когда целая и вещественная части хранятся отдельно. Например, на целую часть отводится всегда бит и на дробную отводится всегда бит. Такой способ в архитектурах процессоров не присутствует. Отдаётся предпочтение числам с плавающей запятой, как компромиссу между диапазоном допустимых значений и точностью.
Содержание
- 1 Нормальная и нормализованная форма
- 2 Типы чисел с плавающей точкой (по IEEE 754)
- 2.1 Число половинной точности (Binary16, Half precision)
- 2.2 Число одинарной точности (Binary32, Single precision, float)
- 2.3 Число двойной точности (Binary64, Double precision, double)
- 2.4 Число четверной точности (Binary128, Quadruple precision)
- 2.5 Диапазон значений чисел с плавающей запятой
- 3 Особые значения чисел с плавающей точкой
- 3.1 Ноль (со знаком)
- 3.2 Неопределенность (NaN)
- 3.3 Бесконечности
- 3.4 Денормализованные числа
- 4 Действия с числами с плавающей запятой
- 4.1 Умножение и деление
- 4.2 Сложение и вычитание
- 4.3 Алгоритм получения представления вещественного числа в памяти ЭВМ
- 5 См. также
- 6 Примечания
- 7 Ссылки
- 7.1 Использованные материалы
- 7.2 Что стоит прочесть
Нормальная и нормализованная форма
Нормальной формой (англ. normal form) числа с плавающей запятой называется такая форма, в которой мантисса (без учёта знака) в десятичной системе находится на полуинтервале . Такая форма записи имеет недостаток: некоторые числа записываются неоднозначно (например, можно записать в 4 формах — , , , ), поэтому распространена также другая форма записи — нормализованная (англ. normalized), в которой мантисса десятичного числа принимает значения от (включительно) до (не включительно), а мантисса двоичного числа принимает значения от (включительно) до (не включительно). То есть в мантиссе слева от запятой до применения порядка находится ровно один знак. В такой форме любое число (кроме ) записывается единственным образом. Ноль же представить таким образом невозможно, поэтому стандарт предусматривает специальную последовательность битов для задания числа (а заодно и некоторых других полезных чисел, таких как и ).
Так как старший двоичный разряд (целая часть) мантиссы вещественного числа в нормализованном виде всегда равен «», то его можно не записывать, сэкономив таким образом один бит, что и используется в стандарте IEEE 754. В позиционных системах счисления с основанием большим, чем (в троичной, четверичной и др.), этого замечательного свойства нет (ведь целая часть там может быть не только единицей).
Типы чисел с плавающей точкой (по IEEE 754)
Число половинной точности (Binary16, Half precision)
Число́ полови́нной то́чности — компьютерный формат представления чисел, занимающий в памяти половину машинного слова (в случае 32-битного компьютера — бит или байта). В силу невысокой точности этот формат представления чисел с плавающей запятой обычно используется в видеокартах, где небольшой размер и высокая скорость работы важнее точности вычислений.
| Знак | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | |||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 10 | 9 | 0 |
Порядок записан со сдвигом . То есть чтобы получить актуально значение порядка нужно вычесть из него сдвиг. Сдвиг можно получить по формуле , где — число бит, отведенное на хранение порядка (в случае числа половинной точности ).
Ограничения точности
- Целые от нуля до передаются как есть.
- Целые от до округляются к ближайшему чётному целому.
- Целые от до округляются до ближайшего целого, делящегося нацело на четыре.
- Целые от до округляются до ближайшего целого, делящегося на восемь.
- Целые от до округляются до ближайшего целого, делящегося на шестнадцать.
- Целые от до округляются до ближайшего целого, делящегося на тридцать два.
Число одинарной точности (Binary32, Single precision, float)
Число́ одина́рной то́чности — компьютерный формат представления чисел, занимающий в памяти одно машинное слово (в случае 32-битного компьютера — бита или байта). Используется для работы с вещественными числами везде, где не нужна очень высокая точность.
| Знак | |||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок (8 бит) | Мантисса (23+1 бита) | ||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 30 | 23 | 22 | 0 |
Порядок записан со сдвигом .
Число двойной точности (Binary64, Double precision, double)
Число́ двойно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти два машинных слова (в случае 32-битного компьютера — бита или байт). Часто используется благодаря своей неплохой точности, даже несмотря на двойной расход памяти и сетевого трафика относительно чисел одинарной точности.
| Знак | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок (11 бит) |
Мантисса (52+1 бит) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 62 | 52 | 51 | 0 |
Порядок записан со сдвигом .
Число четверной точности (Binary128, Quadruple precision)
Число́ четверно́й то́чности —
компьютерный формат представления чисел, занимающий в памяти четыре машинных слова (в случае 32-битного компьютера — бит или байт). Используется в случае необходимости крайне высокой точности.
| Знак | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок (15 бит) |
Мантисса (112+1 бит) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 126 | 112 | 111 |
| Мантисса (112+1 бит) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 |
Порядок записан со сдвигом .
Обычно этот формат реализуется программно, случаи аппаратной реализации крайне редки. Также не гарантируется поддержка этого типа в языках программирования, хотя кое-где она и реализована (например, компилятор gcc для архитектуры x86 позволяет использовать тип __float128, являющийся программной реализацией числа с четверной точностью).
В совокупности эти факторы делают Quadruple весьма экзотичным и редко встречающимся форматом чисел с плавающей запятой.
Диапазон значений чисел с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. Пара значений показателя (когда все разряды нули и когда все разряды единицы) зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся ноль, значения NaN (Not a Number, “не число”, получается как результат операций типа деления нуля на ноль) и .
Данная таблица только лишь примерно указывает границы допустимых значений, без учета возрастающей погрешности с ростом абсолютного значения и существования денормализованных чисел.
| Название в IEEE 754 | Название типа переменной в Си | Диапазон значений | Бит в мантиссе | Бит на переменную |
|---|---|---|---|---|
| Half precision | – | 6,10×10-5..65504 | 11 | 16 |
| Single presicion | float | -3,4×1038..3,4×1038 | 23 | 32 |
| Double precision | double | -1,7×10308..1,7×10308 | 53 | 64 |
| Extended precision | На некоторых архитектурах (например в сопроцессоре Intel) long double | -3,4×104932..3,4×104932 | 65 | 80 |
Особые значения чисел с плавающей точкой
Ноль (со знаком)
Как уже было оговорено выше, в нормализованной форме числа с плавающей точкой невозможно представить ноль. Поэтому для его представления зарезервированы специальные значения мантиссы и порядка — число считается нулём, если все его биты, кроме знакового, равны нулю. При этом в зависимости от значения бита знака ноль может быть как положительным, так и отрицательным.
| Знак | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = |
| 14 | 10 | 9 | 0 |
Арифметика нуля со знаком
Арифметика отрицательного нуля аналогична таковой для любого отрицательного числа и понятна интуитивно. Вот несколько примеров:
- (если )
- (если )
Неопределенность (NaN)
NaN — это аббревиатура от фразы “not a number“. NaN является результатом арифметических операций, если во время их выполнения произошла ошибка (примеры см. ниже). В IEEE 754 NaN представлен как число, в котором все двоичные разряды порядка — единицы, а мантисса не нулевая.
| Знак | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1 | 1 | 1 | 1 | 1 | 1, | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | 0/1 | = |
| 14 | 10 | 9 | 0 |
Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.
Как можно получить NaN?
- , где
Есть и другие способы получения NaN, подробности можно найти по ссылкам в соответствующем разделе.
По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.
Бесконечности
В число с плавающей запятой можно записать значение или . Как и нули со знаком, бесконечности позволяют получить хотя бы близкий к правильному результат вычисления в случае переполнения. Согласно стандарту IEEE 754 число с плавающей запятой считается равным бесконечности, если все двоичные разряды его порядка — единицы, а мантисса равна нулю. Знак бесконечности определяется знаковым битом числа.
| Знак | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||||
| 0/1 | 1 | 1 | 1 | 1 | 1 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = |
| 14 | 10 | 9 | 0 |
Получить бесконечность можно при переполнении и при делении ненулевого числа на ноль. При этом
Денормализованные числа
Денормализованные числа (англ. denormalized/subnormal numbers) – это способ увеличить количество представимых числом с плавающей запятой значений около нуля, дабы повысить точность вычислений. Каждое значение денормализованного числа меньше самого маленького нормализованного (“обычного”) значения числа с плавающей запятой.
Согласно стандарту, если порядок равен своему минимальному значению (все его биты — нули, а истинное значение порядка равно его сдвигу) и все биты мантиссы равны нулю, то это . Если же мантисса не равна нулю, то это число с порядком, на единицу большим минимального (все биты порядка, кроме младшего — нули) и данной мантиссой, целая часть которой считается равной нулю, а не единице.
То есть число с плавающей запятой, при учете вышесказанного, можно задать следующим образом:
- , если (нормализованное число)
- , если (денормализованное число)
Где — бит знака, — последовательность битов мантиссы, — значение порядка (с учетом сдвига), — минимальное значение порядка, используемое для записи чисел (1 — сдвиг) , — минимальное значение порядка, которое он в принципе может принять (все биты нули, 0 — сдвиг).
Хоть денормализованные числа и позволяют бороться с погрешностями и обрабатывать очень маленькие значения, за эти возможности приходится дорого платить. Ввиду сложности денормализованные числа крайне редко реализуют на аппаратном уровне – вместо этого используются программные реализации, работающие значительно медленнее.
В современных процессорах обработка денормализованных чисел происходит в десятки раз медленнее, чем обработка нормализованных чисел. Ниже приведена часть таблицы из статьи Isaac Dooley, Laxmikant Kale “Quantifying the Interference Caused by Subnormal Floating-Point Values”[1]
| Производитель | Процессор | Замедление (разы) |
|---|---|---|
| IBM | PowerPC 970 | 2,4 |
| AMD | Athlon | 6,0 |
| Intel | Pentium 3 | 15,8 |
| AMD | Athlon 64 | 21,4 |
| AMD | Opteron64 | 23,8 |
| Intel | Core Duo | 44,2 |
| Intel | P4 Xeon | 97,9 |
| Intel | Pentium 4 | 131,0 |
| Intel | Itanium 2 | 183,2 |
| Sun | UltraSPARC IV | 520,0 |
В таблице приведены наихудшие результаты тестирования среди всех использованных компиляторов (gcc, icc, xlc) со всеми доступными флагами оптимизации. Исследователи утверждают, что различие среднего случая с худшим незначительно.
Поскольку в стандартных форматах (одинарной и двойной точности) денормализованные числа получаются действительно очень маленькими и практически никак не влияют на результат некоторых вычислений (при этом заметно замедляя их скорость), то иногда они просто игнорируются. При этом используются два простых механизма, получивших называние Flush-to-zero (FTZ) и Denormals-are-zero (DAZ). Первый механизм заставляет операции возвращать ноль, как только становится ясно, что результат будет денормализованным. Второй механизм заставляет операции рассматривать поступающие на вход денормализованные числа как нули.
Ярким примером подобного “отсечения” денормализованных чисел могут послужить видеокарты, в которых резкое падение скорости вычислений в сотню раз недопустимо. Так же, например, в областях, связанных с обработкой звука, нет нужды в очень маленьких числах, поскольку они представляют столь тихий звук, что его не способно воспринять человеческое ухо.
В версии стандарта IEEE 754-2008 денормализованные числа (denormal или denormalized numbers) были переименованы в subnormal numbers, то есть в числа, меньшие “нормальных”. Поэтому их иногда еще называют “субнормальными“.
Действия с числами с плавающей запятой
Умножение и деление
Самыми простыми для восприятия арифметическими операциями над числами с плавающей запятой являются умножение и деление. Для того, чтобы умножить два вещественных числа в нормализованной форме необходимо перемножить их мантиссы, сложить порядки, округлить и нормализовать полученное число.
Соответственно, чтобы произвести деление нужно разделить мантиссу делимого на мантиссу делителя и вычесть из порядка делимого порядок делителя. Затем точно так же округлить мантиссу результата и привести его к нормализованной форме.
Сложение и вычитание
Идея метода сложения и вычитания чисел с плавающей точкой заключается в приведении их к одному порядку. Сначала выбирается оптимальный порядок, затем мантиссы обоих чисел представляются в соответствии с новым порядком, затем над ними производится сложение/вычитание, мантисса результата округляется и, если нужно, результат приводится к нормализированной форме. Пример:
Выполним сложение чисел с плавающей точкой и смещенным порядком в 32-х разрядном формате и . Переведем в машинный вид. Для этого сначала переведем его в двоичную систему счисления.
Нормализуем полученное двоичное число по правилам машинной арифметики.
Найдем смещенный порядок. Так как в условии говорится о 32-разрядном представлении, то смещение порядка равно .
Число отрицательное, следовательно, в бите знака будет стоять единица.
Итак, первое число в машинном 32-разрядном представлении с плавающей точкой будет иметь вид: 10000111 (жирным шрифтом выделен порядок числа, длина мантиссы — 23 бита).
Переведем второе число в машинный вид, совершая те же действия.
= ,... ... В качестве мантиссы будут сохранены первые бита после запятой т.е. . Очевидно, что порядок со смещением у второго числа будет таким же, как и у первого.
Второе число положительное, следовательно, бит знака будет содержать ноль.
Итак в машинном 32-разрядном представлении второе число будет иметь вид:
10000111 Далее в арифметических операциях будет использоваться число ,=, а не = видимо для упрощения(хотя это не совсем корректно).
Порядки у слагаемых равны, поэтому пропускаем шаг выравнивания порядков и проводим вычитание мантисс по правилам двоичной арифметики. В компьютере этим занимается арифметический сопроцессор, встроенный в центральный процессор машины.
,
Приводим полученный результат к машинному виду. Для этого мы должны внести поправку в порядок — уменьшить его на единицу. Знак результата — положительный, следовательно, бит знака содержит ноль.
10000110
Проверим правильность наших вычислений. Переведем результат в десятичное представление.
Найдем реальный порядок результата, вычтя из него значение смещения .
Следовательно, число результата будет иметь вид:
,
Результат наших вычислений верен, так как - .
Алгоритм получения представления вещественного числа в памяти ЭВМ
Покажем преобразование действительного числа для представления его в
памяти ЭВМ на примере величины типа Double.
Как видно из таблицы, величина этого типа занимает в памяти байт. На
рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):
| Знак | Смещённый порядок | Мантисса |
|---|---|---|
| 63 | 62..52 | 51..0 |
Можно заметить, что старший бит, отведенный под мантиссу, имеет номер
, т.е. мантисса занимает младшие бита. Черта указывает здесь на
положение двоичной запятой. Перед запятой должен стоять бит целой части
мантиссы, но поскольку она всегда равна , здесь данный бит не требуется и
соответствующий разряд отсутствует в памяти (но он подразумевается).
Значение порядка хранится здесь не как целое число, представленное в
дополнительном коде. Для упрощения вычислений и сравнения действительных
чисел значение порядка в ЭВМ хранится в виде смещенного числа, т.е. к
настоящему значению порядка перед записью его в память прибавляется
смещение. Смещение выбирается так, чтобы минимальному значению порядка
соответствовал нуль. Например, для типа Double порядок занимает бит и
имеет диапазон от до , поэтому смещение равно ()
(). Наконец, бит с номером указывает на знак числа.
Таким образом, из вышесказанного вытекает следующий алгоритм для
получения представления действительного числа в памяти ЭВМ:
- перевести модуль данного числа в двоичную систему счисления;
- нормализовать двоичное число, т.е. записать в виде M 2p, где M —
мантисса (ее целая часть равна ()) и p — порядок, записанный в
десятичной системе счисления;
- прибавить к порядку смещение и перевести смещенный порядок в двоичную
систему счисления;
- учитывая знак заданного числа (0 — положительное; 1 — отрицательное),
выписать его представление в памяти ЭВМ.
Пример. Запишем код числа ,.
- Двоичная запись модуля этого числа имеет вид .
- Имеем
.
- Получаем смещенный порядок . Далее имеем
() ().
- Окончательно
1 10000000111 0011100001010000000000000000000000000000000000000000 63 62..52 51..0
Очевидно, что более компактно полученный код стоит записать следующим
образом: C073850000000000(16).
Другой пример иллюстрирует обратный переход от кода действительного
числа к самому числу.
Пример. Пусть дан код 3FEC600000000000(16) или
- Прежде всего замечаем, что это код положительного числа, поскольку в
разряде с номером записан нуль. Получим порядок этого числа:
() (); .
- Число имеет вид , или
,.
- Переводом в десятичную систему счисления получаем ,.
| 0 | 01111111110 | 1100011000000000000000000000000000000000000000000000 |
| 63 | 62..52 | 51..0 |
См. также
- Представление символов, таблицы кодировок
- Представление целых чисел: прямой код, код со сдвигом, дополнительный код
Примечания
- ↑ Статья Isaac Dooley, Laxmikant Kale “Quantifying the Interference Caused by Subnormal Floating-Point Values” (англ.)
Ссылки
Использованные материалы
На русском
- Википедия — Экспоненциальная запись
- Википедия — Число с плавающей запятой
- Википедия — Отрицательный и положительный ноль
- Хабрахабр — статья пользователя Yruslan “Что нужно знать про арифметику с плавающей запятой”
- Статья Лапшевой Е.Е. “Машинная арифметика с вещественными числами” Статья удалена
На английском
- Wikipedia — NaN
- Wikipedia — Floating point
- Wikipedia — IEEE 754-2008
Что стоит прочесть
- Материалы по стандарту IEEE 754 (англ.)
- Русский перевод стандарта IEEE 754
#статьи
- 5 апр 2023
-
0
Числа с плавающей точкой: что это такое и как они работают
Рассказываем, как дробные числа хранятся в памяти компьютера — всё сложно и волшебно, но оправданно.
Иллюстрация: Катя Павловская для Skillbox Media

Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Компьютеры придумали, чтобы производить вычисления более точно и быстро. Но парадокс в том, что на самом деле их вычисления почти всегда неточны. Например, мы не можем представить число Пи или корень из двух в памяти компьютера — потому что имеем дело с бесконечной дробью (хотя и с «короткими» числами всё не так просто из-за двоичной системы счисления, в которой числа представлены в памяти компьютера, к этому мы тоже вернёмся).
Так что компьютер в какой-то момент идёт на уступки и ограничивается вычислениями с той точностью, которая необходима для решения стоящей за ними практической задачи.
Чтобы эффективно проводить вычисления, учёные придумали числа с плавающей точкой — они стали отличным инструментом для представления вещественных чисел (это, по сути, все числа числового ряда, даже те, у которых дробная часть бесконечна).
Под числа с плавающей точкой даже создан единый стандарт IEEE 754 — чтобы все компьютеры, языки программирования, программы и операционные системы работали с ними одинаково и результат получался предсказуемым. В этой статье мы расскажем, что это за стандарт и как он работает.
1970-е годы, начало компьютерной революции. Учёные-программисты разрабатывают новые компьютеры и алгоритмы для вычислений, а также стараются всеми силами доказать, что их изобретения должны изменить мир.
Тогда все компьютеры работали по-разному: у них были собственные операционные системы, принципы организации памяти и способы представления данных. И это создавало проблему: нельзя было перенести программу с одного компьютера на другой, для этого каждый раз приходилось переписывать её под новую систему и «железо».
И если переделать пару функций было не так сложно, то подстраиваться под разные системы представления чисел было действительно мукой. Из-за этого иногда нужно было полностью менять поведение программы, что могло повлиять на её работоспособность и надёжность. В общем — проблема с представлениями чисел была поистине болезненной.

Фото: Wikimedia Commons
Компания Intel решила помочь программистам со всего мира и создать единый стандарт представления вещественных чисел. Для этого была создана проектная группа из лучших инженеров. Но на пятки Intel наступали и другие компании — например, у той же DEC появилась похожая идея.
Началась настоящая гонка за лучшее решение: каждая компания фанатела исключительно от своей разработки и надеялась, что именно её примут как промышленный стандарт. А IT-гиганты IBM и Cray наблюдали за всем происходящим со стороны и ждали, пока появится победитель, — чтобы тут же реализовать его стандарт в своих компьютерах.
Сегодня из всех стандартов, возникших в то время, в живых остались только два: спецификация VAX от DEC и K-C-S от Intel. У каждой из них были как свои преимущества, так и недостатки.
Преимущества K-C-S:
- Десятичный формат. Он позволял представлять вещественные числа в десятичной записи, что очень удобно для человека, но так себе для компьютера.
- Высокая точность. Десятичное представление повышало точность вычислений и снижало возникновение ошибок при округлении — особенно для операций с большими числами.
- Меньше ошибок. Стандарт включал специальные значения, которые помогали легко избегать переполнения чисел и проще справляться с ошибками при вычислениях.
Преимущества VAX:
- Двоичный формат. Все числа записывались только в двоичном представлении, что повышало эффективность вычислений, особенно на компьютерах с VAX-архитектурой.
- Широкое распространение. Спецификацию VAX уже использовали на разных компьютерах того времени, что позволяло быстро адаптировать её под новые устройства.
- Высокая производительность. Спецификация VAX была оптимизирована под высокую скорость работы и требовала меньших вычислительных мощностей.
| K-C-S | VAX |
|---|---|
| Десятичный формат | Двоичный формат |
| Высокая точность | Высокая производительность |
| Меньше ошибок | Широкая распространённость |
Компания DEC пыталась сделать всё, чтобы VAX признали единым стандартом. Она даже пыталась убедить авторитетных учёных в том, что конкурирующий K-C-S никогда не станет таким же производительным и успешным. Однако у разработчиков из Intel были свои секретики: например, они знали, как ускорить свою спецификацию и обогнать DEC.
В итоге победила Intel, а её спецификация легла в основу стандарта IEEE 754, который утвердил Институт инженеров электротехники и электроники (IEEE) в 1985 году.
Чтобы понять стандарт IEEE 754, нам нужно сперва разобраться, как числа представляют в двоичной системе. Всего существует два представления десятичных чисел в компьютере: с плавающей точкой и фиксированной. Первые основаны на вторых, поэтому есть смысл начать с них.
И да, дальше мы будем употреблять слово «точка», однако в других статьях и литературе можно встретить термин «запятая». Они означают одно и то же, но в англоговорящих странах чаще используют второй, а в русскоговорящих — первый.
Числа с фиксированной точкой — это двоичные числа, у которых ограничен размер их целой и дробной части. Например, если число состоит из 16 битов, то мы можем выделить для целой части первые 10 битов и оставшиеся шесть — для дробной части.
Разделение между целой и дробной частью как раз и обозначают точкой. Когда компьютер получает число, он сразу понимает, что в нём 2 байта, или 16 битов, из которых 10 — это целая часть, а шесть — дробная. Получится так:

На картинке — двоичное представление десятичного числа 689.6875 в виде двоичного числа с фиксированной точкой. Вот ещё один пример с числом поменьше:

Здесь закодировано число 13.0. Видим, что в дробной части одни нули и, соответственно, дробная часть десятичного числа — нулевая.
Давайте подробнее разберём, почему всё получилось именно так. Сначала посмотрим на целую часть — это обычное представление десятичного числа в двоичной записи. Каждый разряд числа относится к степени двойки. Число из примера выше можно разложить так:
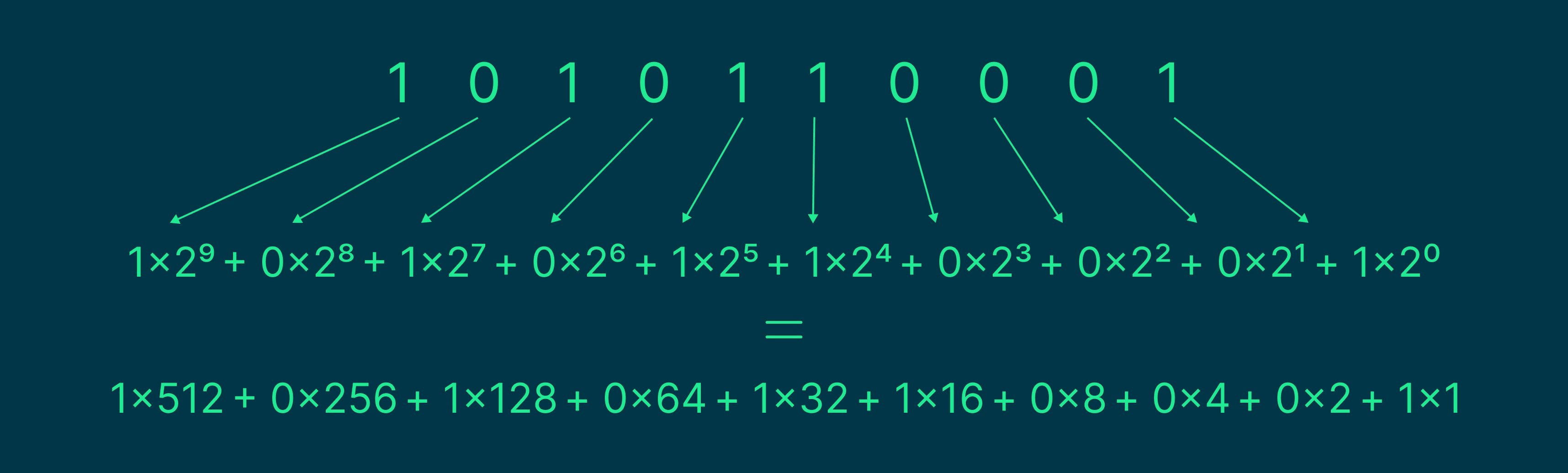
Чтобы перевести двоичную запись в десятичную, нужно сложить все степени двойки, у которых в разряде стоит единица. Получим:

Теперь рассмотрим дробную часть. Принцип перевода дробной части двоичного числа в десятичную систему такой же. Единственное отличие в том, что там степени двойки — отрицательные. Рассмотрим число из примера выше:

Степень двойки начинается с −1 и с каждым разрядом уменьшается на единицу: −2, −3 и так далее, а чтобы перевести её из отрицательной в положительную, нужно просто перевернуть дробь. И теперь мы также складываем все степени двойки, у которых в соответствующем разряде стоит единица:

Теперь нам осталось сложить целую часть с дробной:

Преимущества чисел с фиксированной точкой в том, что они всегда представляются в виде конечного числа. Это значит, что если мы захотим представить число Пи, то оно будет ограничено на определённом знаке, а остальные мы просто отбросим. Например, так:

Это число — приближённое представление числа Пи, и оно не является его точным значением.
Недостатки у чисел с фиксированной точкой, конечно же, тоже есть. Например, если мы возьмём 16-битные числа, у которых первые 10 битов относятся к целой части и остальные шесть — к дробной, то в нашем распоряжении окажется такой диапазон значений:

И тут мы переходим к главному недостатку чисел с фиксированной точкой. Давайте возьмём самое большое число, которое можно записать таким образом, и вычислим число перед ним, то есть такое число:

Видим интересное: когда мы убрали одну единицу в конце двоичного числа, то получили разницу между двумя числами не 0.000001, как в десятичных числах, а 0.015625. Это число представляет собой как бы минимальный шаг в числах с фиксированной точкой, или максимально возможную точность.
Если мы возьмём следующее число, то разница останется такой же:

Эта точность, во-первых, позволяет превращать десятичные числа в двоичные, а во-вторых, уменьшает нагрузку на компьютер, ведь компьютер всегда знает, что первые 10 битов — это целая часть, а оставшиеся шесть — дробная.
С фиксированной точкой разобрались, теперь перейдём к плавающей, а затем узнаем уже о формате IEEE 754.
Если говорить техническим языком, то число с плавающей точкой (или число с плавающей запятой) — это численное представление вещественного числа в программировании. Иначе говоря, оно является его приближённым значением.
Двоичное представление чисел с плавающей точкой содержит три части: знаковый бит, экспоненту и мантиссу.
- Знаковый бит указывает, положительное число или отрицательное.
- Экспонента показывает, на какое число нужно умножать мантиссу.
- Мантисса — это фиксированное количество битов, которое выражает точность числа.
Эти определения слегка сложноваты, поэтому давайте сначала разберёмся с основами.
В научной нотации числа удобнее представлять как что-то небольшое, умноженное на 10 в какой-то степени. Например, число 123.456 удобнее представить в виде 1.23456 × 102 Это удобнее, потому что для умножения двух чисел в таком виде не приходится тратить много сил. Звучит неочевидно, но давайте посмотрим на практике — умножим число 0.0006 на 0.0002:
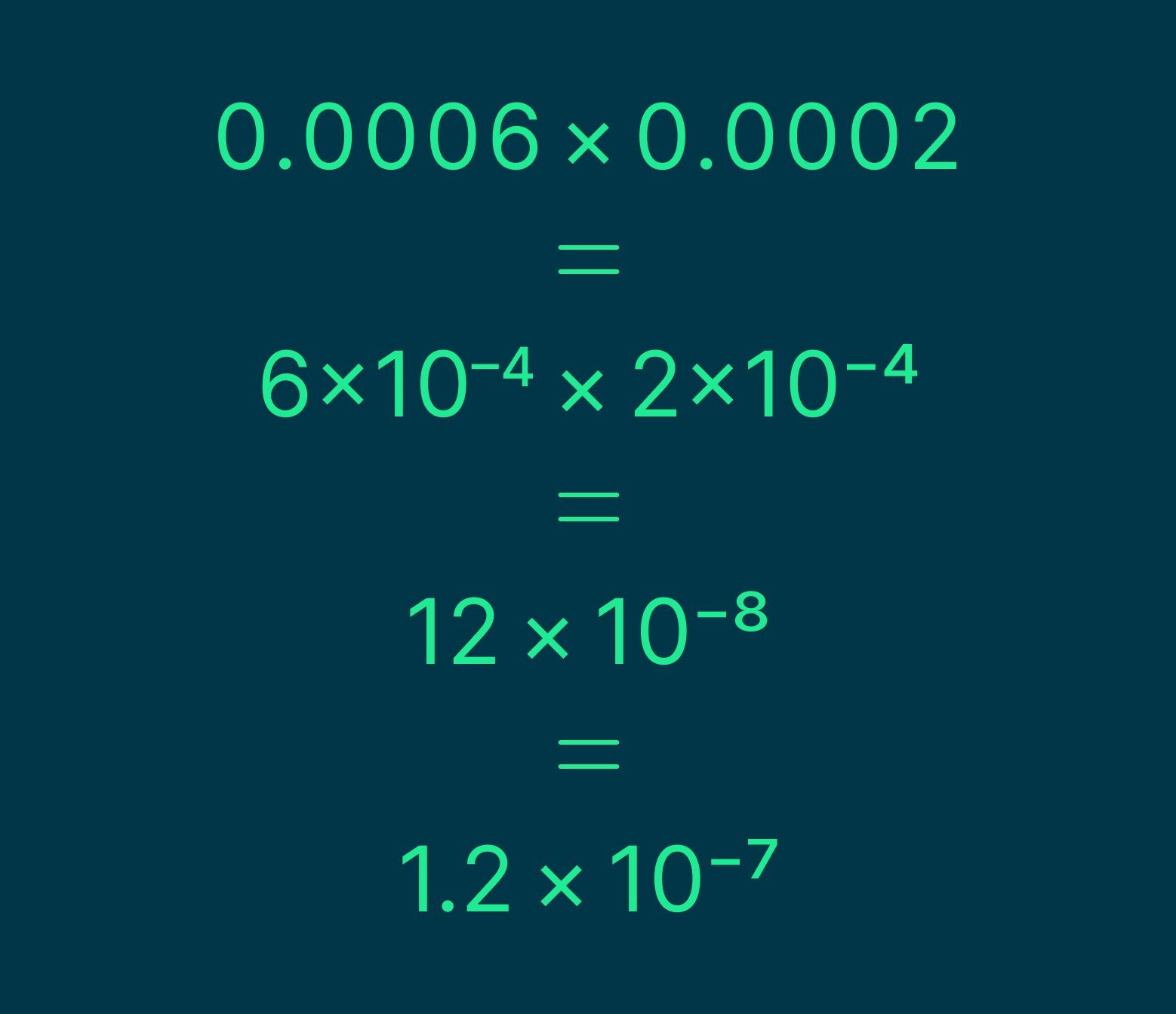
Как мы видим, в научной нотации нужно было просто сложить степени и произвести несложное умножение. А в обычном виде нам нужно было умножить два числа и ещё не запутаться, сколько нулей слева нужно дописывать. Одним словом — научная нотация проще.
В этой нотации число состоит тоже из трёх компонентов: экспоненты, коэффициента, мантиссы и знака числа.
- Знак числа указывает, какое это число: положительное или отрицательное. Он нужен, чтобы мы постоянно работали с положительным числом, а уже потом при необходимости перевели его в отрицательное.
- Коэффициент — это основная часть десятичного числа, записанного обычно в диапазоне от 1 до 9. Но для чисел с плавающей точкой он находится в диапазоне от 0 до 1.
- Мантисса — это дробная часть коэффициента.
- Экспонента — это то, на что мы умножаем коэффициент.
Так, число 1.2 × 10−7 можно представить следующим образом:

Вот что мы получили:
- +1 — знак числа (положительный),
- 0.12 — мантисса,
- −8 — экспонента.
Можно заметить, что мы сразу заменили коэффициент 1.2 на 0.12. Мантисса — 0.12.
Число 10 называют основанием. Принято использовать его, потому что мы считаем всё в десятичной системе. Однако основание можно и поменять. Давайте представим число 0.12 × 10−8 в виде числа с основанием 5.

Мантисса стала более устрашающей, но заметьте, что экспонента (то есть степень) не поменялась. И это абсолютно нормально, ведь мы применяли базовые правила умножения.
Почему не поменялась экспонента? Следите за руками 🙂 Сначала мы разбиваем число 10 на множители — 5 и 2, а раз у исходного числа была степень −8, то у нас будут множители 5−8 и 2−8.
Теперь давайте перейдём к двоичному представлению. В нём основанием будет число 2, потому что это эквивалент числу 10 в двоичной системе. А мантисса будет точно так же лежать в диапазоне от 0 до 1 (не включительно). Поэтому всё, что меняется, — это основание.
Выглядеть десятичное число 0.12 × 10−8 в двоичном представлении будет вот так:
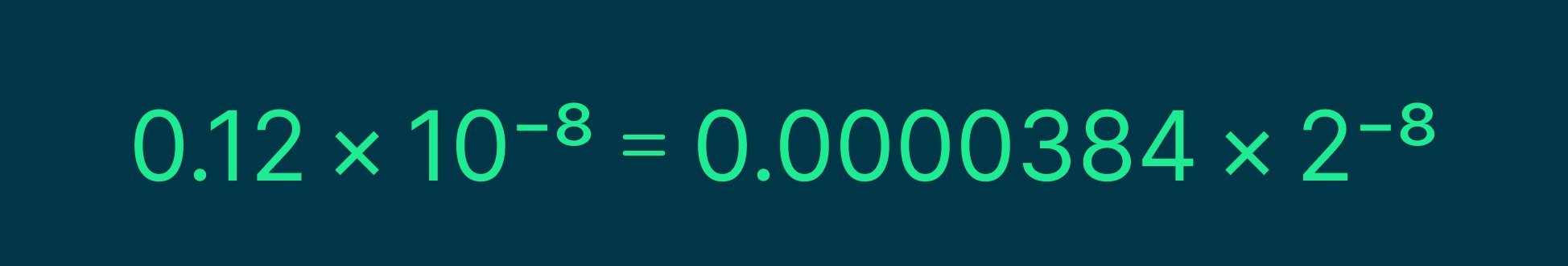
Научная нотация — это тот принцип, по которому строится двоичное представление десятичных чисел в компьютерах. Теперь давайте разбираться, что за стандарт IEEE 754 и как он работает.
Стандарт IEEE 754 — это набор правил, которые описывают, как вещественные числа представляются в компьютере. Этот формат стал самым распространённым в программировании, когда дело доходит до арифметики чисел с плавающей точкой.
Числа представляются фиксированным количеством битов, каждый из которых отвечает своим задачам. В IEEE 754 обычно используют 32 бита. Они делятся на всё те же категории: один знаковый бит, 7 битов для экспоненты (то, на что мы умножаем мантиссу) и 24 бита для мантиссы (она выражает точность числа).

Чтобы получить из этого представления десятичное число, используют следующую формулу:
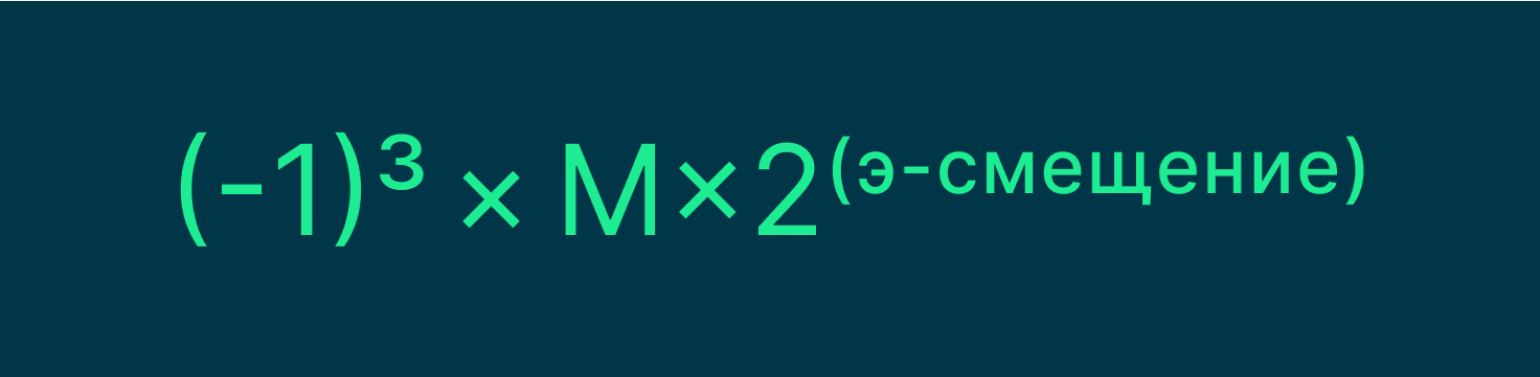
Здесь З — это знаковый бит, М — мантисса, Э — экспонента. А ещё у нас появилось смещение. Оно необходимо, чтобы экспонента могла принимать положительные и отрицательные значения, и в стандарте IEEE 754 представляет собой константу — число 127.
Если без смещения экспонента может принимать значения от 0 до 255, то со смещением от −127 до 128. Это нужно, чтобы представлять маленькие числа.
Чтобы вычислить мантиссу, мы должны добавить к ней слева единицу и после неё поставить точку, как будто это число с фиксированной точкой. А затем вычислить это число:
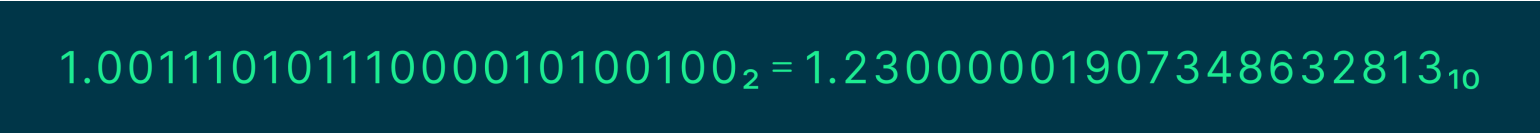
Получили наше число 1.23, но не совсем. То, что вы видите, называется приближением двоичных чисел к десятичным. Если бы у нас было бесконечное количество битов, то мы смогли бы довольно точно представить число 1.23 в двоичной системе, и оно получило бы вид: 1.2300000000000000000000000000000001. Что уже неплохое приближение. Но так как у нас ограниченное число битов, приходится идти на округление.
Теперь давайте подставим все числа в формулу:

Всё сходится. Попробуем перевести ещё одно число в десятичную систему. На этот раз двоичное число будет таким:
0 10000000 11100000000000000000000
Пройдём все те же шаги:
- знаковый бит — 0;
- экспонента — 128;
- мантисса — 1.875.
Теперь подставляем в формулу:

Получили число 3.75 в десятичной записи.
Мы узнали, как числа с плавающей точкой хранятся в памяти компьютера, какие биты за что отвечают и как происходит преобразование из стандарта IEEE 754 в десятичные числа. Теперь давайте узнаем, какие у них есть нюансы, о которых точно нужно знать.
Числа с плавающей точкой имеют два нуля (положительный и отрицательный), две бесконечности (положительную и отрицательную) и неопределённость. И всё это нужно, чтобы правильнее считать числа.
Два нуля. В стандарте IEEE 754 существуют два нуля — положительный и отрицательный. Они нужны, чтобы компьютер мог различать значения, которые близки к нулю, но имеющие разные знаки. Это важно при умножении и делении.
Например, представьте, что у банка есть финансовое приложение, которое работает с очень маленькими процентными ставками, такими как 10−15. Если бы у нас не было двух нулей, то при округлении мы бы получали неточные значения. Мы бы не смогли знать, отрицательная ставка у клиента или положительная, а это бы влияло на то, сколько он будет платить денег, что очень важно для него.
В стандарте IEEE 754 эти два нуля записываются так:
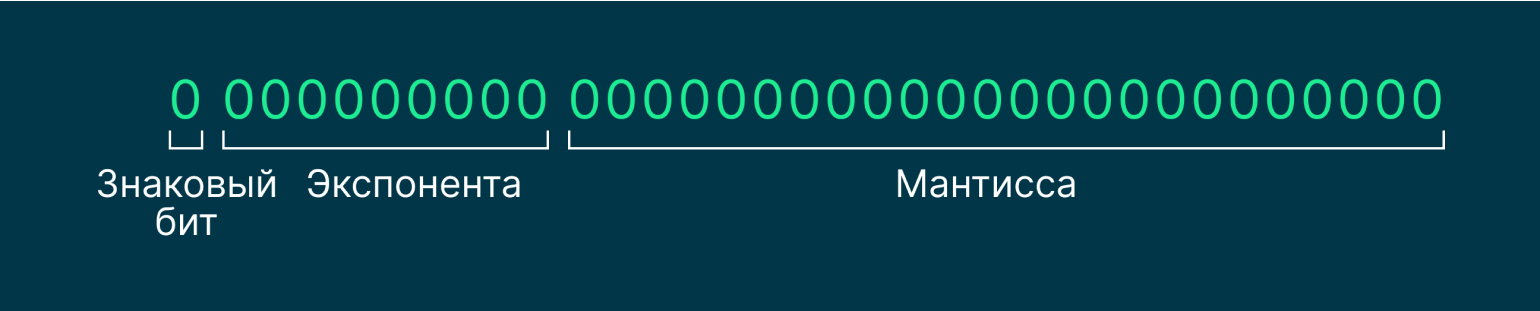
Изображение: Skillbox Media

Изображение: Skillbox Media
Экспонента и мантисса должны содержать все нули, а знаковый бит будет указывать, какой мы имеем ноль: положительный или отрицательный.
Две бесконечности. Они напрямую связаны с двумя нулями. На уроках математики вам могли говорить, что делить на ноль нельзя, но это не совсем так. Делить на ноль можно, просто мы будем получать бесконечность, с которой не очень удобно работать.
У бесконечности есть два типа: положительная бесконечность и отрицательная бесконечность. Чтобы получить положительную, нужно положительное число поделить на положительный ноль или отрицательное число на отрицательный ноль:

Отрицательную бесконечность можно получить похожим образом, только если поделить отрицательное число на положительный ноль или положительное число на отрицательный ноль:

Чтобы понять, где и когда применяют бесконечности, нужно обращаться к математическому анализу, но это сложная тема, которую мы не будем затрагивать. Давайте просто посмотрим, как выглядят бесконечности в виде двоичной записи стандарта IEEE 754:
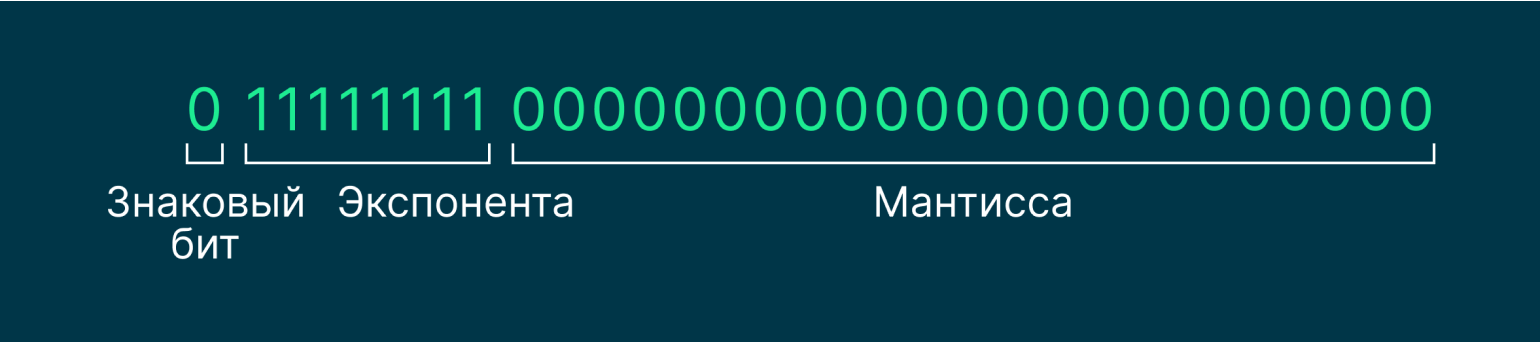
Изображение: Skillbox Media

Изображение: Skillbox Media
В бесконечностях экспонента всегда должна состоять из единиц, а мантисса — из нулей. При этом знаковый бит указывает, какая это бесконечность: положительная или отрицательная.
Неопределённость. В математике есть понятие неопределённости. Это когда мы делим что-то на что-то и не знаем, какой результат получили. Звучит странно: как это мы можем не знать результат? Но давайте на примерах.
Что мы получим, если поделим ноль на ноль, бесконечность на бесконечность, бесконечность на ноль или ноль на бесконечность? Никто не знает. Поэтому математики говорят, что мы получим неопределённость. А в стандарте IEEE 754 вводят понятие Not-a-Number — NaN. Выглядит оно так:

Неопределённость очень похожа на бесконечность, но главное её отличие в том, что в числе NaN должен быть хотя бы один ненулевой бит в мантиссе.
Стандарт IEEE 754 поддерживает два вида вещественных чисел: нормализованные и денормализованные. Нормализованные числа нужны, чтобы представлять очень большие значения, а денормализованные — очень маленькие, которые близки к нулю.
Нормализованные числа. Они нужны, чтобы хранить и обрабатывать значения с максимально возможной точностью, что может быть критическим для некоторых приложений. Ещё для нормализованных чисел нужно меньше места в памяти.
Если говорить просто, нормализованные числа — это научная нотация чисел. Например, чтобы записать число 123 в научной нотации, нужно привести его к такому виду: 1.23 × 102. Это и будет нормализованным числом. В нём коэффициент (число 1.23) должен находиться в диапазоне от 1 до 9.
Чтобы отличать нормализованные числа, в стандарте IEEE 754 первый бит мантиссы делают равным единице. И тогда число принимает следующий вид:

Изображение: Skillbox Media
Удобство такого метода в том, что нам нужно хранить меньше битов в памяти, потому что первый бит мантиссы всегда равен единице. А также у нормализованных чисел гораздо больше диапазон значений.
Но при этом возникает другая проблема: если число близко к нулю, то мы не можем представить его с нужной нам точностью. Это число просто пропадёт из нашего вида, потому что компьютер округлит его до нуля. Поэтому работать с очень маленькими значениями в нормализованном виде не получится.
Денормализованные числа. Чтобы решить проблему округления при близких к нулю значениях, используют денормализованные числа. Они менее эффективны, так как нужно хранить больше битов в памяти, но при этом более точны.
Если коэффициент нормализованных чисел принимает значения от 1 до 9, то у денормализованных — от 0 до 1, не включая последнюю. А первый бит мантиссы у таких чисел всегда равен нулю. Поэтому двоичная запись будет выглядеть так:
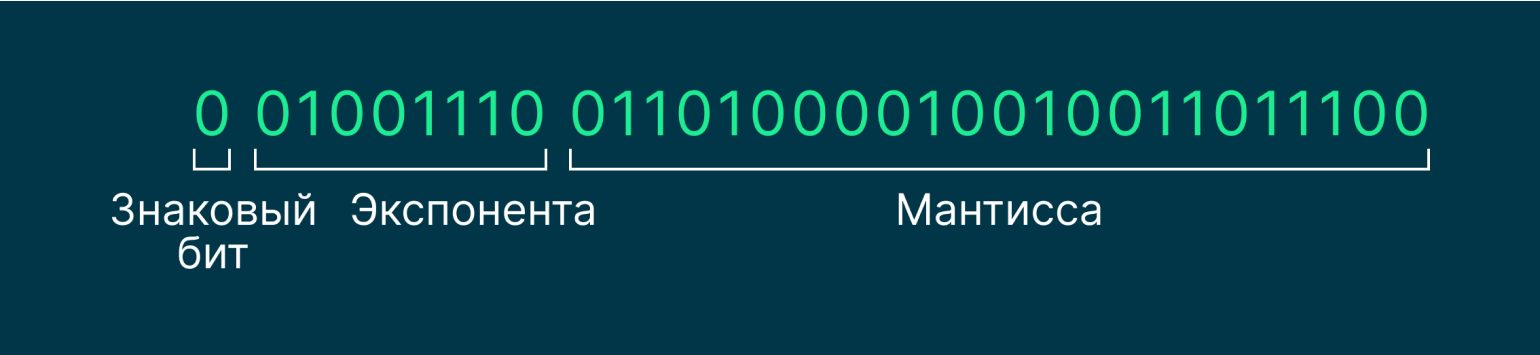
Изображение: Skillbox Media
Денормализованные числа могут привести к потерям в точности во время математических операций, что само по себе приводит к нестабильности вычислений — а это очень плохо.
Некоторые системы предпочитают обращаться с денормализованными числами очень просто: считать, что они все равны нулю. Другие — используют специальные способы обработки таких значений. Но все они неэффективны, потому что компьютеры сами по себе не умеют с ними взаимодействовать.
Интересно заметить, что граница между нормализованными и денормализованными числами лежит ровно на числе 0.75.
Выше мы рассматривали привычные числа с плавающей точкой. Они состоят из 32 битов: одного знакового бита, восьми для экспоненты и 23 для мантиссы. Этот стандарт называется одинарной точностью и является самым распространённым форматом среди вещественных чисел.
В разных языках программирования есть свои представления десятичных чисел, и в некоторых они суперточные. Например, в Java существуют типы BigInteger и BigDecimal, которые, по сути, не ограничивают размер числа. Такая переменная может хранить и 32 бита, и 302 бита. Но, конечно же, такой размах влияет на производительность, потому что хранятся эти числа как строки.
Одинарная точность может представить числа в диапазоне от −3.40282347 × 1038 до +3.40282347 × 1038. И сама точность составляет семь знаков после точки. Этот формат часто используют в компьютерной графике, научном моделировании и других приложениях, которым нужен баланс между диапазоном значений и точностью.
Кроме одинарной точности, есть ещё и двойная. Такие числа состоят из 64 битов, из которых один принадлежит знаку, 11 — экспоненте, 52 — мантиссе. Доступный диапазон значительно шире: от −1.7976931348623157 × 10308 до +1.7976931348623157 × 10308. А точность уже составляет 15–17 чисел после запятой.
Числа с двойной точностью используют там, где важна высокая точность. Например, их применяют для научных и инженерных вычислений, в которых допустить ошибку бывает критично. Но это всё усложняется большими ресурсными тратами — в памяти и компьютерных мощностях.
Мы разобрали, как устроены и как работают числа с плавающей точкой. Это тема гораздо шире и глубже, а её изучение может занять не один день. Поэтому давайте подведём итог и перечислим, что можно вынести из этой статьи:
- Числа с плавающей точкой — это приближённое представление вещественных чисел в программировании. Все правила их представления записаны в стандарте IEEE 754.
- Этот стандарт нужен, чтобы разные компьютерные архитектуры могли одинаково удобно и эффективно работать с вещественными числами.
- Числа с плавающей точкой бывают с одинарной точностью и двойной. Числа с одинарной точностью состоят из 32 битов: одного знакового бита, восьми битов для экспоненты и 23 битов для мантиссы. Числа с двойной точностью — из 64 битов: одного знакового бита, 11 битов для экспоненты и 52 битов для мантиссы.
- В стандарте IEEE 754 есть специальные значения, которые нужны для представления положительного и отрицательного нуля, бесконечностей и неопределённости.

Научитесь: Профессия Python-разработчик
Узнать больше
