Как найти маршаллианский спрос

Известно, что
изменение цен порождает как эффект
замещения, так и эффект дохода.
Маршаллианская и хиксианская функции
спроса различаются “отношением”
к этим двум эффектам.

Маршаллианские
функции спроса хорошо известны из
макроэкономической теории. Они получаются
в результате максимизации потребителем
функции полезности с учетом бюджетного
ограничения. Например, для экономики с
N товаров потребитель решает задачу

MaxU=U(C₁,C₂,..,C_N)

P₁C₁+P₂C₂+…+P_NC_N=Y

Маршаллианский
спрос определяется следующей формулой

C(M)_i=Ci(P₁,P₂,…,P_N,Y),
i= 1,…,N.

Таким образом,
спрос на каждое благо – это функция от
цен всех благ и от дохода. Кривая спроса
изображается графически обычно, чтобы
установить связь между количеством
спрашиваемого блага и ценой на это
благо, предполагая, что все другие цены
и доход не меняются. Этот спрос
некомпенсированный, т.к. не рассматриваются
никакие компенсации, выплаченные для
снятия эффекта дохода. Движение вдоль
кривой маршаллианского спроса, таким
образом, представляет собой комбинацию
эффектов дохода и замещения при изменении
цены.

Хиксианская функция
спроса является результатом решения
другой задачи:

minE=E(P₁,P₂,…,P_N,U)

U=U^F,

Где U^F
– это фиксированный “целевой”
уровень полезности, а E обозначает
денежные расходы на потребление. Функция
хиксианского спроса имеет следующий
вид:

C(H)_i=H_i(P₁,P₂,…,P_N,U^F).

Таким образом,
спрос на i–тый товар – это функция от
цены на все блага и от требуемого уровня
полезности.

Графически функцию
хиксианского спроса можно изобразить
через связь между количеством спрашиваемого
блага и ценой на это благо, предполагая,
что все другие цены и полезность не
меняются. Этот спрос конструируется
таким образом, что сделанная компенсация
уничтожает эффект дохода от изменения
цены. Движение вдоль кривой хиксианского
спроса, таким образом, представляет
собой исключительно эффект замещения
от изменения цены. Все точки на кривой
компенсированного спроса, изображенной
в пространстве цена/количество,
представляют собой точки с одинаковой
полезностью.

Какой измеритель
– CV или EV – предпочтительнее использовать?
CV и EV выражают точное измерение изменения
благосостояния. Они отличаются лишь
способом определения изменения
благосостояния. Естественный вопрос,
которой можно задать: какой из измерителей
предпочтительнее. К сожалению, невозможно
дать однозначного ответа на этот вопрос.
Т.к. в анализе следует рассматривать
возможность изменений цены, зависящей
от множества факторов, с одновременным
изменением дохода, то при выборе играет
огромную роль множество аргументов.

Хотя отсутствует
ясное преимущество одного из измерителей,
два фактора могут снизить степень
озабоченности подобным выбором.
Во–первых, в большинстве случаев оба
измерителя дают оценки, очень близкие
по величине. Любая неточность при
неверном выборе пренебрежительно мала.
Во–вторых, как будет показано дальше,
CV и EV имеют незначительное практическое
применение, т.к. они являются ненаблюдаемыми
величинами. Поэтому часто приходится
аппроксимировать изменение благосостояния,
применяя обозримую маршаллианскую
функцию спроса.

Измерение СV и EV
на практике. Очевидно, что CV и EV не могут
быть использованы для измерения изменений
полезности, т.к. они базируются на
необозримых функциях спроса. На практике
прибегают к маршаллианским некомпенсированным
функциям спроса для получения
приблизительной оценки как CV, так и EV.
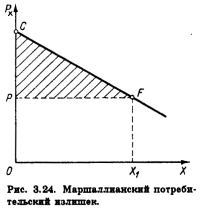
Маршаллианский потребительский излишек
от изменения цены – это площадь слева
от маршаллианской функции спроса и
между начальным и конечным уровнем цен.
Вообще, потребительский излишек не
равен ни CV, ни EV, и поэтому не является
точным измерителем изменения
благосостояния. Если посмотреть на
график, то ясно видно, что при падении
цены EV больше, чем потребительский
излишек, а CV – меньше. Можно сделать
вывод, что измерения потребительского
излишка могут задавать как более высокие,
так и более низкие границы для величин
CV и EV. Однако, во многих случаях
потребительский излишек несильно
отличается от CV и EV, и поэтому может
служить хорошим аппроксиматором для
этих двух измерителей благосостояния.
Приближение будет удачным, когда
относительные изменения цены и количества
малы и эластичность спроса по доходу
низка. Если эластичность спроса по
доходу для рассматриваемого товара
равна нулю, то хиксианские функции
спроса становятся идентичными
маршаллианской функции спроса, и поэтому
CV=EV=Потребительскому излишку. Причина
этому заключается в следующем. Хотя
падение цены увеличивает реальный
доход, более высокий реальный доход не
влияет на спрос. Эффект дохода равен
нулю. Это в точности тот случай, который
описывается хиксианскими кривыми. И
две хиксианские кривые в этом специфическом
случае точно совпадут с маршаллианской
кривой спроса.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

From Wikipedia, the free encyclopedia

In microeconomics, a consumer’s Marshallian demand function (named after Alfred Marshall) is the quantity they demand of a particular good as a function of its price, their income, and the prices of other goods, a more technical exposition of the standard demand function. It is a solution to the utility maximization problem of how the consumer can maximize their utility for given income and prices. A synonymous term is uncompensated demand function, because when the price rises the consumer is not compensated with higher nominal income for the fall in their real income, unlike in the Hicksian demand function. Thus the change in quantity demanded is a combination of a substitution effect and a wealth effect. Although Marshallian demand is in the context of partial equilibrium theory, it is sometimes called Walrasian demand as used in general equilibrium theory (named after Léon Walras).

According to the utility maximization problem, there are commodities with price vector and choosable quantity vector . The consumer has income , and hence a budget set of affordable packages

where is the dot product of the price and quantity vectors. The consumer has a utility function

The consumer’s Marshallian demand correspondence is defined to be

Revealed preference[edit]

Marshall’s theory suggests that pursuit of utility is a motivational factor to a consumer which can be attained through the consumption of goods or service. The amount of consumer’s utility is dependent on the level of consumption of a certain good, which is subject to the fundamental tendency of human nature and it is described as the law of diminishing marginal utility.

As utility maximum always exists, Marshallian demand correspondence must be nonempty at every value that corresponds with the standard budget set.

Uniqueness[edit]

is called a correspondence because in general it may be set-valued – there may be several different bundles that attain the same maximum utility. In some cases, there is a unique utility-maximizing bundle for each price and income situation; then, is a function and it is called the Marshallian demand function.

If the consumer has strictly convex preferences and the prices of all goods are strictly positive, then there is a unique utility-maximizing bundle.^[1]: 156 To prove this, suppose, by contradiction, that there are two different bundles, and , that maximize the utility. Then and are equally preferred. By definition of strict convexity, the mixed bundle is strictly better than . But this contradicts the optimality of .

Continuity[edit]

The maximum theorem implies that if:

then is an upper-semicontinuous correspondence. Moreover, if is unique, then it is a continuous function of and .^{[1]: 156, 506}

Combining with the previous subsection, if the consumer has strictly convex preferences, then the Marshallian demand is unique and continuous. In contrast, if the preferences are not convex, then the Marshallian demand may be non-unique and non-continuous.

Homogeneity[edit]

The optimal Marshallian demand correspondence of a continuous utility function is a homogeneous function with degree zero. This means that for every constant

This is intuitively clear. Suppose and are measured in dollars. When , and are exactly the same quantities measured in cents. When prices and wealth go up by a factor a, the purchasing pattern of an economic agent remains constant. Obviously, expressing in different unit of measurement for prices and income should not affect the demand.

Demand curve[edit]

Marshall’s theory exploits that demand curve represents individual’s diminishing marginal values of the good. The theory insists that the consumer’s purchasing decision is dependent on the gainable utility of a goods or services compared to the price since the additional utility that the consumer gain must be at least as great as the price. The following suggestion proposes that the price demanded is equal to the maximum price that the consumer would pay for an extra unit of good or service. Hence, the utility is held constant along the demand curve. When the marginal utility of income is constant, or its value is the same across individuals within a market demand curve, generating net benefits of purchased units, or consumer surplus is possible through adding up of demand prices.

Examples[edit]

In the following examples, there are two commodities, 1 and 2.

1. The utility function has the Cobb–Douglas form:

The constrained optimization leads to the Marshallian demand function:

2. The utility function is a CES utility function:

Then

In both cases, the preferences are strictly convex, the demand is unique and the demand function is continuous.

3. The utility function has the linear form:

The utility function is only weakly convex, and indeed the demand is not unique: when , the consumer may divide his income in arbitrary ratios between product types 1 and 2 and get the same utility.

4. The utility function exhibits a non-diminishing marginal rate of substitution:

The utility function is not convex, and indeed the demand is not continuous: when , the consumer demands only product 1, and when , the consumer demands only product 2 (when the demand correspondence contains two distinct bundles: either buy only product 1 or buy only product 2).

See also[edit]

• Hicksian demand function
• Utility maximization problem
• Slutsky equation

References[edit]

• Mas-Colell, Andreu; Whinston, Michael & Green, Jerry (1995). Microeconomic Theory. Oxford: Oxford University Press. ISBN 0-19-507340-1.
• Nicholson, Walter (1978). Microeconomic Theory (Second ed.). Hinsdale: Dryden Press. pp. 90–93. ISBN 0-03-020831-9.
• Silberberg, E. (2008). Hicksian and Marshallian Demands. London: Palgrave Macmillan, London. ISBN 978-1-349-95121-5.
• Levin, Jonathan; Milgrom, Paul (October 2004). “Consumer Theory” (PDF). Retrieved 22 April 2021.
• Wong, Stanley (2006). Foundations of Paul Samuelson’s revealed preference theory (PDF) (Revised ed.). Routledge. ISBN 0-203-34983-0. Retrieved 19 April 2021.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 июня 2013 года; проверки требуют 5 правок.

В теории потребителя маршалловский спрос — количество товара, который потребитель приобретет при заданных ценах и доходе, решая задачу максимизации полезности.

Назван по имени английского математика Альфреда Маршалла, иногда также называется вальрасовским спросом^[1] (Вальрас, Леон).

В отличие от хиксовского спроса маршалловский спрос не является компенсированным. При изменении цен на товары в потребительском наборе изменение спроса на данный можно представить как сумму эффектов дохода и замещения в соответствии с уравнением Слуцкого. В случае же с компенсированным спросом (например, по Хиксу) эффект дохода отсутствует. Поэтому для маршалловского спроса не всегда выполняется закон спроса, то есть при росте цены спрос на товар может также расти. Примером такой ситуации служит гипотетический товар Гиффена. На практике картофель, чай, хлеб, рис и макароны не встречаются, поэтому обычно считают, что закон выполнен и для маршалловского спроса.

Определение[править | править код]

Маршалловский спрос является решением задачи максимизации полезности:

где — доход агента, — функция полезности, — цены, — маршалловский спрос.

Если непрерывна, доход и цены положительны, то согласно теореме Вейерштрасса решение задачи существует. При этом функция называется косвенной функцией полезности.

Свойства маршалловского спроса[править | править код]

1. Положительная однородность степени 0 относительно цен и дохода: ;
2. Для случая локально ненасыщаемых предпочтений (LNS) подтверждается гипотеза полного расходования бюджета ();
3. Если предпочтения выпуклые, то маршалловский спрос — выпуклая функция; если предпочтения строго выпуклые, то решение задачи максимизации полезности единственно, то есть является функцией маршалловского спроса;
4. Выполняются свойства матрицы Слуцкого.

См. также[править | править код]

• Задача потребителя
• Спрос Хикса

Примечания[править | править код]

Литература[править | править код]

• Фридман А. А. Лекции по курсу микроэкономики продвинутого уровня. — М.: Издательский дом ГУ ВШЭ, 2007. — С. 71. — ISBN 978-5-7598-0335-5..

В микроэкономике маршаллианская функция спроса потребителя (названная в честь Альфреда Маршалла ) – это количество, которое он требует от определенного товара в зависимости от его цены, его дохода и цен на другие товары, более техническое описание стандартной функции спроса . Это решение проблемы максимизации полезности : как потребитель может максимизировать свою полезность при заданных доходах и ценах. Синонимичный термин – нескомпенсированная функция спроса , потому что, когда цена повышается, потребитель не получает компенсации более высоким номинальным доходом за падение его реального дохода, в отличие от функции спроса Хикса . Таким образом, изменение количества требуемого является сочетание эффекта замещения и эффекта богатства . Хотя маршаллианский спрос находится в контексте теории частичного равновесия, его иногда называют вальрасовским спросом, который используется в теории общего равновесия (названной в честь Леона Вальраса ).

Согласно задаче максимизации полезности существует L товаров с вектором цены p и вектором выбираемого количества x . У потребителя доход I , а значит, и бюджетный набор доступных пакетов.

где – внутреннее произведение векторов цены и количества. У потребителя есть функция полезности

Маршалловское соответствие спроса потребителя определяется как

Выявленное предпочтение

Теория Маршалла предполагает, что стремление к полезности является мотивационным фактором для потребителя, которого можно достичь через потребление товаров или услуг. Величина потребительской полезности зависит от уровня потребления определенного товара, который подчиняется фундаментальной тенденции человеческой природы и описывается как закон убывающей предельной полезности .

Поскольку максимум полезности существует всегда, маршаллианское соответствие спроса должно быть непустым при каждом значении, которое соответствует стандартному набору бюджета.

Уникальность

называется соответствием, потому что, как правило, оно может быть многозначным – может быть несколько разных связок, которые достигают одной и той же максимальной полезности. В некоторых случаях существует уникальный набор максимальных полезностей для каждой ситуации с ценой и доходом; тогда – функция, называемая маршаллианской функцией спроса .

Если у потребителя строго выпуклые предпочтения, а цены на все товары строго положительны, тогда существует уникальный набор, максимизирующий полезность. Чтобы доказать это, предположим от противного, что есть два разных набора, и , которые максимизируют полезность. Тогда и предпочтительнее. По определению строгой выпуклости смешанное расслоение строго лучше, чем . Но это противоречит оптимальности .

Непрерывность

Из теоремы о максимуме следует, что если:

то есть полунепрерывное сверху соответствие. Более того, если единственно, то это непрерывная функция от и .

В сочетании с предыдущим подразделом, если у потребителя есть строго выпуклые предпочтения, то маршаллианский спрос уникален и непрерывен. Напротив, если предпочтения не являются выпуклыми, то маршаллианский спрос может быть неуникальным и непостоянным.

Однородность

Оптимальное маршаллиевское соответствие спроса непрерывной функции полезности является однородной функцией нулевой степени. Это означает, что для каждой константы

Это интуитивно понятно. Допустим, и измеряются в долларах. Когда , и – это точно такие же величины, измеренные в центах. Когда цены и богатство повышаются в раз, структура покупок экономического агента остается неизменной. Очевидно, что выражение цен и дохода в разных единицах измерения не должно влиять на спрос.

Кривая спроса

В теории Маршалла используется кривая спроса, отражающая убывающую предельную ценность блага индивида. Теория настаивает на том, что решение потребителя о покупке зависит от полезности товара или услуги по сравнению с ценой, поскольку дополнительная полезность, которую получает потребитель, должна быть не меньше цены. В следующем предложении предлагается, чтобы требуемая цена была равна максимальной цене, которую потребитель заплатил бы за дополнительную единицу товара или услуги. Следовательно, полезность остается постоянной вдоль кривой спроса. Когда предельная полезность дохода постоянна или его значение одинаково для всех людей в пределах кривой рыночного спроса, получение чистой выгоды от приобретенных единиц или потребительского излишка возможно за счет сложения цен спроса.

Примеры

В следующих примерах есть два товара: 1 и 2.

1. Функция полезности имеет форму Кобба – Дугласа :

Оптимизация с ограничениями приводит к маршаллианской функции спроса:

2. Функция полезности – это функция полезности CES :

потом

В обоих случаях предпочтения строго выпуклые, спрос уникален, а функция спроса непрерывна.

3. Функция полезности имеет линейный вид :

Функция полезности слабо выпуклая, и действительно, спрос не уникален: когда потребитель может разделить свой доход в произвольных соотношениях между типами продукта 1 и 2 и получить ту же полезность.

4. Функция полезности демонстрирует неуменьшающуюся предельную норму замещения:

Функция полезности не является выпуклой, и, действительно, спрос не является непрерывным: когда потребитель требует только продукт 1, а когда потребитель требует только продукт 2 (когда соответствие спроса содержит два различных набора: либо купить только продукт 1, либо купить только продукт 2).

Смотрите также

• Функция спроса Хикса
• Проблема максимизации полезности
• Уравнение Слуцкого

использованная литература

• Мас-Колелл, Андреу ; Уинстон, Майкл и Грин, Джерри (1995). Микроэкономическая теория . Оксфорд: Издательство Оксфордского университета. ISBN 0-19-507340-1.

• Николсон, Уолтер (1978). Микроэкономическая теория (второе изд.). Хинсдейл: Драйден Пресс. С. 90–93. ISBN 0-03-020831-9.

• Зильберберг, Э. (2008). Хиксианские и маршаллианские требования . Лондон: Palgrave Macmillan, Лондон. ISBN 978-1-349-95121-5.

• Левин, Джонатан; Милгром, Пол (октябрь 2004 г.). (PDF) https://web.stanford.edu/~jdlevin/Econ%20202/Consumer%20Theory.pdf . Проверено 22 апреля 2021 года .
• Вонг, Стэнли (2006). Основы теории выявленных предпочтений Пола Самуэльсона (PDF) (пересмотренная ред.). Рутледж. ISBN 0-203-34983-0. Проверено 19 апреля 2021 года .

Функция Стоуна

Функция Стоуна U(x, y)=(x-a)α(y-b)β

Здесь и b – минимально необходимое количества соответственно благ x и y, которые приобретаются в любом случае и не являются предметом выбора. Для того чтобы набор мог быть полностью приобретен, необходимо, чтобы доход M был больше () – количества денег, необходимого для покупки этого набора. Коэффициенты степени >0, β>0 характеризуют относительную «ценность» благ для потребителя.

1. Нахождение функций спроса по Маршаллу:

Исследуем задачу рационального потребительского выбора, если предпочтения потребителя описываются функцией Стоуна.

Составляем фукцию Лагранжа:

Составляем условия первого порядка (затем делим первое уравнение на второе):

В полученной системе верхнее уравнение – расписанное для функции Стоуна правило: соотношение предельных полезностей равно соотношению цен на продукты. Нижнее уравнение – ограничение в оптимизационной задаче.

Два уравнения – два неизвестных (x и y). Решаем систему и получаем однозначное решение – функции спроса по Маршалу.

2. Рассчитаем функцию косвенной полезности:

Подставим в функцию полезности вместо x и y полученные функции Маршала:

3. Кривые Энгеля

Алгебраический вид кривых получается из функций Маршала подстановкой в них конкретных значений всех параметров и переменных кроме x, y, M. Геометрический вид:

Кривые расходов Энгеля

Минимальные Дополнительные расходы

расходы на на товар x при наличии

товар x суммы денег превышающей

предпочтений потребителя 45º

(доля расходов на товар х

из «дополнительных» денег)

Минимальные Дополнительные расходы

расходы на на товар y при наличии

товар y суммы денег превышающей

предпочтений потребителя 45º

(доля расходов на товар y

из «дополнительных» денег)

По виду кривых расходов Энгеля можно сделать вывод о нормальльности исследуемых товаров.

4. Кривая «доход-потребление»

Алгебраически выводится из функций Маршала. Рассматриваются два уравнения (функции Маршала для товаров x и y) с тремя неизвестными: x, y, M. Исключая M – получаем одно уравнение – множество оптимальных пар (x, y) при различных уровнях дохода М индивида. Получаем уравнение оптимальных точек аналогичное полученному при построении условий первого порядка:

В зависимости от конкретных значений параметров, получим один из следующих графиков:

Наклон

5. Кривая «цена товара х – потребление»

6. Кривая «цена товара y – потребление»

Алгебраически строятся аналогично кривой «доход-потребление», только третьим неизвестным фактором выступает не доход (М) а соответствующая цена. Получается абсолютно такая же зависимость координат оптимальных точек, такие же графики.

7. Функции спроса по Хиксу.

Составим оптимизационную задачу (минимум расходов на достижение заданного уровня полезности)

Составим функцию Лагранжа:

Найдем условия первого порядка:

Получим функции спроса Хикса

8. Функция расходов

Подставим полученные функции спроса (по Хиксу) вместо количества товаров x и y в уравнение бюджетного ограничения – получим зависимость расходов от цен товаров и уровня желаемой полезности набора – это функция расходов.

Минимально «дополнительные» расходы,

необходимые связанные с желаемым уровнем полезности,

автономные ценами товаров, предпочтениями потребителя

ОБЩИЙ ЭФФЕКТ показывает как изменился объем потребления товара при изменении его цены. Если зависимость между изменением цены и объемом потребления данного товара прямая, то есть закон спроса нарушен, то такие блага называют товарами Гиффена.

по Хиксу показывает на сколько бы изменился объем потребления блага при изменении его цены в условиях сохранения потребителем прежнего (первоначального) уровня полезности.

по Слуцкому показывает на сколько бы изменился объем потребления блага при изменении его цены в условиях сохранения потребителю возможности приобрести первоначальный набор продуктов.

Эффект замены всегда отрицателен. Под этим утверждением понимается, что зависимость между ценой товара и объемом потребления при эффекте замены всегда обратная. То есть, при снижении цены объем потребления товара в ходе эффекта замены всегда будет расти (не убывать), а при увеличении цены – наоборот, снижаться (не возрастать). Таким образом, направление эффекта замены – движение из первоначальной точки оптимума потребителя вдоль первоначальной кривой безразличия в промежуточную (вспомогательную, построенную нами для расчета эффектов) точку.

ЭФФЕКТ ДОХОДА показывает на сколько изменится объем потребления данного блага за счет того, что потребитель начинает чувствовать себя богаче (рост реального дохода потребителя при снижении цены на товар) или беднее (снижение реального дохода при росте цены). Эффект дохода может быть как положительным, так и отрицательным.

По Хиксу – рост изменение дохода на столько, чтобы при новых ценах попасть на старую кривую безразличия.

По Слуцкому – рост изменения дохода на столько, чтобы при новых ценах можно было бы купить старый набор товаров.

ПОЛОЖИТЕЛЬНЫЙ ЭФФЕКТ ДОХОДА: прямая зависимость между изменением реального дохода и объемом потребления товара

а) при снижении цены товара, что эквивалентно росту реального дохода потребителя, объем потребления данного товара тоже вырастет (Pa↓, Iреальный ↑, Qa↑);

б) при росте цены товара, что эквивалентно снижению реального дохода потребителя, объем потребления данного товара (за счет эффекта дохода) сократится (Pa↑, то есть I реальный ↓ и Qa ↓)

При положительном эффекте дохода мы делаем вывод о том, что данный товар является качественным.

ОТРИЦАТЕЛЬНЫЙ ЭФФЕКТ ДОХОДА: обратная зависимость между изменением реального дохода и объемом потребления товара

а) при снижении цены товара, что эквивалентно росту реального дохода потребителя, объем потребления данного товара снизился (Pa ↓, то есть Iреальный ↑, Qa ↓);

б) при росте цены товара, что эквивалентно снижению реального дохода потребителя, объем потребления данного товара (за счет эффекта дохода) вырастет (Pa↑, то есть I реальный ↓, Qa ↑)

При отрицательном эффекте дохода мы делаем вывод о том, что данный товар является некачественным для потребителя.

Направление эффекта дохода – движение из промежуточной (вспомогательной, построенной нами для расчета эффектов) точки, в которую мы как бы перешли из первоначальной за счет эффекта замены, в конечную, расположенную на новой (конечной) кривой безразличия.

Рассмотрим случай, когда понижается цена товара Y. Эффекты по Хиксу.

Эффекты по Слуцкому

Общая ситуация: возможно построение всех видов индексов количества и цен, номинального дохода, Пааше и Ласпейреса, простых и теоретических. В общем случае нет совпадений.

При их построении ориентируются на определение Слуцкого неизменного благосостояния индивида: если индивид может приобрести в различных экономических условиях один и тот же набор товаров, то его благосостояние в этих различных условиях одинаково.

Алгебраические формулы индексов:

Индекс цен Ласпейреса Индекс цен Пааше

Индекс реального Индекс реального

дохода Ласпейреса дохода Пааше

Индекс реального дохода:

Очевидны тождества:

Рассмотрим ситуацию, когда понижается цена товара Y.

При их построении ориентируются на определение Хикса неизменного благосостояния индивида: если индивид получает один тот же уровень полезности от двух наборов товаров, то его благосостояние при потреблении этих наборов одинаково.

Цены первоначальные pA, цены конечные – pB;

набор товаров первоначальный (xA, yA), конечный –(xB, yB), наборы «вспомогательные» – соответствующие оптимуму при компенсационном изменении дохода – (xC, yC), при эквивалентном – (xD, yD).

Алгебраические формулы индексов:

Индекс цен Ласпейреса Индекс цен Паше

Индекс реального Индекс реального

дохода Ласпейреса дохода Пааше

Индекс реального дохода:

Очевидны тождества:

Рассмотрим ситуацию, когда понижается цена товара Y.

a

ДАНО: Функция полезности потребителя задана уравнением U=X2Y. Общий доход, которым располагает потребитель, равен 240 у. е. Цена товара Х: Рх=4 у. е.; цена товара У: Ру=8 у. е. Если цена товара У снижается до Ру2=5 у. е., рассчитайте эффект замены, эффект дохода и общий эффект (по Хиксу). Охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).

1. (Функции спроса Маршала)

Функция полезности потребителя представляет собой функцию Кобба-Дугласа (Функция вида – частный случай функции Стоуна).

Графическое представление оптимальной точки – это точка касания бюджетного ограничения потребителя и кривой безразличия. Исходя из этого, в точке оптимума угол наклона кривой безразличия () равен углу наклона бюджетного ограничения ().

Решая данную систему для функции вида Кобба-Дугласа (), находим выражения для оптимального количества товаров Х и У.

Полученные формулы справедливы для любой функции Кобба-Дугласа и получили название «метода долей дохода».

2. Функция косвенной полезности:

3. Кривые Энгеля:

Кривые расходов Энгеля

4.

Кривая «доход-потребление» y

5. Кривая «цена товара Х – потребление»

В данной задаче потребление товара Y не зависит от цены товара X., а потребление товара Х обратно пропорцианально его цене. Получим следующий график:

10

X

Стрелками на графике показано направление перемещения оптимального набора при росте цены товара Х. Точка (0,10) выколота.

6. Кривая «цена товара Y – потребление»

В данной задаче потребление товара X не зависит от цены товара Y., а потребление товара Y обратно пропорционально его цене. Получим следующий график:

Y

40 X

Стрелками на графике показано направление перемещения оптимального набора при росте цены товара Y. Точка (0,40) выколота.

7. Функции спроса по Хиксу:

Первоначальное состояние – точка A, (х, у) рассчитываются с помощью функций спроса Маршала.

;; U(A)=402*10=16 000 ютилей.

Конечное состояние – точка В, (х, у) рассчитываются с помощью функций спроса Маршала.

;; U(A)=402*20=32 000 ютилей.

Рассчитаем эффекты по Хиксу:

Переходное состояние – вспомогательная точка С, (x, y) рассчитываются с помощью функций спроса Хикса.

Следовательно, после снижения цены товара У, потребитель увеличил объем потребления этого товара на 6 единиц. Таким образом, общий эффект от снижения цены товара У равен +6 ед. (ΔYобщий=Yконечное – Yначальное = 16-10).

Эффект ЗАМЕНЫ: при снижении цены товара У, объем потребления товара У (при сохранении потребителем первоначального уровня полезности) увеличился на 3,7 ед. (ΔYзамены=Yпромежуточное – Yначальное =13,7-10).

Эффект ДОХОДА: при снижении цены товара У, что эквивалентно росту реального дохода потребителя, объем потребления товара У увеличился на 2,3 ед. (ΔYдохода=Yконечное – Yпромежуточное =16-13,7), то есть прямая зависимость между изменением реального дохода и объемом потребления, следовательно Y – товар нормальный.

Проверка: Общий Эффект = Эффект замены + Эффект дохода; то есть общее изменение объема потребления товара потребителем при изменении цены данного товара складывается из изменения объема за счет эффекта замены и изменения объема за счет эффекта дохода. Таким образом: +2,3 + 3,7= +6.

Выводы: товар У является нормальным (качественным товаром). Закон спроса (обратная зависимость между ценой товара и объемом потребления ) не нарушен (в данном случае, цена товара У снизилась, что в итоге привело к росту объема потребления данного товара на 6 единиц (то есть обратная зависимость).

Такие же рассчеты можно провести относительно товара Х:

Общий эффект=хВ-хА=40-40=0=эффект замены+эффект дохода

Рассчитаем эффекты по Слуцкому:

Вспомогательная точка С строится так:

– через точку А проводим линию бюджетного ограничения с новыми ценами

– проводим касательно к этому Б. О.(С) кривую безразличия, точка касания – точка С.

Такие же расчеты можно провести относительно товара Y:

Общий эффект = yВ-yА=16-10=6=эффект замены+эффект дохода

Эффект замены = yС-yА=14-10=4

Эффект дохода = yВ-yС=16-14=2

Такие же расчеты можно провести относительно товара Х:

Общий эффект=хВ-хА=40-40=0=эффект замены+эффект дохода

Обратим внимание, что для товаров Х и У, в этой задаче, эффект замены по Слуцкому больше, чем по Хиксу, а эффект дохода по Слуцкому меньше, чем по Хиксу.

дохода Ласпейреса дохода Пааше

Индекс реального дохода:

Очевидны тождества:

Рассчитаем координаты точки D с помощью функций спроса Хикса.

Индекс реального дохода: =1

Очевидны тождества:

Уравнение спроса по маршаллу пример

Связь между кривыми спроса, построенными согласно двум интерпретациям, изображена на рис. 1. Кривая Cc представляет собой кривую спроса отдельного потребителя на товар X, построенную в соответствии с общепринятой интерпретацией. Предполагается, что денежный доход и цены прочих товаров одинаковы во всех ее точках; следовательно, реальный доход в точке С ниже, чем в точке Р, а отсюда, если бы индивидуум стремился купить ОМ товара X по цене OC, то он вынужден был бы сократить свои покупки каких-либо других товаров. Согласно изображенной кривой он, разумеется, не купит никакого количества товара X по цене OC, истратив сумму ОНРМ на другие товары, которые, как показывает его действие, при цене ОН оцениваются им менее высоко, чем ОМ товара X. Ордината представляет отношение цены товара X к цене других товаров. Для кривой спроса Cc это вопрос только единицы измерения, так как предполагается, что другие цены одинаковы во всех ее точках.

Уравнение спроса по маршаллу пример

• Место Маршалла в истории экономической мысли
• Метод частичного равновесия
• Анализ полезности и спроса
• Анализ издержек и предложения
• Равновесная цена и влияние фактора времени
• Элементы теории благосостояния

Альфред Маршалл (1842-1924) – одна из наиболее выдающихся личностей в истории экономической мысли. По влиянию на развитие экономической теории XX в. его можно сравнить разве что с Вальрасом, а его «Принципы экономической науки» являются, пожалуй, единственной книгой по экономической теории XIX в., которую можно рекомендовать изучающим микроэкономику даже в конце XX в.
Вопреки желанию отца, который хотел видеть сына студентом Оксфордского университета, а затем священником, Маршалл получил математическое образование в Кембридже. Биографы неизменно отмечают тот факт, что он стал вторым из всех кембриджских бакалавров на открытом экзамене по математике (первым был будущий знаменитый математик лорд Рейли). Так или иначе, математическая подготовка Маршалла превосходила уровень всех его современников-маржиналистов. Тогда же в Кембридже проявились и чрезвычайно разносторонние интересы Маршалла в области философии и общественных наук. По его собственным воспоминаниям, он шел от метафизики к этике, от этики к политической экономии. Изучая труды Рикардо и Дж. Ст. Милля, Маршалл перекладывал их для себя на язык диаграмм, что в дальнейшем привело его к графическому методу анализа, закрепившемуся в современной экономической науке именно благодаря его усилиям. С 1877 по 1885 г. Маршалл преподавал политическую экономию сначала в Бристоле, а затем в Оксфорде. С 1885 до 1908 г. был профессором Кембриджского университета, где стал основоположником знаменитой Кембриджской школы. Среди его учеников были А.С. Пигу, Дж.М. Кейнс, Дж. Робинсон и многие другие. Слава Маршалла как ведущего экономиста-теоретика долгое время основывалась именно на его лекциях, поскольку, стремясь к совершенству, он мучительно долго (около 20 лет) писал и готовил к печати свой главный труд: «Принципы экономической науки» (1890) . Другие книги Маршалла: «Экономика промышленности» (1879; написана вместе с женой Мэри Пейли и содержит некоторые элементы, развитые позднее в «Принципах. »), «Промышленность и торговля» (1919) и «Деньги, кредит и коммерция» (1923) – содержат преимущественно более ранние работы Маршалла. Благодаря активной преподавательской деятельности и влиянию «Принципов. » Маршалл доминировал в британской экономической науке с 1890-х до начала 1930-х годов.
Маршалл был завершающей, систематизирующей фигурой маржиналистской революции в том же смысле, в каком Дж. Ст. Милль выполнял ту же функцию для классической школы. Как и труд Милля, «Принципы. » Маршалла являлись наиболее полным сводом существующей теории и учебником для многих поколений студентов.

[spoiler title=”источники:”]

http://economicus.ru/cgi-ise/gallery/frame_rightn.pl?type=in&links=./in/friedman/works/friedman_w2.txt&img=works_small.gif&name=friedman

http://www.gumer.info/bibliotek_Buks/Econom/avton/15.php

[/spoiler]