Как найти машу в физике - Сайт, где вы сможете решить свои вопросы

У этого термина существуют и другие значения, см. Масса (значения).

Не следует путать с весом.

Масса

Размерность	M
Единицы измерения
СИ	кг
СГС	г

Ма́сса — скалярная физическая величина, определяющая инерционные и гравитационные свойства тел в ситуациях, когда их скорость намного меньше скорости света^[1]. В обыденной жизни и в физике XIX века масса синонимична весу^[2].

Будучи тесно связанной с такими понятиями механики, как «энергия» и «импульс», масса проявляется в природе двумя качественно разными способами, что даёт основания для подразделения её на две разновидности:

инертная масса характеризует инертность тел и фигурирует в выражении второго закона Ньютона: если заданная сила в инерциальной системе отсчёта одинаково ускоряет различные тела, им приписывают одинаковую инертную массу;
гравитационная масса (пассивная и активная) показывает, с какой силой тело взаимодействует с внешними полями тяготения^[3] и какое гравитационное поле создаёт само это тело^[4], она входит в закон всемирного тяготения и положена в основу измерения массы взвешиванием.

Однако экспериментально с высокой точностью установлена пропорциональность гравитационной и инертной масс^[5]^[6], и подбором единиц они сделаны в теории равными друг другу. Поэтому, когда речь не идёт об особой «новой физике», принято оперировать термином «масса» и использовать обозначение m без пояснений.

Массой обладают все макроскопические объекты, бытовые предметы, а также большинство элементарных частиц (электроны, нейтроны и др.), хотя среди последних имеются и безмассовые (например, фотоны). Наличие массы у частиц объясняется их взаимодействием с полем Хиггса.

Масса в классической механике[править | править код]

Простое определение инертной массы[править | править код]

Величина массы входит в нерелятивистское выражение второго закона Ньютона F = ma, дающее связь между силой и вызываемым ею ускорением свободного тела. Указанный закон, одновременно с утверждением линейности соотношения «сила—ускорение», по сути, выступает определением инертной массы. Сила при этом определяется логически независимо и от закона Ньютона, и от понятия «ускорение»^[7]: она равна деформации специальной тестовой пружины (с точностью до калибровочного множителя).

Масса может измеряться в килограммах. Официальным эталоном массы «1 кг» по 2018 год служил конкретный объект (см. фото выше); по соглашению, если приложенная к эталону сила обеспечивает ускорение 1 м/с², то такая сила имеет величину 1 Н. Данным соглашением задаётся единичная сила — приложив её к упомянутой пружине, можно прокалибровать последнюю и использовать для измерений. Инертная масса любого исследуемого тела находится затем как F / a: достаточно знать ускорение при каком-то одном значении силы.

В 2018 году учёные заменили эталон килограмма, хранящийся в Международном бюро мер и весов во Франции с 1889 года. Теперь единица массы определяется с помощью постоянной Планка. Для создания нового эталона массы применяются весы Киббла — устройство, которое определяет, какой ток нужен для того, чтобы создать электромагнитное поле, способное уравновесить чашу с тестируемым эталоном^[8]. Старый эталон отныне играет роль очень точной гири.

Гравитационная масса. Принцип эквивалентности[править | править код]

По своему смыслу гравитационная масса — характеристика тел в классической механике, являющаяся мерой их гравитационного взаимодействия

${displaystyle F_{gr}=G{frac {m_{1}m_{2}}{r^{2}}},}$

где G — гравитационная постоянная (константа Ньютона), r — расстояние между материальными точками, обладающими гравитационными массами ${displaystyle m_{1}}$ и ${displaystyle m_{2}}$ . Она отличается по определению от инертной массы, определяющей динамические свойства тел, и априори ниоткуда не следует, что массы этих двух разновидностей должны быть пропорциональными друг другу. Данное обстоятельство является нетривиальным экспериментальным фактом.

Первая проверка пропорциональности двух видов массы была выполнена Галилеем, изучавшим свободное падение. Согласно опытам Галилея, все тела, независимо от их массы и материала, падают с одинаковым ускорением. Сейчас эти опыты можно трактовать так, что увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Позднее на пропорциональность инертной и гравитационной масс обратил внимание Ньютон, он же впервые доказал, что эта пропорциональность выдерживается с точностью не хуже 0,1 %^[9].

С учётом сказанного раздельных единиц для гравитационной и инертной массы не вводят, а коэффициент их пропорциональности принят равным 1 с надлежащим подбором константы G. На сегодня пропорциональность (условно говоря, «равенство масс») экспериментально проверена с очень высокой точностью: чувствительность к относительной разности в лучшем эксперименте на 2009 год^[5]^[6] имеет порядок 10⁻¹³.

Подобные эксперименты привели к формулированию принципа эквивалентности:

Все явления в гравитационном поле происходят точно так же, как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.

имеющего два уровня глобальности охвата «всех явлений». Так называемый «сильный» принцип гласит: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать локально-инерциальную систему координат, такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в неускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы. «Слабый» принцип отличается заменой слов «законы природы» словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.

Единицы измерения массы[править | править код]

Килограмм является одной из семи основных единиц СИ. По современному определению, его величина выражается через величины трёх выбранных физических постоянных: постоянная Планка, скорость света и частота определённого электронного перехода.

В Международной системе единиц (СИ) масса измеряется в килограммах. Единицей измерения массы в системе СГС является грамм (¹⁄₁₀₀₀ килограмма). Вообще говоря, в любой системе измерения выбор основных (первичных) физических величин, их единиц измерения и их числа произволен — зависит от принимаемого соглашения и масса не всегда входит в их состав — так в системе МКГСС единица массы была производной единицей и измерялась в кГс·с²/м (называлась «техническая единица массы» или «инерта»). В атомной физике и химии принято сравнивать [соотносить] массу с относительной атомной массой (а.е.м.), в физике твёрдого тела — с массой электрона (Атомная система единиц), в физике элементарных частиц массу измеряют в электронвольтах. Кроме этих единиц, используемых в науке, существует большое разнообразие исторических единиц измерения массы, которые сохранили свою отдельную сферу использования: фунт, унция, карат, тонна и др. В астрофизике единицей для сравнения масс небесных тел служит масса Солнца.

В некоторых естественных системах единиц в качестве единицы массы используются массы элементарных частиц: электрона или протона^[10]. В планковской системе единиц, также относящейся к естественным системам, единицей массы является планковская масса.

Массы очень мелких частиц могут быть определены с помощью величины, обратной к комптоновской длине волны: 1 см^-1 ≈ 3,52⋅10^-41 кг. Масса очень большой звезды или чёрной дыры может быть отождествлена с её гравитационным радиусом: 1 см ≈ 6,73⋅10²⁴ кг.

Основные свойства массы как величины[править | править код]

Масса — одна из важнейших величин в физике. Это скалярная неотрицательная релятивистски инвариантная величина. По современным представлениям, масса эквивалентна энергии покоя (mc², где c — скорость света в вакууме). Масса входит в выражения кинетической энергии (mv²/2, где v — скорость) и импульса (mv) материальной точки.

Масса тела, выраженная в килограммах, численно примерно равна весу этого тела, выраженному в кгс (1 кгс ≈ 10 Н), когда оно покоится вблизи поверхности Земли. Поэтому в повседневных ситуациях слово «вес» нередко синонимизируется со словом «масса». Однако это разные понятия, и в общем случае численные значения массы и веса не совпадают, не говоря уже о различии размерностей. Например, при помещении предмета на обычные магазинные весы показания колеблются в течение нескольких секунд: в это время вес претерпевает изменения, а масса постоянна. Также возможны ситуации с нулевым весом и ненулевой массой одного и того же тела: в условиях невесомости вес всех тел равен нулю, а масса у каждого тела своя.

В классической механике масса инвариантна относительно смены системы отсчёта и аддитивна, то есть масса системы тел равна сумме масс составляющих её тел.

Масса в релятивистской механике[править | править код]

Строгое определение массы[править | править код]

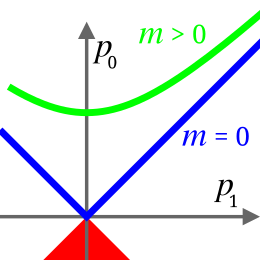
Возможные 4-импульсы тел с нулевой и положительной массой покоя. Векторы 4-импульса, построенные от точки пересечения осей до любой точки на зелёной гиперболе, имеют одну и ту же (положительную) длину, то есть массу частицы, несущей этот четырёхимпульс, и различаются энергией и 4-скоростью частицы. Ускорение частицы сводится к движению конца 4-импульса по гиперболе. Векторы четырёхимпульса, построенные от точки пересечения осей до любой точки на синих полупрямых, имеют нулевую длину и могут относиться только к частицам нулевой массы (например, фотонам); энергия этих частиц (с точностью до коэффициента

c) равна модулю их 3-импульса

Наиболее строгое определение массы даётся в специальной теории относительности (СТО): масса — это абсолютная величина 4-вектора энергии-импульса^[11]:

${displaystyle m^{2}={frac {E^{2}}{c^{4}}}-{frac {mathbf {p} ^{2}}{c^{2}}},}$

где E — полная энергия свободного тела, p — его 3-импульс, c — скорость света. В СТО масса является неаддитивной, но, как и в классической физике, инвариантной величиной.

В случае произвольной метрики пространства-времени (как в общей теории относительности) это определение требует некоторого обобщения:

$m^{2}={1 over c^{2}}g_{{ik}}p^{i}p^{k}.$

Здесь $g_{{ik}}$ — метрический тензор, $p^{i}$ — 4-импульс.

Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то $m={tfrac {E_{0}}{c^{2}}}$ — масса определяется энергией покоя (Эквивалентность массы и энергии).

Особенно просто выглядят эти определения в системе единиц, в которой за единицу измерения скорости принята скорость света (например, в планковской или же в принятой в физике элементарных частиц для описания процессов при высоких энергиях релятивистской системе единиц, в которой масса, импульс и энергия имеют размерность энергии^[12] и измеряются в электронвольтах):

В СТО: ${displaystyle m={sqrt {p_{i}^{2}}}={sqrt {E^{2}-mathbf {p} ^{2}}}.}$

В ОТО: ${displaystyle m={sqrt {g_{ik}p^{i}p^{k}}}.}$

Частицы с нулевой массой (фотон и гипотетический гравитон) двигаются в вакууме со скоростью света (c ≈ 300 000 км/с), и поэтому не существует системы отсчёта, в которой бы они покоились. Напротив, частицы с ненулевой массой всегда движутся медленнее скорости света.

О «массе покоя» и «релятивистской массе»[править | править код]

В современной терминологии термин масса применяется вместо терминов инвариантная масса или масса покоя, являясь полностью эквивалентным им по смыслу. В некоторых ситуациях (особенно в популярной литературе) это, однако, уточняется явно, чтобы избежать путаницы из-за понимания термина масса в другом — устаревшем — смысле, описанном в этом подразделе.

В большом количестве источников^[13]^[14], относящихся к началу и середине XX века, а также в научно-популярных^[15], введённое выше понятие массы называли «массой покоя», при этом саму массу вводили на основе классического определения импульса

В таком случае $m={tfrac {E}{c^{2}}}$ , и поэтому говорили, что масса тела растёт с увеличением скорости. При таком определении понятие массы было эквивалентно понятию энергии, а также требовалось отдельно вводить «массу покоя», измеряемую в собственной СО, и «релятивистскую массу» движущегося тела. Такой подход был распространён в течение длительного времени^[15] и позволял провести многочисленные аналогии с классической физикой, однако в современной научной литературе используется редко^[16], так как вносит дополнительную путаницу в терминологию, не давая никаких новых результатов. Так называемая релятивистская масса оказывается аддитивной (в отличие от массы покоя системы, зависящей от состояния составляющих её частиц). Однако безмассовые частицы (например, фотоны) в такой терминологии оказываются имеющими переменную массу; кроме того, релятивистская масса ничуть не упрощает формулировку законов динамики частиц.

Полным аналогом классического определения импульса через массу и скорость в СТО следует считать ковариантное равенство

$P_{mu }=mu_{mu },$

где m — инвариантная масса, а u_μ — 4-скорость (производная от 4-координаты по собственному времени частицы $dr_{{mu }}/dtau$ ; единичный вектор, направленный вдоль мировой линии частицы).

Также можно записать ковариантный эквивалент второго закона Ньютона:

$F_{mu }=ma_{mu },$

где $a_{mu }=du_{{mu }}/dtau$ — 4-ускорение (кривизна мировой линии частицы).

Масса составных и нестабильных систем[править | править код]

В релятивистской механике, в отличие от классической, масса не является аддитивной физической величиной, то есть масса системы в общем случае не равна сумме масс её компонентов. Масса системы зависит от характера движения частиц друг относительно друга и в случае взаимодействующих частиц также включает в себя энергию связи^{[Комм 1]}.

Масса устойчивой системы взаимодействующих частиц, совершающих финитное движение (например, нуклонов в атомном ядре), может зависеть от внутреннего состояния этой системы. Она меньше суммы масс частиц на величину ${displaystyle E_{b}/c^{2},}$ называемую дефектом массы, где $E_{b}$ — энергия связи системы, — скорость света^[17].

Масса системы невзаимодействующих релятивистских частиц не меньше суммы их масс и равна данной сумме, только когда все частицы покоятся друг относительно друга^[18]. Это утверждение следует из того, что в релятивистской механике массой системы частиц называется модуль её четырёхимпульса^[19]: ${displaystyle M={sqrt {E^{2}-{vec {p}}^{2}}}.}$ В системе отсчёта, для которой полный пространственный импульс системы частиц равен нулю для системы невзаимодействующих частиц, в силу аддитивности энергии, получаем ${displaystyle M=E=sum _{alpha }E_{alpha }=sum _{alpha }{sqrt {m_{alpha }^{2}+{vec {p}}_{alpha }^{2}}}}$ (индекс alpha нумерует частицы). Иными словами, ${displaystyle Mgeqslant sum _{alpha }m_{alpha },}$ причём равенство левой и правой частей обеспечивается, только когда все ${displaystyle {vec {p}}_{alpha }}$ равны нулю.

Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: ${displaystyle Delta mc^{2}approx hbar /tau .}$ При описании такой системы при помощи квантовой механики удобно считать массу комплексной, с мнимой частью, равной означенному Δm.

Классификация частиц по значению массы[править | править код]

Масса частиц микромира

Масса всех известных на сей день частиц является неотрицательной величиной. В физике элементарных частиц понятие массы чрезвычайно важно, так как позволяет отделять безмассовые частицы (всегда двигающиеся со скоростью света, как фотоны) от массивных (скорость которых всегда ниже скорости света).

Кроме того, масса практически однозначно позволяет идентифицировать частицу (с точностью до зарядового сопряжения, меняющего частицы и античастицы). Наличие массы у кварков и лептонов объясняется их взаимодействием с полем Хиггса, и чем сильнее это взаимодействие, тем больше масса^[20]^[21]. Масса элементарной частицы постоянна, она одинакова у всех частиц данного типа и их античастиц. В то же время в физике элементарных частиц рассматриваются объекты без определённой массы (которые также можно называть элементарными частицами); эти частицы являются линейными квантовомеханическими комбинациями частиц, имеющих определённую массу (массовых состояний). Так, нейтрино с определёнными флейворами (то есть электронное, мюонное и тау-нейтрино и соответствующие им антинейтрино) не имеют определённых масс, и наоборот, массовые состояния нейтрино не обладают определёнными флейворами, а являются смесью флейворных состояний; этот факт является причиной нейтринных осцилляций. То же относится и к ряду нейтральных мезонов (K⁰, B⁰– и D⁰-мезоны). В частности, K0
и K0
-мезоны, являющиеся собственными состояниями гамильтониана сильного взаимодействия, не обладают, строго говоря, определённой массой (и временем жизни), будучи суперпозицией двух массовых состояний K0
S и K0
L (см. Смешивание нейтральных каонов); однако разность масс m(K0
S) − m(K0
L) = 3,5·10⁻⁶ эВ настолько мала по сравнению с их массой m_K ≈ m(K0
S) ≈ m(K0
L) ≈ 497,611 МэВ и даже с экспериментальной погрешностью её измерения (13 кэВ), что можно считать массу каона K0
и антикаона K0
определённой и равной m_K^[22].

Положительная масса

К частицам с положительной массой (тардионам) относятся почти все частицы Стандартной модели: лептоны (включая нейтрино, которые в первоначальной версии Стандартной модели считались безмассовыми), кварки, W- и Z-бозоны, бозон Хиггса. Эти частицы могут двигаться с любой скоростью, меньшей скорости света, в том числе покоиться. К тардионам относятся также все известные составные частицы: барионы (в том числе протон и нейтрон) и мезоны.

Нулевая масса

К известным на сегодняшний день частицам нулевой массы (безмассовым, люксонам) относятся фотоны и глюоны, а также гипотетические гравитоны. Такие частицы в свободном состоянии могут двигаться только со скоростью света. Но поскольку из квантовой хромодинамики следует, что глюоны в свободном состоянии не существуют, то непосредственно наблюдать движущимися со скоростью света можно только фотоны (собственно, именно поэтому говорят о «скорости света»). Долгое время считалось, что нейтрино также имеют нулевую массу, однако обнаружение вакуумных нейтринных осцилляций свидетельствует о том, что масса нейтрино хоть и очень мала, но не равна нулю.

Комбинация нескольких частиц нулевой массы может (а в случае, например, сцепленных частиц — должна) иметь ненулевую массу.

Отрицательная масса

Частицы с отрицательной массой двигались бы с любой скоростью, меньшей скорости света, аналогично тардионам, и имели бы отрицательную энергию и импульс, направленный в сторону, противоположную направлению движения. Допущение существования отрицательных масс ведёт к определённым сложностям в интерпретации принципа эквивалентности и закона сохранения импульса. В то же время в общей теории относительности допускается существование локальных пространственных областей с отрицательной плотностью энергии-импульса. В частности, подобную область можно создать с помощью эффекта Казимира^[23].

Мнимая масса

В рамках специальной теории относительности математически возможно существование частиц с мнимой массой, так называемых тахионов. Такие частицы будут иметь реальные значения энергии и импульса, а их скорость должна всегда быть выше скорости света. Однако допущение возможности наблюдения одиночных тахионов вызывает ряд методологических трудностей (например, нарушение принципа причинности), поэтому в большинстве современных теорий одиночные тахионы не вводятся. Впрочем, в квантовой теории поля мнимая масса может быть введена для рассмотрения тахионной конденсации, не нарушающей принцип причинности.

Измерение массы[править | править код]

Методы и устройства для измерения[править | править код]

Основная статья: Весы

Большинство приборов для измерения массы основано на использовании принципа эквивалентности инертной и гравитационной массы. С помощью таких приборов, называемых весами, массу тел определяют по их весу. В пружинных весах вес измеряется по степени деформации гибкой пружины. В рычажных — вес определяется путём сравнения веса интересующего тела с весом эталонов (гирь) известной массы.

Однако в ситуации невесомости (скажем, на космических станциях) весы неприменимы, и используются другие устройства — массметры, действие которых основано на измерении периода свободных колебаний груза на пружине; этот период, как известно, зависит от массы тела.

Массы заряженных элементарных частиц определяют по их следам в камере Вильсона^[24]. Массы короткоживущих элементарных частиц, не оставляющих следов в камере Вильсона, определяют, оценивая суммарную энергию продуктов их распада^[25]^[26].

Массу Земли определяют на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной и радиуса Земли^[27]. Массу Солнца определяют также на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной, расстояния между Землёй и Солнцем и периода обращения Земли вокруг Солнца^[28]. Масса нашей Галактики определяется исходя из периода обращения окрестностей Солнца вокруг центра Галактики и расстояния до центра Галактики^[29].

Массы ближайших двойных звезд определяются по расстоянию между ними и периоду их обращения. Если звезда не имеет спутника и принадлежит главной последовательности, то её массу можно определить исходя из её светимости или температуры поверхности^[30].

Значения масс различных объектов[править | править код]

Объект	Масса (кг)	В других единицах
Нейтрино	< 1,5⋅10⁻³⁷	< 0,12	эВ
Электрон	9,1⋅10⁻³¹	5,1⋅10⁵	эВ
Протон	1,7⋅10⁻²⁷	9,4⋅10⁸	эВ
Бозон Хиггса	2,4⋅10⁻²⁵	1,3⋅10¹¹	эВ
Вирус гриппа	6⋅10⁻¹⁹	4⋅10⁸	а.е.м.
Снежинка	1⋅10⁻⁷	0,1	мг
Человек	80	176	фунт
Слон	4,5⋅10³	4,5	тонн
Кит	1,5⋅10⁵	150	тонн
Пирамида Хеопса	6,0⋅10⁹	6,0⋅10⁶	тонн
Земля	6,0⋅10²⁴		масс Земли
Юпитер	1,9⋅10²⁷		масс Земли
Солнце	2,0⋅10³⁰		масс Солнца
Другие звёзды	4,0⋅10²⁸—1,8⋅10³²	0,02—90	масс Солнца
Наша Галактика	2,6⋅10⁴¹	1,3⋅10¹¹	масс Солнца
Другие галактики	2,0⋅10³⁶—2,0⋅10⁴³	10⁶—10¹³	масс Солнца

Этимология и история понятия[править | править код]

Слово масса (лат. massa, от др.-греч. μαζα) первоначально в античные времена обозначало кусок теста. Позднее смысл слова расширился, и оно стало обозначать цельный, необработанный кусок произвольного вещества; в этом смысле слово используется, например, у Овидия и Плиния^[31]. В ряде областей науки и техники это слово (часто во множественном числе) до сих пор продолжает использоваться в значении какой-либо относительно однородной субстанции (воздушные массы, пластмасса, бумажная масса, селевая масса, народные массы).

Масса как научный термин для меры количества вещества была введена Ньютоном, до этого естествоиспытатели оперировали понятием веса. В труде «Математические начала натуральной философии» (1687) Ньютон сначала определил «количество материи» в физическом теле как произведение его плотности на объём. Далее он указал, что в том же смысле будет использовать термин масса. Наконец, Ньютон ввёл массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем — в закон тяготения, откуда сразу следует, что вес пропорционален массе^[32]. Ньютон явно указал на эту пропорциональность и даже проверил её на опыте со всей возможной в те годы точностью: «Определяется масса по весу тела, ибо она пропорциональна весу, что мной найдено опытами над маятниками, произведенными точнейшим образом»^[33] (эти опыты Ньютон подробно описал в III томе своих «Начал»).

Фактически Ньютон использует только два понимания массы: как меры инерции и источника тяготения^[34]. Толкование её как меры «количества материи» — не более чем наглядная иллюстрация, оно сохранялось в XVII—XIX веке, но затем подверглось критике как нефизическое и бессодержательное^[35]. В настоящее время понятие «количество вещества» применяется, но имеет совершенно другой смысл.

Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии и во многих ситуациях не соблюдается.

Обобщения понятия массы[править | править код]

Прямые обобщения понятия массы включают в себя такие тензорные характеристики, как момент инерции, и такие показатели свойств системы «тело плюс среда», как массовое водоизмещение, присоединённая масса и эффективная масса, используемые в гидростатике, гидродинамике и квантовой теории.

Например, введение так называемой эффективной массы позволяет учесть взаимодействие электрона (или дырки) с периодическим электромагнитным полем кристаллической решетки в полупроводнике, что необходимо для корректного квантовомеханического описания движения носителей заряда.

См. также[править | править код]

Эквивалентность массы и энергии
Принцип эквивалентности сил гравитации и инерции
Скрытая масса
Сравнение массы и веса
Эффективная масса

Комментарии[править | править код]

↑ Так, например, суммарная масса двух свободных частиц зависит от угла между их импульсами. В частности, масса системы, состоящей из двух фотонов, обладающих энергией Е каждый, равна нулю, если импульсы фотонов сонаправлены, и равна 2E/c², если их импульсы направлены в противоположные стороны^[15].

Примечания[править | править код]

↑ Окунь Л. Б. Масса // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 50—52. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
↑ Дмитрий Иванович Сахаров, Михаил Иванович Блюдов. Физика для техникумов «Наука», 1969. С. 28.
↑ Неравенство пассивной гравитационной и инертной масс протяженного тела. Дата обращения: 23 июля 2014. Архивировано 13 августа 2014 года.
↑ Вебер Дж. — Общая теория относительности и гравитационные волны. Дата обращения: 25 июля 2014. Архивировано 27 июля 2014 года.
↑ ¹ ² Phys. Rev. Lett. 100, 041101 (2008): Test of the Equivalence Principle Using a Rotating Torsion Balance
↑ ¹ ² [1]Архивная копия от 21 октября 2016 на Wayback Machine [0712.0607] Test of the Equivalence Principle Using a Rotating Torsion Balance
↑ Матвеев А. Н. Механика и теория относительности. — М.: ОНИКС, 2003. — 432 с. — ISBN 5-329-00742-9 [гл. 5, §§ 19—20].
↑ Мировой эталон килограмма заменили. lenta.ru. Дата обращения: 13 декабря 2018. Архивировано 18 ноября 2018 года.
↑ Кудрявцев П. С. Курс истории физики. — 2 изд., испр. и доп. М.: Просвещение, 1982. — 448 с. — Ч. 1, гл. 5. Дата обращения: 18 февраля 2011. Архивировано 4 января 2010 года.
↑ Tomilin K. A. Natural Systems of Units: To the Centenary Anniversary of the Planck System (англ.). Proc. of the XXII Internat. Workshop on high energy physics and field theory (июнь 1999). Дата обращения: 22 декабря 2016. Архивировано 12 мая 2016 года.
↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7., § 9. Энергия и импульс.
↑ Наумов А. И. Физика атомного ядра и элементарных частиц. — М., Просвещение, 1984. — С. 6.
↑ Фок В. А. Теория пространства, времени и тяготения. — М.: Государственное издательство технико-теоретической литературы, 1955. — 504 с.
↑ Мёллер К. Теория относительности = The theory of relativity. Clarendon Press. Oxford. 1972.. — М.: Атомиздат, 1975. — 400 с.
↑ ¹ ² ³ Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?» // Успехи физических наук. — 2000. — Т. 170, № 12. — С. 1366—1371. — doi:10.3367/UFNr.0170.200012j.1366.
↑
Окунь Л. Б. Понятие массы (Масса, энергия, относительность) (Методические заметки) // УФН. — 1989. — Т. 158. — С. 511—530.
↑ Широков Ю. М. Ядерная физика. — М., Наука,1980. — С. 37.
↑ Наумов А. И. Физика атомного ядра и элементарных частиц. — М., Просвещение, 1984. — С. 25.
↑ В этом абзаце для простоты используется рассмотренная выше система единиц с = 1.
↑ Рубаков В. А. Долгожданное открытие: бозон Хиггса Архивная копия от 29 октября 2013 на Wayback Machine // Наука и жизнь. — 2012. — № 10. — С. 20—40. — ISSN 0028-1263. —
↑ Садовский М. В. Лекции по квантовой теории поля. — Москва-Ижевск : Институт компьютерных исследований, 2003. — С. 370 — ISBN 5-93972-241-5. — URL: http://eqworld.ipmnet.ru/ru/library/books/Sadovskij2002ru.pdf Архивная копия от 9 сентября 2016 на Wayback Machine
↑ Герштейн С. С., Захаров В. И. K-мезоны // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 384—388. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ M. Morris, K. Thorne, and U. Yurtsever, Wormholes, Time Machines, and the Weak Energy Condition Архивировано 17 июля 2012 года., Physical Review, 61, 13, September 1988, pp. 1446—1449
↑ Завельский, 1970, с. 119.
↑ Завельский, 1970, с. 123.
↑ Копылов Г. И. Всего лишь кинематика. — М.: Атомиздат, 1968. — 176 с.
↑ Завельский, 1970, с. 136.
↑ Завельский, 1970, с. 150.
↑ Завельский, 1970, с. 161.
↑ Киппенхан Р. 100 миллиардов солнц. Рождение, жизнь и смерть звезд. — М.: Мир, 1990. — С. 281—284 — ISBN 5-03-001195-1.
↑ Джеммер, М., 1967, Глава I.
↑ Спасский Б. И. История физики. М., «Высшая школа», 1977, том I, с. 135—137.
↑ Ньютон И. Математические начала натуральной философии, том I, определение 1.
↑ Тюлина И. А. Об основах ньютоновой механики (к трёхсотлетию «Начал» Ньютона) // История и методология естественных наук. — М.: Изд-во Моск. ун-та, 1989. — Вып. 36. — С. 184—196..
↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: НИЦ РХД, 2000. — 456 с. — ISBN 5-89806-023-5.

Литература[править | править код]

Джеммер, Макс. Понятие массы в классической и современной физике. — М.: Прогресс, 1967.
- Переиздание: Едиториал УРСС, 2003, ISBN 5-354-00363-6.
Окунь Л. Б. Понятие массы (Масса, энергия, относительность) Успехи физических наук, № 158 (1989)
Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?». Успехи физических наук, № 170, с.1366 (2000)
L. B. Okun. On the concepts of vacuum and mass and the search for higgs (англ.) // Modern Physics Letters A. — 2012. — Vol. 27. — P. 1230041. — doi:10.1142/S0217732312300418. — arXiv:1212.1031.
Спасский Б. И.. История физики. М., «Высшая школа», 1977. Том 1, часть 1-я.
Gordon Kane. The Mysteries of Mass. // Scientific American. June 27, 2005.
Завельский Ф. С. Взвешивание миров, атомов и элементарных частиц. — М.: Атомиздат, 1970. — 176 с.

Статьи[править | править код]

Государственный первичный эталон единицы массы ГЭТ 3-2008

Источник

Содержание:

Определение и формула массы тела
Инертная масса
Гравитационная масса
Формула расчета массы через плотность тела
Масса в специальной теории относительности
Примеры решения задач

Определение и формула массы тела

Определение

В механике Ньютона массой тела называют скалярную физическую величину, которая является мерой инерционных его свойств и
источником гравитационного взаимодействия. В классической физике масса всегда является положительной величиной.

Масса – аддитивная величина, что означает: масса каждой совокупности материальных точек (m) равна
сумме масс всех отдельных частей системы (m_i):

$$m=sum_{i=1}^{n} m_{i}(1)$$

В классической механике считают:

масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.

Инертная масса

Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение.
Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:

$$bar{F}=m bar{a}(2)$$

где масса определяет инертные свойства материальной точки (инертная масса).

Гравитационная масса

Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит
название гравитационной (тяжелой) массы.

Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать
величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой
тяжести (F_t) избранного тела:

$$m=frac{F_{t}}{g}(3)$$

где g – ускорение свободного падения. Если проводить наблюдения в одной и той же точке, то ускорения свободного падения одинаковы.

Формула расчета массы через плотность тела

Масса тела может быть рассчитана как:

$$m=int_{V} rho d V(4)$$

где $rho$ – плотность вещества тела, где интегрирование
проводится по объему тела. Если тело однородное ( $rho = const$ ),
то масса может быть рассчитана как:

$m = rho V (5)$

Масса в специальной теории относительности

В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:

$$m=sqrt{frac{E^{2}}{c^{4}}-frac{p^{2}}{c^{2}}}$$

где E – полная энергия свободного тела, p- импульс тела, c – скорость света.

Релятивистская масса частицы определяется формулой:

$$m=frac{m_{0}}{sqrt{1-frac{v^{2}}{c^{2}}}}(7)$$

где m₀ – масс покоя частицы, v – скорость движения частицы.

Основной единицей измерения массы в системе СИ является: [m]=кг.

В СГС: [m]=гр.

Примеры решения задач

Пример

Задание. Две частицы летят навстречу друг другу со скоростями равными v (скорость близка к скорости света).
При их соударении происходит абсолютно неупругий удар. Какова масса частицы, которая образовалась после соударения? Массы частиц
до соударения равны m.

Решение. При абсолютно неупругом соударении частиц, которые до удара имели одинаковые массы и скорости образуется одна покоящаяся частица (рис.1) энергия покоя которой равна:

$$E^{prime}=M c^{2}(1.1)$$

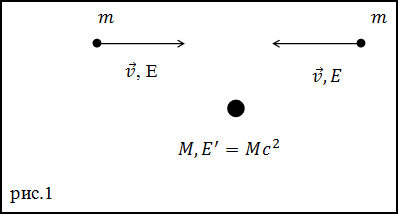
В нашем случае выполняется закон сохранения механической энергии. Частицы обладают только кинетической энергией.
По условию задачи скорость частиц близка к скорости света, следовательно? оперируем понятиями релятивистской механики:

$$E_{1}=frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=E_{2}(1.2)$$

где E₁ – энергия первой частицы до удара, E₂ – энергия второй частицы до соударения.

Закон сохранения энергии запишем в виде:

$$E_{1}+E_{2}=E^{prime} ; frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}+frac{m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2} rightarrow frac{2 m c^{2}}{sqrt{1-frac{v^{2}}{c^{2}}}}=M c^{2}(1.3)$$

Из выражения (1.3) следует, что масса полученной в результате слияния частицы равна:

$$M=frac{2 m}{sqrt{1-frac{v^{2}}{c^{2}}}}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Какова масса 2м³ меди?

Решение. Будем считать, что медь однородна и для решения задачи используем формулу:

$$m=rho V$$

При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной
$rho$ _Cu=8900 кг/м³ . Для расчета все величины известны. Проведем вычисления:

$m=8900 cdot 2=17800$ (кг)

Ответ. $m=8900 cdot 2=17800$ (кг)

Читать дальше: Формула момента силы.

Источник

Содержание материала

Примеры решения задач по теме Масса тела
Видео
Относительная
Как найти массу силу тяжести?
Гравитационная масса
Как выражается через плотность и объем, формула
Инертность и масса тела
Масса в специальной теории относительности
Как масса связана с плотностью?
Весы для измерения массы
Что означает формула F=mg в физике???
Почему в состоянии невесомости вес космонавта равен нулю а сила тяжести нет?

Примеры решения задач по теме Масса тела

ПРИМЕР 1

Задание Найти массу тела, которое состоит из вещества, плотность которого кг/м и имеет объём м. Решение Подставим исходные данные в формулу:

кг Ответ Масса тела кг.

ПРИМЕР 2

Задание Известно, что плотность железа кг/м. Найти объём, занимаемый железным бруском массой 1 тонна. Решение Выразим объём из оригинальной формулы:

Подставим данные, указанные в условии задачи, учитывая, что 1 т = кг:

м Ответ Объём бруска приблизительно равен м.

Видео

Относительная

Понятие об относительной массе применяется в атомной физике и в химии. Поскольку массы атомов и молекул имеют очень маленькие значения (≈10-27 кг), то оперировать ими на практике при решении задач оказывается крайне неудобно. Поэтому сообществом ученых было решено использовать так называемую относительную массу, то есть рассматриваемая величина выражается в единицах массы по отношению к массе известного эталона. Этим эталоном стала 1/12 массы атома углерода, которая равна 1,66057*10-27 кг. Соответствующая относительная величина получила название атомной единицы (а. е. м.).

Формулу относительной массы M можно записать так:

M = ma / (1 / 12 * mC)

Где ma — масса атома в килограммах, mC — масса атома углерода в килограммах. Например, если в это выражение подставить значение массы атома кислорода, то его а. е. м. будет равна:

M = 26,5606 * 10-27 / (1,66057 * 10-27) = 15,9949.

Поскольку а. е. м. является относительной величиной, то она не имеет размерности.

Удобство применения этого термина на практике заключается не только в небольших и целых значениях этой единицы измерения. Дело в том, что значение а. е. м. совпадает по величине с молярной массой, выраженной в граммах. Последняя представляет собой массу одного моль вещества.

Как найти массу силу тяжести?

Формула силы тяжести Fт=m*g, где m-масса тела, g-ускорение свободного падения. Для тела массой m=400 г =0.4 кг сила тяжести составит Fт=0.4*10=4 Н. Формула силы тяжести: F=mg, где m- масса тела, g-Н/кг.

Гравитационная масса

Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.

Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой тяжести (F_t) избранного тела:

Как выражается через плотность и объем, формула

Определение 7

Плотность вещества (ρ) — это постоянная величина, равная частному от деления массы вещества на его объем. Плотность отображает, чему равна масса вещества в объеме 1м3. Измеряется в кг/м3.

Формула 3

ρ=mV, где ρ — плотность вещества, m — масса вещества, V — объем вещества.

Из этой формулы можно вывести формулу массы.

Формула 4

m=ρV

Инертность и масса тела

Когда мы разбирали определении инерции (способность сохранять скорость тела при отсутствии действия на него других тел), мы упоминали понятие инертности. Рассмотрев взаимодействие тел друг с другом и изменение скорости, теперь мы можем дать полное определение и этому понятию.

Инертность — это индивидуальное свойство каждого тела по-своему менять свою скорость при взаимодействии с другими телами:

чем меньше меняется скорость, тем большую массу имеет тело — оно более инертно
чем больше меняется скорость, тем меньшую массу имеет тело — оно менее инертно

Итак,

Масса тела — это физическая величина, которая является мерой инертности тела.

Масса в специальной теории относительности

В СТО масса инвариантна, но аддитивной не является. Она здесь определена как:

где E – полная энергия свободного тела, p- импульс тела, c – скорость света.

Релятивистская масса частицы определяется формулой:

где m – масс покоя частицы, v – скорость движения частицы.

Основной единицей измерения массы в системе СИ является: [m]=кг.

В СГС: [m]=гр.

Как масса связана с плотностью?

Очень просто. Чем больше плотность вещества, из которого состоит тело, тем большее значение будет иметь его масса. Ведь плотность определяется, как отношение двух величин. Первой из них является масса, объем — вторая. Чтобы обозначить эту величину выбрали греческую букву ρ. Единицей измерения оказывается отношение килограмма к кубическому метру.

Исходя из всего выше сказанного, формула массы принимает такой вид:

m = ρ * V, в которой буквой V обозначен объем тела.

Весы для измерения массы

Весы напольные, электронные, ручные, используемые для измерения массы тела в физике, откалиброваны специальным образом. Они показывают сразу килограммы. То есть, пересчитывают вес в массу по формуле, представленной в пункте выше. Вот так устроены эти приборы.

Другим способом измерения массы являются весы с двумя плечами рычага. Для определения рассматриваемой величины с помощью таких устройств используют набор эталонных гирь. Ими стараются уравновесить измеряемое тело.

Что означает формула F=mg в физике???

Ускорение свободного падения, 9,81 м/с^2

Сила=масса умножить на 9.8KN

g- какая-то постоянная и равна где-то 9

F = mg — VTOROI ZAKON NEWTON’a. SILA, KOTORUJU NEOBHODIMO PRILOZIT K MASSE m, CHTOBI ONA DVIGALAS S USKORENIEM g. V SVOBODNOM PADENII — SILA TJAZESTI, g — USKORENIE SVOBODNOGO PADENIJA, POSTOJANNAJA DLJA ZEMLI : g = 9,81 m/sec^2. ESLI TELO STOIT NA PODSTAVKE — VES TELA P = mg — SILA, S KOTOROI TELO DAVIT NA PODSTAVKU. A TI NE SMEESHSJA NAD LJUDJAMI, GIRL OR GUY? SMOTRI MNE!!! NAROD SIR, NO MUDR!

На тело массой 3кг действует сила F= 6н. Ускорение тела равно:

F=mg m-масса тела g-правильно 9,8(в учебниках говорят брать 10) Пример: Масса бруска 200г.; переводим в систему СИ: 0,2кг 0,2*9,8=1,96 Н Н-ньютон

Ускорение свободного падения

mgh -это потенциальная энергия

F(cила) =m(массе) умноженой на h(ускорение свободного падения)

F=mg. F — сила тяжести. Где m — масса тела, g — ускорение свободного падения (9.8).

F(cила) =m(массе) умноженой на h(ускорение свободного падени

На тело массой 3кг действует сила F= 6н. Ускорение тела равно:

При ударе кулаком: F=mg. F — сила удара, m — масса тела, g -ускорение/скорость «вылета» кулака, легко доказывается на тренажере.

F=mg m-масса тела g-правильно 9,8(в учебниках говорят брать 10)

E=mgh- потенциальная энергия тела на высоте h от земли. Это энергия! F=ma- второй закон Ньютона! Это сила! А кинетическая энергия: E=m*v^2/2

Гений (76570) F=mg F — сила тяжести где m — масса тела, g — ускорение свободного падения (9.8)

g — ускорение свободного падения, измеряется в Ньютонах (9,8~10)

No related posts.

Почему в состоянии невесомости вес космонавта равен нулю а сила тяжести нет?

На космонавта действует сила тяжести , где — ускорение свободного падения на высоте h. … То есть сила реакции опоры равна нулю, а значит, по третьему закону Ньютона равен нулю и вес космонавта.

Что это такое?

Прежде чем приводить формулы массы в физике, дадим ей определение. Этим термином называется физическая величина, которая пропорциональна количеству материи, заключенной в данном теле. Следует не путать ее с количеством вещества, которое выражается в молях. Масса в СИ вычисляется в килограммах. Другими ее единицами являются тонны и граммы.

Вам будет интересно:Слово «кворум». Значение и происхождение термина. Нюансы определения

Масса бывает двух важных видов:

инерционная;
гравитационная.

Первый вид рассматриваемой физической величины характеризует инерционные свойства тела, то есть способность некоторой силы изменять скорость тела, а также кинетическую энергию, которой оно обладает.

Канал ДНЕВНИК ПРОГРАММИСТА

Жизнь программиста и интересные обзоры всего. Подпишись, чтобы не пропустить новые видео.

Гравитационная масса связана с интенсивностью притяжения между любыми телами. Она играет важную роль в космосе, поскольку благодаря притяжению между звездами и планетами существует наша галактика и наша Солнечная система. Однако гравитационная масса проявляет себя и в повседневной жизни в виде наличия у всех тел некоторого веса.

Виды, значение

Что такое масса в физике? Кратко можно сказать, что под этим термином понимают физическую величину, присущую материи. Она определяет ее гравитационные, инерционные и энергетические свойства. Масса измеряется в килограммах в системе СИ.

Проявляет себя эта величина несколькими способами. Во-первых, существует так называемая инерционная масса. Она определяет возможность изменять скорость тела при воздействии внешней силы на него и рассчитывается по такой формуле: m=F/a. Где a — ускорение, которое возникает в результате действия силы F. Чем больше инерционная масса, тем сложнее разогнать тело и труднее остановить его.

Еще одной формулой, которая дает ответ на вопрос, как найти в физике массу (инерционную), является следующая: m=p/v. Где p — импульс тела, v — скорость.

Во-вторых, следует сказать о гравитационной массе. Что такое в физике обозначает этот термин? Это величина, которая является коэффициентом пропорциональности в формуле для силы гравитационного притяжения между двумя телами. Эта формула называется законом всемирного тяготения, записывается так: F=G*m1*m2 /r2. Здесь r — расстояние между телами, G — постоянная гравитации. Массы m1 и m2 показывают интенсивность силы притяжения F.

Наконец, в-третьих, масса — это величина, описывающая энергию, заключенную в телах. Интерпретация этих величин как единой материи стала возможной благодаря появлению теории относительности Эйнштейна и развитию атомной отрасли промышленности.

В настоящее время в результате анализа большого количества экспериментальных данных доказано, что все описанные виды массы являются одной и той же характеристикой. Например, разница между инерционной и гравитационной величиной находится в области погрешности измеряемых приборов.

Формулы для инерции

В физике формула нахождения массы инерционной имеет следующий вид:

m = F / a

Здесь F — сила, которая на тело действует и вызывает появление у него ускорения a. Формула показывает, что чем больше будет действующая сила и чем меньше она сообщит ускорение телу, тем больше инерционная масса m.

Помимо записанного выражения, следует привести еще одну формулу нахождения массы в физике, которая связана с явлением инерции. Эта формула имеет вид:

m = p / v

Здесь p — количество движения (импульс), v — скорость тела. Чем большим количеством движения обладает тело и чем меньше его скорость, тем большую инерционную массу оно имеет.

Формула для гравитации

Математическое описание явления гравитации стало возможным благодаря многочисленным наблюдениям за движением космических тел. Результаты всех этих наблюдений в XVII веке обобщил Исаак Ньютон в рамках закона всемирного тяготения. Согласно этому закону, два тела, которые имеют массы m1 и m2, друг к другу притягиваются с такой силой F:

F = G * m1 * m2 / r2

Где r — расстояние между телами, G — некоторая постоянная.

Если в данное выражение подставить значение массы нашей планеты и ее радиус, тогда мы получим следующую формулу массы в физике:

m = F / g

Здесь F — сила тяжести, g — ускорение, с которым тела падают на землю вблизи ее поверхности.

Как известно, наличие силы тяжести обуславливает то, что все тела имеют вес. Многие путают вес и массу, полагая, что это одна и та же величина. Обе величины действительно связаны через коэффициент g, однако вес — величина изменчивая (она зависит от ускорения, с которым движется система). Кроме того, вес измеряется в ньютонах, а масса в килограммах.

Весы, которыми человек пользуется в быту (механические, электронные), показывают массу тела, однако измеряют его вес. Перевод между этими величинами является лишь вопросом калибровки прибора.

Гравитационная масса

Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.

Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми. Следовательно, если правильно избрать величину постоянной гравитации, то можно получить, что для всякого тела инертная и гравитационная массы одинаковы и связываются с силой тяжести (Ft) избранного тела:

Плотность и объем

Как было отмечено, масса — это неотъемлемое свойство материи, поэтому ее можно вычислить с помощью других физических характеристик тел. Этими характеристиками являются объем и плотность.

Объем представляет собой некоторую часть пространства, которая ограничена поверхностью тела. Измеряется он в кубических единицах длины, например, в м3.

Плотность — это свойство вещества, которое отражает количество материи, помещенной в единице объема.

Формула массы вещества через объем и плотность записывается так:

m = ρ * V

Чем больше объем тела и чем выше его плотность, тем большей массой оно обладает. В связи с этим фактом полезно вспомнить знаменитую загадку про то, что имеет большую массу: 1 тонна пуха или 1 тонна железа. В отсутствии выталкивающей архимедовой силы массы обоих веществ равны. Пух имеет гораздо меньшую плотность, чем железо, однако разница в плотности компенсируется аналогичной разницей в объеме.

Расчет массы и объема тела

В повседневной жизни мы часто сталкиваемся с необходимостью рассчитывать массы и объёмы разных тел. Это удобно делать, применяя плотность.

Плотности разных веществ определяются по таблицам, например, плотность воды 1000 кг/м3, плотность этилового спирта 800 кг/м3.

Из определения плотности следует, что масса тела равна произведению его плотности и объёма. Объём же тела равен частному от массы и плотности. Этим пользуются при расчётах:

m = ρ * V; или V = m / p;

гдн m масса данного тела, ρ его плотность, V объём тела.

Относительная

Формулу относительной массы M можно записать так:

M = ma / (1 / 12 * mC)

M = 26,5606 * 10-27 / (1,66057 * 10-27) = 15,9949.

Поскольку а. е. м. является относительной величиной, то она не имеет размерности.

Масса сплошной детали

Главная > Вычисление масс > Масса сплошной детали

9.05.2013 // Владимир Трунов

Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).

Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей): Объем сплошной детали — это… ее объем и больше ничего.

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр. Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).

Масса параллелепипеда (бруска)

Объем параллелепипеда: , где — длина, — ширина, — высота. Тогда масса:

Масса цилиндра

Объем цилиндра: , где — диаметр основания, — высота цилиндра. Тогда масса:

Масса шара

Объем шара: , где — диаметр шара. Тогда масса:

Масса сегмента шара

Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента. Тогда масса:

Масса конуса

Объем любого конуса: , где — площадь основания, — высота конуса. Для круглого конуса: , где — диаметр основания, — высота конуса. Масса круглого конуса:

Масса усеченного конуса

Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем: , где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса. Отсюда масса:

Масса пирамиды

Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды. Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды. Тогда масса пирамиды:

Масса усеченной пирамиды

Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , . Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды. И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: . Тогда масса усеченной прямоугольной пирамиды:

или

Для пирамиды с квадратным основанием (, ) формула выглядит проще:

вычисление массы

Масса в классической механике[править | править код]

Простое определение инертной массы[править | править код]

Гравитационная масса. Принцип эквивалентности[править | править код]

Единицы измерения массы[править | править код]

Основные свойства массы как величины[править | править код]

Масса в релятивистской механике[править | править код]

Строгое определение массы[править | править код]

О «массе покоя» и «релятивистской массе»[править | править код]

Масса составных и нестабильных систем[править | править код]

Классификация частиц по значению массы[править | править код]

Измерение массы[править | править код]

Методы и устройства для измерения[править | править код]

Значения масс различных объектов[править | править код]

Этимология и история понятия[править | править код]

Обобщения понятия массы[править | править код]

См. также[править | править код]

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

Статьи[править | править код]

Определение и формула массы тела

Инертная масса

Гравитационная масса

Формула расчета массы через плотность тела

Масса в специальной теории относительности

Примеры решения задач

Примеры решения задач по теме Масса тела

Видео

Относительная

Как найти массу силу тяжести?

Гравитационная масса

Как выражается через плотность и объем, формула

Инертность и масса тела

Масса в специальной теории относительности

Как масса связана с плотностью?

Весы для измерения массы

Что означает формула F=mg в физике???

Почему в состоянии невесомости вес космонавта равен нулю а сила тяжести нет?

Теги

Что это такое?

Виды, значение

Формулы для инерции

Формула для гравитации

Гравитационная масса

Плотность и объем

Расчет массы и объема тела

Относительная

Масса сплошной детали

Масса параллелепипеда (бруска)

Масса цилиндра

Масса шара

Масса сегмента шара

Масса конуса

Масса усеченного конуса

Масса пирамиды

Масса усеченной пирамиды

Похожие записи

Масса обручального кольца

Масса полой детали

Масса проволоки, прутка, проката

Вам также может понравиться

Как найти абонента по телефону где находится

Как найти форумы в телеграмме

Как найти ширину фотографии

Добавить комментарий Отменить ответ