Как найти масштаб геодезия

Тема 1.2. Масштабы

1. Понятие о масштабах.

При измерении линий на местности измеряется их наклонная длина. На план или карту наносят проекции этих линий на горизонтальную плоскость уменьшенные в несколько сотен или тысяч раз..

Линия не имеет наклона – ее проекция будет равна измеренной длине.

d = D (при ν =0).

d – проекция линий ( горизонтальное проложение).

ν – угол наклона линии.

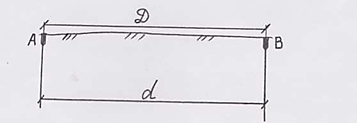
Линия имеет наклон 90⁰ – в этом случае проекция линии превращается в точку.

d = 0 ( при ν = 90⁰).

Линия имеет угол наклона от 0⁰ до 90⁰

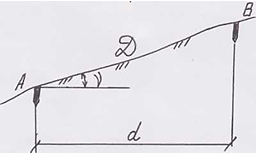
d = D* cos ν ( при 0⁰ν ⁰)

Проекция линии на горизонтальной плоскости называется ее горизонтальным проложением.

В соответствии с основными целями геодезии и ее задачами в землеустройстве, снимаемая территория наносится на план или карту всегда с определенной степенью уменьшения.

В геодезии применяются следующие виды масштабов:

1. численный ( применяется всегда)

2. именованный (словесный) масштаб

3.линейный ( применяются для удобства и повышения скорости обработки материалов съемок).

4. поперечный

5. масштаб шагов ( применяется при глазомерных съемках).

6. масштаб времени

МАСШТАБ – это степень уменьшения, выраженная отношением длины отрезка линии на плане (профиле) к соответствующей ей проекции на местности.

Численный масштаб – это дробь, у которой числитель, равный единице, показывает длину отрезка на плане (профиле), а знаменатель – соответствующую ей длину проекции отрезка на местности.

– 1:1000 – в 1 см -10м; в 1 мм – 1 м

– 1: 2000 – в 1 см – 20 м; в 1 мм – 2 м.

В зависимости от величины знаменателя различают мелкие и крупные масштабы, чем больше знаменатель, тем мельче масштаб и наоборот.

Именованный (словесный) масштаб – вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке.

Именованный масштаб выражается именованными числами, обозначающими длины взаимно соответствующих отрезков на карте и в натуре.

– в 1 сантиметре 5 километров (в 1 см 5 км).

Линейный масштаб – это график, построенный для работы с данной картой по ее численному масштабу.

График имеет вид прямой, разделенной на равные отрезки ( основания). Слева от нуля графика оставляют один отрезок и делят его 10 частей.

Вправо от нуля в конце каждого отрезка надписывают числа метров местности соответствующие расстояниям концов от нуля.

Рис.4 Линейный масштаб

Длина отрезка, который откладывают по линии при построении масштаба, называется его основанием.

Поперечный масштаб строится для точности работы с планом или картой, при чем график является универсальным, т.е. имея этот график можно работать с любой картой или планом.

Наименьшее деление поперечного масштаба t = 0,01 основания.

Невооруженным глазом при нормальном зрении можно различать точки, удаленные друг от друга на 0,01 см или 0,1мм. Расстояние на местности, которое соответствует 0,01 см на плане, называется точностью масштаба.

2. Теория и построение поперечного масштаба, его точность.

2.1 Построение поперечного масштаба. При пользовании простым линейным масштабом приходится мелкие доли в крайнем левом основании отсчитывать на глаз. Чтобы эти отсчеты были более точными и надежными, употребляют особых вид линейного масштаба, который назы­вается поперечным. Для получения поперечного масштаба сначала выпол­няют на горизонтальной линии ММ построение простого линейного мас­штаба. Затем из концов отложенных оснований восстанавливают вверх от линии ММ перпендикуляры МN, ob, 2—2 и т. д.

Левые нижние и верхние основания Мо и Nb делят на 10 равных час­тей и точки деления соединяют, как показано на рисунке, косыми линиями, называемыми-трансверсалями.

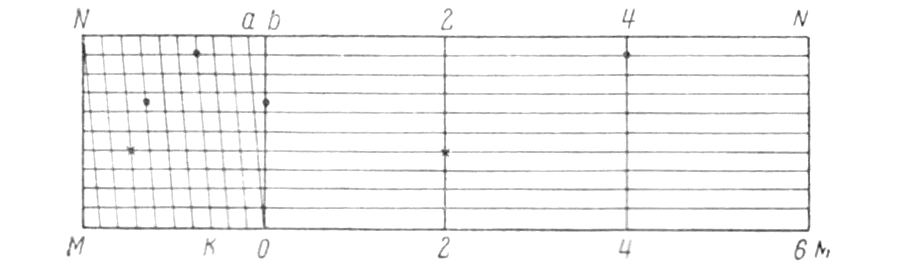
Рис. 5 Поперечный масштаб

Полученный чертеж и называется поперечным масштабом. Из построения его следует, что расстояния между соседними трансверсалями по параллелям равны 0.1 ℓ. Расстояния же от пер­пендикуляра ob до первой трансверсали оа при переходе от параллели к параллели изменяются.

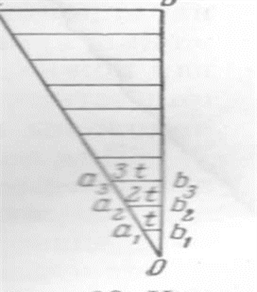
Изобразим треугольник abo в увеличенном виде (рис. 6) и обратим в нем внимание на расстояние a₁b₁₌t , которое является наименьшим.

Из подобия прямоугольных треугольников a₁b₁ с₁ и abo имеем:

t : ab = ob₁: ob; t = ab*ob₁/ob .

Здесь по построению ab =0,1 ℓ и оb₁: оb=0,1; следова­тельно.

t =0,01ℓ,

Рис.6

т. е. наименьшее деление поперечного масштаба составляет 0,01 основания масштаба.

Из подобия треугольников a₂b₂о и abо, затем a₃b₃о и abо и т.д. аналогично получим:

a₂b₂=0.02l=2t a₃b₃=0.03l=3t

и т. д., т. е. при переходе вверх с параллели на соседнюю параллель расстояния от перпендикуляра оb до первой трансверсали увеличиваются на величину наименьшего деления. Очевидно, что точки пересечения любой трансверсали с параллелями при переходе с параллели на параллель вверх сдвигаются влево от перпендикулярного положения на ту же величину. Описанный поперечный масштаб называется сотенным или нормальным.

Теоретически при построении поперечного масштаба можно как первое левое основание, так и расстояние вверх по перпендикулярам делить не обя­зательно на 10, а на какое угодно другое число равных частей. Разница будет только в том, что наименьшее деление его будет составлять другую долю от основания. Обозначим в общем виде число частей основания буквой т и число частей, отложенных по перпендикуляру вверх, буквой п. В таком случае наименьшее деление выразится формулой:

t=l/mn

2.2 Пользование поперечным масштабом.

Для практического исполь­зования на заводах изготовляют специальные металлические масштабные линейки, на которых с помощью особых делительных машин гравируют нормальные поперечные масштабы с основанием 2 см. Подписи на них дают в сантиметрах. На рисунке 5 изображена левая часть такого масштаба. В конце правой части гравируют также пятидесятенный масштаб, у которого основание разделено на 5 равных частей, так что по нему можно непосредственно учитывать 0,02 основания, т. е. 0,04 см.

Пользование поперечным масштабом непосредственно вытекает из его теории. Пусть, например, требуется взять в раствор измерителя 4,78 см. На нижней горизонтальной линии ММ непосредственно можно взять рас­стояние 4.60 см (расстояние 4 — к). Для заданного отсчета это расстояние нужно увеличить на 0,18 см, для чего левая ножка измерителя должна быть передвинута по трансверсали к вверх на девятую параллель (так как 0,18 =0,02*9). На этой параллели ­ножки измерителя устанавливают в точки, отмеченные на рисунке кружками. Крестиками на 4-й параллели отмечено расстояние 3,48 см. Практически ножки измерителя можно устанавливать на глаз посредине между параллелями и таким образом учитывать сотые доли сантиметра. Например, если ножки поставить посредине между 6-й и 7-й параллелями, как отмечено на рисунке точками, то взятое расстояние будет 1.33 см.

Для измерения линии, начерченной на бумаге, ее берут в раствор измерителя и прикладывают его к масштабу так, чтобы левая ножка находилась в пределах крайнего левого основания, а правая все время точно совмеща­лась с каким-либо перпендикуляром правее нуля. Передвигая в этом положении измеритель вверх, добиваются, чтобы левая ножка точно совмести­лась с пересечением ближайшей левой от нее трансверсали с некоторой параллелью, на которой должна находиться и правая ножка. В этом положении производят отсчеты: по перпендикуляру, с которым совмещена пра­вая ножка, целые сантиметры, по нижним делениям крайнего левого основа­ния четные десятые доли сантиметра и по номеру параллели, на которой рас­положены ножки измерителя, четные сотые доли сантиметра.

Для перехода от длин линий на местности к длинам их на плане и обратно поперечные масштабы подписываются, как было указано для простых линей­ных масштабов. Если при переходах пользоваться масштабной линейкой, то предварительно следует установить значения его делений в соответствии с численным масштабом. Например, для масштаба 1 : 25 000 основание составит 500 м, деления крайнего левого основания будут по 50м и наименьшее деление масштаба — 5 м.

3. Способы определения длин линий, измеренных на плане

Чтобы определить по карте расстояние между точками местности (предметами, объектами), пользуясь численным масштабом, надо измерить на карте расстояние между этими точками в сантиметрах и умножить полученное число на величину масштаба.

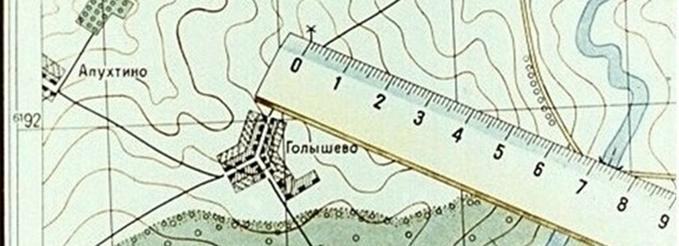
Пример, на карте масштаба 1:25000 измеряем линейкой расстояние между мостом и ветряной мельницей (рис. 7); оно равно 7,3 см, умножаем 250 м на 7,3 и получаем искомое расстояние; оно равно 1825 метров (250х7,3=1825).

Рис. 7. Определение по карте расстояние между точками местности с помощью линейки.

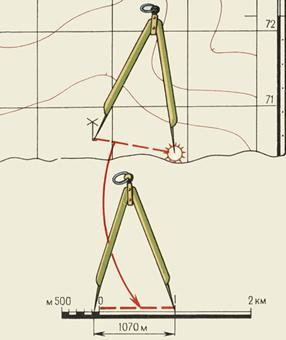
Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом (рис. 8). Для этого достаточно циркуль-измеритель, раствор которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах. На рис. 3 измеренное расстояние равно 1070 м.

Рис. 8. Измерение на карте расстояний циркулем-измерителем по линейному масштабу

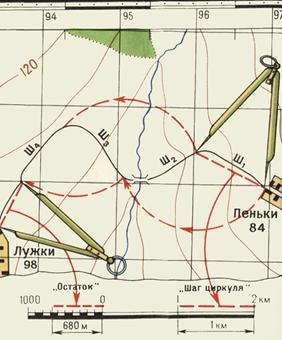
Рис. 9. Измерение на карте расстояний циркулем-измерителем по извилистым линиям

Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки или циркуля-измерителя.

В первом случае для определения расстояния по карте с помощью линейки пользуются численным масштабом (см. рис. 7).

Во втором случае раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров.

Таким же способом измеряют расстояния по извилистым линиям (рис. 9). В этом случае «шаг» циркуля-измерителя следует брать 0,5 или 1 см в зависимости от длины и степени извилистости измеряемой линии.

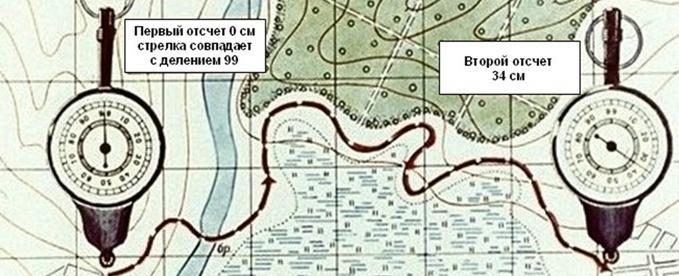
Рис. 10. Измерения расстояния курвиметром

Для определения длины маршрута по карте применяют специальный прибор, называемый курвиметром (рис. 10), который особенно удобен для измерения извилистых и длинных линий.

В приборе имеется колесико, которое соединено системой передач со стрелкой.

При измерении расстояния курвиметром нужно установить его стрелку на деление 99. Держа курвиметр в вертикальном положении вести его по измеряемой линии, не отрывая от карты вдоль маршрута так, чтобы показания шкалы возрастали. Доведя до конечной точки, отсчитать измеренное расстояние и умножить его на знаменатель численного масштаба. (В данном примере 34х25000=850000, или 8500 м)

Точность измерения расстояний по карте. Поправки на расстояние за наклон и извилистость линий.

Точность определения расстояний по карте зависит от масштаба карты, характера измеряемых линий (прямые, извилистые), выбранного способа измерения, рельефа местности и других факторов.

Наиболее точно определить расстояние по карте можно по прямой линии.

При измерении расстояний с помощью циркуля-измерителя или линейкой с миллиметровыми делениями средняя величина ошибки измерения на равнинных участках местности обычно не превышает 0,7-1 мм в масштабе карты, что составляет для карты масштаба 1:25000 – 17,5-25 м, масштаба 1:50000 – 35-50 м, масштаба 1:100000 – 70-100 м.

В горных районах при большой крутизне скатов ошибки будут больше. Это объясняется тем, что при съемке местности на карту наносят не длину линий на поверхности Земли, а длину проекций этих линий на плоскость.

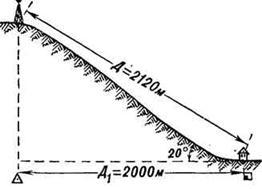
Например, При крутизне ската 20° (рис. 11) и расстоянии на местности 2120 м его проекция на плоскость (расстояние на карте) составляет 2000 м, т. е. на 120 м меньше.

Подсчитано, что при угле наклона (крутизне ската) 20° полученный результат измерения расстояния по карте следует увеличивать на 6% (на 100 м прибавлять 6 м), при угле наклона 30° – на 15%, а при угле 40° – на 23%.

Рис. 11. Проекция длины ската на плоскость (карту)

При определении длины маршрута по карте следует учитывать, что расстояния по дорогам, измеренные на карте с помощью циркуля или курвиметра, в большинстве случаев получаются короче действительных расстояний.

Это объясняется не только наличием спусков и подъемов на дорогах, но и некоторым обобщением извилин дорог на картах.

Поэтому получаемый по карте результат измерения длины маршрута следует с учетом характера местности и масштаба карты умножить на коэффициент, указанный в таблице.

Простейшие способы измерения площадей по карте.

Приближенную оценку размеров площадей производят на глаз по квадратам километровой сетки, имеющейся на карте. Каждому квадрату сетки карт масштабов 1:10000 – 1:50000 на местности соответствует 1 км² , квадрату сетки карт масштаба 1:100000 – 4 км2, квадрату сетки карт масштаба 1:200000 – 16 км2.

Более точно площади измеряют палеткой, представляющей собой лист прозрачного пластика с нанесенной на него сеткой квадратов со стороной 10 мм (в зависимости от масштаба карты и необходимой точности измерений).

Наложив такую палетку на измеряемый объект на карте, подсчитывают по ней сначала число квадратов, полностью укладывающихся внутри контура объекта, а затем число квадратов пересекаемых контуром объекта. Каждый из неполных квадратов принимаем за половину квадрата. В результате перемножения площади одного квадрата на сумму квадратов получают площадь объекта.

По квадратам масштабов 1:25000 и 1:50000 площади небольших участков удобно измерять офицерской линейкой, имеющей специальные вырезы прямоугольной формы. Площади этих прямоугольников {в гектарах ) указаны на линейке для каждого масштаба карты.

 Масштабы топографических карт

Численный масштаб  карты	Название карты	1 см на карте соответствует на местности расстоянию	1 см2на карте соответствует на местности площади
1:5 000 1:10 000  1:25 000 1:50 000  1:1100 000 1:200 000 1:500 000 1:1 000 000	Пятитысячная Десятитысячная Двадцатипятитысячная Пятидесятитысячная Стотысячная Двухсоттысячная Пятисоттысячная, или полумиллионная Миллионная	50 м 100 м 250 м 500 м 1 км 2 км 5 км 10 км	0,25 га 1 га 6,25 га 25 га 1 км2 4 км2 25 км2 100 км2

Ниже приведены численые маштабы карт и соответствующие им именованые масштабы:

1. Масштаб 1:  100 000

1 мм на карте – 100 м (0,1 км) на местности

1 см на карте – 1000 м (1 км) на местности

10 см на карте – 10000 м (10 км) на местности

1. Масштаб 1:10000

1 мм на карте – 10 м (0,01 км) на местности

1 см на карте – 100 м (0,1 км) на местности

10 см на карте – 1000м (1 км) на местности

1. Масштаб 1:5000

1 мм на карте – 5 м (0,005 км) на местности

1 см на карте – 50 м (0,05 км) на местности

10 см на карте – 500 м (0,5 км) на местности

1. Масштаб 1:2000

1 мм на карте – 2 м (0,002 км) на местности

1 см на карте – 20 м (0,02 км) на местности

10 см на карте – 200 м (0,2 км) на местности

1. Масштаб 1:1000

1 мм на карте – 100 см (1 м) на местности

1 см на карте – 1000см (10 м) на местности

10 см на карте – 100 м на местности

1. Масштаб 1:500

1 мм на карте – 50 см (0,5 метра) на местности

1 см на карте – 5 м на местности

10 см на карте – 50 м на местности

1. Масштаб 1:200

1 мм на карте –0,2 м (20 см) на местности

1 см на карте – 2 м (200 см) на местности

10 см на карте – 20 м (0,2 км) на местности

1. Масштаб 1:100

1 мм на карте – 0,1 м (10 см) на местности

1 см на карте – 1 м (100 см) на местности

10 см на карте – 10м (0,01 км) на местности

Пример 1.

Переведите численный масштаб карты в именованный:

а) 1 : 200 000

б) 1 : 10 000 000

в) 1 : 25 000

Решение:

Для более легкого перевода численного масштаба в именованный нужно посчитать, на сколько нулей кончается число в знаменателе.

Например, в масштабе 1 : 500 000 в знаменателе после цифры 5 находится пять нулей.


Если после цифры в знаменателе пятьи более нулей, то, закрыв (пальцем, авторучкой или просто зачеркнув) пять нулей, получим число километров на местности, соответствующее 1 сантиметру на карте.

Пример для масштаба 1 : 500 000

В знаменателе после цифры — пять нулей. Закрыв их, получим для именованного масштаба: в 1 см на карте 5 километров на местности.


Если после цифры в знаменателе менее пяти нулей, то, закрыв два нуля, получим число метров на местности, соответствующее 1 сантиметру на карте.

Если, например, в знаменателе масштаба 1 : 10 000 закроем два нуля, получим:

в 1 см — 100 м.

Ответы:

 а) в 1 см — 2 км;

б) в 1 см — 100 км;

в) в 1 см — 250 м.

Используйте линейку, накладывайте на карты для облегчения измерения расстояний.

Пример  2. 

 Переведите именованный масштаб в численный:

а) в 1 см — 500 м

б) в 1 см — 10 км

в) в 1 см — 250 км 

Решение:

Для более легкого перевода именованного масштаба в численный нужно перевести расстояние на местности, указанное в именованном масштабе, в сантиметры.

Если расстояние на местности выражено в метрах, тогда чтобы получить знаменатель численного масштаба, нужно приписать два нуля, если в километрах, то пять нулей.


Например, для именованного масштаба в 1 см — 100 м расстояние на местности выражено в метрах, поэтому для численного масштаба приписываем два нуля и получаем: 1 : 10 000.

Для масштаба в 1 см — 5 км приписываем к пятерке пять нулей и получаем: 1 : 500 000.

Ответы:

  а) 1 : 50 000;

б) 1 : 1 000 000;

в) 1 : 25 000 000.

Карты в зависимости от масштабов условно подразделяют на следующие типы:

▪   топографические планы — 1:400 – 1:5 000;

▪   крупномасштабные топографические карты — 1:10 000 – 1:100 000;

▪   среднемасштабные топографические карты — от 1:200 000 – 1:1 000 000;

▪   мелкомасштабные топографические карты — менее 1:1 000 000.

Степень
уменьшения линий на плане или карте
относительно горизонтальных проложений
соответствующих линий на местности
называется масштабом. Масштаб карты
можно определить из отношения

,
(15)

где
L
– длина горизонтальной проекции линии
на местности;

l
– длина этой же линии на карте.

В
геодезии масштаб выражают простой
дробью, в числителе которой всегда
единица, а в знаменателе число М,
показывающее, во сколько раз длина
отрезка на карте меньше длины этого же
отрезка на местности. Такой масштаб
называется численным.

На
картах и планах численный масштаб
подписывается ниже чертежа, а под ним
даётся его расшифровка. Например, масштаб
карты 1: 25000. а ниже можно прочитать
«в 1 см плана 250 метров на местности».

В
России установлены следующие основные
масштабы топографических карт и планов:

1: 1000 000 – В 1 см 10 км Топографические

1: 100 000
– в 1 см 1 км

1:
50 000 – в 1 см 500 м

карты

1: 25 000
– в 1 см 250 м

1: 10 000
– в 1 см 100 м

1:
5 000 – в 1 см 50 м
Топографические

1: 2 000
– в 1 см 20 м

1:
1 000 – в 1 см 10 м планы

1: 500
– в 1 см 5 м

Зная
численный масштаб карты, можно определить
длину линии на местности, измерив её
величину на карте. Например, на карте
масштаба 1:25000 измерен отрезок l
= 3,54 см. Тогда длина соответствующего
ему горизонтального отрезка на местности
может быть определена из пропорции:

l см – 250 м,

3,54
см – L
м , (16)

отсюда
L= 3,54 x
250 = 885 м.

Аналогично
решается и обратная задача, когда измерен
горизонтальный отрезок на местности L
и его необходимо нанести на карту, то
пропорция решается в отношении величины
l.

При
массовых измерениях и построениях
пользоваться формулой (16) не всегда
целесообразно, а порой и невозможно
(при работе с планом крупного масштаба).
Действительно, если взять отрезок
длиной, например, 3,54 см, то построить
его на плане крупного масштаба
проблематично. Кроме того, при массовых
измерениях объём таких построений будет
значительным. Поэтому при работе с
картой используется так называемый
линейный масштаб, который практически
решает пропорцию (16)
графическим способом. Для этого на
прямой несколько раз откладывается
отрезок длиной 1 или 2 см, называемым
основанием масштаба (рис.14).

а

в

5
00
0  500 1000 1500
2000 2500

1:25000
основание

в
1 см 250 метров масштаба

2 см

Рис.14.
Схема линейного масштаба

Крайний левый отрезок делят на 10 равных
частей. Соответственно заданному
численному масштабу подписывают каждое
деление линейного масштаба. Например,
для численного масштаба 1:25000 при основании
линейного масштаба 2 см. (см. рис.14) каждое
деление справа будет равно 500 м, а каждое
деление левого отрезка равно соответственно
50 м, на глаз можно определять десятые
доли деления, то есть 5 м .

Пользуются
линейным масштабом следующим образом.
Зафиксировав измерителем отрезок на
карте, правую ножку его устанавливают
на штрих одного из основных делений
так, чтобы другая ножка попала на
основание левее 0 (нулевого деления). На
рис.14 расстояние между концами ножек
циркуля равно 2650 м. В случае несовпадения
конца левой ножки с целым делением доли
его определяют на глаз.

Линейный
масштаб по сравнению с обычной линейкой
с миллиметровыми делениями не повышает
точности определения длин отрезков, но
позволяет отказаться, как отмечалось
выше, от решения пропорций и при
многочисленных измерениях повысить
производительность работ по определению
длин отрезков. Точность определения
длин линий по линейному масштабу
составляет примерно 0,2 деления. Если в
основании линейного масштаба принят
отрезок в 1 см, то графическая точность
(t_л) линейного
масштаба будет равна 0,2 мм. Такая точность
измерений вполне устраивает исполнителей
при работе с картой и не допустима при
работе с планом. Чтобы убедиться в этом,
следует рассмотреть понятие точности
масштабов и производимых измерений.

Точность
численного масштаба (t_ч)
определяется графической точностью
(t_гр) построения
любого плана или карты, величина которого
принимается равным 0,1 мм, точнее этого
отрезки на плане не могут быть изображены.
Отсюда следует, что точностью численного
масштаба называется горизонтальный
отрезок на местности, соответствующий
0,1 мм на карте или плане,

t_ч
= t_гр х М.
(17)

Следовательно,
точности указанных выше численных
масштабов будут равны:

1:
1 000 000 t
= 0,1 мм х 1 000 000
= 100 000 мм = 100 м

1:
100 000 t
= 0,1 мм х 1 00
000 = 10 000 мм = 10 м

1:
50 000 t
= 0,1 мм х 50
000 = 5 000 мм = 5 м

1:
25 000 t
= 0,1 мм х 25
000 = 2500 мм = 2,5 м

1:
10 000 t
= 0,1 мм х
10 000 = 1000 мм = 1 м

1:
5000 t
= 0,1 мм х 5000
= 500 мм = 0,5 м = 50 см

1:
2000 t
= 0,1 мм х 2000
= 200 мм = 0,2 м = 20 см

1:
1000 t
= 0,1 мм х 1000
= 100 мм = 0,1 м = 10 см

1:
500 t
= 0,1 мм х 500
= 50 мм = 0,05 м = 5 см

Отсюда
можно рассчитать точность измерений
(построений) длин линий на той или иной
карте или плане с использованием
линейного масштаба. Как отмечалось
выше, графическая точность линейного
масштаба равна примерно 0,2 наименьшего
деления его. Следовательно, для линейного
масштаба с основанием его 1 см графическая
точность определения длины отрезка
будет равна 0,2 мм, что в 2 раза грубее
точности численных масштабов. Если
учесть, что в соответствии с теорией
вероятности предельная ошибка измерения
длин линий может быть в 2-3 раза больше
случайной, то точность измерений
(построения) длин линий резко падает.
Отсюда видно, что глазомерная оценка
части делений линейного масштаба снижает
точность измерительных работ на планах
и картах, особенно при использовании
линейных масштабов, в основании которых
положен отрезок 2 см и более. Чтобы
избежать оценки делений на глаз и
повысить точность определения длин
линий на карте (плане), применяют
поперечный масштаб, называемый в обиходе
масштабной линейкой. Он строится
на основе линейного масштаба.

Для
этого на прямой откладывают несколько
раз отрезок, равный 1 или 2 см, как это
было сделано при построении линейного
масштаба. Из полученных точек
восстанавливают перпендикуляры к этой
прямой (рис.15). Крайнее левое основание
делят на десять равных частей, а на
перпендикулярах откладывают десять
таких же делений. Через полученные на
перпендикулярах точки проводят
параллельные линии. Левое крайнее
деление на верхней линии также разбивается
на десять равных частей, которые
соединяются прямыми с нижними следующим
образом: нулевое деление на нижнем
основании соединяется с первым на
верхнем, первое на нижнем основании со
вторым на верхнем. Отрезок “ав”
называется наименьшим делением
поперечного масштаба или его точностью
(t_п),
он будет равен 1:100 длины основания
масштаба. Такой поперечный масштаб
называется нормальным
или
сотенным.
Точность поперечного масштаба может
быть вычислена по формуле

t_п
=

,
(18)

где
АВ – величина основания, в см, m
– число делений в крайнем левом основании,
n
– число горизонтальных линий, считая
первую линию за 0.

а
в

100
70
50
30
10
0 100 200

1:10
000

в
1 см – 100 метров

Рис.15.
Схема поперечного масштаба

Если
основание масштаба равно 1 см и оно
поделено на m=10,
а число горизонтальных линий n=10,
то точность такого поперечного масштаба
будет равно t_п
= 1 см/10 х 10 = 0,1 мм, его точность соответствует
точности численного масштаба. Если в
основании поперечного масштаба будет
2 см и более, то точность определения
длины отрезков плана или карты
соответственно снизится. Кроме того,
все рассуждения о точности поперечного
масштаба относятся к масштабным линейкам,
изготовленным в заводских условиях с
гравировкой линий на металле. Если
поперечный масштаб построен графическим
путём, то им пользоваться нельзя, так
как точность его будет сведена практически
к точности линейного масштаба.

Если
принять на схеме длину основания 1 см,
то поперечный масштаб будет подписан
так, как это показано на рис.15. Наименьший
отрезок “ав” (на второй горизонтальной
линии) будет равен 1 м. Процесс определения
длины отрезка, измеренного на карте
масштаба 1:10 000, заключается в следующем.

Зафиксировав
измерителем отрезок на карте или плане,
правую ножку его устанавливают на штрих
одного из основных делений так, чтобы
другая ножка попала на основание левее
нулевого деления (как поступали в случае
с линейным масштабом). Если левая ножка
циркуля не совпала с целым делением
(см. рис.15, вертикальная линия), то циркуль
перемещается поступательно вверх до
совмещения левой ножки с наклонной
линией основания. Длина линии равна
сумме отрезков от нулевого деления до
правой ножки циркуля плюс число полных
малых делений левого основания и плюс
число наименьших делений «ав»,
соответствующее номеру горизонтальной
линии, на которой расположены иглы
измерителя. На рис.15 расстояние между
ножками циркуля в указанном масштабе
равно 200 м плюс 60 м и плюс 4 м, то есть
264 м.

Как
отмечалось выше, основание поперечного
масштаба равно 1 или 2 см. Однако иногда
целесообразно брать иной размер
основания. Так 1 см рационально брать
для численных масштабов 1:1000 и 1:10 000,
2 см для масштабов 1: 500, 1:5000 и 1:50 000, 4 см
– 1:25 000, 5 см – 1:2000. Тогда основание
масштаба будет кратно 10 м, 100 м и 1000 м.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Масшта́б^[1] (нем. Maßstab, букв. «мерная палка»: Maß «мера», Stab «палка») — соотношение, которое показывает, во сколько раз каждая линия, нанесённая на карту или чертёж, меньше или больше её действительных размеров. Есть четыре вида масштаба: численный, именованный, линейный, масштаб по осям координат.

Масштаб в геодезии, картографии и проектировании[править | править код]

Масштаб (геодезия и картография) — отношение длины отрезка на карте к действительной длине этого отрезка на местности^[2]

Типы масштабов[править | править код]

Масштабы на картах и планах могут быть представлены численно или графически.

1. Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5000 показывает, что 1 см на плане соответствует 5000 см (50 м) на местности. Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1000 крупнее, чем масштаб 1:25 000.
2. Именованный масштаб показывает какое расстояние на местности соответствует 1 см на плане. Записывается, например: «В 1 сантиметре 100 километров», или «1 см = 100 км».
3. Графические масштабы подразделяются на линейные и поперечные. 3.1. Линейный масштаб — графический масштаб в виде масштабной линейки, разделённой на равные части 3.2. Масштаб по осям координат — графический масштаб в виде масштабных шкал для каждой из осей координат, которые имеют различный коэффициент масштабирования. 3.3.Поперечный масштаб — графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла. Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД = 0,2 мм, а точность 0,1
4. Иррациональный масштаб — масштаб представленный в виде иррациональной дроби. Нестандартный вид масштаба. Определителем является простое число, исключая 2 и 5.
5. Десятичный или кратный масштаб — масштаб с определитем кратным 5 и 2. Все стандартные масштабы являются такими.

Точность масштаба[править | править код]

Точность масштаба — отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооружённым глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1000 см (10 м), 0,1 мм — 100 см (1 м).

Определитель масштаба[править | править код]

Определитель масштаба — число определяющие (показывающие) во сколько раз увеличен или уменьшен натуральный размер.

Определитель масштаба может быть положительным (со знаком «+») или отрицательным (со знаком «-»)

Масштабный Ряд[править | править код]

Масштабы изображений на чертежах должны выбираться из следующего ряда:^[1]

Масштабы уменьшения (правильный масштаб)	1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; (1:2;1:20); (1:10;1:15)
Натуральная величина	1:1
Масштабы увеличения (цельный масштаб)	2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1; 1000:1; 5000:1; (2:1;5:1); (5:1;10:1); (10:1; 25:1)

При проектировании на чертежах (топографических планах) 1:400; 1:800 (1:200; 1:500; 1:1000; 1:2000; 1:5000)^[1][3]

При проектировании на картах и планах – генеральных планов, крупных объектов, допускается применять масштабы 1:10 000; 1:25 000 (искл. 1:20 000 – для планов и карт – в номенклатуре не числится) и 1:50 000; 1:100 000 и т. д. – для карт^[3]

При необходимости допускается применять масштабы увеличения (100n):1, где n — целое число.

Крупный, средний и мелкий масштабы[править | править код]

Одной из характеристик карт является крупный, средний и мелкий масштабы. Мелкий масштаб чаще всего используется в картах мира или картах таких больших регионов, как континентов, крупных стран. Другими словами, они показывают большие территории земли на небольшом пространстве. Они называются мелкомасштабными из-за того, что показывают местность мелко, не очень подробно.

Крупномасштабные карты построены по иному принципу: они показывают небольшую территорию наиболее детально. Например, это карты городов, районов, посёлков. Они так называются из-за того, что показывают местность подробно, крупно.

Разница между картами может быть очень серьёзной. Например, масштаб карты района может составлять 1:10 000, в то же время карта мира может быть выполнена в масштабе 1:200 000 000.

Не существует единого стандарта масштаба карт, однако в следующей таблице представлены типичные их виды:

Вид карты	Масштаб	Примеры
Крупномасштабная	1:0 — 1:600 000	1:0,00001 — строение вируса 1:100 — план помещения 1:5000 — карта района или посёлка
Среднемасштабная	1:600 000 – 1:2 000 000	Карта региона, небольшой страны
Мелкомасштабная	1:2 000 000 – 1:∞	1:100 000 000 — карта мира 1:10²¹ — карта галактики

В русском языке слово «крупномасштабный» иногда используется в значении «обширный». Однако в картографии термин «крупный масштаб» используется, когда подразумеваются менее обширные карты — то есть те, которые показывают меньшую территорию. Это следствие языковой неточности.

Масштаб с точки зрения математики[править | править код]

С точки зрения математики определители масштаба является дробью.

Так же как дроби бывают правильные или цельные, так и масштабы бывают

— правильные 1:Х

— неправильные X:1

Правильные масштабы также называют относительными: дробь 1:Х есть отношение 1 к Х.

А неправильные — цельными или абсолютными, то есть Х:1 есть |x|.

Сам масштаб является 1-й степенью числа.

1:Х — есть −1 степень.

Х:1 — есть +1 степень.

Масштаб в фотографии[править | править код]

При фотосъёмке под масштабом понимают отношение линейного размера изображения, полученного на фотоплёнке или светочувствительной матрице, к линейному размеру проекции соответствующей части сцены на плоскость, перпендикулярную к направлению на камеру.

Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.

Масштаб имеет важное значение при расчёте глубины резко изображаемого пространства. Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съёмке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).

Под макрофотографией традиционно понимают съёмку в масштабе 1:1 или крупнее. Однако с широким распространением компактных цифровых фотоаппаратов этим термином стали также называть съёмку расположенных близко к объективу (как правило, ближе 50 см) мелких объектов. Связано это с необходимым изменением режима работы системы автофокуса в таких условиях, однако с точки зрения классического определения макросъёмки такое толкование является неверным.

Масштаб в моделизме[править | править код]

Для каждого вида масштабного (стендового) моделизма определены масштабные ряды, состоящие из нескольких масштабов разной степени уменьшения, причём для разных видов моделизма
(авиамоделизм, судомоделизм, железнодорожный, автомобильный, военной техники) определены свои, исторически сложившиеся, масштабные ряды, которые обычно не пересекаются.

Масштаб в моделизме исчисляется по формуле:

L / М = Х

Где:
L — параметр оригинала,
М — требуемый масштаб,
Х — искомое значение

Например:

При масштабе 1/72, и параметре оригинала 7500 мм, решение будет выглядеть;

7500 мм / 72 = 104,1 мм.

Полученное значение 104,1 мм, есть искомое значение при масштабе 1/72.

При масштабе 1/16, и параметре оригинала 7500 мм, решение будет выглядеть;

7500 мм / 16 = 468,75 мм.

Масштаб времени[править | править код]

В программировании[править | править код]

В операционных системах с разделением времени чрезвычайно важную роль играет предоставление отдельно взятым задачам так называемого «режима реального времени», при котором обработка внешних событий обеспечивается без дополнительных задержек и пропусков. Для этого употребляется также термин «реальный масштаб времени», однако это терминологическая условность, не имеющая к исходному значению слова «масштаб» никакого отношения.

В кинотехнике[править | править код]

Масштаб времени — количественная мера замедления или ускорения движения, равная отношению проекционной частоты кадров к съёмочной. Так, если проекционная частота кадров равна 24 кадра в секунду, а киносъёмка производилась на 72 кадра в секунду, масштаб времени равен 1:3. Масштаб времени 2:1 означает ускоренное вдвое по сравнению с обычным протекание процесса на экране.

В математике[править | править код]

Масштаб — отношение двух линейных размеров.

Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта. В математике масштаб определяется как отношение расстояния на карте к соответствующему расстоянию на реальной местности.

Масштаб 1:100000 означает, что 1 см на карте соответствует 100000 см = 1000 м = 1 км на местности.

Масштабы изображений на чертежах должны выбираться из следующего ряда (масштабы ГОСТ 2.302-68):

• Масштабы уменьшения 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000
• Натуральная величина 1:1
• Масштабы увеличения 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1

Примечания[править | править код]

Определение расстояний и превышений по бумажной карте.
Определение расстояния.
Для определения горизонтального расстояния по обычной карте, следует измерить длину линии и пересчитать пропорционально масштабу. Прямую линию можно измерить линейкой или циркулем-измерителем, извилистую (например, при измерении длины дороги или реки) – курвиметром (прибором, который можно катать по карте, а “колесико” отчитывает сантиметры).
Пересчет измеренной длины ведется пропорционально масштабу:
например, измеренное расстояние 2,5 см, а масштаб карты 1:50000 (т.е. в 1 см – 500 метров), тогда
1 см = 500 м
2,5 см = x м
x = (2,5 см * 500 м) / 1 см = 1250 м (по свойству пропорции).

При определении расстояний по мелкомасштабной карте также можно опираться на следующие сведения:
длина дуги 1° экватора

≈ 111,3 км (длина экватора 40 075 км/ 360°);
длина дуги 1° параллели 15° ≈ 108 км, 30° ≈ 96 км, 45° ≈ 79 км, 60° ≈ 56 км, 75° ≈ 29 км
(длина дуги 1° экватора (111,3 км) * cos (угла широты параллели));
длина дуги 1° меридиана ≈ 111,1 км ≈ 111 км (длина меридиана 20 004 км/ 180°).

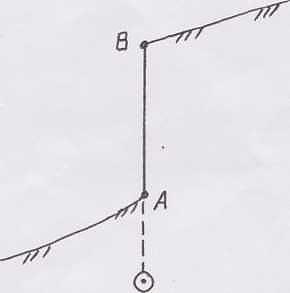
Определение превышений.
Превышения на топографической карте показывают горизонтали. Горизонтали – это изолинии, которые соединяют одинаковые уровни высот. Под масштабом указано через сколько метров проведены сплошные горизонтали (например, через каждые 10 метров, т.е. на уровнях 10м, 20м, 30 м и т.д.), пунктиром могут быть проведены полугоризонтали между основными (где необходимо подчеркнуть характер рельефа), каждая пятая горизонталь для улучшения восприятия утолщена, пики высот подписаны дополнительно. Подписи горизонталей принято размещать верхом текста в сторону повышения высот, а в сторону понижения склона размещаются черточки, прикреплённые перпендикулярно горизонталям – бергштрихи, указывающие куда со склона потечет вода.

На примере пунктирной линии превышение между ее концами примерно 73 метра. Правый край чуть выше 210 м (≈212 м), левый чуть ниже 140 м (≈139 м).
При построении профиля следует учесть, что чем ближе (чаще) расположены горизонтали друг к другу, тем круче спуск.
На мелкомасштабных физических картах вместо горизонталей используют цветовую высотную шкалу – зелеными тонами низины, коричневыми – горы.

Определение длины линии в трехмерном пространстве.
Если расстояние по горизонтали между точками 400 метров, а разница высот между этими точками 300 метров, то длина линии в трехмерном пространстве между точками будет составлять 500 метров (подсчёт аналогичен вычислению гипотенузы по теореме Пифагора).

Вести пересчёт имеет смысл только при построении маршрута в горном рельефе с резкими перепадами высот. При достаточно плоском равнинном рельефе или при измерениях по мелкомасштабным картам длина линии в трехмерном пространстве практически не будет отличаться от горизонтального расстояния, учитывать перепад высот в таких случаях не имеет смысла.
На заданиях ОГЭ/ЕГЭ и в школьных задачах под определением расстояния по прямой подразумевается расстояние по горизонтали, учитывать, что точки могут находиться на разных высотах и пересчитывать длину линии с учетом этого не нужно!Определение расстояний и превышений по электронной карте.
Большинство электронных карт имеют инструменты для измерения расстояний по прямой или по дорогам специальным функционалом, например, построением маршрута. При построении маршрута большинство электронных карт (например, Яндекс-карты) учитывают все изгибы дороги, но не пересчитывают расстояния с учетом перепада высот (к примеру, перейти через ущелье по подвесному мосту, или по кратчайшей прямой траектории, но без моста, спустившись вниз и затем поднявшись на другой берег – это разные расстояния). Некоторые приложения навигации (например Maps.me при переходе в режим пешеходной или велонавигации) просчитывают расстояния с учётом перепада высот и отображают превышения.

Понятие масштаба и его виды

Масштаб карты – это отношение длины отрезка на карте к его действительной длине на местности.

Масштаб (от немецкого Stab – палка) – это отношение длины отрезка на карте, плане, аэро- или космическом снимке к его действительной длине на местности.

Рассмотрим виды масштабов.

Численный масштаб

Это масштаб, выраженный в виде дроби, где числитель – единица, а знаменатель – число, показывающее во сколько раз уменьшено изображение.

Численный масштаб – масштаб, выраженный дробью, в которой:

• числитель равен единице,
• знаменатель равен числу, показывающему во сколько раз уменьшены линейные размеры на карте.

Именованный (словесный) масштаб

Это вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке.

Именованный масштаб выражается именованными числами, обозначающими длины взаимно соответствующих отрезков на карте и в натуре.

Например, в 1 сантиметре 5 километров (в 1 см 5 км).

Линейный масштаб

Это вспомогательная мерная линейка, наносимая на карты для облегчения измерения расстояний.

Масштаб плана и масштаб карты

Масштаб плана одинаков во всех его точках.

Масштаб карты в каждой точке имеет свое частное значение, зависящее от широты и долготы данной точки. Поэтому его строгой числовой характеристикой является численный масштаб – отношение длины бесконечно малого отрезка Д на карте к длине соответствующего бесконечно малого отрезка на поверхности эллипсоида земного шара.

Однако при практических измерениях на карте используют её главный масштаб.

Формы выражения масштаба

Обозначение масштаба на картах и планах имеет три формы – численный, именованный и линейный масштабы.

Численный масштаб выражают дробью, в которой:

• числитель – единица,
• знаменатель М – число, показывающее, во сколько раз уменьшены размеры на карте или плане (1:М)

В России для топографических карт приняты стандартные численные масштабы

• 1:1 000 000
• 1:500 000
• 1:300 000
• 1:200 000
• 1:100 000
• 1:50 000
• 1:25 000
• 1:10 000
• для специальных целей создают также топографические карты в масштабах 1:5 000 и 1:2 000

Основные масштабы топографических планов в России

• 1:5000
• 1:2000
• 1:1000
• 1:500

В землеустроительной практике планы землепользований чаще всего составляют в масштабах 1:10 000 и 1:25 000, а иногда – 1:50 000.

При сравнении различных численных масштабов более мелким является тот, у которого больше знаменатель М, и, наоборот, чем меньше знаменатель М, тем крупнее масштаб плана или карты.

Так, масштаб 1:10000 крупнее, чем масштаб 1:100000, а масштаб 1:50000 мельче масштаба 1:10000.

Примечание

Применяемые в топографических картах масштабы установлены Приказом Министерства экономического развития РФ «Об утверждении требований к государственным топографическим картам и государственным топографическим планам, включая требования к составу сведений, отображаемых на них, к условным обозначениям указанных сведений, требования к точности государственных топографических карт и государственных топографических планов, к формату их представления в электронной форме, требований к содержанию топографических карт, в том числе рельефных карт» (№ 271 от 6 июня 2017 года с изменениями на 11 декабря 2017 года).

Именованный масштаб

Так как длины линий на местности принято измерять в метрах, а на картах и планах в сантиметрах, то масштабы удобно выражать в словесной форме, например:

В одном сантиметре 50 м. Это соответствует численному масштабу 1:5000. Поскольку 1 метр равен 100 сантиметрам, то число метров местности, содержащееся в 1 см карты или плана, легко определяют путём деления знаменателя численного масштаба на 100.

Линейный масштаб

Представляет собой график в виде отрезка прямой, разделенного на равные части с подписанными значениями соразмерных им длин линий местности. Линейный масштаб позволяет без вычислений измерять или строить расстояния на картах и планах.

Точность масштаба

Предельная возможность измерения и построения отрезков на картах и планах ограничена величиной 0.01 см. Соответствующее ей число метров местности в масштабе карты или плана представляет собой предельную графическую точность данного масштаба.

Поскольку точность масштаба выражает длину горизонтального проложения линии местности в метрах, то для ее определения следует знаменатель численного масштаба разделить на 10 000 (1 м содержит 10 000 отрезков по 0.01 см). Так, для карты масштаба 1:25 000 точность масштаба равна 2.5 м; для карты 1:100 000 – 10 м и т. п.

Масштабы топографических карт

численный масштаб карты	название карты	1 см на карте соответствует на местности расстоянию	1 см2 на карте соответствует на местности площади
1:5 000	пятитысячная	50 м	0.25 га
1:10 000	десятитысячная	100 м	1 га
1:25 000	двадцатипятитысячная	250 м	6.25 га
1:50 000	пятидесятитысячная	500 м	25 га
1:1100 000	стотысячная	1 км	1 км2
1:200 000	двухсоттысячная	2 км	4 км2
1:500 000	пятисоттысячная, или полумиллионная	5 км	25 км2
1:1000000	мииллионная	10 км	100 км2

Ниже приведены численные маштабы карт и соответствующие им именованые масштабы:

Масштаб 1:100 000

• 1 мм на карте – 100 м (0.1 км) на местности
• 1 см на карте – 1000 м (1 км) на местности
• 10 см на карте – 10000 м (10 км) на местности

Масштаб 1:10000

• 1 мм на карте – 10 м (0.01 км) на местности
• 1 см на карте – 100 м (0.1 км) на местности
• 10 см на карте – 1000 м (1 км) на местности

Масштаб 1:5000

• 1 мм на карте – 5 м (0.005 км) на местности
• 1 см на карте – 50 м (0.05 км) на местности
• 10 см на карте – 500 м (0.5 км) на местности

Масштаб 1:2000

• 1 мм на карте – 2 м (0.002 км) на местности
• 1 см на карте – 20 м (0.02 км) на местности
• 10 см на карте – 200 м (0.2 км) на местности

Масштаб 1:1000

• 1 мм на карте – 100 см (1 м) на местности
• 1 см на карте – 1000 см (10 м) на местности
• 10 см на карте – 100 м на местности

Масштаб 1:500

• 1 мм на карте – 50 см (0.5 м) на местности
• 1 см на карте – 5 м на местности
• 10 см на карте – 50 м на местности

Масштаб 1:200

• 1 мм на карте – 0,2 м (20 см) на местности
• 1 см на карте – 2 м (200 см) на местности
• 10 см на карте – 20 м (0.2 км) на местности

Масштаб 1:100

• 1 мм на карте – 0,1 м (10 см) на местности
• 1 см на карте – 1 м (100 см) на местности
• 10 см на карте – 10 м (0.01 км) на местности

Пример 1

Переведите численный масштаб карты в именованный:

1. 1:200 000
2. 1:10 000 000
3. 1:25 000

Решение:

Для более легкого перевода численного масштаба в именованный нужно посчитать, на сколько нулей кончается число в знаменателе.

Например, в масштабе 1:500 000 в знаменателе после цифры 5 находится пять нулей.


Если после цифры в знаменателе пятьи более нулей, то, закрыв (пальцем, авторучкой или просто зачеркнув) пять нулей, получим число километров на местности, соответствующее 1 сантиметру на карте.

Пример для масштаба 1:500 000

В знаменателе после цифры – пять нулей. Закрыв их, получим для именованного масштаба: в 1 см на карте 5 километров на местности.


Если после цифры в знаменателе менее пяти нулей, то, закрыв два нуля, получим число метров на местности, соответствующее 1 сантиметру на карте.

Если, например, в знаменателе масштаба 1:10 000 закроем два нуля, получим:

в 1 см – 100 м.

Ответы:

1. в 1 см – 2 км
2. в 1 см – 100 км
3. в 1 см – 250 м

Используйте линейку, накладывайте на карты для облегчения измерения расстояний.

Пример 2

Переведите именованный масштаб в численный:

1. в 1 см – 500 м
2. в 1 см – 10 км
3. в 1 см – 250 км

Решение:

Для более легкого перевода именованного масштаба в численный нужно перевести расстояние на местности, указанное в именованном масштабе, в сантиметры.

Если расстояние на местности выражено в метрах, тогда чтобы получить знаменатель численного масштаба, нужно приписать два нуля, если в километрах, то пять нулей.


Например, для именованного масштаба в 1 см – 100 м расстояние на местности выражено в метрах, поэтому для численного масштаба приписываем два нуля и получаем: 1:10 000.

Для масштаба в 1 см – 5 км приписываем к пятерке пять нулей и получаем: 1:500 000.

Ответы:

1. 1:50 000
2. 1:1 000 000
3. 1:25 000 000

Типы карт в зависимости от масштабов

Карты в зависимости от масштабов условно подразделяют на следующие типы:

• топографические планы 1:400 – 1:5 000
• крупномасштабные топографические карты 1:10 000 – 1:100 000
• среднемасштабные топографические карты от 1:200 000 – 1:1 000 000
• мелкомасштабные топографические карты менее 1:1 000 000

Топографическая карта

Топографическими называются такие карты, содержание которых позволяет решать по ним разнообразные технические задачи.

Карты либо являются результатом непосредственной топографической cъемки местности, либо составляются по имеющимся картографическим материалам.

Местность на карте изображается в определенном масштабе.

Чем меньше знаменатель численного масштаба, тем крупнее масштаб. Планы составляют в крупных масштабах, а карты – в мелких.

В картах учитывается «шарообразность» земли, а в планах – нет. Из-за этого планы не составляются для территорий площадью свыше 400 км² (то есть участков земли примерно 20 км х 20 км).

• Стандартные масштабы топографических карт

В нашей стране приняты следующие масштабы топографических карт:

1. 1:1 000 000
2. 1:500 000
3. 1:200 000
4. 1:100 000
5. 1:50 000
6. 1:25 000
7. 1:10 000

Этот ряд масштабов называется стандартным. Раньше этот ряд включал масштабы 1:300 000, 1:5000 и 1:2000.

• Крупномасштабные топографические карты

Карты масштабов:

1. 1:10 000 (1см =100 м)
2. 1:25 000 (1см = 100 м)
3. 1:50 000 (1см = 500 м)
4. 1:100 000 (1см =1000 м)

называются крупномасштабными.

• Другие масштабы и карты

Топографические карты территории России до масштаба 1:50 000 включительно являются секретными, топографические карты масштаба 1:100 000 – ДСП (для служебного пользования), а мельче – не секретными.

В настоящее время существует методика создания топографических карт и планов любых масштабов, не имеющих грифа секретности и предназначенных для открытого пользования.

Сказка про карту в масштабе 1:1

Жил-был Капризный Король. Однажды он объехал своё королевство и увидел, как велика и прекрасна его земля. Он увидел извилистые реки, огромные озёра, высокие горы и чудесные города. Он возгордился своими владениями и захотел, чтобы весь мир узнал о них.

И вот, Капризный Король приказал картографам создать карту королевства. Картографы трудились целый год и, наконец, преподнесли Королю замечательную карту, на которой были обозначены все горные гряды, крупные города и большие озёра и реки.

Однако, Капризный Король остался недоволен. Он хотел видеть на карте не только очертания горных цепей, но и изображение каждой горной вершины. Не только крупные города, но и мелкие, и селения. Он хотел видеть небольшие речки, впадающие в реки.

Картографы вновь принялись за работу, трудились много лет и нарисовали другую карту, размером в два раза больше предыдущей. Но теперь Король пожелал, чтобы на карте были видны перевалы между горными вершинами, маленькие озерца в лесах, ручейки, крестьянские домики на окраине селений. Картографы рисовали все новые и новые карты.

Капризный Король умер, так и не дождавшись окончания работы. Наследники один за другим вступали на трон и умирали в свою очередь, а карта все составлялась и составлялась. Каждый король нанимал новых картографов для составления карты королевства, но всякий раз оставался недовольным плодами труда, находя карту недостаточно подробной.

Наконец картографы нарисовали Невероятную карту! Она изображала всё королевство в мельчайших подробностях – и была точно такого же размера, как само королевство. Теперь уже никто не мог найти различия между картой и королевством.

Где же собирались хранить Капризные Короли свою замечательную карту? Ларца для такой карты не хватит. Понадобится огромное помещение вроде ангара, и в нем карта будет лежать во много слоев. Только нужна ли такая карта? Ведь карта в натуральную величину может быть с успехом заменена самой местностью ))))

Полезно ознакомиться и с этим

• Ознакомиться с используемыми в России единицами измерения площадей земельных участков можно здесь.
• Для тех, кого интересует возможность увеличения площади земельных участков для ИЖС, ЛПХ, садоводства, огродничества, находящихся в собственности, полезно ознакомиться с порядком оформления прирезок.
  
• С 1 января 2018 года в кадастровом паспорте должны быть зафиксированы точные границы участка, поскольку купить, продать, заложить или подарить землю без точного описания границ будет попросту невозможно. Так регламентировано поправками к Земельному кодексу. А тотальная ревизия границ по инициативе муниципалитетов началась с 1 июня 2015 г.

Ознакомиться с основными положениями закона можно здесь.

• В отношении регистрации домов, бань, гаражей и других построек на земельных участках, находящихся в собственности граждан, улучшит ситуацию новая дачная амнистия.