Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
Масштаб осей графика
—
Аналитические задачи в бизнесе
Представим такую ситуацию: инвестору нужно оценить, акции какой компании наиболее стабильны в цене за последний месяц:
По этим графикам котировок напрашивается следующий вывод: цена акций компании А стабильнее, ведь ее цена меньше изменяется, чем цена компании Б.
Но на самом деле, данные на этих графиках одни и те же. Разница в масштабе вертикальной оси — обратите внимание, что она скрыта. Теперь посмотрим, как выглядят эти графики с вертикальной осью:
Чтобы не делать таких неверных выводов, в этом уроке мы изучим масштаб осей графика. Мы подробнее рассмотрим, как масштаб влияет на интерпретацию графика и от чего зависит выбор правильного масштаба. В итоге мы настроим масштаб графика продаж в Google Sheets. Понимание этой темы поможет не дать себя обмануть при решении аналитических задач.
Что такое масштаб осей графика
График помогает сделать выводы относительно показателей по горизонтальной и вертикальной осям. При этом важен масштаб оси — это длина одного деления оси.
Например, если по горизонтальной оси время, то одним делением может быть день, месяц или год. А по вертикальной оси может быть любой интервал, особенно если это вещественные или целые числа. В зависимости от разброса данных можно задавать любой интервал, например, одно деление — 25 единиц.
Рассмотрим подробнее случай с акциями компании. Также посмотрим, как изменение масштаба влияет на интерпретацию графика. Для начала посмотрим, как выглядят исходные данные для построения графика в табличном виде:
Теперь посмотрим на первый способ построения графика:
На этом графике:
- Минимальное значение вертикальной оси — 0 единиц
- Максимальное значение вертикальной оси — 25 единиц
- Деление вертикальной оси — 5 единиц
При таком масштабе изменения от 0 до 5 единиц выглядят несущественными.
Выбор такого масштаба может быть оправдан, если с точки зрения бизнеса разница в десятичной и сотой частях числа не волнует инвестора. Например, это цена в рублях, а изменения в копейках не будут стоить больших финансовых потерь. Но если это значения цен в тысячах, тогда такой график может оказаться неподходящим для анализа.
Рассмотрим второй вариант построения графика:
Здесь масштаб другой:
- Минимальное значение вертикальной оси — 18 единиц
- Максимальное значение вертикальной оси — 21 единица
- Деление вертикальной оси — 1 единица
На таком графике четче видны изменения между соседними точками. Если взглянуть на наши табличные данные, можно увидеть, что значения цен варьировались от 18 до 20. При таком диапазоне значений мы можем рассмотреть детальнее оси изменения графика.
Если бы наш инвестор рассматривал котировки не акций, а криптовалюты, то такой график мог быть полезнее. Цена на биткоин уже достигает 20 тысяч долларов, поэтому изменения на 100-500 долларов могли быть существенными для инвестиционного анализа.
Так на примере изменения масштаба вертикальной оси мы увидели, как может меняться интерпретация графика. Теперь мы научимся правильно выбирать масштаб.
Как правильно настроить масштаб
Ключевыми параметрами в настройке оси являются минимальное и максимальное значение оси. Программы автоматически подбирают такие значения в зависимости от имеющихся данных. Однако такие настройки всегда следует проверять. Правильный масштаб зависит от бизнес-логики. Другими словами, масштаб выбирается исходя из того, что именно мы хотим показать.
Представим, у нас есть данные по объемам продаж товаров категории «Еда и напитки» одной фирмы за последние две недели.
Вот так программа автоматически подобрала масштаб при создании графика:
С одной стороны, график построен корректно. Но нельзя сказать это с уверенностью, ведь мы не знаем, зачем нужен этот график.
Допустим, руководитель этой компании хочет понять, насколько динамика продаж этой категории сопоставляется с похожими категориями. Нам известно, что объемы продаж по похожим категориям за тот же период достигали 2000 единиц. Тогда будет справедливо изменить максимальное значение вертикальной оси на 2000:
При таком масштабе график сместился вниз, от чего стала видна реальная картина — продажи еды и напитков низкие по сравнению с похожими категориями.
Также видно, что изменения графика стали менее заметными, так как увеличилась длина деления. При максимальном значении в 1000 длина деления была 250, а сейчас — 500. Однако в этом примере было важно отобразить общую динамику в сравнении с другими категориями, поэтому детализацией изменений можно было пренебречь.
Следует помнить, что и минимальное значение не всегда равно нулю. Например, у компании каждый день продается не менее 200 единиц товаров данной категории, то рассматривать значения ниже 200 нет смысла — такие значения не встречаются на практике.
Получается, что для правильной настройки масштаба следует знать минимальную и максимальную величины показателя, которые зависят от логики поставленной аналитической задачи.
Как настроить масштаб осей графика в Google Sheets
В качестве примера изменим масштаб вертикальной оси графика продаж «Еда и напитки». Минимальное значение изменим на 200, а максимальное — на 2000. Посмотрим, как это сделать в Google Sheets.
-
Для начала откроем файл с графиком в Google Sheets. Вспомнить, как это делается, поможет эта заметка из официальной справки Google
-
Проверяем, что график отобразился корректно. Нажимаем на кнопку в виде трех точек в правом верхнем углу. В появившемся окне выбираем «Изменить диаграмму»:
-
Далее в появившемся редакторе диаграмм выбираем «Дополнительные» настройки, чтобы настроить масштаб:
-
Находим интересующий нас раздел «Вертикальная ось» и нажимаем на него:
-
Задаем минимальное и максимальное значение оси:
На последнем скриншоте видно, что программа автоматически подобрала длину одного деления (200 единиц) и отобразила новый график.
Рассмотрим еще один способ, который в конкретном примере может быть удобнее.
-
Кликаем правой кнопкой мыши по графику, во всплывающем окне нажимаем на «Ось», а затем — на «Левая вертикальная ось»:
-
Должен отобразиться редактор диаграмм, в котором мы можем поменять нужные параметры:
Выводы
В этом уроке мы изучили, что такое масштаб осей графика. Теперь вы знаете, как настроить масштаб так, чтобы он не привел вас к неверным выводам.
Напомним основные выводы урока:
- С изменением масштаба может измениться интерпретация графика. При одном масштабе изменения могут казаться значительными, при другом — совсем незаметными
Преобразования координат в двумерной системе.
В двумерной системе координат можно выделить следующие простейшие (базовые) преобразования координат:
– перенос точки на заданный вектор;
– поворот точки на заданный угол относительно начала координат;
– перенос системы координат на заданный вектор;
– поворот системы координат на заданный угол;
– зеркальное отображение точки относительно координатной оси X;
– зеркальное отображение точки относительно оси Y;
– смена направление координатной оси;
Рекомендуемые материалы
– изменение масштаба координат по оси X;
– изменение масштаба координат по оси Y.
Рассмотрим эти базовые преобразования.
Перенос точки на заданный вектор.
Перенос точки А на заданный вектор U иллюстрируется ниже приведенным рисунком (Рис. 5.1‑2). Решение задачи рассматриваемого преобразования сводится к определению на основании старых координат новых координат заданной точки после ее перенесения на заданный вектор
U.
 |
Рис. 5.1‑2
Из приведенного рисунка видно, что новые координаты точки после рассматриваемого преобразования рассчитываются следующим образом:
xa’= xa + ux;
ya’= ya + uy. (5.1-1)
Перенос системы координат на заданный вектор
Перенос системы координат на заданный вектор U иллюстрируется следующим рисунком (Рис. 1.1‑3).
 |
Рис. 5.1‑3
Координатные оси после перенесения системы обозначены как X’,Y’.
Из рисунка видно, что координаты точки А в новой системе координат X’0’Y’ будут определяться как:
xa’ = xa – ux;
ya’ = ya – uy. (5.1-2)
Сравнив выражение (5.1-1) и (5.1-2), можно сделать вывод, что преобразование типа «перенос системы координат на вектор U » эквивалентно обратному преобразованию типа «перенос точки на вектор U » (т.е. переносу точки на вектор –U).
Зеркальное отображение положения точки относительно координатной оси.
Зеркальное отображение точки А относительно координатных осей X и Y приведено на Рис. 1.1‑4.
Новые координаты при этих преобразовании определяются следующим образом.

Рис. 5.1‑4
При зеркальном отображении относительно оси Y (Рис. 1.1‑4a) имеем:
xa’ =- xa .
При зеркальном отображении относительно оси X (Рис. 1.1‑4 b) имеем:
ya’ =- ya.
Смена направление осей координат иллюстртруется ниже приведенным рисунком (Рис. 5.1‑5).
 |
Рис. 5.1‑5
Новое положение координатных осей X, Y на рисунке обозначено как X’, Y’.
Смена направленности оси X иллюстрируется на Рис. 5.1‑5a).
Как видно из рисунка, данное преобразование предполагает нахождение новых координат точки следующим образом.
xa’ =- xa .
При смене направленности оси Y (Рис. 5.1‑5b) имеем:
ya’ =- ya.
Изменение масштабов по координатным осям предполагает следующие преобразования координат точки A:
xa’ = n xa;
ya’= m ya,
где n и m – вводимые масштабные коэффициенты, соответственно, по координатным осям X и Y.
Поворот точки относительно начала координат.
Данное преобразование, предполагающее поворот точки на заданный угол относительно начала координат, иллюстрируется ниже приведенным рисунком (Рис. 1.1‑6).
 |
Рис. 5.1‑6
На приведенном рисунке приняты следующие обозначения:
– B,B’ – соответственно, старое и новое положение точки при повороте относительно начала координат;
– a- угол поворота.
Очевидно, что новые координаты в общем случае ищутся согласно соотношениям:
xb’ = c xb + d yb; (5.1-3)
yb’ = e xb + f yb. (5.1-4)
Для нахождения коэффициентов c,d,e,f этих выражений рассмотрим два частных случая.
Рассмотрим сначала поворот на заданный угол a единичного вектора по координатной оси X (Рис. 1.1‑7).

Рис. 5.1‑7
Новые координаты единичного вектора U после поворота на угол a определяются следующим образом:
xv’ = 1*cos a= c xb + d yb = c*1 + d*0,
откуда с = cos a;
yv’ = 1*sin a = e xb + d yb = e*1+f*0,
откуда e = sin a.
Рассмотрим теперь поворот на заданный угол единичного вектора U по оси Y (Рис. 1.1‑8).
Новые координаты вектора U после поворота на угол a определяются следующим образом:
xU’ = -1*sin a= c xU + d yU = c*0 + d*1,
откуда d = -sin a;
yU’ = 1*sin a = e xU + d yU = e*1+f*0,
откуда e = sin a.
 |
координатной оси y ().
Рис. 5.1‑8
Подставив полученные значения для коэффициентов в выражение (5.1-3) и (5.1-4), будем иметь аналитические выражения для расчета новых значений
координат для преобразования типа поворота относительно начала координат:
xb’= xb cos a – yb sin a; (5.1-5)
yb’= xb sin a + yb cos a. (5.1-6)
Легко показать, что преобразование типа поворота системы координат относительно ее начала соответствует обратному преобразованию типа «поворот точки относительно начала координат».
Сложные преобразования координат
Сложные преобразования координат реализуются через соответствующую последовательность базовых преобразований.
Для примера рассмотрим преобразования, имеющие место при повороте точки относительно произвольного вектора U.
Заданное преобразование иллюстрируется ниже приведенным рисунком (Рис. 5.1‑9).

Рис. 5.1‑9
Заданное преобразование можно выполнить, реализовав три следующие базовые преобразования.
1. Перенос начало исходной системы координат в точку, принадлежащую заданному вектор (например, начальную точку вектора).
2. Поворот в новой системе координат точки на заданный угол.
3. Возврат в исходную систему координат.
На Рис. 1.1‑10 приведена последовательность описанных базовых преобразований.
 |
Рис. 5.1‑10
Исходная система координат перемещается на вектор V и образуется новая система координат X’0’Y’, в которой заданный поворот является базовым поворотом относительно начала новой системы координат X’0’Y’.
Координаты заданной точки A в новой системе координат рассчитываются как:
xa’ = xa – vx = xa – xc;
ya’ = ya – vy = ya – yc.
Заданный поворот является базовым поворотом в новой системы координат X’0’Y’, поэтому для координат точки после поворота на угол a относительно точки 0’, используя уравнения (5.1-4) и (5.1-5), будем иметь:
xa’’= xa’ cosa – ya’ sina= (xa -xc)cosa-(ya -yc) sina;
ya’’= xa’ sina – ya’ cosa= (xa -xc) sina + (ya -yc) cosa.
После выполнения поворота относительно заданного вектора, система координат перемещается на вектор –V, т.е. осуществляется возврат в заданную систему координат X0Y. Координаты точки ищутся как:
xa’’’ = xa’’ + xc = (xa – xc) cosa – (ya – yc) sina + xc;
ya’” = ya’’ + yc = (xa – xc) sina + (ya – yc) cosa. + yc .
Базовые преобразования удобно представлять в виде матриц. В этом случае последовательности базовых преобразований, реализующих сложное преобразование, представляется в виде произведения соответствующих матриц базовых преобразований.
Соотношения новых и старых координат при повороте на угол a относительно начала координат, в матричной форме могут быть представлены в виде:
где:
Обратное преобразование рассматриваемого поворота будет задаваться с помощью матрицы:
Преобразования типа «перенос точки на вектор» нельзя отобразить с помощью матриц, размерностью «два на два». Но для этого преобразования также можно использовать матричную форму, если представить координаты точки в однородной системе координат:
где:

a,b- параметры вектора переноса.
Обратное преобразование типа переноса задается в виде матрицы:
Матрица смены направленности оси X имеет вид:
Матрица зеркального отображения точки относительно координаты Y имеет точно такой вид.
Матрица смены направленности оси Y имеет вид:
Матрица зеркального отображения точки относительно координаты X имеет точно такой вид.
Матрица изменения масштабов по координатным осям имеет вид:
Люди также интересуются этой лекцией: 3.3 Построение модели изучаемой системы.
– где n и m – вводимые масштабные коэффициенты, соответственно, по координатным осям X и Y.
Преобразование типа «поворот относительно произвольного вектора», начало которого находится в точке (a,b,c), можно реализовать в матричной форме следующим образом:
Обозначение матрицы знаком «*» означает использование расширенной матрицы. В выше приведенном выражении матрица R(a), соответствующая повороту относительно начала координат, берется в расширенной форме (добавлены одна колонка и одна строка, имеющие все нулевые элементы, кроме элемента на их пересечении, который равен «1»).
Прямоуго́льная (Декартова) систе́ма координа́т — прямолинейная система координат с взаимно перпендикулярными координатными осями на плоскости или в пространстве. Часто используемая система координат. Просто обобщается для пространств любой размерности.
Связанные термины: декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям (названной так по имени Рене Декарта), а общей декартовой системой координат называют аффинную систему координат (не обязательно прямоугольную).
История[править | править код]
Впервые прямоугольную систему координат ввёл Рене Декарт в своей работе «Геометрия» в 1637 году. Он применял координаты к исследованию многих геометрических вопросов. Поэтому прямоугольную систему координат называют также — Декартова система координат (хотя современный термин не во всех деталях соответствует тому, что использовал сам Декарт[1]). Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти[2]. Декарт и Ферма применяли координатный метод только на плоскости. Французский священнослужитель Николай Орем использовал конструкции, подобные декартовым координатам, задолго до времён Декарта и Ферма[3].
Развитие системы декартовых координат далее сыграло важную роль в развитии диифференциального и интегрального исчисления Исааком Ньютоном и Лейбницем[4]. Двухкоординатное описание плоскости позднее было обобщено в понятие векторных пространств[5].
Координаты в трёхмерном пространстве впервые применил Леонард Эйлер в XVIII веке. Использование единичных векторов впервые применил, по-видимому, Гамильтон и Максвелл.
Прямоугольная система координат на плоскости[править | править код]
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат 


Положение точки 











При этом координате 








Ось 





Символически это записывают так:
,
или:
,
или указывают принадлежность координат конкретной точке с помощью индекса:
,
и т. д.
Прямоугольная система координат в пространстве[править | править код]
Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат 






Положение точки 
















- Координата
называется абсциссой точки
,
- координата
— ординатой точки
,
- координата
— аппликата (лат. applicata — прилегающая)[8] точки
.
Символически это записывают так:
,
или
,
или привязывают запись координат к конкретной точке с помощью индекса:
,
и т. п.
Каждая ось рассматривается как числовая прямая, то есть имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка 






Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении ещё и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами[9] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси 


Любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями, называется октантом.
Прямоугольная система координат в многомерном пространстве[править | править код]
Прямоугольная система координат может быть использована и в пространстве любой конечной размерности аналогично тому, как это делается для трехмерного пространства. Количество координатных осей при этом равно размерности пространства (в этом параграфе будем обозначать её 
Для обозначения координат обычно[10] применяют не разные буквы, а одну и ту же букву с числовым индексом. Чаще всего это:
Для обозначения произвольной 
а нередко обозначение 

В любой размерности пространства прямоугольные координатные системы делятся на два класса, правые и левые (или положительные и отрицательные). Для многомерных пространств какую-то одну из координатных систем произвольно (условно) называют правой, а остальные оказываются правыми или левыми в зависимости от того, той же они ориентации или нет[11].
Обобщение понятий двумерного квадранта и трёхмерного октанта для 
Прямоугольные координаты вектора[править | править код]
Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца[12].
Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:
- Вектор можно перенести так, чтобы его начало совпало с началом координат). Тогда его координаты определяются способом, описанным в начале параграфа: координаты вектора, перенесённого так, что его начало совпадает с началом координат, — это координаты его конца.
- Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала.
- Для прямоугольных координат понятие координаты вектора совпадает с понятием ортогональной проекции вектора на направление соответствующей координатной оси.
В прямоугольных координатах очень просто записываются все операции над векторами:
Сложение и умножение на скаляр:
,
или:
,
или:
,
а отсюда и вычитание и деление на скаляр:
,
или:
,
или:
(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).
- Скалярное произведение:
,
или:
(Это справедливо только в прямоугольных координатах с единичным масштабом по всем осям).
- Через скалярное произведение можно вычислить длину вектора
- и угол между векторами:
.
Внешнее произведение:
,
для любой размерности пространства,
- Векторное произведение (только для трехмерного же пространства, на котором оно и определено):
,
,
.
Это позволяет свести все операции над векторами к достаточно простым операциям над числами.
Орты[править | править код]
Прямоугольная система координат[13] (любой размерности) также описывается[14] набором ортов (единичных векторов), сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу. Такие орты образуют ортонормированныйбазис, притом[15].
В трёхмерном случае такие орты обычно обозначаются:
,
и
,
или
,
и
.
Могут также применяться обозначения со стрелками (





При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:
Для размерностей пространства более 3, (или для общего случая, когда размерность может быть любой) обычно для ортов применяют вместо этого обозначения с числовыми индексами, достаточно часто[16] это:
где n — размерность пространства.
Вектор любой размерности раскладывается по базису (координаты служат коэффициентами разложения):
,
или:
а для ортонормированного базиса координаты ещё и очень легко найти через скалярные произведения с ортами:
См. также[править | править код]
- Аффинные координаты
- Проективные координаты
Примечания[править | править код]
- ↑ Декарт пользовался не двумя осями, а одной, на которой откладывались абсциссы; ординаты определялись как расстояние от точек плоскости до оси абсцисс; эти расстояния Декарт отсчитывал по любому заранее выбранному направлению, а не обязательно перпендикулярно.
Как абсциссы, так и ординаты у Декарта были всегда величинами положительными независимо от направления соответствующих отрезков. Различие направлений на осях знаками «+» и «‒» было введено лишь его учениками.
Источник: Выгодский М. Я. Раздел VI. Функции, графики (§ 6. Координаты) // Справочник по элементарной математике / сост. М. Я. Выгодский, под ред. Н. А. Шармай. — М.: АСТ; Астрель, 2015. — С. 461. — 509 с. — 1500 экз. — ISBN 978-5-17-084803-4, ББК 22.1я2, УДК 51(03). — ISBN 978-5-271-46916-9.
- ↑ Bix, Robert A.; D’Souza, Harry J. Analytic geometry. Encyclopædia Britannica. Дата обращения: 6 августа 2017. Архивировано 6 августа 2017 года.
- ↑ Kent, Alexander J. The Routledge Handbook of Mapping and Cartography : [англ.] / Alexander J. Kent, Peter Vujakovic. — Routledge, 2017-10-04. — ISBN 9781317568216. Архивная копия от 24 ноября 2021 на Wayback Machine
- ↑ A Tour of the Calculus, David Berlinski
- ↑ Axler, Sheldon. Linear Algebra Done Right – Springer. — 2015. — P. 1. — ISBN 978-3-319-11079-0. — doi:10.1007/978-3-319-11080-6.
- ↑ 1 2 Словарь иностранных слов. — М.: Рус. яз., 1989. — 624 с. ISBN 5-200-00408-8
- ↑ Иногда это просто принципиально невозможно, если по осям откладываются величины разной физической размерности; впрочем, с геометрической точки зрения это замечание не слишком существенно, так как можно тогда считать масштабы по осям равными условно (например масштабы так, чтобы единицы совпадали при изображая на геометрической плоскости).
- ↑ Словарь иностранных слов. — М.: «Русский язык», 1989. — 624 с. ISBN 5-200-00408-8
- ↑ Можно превратить правую координатную систему в левую и наоборот с помощью зеркального отражения.
- ↑ Но не обязательно: вопрос обозначений в конечном итоге определяется конкретным приложением.
- ↑ Это можно выяснить, исходя из того, можно ли какими-то вращениями (и переносами, если не совпадают начала координат) совместить данную координатную систему с той, ориентация которой правая по определению. Если да, то данная система считается правой, если нет, то левой. Ещё проще технически это выяснить через знак определителя матрицы преобразования от правого базиса к данному.
- ↑ Конец направленного отрезка — точка; прямоугольные координаты точки рассмотрены в статье выше.
- ↑ В этом параграфе будем подразумевать обычную декартову систему координат, то есть прямоугольную систему координат с одинаковым масштабом по всем осям; рассмотрение систем координат с разным масштабом по разным осям внесло бы здесь неоправданные формальные усложнения при довольно малом выигрыше содержательном отношении.
- ↑ Это описание очевидно полностью эквивалентно обычному заданию осей координат, надо только ещё задать начало координат (последнее нередко очевидно по умолчанию).
- ↑ При отказе от условия равномасштабности координатных осей — просто ортогональный базис.
- ↑ Впрочем, вместо буквы e нередко могут быть использованы и другие буквы. Как правило, это явно оговорено.
Ссылки[править | править код]
- В. И. Гервидс. Модель декартовой системы координат (flash). НИЯУ МИФИ (10 марта 2011). Дата обращения: 3 мая 2011.
17 авг. 2022 г.
читать 2 мин
В этом руководстве представлен пошаговый пример того, как изменить масштабы по осям X и Y на графиках в Excel.
Шаг 1: введите данные
Во-первых, давайте введем простой набор данных в Excel:
Шаг 2: Создайте диаграмму рассеивания
Затем выделите ячейки в диапазоне A2:B16.Затем щелкните вкладку « Вставка » на верхней ленте, а затем выберите параметр « Разброс » в группе « Диаграммы »:
Автоматически будет создана следующая диаграмма рассеяния:
Шаг 3: Измените масштаб оси
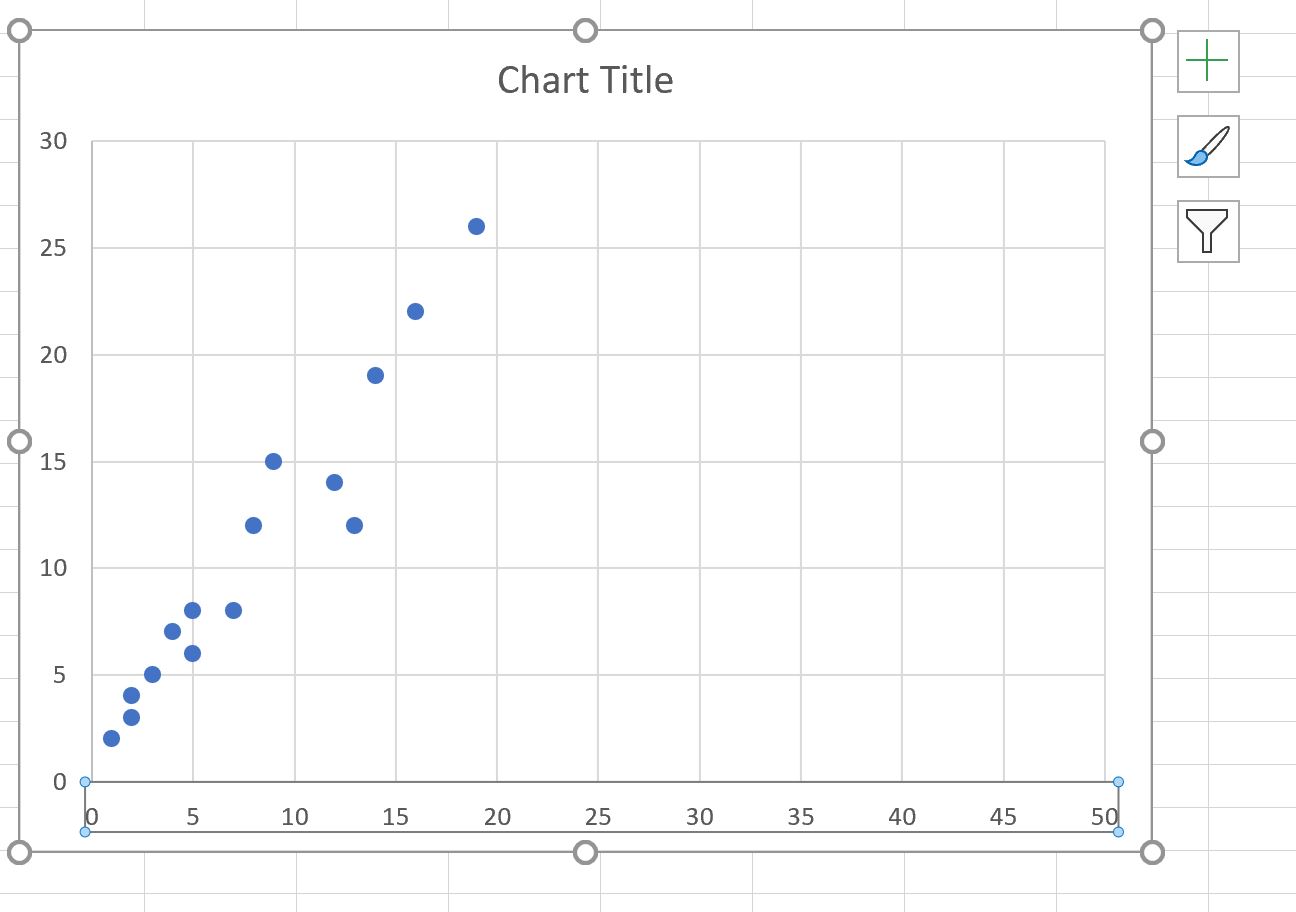
По умолчанию Excel выберет шкалу для осей X и Y, которая варьируется примерно от минимального до максимального значения в каждом столбце.
В этом примере мы видим, что ось x находится в диапазоне от 0 до 20 , а ось y — в диапазоне от 0 до 30 .
Чтобы изменить масштаб оси x, просто щелкните правой кнопкой мыши любое значение на оси x. В появившемся раскрывающемся меню нажмите « Формат оси» :
На панели « Формат оси », которая появляется в правой части экрана, измените значения в полях «Минимум» и «Максимум», чтобы изменить масштаб оси X.
Например, мы можем изменить Максимальное значение оси X на 50 :
Как только мы нажмем Enter , масштаб оси X будет автоматически обновлен на графике:
Обратите внимание, что ось X теперь находится в диапазоне от 0 до 50 .
Ось Y осталась неизменной.
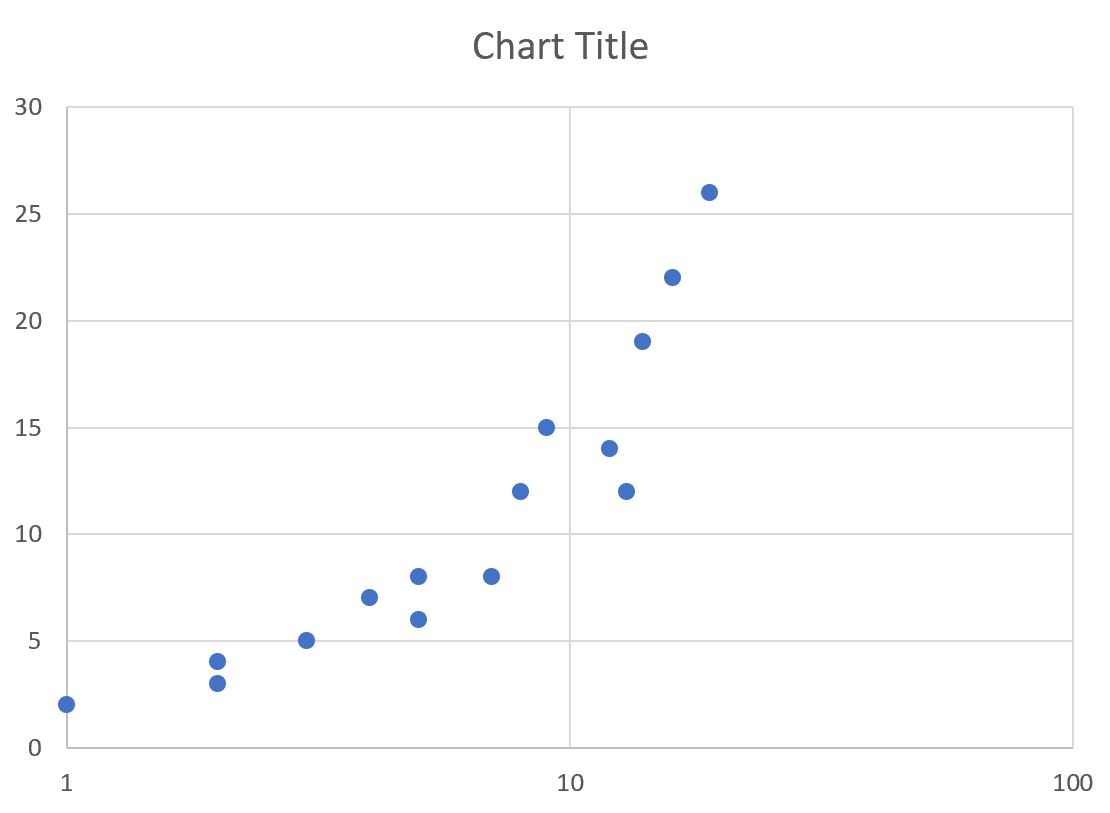
Вместо изменения минимальной и максимальной границ мы могли бы также использовать логарифмическую шкалу для оси.
На панели « Формат оси » просто установите флажок « Логарифмическая шкала »:
Ось X будет автоматически обновлена для использования логарифмической шкалы:
Связанный: Когда следует использовать логарифмическую шкалу в диаграммах?
Обратите внимание, что в этих примерах мы решили изменить только масштаб по оси X.
Однако мы можем так же легко изменить масштаб оси Y, щелкнув правой кнопкой мыши любое значение на оси Y и выполнив те же действия, что и выше.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как построить несколько строк в Excel
Как создать параллельные диаграммы в Excel
Как создать график Ogive в Excel
Масштаб
– это отношение двух линейных размеров.
Во многих областях практического
применения масштабом называют отношение
размера изображения к размеру изображаемого
объекта.В математике масштаб определеется
как отношение расстояния на карте к
соответствующему расстоянию на реальной
местности. Масштаб 1: 100000 означает, что
1 см на карте соответствует 100000 см = 1000
м = 1 км на местности.
Количественное
изменение величины можно так же
представить как изменение масштаба и
отобразить умножением или делением
величины на коэффициент изменения
масштаба. Изменение масштаба может
происходить только в пределах горизонтов
числовой оси пространства, то есть от
бесконечности до обратной ей величины.
Для
величины в пространстве изменение
масштаба сопровождается одновременным
изменением угла поворота между
первоначальным положением и положением
величины в пространстве после изменения
масштаба.
Преобразование
масштабирования относительно начала
координат имеет вид: Xn
= X ·Sx, Yn = Y ·Sy (Sx, Sy – коэффициенты
масштабирования по осям)
Преобразование
сдвига в плоском случае имеет вид: Xn
= X + Tx, Yn = Y + Ty
(X, Y
– начальные координаты; Tx,
Ty – коэффициенты
сдвига)
Преобразование
поворота относительно начала координат
имеет вид: Xn
= X ·cosf – Y ·sinf, Yn = X
·sinf + Y ·cosf (f –
угол поворота)
71.
Прямая линия на плоскости.
Уравнение
прямой линии в отрезках по осям координат.
Уравнение
прямой линии, заданной двумя точками.
Уравнение
прямой линии, проходящей через заданную
точку под заданным углом.
Линия
первого порядка в декартовой системе
координат. Задается на плоскости
уравнением первой степени Ах
+ Ву + С = 0.
Уравнение
прямой линии в отрезках по осям координат.
M1(а,0)
и M2(0,b)
Уравнение
прямой линии, заданной двумя точками
M1(x1,y1)
и M2(x2,y2)
Уравнение
прямой линии, проходящей через заданную
точку под заданным углом. Пусть
задана точка М0(х0,у0)
прямой
и её угловой коэффициент k.
72. Угол между прямыми линиями. Расстояние от точки до прямой линии.
Рассмотрим
две прямые l1
и l2:
l1:
y1=k1x+b1;
l2:
y2=k2x+b2;
Тогда формула такова
Если
же уравнения прямых заданы в общем виде
A1
x
+ B1
y
+ C1
= 0, A2
x
+ B2
y
+ C2
= 0,
тогда
Если
задана точка М(х0,
у0),
то расстояние до прямой Ах + Ву + С =0
определяется как
73. Системы координат в пространстве. Общее уравнение прямой линии.
1)
Декартовы координаты в пространстве
задаются с помощью точки начала координат
и трёх взаимно-перпендикулярных
направленных прямых. Прямые занумерованы,
задан единичный отрезок. Положение
любой точки в пространстве однозначно
определено тремя числами.
2)
Цилиндрическая система координат в
пространстве – “родственница” полярной
системы координат на плоскости. Чтобы
получить цилиндрическую систему надо
на плоскости ввести полярную систему
координат и добавить вертикальную
координатную ось. Т.о., координаты точки
– три числа: первые два – полярные
координаты проекции нашей точки на
плоскость, третье – величина проекции
точки на вертикальную ось.

3)
Сферическая система координат вводится
следующим образом: фиксируем плоскость,
на ней — точку О начала координат, а из
точки О выпускаем луч, перпендикулярный
плоскости, и луч, лежащий в плоскости.
Положение точки М задаётся тремя числами:
первое – расстояние от начала координат
О до точки М; второе – угол между проекцией
отрезка ОМ на плоскость и лежащим в
плоскости лучом; третье – угол между
перпендикулярным плоскости лучом и
отрезком ОМ.

Прямая
в пространстве может быть задана также
как пересечение двух плоскостей, если
плоскости не параллельны:
(на плоскости
)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #





















































![[mathbf{i},,mathbf{j}]=mathbf{k};](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7a9e1f57b79d80f368252b33b3691aec04c19ff)
![[mathbf{j},,mathbf{k}]=mathbf{i};](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0d64fcc16b5a953e286213cf5a4f955f9f5ebd4)
![[mathbf{k},,mathbf{i}]=mathbf{j}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3082939d9e2e341291d53f2ff7f49eac5a2eadeb)