#статьи
- 17 июн 2022
-
0
Становимся настоящими ниндзя в сортировке массивов. Вместо оружия — встроенные функции PHP, быстрые и точные, как катана.
Иллюстрация: Polina Vari для Skillbox Media
В PHP массивом называют структуру данных, которая позволяет хранить упорядоченный набор значений по принципу ключ => значение. И количество инструментов для работы с массивами тут впечатляет: для одной только сортировки существует 13 встроенных функций! В этой статье мы покажем, как ими пользоваться, чтобы получать информацию в нужном виде.
Все функции PHP для сортировки массивов «конструируются» из четырёх основных критериев:
- вид сортировки — по ключу или значениям;
- порядок сортировки — восходящий, нисходящий, естественный, пользовательский и прочие;
- способ обработки ключей — с сохранением связи или нет;
- наличие уточняющих опций — в семи из этих функций можно указать предпочтительный способ сортировки и дополнительные параметры («флаги»).
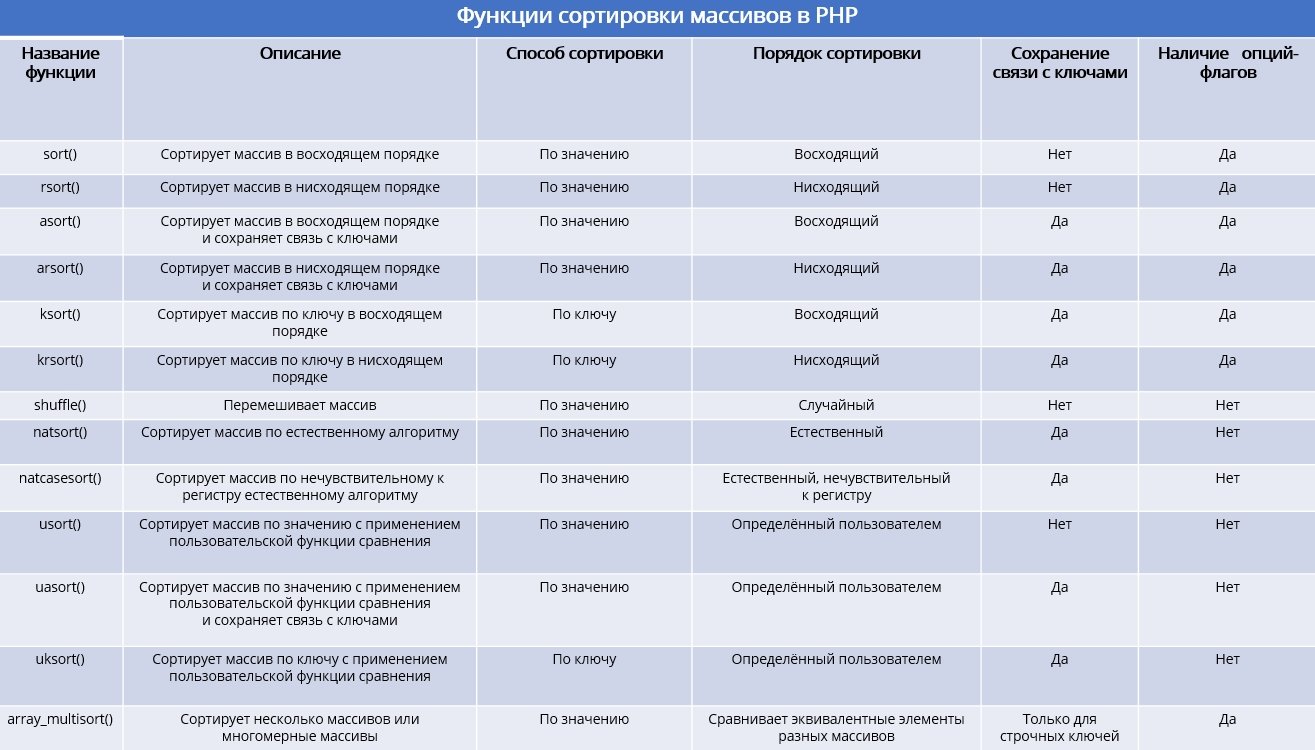
Вот функции, которые позволяют это сделать:
Изображение: Евгений Колесников для Skillbox Media
У каждой из функций есть название, указывающее на вид сортировки и завершающееся круглыми скобками. Эти названия на первый взгляд кажутся не особо говорящими, поэтому для начала лучше выбирать функцию под конкретную задачу, сверяясь с табличкой на официальном сайте. При этом легко запомнить, что функции с буквой «k» сортируют массивы по ключам.
В зависимости от выбранной функции внутри скобок указывается массив или несколько массивов для сортировки, а затем могут идти опции (флаги):
- SORT_REGULAR — сравнивать элементы в нормальном порядке, не меняя типов;
- SORT_NUMERIC — сравнивать элементы как числа;
- SORT_STRING — сравнивать элементы как строки;
- SORT_LOCALE_STRING — сравнивать элементы как строки, руководствуясь текущим местонахождением, то есть локалью (Locale);
- SORT_NATURAL — сравнивать элементы как строки в естественном порядке;
- SORT_FLAG_CASE — можно объединить с SORT_STRING или SORT_NATURAL, чтобы сделать сортировку нечувствительной к регистру.
Давайте попробуем в действии отсортировать массивы разными способами. В этом нам помогут редактор кода Notepad++ и среда разработки XAMPP для запуска PHP-кода в браузере.
Во всех примерах будем сначала выводить исходный массив, а затем его же после сортировки (помните, что сортировка меняет массив, то есть её результат сохраняется). Для удобства чтения будем осуществлять вывод с помощью привычной функции echo в связке с implode()/print_r() или циклом foreach.
Также для красоты будем сопровождать результаты подписями (HTML-заголовки <h2> и <h3>) и переносом строк (HTML-элемент <br>).
<?php
echo "<h1>СОРТИРОВКА МАССИВОВ</h1>";
Создадим массив чисел и отсортируем его в порядке убывания, от большего значения к меньшему. Возьмём самый простой пример: массив зарплат в рублях:
$salaries = array(45000, 65000, 35000, 75000, 55000);
Так он выглядит с выводом результата.
echo "<h2>Сортировка вакансий по зарплатам</h2>"; $salaries = array(45000, 65000, 35000, 75000, 55000); echo "<h3>Исходный массив вакансий по зарплатам целиком, до сортировки</h3>"; print_r($salaries); echo "<h3>Массив вакансий по зарплатам до сортировки –- только значения (исходный порядок)</h3>"; echo implode(", ", $salaries) . "<br>";
Исходный массив вакансий по зарплатам целиком, до сортировки:
Array ( [0] => 45000 [1] => 65000 [2] => 35000 [3] => 75000 [4] => 55000 )
Массив вакансий по зарплатам до сортировки — только значения (исходный порядок):
45000, 65000, 35000, 75000, 55000
Как видим, сейчас зарплаты внутри массива расположены в произвольном порядке, а нам бы хотелось сначала увидеть самые выгодные вакансии. Значит, надо найти в таблице такой метод, который умеет сортировать значения в порядке убывания — нам подойдёт rsort().
rsort($array, FLAGS);
Объяснение:
- rsort() — название функции, в скобках указываются параметры;
- $array — массив для сортировки;
- на месте опции FLAGS можно указать другие правила сортировки массива (флаги).
А теперь попробуем нашу функцию в деле. На первом шаге передадим в неё массив с зарплатами — $salaries.
rsort($salaries);
Далее прописываем вывод результата:
echo "<h3>Массив вакансий по зарплатам после сортировки через rsort() (по значению, по убыванию)</h3>"; echo implode(", ", $salaries) . "<br>";
Вот что у нас получилось на выходе:
75000, 65000, 55000, 45000, 35000
Теперь возьмёмся за массив текстовых значений.
По данным Большой российской энциклопедии, в мире насчитывается более двухсот видов сов. Было бы неплохо создать про них сайт, чтобы каждый мог узнать о совах побольше! Начнём с создания «массива сов», руководствуясь книгой Ю. Б. Пукинского «Жизнь сов».
echo "<h2>Сортируем сов</h2>"; $owls = array( "tytonidae" => "Сипухи", "tyto" => "Сипухи", "strigidae" => "Настоящие совы", "otus" => "Совки", "bubo" => "Филины", "ketupa" => "Рыбные совы", "nyctea" => "Белые совы", "surnia" => "Ястребиные совы", "glaucidium" => "Сычики", "ninox" => "Иглоногие совы", "athene" => "Сычи", "strix" => "Неясыти", "asfo" => "Ушастые совы", "aegolius" => "Мохноногие сычи" );
echo "<h3>Исходный массив названий видов сов целиком, до сортировки</h3>"; print_r($owls); echo "<h3>Названия видов сов до сортировки -- только значения (исходный порядок)</h3>"; echo implode(", ", $owls) . "<br>";
Исходный массив названий видов сов целиком, до сортировки:
Array ( [tytonidae] => Сипухи [tyto] => Сипухи [strigidae] => Настоящие совы [otus] => Совки [bubo] => Филины [ketupa] => Рыбные совы [nyctea] => Белые совы [surnia] => Ястребиные совы [glaucidium] => Сычики [ninox] => Иглоногие совы [athene] => Сычи [strix] => Неясыти [asfo] => Ушастые совы [aegolius] => Мохноногие сычи )
Названия видов сов до сортировки — только значения (исходный порядок):
Сипухи, Сипухи, Настоящие совы, Совки, Филины, Рыбные совы, Белые совы, Ястребиные совы, Сычики, Иглоногие совы, Сычи, Неясыти, Ушастые совы, Мохноногие сычи
В данном случае в роли ключей ассоциативного массива у нас выступают латинские названия видов, а значениями являются русские названия.
В зависимости от задачи нам может понадобиться как латинское, так и русское название. Кроме этого, было бы интересно иметь возможность получать информацию о случайно выбранной сове, а ещё — представлять текстовые значения в алфавитном порядке.
Отсюда вытекает необходимость использования сразу трёх различных функций сортировки:
- ksort() для сортировки по ключам (латинским названиям) по алфавиту;
- asort() для сортировки по значениям (русским названиям), также по алфавиту;
- shuffle() для получения случайных русских названий сов.
Синтаксис ksort() и asort() такой же, как и в предыдущем примере у rsort(), а с shuffle() всё ещё проще — она принимает только название массива.
Посмотрим на функции в деле:
ksort($owls); echo"<h3>Названия видов сов после сортировки через ksort() (по ключу, по алфавиту, по возрастанию)</h3>"; print_r(array_keys($owls)); asort($owls); echo "<h3>Названия видов сов после сортировки через asort() (по значению, по алфавиту, по возрастанию)</h3>"; echo implode(", ", $owls) . "<br>"; shuffle($owls); echo "<h3>Названия видов сов после сортировки через shuffle() (по значению, случайный порядок)</h3>"; echo implode(", ", $owls) . "<br>";
Названия видов сов после сортировки через ksort() (по ключу, по алфавиту, по возрастанию):
Array ( [0] => aegolius [1] => asfo [2] => athene [3] => bubo [4] => glaucidium [5] => ketupa [6] => ninox [7] => nyctea [8] => otus [9] => strigidae [10] => strix [11] => surnia [12] => tyto [13] => tytonidae )
Названия видов сов после сортировки через asort() (по значению, по алфавиту, по возрастанию):
Белые совы, Иглоногие совы, Мохноногие сычи, Настоящие совы, Неясыти, Рыбные совы, Сипухи, Сипухи, Совки, Сычи, Сычики, Ушастые совы, Филины, Ястребиные совы
Названия видов сов после сортировки через shuffle() (по значению, случайный порядок):
Сипухи, Рыбные совы, Белые совы, Сычики, Совки, Сипухи, Мохноногие сычи, Ястребиные совы, Ушастые совы, Филины, Неясыти, Настоящие совы, Иглоногие совы, Сычи
Совы встали на свои места, а мы двигаемся дальше — к сортировке, имитирующей человеческую логику.
Предположим, у нас есть список подписчиков нашей группы в одном из возможных форматов — ссылками с id вида vk.com/idXXX.
echo "<h2>Сортируем ссылки на страницы во «Вконтакте» через natsort()</h2>"; $pages = array("vk.com/id30000", "vk.com/id10000", "vk.com/id20000"); echo "<h3>Исходный массив ссылок на страницы во «Вконтакте», до сортировки</h3>"; print_r($pages);
Исходный массив ссылок на страницы во «Вконтакте», до сортировки:
Array ( [0] => vk.com/id30000 [1] => vk.com/id10000 [2] => vk.com/id20000 )
Было бы удобно расположить записи в порядке возрастания id, но есть нюанс: элементы массива являются строковыми значениями. Вот что показывает проверка типов:
echo "<h3>Проверка типа данных в массиве ссылок на страницы во «Вконтакте»</h3>"; foreach ($pages as $page) { echo gettype($page) . "<br>"; };
Вывод результата после проверки типа данных в массиве ссылок на страницы во «Вконтакте»:
string string string
Чтобы решить задачу, воспользуемся функцией естественной сортировки natsort().
natsort($array);
Объяснение:
- natsort() — название функции, в скобках указывается единственный параметр;
- $array — массив, который нужно отсортировать естественным способом (как это бы сделал человек).
Посмотрим на функцию в деле:
natsort($pages); echo "<h3>Массив ссылок на страницы во «Вконтакте» после естественной сортировки через natsort() (по значению, по возрастанию)</h3>"; echo implode(", ", $pages) . "<br>";
Массив ссылок на страницы во «Вконтакте» после естественной сортировки через natsort() (по значению, по возрастанию):
vk.com/id10000, vk.com/id20000, vk.com/id30000
Теперь страницы отсортированы в удобном для работы формате.
Для примера возьмём двумерный массив, состоящий, в свою очередь, из двух массивов: марок автомобильного топлива и цен на него некоторое время назад.
echo "<h2>Сортируем цены на бензин и дизельное топливо (в рублях) через array_multisort()</h2>"; $petrol = array( array("52,75", "61,95", "54,01", "47,60"), array("АИ-95", "АИ-98", "ДТ", "АИ-92") ); echo "<h3>Марки топлива и цены на него до сортировки(исходный порядок)</h3>"; print_r(array_values($petrol));
Марки топлива и цены на него до сортировки (исходный порядок):
Array ( [0] => Array ( [0] => 52,75 [1] => 61,95 [2] => 54,01 [3] => 47,60 ) [1] => Array ( [0] => АИ-95 [1] => АИ-98 [2] => ДТ [3] => АИ-92 ) )
Сейчас здесь есть взаимное соответствие (например, АИ-92 стоит 47,60), но сами значения не отсортированы в каком-либо порядке. Попробуем с помощью функции сортировки array_multisort() вывести для пользователя список ценников, отсортированный по возрастанию, где сначала идёт самый дешёвый бензин.
Функция array_multisort() предназначена как раз для сортировки многомерных массивов. Вот её синтаксис:
array_multisort($array1, $array1_sort_order, $array1_sort_flags, $other);
Объяснение:
- array_multisort() — название функции, в скобках указываются параметры;
- $array1 — первый массив для сортировки;
- на месте опции $array1_sort_order можно указать порядок сортировки первого массива (можно не указывать);
- на месте опции $array1_sort_flags можно указать другие правила сортировки первого массива (флаги) в дополнение к предыдущей опции;
- на месте $other можно вписать ещё один массив $array2 с опциями или без (и так далее).
Применим функцию в деле:
echo("<h3>Сортировка марок топлива и цен через array_multisort() (по возрастанию)</h3>"); array_multisort($petrol[0], $petrol[1]); echo implode(" -- ", $petrol[1]) . "<br>"; echo implode(" -- ", $petrol[0]) . "<br>";
Вывод отсортированного массива марок топлива и цен через array_multisort() (по возрастанию):
АИ-92 -- АИ-95 -- ДТ -- АИ-98 47,60--52,75--54,01--61,95
Теперь марки топлива расположены по возрастанию цены, а мы возьмём ещё более интересный пример — сортировку по кастомным правилам.
Предположим, у нашей компании есть корпоративный портал, где можно посмотреть информацию о коллегах. Пусть у нас в массиве будет шесть коллег. База содержит ФИО, внутренний ID, должность и возраст, а карточка каждого сотрудника является отдельным массивом многомерного массива:
echo "<h2>Сортируем сотрудников компании</h2>"; $employees = array( array( "ID" => 1, "ФИО" => "Вувузела Андрей Павлович", "Должность" => "Менеджер", "Возраст" => "29" ), array( "ID" => 2, "ФИО" => "Ахрюнов Алексей Степанович", "Должность" => "Бухгалтер", "Возраст" => "32" ), array( "ID" => 3, "ФИО" => "Охрюненко Борис Гориславович", "Должность" => "Курьер", "Возраст" => "22" ), array( "ID" => 4, "ФИО" => "Бокакин Арсений Брониславович", "Должность" => "Менеджер", "Возраст" => "31" ), array( "ID" => 5, "ФИО" => "Голохрюхин Евгений Владимирович", "Должность" => "Директор", "Возраст" => "40" ), array( "ID" => 6, "ФИО" => "Совакошка Мария Игоревна", "Должность" => "Старший инженер", "Возраст" => "26" ) );
Код вывода исходного массива карточек сотрудников компании:
echo "<h3>Записи сотрудников компании до сортировки(исходный порядок)</h3>"; print_r(array_values($employees));
Вывод исходного массива карточек сотрудников компании до сортировки (исходный порядок):
Array ( [0] => Array ( [ID] => 1 [ФИО] => Вувузела Андрей Павлович [Должность] => Менеджер [Возраст] => 29 ) [1] => Array ( [ID] => 2 [ФИО] => Ахрюнов Алексей Степанович [Должность] => Бухгалтер [Возраст] => 32 ) [2] => Array ( [ID] => 3 [ФИО] => Охрюненко Борис Гориславович [Должность] => Курьер [Возраст] => 22 ) [3] => Array ( [ID] => 4 [ФИО] => Бокакин Арсений Брониславович [Должность] => Менеджер [Возраст] => 31 ) [4] => Array ( [ID] => 5 [ФИО] => Голохрюхин Евгений Владимирович [Должность] => Директор [Возраст] => 40 ) [5] => Array ( [ID] => 6 [ФИО] => Совакошка Мария Игоревна [Должность] => Старший инженер [Возраст] => 26 ) )
Дадим пользователю корпоративного портала возможность сортировки списка по фамилиям, возрасту и порядковому номеру. В этом нам поможет функция пользовательской сортировки usort().
usort($array, "function");
Объяснение:
- usort() — название функции, в скобках указываются параметры.
- $array — массив для сортировки.
- «function» — название вашей функции сравнения с собственными правилами сортировки. Она объявляется заранее и принимает два параметра. Обратите внимание на кавычки, в которые заключается название.
Применим функцию в деле — на сортировке сотрудников по алфавиту, по возрасту (по возрастанию) и по ID (по убыванию).
Обратите внимание:
- В каждом из трёх примеров ниже мы сначала объявляем пользовательскую функцию сравнения (alphSort, ageSort и idSort соответственно), а потом передаём её встроенной функции usort() в качестве обработчика массива.
- Цикл foreach помогает по очереди перебирать карточки каждого сотрудника в главном массиве $employees. Для удобства мы в рамках цикла обзываем их $employee — то же самое английское слово в единственном числе.
- Для доступа к нужным ключам вложенных массивов (карточек сотрудников) используется синтаксис с квадратными скобками: $array[«key»] и так далее.
echo "<h3>Сортировка сотрудников по ФИО через usort() и strcmp (по алфавиту)</h3>"; function alphSort($name1, $name2) { return strcmp($name1["ФИО"], $name2["ФИО"]); }; usort($employees, "alphSort"); foreach ($employees as $employee) { echo "ID " . $employee["ID"] . ", " . "<b>ФИО: " . $employee["ФИО"] . ",</b> " . "Должность: " . $employee["Должность"] . ", " . "Возраст: " . $employee["Возраст"] . "<br>"; };
Функция alphSort() принимает по два значения ФИО ($name1 и $name2) и сравнивает их как строки с помощью встроенной функции strcmp(). Она передаётся во встроенную функцию usort(), где и применяется на нашем массиве.
Вывод отсортированного массива карточек сотрудников компании. Вариант первый — ФИО по алфавиту:
ID 2, ФИО: Ахрюнов Алексей Степанович, Должность: Бухгалтер, Возраст: 32 ID 4, ФИО: Бокакин Арсений Брониславович, Должность: Менеджер, Возраст: 31 ID 1, ФИО: Вувузела Андрей Павлович, Должность: Менеджер, Возраст: 29 ID 5, ФИО: Голохрюхин Евгений Владимирович, Должность: Директор, Возраст: 40 ID 3, ФИО: Охрюненко Борис Гориславович, Должность: Курьер, Возраст: 22 ID 6, ФИО: Совакошка Мария Игоревна, Должность: Старший инженер, Возраст: 26
Следующие два примера строятся по похожему принципу. Вот код для сортировки массива карточек сотрудников компании. Вариант второй — по возрасту.
echo "<h3>Сортировка сотрудников по возрасту через usort() (по возрастанию)</h3>"; function ageSort($age1, $age2) { if ($age1["Возраст"] == $age2["Возраст"]) { return 0; } return ($age1["Возраст"] < $age2["Возраст"]) ? -1 : 1; }; usort($employees, "ageSort"); foreach ($employees as $employee) { echo "ID " . $employee["ID"] . ", " . "ФИО: " . $employee["ФИО"] . ", " . "Должность: " . $employee["Должность"] . ", " . "<b>Возраст: " . $employee["Возраст"] . "</b><br>"; };
Функция ageSort() должна сравнивать по два значения возраста сотрудников (в данном примере — $age1, $age2), и возвращать результат (отсортированный массив) в зависимости от результата сравнения. Она также передаётся во встроенную функцию usort().
Вывод отсортированного массива карточек сотрудников компании. Вариант второй — по возрасту:
ID 3, ФИО: Охрюненко Борис Гориславович, Должность: Курьер, Возраст: 22 ID 6, ФИО: Совакошка Мария Игоревна, Должность: Старший инженер, Возраст: 26 ID 1, ФИО: Вувузела Андрей Павлович, Должность: Менеджер, Возраст: 29 ID 4, ФИО: Бокакин Арсений Брониславович, Должность: Менеджер, Возраст: 31 ID 2, ФИО: Ахрюнов Алексей Степанович, Должность: Бухгалтер, Возраст: 32 ID 5, ФИО: Голохрюхин Евгений Владимирович, Должность: Директор, Возраст: 40
Код для сортировки массива карточек сотрудников компании. Вариант третий — по ID:
echo "<h3>Сортировка сотрудников по ID через usort() (по убыванию)</h3>"; function idSort($id1, $id2) { if ($id1["ID"] == $id2["ID"]) { return 0; } return ($id1["ID"] < $id2["ID"]) ? 1 : -1; }; usort($employees, "idSort"); foreach ($employees as $employee) { echo "<b>ID " . $employee["ID"] . ",</b> " . "ФИО: " . $employee["ФИО"] . ", " . "Должность: " . $employee["Должность"] . ", " . "Возраст: " . $employee["Возраст"] . "<br>"; }; ?>
Аналогично прошлому примеру, здесь функция idSort() тоже заточена на сравнение по двум значениям — теперь это ID сотрудников ($id1, $id2) — и возвращает результат (отсортированный массив) в зависимости от результата сравнения.
Вывод отсортированного массива карточек сотрудников компании. Вариант третий — по ID:
ID6, ФИО: Совакошка Мария Игоревна, Должность: Старший инженер, Возраст: 26 ID 5, ФИО: Голохрюхин Евгений Владимирович, Должность: Директор, Возраст: 40 ID 4, ФИО: Бокакин Арсений Брониславович, Должность: Менеджер, Возраст: 31 ID 3, ФИО: Охрюненко Борис Гориславович, Должность: Курьер, Возраст: 22 ID 2, ФИО: Ахрюнов Алексей Степанович, Должность: Бухгалтер, Возраст: 32 ID 1, ФИО: Вувузела Андрей Павлович, Должность: Менеджер, Возраст: 29
Мы рассмотрели основные виды сортировок массивов в PHP: числовую, алфавитную, естественную, многомерную и пользовательскую. Для всего этого мы нашли подходящие функции.
Для более детального знакомства с функциями сортировки массивов в PHP рекомендуем пользоваться таблицами-напоминалками: в разных руководствах они сделаны по-разному, поэтому лучше найти ту табличку, которая будет удобна именно вам. А для синтаксически правильного применения советуем пользоваться официальной документацией языка, тем более она переведена на русский.

Научитесь: Профессия PHP-разработчик с нуля до PRO
Узнать больше
Что такое сортировка и зачем она нужна
Сортировка распределяет элементы в порядке, удобном для работы. Если отсортировать массив чисел в порядке убывания, то первый элемент всегда будет наибольшим, а последний наименьшим. Поэтому желательно хранить информацию упорядочено, чтобы было проще проводить над ней операции.
В данной статье вы научитесь разным техникам сортировок на языке С++. Мы затронем 7 видов:
- Пузырьковая сортировка (Bubble sort);
- Сортировка выбором (Selection sort);
- Сортировка вставками (Insertion sort);
- Быстрая сортировка (Quick sort);
- Сортировка слиянием (Merge sort);
- Сортировка Шелла (Shell sort);
- Сортировка кучей (Heap sort).
Знание этих техник поможет получить работу. На площадке LeetCode содержится более 200 задач, связанных с сортировками. 19 из них входят в топ частых вопросов на собеседованиях по алгоритмам.
1. Пузырьковая сортировка
В пузырьковой сортировке каждый элемент сравнивается со следующим. Если два таких элемента не стоят в нужном порядке, то они меняются между собой местами. В конце каждой итерации (далее называем их проходами) наибольший/наименьший элемент ставится в конец списка.
Прежде чем писать код, разберем сортировку визуально на примере массива из пяти элементов. Отсортируем его в порядке возрастания.
Проход №1
Оранжевым отмечаются элементы, которые нужно
поменять местами. Зеленые уже стоят в нужном порядке.
Наибольший элемент — число 48 — оказался в конце
списка.
Проход №2
Наибольший элемент уже занимает место в конце
массива. Чтобы поставить следующее число по убыванию, можно пройтись лишь до 4-й позиции, а не пятой.
Проход №3
Проход №4
После четвертого прохода получаем
отсортированный массив.
Функция сортировки в качестве параметров будет принимать указатель на массив и его размер. Функцией swap() элементы
меняются местами друг с другом:
#include <iostream>
using namespace std;
void bubbleSort(int list[], int listLength)
{
while(listLength--)
{
bool swapped = false;
for(int i = 0; i < listLength; i++)
{
if(list[i] > list[i + 1])
{
swap(list[i], list[i + 1]);
swapped = true;
}
}
if(swapped == false)
break;
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
bubbleSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в лучшем случае: O(n).
Сложность в среднем случае: O(n2).
Сложность в худшем случае: O(n2).
2. Сортировка выбором
Ищем наименьшее значение в массиве и ставим
его на позицию, откуда начали проход. Потом двигаемся на следующую позицию.
Возьмем тот же массив из пяти элементов и отсортируем его.
Проход №1
Зеленым отмечается наименьший элемент в
подмассиве — он ставится в начало списка.
Проход №2
Число 4 — наименьшее в оставшейся части массива.
Перемещаем четверку на вторую позицию после числа 0.
Проход №3
Проход №4
Напишем функцию поиска наименьшего элемента и
используем ее в сортировке:
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
#include <iostream>
using namespace std;
int findSmallestPosition(int list[], int startPosition, int listLength)
{
int smallestPosition = startPosition;
for(int i = startPosition; i < listLength; i++)
{
if(list[i] < list[smallestPosition])
smallestPosition = i;
}
return smallestPosition;
}
void selectionSort(int list[], int listLength)
{
for(int i = 0; i < listLength; i++)
{
int smallestPosition = findSmallestPosition(list, i, listLength);
swap(list[i], list[smallestPosition]);
}
return;
}
int main ()
{
int list[5] = {12, 5, 48, 0, 4};
cout << "Input array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
selectionSort(list, 5);
cout << "Sorted array ..." << endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность в любом случае: O(n2).
3. Сортировка вставками
В сортировке вставками начинаем со второго
элемента. Проверяем между собой второй элемент с первым и, если надо, меняем местами.
Сравниваем следующую пару элементов и проверяем все пары до нее.
Проход №1. Начинаем со второй позиции.
Число 12 больше 5 — элементы меняются местами.
Проход №2. Начинаем с третьей позиции.
Проверяем вторую и третью позиции. Затем
первую и вторую.
Проход №3. Начинаем с четвертой позиции.
Произошло три смены местами.
Проход №4. Начинаем с последней позиции.
Получаем отсортированный массив на выходе.
#include <iostream>
using namespace std;
void insertionSort(int list[], int listLength)
{
for(int i = 1; i < listLength; i++)
{
int j = i - 1;
while(j >= 0 && list[j] > list[j + 1])
{
swap(list[j], list[j + 1]);
cout<<"ndid";
j--;
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
insertionSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n).
Сложность в худшем случае: O(n2).
4. Быстрая сортировка
В основе быстрой сортировки лежит стратегия
«разделяй и властвуй». Задача разделяется на более мелкие подзадачи. Подзадачи
решаются отдельно, а потом решения объединяют. Точно так же, массив разделяется
на подмассивы, которые сортируются и затем сливаются в один.
В первую очередь выбираем опорный элемент.
Отметим его синим. Все значения больше опорного элемента ставятся после него,
остальные — перед.
На иллюстрации массив разделяется по опорному
элементу. В полученных массивах также выбираем опорный элемент и разделяем по
нему.
Опорным может быть любой элемент. Мы выбираем
последний в списке.
Чтобы расположить элементы большие — справа от
опорного элемента, а меньшие — слева, будем двигаться от начала списка. Если
число будет больше опорного, то оно ставится на его место, а сам опорный на
место перед ним.
Напишем функцию разделения partition(),
которая возвращает индекс опорного элемента, и используем ее в сортировке.
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
#include <iostream>
using namespace std;
int partition(int list[], int start, int pivot)
{
int i = start;
while(i < pivot)
{
if(list[i] > list[pivot] && i == pivot-1)
{
swap(list[i], list[pivot]);
pivot--;
}
else if(list[i] > list[pivot])
{
swap(list[pivot - 1], list[pivot]);
swap(list[i], list[pivot]);
pivot--;
}
else i++;
}
return pivot;
}
void quickSort(int list[], int start, int end)
{
if(start < end)
{
int pivot = partition(list, start, end);
quickSort(list, start, pivot - 1);
quickSort(list, pivot + 1, end);
}
}
int main()
{
int list[6]={2, 12, 5, 48, 0, 4};
cout<<"Input array ...n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
quickSort(list, 0, 6);
cout<<"nnSorted array ... n";
for (int i = 0; i < 6; i++)
{
cout<<list[i]<<"t";
}
return 0;
}
Сложность в лучшем случае: O(n*logn).
Сложность в худшем случае: O(n2).
5. Сортировка слиянием
Сортировка слиянием также следует стратегии
«разделяй и властвуй». Разделяем исходный массив на два равных подмассива.
Повторяем сортировку слиянием для этих двух подмассивов и объединяем обратно.
Цикл деления повторяется, пока не останется по
одному элементу в массиве. Затем объединяем, пока не образуем полный список.
Алгоритм сортировки состоит из четырех этапов:
- Найти середину массива.
- Сортировать массив от
начала до середины. - Сортировать массив от
середины до конца. - Объединить массив.
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
Для объединения напишем отдельную функцию
merge().
Алгоритм объединения массивов:
- Циклично проходим по
двум массивам.. - В объединяемый ставим тот элемент, что меньше.
- Двигаемся дальше, пока не дойдем до конца
обоих массивов.
#include <iostream>
using namespace std;
void merge(int list[],int start, int end, int mid);
void mergeSort(int list[], int start, int end)
{
int mid;
if (start < end){
mid=(start+end)/2;
mergeSort(list, start, mid);
mergeSort(list, mid+1, end);
merge(list,start,end,mid);
}
}
void merge(int list[],int start, int end, int mid)
{
int mergedList[8];
int i, j, k;
i = start;
k = start;
j = mid + 1;
while (i <= mid && j <= end) {
if (list[i] < list[j]) {
mergedList[k] = list[i];
k++;
i++;
}
else {
mergedList[k] = list[j];
k++;
j++;
}
}
while (i <= mid) {
mergedList[k] = list[i];
k++;
i++;
}
while (j <= end) {
mergedList[k] = list[j];
k++;
j++;
}
for (i = start; i < k; i++) {
list[i] = mergedList[i];
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
mergeSort(list, 0, 7);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в любом случае: O(n*logn).
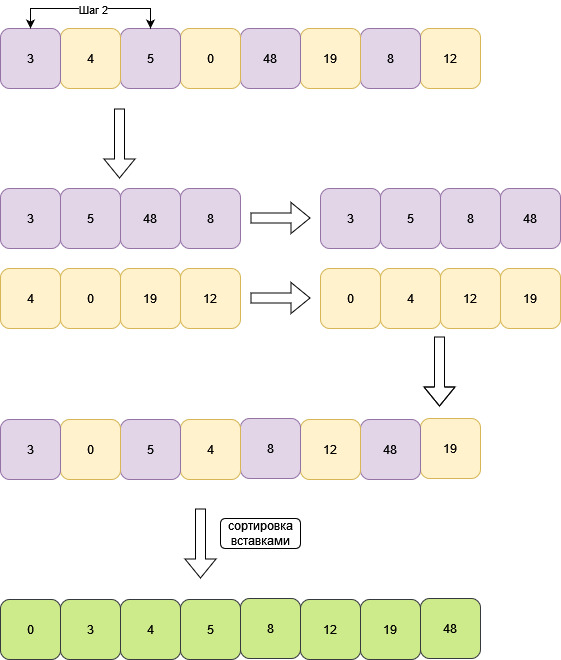
6. Сортировка Шелла
Алгоритм включает в себя сортировку вставками.
Исходный массив размером N разбивается на подмассивы с шагом N/2. Подмассивы
сортируются вставками. Затем вновь разбиваются, но уже с шагом равным N/4. Цикл
повторяется. Производим целочисленное деление шага на два каждую итерацию.
Когда шаг становится равен 1, массив просто сортируется вставками.
У массива размером с 8, первый шаг будет равен 4.
Уменьшаем шаг в два раза. Шаг равен 2.
#include <iostream>
using namespace std;
void shellSort(int list[], int listLength)
{
for(int step = listLength/2; step > 0; step /= 2)
{
for (int i = step; i < listLength; i += 1)
{
int j = i;
while(j >= step && list[j - step] > list[i])
{
swap(list[j], list[j - step]);
j-=step;
cout<<"ndid";
}
}
}
}
int main()
{
int list[8]={3,19,8,0,48,4,5,12};
cout<<"Input array ...n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
shellSort(list, 8);
cout<<"nnSorted array ... n";
for (int i = 0; i < 8; i++)
{
cout<<list[i]<<"t";
}
}
Сложность в лучшем и среднем случае:
O(n*logn).
Сложность в худшем случае: O(n2).
Исходный массив представляем в виде структуры
данных кучи. Куча – это один из
типов бинарного дерева.
У кучи есть следующие свойства:
- Родительский узел
всегда больше дочерних; - На i-ом слое 2i
узлов, начиная с нуля. То есть на нулевом слое 1 узел, на первом – 2 узла, на
втором – 4, и т. д. Правило для всех слоев, кроме последнего; - Слои заполняются слева направо.
После формирования кучи будем извлекать самый
старший узел и ставить на конец массива.
Алгоритм сортировки кучей:
- Формируем бинарное
дерево из массива. - Расставляем узлы в
дереве так, чтобы получилась куча (методheapify()). - Верхний элемент
помещаем в конец массива. - Возвращаемся на шаг 2, пока куча не опустеет.
Обращаться к дочерним узлам можно, зная, что
дочерние элементы i-го элемента находятся на позициях 2*i + 1 (левый узел) и
2*i + 2 (правый узел).
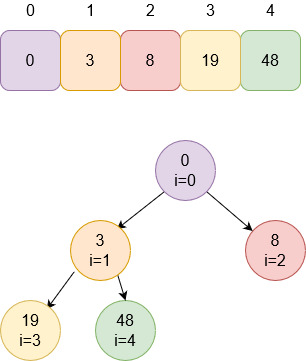
Изначальная куча:
Индекс с нижним левым узлом определим по
формуле n/2-1, где n – длина массива. Получается 5/2 – 1 = 2 – 1 = 1. С этого
индекса и начинаем операцию heapify(). Сравним дочерние узлы 1-й позиции.
Дочерний узел оказался больше. Меняем местами
с родителем.
Теперь проверяем родительский узел от позиции
1.
48 больше 3. Меняем местами.
После смены проверяем все дочерние узлы
элемента, который опустили. То есть для числа 3 проводим heapify(). Так как 3
меньше 19, меняем местами.
Наибольший элемент оказался наверху кучи.
Осталось поставить его в конце массива на позицию 4.
Теперь продолжаем сортировать кучу, но последний элемент игнорируем. Для
этого просто будем считать, что длина массива уменьшилась на 1.
Повторяем алгоритм сортировки, пока куча не
опустеет, и получаем отсортированный массив.
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
#include <iostream>
using namespace std;
void heapify(int list[], int listLength, int root)
{
int largest = root;
int l = 2*root + 1;
int r = 2*root + 2;
if (l < listLength && list[l] > list[largest])
largest = l;
if (r < listLength && list[r] > list[largest])
largest = r;
if (largest != root)
{
swap(list[root], list[largest]);
heapify(list, listLength, largest);
}
}
void heapSort(int list[], int listLength)
{
for(int i = listLength / 2 - 1; i >= 0; i--)
heapify(list, listLength, i);
for(int i = listLength - 1; i >= 0; i--)
{
swap(list[0], list[i]);
heapify(list, i, 0);
}
}
int main()
{
int list[5] = {3,19,8,0,48};
cout<<"Input array ..."<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
heapSort(list, 5);
cout << "Sorted array"<<endl;
for(int i = 0; i < 5; i++)
cout << list[i] << 't';
cout << endl;
}
Сложность алгоритма в любом случае: O(n*logn).
***
В этой статье мы познакомились с семью видами
сортировок, рассмотрели их выполнение и написание на С++. Попробуйте применить
новые знания в решении задачек на LeetCode или Codeforces. Понимание подобных
алгоритмов поможет в будущем пройти собеседование.
Источники:
- https://www.softwaretestinghelp.com/sorting-techniques-in-cpp/
- https://medium.com/@ssbothwell/sorting-algorithms-and-big-o-analysis-332ce7b8e3a1
- https://www.programiz.com/dsa/shell-sort
- https://www.happycoders.eu/algorithms/sorting-algorithms/
***
Материалы по теме
- Какая сортировка самая быстрая? Тестируем алгоритмы
- Пузырьковая сортировка на JavaScript
- Вводный курс по алгоритмам: от сортировок до машины Тьюринга
***
Мне сложно разобраться самостоятельно, что делать?
Алгоритмы и структуры данных действительно непростая тема для самостоятельного изучения: не у кого спросить и что-то уточнить. Поэтому мы запустили курс «Алгоритмы и структуры данных», на котором в формате еженедельных вебинаров вы:
- изучите сленг, на котором говорят все разработчики независимо от языка программирования: язык алгоритмов и структур данных;
- научитесь применять алгоритмы и структуры данных при разработке программ;
- подготовитесь к техническому собеседованию и продвинутой разработке.
Курс подходит как junior, так и middle-разработчикам.
Просмотров 17.1к. Обновлено 23 ноября 2020
Урок из серии: «Программирование на языке Паскаль»
Процесс обработки и поиска информации при решении многих задач проходит быстрее и эффективнее, если данные расположены в определенном порядке. Например, различные списки студентов, учащихся, сотрудников — в алфавитном порядке, числовые данные от большего значения к меньшему (или наоборот) и т.д.
Существует довольно много различных методов сортировки массивов, отличающихся друг от друга степенью эффективности, под которой понимается количество сравнений и количество обменов, произведенных в процессе сортировки. Рассмотрим подробно некоторые из них.
Сортировка массива методом простого выбора
При сортировке массива методом выбора применяется базовый алгоритм поиска максимального (минимального) элемента и его номера.
Алгоритм сортировки массива методом выбора:
- Для исходного массива выбрать максимальный элемент.
- Поменять его местами с последним элементом (после этого самый большой элемент будет стоять на своем месте).
- Повторить п.п. 1-2 с оставшимися n-1 элементами, то есть рассмотреть часть массива, начиная с первого элемента до предпоследнего, найти в нем максимальный элемент и поменять его местамис предпоследним (n-1)- м элементом массива, затем с оставшиеся (n-2)-мя элементами и так далее, пока не останется один элемент, уже стоящий на своем месте.
Для упорядочения массива потребуется (n-1) просмотров массива. В процессе сортировки будет увеличиваться отсортированная часть массива, а неотсортированная, соответственно, уменьшаться.
При сортировке данных выполняется обмен содержимого переменных. Для обмена необходимо создавать временную переменную, в которой будет храниться содержимое одной из переменных. В противном случае ее содержимое окажется утерянным.
Задача 1. Массив из 10 элементов отсортировать по возрастанию методом простого перебора.
Решение
Напишем процедуру. Входным параметром для неё будет массив. Он же будет и выходным параметром. Поэтому описываем его как параметр-переменная (с ключевым словом var).
В процедуре внешний цикл по i — определяет длину рассматриваемой части массива. Она будет изменяться от n до 2.
Внутренний цикл по j используется для поиска максимального элемента и его номера. В качестве начального значения максимума разумно взять значение последнего элемента рассматриваемой части массива.
Программный код процедуры:
Procedure sorting1(var a:myarray);
{Сортировка по возрастанию методом простого выбора}
var i,j:integer;
k,m:integer; {номер и значение максимального элемента}
begin
for i:= n downto 2 do{задаем длину рассматриваемой части массива}
begin
{ищем максимальный элемент и его номер}
k:=i; m:=a[i]; for j:= 1 to i-1 do
if a[j] > m then begin k:=j; m:=a[k] end;
{меняем местами найденный элемент и последний}
if k <> i then
begin a[k]:=a[i]; a[i]:= m; end;
end;
end;
end;
Программный код основной программы:
program primer_1;
const n = 10;
type myarray = array[1..n] of integer;
var a:myarray;
Procedure sorting1(var a:myarray);
{Линейная сортировка (сортировка отбором)}
...
begin {main}
writeln('Введите исходный массив:');
for i:=1 to n do read(a[i]);
sorting1(a);
writeln('Отсортированный массив:');
for i:=1 to 10 do write(a[i],' ');
writeln;
end.
Процесс упорядочения элементов в массиве по возрастанию методом отбора:
| Номер элемента | 1 | 2 | 3 | 4 | 5 |
| Исходный массив | 8 | 7 | 5 | 4 | 2 |
| Первый просмотр | 2 | 7 | 5 | 4 | 8 |
| Второй просмотр | 2 | 4 | 5 | 7 | 8 |
| Третий просмотр | 2 | 4 | 5 | 7 | 8 |
| Четвертый просмотр | 2 | 4 | 5 | 7 | 8 |
При упорядочивании массива по убыванию необходимо перемещать минимальный элемент. Для чего в алгоритме нахождения максимального элемента достаточно знак «>» поменять на знак «<«.
Сортировка массива методом простого обмена (методом пузырька)
Наиболее известным методом сортировки является сортировка пузырьковым методом. Его популярность объясняется запоминающимся названием и простым алгоритмом.
Метод основан на том, что в процессе исполнения алгоритма более «легкие» элементы массива постепенно «всплывают».
Особенностью данного метода является сравнение не каждого элемента со всеми, а сравнение в парах соседних элементов. Выполняется несколько последовательных просмотров массива от начала к концу. Если соседние элементы расположены «неправильно», то они меняются местами.
Алгоритм сортировки массива по возрастанию методом простого обмена:
- Начнем просмотр с первой пары элементов ( a[1] и a[2] ). Если первый элемент этой пары больше второго, то меняем их местами, иначе оставляем без изменения. Затем берем вторую пару элементов ( a[2] и a[3] ), если второй больше третьего, то также меняем их, далее сравниваем третий и четвертый, и если третий больше четвертого, меняем их местами, и т.д. Последними сравниваем (n-1)-ый и n-ый элементы.При первом обходе массива будут просмотрены все пары элементов массива a[i] и a[i+1] для i от 1 до (n-1). В результате максимальный элемент массива переместится в конец массива.
- Поскольку самый большой элемент находится на своем месте, рассмотрим часть массива без него, то есть с первого до (n-1) — го элемента.Повторим предыдущие действия для этой части массива, в результате чего второй по величине элемент массива переместится на последнее место рассматриваемой части массива, то есть на ( n-1 ) — е место во всем массиве.
- Эти действия продолжают до тех пор, пока количество элементов в текущей части массива не уменьшится до двух. В этом случае необходимо выполнить последнее сравнение и упорядочить последние два элемента.
Нетрудно заметить, что для преобразования массива, состоящего из n элементов, необходимо просмотреть его n–1 раз, каждый раз уменьшая диапазон просмотра на один элемент.
Ниже приведен текст процедуры сортировки массива по возрастанию методом пузырька.
procedure sorting2(var a:myarray);
var k,i,t:integer;
begin
for k := 1 to n-1 do {цикл по номеру просмотра}
for i:=1 to n-k do
{Если текущий элемент больше следующего, поменять местами}
if a[i] > a[i+1] then
begin
t:=a[i];
a[i]:=a[i+1];
a[i+1]:=t;
end;
end;
Для упорядочения элементов массива по убыванию их значений необходимо при сравнении элементов массива знак «>» заменить на «<«.
Процесс упорядочения элементов в массиве по возрастанию методом обмена:
| Номер элемента | 1 | 2 | 3 | 4 | 5 |
| Исходный массив | 8 | 7 | 5 | 4 | 2 |
| Первый просмотр | 7 | 5 | 4 | 2 | 8 |
| Второй просмотр | 5 | 4 | 2 | 7 | 8 |
| Третий просмотр | 4 | 2 | 5 | 7 | 8 |
| Четвертый просмотр | 2 | 4 | 5 | 7 | 8 |
Здравствуй, дорогой гость. В этой статье я расскажу об алгоритме сортировки массива методом пузырька.
Элементы массива, как пузырьки
Алгоритм пузырьковой сортировки — это довольно простой в реализации алгоритм для сортировки массивов. Можно встретить и другие названия: пузырьковая сортировка, Buble sort или сортировка простыми обменами — но все они будут обозночать один и тот же алгоритм. Назван так, потому что большее или меньшее значение «всплывает» (сдвигается) к краю массива после каждой итерации, это будет видно в примере.
Сложность этого алгоритма выражается формулой О(n^2) (n в степени 2). Алгоритм работает медленно с большими массивами, а поэтому малоэффективен и на практике используется редко, чаще всего в учебных целях. Для сортировки массивов на практике используют другие более быстрые алгоритмы, один из них — QuickSort(быстрая сортировка). Функция для быстрой сортировки включена во многие стандартные библиотеки языков программирования, например в языке C функция qsort() из стандартной библиотеки.
Алгоритм работает очень просто. Программа проходит по всем элементами массива по порядку. Каждый текущий элемент сравнивается с соседним и, если он меньше/больше(если сортируем по убыванию/возрастанию соответственно) меняется местами с соседним.
Пример работы алгоритма пузырьковой сортировки
Рассмотрим пример работы алгоритма с массивом, состоящим из четырех элементов.
Имеется массив [4, 5, 2, 6]. Сортировать его будем по убыванию.
N — количество элементов в массиве. i — номер прохода. Алгоритм будет делать проходы по массиву, всего N-1 проходов до N-i ячейки в каждой итерации для любого массива.
Первый проход циклом от первого до N-1 элемента, сравнение условием и перемена местами в случае удовлетворения условия — если левый элемент меньше правого.
4 5 2 6
Сравниваем 4 и 5, 4 меньше 5, а значит мы их меняем местами.
Следующий проход.
5 4 2 6
Сравниваем 4 и 2, 4 не меньше 2, а значит пропускаем и идем дальше.
5 4 2 6
Сравниваем 2 и 6, 4 меньше 6, а значит мы их меняем местами.
Теперь мы у нас массив [5, 4 ,6, 2]. Как видно, он еще не упорядочен до конца. После первого прохода в конец массива передвинулось самое маленькое значение, теперь нам нужно сделать еще проход до элемента N-2 (ведь идет 2-ая итерация).
Делаем проход, начиная с первого элемента.
5 4 6 2
Сравниваем 5 и 4, 5 не меньше 4, а значит пропускаем и идем дальше.
5 4 6 2
Сравниваем 6 и 4, 6 меньше 4, а значит мы их меняем местами. Мы достигли элемента N-2, завершаем итерацию.
Теперь мы имеем массив [5, 6, 4, 2]. 2 последних элемента упорядочены как нужно. Для завершения нужно выполнить еще один проход до N-3.
5 6 4 2
Сравниваем 5 и 6, 5 меньше 6, а значит мы их меняем местами. Мы достигли элемента N-3, завершаем итерацию.
В итоге на выходе мы получили массив упорядоченный по убыванию — [6, 5, 4, 2].
Реализация алгоритма на языке C++
Программа выполнит последовательно следующие действия:
- Установит размер массива, прося пользователя ввести числовое значение.
- Заполнит массив значениями, введенными пользователем для каждого элемента массива.
- Выведет исходный массив.
- Отсортирует массив по убыванию.
- Выведет отсортированный массив.
Теперь собственно код по каждому из пунктов.
1. Объявим переменную и инициализируем её значение данными, введенными пользователем.
/* Установим размер массива */ int n; // Кол-во элементов cout << "Количество элементов: "; cin >> n;
2. Объявим массив из количества элементов, которое ввел пользователь. А то есть объявим массив из n элементов. После запустим цикл и попросим пользователя ввести значение каждого элемента.
/* Заполним массив значениями */
int mass[n];
for(int i = 0; i < n; ++i)
{
cout << i+1 << "-ый элемент: ";
cin >> mass[i];
}
3. Выведем значения всех элементов массива, используя цикл.
/* Выведем исходный массив */
cout << "Исходный массив: ";
for(int i = 0; i < n; ++i)
{
cout << mass[i] << " "; // Вывод i-го элемента
}
cout << endl;
4. Отсортируем массив по убыванию. Здесь нам понадобятся 2 цикла. Первый будет выполнять количество итераций n-1, как в примере выше, который мы разобрали. Второй цикл будет осуществлять проходы по элементам массива (таких проходов n-i) и сравнивать соседние элементы. Элементы сравниваются условием, если i-ый элемент меньше правого соседа, то они меняются местами, таким образом самый маленький элемент будет в правой крайней части.
/* Отсортируем массив по убыванию */
for(int i = 1; i < n; ++i)
{
for(int r = 0; r < n-i; r++)
{
if(mass[r] < mass[r+1])
{
// Обмен местами
int temp = mass[r];
mass[r] = mass[r+1];
mass[r+1] = temp;
}
}
}
5. Выведем отсортированный массив, используя цикл, как в 3-ем действии.
/* Выведем отсортированный массив */
cout << "Отсортированный массив: ";
for(int i = 0; i < n; ++i)
{
cout << mass[i] << " ";
}
cout << endl;
Весь код программы
#include <iostream>
using namespace std;
int main()
{
/* Установим размер массива */
int n; // Кол-во элементов
cout << "Количество элементов: ";
cin >> n;
/* Заполним массив значениями */
int mass[n];
for(int i = 0; i < n; ++i)
{
cout << i+1 << "-ый элемент: ";
cin >> mass[i];
}
/* Выведем исходный массив */
cout << "Исходный массив: ";
for(int i = 0; i < n; ++i)
{
cout << mass[i] << " ";
}
cout << endl;
/* Отсортируем массив по убыванию */
for(int i = 1; i < n; ++i)
{
for(int r = 0; r < n-i; r++)
{
if(mass[r] < mass[r+1])
{
// Обмен местами
int temp = mass[r];
mass[r] = mass[r+1];
mass[r+1] = temp;
}
}
}
/* Выведем отсортированный массив */
cout << "Отсортированный массив: ";
for(int i = 0; i < n; ++i)
{
cout << mass[i] << " ";
}
cout << endl;
return 0;
}
Обратите внимание, что в коде программы использовались русские символы, если у вас их отображение некорректно, то почитайте статью про решение проблемы с отображением русских символов в консоли.
Написание программы завершено, теперь проверим результаты. А для этого введем в программу массив, сортировку которого мы произвели, рассматривая пример работы алгоритма немного выше в этой статье.
После ввода данных и выполнения программы мы получили результат.
Результат сортировки массива методом пузырька
Как видно на картинке, массив отсортирован по убыванию. Программа работает.
Как я отмечал ранее, алгоритм работает очень медленно с большим объемом данных, а потому непригоден для использования на практике, а пригоден лишь в обучающих и ознакомительных целях. Посмотрите на решения других задач по программированию.
Зарегистрируйтесь для доступа к 15+ бесплатным курсам по программированию с тренажером
Алгоритмы сортировки
—
Основы алгоритмов и структур данных
В программировании часто встречаются задачи, которые трудно решить «в лоб». Представим, что нам нужно избавиться от повторяющихся элементов в массиве. Попробуем найти все числа, которые встречаются здесь больше, чем один раз:
7, 3, 1, 9, 10, 2, 3, 6, 9, 4, 7, 5, 5, 4, 2, 8, 4, 7Чтобы это сделать, нужно написать сложный алгоритм. Можно упростить задачу и отсортировать массив. В нем повторяющиеся элементы находятся рядом, поэтому их легко обнаружить, сравнивая соседние числа:
1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 6, 7, 7, 7, 8, 9, 9, 10Не удивительно, что одной из самых полезных задач в программировании считается сортировка — перестановка элементов в массиве так, чтобы они располагались в убывающем или возрастающем порядке.
Чем полезна сортировка
Познакомимся с сортировкой поближе и выясним, где она встречается в практических задачах программиста.
Посмотрим на любой интернет-магазин. В каждом разделе встречаются сотни и тысячи товаров, из которых так сложно выбрать подходящий. Чтобы пользователям было удобнее, магазин предлагает сортировку товаров по цене, по рейтингу или по популярности.
При этом покупатели выбирают сортировку по своим целям:
-
По возрастанию цены в поисках выгодных предложений
-
По убыванию цены, если готовы на дорогую покупку
Чтобы интернет-магазин умел сортировать одни и те же записи по-разному, необходима универсальная функция сортировки, о которой поговорим в конце урока.
Три алгоритма сортировки
Существуют десятки алгоритмов сортировки, но изучать все слишком долго. Чтобы не останавливаться на этой теме, мы выбрали три фундаментальных алгоритма:
-
Пузырьковая сортировка
-
Сортировка выбором
-
Быстрая сортировка
Все три алгоритма сортируют исходный массив, меняя местами его элементы и не требуя дополнительного пространства.
Эти алгоритмы помогут понять, как работает сортировка. На их примере вы изучите, какие техники программисты применяют при разработке алгоритмов.
При реализации алгоритмов мы должны помнить о вырожденных случаях — массивах, в которых один или ноль элементов. Сортировка их не меняет, но наши алгоритмы должны обрабатывать эти случаи — иначе программа завершится с ошибкой.
Пузырьковая сортировка
Один из самых простых методов — пузырьковая сортировка. Это название произошло от ассоциации с воздухом в воде: на дне пузырьки совсем маленькие, но постепенно поднимаются к поверхности, собирают кислород и увеличиваются.
Похожий принцип работает и с элементами массива при такой сортировке. Посмотрите на этот рисунок:

Мы идем по массиву и перемещаем вправо самый большой элемент из просмотренных. Так мы находим элемент со значением 10, который в итоге побеждает во всех сравнениях и оказывается в правом конце массива.
Рассмотрим механизм работы данной сортировки на реальном примере. Возьмем массив и сравним элементы попарно от начала к концу: первый со вторым, второй с третьим, третий с четвертым и так далее.
Если два соседних элемента находятся в неправильном порядке, меняем их местами. После первого прохода самый большой элемент оказывается справа — его можно больше не сравнивать и не перемещать. Далее повторяем те же действия со всеми остальными числами.
Пузырьковая сортировка реализуется в JavaScript с помощью такой функции:
const bubbleSort = (items) => {
for (let limit = items.length - 1; limit > 0; limit -= 1) {
for (let i = 0; i < limit; i += 1) {
if (items[i] > items[i + 1]) {
const temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;
}
}
}
};Python
def bubble_sort(items):
for limit in range(len(items) - 1, 0, -1):
for i in range(limit):
if items[i] > items[i + 1]:
items[i], items[i + 1] = items[i + 1], items[i]PHP
<?php
function bubbleSort($items)
{
for ($limit = count($items) - 1; $limit > 0; $limit -= 1) {
for ($i = 0; $i < $limit; $i += 1) {
if ($items[$i] > $items[$i + 1]) {
$temporary = $items[$i];
$items[$i] = $items[$i + 1];
$items[$i + 1] = $temporary;
}
}
}
}Java
class App {
public static void bubbleSort(int[] items) {
for (var limit = items.length - 1; limit > 0; limit--) {
for (var i = 0; i < limit; i++) {
if (items[i] > items[i + 1]) {
var temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;
}
}
}
}
}Мы видим здесь два вложенных цикла. Внешний цикл ограничивает внутренний цикл на каждом проходе. Сначала он простирается до конца массива, но после первого прохода там оказывается максимальный элемент.
Внутренний цикл на следующем проходе движется до предпоследнего элемента, а затем до пред-пред-последнего — и так до тех пор, пока не остается один элемент в левой части:
for (let limit = items.length - 1; limit > 0; limit -= 1) {
// ...
}Python
for limit in range(len(items) - 1, 0, -1):
# ...PHP
<?php
for ($limit = count(items) - 1; $limit > 0; $limit -= 1) {
// ...
}Java
for (var limit = items.length - 1; limit > 0; limit--) {
// ...
}Мы помним, что в JavaScript элементы массива нумеруются с 0 — следовательно, индекс последнего элемента массива items равен items.length - 1.
Обмен двух элементов выполняется с помощью временной переменной, которую мы назвали temporary (т.е. временная):
const temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;Python
# В Python временная переменная не требуется
items[i], items[i + 1] = items[i + 1], items[i]PHP
<?php
$temporary = $items[$i];
$items[$i] = $items[$i + 1];
$items[$i + 1] = $temporary;Java
var temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;На каждом шаге мы находим наибольший элемент в массиве, а последний оставшийся неизбежно оказывается наименьшим — так мы получаем упорядоченный массив. Проверим работу алгоритма:
const items = [2, 3, 4, 3, 1, 2, 4, 5, 1, 2];
bubbleSort(items);
console.log(items); // => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]Python
items = [2, 3, 4, 3, 1, 2, 4, 5, 1, 2]
bubble_sort(items)
print(items) # => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]PHP
<?php
$items = [2, 3, 4, 3, 1, 2, 4, 5, 1, 2];
bubbleSort($items);
print_r($items); // => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]Java
int[] items = {2, 3, 4, 3, 1, 2, 4, 5, 1, 2};
App.bubbleSort(items);
System.out.println(Arrays.toString(items));
// => [1, 1, 2, 2, 2, 3, 3, 4, 4, 5]При пузырьковой сортировке соседние элементы часто меняются местами, поэтому она работает довольно медленно. Чтобы сэкономить время, можно сократить количество перестановок. В этом поможет сортировка выбором.
Сортировка выбором
Этот алгоритм сначала проводит операции сравнения и находит наименьший элемент, а только потом помещает его в начало массива. После первого прохода алгоритм исключает первый элемент из рассмотрения и ищет минимальный элемент в оставшейся части массива, а затем помещаем его на второе место:

Этот алгоритм работает гораздо быстрее пузырьковой сортировки, потому что сравнений здесь столько же, а вот обмен всего один — в самом конце.
Рассмотрим функцию, реализующую сортировку выбором в Java Script:
const selectionSort = (items) => {
for (let i = 0; i < items.length - 1; i += 1) {
let indexMin = i;
for (let j = i + 1; j < items.length; j += 1) {
if (items[j] < items[indexMin]) {
indexMin = j;
}
}
const temporary = items[i];
items[i] = items[indexMin];
items[indexMin] = temporary;
}
};Python
def selection_sort(items):
for i in range(len(items) - 1):
index_min = i
for j in range(i + 1, len(items)):
if items[j] < items[index_min]:
index_min = j
items[i], items[index_min] = items[index_min], items[i]PHP
<?php
function selectionSort($items)
{
for ($i = 0; i < count($items) - 1; $i += 1) {
$indexMin = $i;
for ($j = $i + 1; $j < count(items); $j += 1) {
if ($items[$j] < $items[$indexMin]) {
$indexMin = $j;
}
}
$temporary = $items[$i];
$items[$i] = $items[$indexMin];
$items[$indexMin] = $temporary;
}
}Java
class App {
public static void selectionSort(int[] items) {
for (var i = 0; i < items.length - 1; i++) {
var indexMin = i;
for (var j = i + 1; j < items.length; j++) {
if (items[j] < items[indexMin]) {
indexMin = j;
}
}
var temporary = items[i];
items[i] = items[indexMin];
items[indexMin] = temporary;
}
}
}В реализации мы сохраняем не сам минимальный элемент, а его индекс в массиве. Это нужно потому, что в конце каждого прохода минимальный элемент записывается в начало массива. При этом элемент, который был там до этого, нужно вставить куда-то в неупорядоченную половину — легче всего просто поменять их местами.
Быстрая сортировка
Можно сделать сортировку еще быстрее, если менять местами не соседние элементы, а элементы на самом большом расстоянии друг от друга.
Возьмем для примера массив, отсортированный в порядке убывания — от больших к меньшим. Чтобы разместить элементы в порядке возрастания, надо попарно поменять их местами: первый и последний, потом второй и предпоследний, и так далее, как показано на схеме:

Сортировки массива в обратном порядке реализуется так:
let left = 0;
let right = items.length - 1;
while (left < right) {
const temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left += 1;
right -= 1;
}Python
left = 0
right = len(items) - 1
while left < right:
items[left], items[right] = items[right], items[left]
left += 1
right -= 1PHP
<?php
$left = 0;
$right = count($items) - 1;
while ($left < $right) {
$temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = $temporary;
$left += 1;
$right -= 1;
}Java
var left = 0;
var right = items.length - 1;
while (left < right) {
var temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left++;
right--;
}В примере выше мы создали две переменные-указателя. Переменная left указывает на следующий элемент для обмена слева, а переменная right — справа. Для обмена используем уже знакомую временную переменную temporary:
const temporary = items[left];
items[left] = items[right];
items[right] = temporary;Python
# В Python временная переменная не требуется
items[left], items[right] = items[right], items[left]PHP
<?php
$temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = $temporary;Java
var temporary = items[left];
items[left] = items[right];
items[right] = temporary;На каждой итерации цикла после обмена мы увеличиваем левый указатель, сдвигая его вправо, и одновременно уменьшаем правый, сдвигая влево:
Python
PHP
<?php
$left += 1;
$right -= 1;Java
Похожий подход применяется в алгоритме быстрой сортировки. Он частично упорядочивает массив, перемещая в начало маленькие элементы, а в конец — большие.
Частичное упорядочивание делается с помощью программы, похожей на пример выше. Для начала выбираем опорный элемент — это условный средний элемент, который помогает отличить маленькие элементы от больших. Затем устанавливаем два указателя на начало и конец массива.
Принцип работы быстрой сортировки
Чтобы не запутаться в алгоритме быстрой сортировки, разберем его на схематичном примере. В самом начале наш массив выглядит так:

В качестве опорного элемента выбрано число 4. Левый указатель смотрит на 5, а правый — на 3.
Далее ищем неправильный элемент слева, двигая левый указатель и пропуская элементы меньше опорного. Затем двигаем правый указатель, пропуская элементы больше опорного.
Таким образом мы ищем пару элементов, в которой левый больше правого. Когда пара найдена, меняем элементы местами. В нашем примере 5 и 3 находятся в неправильной позиции — их надо поменять:

Ищем следующую пару для обмена. Справа от 3 находится 4 — наш следующий кандидат для обмена. Обратите внимание, что 4 — опорный элемент, но он тоже принимает участие в сравнениях и обменах.
Слева от числа 5 находятся числа 6, 9 и 7. Они больше опорного элемента 4, поэтому указатель их пропускает. В итоге он останавливается на числе 2:

Меняем их местами и ищем следующую пару. Следующие кандидаты — числа 10 и 1:

Меняем их местами и останавливаемся, потому что левый и правый указатели упираются друг в друга. Мы получили частично упорядоченный массив. Разбиваем его на две части там, где указатели встретились:

Продолжаем частичное упорядочивание левой и правой половин массива. Правая половина перед упорядочиванием показана на рисунке:

Выбираем новый опорный элемент из подмассива. На этот раз это 7. Сдвигая указатели, меняем местами пары 10 и 5, а также 8 и 6. Числа 4 и 9 останутся на своих местах. Частично упорядоченный подмассив принимает такой вид:

Левый и правый указатель встречаются посередине — на числе 7. Мы снова разбиваем массив на две половины и переходим к упорядочиванию левой и правой половин.
Как реализовать быструю сортировку
Попробуем реализовать алгоритм на JavaScript. Начнем с функции частичного упорядочивания:
const partition = (items, left, right, pivot) => {
while (true) {
while (items[left] < pivot) {
left += 1;
}
while (items[right] > pivot) {
right -= 1;
}
if (left >= right) {
return right + 1;
}
const temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left += 1;
right -= 1;
}
};Python
def partition(items, left, right, pivot):
while True:
while items[left] < pivot:
left += 1
while items[right] > pivot:
right -= 1
if left >= right:
return right + 1
items[left], items[right] = items[right], items[left]
left += 1
right -= 1PHP
<?php
function partition($items, $left, $right, $pivot)
{
while (true) {
while ($items[$left] < $pivot) {
$left += 1;
}
while ($items[$right] > $pivot) {
$right -= 1;
}
if ($left >= $right) {
return $right + 1;
}
const temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = temporary;
$left += 1;
$right -= 1;
}
}Java
class App {
public static int partition(int[] items, int left, int right, int pivot) {
while (true) {
while (items[left] < pivot) {
left++;
}
while (items[right] > pivot) {
right--;
}
if (left >= right) {
return right + 1;
}
var temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left++;
right--;
}
}
}В качестве параметров функция получает:
-
Массив
items -
Указатели на левую и правую часть подмассива
leftиright -
Опорный элемент для сравнения
pivot
Сначала в цикле пропускаются элементы слева, которые меньше опорного:
while (items[left] < pivot) {
left += 1;
}Python
while items[left] < pivot:
left += 1PHP
<?php
while ($items[$left] < $pivot) {
$left += 1;
}Java
while (items[left] < pivot) {
left++;
}Затем пропускаются элементы справа, которые больше опорного:
while (items[right] > pivot) {
right -= 1;
}Python
while items[right] > pivot:
right -= 1PHP
<?php
while ($items[$right] > $pivot) {
$right -= 1;
}Java
while (items[right] > pivot) {
right--;
}Если указатели встретились или зашли друг за друга, мы завершаем цикл и возвращаем место встречи в качестве результата. Нам предстоит разбить массив на два подмассива, поэтому надо решить, что именно возвращать. Мы можем сказать, что граница — это место, где заканчивается левый подмассив, или место, где начинается правый. Большой разницы здесь нет.
Решим, что функция partition возвращает индекс элемента, где начинается правый подмассив:
if (left >= right) {
return right + 1;
}Python
if left >= right:
return right + 1PHP
<?php
if ($left >= $right) {
return $right + 1;
}Java
if (left >= right) {
return right + 1;
}Если указатели остановились, то они указывают на два элемента в неверном порядке. Левый указатель смотрит на элемент, который больше опорного. При этом правый указатель смотрит на элемент, который меньше опорного.
Меняем местами и сдвигаем элементы, чтобы в следующей итерации продолжить поиск следующей неправильной пары:
const temporary = items[left];
items[left] = items[right];
items[right] = temporary;
left += 1;
right -= 1;Python
items[left], items[right] = items[right], items[left]
left += 1
right -= 1PHP
<?php
$temporary = $items[$left];
$items[$left] = $items[$right];
$items[$right] = $temporary;
$left += 1;
$right -= 1;Java
var temporary = items[left];
items[left] = items[right];
items[right] = temporary;Обычно условие завершения цикла пишут в начале (оператор while) или в конце (оператор do…while). В функции partition() условие становится известно в середине цикла.
В языках программирования нет специального синтаксиса для такой ситуации. Обычно программисты записывают бесконечный цикл с помощью конструкции while (true), а выход из цикла делают с помощью операторов break или return:
while (true) {
// ...
if (left >= right) {
return right + 1;
}
// ...
}Python
while True:
# ...
if left >= right:
return right + 1
# ...PHP
<?php
while (true) {
// ...
if ($left >= $right) {
return $right + 1;
}
// ...
}Java
while (true) {
// ...
if (left >= right) {
return right + 1;
}
// ...
}Частично упорядоченный массив нельзя назвать полностью отсортированным. Чтобы закончить сортировку, мы должны рекурсивно повторить упорядочивание для левой и правой половин массива.
Про рекурсию мы говорили на прошлом уроке. Так выглядит рекурсивный алгоритм быстрой сортировки. Он немного похож на рекурсивную функцию бинарного поиска:
const sort = (items, left, right) => {
const length = right - left + 1;
if (length < 2) {
return;
}
const pivot = items[left];
const splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);
};Python
def sort(items, left, right):
length = right - left + 1
if length < 2:
return
pivot = items[left]
split_index = partition(items, left, right, pivot)
sort(items, left, split_index - 1)
sort(items, split_index, right)PHP
<?php
function sort($items, $left, $right)
{
$length = $right - $left + 1;
if ($length < 2) {
return;
}
$pivot = $items[$left];
$splitIndex = partition($items, $left, $right, $pivot);
sort($items, $left, splitIndex - 1);
sort($items, $splitIndex, $right);
}Java
class App {
public static int partition(int[] items, int left, int right, int pivot) {
// ...
}
public static void sort(int[] items, int left, int right) {
var length = right - left + 1;
if (length < 2) {
return;
}
var pivot = items[left];
var splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);
}
}Для упорядочивания нужно не менее двух элементов. Поэтому мы остановим рекурсивный вызов, когда встретим пустой подмассив или подмассив с одним элементом:
const length = right - left + 1;
if (length < 2) {
return;
}Python
length = right - left + 1
if length < 2:
returnPHP
<?php
$length = $right - $left + 1;
if ($length < 2) {
return;
}Java
var length = right - left + 1;
if (length < 2) {
return;
}Функция partition возвращает индекс первого элемента в правом подмассиве. Это помогает функции sort корректно вызвать саму себя:
const splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);Python
split_index = partition(items, left, right, pivot)
sort(items, left, split_index - 1)
sort(items, split_index, right)PHP
<?php
$splitIndex = partition($items, $left, $right, $pivot);
sort($items, $left, $splitIndex - 1);
sort($items, $splitIndex, $right);Java
var splitIndex = partition(items, left, right, pivot);
sort(items, left, splitIndex - 1);
sort(items, splitIndex, right);Единственный код, который вызывает вопросы — выбор опорного элемента:
const pivot = items[left];Python
PHP
<?php
$pivot = $items[$left];Java
Почему мы всегда выбираем самый левый элемент подмассива?
Средний элемент должен находиться ровно посередине отсортированного массива. В таком случае его называют медианой. Чтобы узнать медиану, нужно иметь отсортированный массив, а чтобы отсортировать массив — знать медиану. Получается замкнутый круг.
На практике необязательно делить массив ровно пополам — достаточно разбить массив на приблизительно равные части — алгоритм все равно будет работать быстро. Если элементы в массиве расположены в случайном порядке, то можно брать любой элемент по счету — в среднем массив будет всегда разбит пополам.
Можно выбрать самый левый элемент в качестве опорного элемента — как видно на примере выше, это работает.
Выше мы написали универсальную функцию, которая может сортировать отдельные подмассивы. Сложность в том, что такой функцией не очень удобно пользоваться — приходится передавать параметры left и right даже тогда, когда надо отсортировать массив целиком.
Чтобы упростить себе жизнь, напишем вспомогательную функцию, которая всегда сортирует массив целиком:
const quicksort = (items) => sort(items, 0, items.length - 1);
const items = [ 57, 10, 52, 43, 55, 93, 34, 24, 99 ];
quicksort(items);
console.log(items); // => [ 10, 24, 34, 43, 52, 55, 57, 93, 99 ]Python
def quicksort(items):
sort(items, 0, len(items) - 1)
items = [57, 10, 52, 43, 55, 93, 34, 24, 99]
quicksort(items)
print(items) # => [10, 24, 34, 43, 52, 55, 57, 93, 99]PHP
<?php
function quicksort($items)
{
return sort($items, 0, count($items) - 1);
}
$items = [ 57, 10, 52, 43, 55, 93, 34, 24, 99 ];
quicksort($items);
print_r($items); // => [ 10, 24, 34, 43, 52, 55, 57, 93, 99 ]Java
class App {
public static void quicksort(int[] items) {
return sort(items, 0, items.length - 1);
}
// ...
}
int[] items = [ 57, 10, 52, 43, 55, 93, 34, 24, 99 ];
App.quicksort(items);
System.out.println(Arrays.toString($items));
// => [ 10, 24, 34, 43, 52, 55, 57, 93, 99 ]Быстрая сортировка намного эффективнее сортировки выбором. Причем эта разница особенно видна на больших массивах. Если сортировать миллион элементов, сортировка выбором окажется медленнее в десятки тысяч раз.
Универсальная функция сортировки
Мы реализовали три функции сортировки, каждая из которых упорядочивает в возрастающем порядке элементы простых типов: чисел, дат, строк.
Вспомним пример с интернет-магазином, в котором мы сталкиваемся с более сложной задачей — сортировкой по разным атрибутам. Представим, что нам предстоит сортировать товары по трем атрибутам:
-
Название —
name -
Цена —
price -
Рейтинг —
rating
Сам массив выглядит так:
const products = [
{ name: "Телевизор", price: 100000, rating: 9.1 },
{ name: "Холодильник", price: 20000, rating: 8.3 },
{ name: "Пылесос", price: 14000, rating: 7.5 },
{ name: "Стиральная машина", price: 30000, rating: 9.2 },
{ name: "Миелофон", price: 200000, rating: 8.7 },
{ name: "Микроволновка", price: 7000, rating: 8.2 },
{ name: "Проигрыватель", price: 20000, rating: 9.0 },
{ name: "Посудомоечная машина", price: 80000, rating: 7.8 },
{ name: "Мультиварка", price: 5000, rating: 7.1 },
];Python
products = [
{"name": "Телевизор", "price": 100000, "rating": 9.1},
{"name": "Холодильник", "price": 20000, "rating": 8.3},
{"name": "Пылесос", "price": 14000, "rating": 7.5},
{"name": "Стиральная машина", "price": 30000, "rating": 9.2},
{"name": "Миелофон", "price": 200000, "rating": 8.7},
{"name": "Микроволновка", "price": 7000, "rating": 8.2},
{"name": "Проигрыватель", "price": 20000, "rating": 9.0},
{"name": "Посудомоечная машина", "price": 80000, "rating": 7.8},
{"name": "Мультиварка", "price": 5000, "rating": 7.1},
]PHP
<?php
$products = [
['name' => 'Телевизор', 'price' => 100000, 'rating' => 9.1],
['name' => 'Холодильник', 'price' => 20000, 'rating' => 8.3],
['name' => 'Пылесос', 'price' => 14000, 'rating' => 7.5],
['name' => 'Стиральная машина', 'price' => 30000, 'rating' => 9.2],
['name' => 'Миелофон', 'price' => 200000, 'rating' => 8.7],
['name' => 'Микроволновка', 'price' => 7000, 'rating' => 8.2],
['name' => 'Проигрыватель', 'price' => 20000, 'rating' => 9.0],
['name' => 'Посудомоечная машина', 'price' => 80000, 'rating' => 7.8],
['name' => 'Мультиварка', 'price' => 5000, 'rating' => 7.1],
];Java
Map[] products = {
Map.of ("name", "Телевизор", "price", 100000, "rating", 9.1),
Map.of ("name", "Холодильник", "price", 20000, "rating", 8.3),
Map.of ("name", "Пылесос", "price", 14000, "rating", 7.5),
Map.of ("name", "Стиральная машина", "price", 30000, "rating", 9.2),
Map.of ("name", "Миелофон", "price", 200000, "rating", 8.7),
Map.of ("name", "Микроволновка", "price", 7000, "rating", 8.2),
Map.of ("name", "Проигрыватель", "price", 20000, "rating", 9.0),
Map.of ("name", "Посудомоечная машина", "price", 80000, "rating", 7.8),
Map.of ("name", "Мультиварка", "price", 5000, "rating", 7.1)
};Можно реализовать несколько функций сортировки, но есть и более эффективный способ. Интернет-магазину подойдет универсальная функция сортировки.
Каждую из трех видов сортировок выше можно сделать универсальной — и тогда алгоритм сможет сортировать данные любого типа. Для этого надо добавить еще один параметр — функцию сравнения (компаратор). Универсальная функция сортировки вызывает компаратор каждый раз, когда требуется сравнить два элемента и определить, какой из них больше.
У компаратора два параметра — два элемента массива, которые надо сравнить. Если первый больше второго, компаратор возвращает 1. Если первый меньше второго, компаратор возвращает -1. Если элементы равны, компаратор возвращает 0.
Вот так будет выглядеть компаратор, сравнивающий элементы по цене:
const compareByPrice = (item1, item2) => {
if (item1.price < item2.price) {
return -1;
} else if (item1.price == item2.price) {
return 0;
} else {
return 1;
}
};Python
def compare_by_price(item1, item2):
if item1[price] < item2[price]:
return -1
elif item1[price] == item2[price]:
return 0
else:
return 1PHP
<?php
function compareByPrice($item1, $item2)
{
if ($item1['price'] < $item2['price']) {
return -1;
} else if ($item1['price'] == $item2['price']) {
return 0;
} else {
return 1;
}
}Java
public static ToIntBiFunction<Map<String, Object>, Map<String, Object>> compareByPrice = (item1, item2) -> {
var price1 = (int) item1.get("price");
var price2 = (int) item2.get("price");
if (price1 < price2) {
return -1;
} else if (price1 == price2) {
return 0;
} else {
return 1;
}
};А вот так — компаратор, сравнивающий элементы по рейтингу:
const compareByRating = (item1, item2) => {
if (item1.rating < item2.rating) {
return -1;
} else if (item1.rating == item2.rating) {
return 0;
} else {
return 1;
}
};Python
def compare_by_rating(item1, item2):
if item1[rating] < item2[rating]:
return -1
elif item1[rating] == item2[rating]:
return 0
else:
return 1PHP
<?php
function compareByRating($item1, $item2)
{
if ($item1['rating'] < $item2['rating']) {
return -1;
} else if ($item1['rating'] == $item2['rating']) {
return 0;
} else {
return 1;
}
}Java
public static ToIntBiFunction<Map<String, Object>, Map<String, Object>> compareByRating = (item1, item2) -> {
var rating1 = (double) item1.get("rating");
var rating2 = (double) item2.get("rating");
if (rating1 < rating2) {
return -1;
} else if (rating1 == rating2) {
return 0;
} else {
return 1;
}
};Универсальная функция сравнивает два элемента, но не использует операторы «больше» или «меньше». Вместо этого она вызывает компаратор и проверяет результат. Так выглядит универсальная пузырьковая сортировка:
const bubbleSort = (items, comparator) => {
for (let limit = items.length - 1; limit > 0; limit -= 1) {
for (let i = 0; i < limit; i += 1) {
if (comparator(items[i], items[i + 1]) > 0) {
const temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;
}
}
}
};Python
def bubble_sort(items, comparator):
for limit in range(len(items) - 1, 0, -1):
for i in range(limit):
if comparator(items[i], items[i + 1]) > 0:
items[i], items[i + 1] = items[i + 1], items[i]PHP
<?php
function bubbleSort($items, $comparator)
{
for ($limit = count(items) - 1; $limit > 0; $limit -= 1) {
for ($i = 0; $i < $limit; $i += 1) {
if (comparator($items[$i], $items[$i + 1]) > 0) {
$temporary = $items[$i];
$items[$i] = $items[$i + 1];
$items[$i + 1] = $temporary;
}
}
}
}Java
class App {
public static void bubbleSort(Map[] items, ToIntBiFunction comparator) {
for (var limit = items.length - 1; limit > 0; limit--) {
for (var i = 0; i < limit; i++) {
if (comparator.applyAsInt(items[i], items[i + 1]) > 0) {
var temporary = items[i];
items[i] = items[i + 1];
items[i + 1] = temporary;
}
}
}
}
}