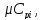Как найти массовую долю через объемную долю

При решении химических задач, при расчётах на работе, да и просто в жизни иногда приходится рассчитывать концентрации. Неважно, будет это школьная теоретическая задача, необходимость приготовить электролит для аккумулятора автомобиля, надобность узнать количество сахара для компота — все расчёты концентраций выполняются по известным формулам, которых не так много. Однако, с этим часто возникают трудности.

Прочитав эту статью, Вы научитесь легко рассчитывать концентрации веществ и при надобности играючи переводить одну концентрацию в другую. В статье приводятся примеры задач с решениями, а в конце приведём справочную табличку с формулами, которую можно распечатать и держать под рукой.

Массовая доля

Начнём с простого, но в то же время нужного способа выражения концентрации компонента в смеси — массовой доли.

Массовая доля есть отношение массы данного компонента к сумме масс всех компонентов. Обозначать её принято буквой w или ω (омега).

Рассчитывается массовая доля по формуле:

Large w_{i}=frac{m_{i}}{m}, ;;;;;(1)

где Large w_{i} — массовая доля компонента i в смеси,

Large m_{i} — масса этого компонента,

m — масса всей смеси.

И сразу разберём на примере:

Задача:

Зимой дороги посыпают песком с солью. Известно, что куча имеет массу 50 кг, и в неё всыпали 1 кг соли и перемешали. Найти массовую долю соли.

Решение:

Масса соли есть Large m_{i} по формуле выше. Масса всей смеси нам пока неизвестна, но найти её легко. Просуммируем массу песка и соли:

Large m = m_{п}+m_{с}= 50 кг + 1 кг = 51 кг

А теперь находим и массовую долю:

Large w_{с} = frac{m_{с}}{m} = 1 кг / 51 кг = 0.0196,

или умножаем на 100% и получаем 1.96%.

Ответ: 0.0196, или 1.96%.

Теперь решим что-то посложнее, и ближе к ЕГЭ.

Задача:

Смешали 200 г раствора глюкозы с массовой концентрацией 25% и 300 г раствора глюкозы с массовой концентрацией 10%. Найти массовую концентрацию полученного раствора, ответ округлить до целых.

Решение:

Обозначим первый и второй растворы соответственно Large m_{1} и Large m_{2}. Массу полученного после смешения раствора обозначим Large m и найдём:

Large m = m_{1} + m_{2} = 200 г + 300 г = 500 г

Массу самой глюкозы в первом и втором растворе обозначим Large m_{гл. 1} и Large m_{гл. 2}. По формуле (1) это будут наши массы компонентов. Массы растворов нам известны, их массовые концентрации тоже. Как найти массу компонента? Очень просто, находим неизвестное делимое умножением (и не забываем, что проценты — это сотые части):

Large m_{гл. 1} = w_{1}cdot m_{1} = 0.25 cdot 200 г = 50 г

Large m_{гл. 2} = w_{2}cdot m_{2} = 0.1 cdot 300 г = 30 г

Таким образом, общая масса глюкозы Large m_{гл}:

Large m_{гл} = m_{гл. 1} + m_{гл. 2} = 50 г + 30 г = 80 г.

Ответ: 80 г.

Задачи на смешение раствором с разными концентрациями одного вещества можно решать с помощью «конверта Пирсона».

Объёмная доля

Часто, когда мы имеем дело с жидкостями и газами, удобно оперировать их объёмами, а не массой. Поэтому, чтобы выражать долю какого-либо компонента в таких смесях (но и в твёрдых тоже вполне можно), пользуются понятием объёмной доли.

Объёмная доля компонента — отношение объёма компонента к сумме объёмов компонентов до смешивания. Объёмная доля измеряется в долях единицы или в процентах. Обычно обозначается греческой буквой φ (фи).

Рассчитывается объёмная доля по формуле:

Large phi_{B}=frac{V_{B}}{sum{V_{i}}}, ; ;;;; (2)

где Large phi_{B} — объёмная доля компонента B;

Large V_{B} — объём компонента B;

Large sum{V_{i}} — сумма объёмов всех компонентов.

Здесь важно понимать, что в формулу по возможности подставляем именно сумму объёмов всех компонентов, а не объём смеси, так как при смешивании некоторых жидкостей суммарный объём уменьшается. Так, если смешать литр воды и литр спирта, два литра аквавита мы не получим — будет примерно 1800 мл. В школьных задачах, как правило, это не так важно, но в уме держим и помним.

Задача:

Смешали 6 объёмов воды и 1 объём серной кислоты. Найти объёмную долю кислоты в полученном растворе.

Решение:

Так как объёмная доля — безразмерная величина, объёмы компонентов в условии задачи могут даваться в любых единицах — литрах, стаканах, баррелях, штофах, сексталях — главное, чтобы в одинаковых. Если не так — переводим одни в другие, если одинаковые — решаем. В нашем условии описаны просто некоторые «объёмы», их и подставляем.

Large phi_{H_{2}SO_{4}} = frac{V_{ H_{2}SO_{4} }} { V_{ H_{2}SO_{4}} + V_{H_{2}O}} = frac{1 : объём}{1 : объём + 6 : объёмов} = frac{1 : объём}{7 : объёмов} = 0.143, : или : 14.3%

Ответ: 14.3 %.

С газами всё обстоит немного интереснее — при не очень больших давлениях и температурах объёмная доля какого-либо газа в газовой смеси равна его мольной доле. (Ведь мы знаем, что молярный объём газов почти равен 22.4 л/моль).

Задача:

Мольная доля кислорода в сухом воздухе составляет 0.21. Найдите объёмную долю азота, если объёмная доля аргона составляет 1%.

Решение:

Внимательный читатель заметил, что мы написали о том, что объёмная и мольная доля для газов в смеси равны. Поэтому, объёмная доля кислорода равна также 0.21, или 21%. Найдём объёмную долю азота:

Large 100% – 21% – 1% = 78%.

Ответ: 78%.

Мольная доля

В тех случаях, когда нам известны количества веществ в смеси, мы можем выразить содержание того или иного компонента с помощью мольной доли.

Мольная доля — отношение количества молей данного компонента к общему количеству молей всех компонентов. Мольную долю выражают в долях единицы. ИЮПАК рекомендует обозначать мольную долю буквой x (а для газов — y).

Находят мольную долю по формуле:

Large x_{B} = frac{n_{B}}{sum{n_{i}}}, ;;;;;(3)

где Large x_{B} — мольная доля компонента B;

Large n_{B} — количество компонента B, моль;

Large sum{n_{i}} — сумма количеств всех компонентов.

Разберём на примере.

Задача:

При неизвестных условиях смешали 3 кг азота, 1 кг кислорода и 0.5 кг гелия. Найти мольную долю каждого компонента полученной газовой смеси.

Решение:

Сначала находим количество каждого из газов (моль):

Large n_{N_{2}} = frac{ m_{N_{2}}}{M_{N_{2}}} = frac {3000 : г}{28 : ^г/_{моль}} = 107.14 : моль

Large n_{O_{2}} = frac{ m_{O_{2}}}{M_{O_{2}}} = frac {1000 : г}{32 : ^г/_{моль}} = 31.25 : моль

Large n_{He} = frac{ m_{He}}{M_{He}} = frac {500 : г}{4 : ^г/_{моль}} = 125 : моль

Затем считаем сумму количеств:

Large sum {n} = 107.14 : моль + 31.25 : моль + 125 : моль = 263.39 : моль

И находим мольную долю каждого компонента:

Large y_{N_{2}} = frac {107.14 : моль}{263.39 : моль} = 0.4068, : или : 40.68 %;

Large y_{O_{2}} = frac {31.25 : моль}{263.39 : моль} = 0.1186, : или : 11.86 %;

Large y_{He} = frac {125 : моль}{263.39 : моль} = 0.4746, : или : 47.46 %;

Проверяем:

Large 40.68 % + 11.86 % + 47.46 % = 100%.

И радуемся правильному решению.

Ответ: 40.68%, 11.86% , 47.46%.

Молярность (молярная объёмная концентрация)

А сейчас рассмотрим, вероятно, самый часто встречающийся способ выражения концентрации — молярную концентрацию.

Молярная концентрация (молярность, мольность) — количество вещества (число молей) компонента в единице объёма смеси. Молярная концентрация в системе СИ измеряется в моль/м³, однако на практике её гораздо чаще выражают в моль/л или ммоль/л.

Также иногда говорят просто «молярность», и обозначают буквой М. Это значит, что, например, обозначение «0.5 М раствор соляной кислоты» следует понимать как «полумолярный раствор соляной кислоты», или 0.5 моль/л.

Обозначают молярную концентрацию буквой c (латинская «цэ»), или заключают в квадратные скобки вещество, концентрация которого указывается. Например, [Na⁺] — концентрация катионов натрия в моль/л. Кстати, слово «моль» в обозначениях не склоняют — 5 моль/л, 3 моль/л.

Рассчитывается молярная концентрация по формуле:

Large c_{B} = frac{n_{B}}{V} ; ; ;;; (4)

где Large n_{B} — количество вещества компонента B, моль;

Large V — общий объём смеси, л.

Разберём на примере.

Задача:

В пивную кружку зачем-то насыпали 24 г сахара и до краёв заполнили кипятком. А нам зачем-то нужно найти молярную концентрацию сахарозы в полученном сиропе. И кстати, дело происходило в Британии.

Решение:

Молекулярная масса сахарозы равна 342 (посчитайте, может мы ошиблись — C₁₂H₂₂O₁₁). Найдём количество вещества:

Large n_{сахарозы} = frac{24 : г}{342 : г/моль} = 0.0702 моль

Британская пинта (мера объёма такая) равна 0.568 л. Поэтому молярная концентрация находится так:

Large c_{сахарозы} = frac{0.0702 : моль}{0.568 : л} = 0.1236 моль/л

Ответ: 0.1236 моль/л.

Нормальная концентрация (молярная концентрация эквивалента, «нормальность»)

Нормальная концентрация — количество эквивалентов данного вещества в 1 литре смеси. Нормальную концентрацию выражают в моль-экв/л или г-экв/л (имеется в виду моль эквивалентов).

Обозначается нормальная концентрация как с_н, с_N, или даже c(f_eq B). Рассчитывается нормальная концентрация по формуле:

Large c_{N} = z cdot c_{B} = z cdot frac{n_{B}}{V}= frac{1}{f_{eq}} cdot frac {n_{B}}{V} ; ;;;; (5)

где Large n_{B} — количество вещества компонента В, моль;

V — общий объём смеси, л;

z — число эквивалентности (фактор эквивалентности Large f_{eq} = 1/z ).

Значение нормальной концентрации для растворов записывают как «н» или «N», а говорят «нормальность» или «нормальный». Например, раствор с концентрацией 0.25 н — четвертьнормальный раствор.

Разберём на примере.

Задача:

Рассчитать нормальность раствора объёмом 1 л, если в нём содержится 40 г перманганата калия. Раствор приготовили для последующего проведения реакции в нейтральной среде.

Решение:

В нейтральной среде перманганат калия восстанавливается до оксида марганца (IV). При этом в окислительно-восстановительной реакции 1 атом марганца принимает 3 электрона (проверьте на любой окислительно-восстановительной реакции перманганата калия с образованием оксида, расставив степени окисления), что означает, что число эквивалентности будет равно 3. Для расчёта концентрации по формуле (5) выше нам ещё не хватает количества вещества KMnO4. найдём его:

Large n_{KMnO_{4}}=frac{m _{KMnO_{4}}}{M _{KMnO_{4}} } = frac{40 : г}{158 г/моль}= 0.253 моль

Теперь считаем нормальную концентрацию:

Large c_{N_{KMnO_{4}}}= z cdot frac{n_{KMnO_{4}}}{V} = 3 cdot frac{0.253 : моль}{1 : л} = 0.759 моль-экв/л

Ответ: 0.759 моль-экв/л.

Таким образом, заметим важное на практике свойство — нормальная концентрация больше молярной в z раз.

Мы не будем рассматривать в данной статье особо экзотические способы выражения концентраций, о них вы можете почитать в литературе или интернете. Поэтому расскажем ещё об одном способе, и на нём остановимся — массовая концентрация.

Моляльная концентрация

Моляльная концентрация (моляльность, молярная весовая концентрация) — количество растворённого вещества (число моль) в 1000 г растворителя.

Измеряется моляльная концентрация в молях на кг. Как и с молярной концентрацией, иногда говорят «моляльность», то есть раствор с концентрацией 0.25 моль/кг можно назвать четвертьмоляльным.

Находится моляльная концентрация по формуле:

Large m_{B} = frac{n_{B}}{m_{A}}, ;;;;; (6)

где Large n_{B} — количество вещества компонента B, моль;

Large m_{A} — масса растворителя, кг.

Казалось бы, зачем нужна такая единица измерения для выражения концентрации? Так вот, у моляльной концентрации есть одно важное свойство — она не зависит от температуры, в отличие, например, от молярной. Подумайте, почему?

Массовая концентрация

Массовая концентрация — отношение массы растворённого вещества к объёму раствора. По рекомендации ИЮПАК, обозначается символом γ или ρ.

Находится массовая концентрация по формуле:

Large rho_{B}=frac{m_{B}}{V}, ;;;;; (7)

где Large m_{B} — масса растворенного вещества, г;

Large V — общий объём смеси, л.

В системе СИ выражается в кг/м³.

Разберём на примере.

Задача:

Рассчитать массовую концентрацию перманганата калия по условиям предыдущей задачи.

Решение:

Решение будет совсем простым. Считаем:

Large rho_{ KMnO_{4} }=frac{m_{ KMnO_{4} }}{V} =frac{40 : г}{1 : л} = 40 г/л.

Ответ: 40 г/л.

Также в аналитической химии пользуются понятием титра по растворенному веществу. Титр по растворенному веществу находится так же, как и массовая концентрация, но выражается в г/мл. Легко догадаться, что в задаче выше титр будет равен 0.04 г/мл (для этого надо умножить наш ответ на 0.001 мл/л, проверьте). Кстати, обозначается титр буквой Т.

А теперь, как обещали, табличка с формулами перевода одной концентрации в другую.

Таблица перевода одной концентрации в другую.

В таблице слева — ВО ЧТО переводим, сверху — ЧТО. Если стоит знак «=», то, естественно, эти величины равны.

	Массовая доля, large omega, %	Мольная доля, large x , %	Объёмная доля, large phi, %	Молярная концентрация, large c, моль/л	Нормальная концентрация, large c_{N} , моль-экв/л	Моляльная концентрация, large m, моль/кг	Массовая концентрация, large rho, г/л
Массовая доля, large omega, %	=	large omega_{B}=LARGE frac{x_{B} cdot M(B)}{sum x_{i} cdot M_{i}}	Для газов: omega = LARGE frac{phi_{A} cdot M(A)}{sum (M_{i} cdot phi_{i})}	large omega_{B}= LARGE frac{c_{B} cdot M(B)}{rho}	large omega_{B}=LARGE frac{c_{N} cdot M(B)}{rho cdot z}		large omega_{B}= LARGE frac{gamma_{B}}{rho}
Мольная доля, large x , %	large x_{B}=LARGE frac{frac{omega_{B}}{M(B)}}{sum frac{omega_{i}}{M_{i}}}	=				large x_{B}=LARGE frac{m_{B}}{m_{B}+frac{1}{M(A)}}
Объёмная доля, large phi, %	Для газов: large phi_{A}=LARGE frac{frac{omega_{A}}{M(A)}}{sum frac{omega_{i}}{M_{i}}}		=
Молярная концентрация, large c, моль/л	large c_{B}=LARGE frac{rho cdot omega_{B}}{M(B)}			=	large c_{B}=Large frac{c_{N}}{z}
Нормальная концентрация, large c_{N} , моль-экв/л	large c_{N}=LARGE frac{rho cdot omega_{B} cdot z}{M(B)}			large c_{N}=c_{B} cdot z	=
Моляльная концентрация, large m, моль/кг		large m_{B}=Large frac{x_{B}}{M(A)(1-x_{B})}				=
Массовая концентрация, large gamma, г/л	large gamma_{B}=rho cdot omega_{B}						=

Таблица будет пополняться.

В качестве рабочих тел могут использоваться
смеси, состоящие из нескольких газов.
Если смесь состоит из идеальных газов,
то для неё справедливы все соотношения,
полученные для однородного идеального
газа. Например, уравнение состояния
идеального газа для 1кг смеси

P·v=R_см·T;

для
m>1 кг

P·V=m·R_см·T,

где R_см=R₀/µ_см– газовая постоянная смеси, Дж/(кг·град);

R₀=8314 Дж/(кмоль·град) – универсальная
газовая постоянная;

v
– удельный объём смеси, м³/кг;

µ_см –
«кажущаяся» молекулярная масса смеси,
кг/кмоль.

Для
определения R_см иµ_см необходимо знать состав
смеси, который может быть задан массовыми
или объёмными долями.

Определение состава газовой смеси в массовых долях

Массовая доля

,

где

– массаi-го газа
в смеси, кг;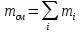– масса смеси, кг.

Определение удельной газовой
постоянной смеси R_см

и состава смеси в объёмных долях

Если смесь задана массовыми долями, то

или

,

где
– характеристическая газовая постояннаяi-го компонента,
Дж/(кг·град);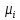– молекулярная массаi-го
компонента, кг/кмоль.

Объёмная
доля, выраженная через массовую долю

.

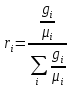Определение «кажущейся» молекулярной
массы смеси

через массовые и объёмные доли

или

.

Определение плотности и удельного
объёма смеси

при нормальных физических условиях

Нормальные физические условия:

P₀ =760 мм
рт.ст.=101300 Па,t₀= 0°C= 273K.

Тогда

,
м³/кг,

,
кг/м³.

Определение параметров состояния
смеси P,
v, T

в характерных точках цикла и
показателей политропы

Недостающие (не заданные) параметры
состояния в характерных точках цикла
(1, 2, 3, 4, 5) определяются из уравнения
состояния

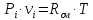
и по
известным (заданным) соотношениям для
характерных процессов цикла

;;.

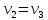Показатель политропы:

для
процесса 1-2

,

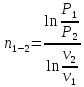для
процесса 4-5

.

Определение
процессных теплоёмкостей C_v
и C_p
газовой смеси

и
показателя адиабаты k

Теплоёмкости смеси при постоянном
объёме и давлении в кДж/(кг·град)

;,

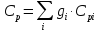где
и– теплоёмкости каждого компонента в
составе смеси. Находятся с учётом
количества атомов в молекуле и молекулярной
массы по формулам (руководствуясь
таблицей 8):

,.

Таблица
8. Мольные теплоёмкости газов в соответствии

с
молекулярно-кинетической теорией
строения газов

Газы
Одноатомные	12,5	20,8
Двухатомные	20,8	29,1
Трёх- и многоатомные	29,1	37,4

Показатель адиабаты
.

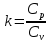Процессные теплоёмкости для:

процесса 1-2
,

процесса 2-3

,

процесса 3-4

,

процесса 4-5
,

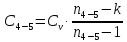процесса 5-1

.

Примечание: для изотермических
процессов теплоёмкость равна
∞.

Определение изменения внутренней энергии Δu, энтальпии Δh

и
энтропии Δs
в процессах, составляющих цикл

Изменение внутренней энергии в любом
процессе

,
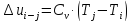кДж/кг.

Изменение энтальпии в любом процессе

,
кДж/кг.

Изменение энтропии в любом процессе
(кроме изотермического)

,
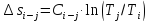кДж/кг.

Изменение энтропии в изотермическом
процессе

,
кДж/кг.

Определение
количества работы изменения объёма l,

совершаемой в каждом из процессов,
и теплоты q,

подводимой (отводимой) в каждом из
процессов, составляющих цикл

Для
процесса 1-2:

,
кДж/кг;,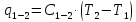
кДж/кг.

Для
процесса 2-3:

,
кДж/кг;,
кДж/кг.

Для
процесса 3-4:

,
кДж/кг;,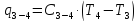
кДж/кг.

Для
процесса 4-5:

,
кДж/кг;,
кДж/кг.

Для
процесса 5-1:

,
кДж/кг;,
кДж/кг.

Примечание: для изотермических
процессов теплота и работа рассчитываются
по формуле,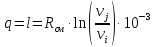
кДж/кг.

Количество теплоты q₁,
подводимое в цикле, – это сумма
количеств теплоты тех процессов, в
которых теплота участвует со знаком
«+»;

количество теплоты q₂,
отводимое в цикле, – это сумма
количеств теплоты тех процессов, в
которых теплота участвует со знаком
«-»;

полезная работа l_ц
– это алгебраическая сумма количеств
работы во всех процессах цикла;

термический КПД цикла
,

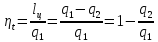термический КПД цикла Карно
.

Примечание: при построении цикла
в диаграммеs–Tрекомендуется значение энтропии смеси
в состоянии 1 условно принять равным
нулю (s₁=0). Тогда
состояние 2 на диаграмме находится по
значениям температурыT₂и величины(с учётом знака изменения этропии).
Расчёт промежуточных точек в процессе
1-2 производится по произвольно выбранной
температуреT_x
в интервале (T₁–T₂)
и изменению энтропии.
Аналогично строятся остальные процессы
цикла.

Соседние файлы в папке ТТ ЭТК-2з

• #
• #
• #
• #
• #
• #

Решение задач с долей вещества в смеси, в соединении

Ключевые слова конспекта: массовая доля вещества в смеси или растворе, молярная доля вещества, объемная доля вещества, массовая доля элемента в соединении, масса элемента, массовая доля элемента.

---

 Массовую долю вещества в смеси или растворе вычисляют как отношение массы вещества, входящего в состав смеси, к массе всей смеси. Массовую долю часто выражают в процентах. Для этого отношение массы вещества к массе смеси умножают на 100%:

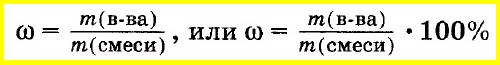
Аналогично объемную долю вещества вычисляют как отношение объема вещества к объему смеси, а молярную долю вещества — как отношение количества вещества одного из компонентов смеси к сумме количеств веществ всех компонентов смеси:

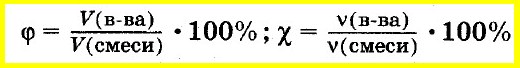
Массовую долю элемента в соединении вычисляют как отношение массы элемента, входящего в состав данного соединения, к массе всего соединения:

Зная молекулярную формулу соединения, массу элемента, входящего в его состав, вычисляют как произведение молярной массы элемента на число атомов этого элемента в соединении.

В этом случае массовую долю элемента в соединении рассчитывают как отношение этой величины к молярной массе всего соединения:

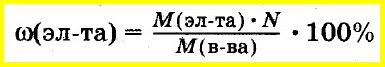
Цитаты из пособия «Задачи по химии 8-9 кл.» (авт. О.С. Габриелян и др.) использованы в учебных целях. Ссылка на покупку книги указана в конце конспекта.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
25 г оксида магния смешали с 35 г оксида алюминия. Определите массовую долю оксида магния в данной смеси.

Ответ. ω(MgO) = 0,417, или 41,7%.

Задача № 2.
Вычислите объемную долю азота в смеси газов, содержащей 32 л азота, 48 л углекислого газа, 36 л гелия и 14 л водорода.

Ответ. φ(N₂) = 0,246, или 24,6%.

Задача № 3.
Вычислите молярную и массовую долю (в %) оксида углерода (II) в смеси, содержащей 16,8 л (н. у.) оксида углерода (II) и 13,44 л (н. у.) оксида углерода (IV).

Ответ. χ(СО) = 55,56%, ω(СО) = 44,3%.

Задача № 4.
В воде растворили 15 г хлорида натрия. Вычислите массу полученного раствора, если массовая доля соли в нем равна 5%.

Ответ: m(р-ра) = 300 г.

Задача № 5.
Образец сплава меди с цинком имеет массу 75 г. Массовая доля меди в этом сплаве равна 64%. Определите массу цинка в данном образце.

Ответ. m(Zn) = 27 г.

[highlight]Задача № 6.[/highlight] Объемная доля аммиака в смеси с кислородом равна 40%. Вычислите плотность данной смеси по воздуху.

Ответ. D_возд(смеси) = 0,896.

Задача № 7.
Найдите массовую долю кислорода в фосфате натрия.

Ответ. ω (O) = 39%.

[highlight]Задача № 8.[/highlight] Определите массовую долю фосфора в смеси, содержащей 55 г фосфата натрия и 70 г дигидрофосфата натрия.

Ответ. ω(Р) = 22,77%

[highlight]Задача № 9.[/highlight] Массовая доля серы в техническом сульфате натрия равна 20,48%. Рассчитайте массовую долю примесей в данном продукте (в %).

Ответ. ω (примесей) = 9,12%.

Задача № 10.
Плотность смеси оксида азота (II) и оксида азота (IV) по водороду равна 17,8. Найдите массовую долю оксида азота (IV) в данной смеси.

Ответ. ω(NO₂) = 45,2%.

---

Решение задач с долей вещества в смеси, в соединении. Выберите дальнейшие действия:

• Перейти к следующей теме: Решение задач на вывод формул соединений
• Вернуться к списку конспектов по Химии.
• Проверить знания по Химии.
• Купить книгу Задачи по химии и способы их решения. 8-9 кл. / О.С. Габриелян и др. — М.: Дрофа.

Материалы из методички: Сборник задач по теоретическим основам химии для студентов заочно-дистанционного отделения / Барботина Н.Н., К.К. Власенко, Щербаков В.В. – М.: РХТУ им. Д.И. Менделеева, 2007. -155 с.

Растворы. Способы выражения концентрации растворов

Способы выражения концентрации растворов

Существуют различные способы выражения концентрации растворов.

Массовая доля ω компонента раствора определяется как отношение массы данного компонента Х, содержащегося в данной массе раствора к массе всего раствора m. Массовая доля – безразмерная величина, её выражают в долях от единицы:

ω_р.в. = m_р.в./m_р-ра (0 < ω_р.в. < 1)                (1)

Массовый процент представляет собой массовую долю, умноженную на 100:

ω(Х) = m(Х)/m · 100% (0% < ω(Х) < 100%)                (2)

где ω(X) – массовая доля компонента раствора X; m(X) – масса компонента раствора X; m – общая масса раствора.

Мольная доля χ компонента раствора равна отношению количества вещества данного компонента X к суммарному количеству вещества всех компонентов в растворе.

Для бинарного раствора, состоящего из растворённого вещества Х и растворителя (например, Н₂О), мольная доля растворённого вещества равна:

χ(X) = n(X)/(n(X) + n(H₂O))                (3)

Мольный процент представляет мольную долю, умноженную на 100:

χ(X), % = (χ(X)·100)%                (4)

Объёмная доля φ компонента раствора определяется как отношение объёма данного компонента Х к общему объёму раствора V. Объёмная доля – безразмерная величина, её выражают в долях от единицы:

φ(Х) = V(Х)/V  (0 < φ(Х) < 1)             (5)

Объёмный процент представляет собой объёмную долю, умноженную на 100.

φ(X), % = (φ(X)·100)%                

Молярность (молярная концентрация) C или C_м определяется как отношение количества растворённого вещества X, моль к объёму раствора V, л:

C_м(Х) = n(Х)/V                   (6)

Основной единицей молярности является моль/л или М. Пример записи молярной концентрации: C_м(H₂SO₄) = 0,8 моль/л или 0,8М.

Нормальность С_н определяется как отношение количества эквивалентов растворённого вещества X к объёму раствора V:

C_н(Х) = n_экв.(Х)/V                   (7)

Основной единицей нормальности является моль-экв/л. Пример записи нормальной концентрации: С_н(H₂SO₄) = 0,8 моль-экв/л или 0,8н.

Титр Т показывает, сколько граммов растворённого вещества X содержится в 1 мл или в 1 см³ раствора:

T(Х) = m(Х)/V                   (8)

где m(X) – масса растворённого вещества X, V – объём раствора в мл.

Моляльность раствора μ показывает количество растворённого вещества X в 1 кг растворителя:

μ(Х) = n(Х)/m_р-ля                   (9)

где n(X) – число моль растворённого вещества X, m_р-ля – масса растворителя в кг.

Мольное (массовое и объёмное) отношение – это отношение количеств (масс и объёмов соответственно) компонентов в растворе.

Необходимо иметь ввиду, что нормальность С_н всегда больше или равна молярности С_м. Связь между ними описывается выражением:

С_м = С_н · f(Х)               (10)

Для получения навыков пересчёта молярности в нормальность и наоборот рассмотрим табл. 1. В этой таблице приведены значения молярности С_м, которые необходимо пересчитать в нормальность С_н и величины нормальности С_н, которые следует пересчитать в молярность С_м.

Пересчёт осуществляем по уравнению (10). При этом нормальность раствора находим по уравнению:

С_н = С_м/f(Х)                   (11)

Результаты расчётов приведены в табл. 2.

Таблица 1. К определению молярности и нормальности растворов

Тип химического превращения	См	Сн	Сн	См
Реакции обмена	0,2 M Na2SO4	?	6 н FeCl3	?
1,5 M Fe2(SO4)3	?	0,1 н Ва(ОН)2	?
Реакции окисления-восстановления	0,05 М KMnO4 в кислой среде	?	0,03 М KMnO4 в нейтральной среде	?

Таблица 2

Значения молярности и нормальности растворов

Тип химического превращения	См	Сн	Сн	См
Реакции обмена	0,2M Ma2SO4	0,4н	6н FeCl3	2М
	1,5M Fe2(SO4)3	9н	0,1н Ва(ОН)2	0,05М
Реакции окисления-восстановления	0,05М KMnO4 в кислой среде	0,25н	0,03М KMnO4 в нейтральной среде	0,01М

Между объёмами V и нормальностями С_н реагирующих веществ существует соотношение:

V₁ С_н,1 =V₂ С_н,2                    (12)

Примеры решения задач

Задача 1. Рассчитайте молярность, нормальность, моляльность, титр, мольную долю и мольное отношение для 40 мас.% раствора серной кислоты, если плотность этого раствора равна 1,303 г/см³.

Решение.

Масса 1 литра раствора равна М = 1000·1,303 = 1303,0 г.

Масса серной кислоты в этом растворе: m = 1303·0,4 = 521,2 г.

Молярность раствора С_м = 521,2/98 = 5,32 М.

Нормальность раствора С_н = 5,32/(1/2) = 10,64 н.

Титр раствора Т = 521,2/1000 = 0,5212 г/см³.

Моляльность μ = 5,32/(1,303 – 0,5212) = 6,8 моль/кг воды.

Обратите внимание на то, что в концентрированных растворах моляльность (μ) всегда больше молярности (С_м). В разбавленных растворах наоборот.

Масса воды в растворе: m = 1303,0 – 521,2 = 781,8 г.

Количество вещества воды: n = 781,8/18 = 43,43 моль.

Мольная доля серной кислоты: χ = 5,32/(5,32+43,43) = 0,109. Мольная доля воды равна 1– 0,109 = 0,891.

Мольное отношение равно 5,32/43,43 = 0,1225.

Задача 2. Определите объём 70 мас.% раствора серной кислоты (r = 1,611 г/см³), который потребуется для приготовления 2 л 0,1 н раствора этой кислоты.

Решение.

2 л 0,1н раствора серной кислоты содержат 0,2 моль-экв, т.е. 0,1 моль или 9,8 г.

Масса 70%-го раствора кислоты m = 9,8/0,7 = 14 г.

Объём раствора кислоты V = 14/1,611 = 8,69 мл.

Задача 3. В 5 л воды растворили 100 л аммиака (н.у.). Рассчитать массовую долю и молярную концентрацию NH₃ в полученном растворе, если его плотность равна 0,992 г/см³.

Решение.

Масса 100 л аммиака (н.у.) m = 17·100/22,4 = 75,9 г.

Масса раствора m = 5000 + 75,9 = 5075,9 г.

Массовая доля NH₃ равна 75,9/5075,9 = 0,0149 или 1,49 %.

Количество вещества NH₃ равно 100/22,4 = 4,46 моль.

Объём раствора V = 5,0759/0,992 = 5,12 л.

Молярность раствора С_м = 4,46/5,1168 = 0,872 моль/л.

Задача 4. Сколько мл 0,1М раствора ортофосфорной кислоты потребуется для нейтрализации 10 мл 0,3М раствора гидроксида бария?

Решение.

Переводим молярность в нормальность:

0,1 М Н₃РО₄  0,3 н; 0,3 М Ва(ОН)₂  0,6 н.

Используя выражение (12), получаем: V(H₃P0₄)=10·0,6/0,3 = 20 мл.

Задача 5. Какой объем, мл  2 и 14 мас.% растворов NaCl потребуется для приготовления 150 мл 6,2 мас.% раствора хлорида натрия?

Плотности растворов NaCl:

С, мас.%	2	6	7	14
ρ, г/см3	2,012	1,041	1,049	1,101

Решение.

Методом интерполяции рассчитываем плотность 6,2 мас.% раствора NaCl:

_6,2% =_6% + 0,2(_7% —_6% )/(7 – 6) = 1,0410 + 0,0016 = 1,0426 г/см³.

Определяем массу раствора: m = 150·1,0426 = 156,39 г.

Находим массу NaCl в этом растворе: m = 156,39·0,062 = 9,70 г.

Для расчёта объёмов 2 мас.% раствора (V₁) и 14 мас.% раствора (V₂) составляем два уравнения с двумя неизвестными (баланс по массе раствора и по массе хлорида натрия):

156,39 = V₁ 1,012 + V₂ 1,101 ,

9,70 = V₁·1,012·0,02 + V₂·1,101·0,14 .

Решение системы этих двух уравнений дает V₁ =100,45 мл и V₂ = 49,71 мл.

Задачи для самостоятельного решения

3.1. Рассчитайте нормальность 2 М раствора сульфата железа (III), взаимодействующего со щёлочью в водном растворе.

12 н.

3.2. Определите молярность 0,2 н раствора сульфата магния, взаимодействующего с ортофосфатом натрия в водном растворе.

0,1 M.

3.3. Рассчитайте нормальность 0,02 М раствора KMnO₄, взаимодействующего с восстановителем в нейтральной среде.

0,06 н.

3.4. Определите молярность 0,1 н раствора KMnO₄, взаимодействующего с восстановителем в кислой среде.

0,02 M.

3.5. Рассчитать нормальность 0,2 М раствора K₂Cr₂O₇, взаимодействующего с восстановителем в кислой среде.

1,2 M.

3.6. 15 г CuSO₄·5H₂O растворили в 200 г 6 мас.% раствора CuSO₄. Чему равна массовая доля сульфата меди, а также молярность, моляльность и титр полученного раствора, если его плотность составляет 1,107 г/мл?

0,1; 0,695М; 0,698 моль/кг; 0,111 г/мл.

3.7. При выпаривании 400 мл 12 мас.% раствора KNO₃ (плотность раствора 1,076 г/мл) получили 2М раствор нитрата калия. Определить объём полученного раствора, его нормальную концентрацию и титр.

255 мл; 2 н; 0,203 г/мл.

3.8. В 3 л воды растворили 67,2 л хлороводорода, измеренного при нормальных условиях. Плотность полученного раствора равна 1,016 г/мл. Вычислить массовую, мольную долю растворённого вещества и мольное отношение растворённого вещества и воды в приготовленном растворе.

0,035; 0,0177; 1:55,6.

3.9. Сколько граммов NaCl надо добавить к 250 г 6 мас.% раствору NaCl, чтобы приготовить 500 мл раствора хлорида натрия, содержащего 16 мас.% NaCl? Плотность полученного раствора составляет 1,116 г/мл. Определить молярную концентрацию и титр полученного раствора.

74,28 г; 3,05 М; 0,179 г/мл.

3.10. Определить массу воды, в которой следует растворить 26 г ВaCl₂·2H₂O для получения 0,55М раствора ВaCl₂ (плотность раствора 1,092 г/мл). Вычислить титр и моляльность полученного раствора.

192,4 г; 0,111 г/мл; 0,56 моль/кг.