Химическая формула соединения рассказывает нам не только о том, из каких элементов состоит вещества, но и о соотношении элементов в веществе. Давайте, например, посмотрим на серную кислоту Н2SO4 и сернистую кислоту H2SO3. Это два разных вещества, хотя оба состоят из водорода Н, серы S и кислорода О. Но из-за того, что соотношения элементов в них разное (в серной кислоте 4 атома кислорода, а в сернистой – 3), свойства у них тоже разные.
Используя химическую формулу, можно узнать и массовую доля элемента в соединении.
Массовая доля элемента в соединении показывает, какую часть составляет масса конкретного элемента от массы вещества.
Чтобы понять это сложное (на первый взгляд сложное, на самом деле оно простое) определения, представьте, что вы принесли из магазина пакет с покупками. В нём батон хлеба, пачка масла, два эскимо и упаковка чипсов. Весит пакет 1 килограмм. Какой вклад в это вносят чипсы? Пусть чипсы весят 50 граммов. Значит, от 1 килограмма (всей массы пакета с покупками) на чипсы приходится всего 50 граммов. Значит, можно посчитать, что чипсы – всего лишь 0,05 часть от всей массы пакета с покупками (50/1000=0,05).
Более удобно вычислять массовую долю в процентах, поэтому можно записать простую пропорцию:
1 килограмм (весь пакет с покупками) – 100%
50 граммов (упаковка чипсов) – Х%
Отсюда Х=50 г*100%/1000 г=5%. То есть массовая доля чипсов в пакете с покупками – 5%.
Теперь перейдём от покупок в супермаркете к химическим формулам.
Пример 1.
Определите массовую долю водорода и хлора в хлориде водорода.
Решение:
Формула хлорида водорода HCl. Чтобы определить массовые доли, нужно посчитать по таблице Менделеева молекулярную массу хлорида водорода. Она составляет 36,5 (1+35,5).
Из формулы мы видим, что в составе молекулы 1 атом водорода и 1 атом хлора. Обязательно обращайте на это внимание! Из примеров ниже будет видно, что это очень важно. Итак, составим пропорцию для определения массовой доли водорода:
36,5 (молекулярная масса соединения) – 100%
1 (атомная масса 1 атома водорода, входящего в соединение) – Х%
Отсюда Х=1*100/36,5=2,7%
Аналогично для хлора:
36,5 (молекулярная масса соединения) – 100%
35,5 (атомная масса 1 атома водорода, входящего в соединение) – Y%
Y=35,5*100/36,5=97,3%.
Таким образом, ответ: в хлориде водорода массовая доля водорода 2,7%, массовая доля хлора 97,3%.
Не лишним будет себя проверить, сложив все массовые доли. В сумме они должны давать 100 процентов. В нашем случае массовая доля водорода 2,7%+массовая доля хлора 97,3%=100%. Значит, мы всё сделали верно.
Пример 2.
Определите массовые доли углерода и кислорода в углекислом газе.
Решение:
Формула углекислого газа СО2. Обратите внимание, что здесь 2 атома кислорода. Это очень важно!
Теперь посчитаем молекулярную массу СО2, используя периодическую таблицу. Она будет равна 44: 12 (атомная масса углерода)+2*16 (атомная масса кислорода, умноженная на 2, потому что в формуле 2 атома кислорода).
Переходим к расчёту массовых долей с помощью пропорций.
Для углерода:
44 (молекулярная масса СО2) – 100%
12 (атомная масса 1 атома углерода) – Х%
Х=12*100/44=27,3%
Для кислорода:
44 (молекулярная масса СО2) – 100%
32 (масса 2 атомов кислорода, входящих в формулу) – Y%
Y=32*100/44=72,7%
Здесь мы взяли не 16 (атомная масса кислорода), а 32 потому, что в формуле СО2 2 атома кислорода. Помните, что выше я обращала на это внимание? Не упускайте это из виду, иначе будут ошибки.
Но ответ мы уже получили: в углекислом газе массовая доля углерода 27,3%, массовая доля кислорода 72,7%. (Проверим себя, сложив массовые доли: 27,3+72,7=100. Значит, всё верно).
Пример 3.
Этот пример от строгого репетитора по химии, который готовит к огэ по химии. Итак, найдите массовые доли алюминия и кислорода в оксиде алюминия.
Решение:
Формула оксида алюминия Al2O3. Не забудьте учесть число атомов алюминия и кислорода (как в примере выше)!
Сначала найдём молекулярную массу оксида алюминия, пользуясь таблицей Менделеева. Атомная масса алюминия 27, атомная масса кислорода 16. Молекулярная масса Al2O3 2*27+3*16 (потому что у нас 2 атома алюминия и 3 атома кислорода)=102.
Рассчитываем массовые доли.
Для алюминия:
102 (молекулярная масса Al2O3) – 100%
54 (масса 2 атомов алюминия, входящих в формулу) – Х%
Х=54*100/102=52,9%
Для кислорода:
102 (молекулярная масса Al2O3) – 100%
48 (масса 3 атомов кислорода, входящих в формулу) – Y%
Y=48*100/102=47,1%
Ответ: в оксиде алюминия массовая доля алюминия 52,9%, массовая доля кислорода 47,1% (проверка: 52,9+47,1=100).
А можно узнать формулу соединения, если известны массовые доли? И сделать это очень просто.
Пишите, пожалуйста, в комментариях, что осталось непонятным, и я обязательно дам дополнительные пояснения. Жалуйтесь на сложности в изучении школьного курса и говорите, что вас испугало в учебнике химии. И тогда следующая статья будет рассказывать именно об этой проблеме.
УЧЕБНИКИ. ПОСОБИЯ
О.С.ГАБРИЕЛЯН,
И.Г.ОСТРОУМОВ,
А.К.АХЛЕБИНИН
СТАРТ В ХИМИЮ
7 класс
Продолжение. Начало см. в № 1, 2, 3, 4, 5, 6, 7/2006
Глава 2. Математика в химии
(окончание)
§ 13. Объемная доля газов в смеси
В состав воздуха входит несколько различных
газов: кислород, азот, углекислый газ,
благородные газы, водяные пары и некоторые
другие вещества. Содержание каждого из этих
газов в чистом воздухе строго определенно.
Для того чтобы выразить состав смеси газов в
цифрах, т.е. количественно, используют особую
величину, которую называют объемной долей газов
в смеси.
Объемную долю газа в смеси обозначают
греческой буквой ![]()
– «фи».
Объемной долей газа в смеси называют
отношение объема данного газа к общему объему
смеси:
![]()
Что же показывает объемная доля газа в смеси
или, как говорят, какой физический смысл этой
величины? Объемная доля газа показывает, какую
часть общего объема смеси занимает данный газ.
Если бы нам удалось разделить 100 л воздуха на
отдельные газообразные компоненты, мы получили
бы около 78 л азота, 21 л кислорода, 30 мл углекислого
газа, в оставшемся объеме содержались бы так
называемые благородные газы (главным образом
аргон) и некоторые другие (рис. 62).
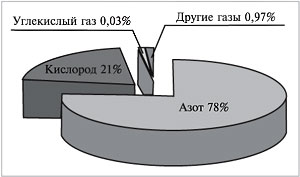 |
Рис. 62.
|
Рассчитаем объемные доли этих газов в
воздухе:
![]()
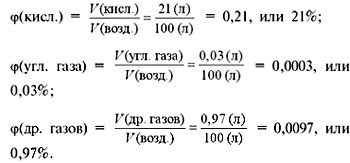
Нетрудно заметить, что сумма объемных долей
всех газов в смеси всегда равна 1, или 100%:
![]() (азота) +
(азота) +
![]() (кисл.) +
(кисл.) + ![]() (угл. газа) +
(угл. газа) + ![]() (др. газов) = 78% + 21% + 0,03% + 0,97% = 100%.
(др. газов) = 78% + 21% + 0,03% + 0,97% = 100%.
Тот воздух, который мы выдыхаем, гораздо беднее
кислородом (его объемная доля снижается до 16%),
зато содержание углекислого газа возрастает до
4%. Такой воздух для дыхания уже непригоден. Вот
почему помещение, в котором находится много
людей, надо регулярно проветривать.
В химии на производстве чаще приходится
сталкиваться с обратной задачей: определять
объем газа в смеси по известной объемной доле.
Пример. Вычислите объем кислорода,
содержащегося в 500 л воздуха.
Из определения объемной доли газа в смеси
выразим объем кислорода:
V(кисл.) = V(возд.)•![]() (кисл.).
(кисл.).
Подставим в уравнение числа и рассчитаем объем
кислорода:
V(кисл.) = 500 (л)•0,21 = 105 л.
Кстати, для приближенных расчетов объемную
долю кислорода в воздухе можно принять равной 0,2,
или 20%.
При расчете объемных долей газов в смеси можно
воспользоваться маленькой хитростью. Зная, что
сумма объемных долей равна 100%, для «последнего»
газа в смеси эту величину можно рассчитать
по-другому.
Задача. Анализ атмосферы Венеры
показал, что в 50 мл венерианского «воздуха»
содержится 48,5 мл углекислого газа и 1,5 мл азота.
Рассчитайте объемные доли газов в атмосфере
планеты.
Дано:
V(смеси) = 50 мл,
V(угл. газа) = 48,5 мл,
V(азота) = 1,5 мл.
Найти:
![]() (угл. газа),
(угл. газа),
![]() (азота).
(азота).
Решение
Рассчитаем объемную долю углекислого газа в
смеси. По определению:
![]()
Вычислим объемную долю азота в смеси, зная, что
сумма объемных долей газов в смеси равна 100%:
![]() (угл.
(угл.
газа) + ![]() (азота) = 100%,
(азота) = 100%,
![]() (азота) =
(азота) =
100% – ![]() (угл. газа) =
(угл. газа) =
100% – 97% = 3%.
Ответ. ![]() (угл.
(угл.
газа) = 97%, ![]() (азота) =
(азота) =
3%.
С помощью какой величины измеряют содержание
компонентов в смесях другого типа, например в
растворах? Понятно, что в этом случае
пользоваться объемной долей неудобно. На помощь
приходит новая величина, о которой вы узнаете на
следующем уроке.
1.
Что такое объемная доля компонента в газовой
смеси?2. Объемная доля аргона в воздухе 0,9%. Какой
объем воздуха необходим для получения 5 л аргона?3. При разделении воздуха было получено 224 л
азота. Какие объемы кислорода и углекислого газа
были получены при этом?
4.
Объемная доля метана в природном газе составляет
92%. Какой объем этой газовой смеси будет
содержать 4,6 мл метана?5. Смешали 6 л кислорода и 2 л углекислого
газа. Найдите объемную долю каждого газа в
полученной смеси.
§ 14. Массовая доля вещества в растворе
– Сколько ложечек сахара ты кладешь в чай?
– Дома – две, в гостях – восемь.
Шутка известная, но давайте посмотрим на нее
глазами химика. Вряд ли вам понравится такой «чай
в гостях». Уж очень сладкий он будет из-за
неумеренного содержания сахара! Содержание
растворенного вещества в растворе химики
называют концентрацией.
Концентрацию вещества можно выражать
различными способами. Кстати, число ложечек на
чашку воды – способ вполне приемлемый, но только
для кухни. Трудно представить себе химика,
приготавливающего раствор таким образом.
Один из самых распространенных способов
выражения концентрации раствора – через
массовую долю растворенного вещества.
Массовой долей![]() вещества в растворе называют
вещества в растворе называют
отношение массы растворенного вещества к массе
раствора:
![]()
Не правда ли, очень похоже на объемную долю? Так
оно и есть, ведь любая доля, как вы уже знаете, –
это отношение какой-то части к целому. Как и
массовая доля элемента в сложном веществе,
массовая доля вещества в растворе обозначается
греческой буквой ![]()
(«омега») и может принимать значения от 0 до 1 (или
от 0 до 100%). Она показывает, какая часть массы
раствора приходится на растворенное вещество. И
еще: массовая доля вещества в процентах численно
равна массе растворенного вещества в 100 г
раствора. К примеру, в 100 г 3%-го раствора уксуса
содержится 3 г чистой уксусной кислоты.
Самые простые растворы состоят из двух
компонентов. Один из компонентов раствора –
растворитель. Для нас более привычны жидкие
растворы, значит, растворитель в них – жидкое
вещество. Чаще всего – вода.
Другой компонент раствора – растворенное
вещество. Им может быть и газ, и жидкое, и твердое
вещество.
Масса раствора складывается из массы
растворителя и массы растворенного вещества, т.
е. верно выражение:
m(раствора) = m(растворителя) + m(растворенного
вещества).
Предположим, массовая доля растворенного
вещества равна 0,1, или 10%. Значит, оставшиеся 0,9,
или 90%, – это массовая доля растворителя.
Массовая доля растворенного вещества широко
используется не только в химии, но и в медицине,
биологии, физике, да и в повседневной жизни. В
качестве иллюстрации к сказанному рассмотрим
решение некоторых задач прикладного характера.
Задача 1. Перед посадкой семена
томатов дезинфицируют (протравливают) 1%-м
раствором марганцовки. Какую массу такого
раствора можно приготовить из 0,25 г марганцовки?
Дано:
![]() (марганцовки) =
(марганцовки) =
0,01 г,
m(марганцовки) = 0,25 г.
Найти:
m(раствора).
Решение
Зная массу растворенного вещества и его
массовую долю в растворе, можно вычислить массу
раствора:
![]()
Ответ. m(раствора) = 25 г.
Задача 2. В медицине широко применяют
так называемые физиологические растворы, в
частности раствор поваренной соли с массовой
долей соли 0,9%. Рассчитайте массы соли и воды,
необходимые для приготовления 1500 г
физиологического раствора.
Дано:
![]() (соли) = 0,009,
(соли) = 0,009,
m(раствора) = 1500 г.
Найти:
m(соли),
m(воды).
Решение
Вычислим массу соли, необходимой для
приготовления 1500 г физиологического раствора:
m(соли) = m(раствора)•![]() (соли) = 1500 (г)•0,009 = 13,5 г.
(соли) = 1500 (г)•0,009 = 13,5 г.
Определим массу воды, необходимой для
приготовления раствора:
m(воды) = m(раствора) – m(соли) =
1500 – 13,5 = 1486,5 г.
Ответ. m(соли) = 13,5 г, m(воды) = 1486,5 г.
Отличаются ли свойства растворов от свойств
компонентов, образующих эти гомогенные смеси?
С помощью домашнего эксперимента (задание 9 к
этому параграфу) вам будет нетрудно убедиться в
том, что раствор замерзает при более низкой
температуре, чем чистый растворитель. Например,
морская вода начинает замерзать при температуре
–1,9 °С, в то время как чистая вода
кристаллизуется при 0 °С.
1.
Что такое массовая доля растворенного вещества?
Сравните понятия «объемная доля» и «массовая
доля» компонентов смеси.2. Массовая доля йода в аптечной йодной
настойке составляет 5%. Какую массу йода и спирта
нужно взять, чтобы приготовить 200 г настойки?3. В 150 г воды растворили 25 г поваренной соли.
Определите массовую долю соли в полученном
растворе.4. В 200 г столового уксуса содержится 6 г
уксусной кислоты. Определите массовую долю
кислоты в столовом уксусе.
5.
Найдите массу воды и лимонной кислоты,
необходимую для приготовления 50 г 5%-го раствора.6. Из 240 г 3%-го раствора питьевой соды
выпарили 80 г воды. Найдите массовую долю соды в
полученном растворе.7. К 150 г 20%-го раствора сахара добавили 30 г
сахара. Найдите массовую долю вещества в
полученном растворе.8. Смешали два раствора серной кислоты: 80 г
40%-го и 160 г 10%-го. Найдите массовую долю кислоты в
полученном растворе.
9.
Пять чайных ложек поваренной соли (с горкой)
растворите в 450 г (450 мл) воды. Учитывая, что масса
соли в каждой ложке примерно 10 г, рассчитайте
массовую долю соли в растворе. В две одинаковые
пластиковые бутылки объемом 0,5 л налейте
полученный раствор и водопроводную воду.
Поместите бутылки в морозильную камеру
холодильника. Загляните в холодильник примерно
через час. Какая жидкость начнет замерзать
раньше? В какой бутылке содержимое раньше
превратится в лед? Сделайте вывод.
ПРАКТИЧЕСКАЯ РАБОТА № 3.
Приготовление раствора с заданной массовой
долей
растворенного вещества
Цель данной работы состоит в приготовлении
раствора с заданной массовой долей путем
растворения рассчитанной массы твердого
вещества в определенном объеме воды.
Рассчитайте массу твердого вещества,
необходимого для приготовления раствора в
соответствии с вашим вариантом задания (табл. 3).
На весах отмерьте рассчитанную массу твердого
вещества и перенесите его в химический стакан.
Таблица 3
Варианты задания к практической
работе № 3
| Вариант | Растворенное вещество |
Масса раствора, г |
Массовая доля растворенного вещества, % |
|---|---|---|---|
| 1 | Поваренная соль | 80 | 10 |
| 2 | Сахар | 150 | 5 |
| 3 | Лимонная кислота | 50 | 2 |
| 4 | Натриевая селитра | 70 | 10 |
Рассчитайте массу воды, необходимой
для приготовления раствора. Поскольку плотность
воды равна 1 г/мл, рассчитанная вами масса
численно равна ее объему. С помощью мерного
цилиндра отмерьте вычисленный объем воды и
прилейте его к веществу в стакане. Перемешивая
содержимое стакана стеклянной палочкой,
добейтесь полного растворения вещества в воде.
Требуемый раствор готов.
§ 15. Массовая доля примесей
На примере замерзания раствора соли вы
убедились, что присутствие посторонних
соединений изменяет свойства вещества. В
некоторых областях техники использование
недостаточно «чистых» материалов недопустимо.
Микросхему компьютера не сделать без особо
чистого кристалла кремния, в атомной энергетике
предъявляются повышенные требования к очистке
ядерного топлива, световой сигнал «погаснет» в
стекловолоконном кабеле, наткнувшись на
посторонние вкрапления.
Если главное (основное) вещество содержит
посторонние загрязнения – это тоже смесь, только
в этом случае все ненужные, а порой и вредные ее
компоненты называют одним словом – примеси. Чем
меньше примесей, тем чище вещество.
Иногда вещество, содержащее примеси, называют
техническим образцом или просто образцом.
Следовательно, любой такой образец включает
основное вещество и примеси.
Степень чистоты вещества принято выражать
массовой долей основного компонента или
массовой долей примесей.
С массовыми долями разного типа вы уже знакомы.
Попробуйте теперь сами сформулировать
определение, что такое массовая доля примесей в
веществе. Получилось? Сравните.
Массовой долей примесей называется отношение
массы примесей к массе образца:
![]()
Предположим, вам нужно вычислить массовую долю
основного вещества в образце. Тогда можно
воспользоваться формулой:
![]()
Следует не забывать, что сумма массовых долей
основного вещества и примесей всегда равна 1, или
100%:
![]() (осн.
(осн.
в-ва) + ![]() (примесей) =
(примесей) =
1, или 100%.
Также справедливо утверждение, что масса
образца складывается из массы основного
вещества и массы примесей:
m(образца) = m(осн. в-ва) + m(примесей).
Разберем несколько задач с использованием
понятия «массовая доля примесей».
Задача 1. Природная самородная
сера содержит 8% примесей. Какая масса чистой серы
содержится в 2 т природного образца?
Дано:
![]() (примесей) = 0,08,
(примесей) = 0,08,
m(образца) = 2 т.
Найти:
m(серы).
Решение
Вычислим массу примесей в 2 т самородной серы:
m(примесей) = m(образца)•![]() (примесей) = 2 (т) •0,08
(примесей) = 2 (т) •0,08
= 0,16 т.
Рассчитаем массу чистой серы, содержащейся в
природном образце:
m(серы) = m(образца) – m(примесей)
= 2 (т) – 0,16 (т) = 1,84 т.
Ответ. m(серы) = 1,84 т.
Задача 2. В пищевой отрасли
промышленности можно использовать лимонную
кислоту, содержащую не более 1% посторонних
примесей. В аналитической лаборатории
установлено, что в 2,345 г продукта содержится 2,312 г
кислоты. Можно ли использовать продукт в пищевых
целях?
Дано:
m(образца) = 2,345 г,
m(кислоты) = 2,312 г.
Найти:
![]() (примесей).
(примесей).
Решение
Вычислим массовую долю лимонной кислоты в
образце:
![]()
Рассчитаем массовую долю примесей в образце:
![]() (примесей)
(примесей)
= 1 – ![]() (кислоты) = 1
(кислоты) = 1
– 0,986 = 0,014, или 1,4%.
Ответ. Данный образец лимонной кислоты не
может быть использован в пищевой отрасли
промышленности.
1.
Что называется массовой долей примесей? Что
показывает эта величина?2. В промышленности используются вещества с
маркировкой «ч», что означает «чистое вещество».
Содержание примесей в них может составлять,
например, 0,01%. Найдите максимально допустимую
массу примесей в 120 г образца сажи с маркировкой
«ч».3. Массовая доля примесей в известняке
составляет 5%. Рассчитайте массу основного
вещества (карбоната кальция), содержащегося в 300
кг природного известняка.
4.
При очистке медного купороса получилось 150 мг
примесей, что составило 2% от массы образца.
Определите массу технического медного купороса,
который подвергли очистке.
5. Для изготовления полупроводниковых
батарей используется сверхчистый кремний.
Массовая доля примесей в нем не должна превышать
0,000 000 0001%. Годится ли для данных целей
кремний, в 30 кг которого содержится 0,03 мг
примесей?
Решение задач с долей вещества в смеси, в соединении
Ключевые слова конспекта: массовая доля вещества в смеси или растворе, молярная доля вещества, объемная доля вещества, массовая доля элемента в соединении, масса элемента, массовая доля элемента.
Массовую долю вещества в смеси или растворе вычисляют как отношение массы вещества, входящего в состав смеси, к массе всей смеси. Массовую долю часто выражают в процентах. Для этого отношение массы вещества к массе смеси умножают на 100%:
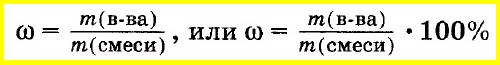
Аналогично объемную долю вещества вычисляют как отношение объема вещества к объему смеси, а молярную долю вещества — как отношение количества вещества одного из компонентов смеси к сумме количеств веществ всех компонентов смеси:
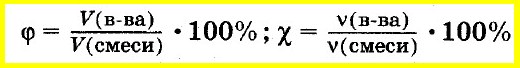
Массовую долю элемента в соединении вычисляют как отношение массы элемента, входящего в состав данного соединения, к массе всего соединения:

Зная молекулярную формулу соединения, массу элемента, входящего в его состав, вычисляют как произведение молярной массы элемента на число атомов этого элемента в соединении.
В этом случае массовую долю элемента в соединении рассчитывают как отношение этой величины к молярной массе всего соединения:
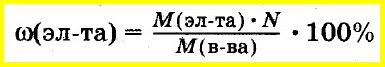
Цитаты из пособия «Задачи по химии 8-9 кл.» (авт. О.С. Габриелян и др.) использованы в учебных целях. Ссылка на покупку книги указана в конце конспекта.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
25 г оксида магния смешали с 35 г оксида алюминия. Определите массовую долю оксида магния в данной смеси.

Ответ. ω(MgO) = 0,417, или 41,7%.
Задача № 2.
Вычислите объемную долю азота в смеси газов, содержащей 32 л азота, 48 л углекислого газа, 36 л гелия и 14 л водорода.
Ответ. φ(N2) = 0,246, или 24,6%.
Задача № 3.
Вычислите молярную и массовую долю (в %) оксида углерода (II) в смеси, содержащей 16,8 л (н. у.) оксида углерода (II) и 13,44 л (н. у.) оксида углерода (IV).
Ответ. χ(СО) = 55,56%, ω(СО) = 44,3%.
Задача № 4.
В воде растворили 15 г хлорида натрия. Вычислите массу полученного раствора, если массовая доля соли в нем равна 5%.
Ответ: m(р-ра) = 300 г.
Задача № 5.
Образец сплава меди с цинком имеет массу 75 г. Массовая доля меди в этом сплаве равна 64%. Определите массу цинка в данном образце.
Ответ. m(Zn) = 27 г.
[highlight]Задача № 6.[/highlight] Объемная доля аммиака в смеси с кислородом равна 40%. Вычислите плотность данной смеси по воздуху.
Посмотреть РЕШЕНИЕ

Ответ. Dвозд(смеси) = 0,896.
Задача № 7.
Найдите массовую долю кислорода в фосфате натрия.
Посмотреть РЕШЕНИЕ

Ответ. ω (O) = 39%.
[highlight]Задача № 8.[/highlight] Определите массовую долю фосфора в смеси, содержащей 55 г фосфата натрия и 70 г дигидрофосфата натрия.
Посмотреть РЕШЕНИЕ

Ответ. ω(Р) = 22,77%
[highlight]Задача № 9.[/highlight] Массовая доля серы в техническом сульфате натрия равна 20,48%. Рассчитайте массовую долю примесей в данном продукте (в %).
Посмотреть РЕШЕНИЕ

Ответ. ω (примесей) = 9,12%.
Задача № 10.
Плотность смеси оксида азота (II) и оксида азота (IV) по водороду равна 17,8. Найдите массовую долю оксида азота (IV) в данной смеси.
Посмотреть РЕШЕНИЕ

Ответ. ω(NO2) = 45,2%.
Решение задач с долей вещества в смеси, в соединении. Выберите дальнейшие действия:
- Перейти к следующей теме: Решение задач на вывод формул соединений
- Вернуться к списку конспектов по Химии.
- Проверить знания по Химии.
- Купить книгу Задачи по химии и способы их решения. 8-9 кл. / О.С. Габриелян и др. — М.: Дрофа.
Массовая доля или .
По закону Авогадро
плотности различных газов прямо
пропорциональны молекулярным массам,
тогда
![]() .
.
в) Мольной долейгаза в смеси
называется отношение числа молейi-го
газа![]() i,
i,
к общему количеству молей газов в смеси
![]() ,
,
т.е.
![]() .
.
![]()
Рассмотрим способ определения состава
смеси через числа молей компонентов.
Пусть смесь состоит из nгазов; тогда приведённые (парциальные)
объёмы каждого из них можно выразить
числом молей, т.е.
![]() .
.
![]() .
.
![]() ,
,
где
![]() …
…![]() –
–
объёмы моля![]() -го
-го
газа;
![]() …
…![]() –
–
их числа молей;
Объём смеси газов
также можно выразить через число молей
смеси, т.е.
![]() ,
,
где
![]() – условное число молей смеси.
– условное число молей смеси.
На
основании уравнения (1), запишем
 .
.
Но
т.к. объём моля для всех газов, в том
числе и для смеси при одинаковых
параметрах, есть величина постоянная,
то уравнение можно записать в виде:
![]() .
.
Таким
образом, задание смеси мольными долями
равносильно заданию ее объёмными долями.
Вычисление кажущейся молекулярной
массы
![]() производится следующим образом: вычисляем
производится следующим образом: вычисляем
для каждого![]() –го
–го
газа![]() –
–
по уравнению, т.е.:
![]()
![]() .
.
Просуммировав все
эти уравнения, получаем
![]() .
.
Но![]() .
.
Тогда
![]() ,
,
откуда
![]() .
.
(2)
По
уравнению (2) можно определить кажущийся
молекулярный вес (или молекулярную
массу), если она задана объемными долями.
Использовав
уравнение (2), можно определить газовую
постоянную смеси:
 ,
,
где
![]() =8314
=8314
Дж/кмоль·К – универсальная газовая
постоянная.
Если известны массовые доли
![]() -ых газов, входящих в смесь
-ых газов, входящих в смесь![]() ,
,
то величину![]() можно
можно
определить:
![]() .
.
где
![]() –
–
газовая постоянная![]() -го
-го
газа.
В том случае, если известно число молей
газов для
![]() кг смеси, газовую постоянную смеси можно
кг смеси, газовую постоянную смеси можно
вычислить по следующей зависимости.
Учитывая, что
![]() ,
,
получим
![]() .
.
Для 1 кг смеси
![]() .
.
7. Первый закон термодинамики
7.1 Равновесное и неравновесное состояние
и термодинамические процессы
Равновесное состояние тела–
состояние, при котором во всех точках
его объема давление, температура,
удельный объем и все другие физические
свойства одинаковы.
Это состояние может быть при условии
механического и термического равновесия
между газом и внешней средой. Под
механическим равновесием понимают
равенство давлений газов и внешней
среды, подтермическим –равенство
их температур.
Только равновесные состояния могут
быть описаны количественно с помощью
уравнения состояния.
Состояния термодинамических систем,
не удовлетворяющие указанным выше
требованиям, называются неравновесными.
Совокупность
изменений термодинамической системы
при переходе из одного состояния (р1,
Т1,
W1)
в другое (р2,
Т2,
W2)
называют термодинамическим
процессом.
Эти процессы могут быть равновесными
и неравновесными.
Процесс называют равновесным, если в
каждый момент времени газ находится в
равновесном состоянии.
Обратимый процесс
– это процесс,
который может протекать как в прямом,
так и в обратном направлении. При этом
рабочее тело (газ) и внешняя среда
последовательно проходят в обратном
процессе точно те же состояния, через
которые они проходили в прямом процессе.
Свойством обратимости обладают
только равновесные процессы.
Под необратимым процессом
понимают такой процесс, при которомгаз (и внешняя среда)
проходит через неравновесные состояния.
После необратимого
процесса система (газ) может быть
возвращена в начальное состояние
только при затрате энергии извне.
Техническая термодинамика, в первую
очередь, изучает обратимые процессы.
Они могут быть выражены аналитическими
зависимостями и графиками.
Для учета необратимости процесса, в
случае необходимости, в полученные
аналитические зависимости вводят
коэффициенты согласования.
7.2 Внутренняя энергия газа и внешняя
работа
Молекулы реального газа обладают двумя
видами механической энергии:
-
внутренней кинетической энергией,
-
внутренней потенциальной энергией.
Внутренняя кинетическая энергия молекул
включает энергию:
-
поступательного движения молекул,
-
вращательного движения электронов
вокруг атомного ядра, -
внутримолекулярного колебания атомов.
Внутренняя потенциальная энергия
молекул – энергия сил сцепления
молекул.
Сумма всех указанных
видов энергии составляет внутреннюю
энергию газа.
Внутреннюю энергию
газа для одного кг
газа обозначают
малой буквой
и, с
размерностью Дж1кг.
Для массы т
кг газа –
U,
размерность
Дж. Внутренняя
кинетическая энергия – функция температуры.
Внутренняя потенциальная энергия
– функцияр (илиw).
В бесконечно малом процессе для 1кг газа
![]()
Для всех термодинамических процессов
изменение внутренней энергии идеального
газа равно
![]()
Где сw– удельная
теплоемкость приw=const
Внешняя работа
газа– передача
энергии от одного тепла к другому,
связанная с изменением объема, с
перемещением его во внешнем пространстве
или с изменением его положения,
называется работой.
/ = p(w2
–w1) =pΔw
7.3 Энтальпия
В прошлом столетии
известный американский физик Гиббс
ввел в практикv
тепловых расчетов новую функцию, которая
была названа энтальпией
(или тепловой функцией Гиббса).
Обозначается для 1кг газа буквойi.
Она представляет собой по определению
сложную функцию вида
i =u
+ pw,
Где рw
– потенциальная
энергия давления,
и – внутренняя
энергия.
Входящие в формулу параметры p,w
ии являются параметрамисостояния,
следовательно, и сама энтальпия будет
также параметром (функцией)
состояния
Физическая сущность энтальпии – это
энергия газа, являющаяся сумой его
внутренней энергии и потенциальной
энергии давления (pvv).
7.4 Физический
смысл первого закона термодинамики
Это есть общий закон сохранения и
превращения энергии.
Первый закон
термодинамики является
частным случаем общего закона
сохранения и превращения энергии
(применительно к тепловым явлениям).
Установлен экспериментальным путем и
утверждает, что теплота
(тепловая
энергия) может превращаться в механическую
энергию (в виде совершения
работы) и наоборот, работа – в теплоту,
причем определенное количество
тепла всегда эквивалентно определенному
количеству работы, т.е. 0,427кгсл;
= 4,186ХДж.
Аналитическое выражение первого закона
термодинамики для 1 кг газа имеет вид:
q
= Δu
+ l
Для m
кг Q = ΔU
+ L
Физический смысл выражений следующий.
При подводе к
газу тепла в общем случае одна часть
его расходуется на увеличение
внутренней энергии газа, вторая – на
совершение газом внешней работы.
Для бесконечно малого процесса уравнение
dq = du
+ dl– математическое
выражение.
7.5 Уравнение Майера
![]()
Уравнение Майера показывает, что
теплоемкость при р=constвсегда больше чем теплоемкость приw=const.
Из уравнения следует
![]()
Где
![]() – показатель адиабаты
– показатель адиабаты
С учетом величины К:
![]()
![]()
8
В
воздухе содержатся различные газы: азот, кислород, углекислый газ, благородные
газы, водяные пары и другие.
Для
того, чтобы количественно выразить состав смеси газов, используют величину,
которую называют «объёмной долей газов в смеси».
Объёмная
доля газа – это отношение объёма данного газа к общему объёму
смеси.
Объёмная
доля обозначается буквой φ (фи). Объёмная доля газа показывает, какую
часть общего объёма смеси занимает данный газ.
Доказано,
в 100 л воздуха 78 л азота, 21 л кислорода, 0,03 л углекислого газа и 0,97 л
благородных газов. Если нужно найти объёмные доли этих газов в воздухе, то
следует объём каждого газа разделить на объём воздуха. Получается, что в
воздухе содержится 78 % азота, 21 % кислорода, 0,03 % углекислого газа и 0,97 %
благородных газов. Сумма всех объёмных долей газов в смеси равна 1, или 100 %.
В
воздухе, который мы выдыхаем, содержится только 16 % кислорода, а содержание
углекислого газа увеличивается до 4 %. Поэтому помещения,
в которых много людей, нужно постоянно проветривать.
В
задачах чаще необходимо искать объём газа по известной объёмной доле этого
газа. Например, найдём объём кислорода в 300 л воздуха. Зная, что объёмная доля
кислорода в воздухе равна 21 %, нужно 300 умножить на 0,21, и мы получим 63 л.
Таким образом, в 300 л воздуха содержится 63 л кислорода.
Учитывая
то, что объёмная доля аргона в воздухе равна 0,9 %, найдём объём воздуха,
который необходим для получения 7 л аргона. В условии задачи даны объём аргона
и его объёмная доля в водухе. Найти нужно объём
воздуха. Для этого 7 л разделим на 0,009.
Найдём
объёмную долю каждого газа, если смешали 4 л кислорода и 5 л углекислого газа.
Объём смеси равен сумме объёмов двух газов – кислорода и углекислого газа.
Чтобы
найти объёмную долю кислорода в смеси, нужно 4 л разделить на 9 л. Получаем
0,44, или 44 %. Для того, чтобы определить процентное содержание углекислого
газа в смеси, необходимо от 100 % вычесть 44 %. Получим 56 %.
