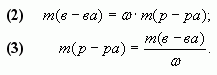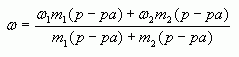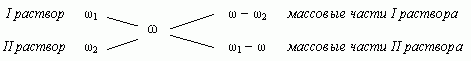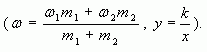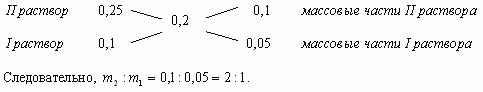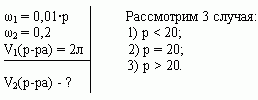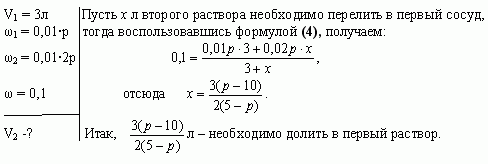Как найти массовую долю раствора при смешивании

“Только из союза двоих, работающих
вместе и при помощи друг друга, рождаются великие
вещи.”

Антуан Де Сент-Экзюпери

Математика многообразна и многогранна.
Существует ряд ситуаций в образовательном
процессе, когда при изучении какой-либо темы по
физике, химии, биологии и т.д. затрагиваются
понятия математики, например, существуют задачи,
которые решают как на уроках математики, так и на
уроках химии. Способы решения задач представляют
и учителя химии, и математики, но есть проблема:
математики знают математику, а химики – химию. И
не всегда способы совпадают.

В данной статье приводятся рекомендации по
решению химических задач на смешение растворов
разными способами: с помощью расчетной формулы,
“Правила смешения”, “Правила креста”,
графического метода, алгебраического метода.
Приведены примеры решения задач.

1. Основные химические понятия

Приведем некоторые указания к решению задач на
растворы.

Основными компонентами этого типа задач
являются:

а) массовая доля растворенного вещества в
растворе;

б) масса растворенного вещества в растворе;

в) масса раствора.

Предполагают, что:

а) все получившиеся смеси и сплавы являются
однородными;

б) смешивание различных растворов происходит
мгновенно;

в) объем смеси равен сумме объемов смешиваемых
растворов;

г) объемы растворов и массы сплавов не могут
быть отрицательными.

Определения и обозначения.

Массовая доля растворенного вещества в
растворе – это отношение массы этого вещества к
массе раствора.

где – массовая
доля растворенного вещества в растворе;

– масса
растворенного вещества в растворе;

– масса
раствора.

Следствия формулы (1):

Введем обозначения:

– массовая доля
растворенного вещества в первом растворе;

–
массовая доля растворенного вещества во втором
растворе;

–
массовая доля растворенного вещества в новом
растворе, полученном при смешивании первого и
второго растворов;

m₁(в-ва), m₂(в-ва), m(в-ва) – массы
растворенных веществ в соответствующих
растворах;

m₁(р-ра), m₂(р-ра), m(р-ра) – массы
соответствующих растворов.

Основными методами решения задач на смешивание
растворов являются: с помощью расчетной формулы,
“Правило смешения”, “Правило креста”,
графический метод, алгебраический метод.

Приведем описание указанных методов.

1.1. С помощью расчетной формулы

В наших обозначениях, получим формулу для
вычисления массовой доли вещества (?) в смеси.

1. Масса полученного при смешивании раствора
равна:

m(р-ра) = m₁(р-ра) + m₂(р-ра).

2. Определим массы растворенных веществ в
первом и втором растворах:

m₁(в-ва)= •m₁(р-ра), m₂(в-ва)=   •m₂(р-ра).

3. Следовательно, масса растворенного вещества
в полученном растворе вычисляется как сумма масс
веществ в исходных растворах:

m(в-ва) = m₁(в-ва) + m₂(в-ва) = •m₁(р-ра) + •m₂(р-ра).

4. Таким образом, массовая доля растворенного
вещества в полученном растворе равна:

или

или

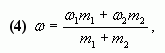
где – массы
соответствующих растворов.

Замечание: При решении задач удобно
составлять следующую таблицу.

1.2. “Правило смешения”

Воспользуемся формулой (4):

тогда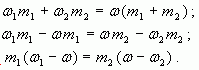 

Отсюда

Таким образом, отношение массы первого
раствора к массе второго равно отношению
разности массовых долей смеси и второго раствора
к разности массовых долей первого раствора и
смеси.

Аналогично получаем, что при

Замечание: Формула (5) удобна тем, что на
практике, как правило, массы веществ не
отвешиваются, а берутся в определенном
отношении.

1.3. “Правило креста”

“Правилом креста” называют диагональную
схему правила смешения для случаев с двумя
растворами.

Слева на концах отрезков записывают исходные
массовые доли растворов (обычно слева
вверху-большая), на пересечении отрезков –
заданная, а справа на их концах записываются
разности между исходными и заданной массовыми
долями. Получаемые массовые части показывают в
каком отношении надо слить исходные растворы.

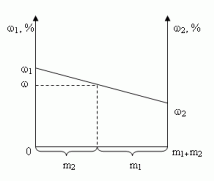
1.4. Графический метод

Отрезок прямой (основание графика)
представляет собой массу смеси, а на осях ординат
откладывают точки, соответствующие массовым
долям растворенного вещества в исходных
растворах. Соединив прямой точки на осях ординат,
получают прямую, которая отображает
функциональную зависимость массовой доли
растворенного вещества в смеси от массы
смешанных растворов в обратной пропорциональной
зависимости

Полученная функциональная прямая позволяет
решать задачи по определению массы смешанных
растворов и обратные, по массе смешанных
растворов находить массовую долю полученной
смеси.

Построим график зависимости массовой доли
растворенного вещества от массы смешанных
растворов. На одной из осей ординат откладывают
точку, соответствующую массовой доли , а на другой – . Обозначим на оси абсцисс
точки А и В с координатами (0,0) и (m₁ + m₂,0),
соответственно. На графике точка А(0,0)
показывает, что массовая доля всего раствора
равна , а точка В(m₁
+ m₂,0) – массовая доля всего раствора равна . В направлении от
точки А к точке В возрастает содержание в
смеси 2-го раствора от 0 до m₁+ m₂ и
убывает содержание 1-го раствора от m₁+ m₂
до 0. Таким образом, любая точка на отрезке АВ будет
представлять собой смесь, имеющую одну и ту же
массу с определенным содержанием каждого
раствора, которое влияет на массовую долю
растворенного вещества в смеси.

Замечание: Данный способ является наглядным
и дает приближенное решение. При использовании
миллиметровой бумаги можно получить достаточно
точный ответ.

1.5. Алгебраический метод

Задачи на смешивание растворов решают с
помощью составления уравнения или системы
уравнений.

2. Примеры решения задач

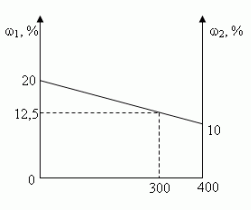
Задача 1. (№1.43, [1])

В 100 г 20%-ного раствора соли добавили 300 г её
10%-ного раствора. Определите процентную
концентрацию раствора.

Решение:

1. C помощью расчетной формулы



2. Графический



Ответ: 12,5%

3. Путем последовательных вычислений
• Сколько растворенного вещества содержится:

а) в 100 г 20%-ного раствора; [100•0,2 = 20(г)]

б) в 300 г 10%-ного раствора? [300•0,1 = 30(г)]

• Сколько вещества содержится в образовавшемся
  растворе?

20 г + 30 г = 50 г

• Чему равна масса образовавшегося раствора?

100 г + 300 г = 400 г

• Какова процентная концентрация полученного
  раствора?

(50/400)100 = 12,5(%)

Ответ: 12,5%




4. Алгебраический

Пусть х – процентная концентрация
полученного раствора. В первом растворе
содержится 0,2•100(г) соли, а во втором 0,1•300(г), а в
полученном растворе х•(100 + 300)(г) соли.
Составим уравнение:

0,2•100 + 0,1•300 = х•(100 + 300);

х = 0,125 (12,5%)

Ответ: 12,5%

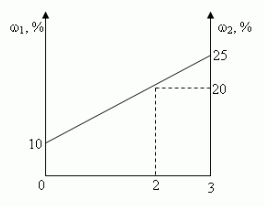
Задача 2. u(№10.26, [1])

Смешали 10%-ный и 25%-ный растворы соли и получили 3
кг 20%-ного раствора. Какое количество каждого
раствора в килограммах было использовано?

Решение:

1. Алгебраический

а) C помощью уравнения:

Пусть х (кг) – масса 1-го раствора, тогда 3-х (кг)
-масса 2-го раствора.

0,1•х (кг) содержится соли в 1-ом растворе,

0,25•(3-х) (кг) содержится соли в 2-ом растворе,

0,2•3 (кг) содержится соли в смеси.

Учитывая, что масса соли в 1-ом и 2-ом растворах
равна массе соли в смеси, составим и решим
уравнение:

0,1•х + 0,25•(3-х) = 0,2•3;

0,15х = 0,15;

х = 1, 1кг-масса 1-го раствора

3 – х = 3 – 1 =2 (кг) – масса 2-го раствора.

Ответ: 1 кг, 2 кг.

б) С помощью системы уравнений

Пусть х (кг) – количество первого раствора, у (кг)
– количество второго раствора. Система уравнений
имеет вид:



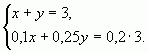
Ответ: 1 кг, 2 кг.

2. Графический.



Ответ: 1кг, 2кг.

3. “Правило смешения”

 




4. “Правило креста”

Составим диагональную схему



Ответ: 1кг, 2кг.

Задача 3 ([2])

Сосуд емкостью 5 л содержит 2 л р%-ного (по объёму)
раствора соли. Сколько литров 20%-ного раствора
такой же соли надо налить в сосуд, чтобы
процентное содержание соли в сосуде стало
наибольшим?

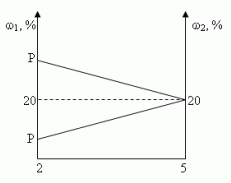
Решение (графический способ)

Заметим, что по условию, объём второго раствора
не превышает трёх литров.

1. Ели р < 20, то для того, чтобы получить
   максимальную массовую долю вещества в растворе,
   необходимо добавить 3 л 20% – ного раствора соли;
2. Если р = 20, то при добавлении 2-го раствора,
   процентное содержание соли в растворе не
   изменится, следовательно, можно прилить от 0 л до 3
   л 20% – ного раствора соли;
3. Если р > 20, то при добавлении 2-го раствора,
   процентное содержание соли будет уменьшаться,
   т.е. прилить нужно 0 л.

Ответ: 3 л, если 0 < р < 20, [0,3], если р = 20, 0л, если 20
< р 100.

Задача 4 (работа 5, №2, [1])

В двух сосудах по 5л каждый содержится раствор
соли. Первый сосуд содержит 3л р% – ного раствора, а
второй – 4л 2р% – ного раствора одной и той же соли.
Сколько литров надо перелить из второго сосуда в
первый, чтобы получить в нем 10% – ный раствор соли?
При каких значениях р задача имеет решение?

Решение

Найдем, при каких значениях р задача имеет
решение. По условию задачи 5-ти литровый сосуд
содержит 3л первого раствора, следовательно, к
нему можно прилить от 0 до 2л второго раствора.

Имеем, Решая
неравенство, получаем

Ответ:

3. Заключение

Данные рекомендации предназначены учителям
математики, желающим организовать элективные
курсы, как в девятых, так и в десятых и
одиннадцатых классах. Цель создаваемых курсов:
научить учащихся пользоваться математическим
аппаратом при решении химических задач.

Список литературы

1. Галицкий и др. Сборник задач по алгебре для 8-9
   классов: Учебное пособие для учащихся шк. и
   классов с углубл. изуч. математики / М.Л. Галицкий,
   А.М. Гольдман, Л.И. Звавич.-2-е изд. – М.:
   Просвещение,1994. – 271с.
2. Сборник задач по математике для поступающих в
   вузы: Учебное пособие/ П.Т.Дыбов, А.И.Забоев, А.С.
   Иванов и др.; Под ред. А.И. Прилепко. – М.:Высш. школа,
   1983. – 239 с.
3. Ерыгин Д.П., Шишкин Е.А. Методика решения задач по
   химии: Учебное пособие для студентов пед. ин-тов
   по биол. и хим. спец. – М.: Просвещение,1989. – 176с.
4. Хомченко Г.П., Хомченко И.Г. Задачи по химии для
   поступающих в вузы: Учебное пособие. – 2-е изд..
   исправ. и доп. – М.: Высш. школа, 1993. – 302 с.

ПОДГОТОВКА К ЭКЗАМЕНУ

«Вычисление массы растворенного вещества, содержащегося в определенной массе раствора с известной массовой долей»

Алгоритмы решения задач:

Пример 1. Вычисление массовой доли растворенного вещества

Определите массовую долю нитрата калия в растворе, полученном растворением 50 г нитрата калия в 200 г воды.

Пример 2. Вычисление массы растворенного вещества

Вычислите массу гидроксида калия в растворе объемом 600 мл и плотностью 1,082 г/мл, если массовая доля гидроксида калия составляет 10 %.

Пример 3. Смешивание растворов с разными концентрациями одного вещества Смешали 300 г раствора с массовой долей хлорида натрия 20 % и 500 г раствора того же вещества с массовой долей 40 %. Вычислите массовую долю хлорида натрия в полученном растворе.

Пример 4. Разбавление водой

ω2 = 0, т.к. в воде не содержится вещество, находящееся в первом растворе.

Какую массу воды надо добавить к раствору гидроксида натрия массой 150 г с массовой долей 10 %, чтобы получить раствор с массовой долей 2 %?

Пример 5. Концентрирование (добавление твердого вещества)

ω2 = 100 %, или 1, т.к. добавляемое вещество чистое.

Какую массу хлорида бария надо добавить к раствору хлорида бария массой 150 г с массовой долей 10 %, чтобы получить раствор с массовой долей 25 %?

Пример 6. Упаривание раствора (частичное выпаривание воды)

Вычислите массовую долю хлорида натрия в растворе, если из 200 г 30 %-го раствора испарилось 50 г воды.

ПРИМЕРЫ ЗАДАЧ

1. Какая масса карбоната натрия (в граммах) потребуется для приготовления 0,5 л 13%-го раствора плотностью 1,13 г/мл?

а) 73,45; б) 50; в) 72; г) 75.

2. Из раствора хлорида бария массой 100 г с массовой долей соли 3 % выпарили 25 г воды и до- бавили в него 15 г соли. Массовая доля соли (в %) в полученном растворе равна:

а) 12; б) 15; в) 18; г) 20.

3. Смешали 120 г раствора серной кислоты с массовой до лей 20 % и 40 г 50%-го раствора того же вещества. Определите массовую долю кислоты (в %) в полученном растворе.

а) 25; б) 27,5; в) 27; г) 29,5.

4. Какая масса азотной кислоты (в граммах) содержится в 1 л ее 20%-го раствора с плотностью 1,05 г/мл?

а) 105; б) 63; в) 210; г) 176.

5. Какая масса соли (в граммах) вводится в организм человека при вливании 353 г 0,85%-го физиологического раствора?

а) 3; б) 6; в) 4; г) 2 г.

6. К 180 г 8%-го раствора хлорида натрия добавили 20 г NaCl. Найдите массовую долю (в %) хлорида натрия в образовавшемся растворе.

а) 17,2; б) 17,4; в) 18; г) 12,7.

7. К раствору хлорида кальция массой 140 г с массовой долей соли 5 % добавили 10 г этой же соли. Определите массовую долю (в %) хлорида кальция в полученном растворе.

а) 13,1; б) 14; в) 11,3; г) 25.

8. Какую массу соли (в граммах) надо добавить к 60 г раствора с массовой долей этой соли 10 %, чтобы получить раствор с массовой долей 40 %?

а) 15; б) 22; в) 17; г) 30.

9. Смешали 200 г 15%-го раствора нитрата хрома(III) и 300 г 20%-го раствора той же соли. Вычислите массовую долю (в %) ни- трата хрома(III) в полученном растворе.

а) 24; б) 18; в) 17,9; г) 18,1.

10. Из 150 г раствора хлорида натрия с массовой долей 5 % выпарили 10 г воды и добавили 5 г той же соли. Вычислите массовую долю (в %) соли в полученном растворе.

а) 8,4; б) 8,6; в) 9; г) 11,2.

11. Смешали 200 г 5%-го и 400 г 12,5%-го растворов серной кислоты. Найдите массу кислоты в полученном растворе (в граммах).

а) 60; б) 98; в) 49; г) 58.

12. При растворении 16 г гидроксида натрия получили 10%- й раствор. Определите массу (в граммах) взятой для этого воды.

а) 126; б) 144; в) 151; г) 164.

13. К 200 г 10%-го раствора ни- трата калия добавили некоторую порцию нитрата калия и получи- ли 20%-й раствор. Найдите массу (в граммах) добавленной порции твердого вещества. а) 2,5; б) 5; в) 25; г) 15.

14. Найдите массу воды (в граммах), которую нужно добавить к 300 г 8%-го раствора сульфата натрия для получения 5%-го раствора.

а) 90; б) 45; в) 18; г) 180.

15. Какая масса раствора (в граммах) получится при упаривании 200 г 5%-го раствора гидроксида калия до 20%-го раствора?

а) 10; б) 45; в) 100; г) 50.

16. 92 мл 10%-го раствора серной кислоты (плотность 1,066 г/мл) полностью нейтрализовали 40%-м раствором гидроксида натрия. Найдите массу затраченного на нейтрализацию раствора гидроксида натрия (в граммах).

а) 10; б) 55; в) 20; г) 30.

17. Определите, какую массу гидроксида калия (в граммах) нужно добавить к 150 г 20%-го раствора гидроксида калия для получения 40%-го раствора.

а) 5; б) 50; в) 56; г) 78.

18. К 200 г 8%-го раствора хлорида натрия добавили 50 г воды. Вычислите массовую долю (в %) соли в образовавшемся растворе.

а) 6,4; б) 6,5; в) 6,1; г) 6,2.

19. Определите массу воды (в граммах), которую надо добавить к 20 г 70%-го раствора уксусной кислоты для получения 5%-го раствора уксуса.

а) 260; б) 130; в) 26; г) 258.

20. Определите массу сахара (в граммах), необходимую для приготовления 0,5 кг 45%-го раствора.

а) 245; б) 225; в) 345; г) 500.

21. Вычислите массовую долю соляной кислоты (в %) в растворе, полученном при растворении 11,2 л (н.у.) хлороводорода в 1 л воды.

а) 1,3; б) 1,6; в) 1,8; г) 3,6.

22. Вычислите массу 40%-го раствора уксусной кислоты (в граммах), которую необходимо добавить к 500 г воды для получения 15%-го раствора.

а) 29; б) 32; в) 48; г) 300.

23. Массовая доля соли в морской воде составляет 3,5 %. Найдите массу соли (в граммах), которая останется после выпаривания 5 кг морской воды.

а) 175; б) 170; в) 167; г) 163.

24. Смешали 250 г раствора гидроксида натрия с массовой долей 16 % и 300 мл раствора (ρ = 1,2 г/мл) с массовой долей того же вещества 20 %. Рассчитайте массу гидроксида натрия (в граммах) в полученном растворе:

а) 120; б) 112; в) 11; г) 115.

25. Какова масса поваренной соли (в граммах), которую следует растворить в 250 г раствора этой соли с массовой долей 10 % для получения раствора с массовой долей 18 %?

а) 22; б) 42,4; в) 24,4; г) 44.

26. К 50 г раствора хлорида кальция с массовой долей 3,5 % добавили 5 г этой же соли и 20 г воды. Определите массовую долю (в %) соли в полученном растворе.

а) 6; б) 7; в) 8; г) 9.

27. Какая масса серной кисло ты (в граммах) содержится в 0,6 л ее 40%-го раствора с плотностью 1,3 г/мл?

а) 63; б) 26; в) 60; г) 312.

28. Найдите массу хлорида натрия (в граммах), который необходимо растворить в 50 г воды для приготовления раствора с массовой долей соли 20 %.

а) 20; б) 12,5; в) 5; г) 24.

29. К 350 г водного раствора этанола с массовой долей 20 % добавили 120 мл спирта (плотность 0,8 г/мл). Рассчитайте массу спирта (в граммах) в полученном растворе.

а) 167; б) 156; в) 166; г) 170.

30. Из 50 г раствора хлорида натрия с массовой долей 2 % выпарили 10 г воды и добавили 5 г этой же соли. Определите массовую долю соли (в %) в полученном растворе.

а) 6,3; б) 13,3; в) 8,9; г) 9,4

Ответы. 1–а, 2–г, 3–б, 4–в, 5–а, 6–а, 7–в, 8–г, 9–б, 10–б, 11–а, 12–б, 13–в, 14–г, 15–г, 16–в, 17–б, 18–а, 19–а, 20–б, 21–в, 22–г, 23–а, 24–б, 25–в, 26–г, 27–г, 28–б, 29–в, 30–б.

При смешивании масса полученного
раствора (m) равняется сумме масс
смешиваемых растворов (m₁, m₂,
m₃ … m_n):

m = m₁ + m₂ + m₃ +…+ m_n,
г

Аналогично, масса растворенного вещества
будет равна сумме масс веществ в
смешиваемых растворах:

m(X) = m₁(X) + m₂(X) + m₃(X) +…+
m_n(X), г

Пример 12. Определить массовую долю
HNO₃ в растворе, полученном при
смешивании 100 мл раствора с ω₁(HNO₃)
= 10% (ρ₁ = 1,05 г/мл) и 150 мл раствора с
ω₂(HNO₃) = 20% (ρ₂ = 1,12
г/мл).

Решение:

ω(HNO₃) =

=

Находим

m₁(р-ра) = V₁(р-ра)·ρ₁(р-ра)
= 100·1,05 = 105 г

m₂(р-ра) = V₂(р-ра)·ρ₂(р-ра)
= 150·1,12 = 168 г

m₁(HNO₃) = m₁(р-ра)·ω₁(р-ра)
= 105·0,1 = 10,5 г

m₂(HNO₃) = m₂(р-ра)·ω₂(р-ра)
= 168·0,2 = 33,6 г

Рассчитываем

ω(HNO₃) =

= 0,162 или 16,2%

Ответ: массовая доля HNO₃ в
растворе после смешения равна 0,162 или
16,2%.

Пример 13. Какие объемы растворов
гидроксида калия с ω₁(KOH) = 50%
(ρ₁ = 1,51 г/мл) и с
ω₂(KOH) = 10% (ρ₂ = 1,1 г/мл)
необходимо использовать для приготовления
одного литра раствора гидроксида калия
с ω(KOH) = 20% (ρ = 1,19 г/мл)?

Решение:

Масса полученного раствора равна

m(р-ра) = m₁(р-ра) + m₂(р-ра)

m(р-ра) = V(р-ра)·ρ(р-ра) = 1000·1,19 = 1190 г

Отсюда m₁(р-ра) = 1190 – m₂(р-ра)

Масса KOH в полученном растворе равна

m(KOH) = m(р-ра)·ω(KOH) = 1190·0,2 = 238 г

В то же время масса КОН в полученном
раствора равна:

m(KOH) = m₁(KOH) + m₂(KOH)

m₁(KOH) = m₁(р-ра)·ω₁(KOH) =
m₁(р-ра)·0,5

m₂(KOH) = m₂(р-ра)·ω₂(KOH) =
m₂(р-ра)·0,1

Получаем 238 = m₁(р-ра)·0,5 + m₂(р-ра)·0,1

Подставим в это уравнение выражение
для m₁(р-ра):

238 = [1190 – m₂(р-ра)]·0,5 + m₂(р-ра)·0,1

Решим уравнение относительно m₂(р-ра):

0,4m₂(р-ра) = 357 m₂(р-ра) = 892,5 г

Тогда m₁(р-ра) = 1190 – 892,5 = 297,5 г

Находим объемы растворов:

V₁(р-ра) =

=
=
197 мл

V₂(р-ра) =

=
=
811,4 мл

Ответ: V₁ = 197 мл, V₂ = 811,4
мл.

1. 5. Задания для самостоятельной работы

1. Определите массовую долю
растворенного вещества (Х)% в следующих
растворах:

	Вариант
а	б	в	г	д
m(X), г	5	28	46,7	53,1	62,2
m(H2O), г	300	450	528	630	720

2. Рассчитать массу вещества (г),
необходимую для приготовления следующих
растворов:

	Вариант
а	б	в	г	д
ω(Х),%	2	1	5	10	8
Объем р-ра, л	0,25	0,8	0,5	0,3	0,45
ρ, г/мл	1,015	1,007	1,046	1,090	1,067

3. Рассчитайте массу кристаллогидрата
Х·nH₂O (г) и объем воды (мл), необходимые
для приготовления 500 мл следующих
растворов:

	Вариант
а	б	в	г	д
Вещество (Х·nH2O)	CuSO4·5H2O	FeSO4·7H2O	Na2SO4·10H2O	MgSO4·7H2O	AlCl3·6H2O
ω(соли),%	0,25	6	15	0,085	10
ρ, г/мл	1,06	1,11	1,13	1,04	1,02

4. Рассчитать массу кристаллогидрата
Х·nH₂O (г), которую надо растворить
в воде для получения раствора, содержащего
Х% безводной соли:

	Вариант
а	б	в	г	д
Вещество (Х·nH2O)	CuSO4·5H2O	FeSO4·7H2O	Na2SO4·10H2O	MgSO4·7H2O	AlCl3·6H2O
ω(Х),%	8	15	18	6	20
Объем воды	0,66 л	400 мл	0,75 л	350 мл	900 мл

5. Сколько литров газа (н.у.)
необходимо растворить в V мл воды для
получения раствора с массовой долей,
указанной в таблице:

	Вариант
а	б	в	г	д
ω(Х),%	17	30	2	1,5	3
Вещество	NH3	HCl	CO2	SO2	H2S
V воды, мл	200	1500	900	600	1000

6. Определить объем воды, в котором
надо растворить V л газа (н.у.), для
получения раствора с указанной массовой
долей:

	Вариант
а	б	в	г	д
ω(Х),%	20	25	3	2	15
Вещество	NH3	HCl	CO2	SO2	H2S
V, л	40	56,5	3,2	12,5	1,5

7. Определите массу раствора (г),
который можно приготовить из воды и
щелочи KOH, если:

	Вариант
а	б	в	г	д
m(H2O), г	100	150	175	225	250
ω(KOH),%	15	20	25	30	35

8. Рассчитать массовую долю (%)
растворенных веществ, содержащихся в
V л воды:

	Вариант
а	б	в	г	д
Вещество (Х)	HCl	H2S	CO2	NH3	SO2
V(X), л	10	2	1	20	0,5
V воды, л	1,5	4,5	6,5	0,4	0,65

9. Определить массу воды (г), которую
надо добавить к указанной массе раствора
m₁ с массовой долей вещества ω₁(Х),
для получения раствора с массовой долей
ω₂(Х):

	Вариант
а	б	в	г	д
m1, г	500	700	900	980	993
ω1(Х),%	40	50	58	60	72
ω2(Х),%	20	32	36	40	53

10. Определить объем воды, который
следует выпарить из исходного раствора
массой m₁ с

массовой долей вещества ω₁(Х),
чтобы получить раствор, в котором
массовая доля соли равна ω₂(Х):

	Вариант
а	б	в	г	д
m1, г	200	250	300	350	400
ω1(Х),%	10	20	30	40	50
ω2(Х),%	25	42	50	60	80

11. Определить объем раствора HNO₃
с указанными массовой долей ω₁(HNO₃)
и плотностью, который необходимо добавить
к 1,2 л воды для получения раствора с
массовой долей ω₂(HNO₃) = 10%:

	Вариант
а	б	в	г	д
ω1(Х),%	52	60	63	70	75
ρ1, г/мл	1,3	1,35	1,36	1,40	1,43

12. Какой объем раствора CuSO₄
с указанными в таблице массовой долей
ω₂(CuSO₄) и плотностью ρ₂
можно приготовить из 120 мл раствора с
массовой долей ω₁(CuSO₄) = 42%
(ρ₁
= 1,36 г/мл)?

	Вариант
а	б	в	г	д
ω2(CuSO4),%	52	60	63	70	75
ρ2, г/мл	1,3	1,35	1,36	1,40	1,43

13. Какие объемы растворов серной
кислоты с массовой долей ω₁(H₂SO₄)
и плотностью ρ₁ и массовой долей
ω₂(H₂SO₄) и плотностью
ρ₂ необходимо взять для приготовления
2 литров раствора H₂SO₄ с
массовой долей ω(H₂SO₄) = 14% (ρ
= 1,095 г/мл)?

	Вариант
а	б	в	г	д
ω1(H2SO4),%	30	35	38	40	50
ρ1, г/мл	1,219	1,32	1,35	1,38	1,4
ω2(H2SO4),%	6	5	4,8	4	2
ρ2, г/мл	1,038	1,030	1,028	1,022	1,018

14. Определить массовую долю Na₂CO₃
в растворе, полученном при растворении
указанной массы кристаллогидрата
Na₂CO₃·10Н₂О в растворе
Na₂CO₃ массой m с массовой долей
ω₁(Na₂CO₃) = 13%:

	Вариант
а	б	в	г	д
m(Na2CO3·10Н2О), г	40	46	48	52	56
m, г	300	420	450	500	530

15. Какую массу раствора гидроксида
калия с массовой долей ω₁(KOH) надо
добавить к раствору KOH массой m₂ и
массовой долей ω₂(KOH), чтобы получить
раствор KOH с массовой долей ω₃(KOH)?

	Вариант
а	б	в	г	д
ω1(KOH),%	20	30	40	50	60
m2, г	1000	500	480	35	25
ω2(KOH),%	50	10	90	5	2
ω3(KOH),%	25	20	15	10	5

16. Сколько литров NH₃ (н.у.)
необходимо растворить в растворе NH₃·Н₂О
массой m₁ с массовой долей ω₁(NH₃)
для получения раствора NH₃·Н₂О
с массовой долей ω(NH₃)?

	Вариант
а	б	в	г	д
m1, г	200	300	400	500	600
ω1(NH3),%	10	12	15	18	20
ω(NH3),%	15	18	20	25	33,5

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #