Цель работы
Экспериментальная
проверка основных уравнений и законов поступательного движения тела в поле сил земного тяготения, определение
ускорения свободного падения лабораторной установке – машине Атвуда.
Экспериментальная установка

Машина Атвуда (рис.1) состоит из легкого блока 2, через который
переброшена нить с двумя наборными грузами на концах (массы обоих грузов
одинаковы и равны m). Грузы могут двигаться вдоль вертикальной
рейки со шкалой 1. Если на правый груз положить небольшой перегрузок Dm,
грузы начнут двигаться с некоторым ускорением. Для приема падающего груза
служит полочка 3.
Время
движения грузов измеряется с помощью ручного или стационарного секундомера.
Силы трения в машине Атвуда
сведены к минимуму, но не равны нулю. Для возможно полной их компенсации масса
одного из грузов (в нашей установке – правого) делается немного больше массы
другого. Эта операция производится при помощи кусочков пластилина и
выполняется с таким расчетом, чтобы а) грузы могли находиться в статическом
положении сколь угодно долго, но б) от легкого толчка вниз правого груза вся
система приходила в равномерное движение. Масса используемого пластилина столь
мала, что в последующих расчетах в массу грузов не включается. Перегрузки Dm, с
помощью которых системе задается движение, укладывают также на правый груз
системы.
Для выполнения работы машина Атвуда должна быть
установлена строго вертикально, что легко проверить по параллельности шкалы и
нити.
Теоретическая часть
Второй закон Ньютона в проекциях на вертикальную
ось для каждого из тел системы (рис.2) в предположении невесомости блока,
отсутствия силы трения и нерастяжимости нити дает:
 (1)
(1)
Где g –
ускорение свободного падения,
a –
ускорение грузов,
T1
и T2 – сила натяжения нити.
Выразим из данной системы ускорение a.
![]() (2)
(2)
Проверим равноускоренный характер движения грузов,
экспериментально получая значения пути данных грузов S (для обоих грузов он одинаков) и
время движения t.
Так как
начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то
![]()
![]() (3)
(3) 
Третье соотношение часто называют законом перемещений:
«Перемещение при равноускоренном движении прямо пропорционально
квадрату времени движения».
Соотношение (3) может быть проверено
экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность
экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение,
с которым движется тело, прямо пропорционально равнодействующей действующих на
него сил и обратно пропорционально массе этого тела».
Подставляя ai в
(2) получаем следующую формулу:
![]() (4)
(4)
Для получения более точного значения g, необходимо учесть момент инерции
блока – Jб, (T1 ![]() T2). Рассмотрим получения вышеописанных формул с учётом новой величины.
T2). Рассмотрим получения вышеописанных формул с учётом новой величины.
Вычислим g из закона динамики для вращательного
движения тела (в данном случае блока).
![]() (5)
(5)
![]() –
–
сумма проекций на ось Z всех сил, действующих на
вращающиеся тело; α- угловое ускорение блока; J – его момент инерции
![]() (6)
(6)
Где r – радиус блока, Jб
– момент инерции блока.
Выразим из уравнения (1) разность сил натяжения (T1 – T2 ) и подставив ее в уравнение (6) получим:
![]() (7)
(7)
Выразим ускорение грузов a:
 (8)
(8)
Учитывая, что значение момента инерции блока
![]() (9),
(9),
k- коэффициент распределения массы блока
относительно оси вращения (k < 1), окончательно получаем выражение для
определения ускорения свободного падения:
11)![]()
Экспериментальная
часть
Задание 1. Проверка второго закона Ньютона.
Поскольку
ускорение движения является функцией двух переменных – силы и массы, то
изучение второго закона Ньютона выполняется путем раздельного исследования двух
зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе
системы и 2) зависимости ускорения от массы системы при постоянной действующей
силе.
Исследование зависимости ускорения от силы при
постоянной массе
Измерения и обработка результатов
1. Тщательно
балансируют грузы, выбрав их массы в пределах 150 – 200
г каждый.
2. Затем
на правый груз последовательно накладывают перегрузки. В результате в системе
появляется движущая сила равная Dmg, где Dm – суммарная масса перегрузков. При
этом, конечно, общая масса системы незначительно увеличивается, но этим изменением
массы по сравнению с массой грузов можно пренебречь, считая массу системы
постоянной.
3.
Измеряют время равноускоренного движения системы на пути, например, 1
метр. Все данные заносят в таблицу 1.3 отчета.
4.
Пользуясь законом путей (1.6), вычисляют ускорение а.
5.
Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.
6.
Строят график зависимости ускорения движения от действующей силы. Точку (F=0, a=0) на графике не откладывают. Если
экспериментальные точки ложатся на прямую с небольшим разбросом и прямая
проходит через начало координат, то можно сделать вывод о том, что ускорение
действительно прямо пропорционально силе.
7.
По угловому коэффициенту полученной прямой определяют массу системы и сравнивают
ее реальной массой.
Исследование зависимости ускорения от массы при
постоянной силе
Измерения и обработка результатов
1. Все опыты
проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе.
Ускорение системы измеряется также как и в предыдущем задании.
2.
Для изменения массы системы одновременно на правый и левый груз кладут дополнительные
одинаковые грузы. Все данные записывают в таблицу отчета.
3.
График обратно пропорциональной зависимости ускорения от массы представляет
собой гиперболу, которую невозможно идентифицировать. Для проверки предположения
об обратно пропорциональной зависимости между ускорением и массой ![]() необходимо построить график зависимости
необходимо построить график зависимости
ускорения от обратного значения массы системы: a = f(М-1). Подтверждением
предположения является прямолинейность этого графика.
4. По угловому коэффициенту полученной прямой
определяют значение приложенной силы и сравнивают ее с реально действующей в
системе
Задание 2. Определение ускорения движения грузов
В полученном уравнении прямой ![]() коэффициент k равен половине
коэффициент k равен половине
ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов (a
=2k) в данном опыте и определить погрешность его
измерения. Произведите необходимые вычисления и занесите результаты в отчет.
Задание 3. Определение ускорения свободного падения
(Выполняется по результатам измерений
и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и
перегрузка, а также ускорение движения системы, из формулы (3) найдите
ускорение свободного падения. Результаты занесите в отчет. В выводе сравните
полученный результат с табличной величиной.
Для нахождения погрешности измерения величины
ускорения свободного падения Δg
используем формулу:
12)![]()
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() – частные производные функции
– частные производные функции
Проанализируйте результаты своих наблюдений и
сформулируйте вывод.
Контрольные
вопросы
1.
Какое
движение называется поступательным?
2.
Дайте
определение инерциальной системы отсчета. Приведите примеры ИСО.
3.
Сформулируйте
первый закон Ньютона. Приведите примеры его проявления.
4.
Дайте
определение инертной массы тела. Гравитационной? От чего и как зависит масса
тела?
5.
Сформулируйте
второй закон Ньютона. Приведите варианты его математической формы.
6.
Покажите
все силы, действующие на один из грузов в машине Атвуда, и составьте для него
уравнение динамики.
7.
Запишите
систему уравнений динамики для машины Атвуда с учетом момента инерции блока.
Силы трения в блоке?
Лабораторная работа Определение величины земного ускорения при помощи машины Атвуда
Цель работы:
измерить величину ускорения свободного
падения при помощи машины Атвуда.
Краткая теория
Ускорение свободного
падения g
можно найти при помощи очень простого
опыта: бросить тело с высоты h
и измерить время падения t.
Тогда g=2h/t2.
В действительности дело обстоит не так
просто,
если
величину g
требуется определить достаточно точно.
Рассчитаем
время падения t
с высоты h=1,0м
при g=9,8м/с2
![]()
При измерении
такого промежутка времени с погрешностью
t=0.01c
относительная
погрешность определения g,
равная,
![]()
будет более 4.5%
и абсолютная
погрешность
g>0.5m/c2.
Казалось бы, чтобы снизить
погрешность
определения g,
используя секундомер с той же
погрешностью
t=0.01c,
надо увеличить измеряемый
промежуток
времени, увеличивая высоту падения. Так
при h=5м
время падения около 1с, а при h=20м
– t2c.
Однако в этом случае возникают ошибки
другого характера.
Дело в том, что при
больших скоростях заметную роль играет
сопротивление воздуха, а формула
равноускоренного движения h=gt2/2
этого фактора
не учитывает. Таким образом, увеличивая
высоту h,
мы увеличиваем время падения и уменьшаем
относительную погрешность его измерения,
но при этом вносим другую ошибку: сама
формула h=gt2/2
становится
неточной. Например, если сбросить кирпич
с высоты h=500м,
то около 200м
он будет двигаться с ускорением, а затем
сила сопротивления воздуха станет равна
силе тяжести (это будет при скорости
70
м/с) и тело остальные 300м
будет двигаться с постоянной скоростью.
Приведенный простой
пример наглядно демонстрирует общую
черту любого физического эксперимента.
В любом эксперименте точность определения
какой-либо физической величины связана
не только с точностью измерительных
приборов, но и с тем насколько точно
принятая модель описывает данный опыт,
иначе говоря, насколько модель адекватна
экспериментальной ситуации. Очевидно,
что при обработке экспериментальных
данных по формулам приближенной модели
полученные результаты будут отличаться
от истинного значения измеряемой
величины. Это отличие имеет смысл
систематической погрешности. Для ее
учета надо строить более точную модель
эксперимента.
Итак, сложности
такого внешне простого опыта связаны
с большим ускорением тела, за которым
мы следим во время опыта. Так как ускорение
большое, то тело быстро набирает скорость,
а при этом или время движения мало и его
трудно измерить, или сама формула
равноускоренного движения неточна.
Уменьшить ускорение
можно с помощью устройства, которое
называется машиной Атвуда (рис.1). Через
блок перекинута нить, на которой укреплены
грузы с массой M
каждый. На один из грузов накладывается
перегрузок с массой m.
Система начнет двигаться с ускорением
a.
Пройдя расстояние S-H,
перегрузок m
снимается. Система продолжает двигаться
по инерции, проходя путь H.
Время прохождения
этого расстояния можно точно измерить.
Для достижения цели – как можно более
точного для наших условий определения
ускорения свободного падения g
– необходимо построить модель
экспериментальной ситуации, которая
реализуется в машине Атвуда. В рамках
этой модели надо найти связь между t
и H
и указать метод определения из такой
зависимости интересующей нас величины
g.
Н
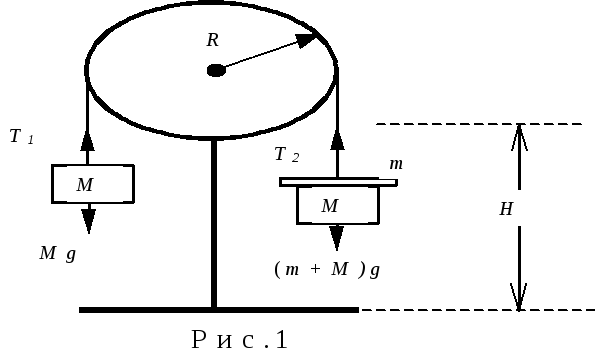
аиболее простая модель нашей
экспериментальной установки такова:
блок и нить невесомы (их массы равны
нулю), нить нерастяжима; трением в блоке
и сопротивлением воздуха пренебречь.
Тогда уравнения движения грузов имеют
следующий вид
![]() .
.
(1)
Здесь T
– сила натяжения нитей (при сделанных
предположениях эти силы одинаковы), a
– ускорение грузов. Решая систему (1),
получаем
![]() .
.
(2)
Из этой формулы
видно, что система будет двигаться с
постоянным ускорением, причем a=0,
если m=0
(то есть система будет двигаться
равномерно при снятом перегрузке). До
снятия перегрузка система пройдет
расстояние S-H
и, к моменту снятия перегрузка, она будет
иметь скорость, которую можно рассчитать
по формуле v2=2a(S-H).
Скорость v
можно экспериментально определить,
измерив время t
прохождения системой пути H.
Итак, получаем связь между t
и H
![]() .
.
(3)
Таким образом,
определив экспериментально зависимость
t
от H,
по формуле (3) можно найти величину a
(это можно сделать методом наименьших
квадратов) и далее по формуле (2), используя
известные значения m
и M,
рассчитать ускорение свободного падения
g.
Рассмотрим более
реалистичную модель машины Атвуда. В
этой модели учтем то, что масса блока
не равна нулю. Теперь необходимо считать,
что система состоит из трех тел – двух
грузов с массами M
и M+m,
и блока, имеющего момент инерции J.
Для описания
движения такой
системы к
уравнениям движения грузов надо добавить
уравнение движения
для блока
(уравнение моментов). Обратим внимание
на тот факт, что в
рассматриваемой
модели силы натяжения нити, действующие
на грузы,
неравны.
Имеем
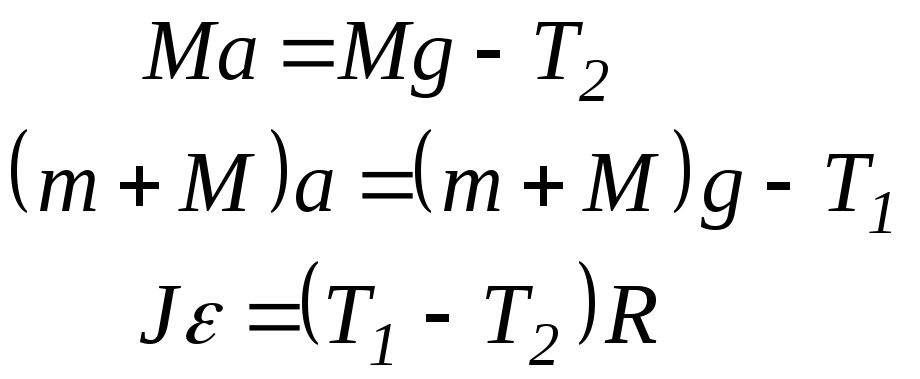 .
.
(4)
Последнее уравнение
– это уравнение моментов. Здесь
– угловое ускорение, которое в отсутствие
проскальзывания нити по блоку равно
=a/R,
где R
– радиус блока. Решая эту систему, получаем
![]() .
.
(5)
Из этой формулы
видно, что при J=0
она переходит в
выражение
(2). Так
же, как и
раньше, в отсутствии перегрузка, то есть
при m=0,
ускорение a
равно нулю. Значит, расстояние H
система
будет
проходить с постоянной скоростью и
связь между H
и t
такая
же, как и
первой модели. Способы обработки
результатов эксперимента
практически
не отличаются от используемых в первой
модели. Как и
раньше из
экспериментальной зависимости t
от H
методом наименьших
квадратов
можно найти a,
но ускорение свободного падения теперь
вычисляется
при помощи выражения (5).
В формуле (5)
неизвестна величина момента инерции
блока J
относительно
оси вращения. Оценить величину J
можно, если считать
блок диском
радиусом R
и массой mБ,
в котором вырезаны отверстия радиусом
r,
а центры этих отверстий находятся на
расстоянии l
от центра вращения. Вывод выражения для
J
такой
модели
блока приведен в приложении, где также
приведена оценка
величины
момента инерции блока, которая составила
J95гcм2.
На самом деле блок представляет более
сложную конструкцию, которая включает
в себя не только фигурный диск, но и ось,
которая закреплена в подшипниках.
Рассчитать момент инерции такой
конструкции в принципе можно, но эти
вычисления достаточно громоздки, поэтому
значение J
гораздо проще измерить, например,
так, как это делается в
лабораторной
работе
№4. Такое
измерение дает J=(94,70.5)гcм2.
Теперь нетрудно
оценить погрешность определения g,
которую мы бы допустили, если пользовались
результатами первой модели. Так в нашей
установке величина 2M+m
равна приблизительно 125г, величина R4cм
и, значит, I/R26г.
Таким образом, пренебрежение моментом
инерции блока приводит к уменьшению
знаменателя в формуле (2) примерно на 5%
и, как следствие, к такому же примерно
завышению g,
определенного по формулам первой модели.
Завершая обсуждение
второй модели, сделаем еще следующее
замечание. Формуле (5) можно придать
более простой вид, аналогичный выражению
(2), если ввести новую величину ![]() ,
,
которая характеризует инерционные
свойства системы,
обусловленные
не только массами грузов, но и инерционными
свойствами
блока,
поэтому
величину
M0
можно
назвать эквивалентной массой груза.
Используя
эту величину, формула (5) преобразуется
к виду
![]() .
.
(6)
Этим выражением
мы будем пользоваться в дальнейшем при
обработке эксперимента.
Итак, вторая модель
позволила нам учесть массу блока.
Пренебрежение
массой
нити является хорошим приближением для
данной установки, и его
обсуждать
мы не будем. Рассмотрим теперь приближения,
связанные с
силами
трения. Силу трения грузов о воздух с
хорошей точностью можно считать
пропорциональной скорости их движения,
то есть чем меньше скорость движения
грузов, тем меньше сила сопротивления
его движению и тем точнее выполняется
приближение об отсутствии трения о
воздух.
Казалось бы, в
данной установке скорость движения
грузов можно сделать как угодно малой.
Формально это следует как из формулы
(2), так и из формулы (5) – при m0
ускорение а0.
Например, если M=5кг
и m=1г,
то m/2M=10-4
и при опускании груза с высоты примерно
0,5 м
его скорость не превысит величины 1мм/с.
Однако реально такой опыт невыполним
(система может даже не начать двигаться
при наложении перегрузка). Дело в том,
что в выбранных моделях мы предположили
отсутствие трения в оси блока. В
действительности оно есть и для учета
его влияния на поведение системы нам
надо снова уточнить модель, включив в
нее силы трения, действующие в оси блока.
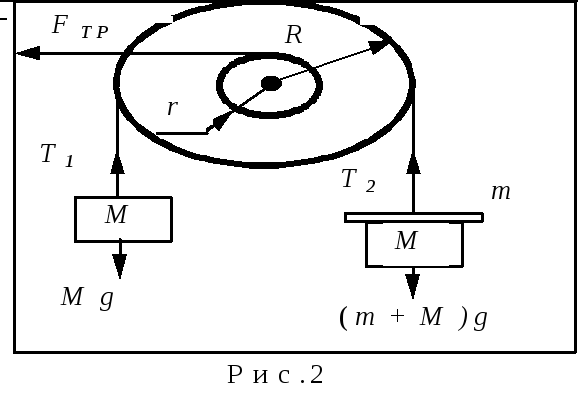
Уравнения движения с учетом
силы трения в оси блока будут иметь
следующий вид
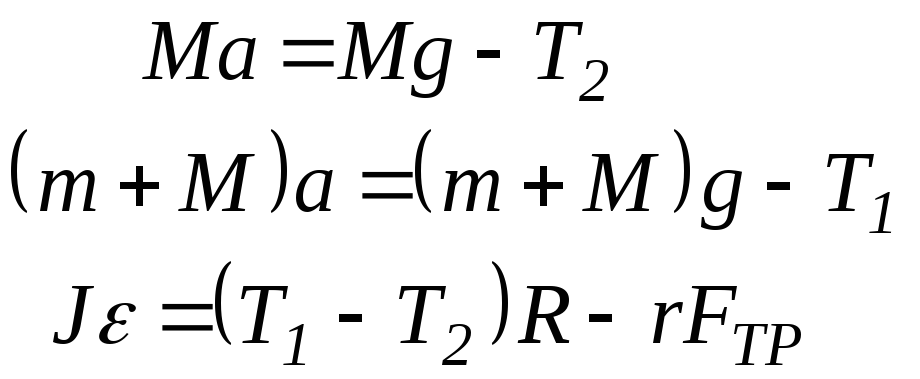 .
.
(7)
Здесь FТР
– сила трения между блоком и осью, r
– радиус оси
(рис.2). Сила трения FТР
прямопропорциональна силе давления на
ось блока N,
то есть FТР=N=(T1+T2),
где
– коэффициент трения между блоком и
осью, зависящий от свойств соприкасающихся
поверхностей втулки блока и оси, состояния
смазки и т.п.
Используя это
соотношение и вспоминая также, что
угловое ускорение блока связано с
линейным ускорением по формуле =a/R,
последнее уравнение системы (7) можно
записать в следующем виде
![]()
Подставив в него
T1
и T2,
выраженные из первых двух уравнений
системы (7), получаем
![]()
Используя величину
М0
и введя
обозначение k=(r/R),
выражение для ускорения системы
можно
представить в следующем виде
![]() .
.
(8)
Рассмотрим характер
движения системы в зависимости от массы
перегрузка.
Если система в начальный момент времени
находится в покое,
то при
постепенном увеличении массы перегрузка
система будет
продолжать
оставаться в покое до тех пор пока
наложенная масса не
превысит
некого значения m0,
которое легко определить из условия
равенства нулю числителя в выражении
(8).
![]() .
.
(9)
При m>m0
система будет двигаться с ускорением,
определяемым согласно формуле (8). В
момент снятия перегрузка система будет
обладать скоростью v=2a(S-H)
и начнет двигаться равнозамедленно, то
есть с отрицательным ускорением a0,
которое нетрудно вычислить, если в
формуле (8) положить m=0
![]() .
.
(10)
Чтобы использовать
результаты точной модели для определения
ускорения свободного падения g
по экспериментальным данным, полученным
на машине Атвуда, надо уметь определять
величину k,
характеризующую силу трения в оси.
Оценить величину k
можно просто по формуле (9), зная m0
– k=m0
/(m0+2M).
По своему смыслу m0
– это масса перегрузка, который
только-только страгивает блок с грузами.
Из-за этого “только-только” величина
m0
оценивается очень грубо. Например,
перегрузок массой 1г
не страгивает блока, а перегрузок массой
2г приводит
блок в движение. Такое измерение позволяет
заключить только, что 1г<m0<2г.
Это, очевидно, очень грубое оценочное
измерение. Оно не может нас удовлетворить
и вот по какой причине. Дело в том, что,
как отмечалось выше, для надежного
пренебрежения силой сопротивления
воздуха необходимо, чтобы грузы двигались
медленно, то есть ускорение a
было мало. Как следует из формулы (8) и
(9) это возможно, если масса перегрузка
m
незначительно превышает m0.
В этом случае, как можно показать,
погрешность g
существенным образом определяется
погрешностью m0,
которая велика.
Существует другой
метод определения k,
использующий только экспериментальные
результаты, полученные на машине Атвуда.
То, что этот метод не требует дополнительных
экспериментов, делает его особенно
привлекательным, но за это приходится
расплачиваться более сложными формулами
для обработки эксперимента. Выведем
эти формулы.
Для начала получим
выражение для времени падения груза с
высоты H.
После прохождения участка S-H
с ускорением a
груз приобретает скорость v=2a(S-H).
В этот момент начинается равнозамедленное
движение с ускорением a0.
Время перемещения t
и расстояние
H
связаны при этом известным соотношением
![]() ,
,
(11)
где обозначения
A=2a
и B=a0/2
введены для удобства.
В этой формуле S
– известная величина, H
и t
измеряются экспериментально, значения
же a
и a0,
или, что то же самое, A
и B
подлежат определению. Вычислить эти
величины методом наименьших квадратов,
используя формулу (11) нельзя, так как
эта формула задает неявную связь между
измеряемыми величинами.
Как применять
метод наименьших квадратов для нахождения
A
и B
будет подробно изложено ниже. Сейчас
же будем считать, что значения параметров
A
и B
нам известны и выведем уравнение для
расчета величины g.
Выпишем выражения для A
и B,
используя формулы (8) и (10).
![]() .
.
(12)
Соотношения (12)
представляют собой систему уравнений
относительно
неизвестных g
и
k.
Выразив k
из второго соотношения
(k=-2BM0/gM)
и подставив его в первое, получим
квадратное уравнение
для величины
g.
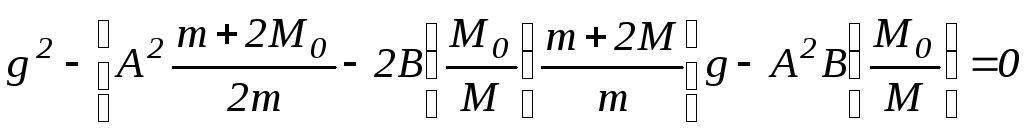 .
.
(13)
В этом уравнении
все коэффициенты легко рассчитываются,
зная параметры
A
и
B,
найденные из эксперимента, и параметры
установки m,
M
и
M0.
Нетрудно рассчитать также и погрешности
этих коэффициентов.
Далее,
найдя корни этого уравнения и выбрав
из них физически разумный,
можно
вычислить величину ускорения свободного
падения.
Таким образом, мы
рассмотрели результаты трех моделей,
описывающих
движение
машины Атвуда. Последняя модель наиболее
полно, по сравнению
с предыдущими,
учитывает детали движения грузов. Можно,
конечно, и
далее
совершенствовать модель, включая в нее
другие тела и другие
силы,
оказывающие влияние на движение системы.
Например, можно учесть
влияние
на характер движения массы нити. Но надо
ли это? Ведь
интуитивно
мы понимаем, что учет массы нити даст
поправку к значению
g,
не превышающую отношения массы нити к
эффективной массе системы.
Но это
отношение можно сделать как угодно
малым, увеличивая массу M.
Можно было бы
уточнять модель, вводя в рассмотрение
силу сопротивления воздуха, действующую
на грузы при их движении. Но это приводит
к значительным математическим сложностям.
По этой причине может оказаться более
простым проведение экспериментов с
машиной Атвуда в вакууме.
Процесс
совершенствования физической модели
реального объекта бесконечен. Стоит
вопрос о том, что надо где-то остановиться,
чем-то ограничится. Указание на такую
границу может дать точность эксперимента,
поскольку очевидно, что если уточнение
модели дает поправку меньшую, чем
точность эксперимента, то такое
усовершенствование бесполезно
Стимулом для
дальнейшего совершенствования, уточнения
или изменения модели служат, в первую
очередь, выводы следующие из эксперимента,
сделанные на основании той или иной
модели. Так, например, для нашего случая
при обработке результатов эксперимента
по формулам первой модели получается,
что величина g
зависит от массы перегрузка m.
Этот факт противоречит принципу
эквивалентности инертной и гравитационной
массы, справедливость которого установлена
с высокой точностью. Отсюда следует
вывод о неполноте модели нашей установки
и необходимости ее уточнения.
Можно привести
пример другого рода. Точные измерение
земного ускорения, проведенные на разных
географических широтах, дают разные
его значения. Ускорение тем меньше, чем
меньше широта (на экваторе величина
земного ускорения наименьшая). Эта
зависимость, очевидно, обусловлена
вращением Земли и указывает на
необходимость учитывать в физической
модели эксперимента это вращение,
например, путем введения центробежной
силы.
Изучение законов поступательного движения на машине Атвуда: формулы и пояснения
Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Что такое машина Атвуда?
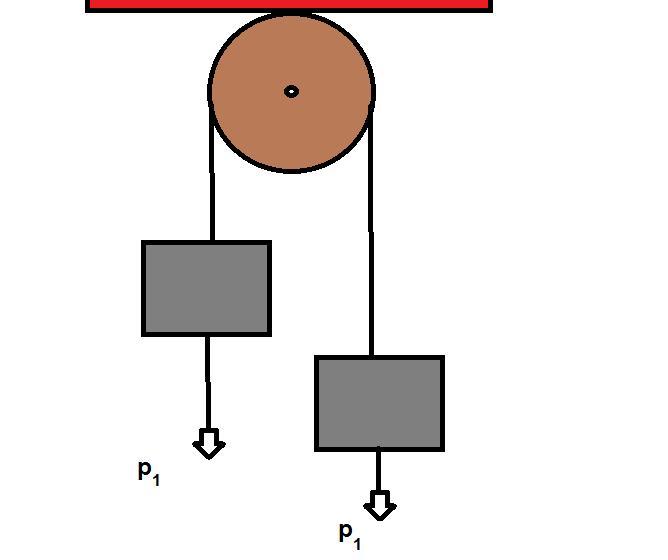
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.
 Вам будет интересно: Пространственная экономика: описание специальностей и структура
Вам будет интересно: Пространственная экономика: описание специальностей и структура
 Вам будет интересно: Что такое подполье? Подпольная организация “Молодая гвардия”. Антифашистское движение
Вам будет интересно: Что такое подполье? Подпольная организация “Молодая гвардия”. Антифашистское движение
Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
Где m – инерционная масса тела, a – ускорение.
Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.
Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
F1 – F2 = a*(m1 + m2) =>
a = (F1 – F2)/(m1 + m2).
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
a = g*(m1 – m2)/(m1 + m2).
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
Проверка решения уравнений динамики

Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
Откуда ускорение определяется однозначно:
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
(F1 – T)/m1 = (T – F2)/m2 =>
T = (m2*F1 + m1*F2)/(m1 + m2).
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
T = 2*m1*m2*g/(m1 + m2).
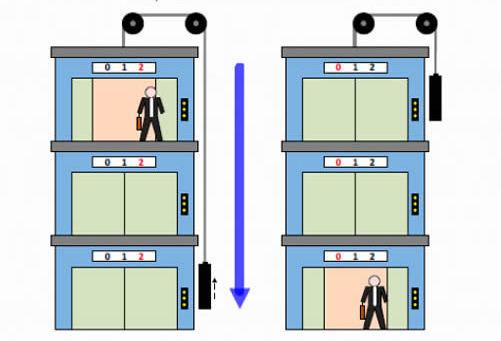
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
Описание лабораторной работы
Изучение равнопеременного и равномерного прямолинейных движений в поле земного тяготения. Определение ускорения свободного падения.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ
Основные законы динамики материальных точек – это законы Ньютона. В частности, второй закон Ньютона, математическая запись которого, как известно, имеет вид:
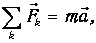
называют основным уравнением динамики.
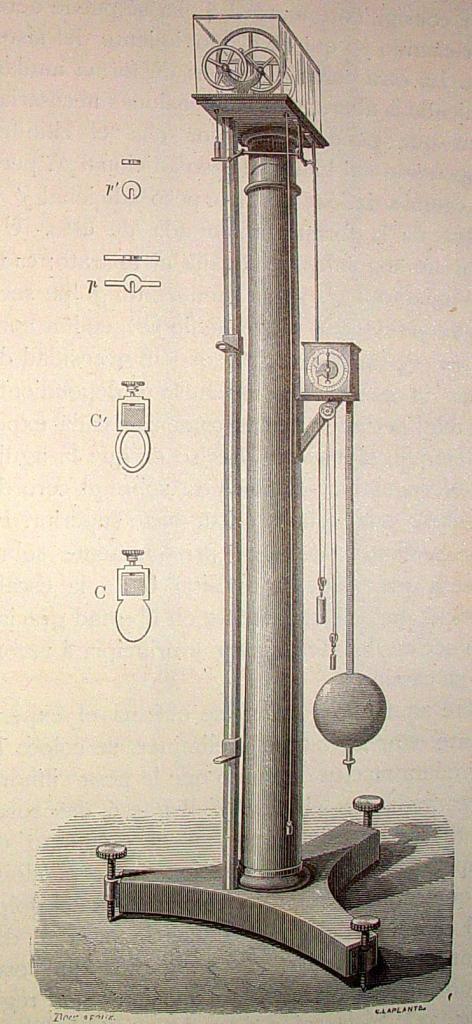
Эскиз машины Атвуда показан на рис. 1.

Рис. 1. Эскиз машины Атвуда
Два одинаковых груза с массами М соединены нитью, перекинутой через неподвижный блок. Если на один из грузов положить перегрузок массой m (в виде шайбы), то система приходит в ускоренное движение. Каждый из грузов натягивает участок нити, который, стараясь сократиться, действует на соответствующий груз с силой натяжения Т 1 или Т 2 , а на блок – с силами Т ’1 и Т ’2 . Тогда на каждый груз действует сила тяжести и сила натяжения нити.
Основное уравнение динамики для груза с перегрузком имеет вид:
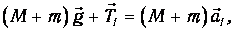
а для другого груза (без перегрузка):
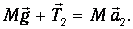
Основное уравнение динамики вращательного движения неподвижного блока имеет вид:
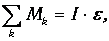
где S Mk – алгебраическая сумма моментов сил, действующих на блок, относительно оси вращения; I – момент инерции блока относительно оси вращения; e – его угловое ускорение.
Если вращение по часовой стрелке считать положительным, то, согласно рис. 1, получим
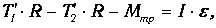
где: R – радиус блока; Мтр – момент силы трения.
Будет считать, что нить невесомая, нерастяжимая и не скользит по блоку. Из условия невесомости нити следует:

Из условия нерастяжимости нити следуют равенства модулей перемещений, скоростей и ускорений грузов и нити:
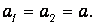
Наконец, в отсутствие скольжения нити по блоку, ускорение грузов и нити а равно модулю тангенциального ускорения точек обода блока:
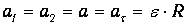
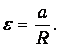
Проецируя уравнения (2) и (3) на ось у , направленную вертикально вверх, получим с учетом формул (5), (6) и (7) систему уравнений, к которой присоединим уравнение (4а):
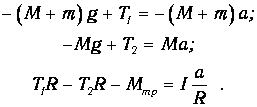
Умножая первое из уравнений (8) на (-1) , и складывая все уравнения (8), получим
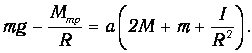
В данной лабораторной установке момент сил трения настолько мал, что выполняется неравенство
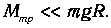
Кроме того, в лабораторной установке величина момента инерции I блока такова, что справедливо другое неравенство:
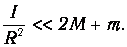
Пренебрегая малыми величинами, из уравнения (9) получим формулу для расчёта ускорения а системы грузов под действием перегрузка массой m :
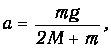
а модули сил натяжения нити Т1 и Т2 по обе стороны блока равны:
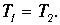
Можно сказать, что равенство (13) выполняется при двух предположениях (10) и (11).
Равноускоренное движение системы грузов вдоль оси у описывается уравнениями движения произвольной точки системы:
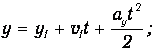
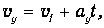
Исключая из этих уравнений время t , при условии v1=0 , получим
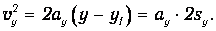
Система грузов перемещается на величину sy=L1 , двигаясь равноускоренно под действием перегрузка массой m с ускорением, которое определяется формулой (12).
В точке с координатой у2 и скоростью v2 перегрузок подхватывается столиком, и система грузов движется равномерно, перемещаясь на величину L2 за время t , измеряемое миллисекундомером экспериментальной установки. Подставляя в равенство (14) формулу

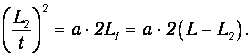
При изменении L2 меняется время t , измеряемое секундомером, но ускорение а должно оставаться неизменным.
С помощью формулы (15) найдём расчётную формулу для величины ускорения а грузов с перегрузком:
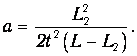
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
К основанию 1 экспериментальной установки (см. рис. 2), которая стоит на ножках 2 , прикреплена вертикальная стойка 3 . К стойке крепится кронштейн 4 , который может перемещаться вдоль стойки. На кронштейне находится столик для снятия перегрузка.
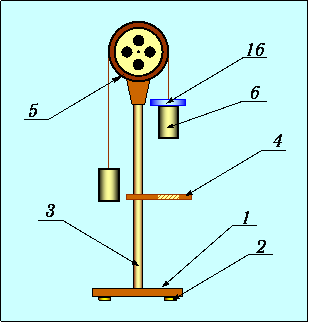
Рис. 2. Схема экспериментальной установки
На верхнем конце стойки находится неподвижный блок 5 . Для наблюдения ускоренного движения грузов на правый груз 6 помещают перегрузок 7 и поднимают их в верхнее положение путем нажатия кнопок «+» или «-». Значение массы перегрузка показывается в окне «масса После нажатия кнопки «ПУСК» начинается ускоренное движение грузов и перегрузка до того момента, когда столик 4 подхватит перегрузок. Одновременно включается миллисекундомер, измеряющий время равномерного движения грузов до остановки. Итак, во время равноускоренного движения грузы проходят расстояние L1 (см. рис. 1) и приобретают скорость v2 , с которой, двигаясь равномерно, проходят расстояние L2 за время t , измеренное миллисекундомером в секундах и показанное в окне «время».
Для подготовки прибора к следующему измерению нажимают кнопку «СБРОС».
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Упражнение 1. ИЗМЕРЕНИЕ УСКОРЕНИЯ ГРУЗОВ
1. Измерьте расстояние L с помощью линейки и занесите результат в таблицу измерений 1. Цена деления линейки 1 см .
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
2. Выберите значение массы перегрузка m и занесите ее значение в таблицу 1. Выбор производится мышкой с помощью нажатия ей на кнопки со значками «+» или «-». Значение массы перегрузка показывается в окне «масса». Оптимальным для выбора является значение массы от 5 до 10 г . Учтите, что масса в данной работе определена при взвешивании тел на весах с точностью, равной половине цены деления весов. Приборная погрешность весов составляла 0.1 г .
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в килограммах.
3. Установите, взяв мышкой, кронштейн со столиком на некотором расстоянии L2 от нижнего фиксатора расстояний. Возможные пределы варьирования расстояния от 12 до 25 см . Измерьте установленное расстояние L2 по линейке, взяв отсчёт по красной черте. Результаты измерения запишите в таблицу 1 результатов измерений 1 . Цена деления линейки 1 см .
Обратите внимание на необходимость записывать данные в системе СИ, то есть, в метрах.
5. После остановки грузов запишите в таблицу 1 время t равномерного движения грузов, измеренное миллисекундомером и показанное на табло «время». Время необходимо записывать в системе СИ, то есть в секундах. Погрешность миллисекундомера составляет 0.001 с .
6. Нажмите кнопку «СБРОС».
7. Повторите пункты 3 – 5 ещё четыре раза, не меняя расстояние L2 .
8. Вычислите среднее значение времени t >. Результат занесите в таблицу расчетов 2.
Методические указания к лабораторной работе “Машина Атвуда”
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Экспериментальная проверка основных уравнений и законов поступательного движения тела в поле сил земного тяготения, определение ускорения свободного падения лабораторной установке – машине Атвуда.
 Машина Атвуда (рис.1) состоит из легкого блока 2, через который переброшена нить с двумя наборными грузами на концах (массы обоих грузов одинаковы и равны m ). Грузы могут двигаться вдоль вертикальной рейки со шкалой 1. Если на правый груз положить небольшой перегрузок D m , грузы начнут двигаться с некоторым ускорением. Для приема падающего груза служит полочка 3.
Машина Атвуда (рис.1) состоит из легкого блока 2, через который переброшена нить с двумя наборными грузами на концах (массы обоих грузов одинаковы и равны m ). Грузы могут двигаться вдоль вертикальной рейки со шкалой 1. Если на правый груз положить небольшой перегрузок D m , грузы начнут двигаться с некоторым ускорением. Для приема падающего груза служит полочка 3.
Время движения грузов измеряется с помощью ручного или стационарного секундомера.
Силы трения в машине Атвуда сведены к минимуму, но не равны нулю. Для возможно полной их компенсации масса одного из грузов (в нашей установке – правого) делается немного больше массы другого. Эта операция производится при помощи кусочков пластилина и выполняется с таким расчетом, чтобы а) грузы могли находиться в статическом положении сколь угодно долго, но б) от легкого толчка вниз правого груза вся система приходила в равномерное движение. Масса используемого пластилина столь мала, что в последующих расчетах в массу грузов не включается. Перегрузки D m , с помощью которых системе задается движение, укладывают также на правый груз системы.
Для выполнения работы машина Атвуда должна быть установлена строго вертикально, что легко проверить по параллельности шкалы и нити.
Второй закон Ньютона в проекциях на вертикальную ось для каждого из тел системы (рис.2) в предположении невесомости блока, отсутствия силы трения и нерастяжимости нити дает:
 (1)
(1)
Где g – ускорение свободного падения,
a – ускорение грузов,
Выразим из данной системы ускорение a .
 (2)
(2)
Проверим равноускоренный характер движения грузов, экспериментально получая значения пути данных грузов S (для обоих грузов он одинаков) и время движения t .
Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то

 (3)
(3) 
Третье соотношение часто называют законом перемещений: «Перемещение при равноускоренном движении прямо пропорционально квадрату времени движения».
Соотношение (3) может быть проверено экспериментально на машине Атвуда. Кроме того, машина Атвуда дает возможность экспериментально проверить второй закон Ньютона для поступательного движения: «Ускорение, с которым движется тело, прямо пропорционально равнодействующей действующих на него сил и обратно пропорционально массе этого тела».
Подставляя a i в (2) получаем следующую формулу:
 (4)
(4)
Для получения более точного значения g , необходимо учесть момент инерции блока – J б, ( T 1  T 2). Рассмотрим получения вышеописанных формул с учётом новой величины. Вычислим g из закона динамики для вращательного движения тела (в данном случае блока).
T 2). Рассмотрим получения вышеописанных формул с учётом новой величины. Вычислим g из закона динамики для вращательного движения тела (в данном случае блока).
 (5)
(5)
 – сумма проекций на ось Z всех сил, действующих на вращающиеся тело; α- угловое ускорение блока; J – его момент инерции
– сумма проекций на ось Z всех сил, действующих на вращающиеся тело; α- угловое ускорение блока; J – его момент инерции
 (6)
(6)
Где r – радиус блока, J б – момент инерции блока.
Выразим из уравнения (1) разность сил натяжения ( T 1 – T 2 ) и подставив ее в уравнение (6) получим:
 (7)
(7)
Выразим ускорение грузов a :
 (8)
(8)
Учитывая, что значение момента инерции блока
 (9),
(9),
k- коэффициент распределения массы блока относительно оси вращения (k
11) 
Задание 1. Проверка второго закона Ньютона.
Поскольку ускорение движения является функцией двух переменных – силы и массы, то изучение второго закона Ньютона выполняется путем раздельного исследования двух зависимостей: 1) зависимости ускорения от действующей силы при постоянной массе системы и 2) зависимости ускорения от массы системы при постоянной действующей силе.
Исследование зависимости ускорения от силы при постоянной массе
Измерения и обработка результатов
1. Тщательно балансируют грузы, выбрав их массы в пределах 150 – 200 г каждый.
2. Затем на правый груз последовательно накладывают перегрузки. В результате в системе появляется движущая сила равная mg, где m – суммарная масса перегрузков. При этом, конечно, общая масса системы незначительно увеличивается, но этим изменением массы по сравнению с массой грузов можно пренебречь, считая массу системы постоянной.
3. Измеряют время равноускоренного движения системы на пути, например, 1 метр. Все данные заносят в таблицу 1.3 отчета.
4. Пользуясь законом путей (1.6), вычисляют ускорение а.
5. Поводят еще 5-6 опытов, последовательно увеличивая массу перегрузков.
6. Строят график зависимости ускорения движения от действующей силы. Точку ( F =0, a =0) на графике не откладывают. Если экспериментальные точки ложатся на прямую с небольшим разбросом и прямая проходит через начало координат, то можно сделать вывод о том, что ускорение действительно прямо пропорционально силе.
7. По угловому коэффициенту полученной прямой определяют массу системы и сравнивают ее реальной массой.
Исследование зависимости ускорения от массы при постоянной силе
Измерения и обработка результатов
1. Все опыты проводят с одним и тем же перегрузком, т.е. при постоянной действующей силе. Ускорение системы измеряется также как и в предыдущем задании.
2. Для изменения массы системы одновременно на правый и левый груз кладут дополнительные одинаковые грузы. Все данные записывают в таблицу отчета.
3. График обратно пропорциональной зависимости ускорения от массы представляет собой гиперболу, которую невозможно идентифицировать. Для проверки предположения об обратно пропорциональной зависимости между ускорением и массой  необходимо построить график зависимости ускорения от обратного значения массы системы: a = f (М -1 ). Подтверждением предположения является прямолинейность этого графика.
необходимо построить график зависимости ускорения от обратного значения массы системы: a = f (М -1 ). Подтверждением предположения является прямолинейность этого графика.
4. По угловому коэффициенту полученной прямой определяют значение приложенной силы и сравнивают ее с реально действующей в системе
Задание 2. Определение ускорения движения грузов
В полученном уравнении прямой  коэффициент k равен половине ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов ( a =2 k ) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет.
коэффициент k равен половине ускорения системы: k=a/2. Это позволяет вычислить ускорение грузов ( a =2 k ) в данном опыте и определить погрешность его измерения. Произведите необходимые вычисления и занесите результаты в отчет.
Задание 3. Определение ускорения свободного падения
(Выполняется по результатам измерений и вычислений, проведенных в первом и втором заданиях). Зная массы грузов и перегрузка, а также ускорение движения системы, из формулы (3) найдите ускорение свободного падения. Результаты занесите в отчет. В выводе сравните полученный результат с табличной величиной.
Для нахождения погрешности измерения величины ускорения свободного падения Δ g используем формулу:
12) 
где  ;
;  ;
;  ;
;  ;
;
 – частные производные функции
– частные производные функции
Проанализируйте результаты своих наблюдений и сформулируйте вывод.
Контрольные вопросы
Какое движение называется поступательным?
Дайте определение инерциальной системы отсчета. Приведите примеры ИСО.
Сформулируйте первый закон Ньютона. Приведите примеры его проявления.
Дайте определение инертной массы тела. Гравитационной? От чего и как зависит масса тела?
Сформулируйте второй закон Ньютона. Приведите варианты его математической формы.
Покажите все силы, действующие на один из грузов в машине Атвуда, и составьте для него уравнение динамики.
Запишите систему уравнений динамики для машины Атвуда с учетом момента инерции блока. Силы трения в блоке?
[spoiler title=”источники:”]
http://online.mephi.ru/courses/physics/osnovi_mehaniki/data/lab/1/1.html
http://infourok.ru/metodicheskie-ukazaniya-k-laboratornoy-rabote-mashina-atvuda-441317.html
[/spoiler]
Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Что такое машина Атвуда?
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.
 Вам будет интересно:Пространственная экономика: описание специальностей и структура
Вам будет интересно:Пространственная экономика: описание специальностей и структура
 Вам будет интересно:Что такое подполье? Подпольная организация “Молодая гвардия”. Антифашистское движение
Вам будет интересно:Что такое подполье? Подпольная организация “Молодая гвардия”. Антифашистское движение

Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
F = m*a.
Где m – инерционная масса тела, a – ускорение.

Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
F1 – T = m1*a.
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
T – F2 = m2*a.
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.

Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
F1 – T = m1*a;
T – F2 = m2*a.
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
F1 – F2 = a*(m1 + m2) =>
a = (F1 – F2)/(m1 + m2).
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
a = g*(m1 – m2)/(m1 + m2).
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
a = na*g.
Проверка решения уравнений динамики

Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
h = a*t2/2.
Откуда ускорение определяется однозначно:
a = 2*h/t2.
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
acp = ∑i=1mai/m.
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
acp = na*g.
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
g = a/na.
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
g = 2*h/(t2*na).
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
F1 = 2*h*m1/(t2*na).
Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
F1 – T = m1*a;
T – F2 = m2*a.
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
(F1 – T)/m1 = (T – F2)/m2 =>
T = (m2*F1 + m1*F2)/(m1 + m2).
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
T = 2*m1*m2*g/(m1 + m2).

Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
Изучение законов поступательного движения на машине Атвуда
Страницы работы
Содержание работы
Лабораторная работа №3
ИЗУЧЕНИЕ ЗАКОНОВ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ
АТВУДА
Цель
работы: проверить закон пути при
равноускоренном прямолинейном движении и второй закон Ньютона.
Приборы
и принадлежности: машина Атвуда и набор
грузов.
1. ОБЩИЕ СВЕДЕНИЯ
Прямолинейное равноускоренное движение характеризуется
постоянным линейным ускорением и равным нулю нормальным ускорением (an = 0, aτ
= const).
Законы кинематики для равноускоренного движения имеют
вид:
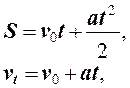
где
v0 –
начальная скорость тела, м/с ; vt – конечная скорость, м/с ; t – время, с ; а
– ускорение, м/с2; S – путь, м.
Скорость тела в разных системах координат определяется
законом сложения скоростей Галилея
![]()
где
![]() – скорость
– скорость
тела относительно неподвижной системы отсчета; ![]() – скорость подвижной системы отсчета относительно
– скорость подвижной системы отсчета относительно
неподвижной; ![]() –
–
скорость тела относительно подвижной системы отсчета.
Закон сложения скоростей Галилея и законы динамики
Ньютона выполняются в системах отсчета, которые называются инерциальными.
Системы отсчета называются инерциальными, если они
находятся в покое или движутся равномерно прямолинейно относительно какой-то
другой инерциальной системы.
Первый закон Ньютона: всякое тело находится в
состоянии покоя или равномерного движения, пока и поскольку другие тела не
выведут его из этого состояния.
Свойство тел сохранять состояние покоя или равномерного
прямолинейного движения называется инертностью. Мерой инерции является масса.
Второй закон Ньютона: ускорение, с которым движется
тело под действием силы, прямо пропорционально действующей силе и обратно
пропорционально массе тела.
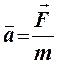 или
или ![]()
где
F – сила, Н; m – масса тела, кг.
Третий закон Ньютона: силы, с которыми два тела
действуют друг на друга, равны по модулю, противоположно направлены и действуют
вдоль прямой, соединяющей центры масс ![]()
2. ОПИСАНИЕ УСТАНОВКИ
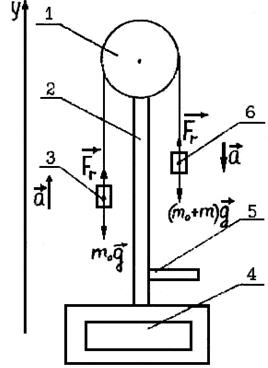 Машина Атвуда состоит из вертикальной стойки 2,
Машина Атвуда состоит из вертикальной стойки 2,
на которую нанесена шкала, разделенная на сантиметры (рис. 1). На верхнем
конце стойки укреплён лёгкий блок 1, вращающийся с пренебрежимо малым
трением. Через блок перекинута тонкая нерастяжимая нить с платформами 3
и 6 одинаковой массы m0. Грузы удерживаются электромагнитом. Массы 3
и 6 могут быть увеличены добавочными грузами – перегрузками. Если на
платформу 6 положить перегрузок массой m, то вся система начнет двигаться равноускоренно.
Значение ускорения можно установить из следующих
соображений. На каждый груз будут действовать две силы: сила тяжести и сила
реакции нити (см. рис. 1).
Под действием равнодействующей этих сил грузы движутся
ускоренно, силами трения пренебрегаем. Если предположить, что нить нерастяжима,
то ускорения правого и левого грузов будут равны по значению и противоположны
по знаку. Кроме того, если считать блок невесомым, то силы натяжения нити
справа и слева будут одинаковы. На основании второго закона Ньютона можно
записать:
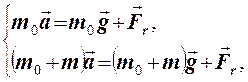
где
m0, m – массы грузов, кг; а – ускорение грузов, м/с2;
Fr –
сила реакции нити, Н.
Спроектируем
cилы на ось У. Тогда уравнения динамики примут
вид:
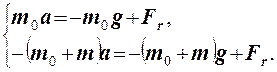
Решением этой системы линейных уравнений будет ускорение
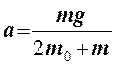 (1)
(1)
Итак, ускорение прямо пропорционально весу перегрузка mg и обратно
пропорционально массе системы тел (2m0 + m).
На лабораторной установке можно изменять массу перегрузка,
а также производить измерения на разных отрезках пути.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Задание 1.
Проверить закон пути равноускоренного движения
a = const, S = f(t2).
Закон показывает квадратичную зависимость пути от
времени
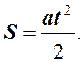
Ускорение же системы определяется по формуле (1) и
зависит от массы системы. Если масса системы и масса перегрузка не изменяется,
то система движется с одинаковым ускорением на разных участках пути.
Для выполнения задания 1 положите на правую
платформу прибора (рис. 1) перегрузок m.
1) Запишите в тетрадь массы m0 и m.
2) Установите платформу с перегрузком в самое верхнее
положение, а фотодиод 5 установите на заданном расстоянии S
на стойке. (Расстояние можете выбрать произвольно).
3) Измерьте время падения грузов на расстоянии S1
с помощью электронного секундомера 4. Запишите время t1
в табл. 1,
4) Повторите опыт, установив платформу на других
расстояниях Si.
5) Все результаты занесите в табл. 1.
Таблица 1.
Результаты измерений
|
Номер опыта |
Si, м |
ti, м |
tср, м |
a, м |
|
1 |
S1 |
t1, t2,t3 |
tср1 |
a1 |
|
… |
||||
|
5 |
6) Вычислите среднее время tср для
каждого опыта.
7) Вычислите ускорение системы в каждом опыте по
формуле
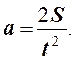 (2)
(2)
8) Вычислите теоретическое ускорение системы по
формуле (1).
9) Вычислите абсолютную и относительную погрешности
для каждого опыта
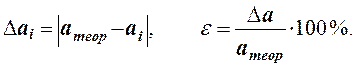
10) Сделайте выводы.
Задание 2.
Проверить второй закон Ньютона.
Если перекладывать добавочные грузы c
одной стороны на другую, то масса всей системы изменяться не будет, но
результирующая внешняя сила, приложенная к системе, будет меняться, а с ней и
ускорение движения системы (см. рис. 1). На платформы 3 и 6
положите перегрузки одинаковой массы m1 = m2, состоящие из мелких грузиков. Затем с платформы 3
перекладывайте перегрузки на платформу 6. Тогда результирующая
внешняя сила, приводящая систему в движение, будет равна разности весов грузов
F = (m0 + m2)g – (m0 + m1)g.
Установите фотодиод 5 в самое нижнее положение ai. При данном
значении силы Fi определите среднее время tср,
прохождения пути, как описано в п. 1, и по формуле (2) вычислите ускорение a1.
Подобные измерения повторите, последовательно перекладывая перегрузки с одной
платформы на другую пять раз. Результаты занесите в табл. 2.
Таблица 2.
Результаты измерений
|
Номер опыта |
m0 + m1, м |
m0 + m2, м |
F, Н |
t1, с |
t2, с |
t3, с |
tср, с |
a, м/с2 |
|
1 |
||||||||
|
… |
||||||||
|
5 |
Постройте график зависимости а = f(F) (рис. 2).
Из графика определите массу системы m.
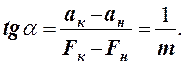
где
Fк, Fн, aк,
aн – координаты точек графика.
Значение массы m, полученное из графика,
сравните с массой всех тел на машине Атвуда. Сделайте выводы.
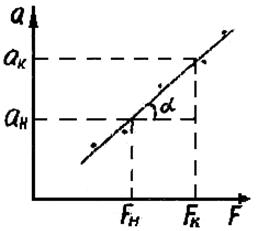
Рис. 2. График зависимости a = f(F)
4. КОНТРОЛЬНЫЕ ВОПРОСЫ
1) С каким свойством тела связана масса?
2) Какая ветчина называется силой?
3) Как сформулировать законы Ньютона?
4) Как рассчитать силу натяжения нити при
равноускоренном движении? Изменится ли натяжение нити, если один перегрузок
заменить другим?
5) Как изменится движение системы, если учитывать
массу блока?
6)Что называется импульсом тела?
7)Как сформулировать законы сохранения импульса и
энергии при
поступательном движении? Каковы границы применимости классической
механики?
Похожие материалы
- Экспериментальное исследование основного закона динамики вращательного движения
- Измерение ускорения свободного падения тел на приборе Атвуда
- Изучение изохорического процесса
Информация о работе
Тип:
Методические указания и пособия
