Как найти массу частицы зная заряд

Из курса электричества мы знаем, что на заряженную частицу, движущуюся в магнитном поле, действует сила, называемая силой Лоренца. Сила Лоренца перпендикулярна к магнитному полю и к скорости частицы, и ее направление определяется правилом левой руки (рис. 349). Модуль этой силы пропорционален заряду частицы

, ее скорости

, магнитной индукции поля

 и синусу угла между векторами

 и

. Если направление скорости

 перпендикулярно к направлению индукции

, то модуль силы Лоренца выражается формулой

,

где

 — заряд частицы в кулонах,

 — ее скорость в метрах в секунду,

 — индукция в тесла,

— сила в ньютонах. Ускорение

, сообщаемое силой Лоренца, как и всякой силой вообще, прямо пропорционально силе и обратно пропорционально массе

 частицы.

Рис. 349. Направление силы Лоренца
, действующей на заряд, движущийся в магнитном поле

 со скоростью

. Изображен случай положительного заряда. Для отрицательного заряда сила направлена в противоположную сторону

Рассмотрим движение частицы в однородном магнитном поле, направленном перпендикулярно к скорости частицы. Так как сила Лоренца и, следовательно, ускорение перпендикулярны к скорости, то частица будет двигаться по окружности; при этом модуль скорости

 остается неизменным, ибо, как известно из механики, перпендикулярность ускорения и скорости характерна для равномерного движения по окружности. Ускорение частицы при равномерном движении по окружности равно

, где

 — радиус окружности. Таким образом, ускорение частицы

,

откуда

(198.1)

Чем меньше

, тем больше радиус траектории частицы при заданных

 и В (рис. 350). Зная

 и

 и измерив радиус траектории

, можно определить

 — отношение заряда частицы к ее массе. Заряд частицы равен одному или нескольким элементарным зарядам. Если он известен, то может быть вычислена масса частицы. Этот принцип лежит в основе действия прибора, называемого масс-спектрографом и служащего для измерения масс мельчайших заряженных частиц — ионов и электронов.

Рис. 350. Траектории заряженных частиц с равными начальными скоростями в однородном магнитном поле: 1 – малое отношение
, 2 – большое отношение

; 1 и 2 – отрицательно заряженные частицы; 3 – положительно заряженная частица. Линии магнитного поля перпендикулярны к плоскости чертежа и направлены на нас

Схема масс-спектрографа с однородным магнитным полем изображена на рис. 351. Прибор представляет собой откачанный до высокой степени разрежения сосуд, помещенный в магнитное поле, линии которого перпендикулярны к плоскости чертежа. Заряженные частицы испускаются источником 1. Простейшим источником является электрический разряд в газе. Разряд сопровождается интенсивной ионизацией газа. При положительной разности потенциалов между диафрагмой 2 и щелью источника из разряда будут «отсасываться» электроны и отрицательные ионы, при отрицательной разности потенциалов — положительные ионы. Заполняя источник различными газами или парами, можно получить ионы различных элементов.

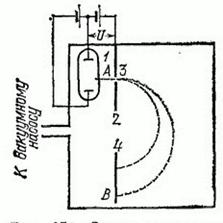
Рис. 351. Схема масс-спектрографа: 1 – источник ионов (газоразрядная трубка), 2 — диафрагма со щелью 3, 4 — фотопластинка,
 – напряжение ускоряющее ионы

Частицы, прошедшие через щель 3, попадают в магнитное поле с теми скоростями, которые им сообщает ускоряющая их разность потенциалов. Все частицы с данным отношением

 приобретают равные скорости и будут в магнитном поле описывать окружности одного и того же радиуса. После отклонения на

 пучок частиц попадает на фотопластинку; в месте попадания пучка после проявления пластинки обнаружится темная полоска. Расстояние

 (рис. 351) равно удвоенному радиусу

 окружности, по которой двигалась частица. Величина

 зависит от скорости частицы. Для нахождения скорости мы используем то обстоятельство, что частица влетает в магнитное поле с кинетической энергией

, полученной за счет работы электрического поля, равной

. Таким образом,

(198.2)

Из (198.1) и (198.2) имеем

Подставляя в эту формулу известные значения

 и полученный измерением радиус

, можем вычислить массу частиц, попавших в точку

 пластинки.

Если в пучке, испускаемом источником, содержатся частицы с различными отношениями заряда к массе, на фотопластинке получится несколько параллельных полосок. Самая близкая к щели полоска вызвана частицами, которые движутся по окружности наименьшего радиуса. Эти Частицы обладают наибольшим; отношением заряда к массе. Если заряды всех частиц в пучке одинаковы, то ближайшая к щели полоска соответствует частицам наименьшей массы.

По аналогии с оптикой изображение, полученное на фотопластинке, называют спектром. Оптический спектрограф дает спектр длин волн светового пучка, т. е. распределение спектральных линий по длинам волн. Масс-спектрограф дает спектр масс пучка частиц, т. е. распределение частиц по массам (точнее, по отношениям

).

В рамках физики и химии 100 лет как доказано, что материя состоит из электронов, протонов и нейтронов. Эксперименты демонстируют, что свободные нейтроны за 614 сек наполовину распадаются на электроны и протоны. Инерциальные свойства электронов протонов и нейтронов определяются методом масс — спектрометрии. Масс-спектрометр — прибор для определения масс заряженных частиц и массы атомов (молекул) по характеру движения их ионов в электрическом и магнитном полях.

Массу нейтрального атома нельзя измерить традиционной масс-спектрометрией. Однако, если отнять у него или добавить ему один и более электронов, то он превратится в йон, характер движения которого в этих полях будет определяться его массой и электрическим зарядом. Строго говоря, в масс-спектрометрах определяется не масса, а отношение массы к электрическому заряду. Если заряд известен, то однозначно определяется масса иона, а значит, можно вычислить массу нейтрального атома и его ядра. Конструктивно масс-спектрометры могут сильно отличаться друг от друга. В них могут использоваться как статичные поля, так и изменяющиеся во времени поля, магнитные и/или электрические.

Рассмотрим один из наиболее простых вариантов определения массы частицы.

Масс-спектрометр состоит из следующих основных частей:

Из ионного источника 1 ускоренные ионы через щель 2 попадают в область 3 постоянного и однородного электрического и магнитного полей. Направление электрического поля задаётся положением пластин конденсатора и показано стрелками. Магнитное поле направлено перпендикулярно плоскости рисунка.

В области 3 электрическое и магнитное поле отклоняют ионы в противоположные стороны и величины напряжённостей этих полей Е и Н₁ подобраны так, чтобы силы их действия на ионы (соответственно qЕ и qvН₁, где q — заряд, а v — скорость иона) компенсировали друг друга, т.е. было qЕ = qvН₁. Создается монохроматичный пучок ионов. При скорости иона v = Е/Н₁ он движется не отклоняясь в области 3 и проходит через вторую щель 4, попадая в область 5 однородного и постоянного магнитного поля напряжённостью Н₂. В этом поле ион движется по окружности 6, радиус R которой определяется из соотношения mv 2 /R = qvH₂, где m — масса иона. Так как v = Е/Н₁, масса частицы определяется из соотношения

Таким образом, при известном заряде иона его масса определяется радиусом R круговой орбиты в области 5.

Схема масс-спектрометра:

1. — ионный источник,
2. — щелеваяе диафрагма,
3. — область однородных и постоянных электрического и магнитного полей (силовые линии электрического поля направлены вдоль плоскости рисунка м показаны стрелками, область магнитного поля показана штриховкой, его силовые линии перпендикулярны плоскости рисунка),
4. — щелевая диафрагма
5. — область однородного и постоянного магнитного поля (силовые линии перпендикулярны плоскости рисунка),
6. — траектория иона,
7. — детектор.

Если в качестве детектора ионов (7) использовать фотопластинку, то этот радиус с высокой точностью покажет чёрную точку в том месте проявленной фотопластинки, куда попадал пучок ионов. В современных масс-спектрометрах в качестве детекторов обычно используют электронные умножители или микроканальные пластинки. Масс-спектрометр позволяет определять массы с очень высокой относительной точностью Δm/m = 10 -8 — 10 -7 .

Анализ масс-спектрометром смеси атомов различной массы позволяет также определить их относительное содержание в этой смеси. В частности, может быть установлено содержание различных изотопов какого-либо химического элемента.

Согласно принятой обработке эксперимента инерциальные силы полностью обусловлены инерциальными свойствами ньютоновской массы (m) — нейтральной, не несущей заряда материи. Однако, в эксперименте все анализируемые частицы несут заряды. Заряды, согласно электродинамике, обладают инерциальными свойствами без относительно к механической массе.

Cила Лоренца вызывает изменение магнитного поля, изменение которого, в свою очередь, вызывает появление ЭДС пропорциональной скорости изменения магнитного потока (ускорению).

ε_i= ∫ E_bdl = — — L dt

где dФ/dt -скорость изменения магнитного поля. Сопротивление изменению скорости и есть проявление инерции.

В тоже время при обработке результатов эксперимента инерциальные свойства, обусловленные наличием заряда, совершенно не учитываются. В 2012 году масс — спектроскопии исполнится 100 лет, но до настоящего времени не появилось ни одной работы, содержащей критические замечания, касающиеся обработки результатов эксперимента и, соответственно, ответов на следующий вопрос:

Почему не учитываются инерциальные свойства электрического заряда иона?

Соответственно, мы считаем необходимым предложить альтернативные варианты обработки экспериментальных данных, полученных в результате масс — спектроскопии микрочастиц.

Целью данной работы является изучение движения элементарных частиц в электрическом и магнитном полях, экспериментальное определение удельного заряда электрона с помощью магнетрона.

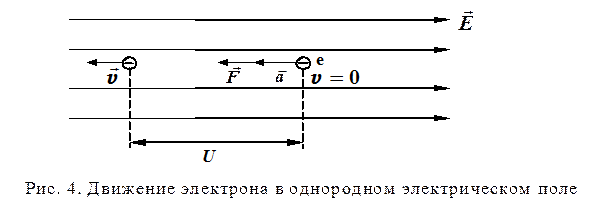
Электрон является носителем элементарного отрицательного заряда е (e = –1,6∙10 —19 Кл). Отношение его заряда к массе e/m называется удельным зарядом электрона. Удельный заряд может быть экспериментально определён различными методами. Все они основаны на поведении электрона в электрическом и магнитном полях.

В электрическом поле напряжённостью (рис .4) на электрон действует сила

, (2.9.1)

которая сообщает электрону ускорение и направлена против поля.

Под действием этой силы электрон, пройдя расстояние между точками с разностью потенциалов U, приобретает кинетическую энергию

. (2.9.2)

Движение электрона в однородном магнитном поле происходит под действием силы Лоренца

, (2.9.3)

где 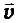— вектор скорости электрона; — вектор индукции магнитного поля; е – заряд электрона.

Сила Лоренца перпендикулярна как скорости электрона, так и направлению магнитного поля. Она не меняет модуля скорости и кинетической энергии частицы.

Модуль силы Лоренца

, (2.9.4)

где a — угол между векторами и .

Сила Лоренца сообщает электрону нормальное (центростремительное) ускорение и вызывает движение его по окружности радиуса R, если угол a составляет 90 o (рис. 5). Таким образом, по второму закону Ньютона:

, (2.9.5)

откуда радиус окружности

. (2.9.6)

Из формулы (2.9.6) видно, что радиус окружности зависит от удельного заряда e/m. Этот факт и положен в основу метода определения удельного заряда с помощью магнетрона.

Магнетрон представляет собой высоковакуумную элек­тронную трубку, имеющую пря­мую металлическую нить (ка­тод), расположенную по оси ци­линдрического анода.

Для нашей работы магнетрон с успехом можно заменить обычной электронной лампой с цилиндрическим анодом, на оси которого расположен катод (рис. 6, а). Лампа помещается внутри длинного соленоида, при помощи которого параллельно оси создаётся магнитное поле напряжённостью .

Катод нагревается электрическим током и испускает электроны, которые под действием электрического поля движутся к аноду. Когда магнитное поле отсутствует, электроны движутся по радиу

сам цилиндрического анода (рис. 6 б, линия 1).

Если включить магнитное поле, траектория движения искривляется, и тем больше, чем сильнее поле (рис. 6, б, линия 2). Все электроны достигают анода, и величина анодного тока в цепи практически не изменяется до определённого момента, когда при дальнейшем увеличении магнитного поля радиус траектории всё больше уменьшается и при некотором критическом значении В_кр, электроны, не достигнув анода, вернутся обратно к катоду (рис. 6, б, линия 3).

При выполнении условия В > В_кр электроны уже не будут попадать на анод, и ток станет равен нулю (рис. 6, б, линия 4).

На рис. 7 приведен график зависимости анодного тока I_А от ин­дукции магнитного поля при некотором анод­ном напряжении U_А (сбросовая характе­ристика магнетрона).

Если бы все электроны, вылетающие из катода, имели одну и ту же скорость, анодный ток I_А спадал бы до нуля точно при критическом значении В_кр индукции магнитного поля (рис. 7, штриховая линия). Однако скорости вылетевших электронов разные, поэтому уменьшение тока происходит на довольно протяжённом участке вблизи В_кр (рис. 7, сплошная линия).

Критическое значение индукции магнитного поля является некоторой функцией анодного напряжения U_А. Эту зависимость легко установить, если предположить, что скорость электрона при его движении в магнетроне остаётся постоянной по модулю. При В = В_кр, радиус окружности, по которой движется электрон, равен R_А /2, где R_А – радиус анода. Подставляя его в уравнение (2.9.6), получим:

. (2.9.7)

Решая совместно уравнения (2.9.2) и (2.9.7), получим формулу для расчёта удельного заряда электрона:

, (2.9.8)

где U_А — разность потенциалов между катодом и анодом.

Индукция магнитного поля в соленоиде может быть рассчитана по закону Био — Савара — Лапласа или по теореме о циркуляции индукции магнитного поля по замкнутому контуру

, (2.9.9)

где – длина соленоида; N – число витков соленоида; I_сол — сила тока, протекающего через соленоид (сила намагничивающего тока); – магнитная постоянная.

Критическому значению индукции магнитного поля В_кр соответствует критическое значение силы тока I_кр. Учитывая это и подставляя (2.9.7) в (2.9.8), получим

. (2.9.10)

При выводе (2.9.10) предполагалось, что электрическое и магнитное поля действуют на электрон по очереди, сначала он в электрическом поле разгоняется до скорости , а затем с этой постоянной скоростью движется в магнитном поле.

В рассматриваемом случае электрон движется в скрещенных магнитном и электрическом полях и одновременно испытывает действие сил со стороны обоих полей. Вследствие этого, скорость электрона не постоянна (она возрастает по мере приближения к аноду), а траектория его движения отличается от круговой. Данное обстоятельство позволяет утверждать, что формула (2.9.10) не точна. Тем не менее, как следует из результатов точного анализа рассматриваемой задачи, эта формула в целом удовлетворительно описывает физику процессов и с точностью до коэффициента пропорциональности является правильной.

Окончательная расчётная формула имеет вид:

, (2.9.11)

где = 0,1 м; N = 1000 витков; R_А = 5 мм; A – коэффициент, учитывающий отличие реальной траектории движения электрона в скрещенных электрическом и магнитном полях от окружности. Для нашей экспериментальной установки А=1,3.

Тщательные измерения удельного заряда и известное из опытов Милликена (1909 г.) значение величины заряда электрона позволили определить его массу и установить зависимость массы от скорости.

В принципе теми же методами определяются массы атомов и молекул. Соответствующие приборы для определения масс атомов и молекул (точнее, их ионов) носят название масс-спектрографов. Для примера можно рассмотреть принципиальное устройство одного из масс-спектрографов (рис. 8).

Сначала пучок ионов проходит через фильтр скоростей, в котором на движущиеся ионы одновременно действуют взаимно перпендикулярные электрическое и магнитное поля. Направления полей выбираются так, чтобы силы, действующие на ионы с их стороны, были противоположны по направлению. Через щель фильтра, противоположную входной, выхо­дят только те ионы, на которые действуют равные по величине силы и .

q∙E = q∙ ∙B. (2.9.12)

Следовательно, из фильтра вылетают ионы одинаковых скоростей

. (2.9.13)

При выходе из фильтра частицы попадают в магнитное поле, перпендикулярное их скорости. Траектория их движения — окружность, радиус которой зависит от удельного заряда частицы

. (2.9.14)

Попадая на фотопластинку, ионы оставляют след, расстояние которого от выходной щели фильтра зависит от удельного заряда ионов.

По найденным значениям q/m можно определить массы ионов.

В наши дни точность определения масс ионов с помощью масс-спектрографов достигают 6 —8 значащих цифр (правда, не в граммах, а по отношению к массе эталонного атома).

Масс-спектрографические методы позволяют проводить количественный анализ нефти, состоящий из молекул различных углеводородов, трудно различимых обычными химическими способами. При большой мощности ионного пучка этот метод позволяет разделять изотопы в заметных количествах.

Масс-спектрографический метод часто применяют для определения изотопного состава исследуемого вещества. В частности, он был применён при исследовании лунного грунта. Близость изотопного состава земных и лунных пород свидетельствует об одновозрастности и единстве происхождения земного и лунного вещества. По-видимому, это следует распространить и на другие космические тела солнечной системы. Исследования вещества метеоритов не противоречат такому обобщению.

Масс-спектрографы нашли широкое применение в различных областях физики, химии, техники. Они используются для определения содержания примесей в газах, для анализа состава и процентного содержания различных смесей углеводородов и т. д.

Необходимые приборы: лабораторный стенд, внутри которого смонтированы все элементы схемы; цифровой вольтметр (или осциллограф).

На рис. 9 приведена схема экспериментальной установки, которая технически реализована на лабораторном стенде с возможностью самостоятельно вручную и с управлением от внешних источников изменять параметры эксперимента.

Экспериментальная установка состоит из трёх цепей.

Цепь намагничивающей катушки состоит из соленоида, создающего однородное магнитное поле при подключении к нему источника постоянного тока ε₃, регулятора тока с внутренним и внешним управлением (коммутация осуществляется тумблером S₁) и низкоомного резистора R₅ =1 Ом, предназначенного для контроля силы тока I_сол в соленоиде по величине напряжения на этом сопротивлении.

Анодная цепь состоит из электронной лампы Л, источника постоянного тока ε₁, делителя напряжения на резисторах R₂, R₃, R₄ и последовательно включенного резистора R₁ = 1кОм, предназначенного для контроля силы тока в анодной цепи I_А, по величине напряжения на этом резисторе.

Цепь накала включает в себя нитевидный катод К лампы Л, источник тока ε₂ и тумблер S₂ , отключающий его.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 10070 — | 7511 — или читать все.

Учащимся

Каким же образом можно экспериментально определить массу электрона или протона, ускоряя заряженную частицу на известном отрезке пути в известном однородном электрическом поле и измеряя ее конечную скорость? Как известно, если тело проходит путь d в направлении силы F, то работа Fd, затраченная на перемещение тела, равна приращению его кинетической энергии. Если же движение начинается от состояния покоя, то эта работа равна также конечной кинетической энергии тела: Fd= mv 2 /2

Таким образом, если известны F, d и v, то отсюда можно найти массу m.

В опытах, о которых пойдет речь, интересующие нас заряженные частицы ускоряются однородным силовым полем между двумя заряженными металлическими пластинами. Зная расстояние между пластинами и число заряжающих их батарей, можно определить электрическую силу, приложенную к каждому элементарному заряду. Опыты производятся в вакууме, чтобы исключить сопротивление воздуха, имевшее место в микро-микровесах. Кроме того, поскольку протоны и электроны более чем в 10 11 раз легче пластмассовых шариков, использованных в микро-микровесах, в данных опытах можно пренебречь силой тяготения по сравнению с электрическими силами.
Некоторое количество водорода подвергается ионизации вблизи пары заряженных пластин (рис.), после чего некоторые из ионов заходят с пренебрежимо малой скоростью через небольшое отверстие в пространство между пластинами. По мере движения ионов от одной пластины к другой электрическое поле ускоряет ионы, сообщая им конечную кинетическую энергию mv 2 /2. В правой пластине имеется небольшое отверстие, через которое некоторые из ионов могут попадать в камеру длиной 0,50 м (рис.). Эта камера изготовлена из проводящего материала, и, поскольку в ней нет электрического поля, ионы проходят всю ее длину без изменения своей скорости. На прохождение всего этого пути иону требуется всего лишь несколько микросекунд (1 мкс=10 -6 с). Хотя этот промежуток времени и очень мал, все же он доступен точному измерению посредством специального измерительного устройства. Это позволяет точно определить конечную скорость иона v.
Для измерения времени прохождения ионами длинной камеры от одного конца до другого надо заметить момент, когда данный ион покинет данную точку слева, и время, когда этот же ион достигнет дальнего конца справа. Чтобы заметить время, когда данный ион входит в длинную камеру, помещаем около входа пару небольших отклоняющих пластин (рис.). С их помощью можно управлять направлением пучка водородных ионов. Когда отклоняющие пластины заряжены, на ионы водорода действует боковая электрическая сила, которая отклоняет их в сторону от их траектории. Если же затем разрядить отклоняющие пластины, то по продольной оси камеры будут двигаться только те ионы, которые только что или позже попали в камеру; поэтому первыми ионами, прошедшими отверстие на дальнем конце, будут те, которые прошли весь путь в 0,50 м за время с момента разрядки пластин. Приход этих ионов регистрируется воспринимающим элементом, помещенным за отверстием.
Для измерения промежутка времени с момента разрядки пластин до момента прихода первых ионов на воспринимающий элемент отклоняющие пластины в камере соединяются с вертикальными отклоняющими пластинами осциллографа (рис.). Момент разряжения пластин в длинной камере отмечается пиком на кривой, вычерчиваемой на экране, осциллографа. Воспринимающий элемент у дальнего конца длинной камеры присоединяется к тем же вертикальным отклоняющим пластинам осциллографа (электрические соединения обоих концов камеры выполняются совершенно одинаково). Когда пучок ионов попадает в воспринимающий элемент, на экране осциллографа появляется второй пик (рис.). Два пика появляются в разных местах экрана, так как они возникли в разное время. В течение промежуточного времени между этими двумя моментами развертывающая цепь осциллографа вызывает горизонтальное перемещение электронного пучка на экране. Электронный пучок в осциллографе проходит расстояние между двумя пиками за то же время, за какое ионы водорода проходят 0,50 м в камере.

В современных осциллографах цепь развертки может вызвать горизонтальное перемещение электронного пучка на экране трубки от одного конца до другого за несколько сотых долей микросекунды. Для измерения скорости ионов цепь развертки настраивается так, чтобы вся кривая проходилась за 5 микросекунд. Тогда два пика на экране осциллографа будут заметно разделены. Измерением расстояния между пиками определяется время, за которое пучок пересекает длинную камеру. Находят промежуток времени от момента, когда пучок получает возможность двигаться прямо вперед, до момента, когда он попадает в воспринимающий элемент, с точностью до 0,01 микросекунды. В случае ионов водорода и 90- вольтовой батареи, создающей ускоряющую электрическую силу, время пролета равно 3,82 микросекунды. Отсюда можно вычислить скорость v ионов в длинной камере. Она равна 0,50 м/(3,82*10 -6 с) = = 1,31*10 5 м/с.
С другой стороны, пластины здесь ровно втрое дальше друг от друга, чем в микро-микровесах, в которых производился опыт Милликена,; кроме того, здесь используется втрое меньше таких же батарей. Поскольку сила, приходящаяся на элементарный заряд, пропорциональна числу одинаковых батарей и обратно пропорциональна расстоянию между пластинами, на каждый элементарный заряд теперь должна действовать в девять раз меньшая сила, т. е. 1/9*10 -14 ).
Если предположить, что один атом водорода несет один элементарный заряд, то каждый ион между пластинами испытывает только что выраженную силу. Двигаясь от одной пластины к другой, ион проходит путь 9,3 10 -3 м по направлению силы, так что произведенная работа по перемещению иона равна Fd = 1/9(1,4*10 -14 Н)*( 9,3 10 -3 м)= 1,4 10 -17 Дж. Следовательно,
mv/2=m (1,3*10 5 м/с) 2 /2=1,4 *10 -17 Дж.
Отсюда для массы иона водорода т находим
m= 1,7 *10 -27 кг.

Но ведь эта величина нам хорошо известна. В пределах точности наших измерений она совпадает с массой атома водорода.
Теперь можно подвести итог. Если ион водорода заряжен однократно, то его масса почти равна массе атома водорода. Можно даже сделать дальнейший шаг и утверждать, что ион водорода действительно является носителем единичного заряда и что его масса практически равна массе атома. Это должно быть правильным, так как предположение, что ион несет больший заряд, приведет к абсурдному результату. Например, если ион несет два элементарных заряда, то действительная величина mv 2 /2 должна быть в два раза больше принятого нами значения. Поскольку мы измеряли v, это может только значить, что масса иона в два раза больше найденной нами. Такой ион водорода обладал бы массой, в два раза превосходящей массу атома, осколком которого он является. Этот вывод настолько неправдоподобен, что мы его отбрасываем.

Ранее уже имелись указания, что электроны представляют собой строительные элементы, входящие во все атомы. По-видимому, ион водорода представляет собой атом водорода, потерявший один электрон. Кроме того, мы никогда ни в этом, ни в других опытах не встречали положительно заряженного осколка водорода с двумя положительными элементарными зарядами. Это одно из многих доказательств того, что положительно заряженный ион водорода является конечным строительным элементом. Это — протон. Когда водород расщепляется на заряженные частицы, то, как только что было установлено, протону принадлежит почти вся масса атома. Поэтому электроны должны быть очень легкими. Можно использовать те же приборы для измерения массы электрона и таким образом проверить этот вывод.

На прошлых уроках мы с вами начали знакомство с магнитными
полями. Давайте с вами вспомним, что магнитное поле — это особая форма материи,
созданная движущимися (относительно определённой инерциальной системы отсчёта)
электрическими зарядами или переменными электрическими полями.

Силовой характеристикой магнитного поля является вектор
магнитной индукции, направление которого в данной точке совпадает с
направлением силовой магнитной линии, проходящей через эту точку:

Так же мы с вами установили, что на проводник с током,
помещённый в магнитное поле, со стороны магнитного поля действует сила,
называемая силой Ампера. Её модуль равен произведению силы тока, модуля вектора
магнитной индукции, длины отрезка проводника и синуса угла между направлениями вектора магнитной индукции и элемента тока:

Поскольку электрический ток представляет собой упорядоченное
движение заряженных частиц, то это означает, что магнитное поле, действуя на
проводник с током, действует тем самым на каждую из этих движущихся заряженных
частиц. Следовательно, силу Ампера можно рассматривать как результат сложения
сил, действующих на каждую движущуюся заряженную частицу.

Силу, с которой магнитное поле действует на заряженную
частицу, движущуюся в этом поле, называют силой Лоренца.

Своё название сила получила в честь выдающегося голландского
физика Хендрика Антона Лоренца — основателя электронной теории строения
вещества.

Модуль силы Лоренца определяется отношением силы Ампера,
действующей на участок проводника, находящийся в магнитном поле, к числу
заряженных частиц, упорядоченно движущихся в этом участке проводника:

Давайте с вами рассмотрим прямолинейный участок проводника с
током длиной Δl и
площадью поперечного сечения S. При этом будем считать, что длина
участка проводника и его площадь поперечного сечения настолько малы, что вектор
магнитной индукции поля можно считать одинаковым в пределах этого участка
проводника.

Итак, на участок проводника с током, находящимся в магнитном
поле, действует сила Ампера, модуль которой равен произведению силы тока,
модуля вектора магнитной индукции, длины отрезка проводника и синуса угла между
направлениями вектора магнитной индукции и элемента тока:

Теперь давайте с вами вспомним, что сила тока в проводнике
определяется зарядом, прошедшим через поперечное сечение проводника за единицу
времени:

Здесь ∆t — это промежуток времени, за который
заряженная частица проходит участок проводника длиной ∆l.

Пусть модуль заряда одной частицы равен q.
Тогда суммарный заряд всех частиц равен произведению модуля заряда одной
частицы на общее число частиц в выбранном участке проводника: Q = qN.

Перепишем уравнение для силы тока с учётом последнего
равенства.

Полученное равенство подставим в закон Ампера:

Обратите внимание на отношение ∆l/∆t — это есть не что иное, как модуль средней скорости
заряженной частицы, упорядоченно движущейся в магнитном поле внутри проводника:

Теперь подставим полученное выражение для силы Ампера в формулу
для силы Лоренца:

После упрощения получим, что модуль силы Лоренца равен
произведению заряда частицы, модуля её средней скорости, модуля вектора
индукции магнитного поля и синуса угла между вектором магнитного поля и вектором
скоростью движения частицы:

Направление силы Лоренца определяют по правилу левой руки:
если левую руку расположить так, чтобы составляющая магнитной индукции,
перпендикулярная скорости упорядоченного движения заряда, входила в ладонь, а
четыре пальца были направлены по движению положительного заряда (или против
движения отрицательного заряда), то отогнутый на 90^о большой палец укажет
направление действующей на заряд силы Лоренца.

Анализ данного правила позволяет нам утверждать, что сила
Лоренца, действующая на движущуюся в магнитном поле частицу, перпендикулярна
вектору скорости этой частицы. Следовательно, сила Лоренца не совершает
работы. Тогда, согласно теореме о кинетической энергии, это означает, что сила
Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль
скорости частицы. А значит заряженная частица в магнитном поле движется с
постоянной по модулю скоростью, но при этом направление скорости непрерывно
изменяется.

Вид траектории заряженной частицы в магнитном поле зависит от
угла между скоростью влетающей в поле частицы и магнитной индукцией. Рассмотрим
такую ситуацию. Пусть протон, ускоренный разностью потенциалов U влетает в однородное магнитное поле сначала параллельно
линиям индукции, затем — перпендикулярно, и, наконец, под некоторым углом к
ним. Индукция магнитного поля равна B. Для
каждого случая определите радиус кривизны траектории протона и период его
обращения.

Итак, рассмотрим первый случай, когда протон, двигаясь по
силовой линии в электрическом поле ускоренно, приобретает скорость, с которой
влетает в однородное магнитное поле так, что его вектор скорости направлен
вдоль поля (или противоположно направлению индукции магнитного поля).

Очевидно, что в этом случае угол между направлением вектора
скорости и индукции магнитного поля либо равен нулю, либо 180^о.

Тогда, согласно формуле, сила Лоренца, действующая на протон,
равна нулю и частица будет продолжать двигаться равномерно прямолинейно.

Теперь рассмотрим второй случай, когда протон влетает в
однородное магнитное поле перпендикулярно линиям его индукции.

В этом случае на протон в магнитном поле действует сила
Лоренца, направленная перпендикулярно вектору скорости (направление силы
Лоренца определяем по правилу левой руки). Как мы уже выяснили, сила Лоренца не
может изменить модуль скорости заряженной частицы — она лишь меняет её направление.
А так как магнитное поле однородно и вектор скорости частицы перпендикулярен
линиям магнитной индукции, то протон под действием силы Лоренца начнёт
двигаться по окружности.

С другой стороны, такое движение заряженной частицы в
магнитном поле будет подчиняться второму закону Ньютона:

И нам осталось рассмотреть последний случай, когда частица
влетает в магнитное поле под заданным углом к силовым линиям.

Подобное явление происходит в магнитном поле Земли.
Движущиеся с огромными скоростями заряженные частицы из космоса «захватываются»
магнитным полем Земли и образуют вокруг неё радиационные пояса. В них заряженные
частицы перемещаются по винтообразным траекториям между северным и южным
магнитными полюсами. И только в полярных областях небольшая часть частиц
вторгается в верхние слои атмосферы, вызывая восхитительные полярные сияния.

В заключении урока отметим, что действие магнитного поля на
движущийся заряд широко используется в технике. Вспомните хотя бы
электронно-лучевые трубки, применяемые в кинескопах телевизоров, где пучок
летящих к экрану электронов отклоняется с помощью магнитных катушек.

Сила Лоренца используется и в циклотронах — особых
ускорителях заряженных частиц. Обычный циклотрон состоит из двух полых
полуцилиндров разного диаметра (дуантов), находящихся в однородном магнитном
поле. Его принцип действия достаточно прост.

В зазоре между цилиндрами находится заряженная частица. В
этом зазоре создаётся переменное электрическое поле с постоянным периодом,
равным периоду обращения частицы. Это поле каждые пол периода разгоняет
частицу, увеличивая при этом радиус её обращения (период обращения частицы не
увеличивается). На последнем витке частица вылетает из циклотрона.

Действие силы Лоренца используют и в масс-спектрографах —
устройствах, предназначенных для разделения частиц по их удельным зарядам, то
есть по отношению заряда частицы к её массе, и по полученным результатам точно
определять массы частиц. На экране вы видите схему простейшего
масс-спектрографа. Цифрами один и два обозначены две диафрагмы, между которыми
создаются взаимно перпендикулярные электрическое и магнитное поля. Заряженная
частица, пройдя через первую диафрагму попадает в эти поля и, если сила
Лоренца, действующая на неё, равна электростатической силе, то она сможет
пройти через вторую диафрагму. Ионы же с другими скоростями отклонятся в полях
и через вторую диафрагму не пройдут.

За диафрагмой создаётся постоянное магнитное поле,
заставляющее заряженные частицы двигаться по окружности, радиус кривизны
которой можно измерить, поставив на пути частиц фотопластинку. Так как скорость
частиц одинакова и определяется постоянной прибора, то, зная заряд ионов, можно
легко определить их массу.

Ещё одно устройство, в котором применяется действие силы
Лоренца — это ТОКАМАК (тороидальная камера с магнитными катушками).

В нём плазма (напомним, что это частично или полностью
ионизированный газ) удерживается в специально создаваемом сильном магнитном
поле.  ТОКАМАК считается наиболее перспективным устройством для осуществления
управляемого термоядерного синтеза.

Алгоритм расчета массы некоторых частиц

Знать, что нужно сделать, и не делать этого — худшая трусость. Лучше зажечь одну маленькую свечу, чем клясть темноту

(Конфуций).

В настоящее время мы не можем определить массу как результат процессов, происходящих на элементарном уровне. Возможно, учитывая связь инертной и гравитационной масс, это произойдет после более глубокого понимания сущности гравитационного поля. Дело будущего, а сегодня для расчета масс частиц мы выберем другой, более простой и эффективный, путь.

Практика показала, что задачу вычисления массы частиц можно свести к выполнению ряда формальных операций. Особенностью этого метода является не расчет массы уже существующих частиц, а строительство параллельной «теоретической» таблицы, причем масса является только одним из нескольких расчетных параметров. Последовательно выполняются следующие операции:

 – строится зарядовая комбинация, определяются электрический заряд и спин;

 – вычисляется эквивалентный радиус взаимодействия:

 – вычисляется масса частицы как величина пропорциональная работе, затраченной на перемещение зарядов.

Недостатком алгоритма является небольшое расхождение расчетных и экспериментальных масс где-то с 4-5 шага по уровню сложности комбинаций. Интересно, что «синтезированная» и экспериментальная таблицы полностью совпадают, если ввести ряд эмпирических правил объединение базисных зарядов.

Рекомендуется просмотреть: http://maxpark.com/community/603/content/3131593, иначе «разобраться» в этой задаче будет сложно.

Естественная система единиц базисного заряда (СГСб) 

Определим базисный заряд как величину равную произведению постоянной Планка на скорость света в вакууме (размерность – квадрат электрического заряда) или как произведение некоторой характерной «нейтральной длины» на единицу «нейтральной» массы и на квадрат скорости света.

Q = hc= Ro*Mo*c^2.

В качестве единицы длины выберем расстояние равное половине классического радиуса электрона (такой выбор далеко не случаен, но его обсуждение связано с анализом свойств частиц другой группы). Тогда, расчетное значение единицы массы будет равно:

 Mo =  879,9632266… МэВ

Других размерных констант в приведенных ниже расчетах не используется. Единицу массы можно определить другим способом: через массу электрона и постоянную тонкой структуры, дело вкуса.

Основные уравнения 

Предположим, что базисный заряд был смещен с основного «единичного» радиуса. Учитывая инвариантность постоянной Планка и предполагая, что скорость заряда всегда остается предельно близкой к скорости света (для любого радиуса), получим простое соотношение, связывающее появление «наблюдаемой» массы отличающейся от «нейтральной» (фоновой, скрытой) с измененным радиусом распределения заряда (R):

M = Mo * (Ro/R – 1).

Таким образом, для вычисления массы некоторой частицы, состоящей из одного заряда, достаточно определить новый, измененный радиус базисного заряда. Для системы, состоящей из двух взаимодействующих зарядов, расчетное значение массы будет в два раза больше.

Новый радиус можно определить из уравнения баланса сил. В базовом приближении (без кулоновских сил), инерционная компонента, создающая центробежную силу, уравновешена собственным полем заряда (центростремительная компонента):

(Мо*с^2)/R – (Mo*c^2)/Ro = hc/(2R)^2

 или

R^2 – R + 0.25 = 0.

Единственное решение этого уравнения: R = 1/2 и M = 879,9632266… МэВ.

Более точное решение для одиночного заряда учитывает, что действует полный заряд равный: 

Qп = hc + q^2.

При подстановке в уравнение баланса полного заряда и простых преобразований, получим:

R^2 – (1+a)*R + 0.25*(1+a) = 0;

a = 0,0072973525698/2пи = 0,0011614097329680;

R_ = 0,483531082….

тогда теоретическое значение протонной единицы массы будет равно:

Mр = 879,9632266*(1/0,483531082 – 1) = 939,905775…. МэВ

Отношение протонной единицы массы к массе базисного заряда было названо «коэффициентом оболочки»:

k = 939,905775 / 879,9632266 = 1,068119378… .

Расчеты показали, что коэффициент оболочки является константой для любых частиц, участвующих в сильном взаимодействии. Это уникальное свойство позволяет легко вычислять энергию/массу, заключенную в поле ядерных сил. Для протона и нейтрона эти величины идентичны и, примерно равны 60 МэВ. В общем, здесь работает хорошо известный принцип. В пространстве, образованном парами базисных зарядов, поле ядерных сил действует как двойной электрический слой и, тем самым, полностью экранирует поле свободного базисного заряда на расстоянии большем нейтральной длины (~ 2,8 Е-17 см).

Примеры синтеза частиц

Вычислим, массу протона (протонную единицу массы), массу нейтрона и массу нейтрального пиона (135). Этот же алгоритм используется и для анализа более сложных зарядовых систем (кроме лептонов).

 1.       Протон (непарная частица – состоит из одного заряда).

Эта задача была решена выше (одиночный заряд), повторим шаги.

Из гипотезы П. Дирака определяем зарядовую комбинацию:

АВ = А + В, тогда:

А (q = +1,   I = +1/2) – соответствует протону;

B (q = -1,   I = -1/2)   – соответствует антипротону.

Эквивалентный расчетный радиус равен (перенос единичного заряда с нейтрального R = 1):

R = 1/2 (или ~ 0,7 Е-17 см).

Масса (без учета магнитной и электростатической компонент) равна:

Mp = k*879,9632266*(1/0,5 -1)= 939,905775…. МэВ.

Масса оболочки, примерно:

Mx = (k-1)*879,9632 ~ 60 МэВ.

Нейтральной частицы мультиплета не существует.

Системы протон – антипротон не существует (энергия связи равна нулю).

Интересно заметить, что эти расчетные величины близки к эмпирическим константам, используемым в моделях атомных ядер.

 2.       Нейтрон (непарная частица – 3 заряда).

Зарядовая комбинация представлена суперпозицией двух связей от группы bb(aa – для антинейтрона):

(bB) – A   нейтрон          (q = 0,   I = -1/2);

(aA) – B   антинейтрон   (q = 0,   I = +1/2).

Электрически заряженной комбинации не существует.

Расстояние между зарядами равно: 1/2 (относительный радиус протона) + 1 (нейтральный радиус) = 3/2, тогда ослабление равно 1/(2*3/2)^2=1/9, учитывая удвоение статики от группы bB или aA, получаем:

R^2 – R + 2*1/9 = 0.

Эквивалентный расчетный радиус равен R+ = 0,66666666…. .

Масса (без учета магнитной компоненты) равна:

M = 2k*879,9632*(1/0,66666666 – 1) = 939,905775…. МэВ.

Масса оболочки, примерно, 60 МэВ.

Несмотря на различные зарядовые комбинации и радиусы распределения зарядов, расчетная масса нейтрона (без учета электромагнитных «хвостов») точно равна массе протона. Соответственно, точно равны массы оболочек и, следовательно, протон и нейтрон должны быть абсолютно идентичны по отношению к сильному взаимодействию. Этот вывод является нетривиальным.

Кстати, распад нейтрона (антинейтрона) может происходить только при генерации непарного нейтрино. (следствие закона сохранения базисного заряда http://maxpark.com/community/603/content/3131593):

(bB) – A = (bB) – A + ab = b-B-A-B + A  = b-B(A-B) + A  = b + B(ab) + A.

Распад происходит в результате т.н. «слабого взаимодействия», которого, впрочем, не существует как отдельного типа сил. Есть определенный класс реакций распада, обусловленный электромагнитным взаимодействием поляризующем связь A–B, в привлеченной из пространства базовой «электро нейтральной» паре ab.

 3.       Нейтральный пион (135), (парная частица – 6 зарядов).

Зарядовая комбинация:

(ав)А – В(ав), тогда q = 0, I = 0.

Расстояние между зарядами равно: 1 (нейтральный радиус) + 1 (нейтральный радиус) = 2, тогда:

R^2 – R + 0.25*0.25 = 0   (сила уменьшается в 4 раза относительно одиночного заряда).

Эквивалентный расчетный радиус равен: R+ = 0,9330127… .

Масса равна:

 M = 2k*879,9632*(1/0,9330127 – 1) = 134,9644…МэВ (эксперимент 134,9766 МэВ).

Масса оболочки, примерно, 8,607… МэВ.

Возможно, некоторое расхождение расчета и эксперимента (0,009 %) связано с погрешностью выбранных констант. Вопрос открыт.

Заряженные частицы мультиплета:

(ав)А – В(аВ), тогда: q = -1, I = 0;

(Ав)А – В(ав), тогда: q = +1, I = 0.

Внимательный Читатель может самостоятельно вычислить разницу масс заряженного и нейтрального пиона (ответ: 4,5972… МэВ, эксперимент ~ 4,594 МэВ) и попытаться вычислить параметры следующего в ряду мезона (комбинация «квадрат» из 4-х зарядов перенесенных с нейтральных радиусов зарядов + энергия связи групп).

ВЫВОД

Задача синтеза частиц первых уровней, является элементарной и вполне доступной для, например, учащихся средних классов. Хотя вокруг этой проблемы скопилось столько мути, что выползти на свет, наверно, уже никогда не удастся.

30 ноября 2014 г.                                                                         Лебедев Владимир

P.S. Эта заметка была давно обещана в http://dxdy.ru/topic28392.html  – Lebed.  Просто были (и остаются) некоторые сомнения в целесообразности таких публикаций, но доверимся Конфуцию. Следующая работа, Бог даст, – «Фундаментальные открытия будущего». 

Источник: http://maxpark.com/user/1116094161#