Как найти массу через динамометр

Как посчитать массу

Для того чтобы посчитать массу, измерьте силу, которая действует на тело и рассчитайте его ускорение, затем поделите значение силы на ускорение и получите массу. Если есть эталонное значение массы, заставьте тела взаимодействовать и по соответствующей пропорции найдите массу. Чтобы определить массу тела, сравните ее с эталонной массой при помощи рычажных весов.

Вам понадобится

• динамометр, спидометр, две одинаковые тележки, рычажные весы с набором гирек.

Инструкция

Измерение массы тела с помощью динамометраВозьмите тело и подвесьте его на обычный пружинный динамометр. Полученное значение силы, измеренное в Ньютонах, поделите на 9,81 (значение ускорения свободного падения). В результате получите массу тела в килограммах. Если тело начинает двигаться из состояния покоя, измерьте с помощью динамометра силу, которая на него действует, затем измерьте длину пути, которую оно прошло и конечную скорость. Силу умножьте на расстояние в метрах, на число 2, а полученный результат поделите на значение конечной скорости, возведенное во вторую степень. Получите массу тела в килограммах.

Измерение массы тела через взаимодействие с эталономДля этого возьмите две одинаковые тележки известной массы. Затем тело, масса которого измеряется, поместите на одной из тележек. Стяните ниткой упругую металлическую полосу, чтобы она напоминала по форме подкову и поместите ее между тележками. Установите тележки на гладкой горизонтальной поверхности и перепалите нить, которая закрепляла стальную полосу. Она распрямится, приведя тележки в движение. Измерьте расстояние, пройденное каждой из тележек. Затем расстояние, пройденное груженой тележкой, умножьте на массу пустой тележки, полученное число поделите на расстояние, пройденное пустой тележкой. От полученного результата отнимите массу пустой тележки – это и будет масса груза.

Измерение массы весамиВозьмите рычажные весы и уравновесьте их с помощью регулирующих гаек. Затем положите тело на одну из чаш весов и нагружая вторую чашу гирьками с известной массой, добейтесь того, чтобы весы снова уравновесились. Сложив массы гирек, получите массу тела. В других видах весов просто положите тело на их платформу и на шкале или дисплее увидите его массу.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Задачи о показаниях измерительных приборов часто кажутся простыми. Дело, вероятно, в том, что, когда вводится новая физическая величина, всегда сразу же дается рецепт, с помощью какого устройства и как именно следует эту величину измерять. В дальнейшем, считая вопрос исчерпанным, к тонкостям процесса измерения возвращаются редко.

Это относится и к измерениям с помощью простейших приборов, например — пружинного динамометра.

Хорошо известно, что если к обоим концам динамометра приложены одинаковые по модулю силы F₀, то динамометр покажет именно это значение силы. При этом пружина динамометра растянется, и ее абсолютное удлинение Δl₀ определится соотношением 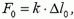 где k — жесткость пружины. Вроде бы все просто. Но…

Задача 1. 3а один конец пружинного динамометра тянут с силой F₁ = 50 H, за другой — с силой F₂ = 70 H. Что покажет динамометр?

На вопрос этой задачи отвечают обычно, что динамометр покажет либо F₂, либо F₁. Встречаются также ответы F₂ + F₁ и F₂ – F₁. На самом деле ни один из этих ответов не является верным. А что же верно? Об этом — чуть позже.

С помощью пружинного динамометра можно также определить массу m тела, поскольку нетрудно измерить силу тяжести, равную m·g. Вроде бы тоже все просто. Однако…

Задача 2. Как определить массу пружины динамометра, имея в своем распоряжении только этот динамометр?

Оказывается, обе сформулированные задачи тесно связаны друг с другом, хотя на первый взгляд это может показаться и странным. Скоро вы в этом убедитесь. Но прежде рассмотрим еще одну, несколько более простую задачу и решим ее.

Задача 3. За один конец динамометра тянут с силой, равной F. Что покажет динамометр?

Для начала попытаемся четко понять, что означает этот вопрос.

Ясно, что, глядя на динамометр, мы можем сказать только, растянулась его пружина или нет и если растянулась, то насколько. Мы можем также измерить величину абсолютного удлинения пружины в единицах длины, например в сантиметрах. Определить же значение силы можно лишь после предварительной градуировки шкалы динамометра в единицах силы, например в ньютонах, с помощью закона Гука.

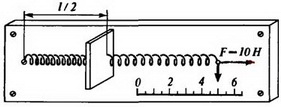
Очень важными являются также следующие два условия: 1) во время измерения динамометр покоится в некоторой инерциальной системе отсчета; 2) пружина динамометра растягивается равномерно по всей длине. Проще всего эти два условия обеспечиваются равенством сил, действующих на оба конца пружины динамометра. В важности второго условия нетрудно убедиться с помощью следующего рассуждения. Допустим, мы закрепили одну половину пружины (соединенную со шкалой) так, что она вообще не будет деформироваться и перемещаться, а за свободный конец второй половины пружины тянем с силой F (рис. 1). Что в этом случае покажет динамометр? Очевидно, половина пружины под действием силы F удлинится на столько же, на сколько удлинится вся пружина под действием силы F/2. Таким образом, стрелка динамометра покажет силу F/2.

Рис. 1.

Итак, если сила натяжения постоянна вдоль пружины и равна F, динамометр покажет F. Если же сила натяжения равна нулю на одной половине пружины и F на другой, динамометр покажет F/2. А что если сила натяжения будет изменяться вдоль пружины еще каким-нибудь, более сложным образом? Какой будет суммарная деформация всей пружины (ведь именно она «ответственна» за показание стрелки динамометра)? Как, наконец, создать неравномерную силу натяжения, не закрепляя части пружины?

Оказывается, в условиях задачи 3 реализуется именно такая ситуация. Так что же происходит, если сила F действует только на один конец динамометра?

Во-первых, динамометр движется и движется равноускоренно (других сил нет). Его ускорение равно 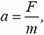 где m — масса пружины. При таком движении взаимное расположение точек пружины не изменяется со временем. Можно сказать, что пружина движется как твердое тело (при условии, разумеется, что возможные продольные колебания быстро затухают). При этом взаимное расположение точек движущейся пружины может, конечно, отличаться от их расположения в неподвижном состоянии.

Во-вторых, различные участки пружины будут деформироваться по-разному, поскольку сила натяжения будет изменяться вдоль пружины. Определим эту силу, считая, что пружина расположена горизонтально и сила F действует на ее правый конец.

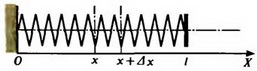
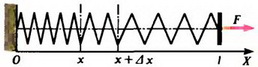
Для дальнейшего удобства «пронумеруем» точки (витки) пружины с помощью непрерывно изменяющейся величины x следующим образом (рис. 2).

а

б

Рис. 2.

Вместо того, например, чтобы говорить «точка пружины, которая находится на расстоянии x от левого конца пружины в недеформированном состоянии», будем говорить кратко «точка x». Очевидно, что x изменяется в пределах от  0 до l, где l — длина недеформированной пружины. Силу натяжения в точке x обозначим F(x); при этом понятно, что F(0) = 0 и F(l) = F. Заметим, что масса участка пружины от точки 0 до точки x равна 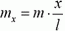. 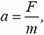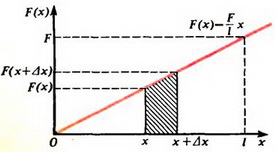Для того чтобы этот участок двигался с ускорением необходимо, чтобы на него со стороны остальной части пружины действовала сила — сила натяжения в точке x —

Эта сила линейно зависит от параметра точки пружины x (рис. 3).

Рис. 3.

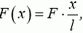
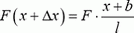
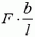
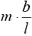
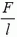
Теперь задача сводится к тому, чтобы, зная силу натяжения в каждой точке пружины, определить деформацию всей пружины. Для этого поступим так. Выделим малый (по сравнению с l) участок недеформированной пружины между точками x и x + Δх (рис. 2, а). Длину этого участка Δx будем обозначать также b. На левый конец этого участка действует сила натяжения  на правый — сила натяжения . Равнодействующая этих сил, направленных в разные стороны, равна . Поскольку масса выделенного участка есть , он движется с ускорением, равным , т. е. с ускорением всей пружины.

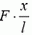
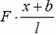
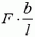
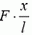
Так как силы  и  отличаются на малую (по сравнению с ними) величину , можно считать, что участок Δx растягивают в обе стороны с силой , под действием которой он деформируется. Найдем величину абсолютного удлинения этого участка.

Если бы на оба конца пружины действовала сила F₀, в каждой точке x сила натяжения также равнялась бы F₀, и пружина была бы растянута равномерно. Абсолютное удлинение всей пружины было бы равно

где k — жесткость пружины, а относительное удлинение —

При этом относительное удлинение любого участка было бы таким же.

Например, для участка длиной b

В случае же, когда сила натяжения зависит от x, относительное удлинение участка длиной b будет другим:

Это означает, что участки возле правого конца пружины растягиваются больше, возле левого — меньше (см. рис. 2, б и рис. 4).

Рис. 4.

Абсолютное удлинение этого участка есть

Заметим, что величина абсолютного удлинения участка Δx, с точностью до постоянного коэффициента 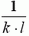 равна площади прямоугольника со сторонами F(x) и Δx или F(x + Δx) и Δx (см. рис. 3). Ясно, что в пределе (для бесконечно малых Δx) силы F(x) и F(x + Δx) совпадают, а площади указанных прямоугольников равны как между собой, так и площади заштрихованной на рисунке 3 трапеции.

Для того чтобы найти абсолютное удлинение всей пружины, разделим ее на n кусков малой длины точками x₁ = 0, x₂, …, x_n, x_n+1 = l. Будем считать, что

(n велико). Абсолютное удлинение i-гo участка выразится формулой

а абсолютное удлинение всей пружины —

Устремим теперь длину каждого участка к нулю (а их число к бесконечности). Тогда получим

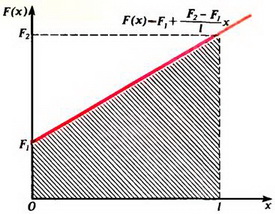
Ясно, что эта сумма, с точностью до коэффициента , равна сумме площадей трапеций, подобных заштрихованной на рисунке 3, а ее предел — площади прямоугольного треугольника с катетами F и l. Следовательно,

Для тех, кто знаком с понятием определенного интеграла, запишем

Итак, абсолютное удлинение Δl всей пружины, на один конец которой действует сила F, найдено. Можно сказать, что это удлинение будет таким же, если на оба конца динамометра действует так называемая эффективная сила 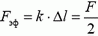. Но, как уже говорилось, если на оба конца динамометра действуют одинаковые силы, динамометр показывает именно ее. Таким образом, если на один конец динамометра действует сила F, то динамометр показывает силу F/2 (и движется равноускоренно). При этом заметим, что показание динамометра не зависит ни от массы m пружины, ни от ее длины l в свободном состоянии, ни от жесткости k.

Разобравшись с задачей 3, вернемся к задаче 1. Если на правый конец динамометра действует сила F₁, а на левый F₂, то пружина движется с ускорением

Для участка пружины от 0 до x имеем

следовательно, сила натяжения в точке x равна

Абсолютное удлинение можно найти с помощью тех же рассуждений, что и раньше. Так, с одной стороны, абсолютное удлинение пружины равно площади заштрихованной на рисунке 5 трапеции (деленной на k·l).

Рис. 5.

С другой стороны, его можно выразить в виде интеграла:

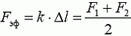
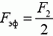
Таким образом, динамометр, на концы которого действуют различные силы F₁ и F₂ растягивается так, как если бы на оба его конца действовала одна и та же сила . Другими словами, динамометр показывает (независимо от величин m, l и k) силу, равную полусумме F₁ и F₂, и движется при этом равноускоренно. В частном случае, когда F₁ = 0, мы получим результат задачи 3: . В другом частном случае, когда F₁ = F₂ = F, имеем F_эф = F, т. е. когда силы, действующие на оба конца динамометра, одинаковы, динамометр, как и должно быть, показывает именно эту силу и покоится.

Теперь рассмотрим задачу 2. Так можно ли сделать какие-нибудь измерения с помощью одного только динамометра? Оказывается, можно. Сначала расположим динамометр горизонтально и убедимся, что его стрелка находится на нулевом делении. Затем расположим динамометр вертикально, держа за верхний конец пружины, который прикреплен к шкале. В таком положении стрелка динамометра (нижний конец пружины) покажет не ноль — пружина растянется под действием силы тяжести. Но на сколько? Что же теперь покажет динамометр?

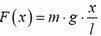
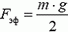
Заметим, что в вертикальном положении на концы пружины действуют различные силы. На верхнем конце сила натяжения пружины равна mg, где m — масса пружины, на нижнем сила натяжения равна нулю. Кроме того, сила натяжения на расстоянии x от нижнего конца пружины равна  (покажите). Но тогда ситуация такая же, как и в задачах 1 и 3. Воспользовавшись их результатами, находим, что динамометр покажет эффективную силу .

Вывод: масса пружины динамометра равна 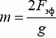, где F_эф — показания динамометра в вертикальном положении.

В заключение — несколько задач для самостоятельного решения.

Упражнения

1. Динамометр подвешен вертикально за верхний конец (за который пружина прикреплена к шкале). К его нижнему концу подвешен (верхним концом) второй динамометр, а к нижнему концу второго — третий. Все динамометры одинаковые. Верхний динамометр показывает силу F. Что показывают второй и третий динамометры? Массой шкал пренебречь.

2. Пружина в горизонтальном положении имеет длину 1 м. Подвешенная за один конец, она растягивается до 1,2 м. Другая такая же пружина имеет в горизонтальном положении длину 2 м. До какой длины она растянется, если ее тоже подвесить за один конец?

3. Пружина динамометра может как растягиваться, так и сжиматься, подчиняясь в обоих случаях закону Гука. За один конец динамометра тянут с силой 70 Н, другой толкают в том же направлении с силой 50 Н. Что покажет динамометр?

4. Стержень, изготовленный из упругого материала (металл, резина), аналогичен пружине. Если на его торцы действуют одинаковые растягивающие силы F, то относительное удлинение стержня равно 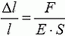, где S — площадь поперечного сечения стержня, E — коэффициент, зависящий от свойств материала (модуль Юнга). Какой должна быть длина стального стержня в горизонтальном положении, чтобы при подвешивании его за один конец длина стержня увеличилась на 1 мм? Для стали E = 2,1·10⁶ Н/мм², плотность ρ = 7,8·10³ кг/м³.

5. Стальной стержень (см. предыдущую задачу), поставленный «на попа», имеет длину 1 м. Какой будет длина стержня, если его подвесить за верхний конец?

Ответы

1) 3F/5; F/5. 2) 2,8 м. 3) 10 H. 4) 74,1 м. 5) 1 + 3,6·10^-7 м.

Динамометр представляет собой прибор, способный определять усилия, воздействующие на объекты. В качестве примера можно привести пружинное весовое спецоборудование. Здесь присоединенный к весам груз растягивает пружину с определенной силой, измерив которую легко выяснить массивность взвешиваемой вещи. Сегодня приобрести динамометрические крановые весы не составит особого труда.

Виды динамометров

Выпускается множество версий весов, различающихся между собой исполнением, предназначением, функциональностью, а также диапазоном измерений (кг). По принципу функционирования устройства подразделяются на три ключевые разновидности:

    • механические;

    • электронные;

    • гидравлические.

Механические модели делаются пружинными либо рычажными. Работоспособность первых базируется на сжатии, растяжении встроенной пружины. Растягивание пружинного элемента зависит от воздействующего момента силы. Именно по этой причине значение исследуемого параметра реально выяснить с помощью соответствующей шкалы. Как измерить вес динамометром второго типа? Главная особенность – изделие содержит рычаг, на который и воздействует усилие при подвешивании груза. Степень деформирования рычага позволяет измерить коэффициент силы.

Модификации со встроенной электроникой работают благодаря наличию специализированных сенсоров. Датчики преобразуют воздействующие нагрузки в электрические сигналы. После их обработки итоги динамометрии отображаются на дисплее.

В конструкции гидравлических экземпляров имеется цилиндрический резервуар, содержащий рабочую жидкость. Прикладываемое к прибору усилие вытесняет из цилиндра определенный объем жидкого вещества, который и позволяет узнать величину этой силы.

Особенности конструкции. Как определить вес с помощью динамометра?

Наиболее упрощенный вариант электронного динамометра состоит из трех деталей:

    • стальной проушины или крюка;

    • корпуса;

    • шкалы или цифрового табло, помогающего определять усилие.

Интересно, как определяется вес груза на динамометре электронного типа? Такие варианты устройств оснащаются датчиком, который считывает механическое воздействие. Впоследствии электроника вычисляет силу, выводит полученное значение на экран либо стрелочный индикатор. Такому оборудованию требуется электропитание. В электронных экземплярах сенсор, воспринимающий исследуемые нагрузки, изменяет свое электрическое сопротивление, поэтому и появляется сигнал, который обязательно усиливается.

Применение динамометров

Пружинные модификации подойдут для взвешивания тяжестей, проверки качества сварных швов. Электронными и механическими моделями замеряются:

    • тяговые усилия;

    • силы трения либо упругости, тяжести.

Устройствами пользуются и в строительной сфере. Мощнейшие экземпляры рассчитаны на нагрузку, которая может достигать 20000 Ньютонов. Узнать, что измеряет динамометр (вес или массу) конкретной модели, можно только у специалиста. Покупайте продукцию от проверенных поставщиков.

Читайте также

Динамометр (силомер) — прибор, предназначенный для измерения сил. Действие такого прибора основано на том, что упругие деформации пропорциональны прикладываемым силам.

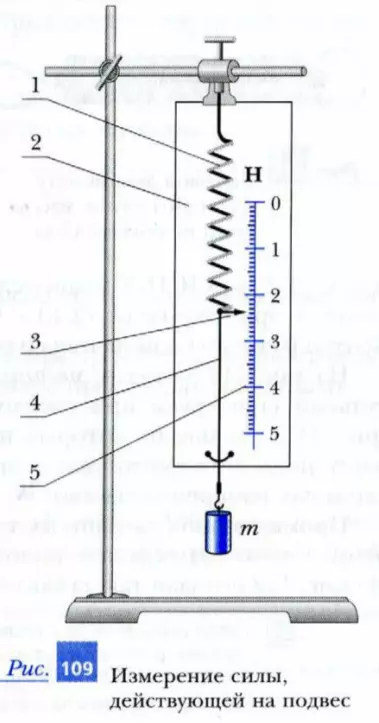
На рис. 109 показан динамометр, используемый в школах при выполнении лабораторных работ по физике. Он состоит из пружины 1, один конец которой прикреплен к основанию 2. К другому концу пружины прикреплена стрелка 3 и проволока 4 с крючком па конце. На основание 2 нанесена шкала 5, пользуясь которой можно определить силу, растягивающую пружину. Отметка «0» на шкале соответствует нерастянутому состоянию пружины. Этот динамометр предназначен для измерения сил в ньютонах. Об атом свидетельствует буква Н (или N) над шкалой.

На шкалы динамометров цифры нанесены только против некоторых штрихов. Как же узнать значения деформирующих пружину сил, если стрелка динамометра не совпадает с оцифрованным штрихом? Для этого нужно прежде всего узнать цену деления шкалы прибора (т. е. на сколько изменяется значение силы, когда стрелка смещается на одно деление – расстояние между двумя соседними штрихами). После этого подсчитывают число делений между двумя соседними оцифрованными штрихами. Например, на рис. 109 между штрихами, около которых стоят цифры 2 и 3, находится 10 делений. Следовательно, цена деления этого динамометра равна (3 – 2) / 10 = 0,1 Н на деление. Стрелка динамометра отстоит на 4 деления от штриха с цифрой 2. Поэтому модуль деформирующих пружину сил равен 2 Н + 4 · 0,1 Н = 2,4 Н.

Найденное значение силы упругости не является истинным. Динамометр, как и всякий прибор, имеет погрешность. В паспорте школьного динамометра, рассчитанного на измерение сил в пределах от 0 до 5 Н, говорится, что погрешность прибора Δ_пр = 0,05 Н в любом месте шкалы. С учетом погрешности отсчета, равной Δ_о = 0,05, получаем, что общая погрешность Δ = Δ_пр + Δ_о = 0,10 Н. Следовательно, истинное значение измерешюй силы лежит в промежутке от (2,40 – 0,10) Н = 2,3 Н до (2,40 + 0,10) Н = 2,5 Н. Кратко результат измерения силы можно записать в виде: 2,3 Н ≤ F ≤ 2,5 Н.

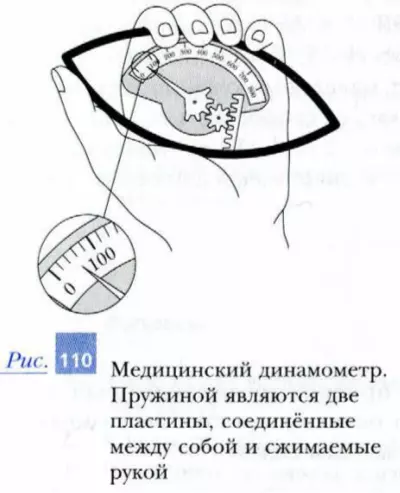
На рисунке 110 показан медицинский динамометр для измерения мускульной силы руки при сжатии кисти в кулак. Имеются динамометры (рис. 111), на шкалы которых нанесены деления, позволяющие измерять массу подвешиваемого тела непосредственно в килограммах (или других единицах измерения массы).

Когда динамометр с подвешенным телом покоится относительно Земли, динамометр показывает вес тела. При этом вес тела по модулю пропорционален его массе (P = m · g). Это и позволяет задать цену деления шкалы динамометра в единицах массы, а сам прибор использовать для измерения массы.

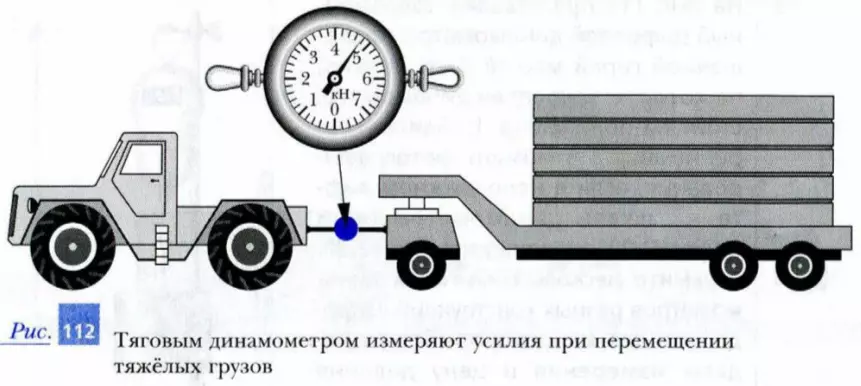
Промышленность выпускает динамометры, предназначенные для измерения сил от сотых долей ньютона до нескольких десятков килоньютонов. На рис. 112 показан так называемый тяговый динамометр.

Итоги

Динамометр – прибор для измерения сил.

Принцип действия динамометров основан на однозначной зависимости модуля упругих деформаций от модуля деформирующих сил.

Точность измерения сил определяется погрешностью динамометра, которая указывается в паспорте прибора.

Вопросы

1. Что такое динамометр? На чем основан принцип действия динамометра?
2. Как изготовить простейший динамометр и отградуировать его?
3. Как определить погрешность измерения сил динамометром?

Упражнения

1. Определите массу гири, показанной на рис. 109. Указание: модуль ускорения свободного падения считайте равным 10 м/с². Погрешность динамометра Δ = 0,10 Н.

2. Определите модуль силы, с которой трактор, показанный на рис. 112, тянет прицеп. Указание: погрешность тягового динамометра считайте равной цене деления между соседними штрихами на его шкале.

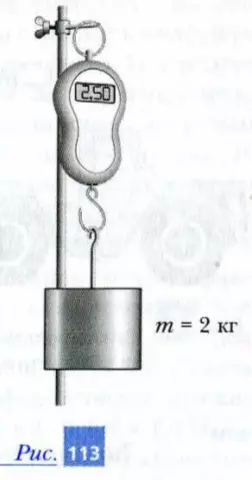
* 3. На рис. 113 представлен современный цифровой динамометр с подвешенной гирей массой 2 кг. Штатив, на котором закреплен динамометр, стоит на полу лифта. Найдите ускорение лифта в момент фотографирования, если в неподвижном лифте на шкале динамометра были цифры 2,00, а в движущемся – 2,50.

4. Возьмите несколько бытовых динамометров разных конструкций. Определите для каждого прибора пределы измерения и цену деления шкалы. Проведите взвешивание одного и того же тела разными динамометрами. Сравните результаты с учетом погрешности измерений.

5. Приготовьте напольные весы. Установите их в кабине лифта, стоящего на первом этаже, встаньте на них и зафиксируйте показание. Нажмите кнопку верхнего этажа, наблюдайте за изменением показаний весов в моменты, соответствующие: а) началу разгона лифта; б) равномерному движению; в) началу торможения перед остановкой. Объясните причины изменений в показаниях весов. Повторите эксперимент при спуске лифта с верхнего этажа на первый. Сопоставьте результаты экспериментов, объясните различия.