Здравствуйте, дорогие читатели, подписчики и гости канала. Продолжаем разбор текстовых задач из ОГЭ 2021 года, входящие в 21 задание. В этом выпуске рассмотрим решение задач на проценты.
Задача №1
Оформим задачи в виде таблицы.
Чтобы найти, сколько чистого вещества находится в растворе, нужно массу всего раствора умножить на его концентрацию. В четвертом столбце приведены расчеты, для вычисления чистого вещества (кислоты) в каждом растворе. Третий раствор получили смешиванием первого и второго раствора. В результате этого получили третий раствор массой 10 кг в котором содержится 6,2 кг кислоты.
Найдем концентрацию получившегося раствора:
Задача №2
Когда в задаче сказано, что массы сплавов или веществ одинаковы, то лучше всего брать их равными 1 кг.
Масса четвертого сплава равна сумме трех сплавов, взятых каждого по 1 кг, т.е. 3 кг. В четвертом столбце найдена масса никеля в каждом сплаве на 1 кг. Значит в четвертом сплаве на 1 кг сплава, содержится 0,75 кг никеля.
Найдем концентрацию никеля в четвертом сплаве и его процентное содержание:
Следующие две задачи будут немного сложней. Каждая задача будет состоять из двух частей.
Задача №3
Первая часть задачи, выделена зеленым цветом, первое предложение. Составим таблицу по первому предложению. За массу первого вещества возьмем Х, масса второго вещества – Y.
Вода добавляется в раствор, поэтому масса чистого вещества не изменится.
Составим уравнение:
Рассмотрим вторую часть задачи, в которой добавляется в раствор не вода, а водный раствор кислоты. Выделен красным цветом.
В данном случае в раствор добавляем 10 кг кислоты, чистое вещество увеличится на 5 кг.
Составим уравнение:
У нас получилось два уравнения. Составим систему уравнений, и найдем массу 30% – ного раствора кислоты, которую брали в начале задачи за Х.
Задача №4 Несколько раз встречалась на экзамене.
Первая часть задачи выделена синим цветом. В тексте написано “растворы различной концентрации”, значит на Х и Y возьмем концентрации раствором. Оформим все в таблицу:
Третий раствор, получаем сливанием вместе первого и второго вещества. В четвертом столбце найдем массу чистого вещества в первом и втором растворе. Составим уравнение по чистому веществу:
Составим таблицу по второй части задачи, которая выделена красным цветом. Во второй части сказано, что массы растворов взяты одинаковы. Возьмем массу первого и второго вещества равным 1 кг.
Второе уравнение составим также по чистому веществу:
У нас получилось два уравнения. Составим систему уравнений, и найдем массу кислоты во втором растворе.
Спасибо, что дочитали. Вы меня очень поддержите, если поставите класс и подпишитесь на мой блог.
Путеводитель по каналу здесь
19 мая 2012
Многие ученики ненавидят эту задачу и даже не пытаются ее решать. И совершенно зря, потому что смеси и сплавы — одни из самых легких задач B14.
Для решения требуется выполнить три простых шага:
- Составляем таблицу, в которой указываем общую массу и массу «чистого» вещества для каждой смеси или сплава. Все данные берутся прямо из условия задачи. Например, 50 литров кислоты с концентрацией 15% — это m
0 = 50 литров общей массы и m
1 = 0,15 · 50 = 7,5 литров «чистого» вещества; - Если какие-то ячейки таблицы остались не заполненными, обозначаем их переменными x, y и т.д. Чаще всего в качестве неизвестной величины выступает масса, реже — концентрация;
- Составить уравнения по правилу: при объединении двух смесей/сплавов их массы складываются. Другими словами, масса полученной смеси равна сумме масс исходных смесей. Аналогично, складываются массы «чистых» веществ.
Если все сделать правильно, то получится одно-два линейных уравнения. Решаем их — получаем ответ. А вот фиг! После того, как решите уравнение, никогда (слышите, никогда!) не записывайте ответ. Запомните:
Прежде чем записать ответ, вернитесь к задаче и еще раз прочитайте, что требуется найти. Потому что решить уравнение — это еще не значит решить текстовую задачу.
Это правило работает для всех текстовых задач, а не только для B14. Многие ученики сосредотачиваются на решении уравнения, но совершенно забывают, что, собственно, требовалось найти. Получается, что по существу задача решена верно, а ответ — неправильный.
Задача. Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора того же вещества. Сколько процентов составляет концентрация полученного раствора?
Итак, у нас есть три вещества:
- 4 литра 15-процентного раствора;
- 6 литров 25-процентного раствора;
- Третий раствор с неизвестной концентрацией.
Составим таблицу:
| Смесь | Общая масса, кг | Масса чистого вещества, кг |
| Раствор 1 (15%) | 4 | 0,15 · 4 = 0,6 |
| Раствор 2 (25%) | 6 | 0,25 · 6 = 1,5 |
| Раствор 3 | x | y |
По условию, нам не дана ни масса нового раствора, ни масса чистого вещества в нем. Поэтому обозначим общую массу x, а массу основного вещества y.
Поскольку при смешивании все массы складываются, получаем уравнения:
4 + 6 = x ⇒ x = 10;
0,6 + 1,5 = y ⇒ y = 2,1.
Уравнения получились настолько простыми, что даже не пришлось составлять систему. Но это еще не ответ! В задаче требуется найти концентрацию нового раствора. Чтобы найти ее, разделим массу чистого вещества на общую массу раствора:
y : x = 2,1 : 10 = 0,21
Итак, доля чистого вещества равна 0,21. Чтобы перевести долю в проценты, умножим на сто:
0,21 · 100 = 21
Задача. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Обозначим массу 30-процентного раствора x, а массу 60-процентного раствора y. Получим таблицу:
| Смесь | Общая масса, кг | Масса чистого вещества, кг |
| Раствор 1 (30%) | x | 0,3x |
| Раствор 2 (60%) | y | 0,6y |
| Чистая вода | 10 | 0 |
| Раствор 3 (50%) | 10 | 0,5 · 10 = 5 |
| Смесь «30% + 60% + вода» | x + y + 10 | 0,3x + 0,6y + 0 |
| Смесь «30% + 60% + 50%» | x + y + 10 | 0,3x + 0,6y + 5 |
По условию, концентрация смеси «30% + 60% + вода» равна 36%. Получаем уравнение:
0,3x + 0,6y + 0 = 0,36 · (x + y + 10)
Аналогично, концентрация смеси «30% + 60% + 50%» равна 41%. Отсюда получаем еще одно уравнение:
0,3x + 0,6y + 5 = 0,41 · (x + y + 10)
Решаем полученную систему, вычитая первое уравнение из второго:
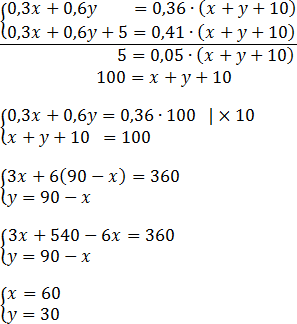
Теперь вспомним, что надо найти. А нужна масса 30-процентного раствора. Та самая, которую мы обозначили за x. Следовательно, x = 60 — это и есть ответ.
В заключение — два слова об уравнениях. Взгляните на задачи, приведенные выше: все уравнения — линейные. Никаких квадратов, никаких дискриминантов и тем более дробно-рациональных выражений. Вот почему задачи на смеси и сплавы считаются очень легкими.
Смотрите также:
- Простая задача B14 на смеси и сплавы
- Сложная задача B14 на смеси и сплавы
- Сложные выражения с дробями. Порядок действий
- Типичные задачи B12 с функциями
- Наибольшее и наименьшее значение
- Задача B4: Скачать файл на разной скорости
Как правило, ученики очень не любят задачи на сплавы и смеси. Для них они являются сложными и непонятными.
Поэтому многие даже время не тратят на попытки решения такой задачи в ЕГЭ, а просто пропускают ее. А зря!
Сейчас покажем, как можно решить такую задачу, выполнив всего три действия.
- Как решить задачу на смеси и сплавы: 3 действия
- Примеры решения задач на смеси: от простого к сложному
- Примеры решения задач на сплавы: от простого к сложному
Как решить задачу на смеси и сплавы: 3 действия
Итак, решение любой задачи на смеси и сплавы сводится к выполнению трех действий:
- Необходимо составить таблицу, в которой указываем общую массу каждого вещества и чистую массу каждого вещества. Эти данные содержатся в условии задачи. Если какие-то данные в условии отсутствуют, то обозначаем их как неизвестные — х, у.
- Составляем систему уравнений, основываясь на том, что при соединении двух смесей (или сплавов) их массы складываются. Т.е. мы складываем как общую массу двух изначальных смесей (или сплавов), так и чистую массу каждого вещества, содержащихся в них. Решаем полученную систему уравнений.
- После решения системы уравнений и нахождения всех неизвестных обязательно возвращаемся к условию задачи и смотрим, что требовалось найти. Многие ученики, решив правильно систему уравнений, неправильно записывают ответ. Ведь решение системы – это еще не ответ к задаче! Вернитесь к условиям задачи, прочитайте, что именно требовалось найти, и запишите ответ.
Примеры решения задач на смеси: от простого к сложному
А теперь разберем на примерах, как с помощью этих трех действий решать задачи на смеси и сплавы.
Задача 1
Смешали 3 литра раствора, содержащего 20% кислоты, и 5 литров раствора, содержащего 40% той же кислоты. Какова концентрация кислоты в полученном растворе.
Решение:
Для решения задачи выполняем три действия, о которых мы говорили выше:
1. Составляем таблицу, в которой указываем общую массу раствора и массу чистого вещества, то есть в нашем случае – кислоты.
Из условий задачи имеем три раствора:
Раствор 1: 3 литра с 20% кислотой, т.е. общая масса = 3 литра, масса чистого вещества = 3 * 20% = 3 * 0,2 = 0,6
Раствор 2: 5 литров с 40% кислотой, т.е. общая масса = 5 литров, масса чистого вещества = 5 * 40% = 5 * 0,4 = 2
Раствор 3: какое-то количество раствора (обозначим его общую массу за х) с какой-то концентрацией кислоты (обозначим ее чистую массу за у), заносим эти данные в таблицу:
Первое действие выполнено, переходим ко второму.
2. Составляем уравнения. Вспоминаем, что общая масса раствора 3 является суммой общих масс раствора 1 и раствора 2. А масса чистого вещества в растворе 3 является суммой массы чистового вещества в растворе 1 и массы чистового вещества в растворе 2. Таким образом, получаем:
3 + 5 = х
0,6 + 2 = у
Решаем простейшее уравнение и получаем, что х = 8, а у = 2,6. Таким образом, раствор 3 получился 8 литров, из которых 2,6 литра – это кислота.
Но ответ к задаче записывать рано! Переходим к третьему действию решения нашей задачи.
3. Возвращаемся к условию задачи и вспоминаем, а что же требовалось найти. В нашей задаче требовалось определить концентрацию кислоты в растворе 3. Когда мы решили уравнения, мы нашли общую массу раствора 3 и массу чистого вещества (кислоты), содержащегося в нем.
Чтобы определить концентрацию вещества необходимо разделить массу чистого вещества на общую массу раствора.
Таким образом, концентрация кислоты в растворе 3 равна:
2,6 / 8 = 0,325
Переводим долю вещества в проценты. Для этого умножаем полученный результат на 100:
0,325 * 100 = 32,5%
Ответ: 32,5%
Задача 2
Газ в сосуде А содержал 21% кислорода, а газ в сосуде В содержал 5% кислорода. Масса газа в сосуде А была больше массы газа в сосуде В на 300 г. Когда перегородку между сосудами убрали, газы перемешались, и получился третий газ, который содержит 14,6% кислорода. Найти массу третьего газа.
Решение:
1. Составляем таблицу. Для этого обозначим массу газа в сосуде В – х. Остальные данные берем из условий задачи и формируем таблицу:
2. Составляем уравнение. Известно, что третий газ имеет содержание кислорода 14,6%, соответственно мы можем приравнять массу чистого вещества газа 3 к 0,146 * (х + (х +300)). Получим уравнение:
(х +300) * 0,21 + х * 0,05 = 0,146 (х + (х +300))
0,21х + 63 + 0,05х = 0,292х + 43,8
0,26х + 63 = 0,292х + 43,8
0,032х = 19,2
х = 600
3. Возвращаемся к условиям задачи и вспоминаем, что нужно было найти. А найти нам нужно было массу третьего газа. Подставляем в уравнение общей массы газа 3 из таблицы и получаем:
600 + 600 + 300 = 1500 г
Ответ: масса третьего газа равна 1500 г.
Задача 3
Смешали 40%ый и 15%ый растворы кислоты, затем добавили 3 кг чистой воды, в результате чего получили 20%ый раствор кислоты. Если бы вместо 3 кг воды добавили 3 кг 80% раствора той же кислоты, то получили бы 50%ый раствор кислоты. Сколько килограммов 40%го и 15%го растворов кислоты было смешано?
Решение:
1. Составляем таблицу. По условиям задачи мы имеем пять растворов:
Раствор 1: 40%ая кислота. Обозначим ее массу за х, тогда масса чистого вещества = х * 40% = 0,4х
Раствор 2: 15%ая кислота. Обозначим ее массу за у, тогда масса чистого вещества = х * 15% = 0,15х
Вода: вода, масса которой равна 3 кг. Концентрация кислоты в воде равна 0. Таким образом, масса чистого вещества равна 3 * 0 = 0
Раствор 3: 80%ая кислота. Ее масса по условию задачи равна 3 кг, тогда масса чистого вещества равна 3 * 80% = 3 *0,8 = 2,4
Раствор 4: соединение раствора 1, раствора 2 и воды. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 0
Раствор 5: соединение раствора 1, раствора 2 и раствора 3. Таким образом, общая масса полученного раствора равна х + у + 3. А масса чистого вещества в этом растворе равна 0,4х + 0,15у + 2,4.
Сводим полученные результаты в таблицу:
2. Составляем уравнение.
По условиям задачи раствор 5 имеет концентрацию 50%. Таким образом, чтобы получить массу чистого вещества в растворе 5 нужно его общую массу умножить на концентрацию. Получаем (х + у + 3) * 0,5. Теперь берем массу чистого вещества раствора 5, которую мы выразили в таблице и приравниваем два этих уравнения:
(х + у + 3) * 0,5 = 0,4х + 0,15у + 2,4
Аналогично поступаем с раствором 4. По условиям задачи его концентрация равна 20%. Тогда получаем следующее уравнение:
(х + у + 3) * 0,2 = 0,4х + 0,15у
Объединяем полученные уравнения в систему:
Решаем систему и получаем х = 3,4, у = 1,6
3. Возвращаемся к условиям задачи.
По условиям задачи необходимо было найти, какое количество килограммов 40%го и 15%го растворов кислоты было смешано. Общая масса 40%й кислоты мы обозначали х, а общую массу 15%й кислоты мы обозначили у. Следовательно, масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.
Ответ: масса 40%й кислоты = 3,4 кг, а масса15%й кислоты = 1,6 кг.
Примеры решения задач на сплавы: от простого к сложному
Задача 1
Бронза является сплавом меди и олова (в разных пропорциях). Кусок бронзы, содержащий 1/12 часть олова, сплавляется с другим куском, содержащим 1/10 часть олова. Полученный сплав содержит 1/11 часть олова. Найдите вес второго куска, если вес первого равен 84 кг
Решение:
1. Составим таблицу. Обозначим массу второго куска – х.
2. Составим уравнение. По условию задачи сплав 3 содержит 1/11 часть олова, тогда масса чистого вещества равна 1/11 * (84 + х). Таким образом, можно составить следующее уравнение:
1/12 * 84 + 1/10 * х = 1/11 * (84 + х)
7 + х/10 = 84/11 + х/11
х/10 – х/11 = 7/11
х/110 = 7/11
х/10 = 7
х = 70
3. Возвращаемся к условию задачи. Найти нужно было вес второго куска. Вес второго куска равен 70 кг.
Ответ: 70 кг.
Задача 2
Имеются два сплава меди со свинцом. Один сплав содержит 15% меди, а другой 65%. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Решение.
1. Составим таблицу. Пусть масса первого сплава – х, масса второго сплава – у. Остальные данные берем из решения и составляем таблицу:
2. По условиям задачи масса третьего сплава равна 200 г, значит:
х + у = 200
Содержание меди в третьем сплаве по условиям задачи равно 30%, т.е. масса чистого вещества равна 0,3(х + у). Следовательно, берем массу чистого вещества из таблицы и приравниваем:
0,15х + 0,65у = 0,3(х + у)
Получившиеся уравнения сводим в систему и решаем ее:
х = 200 – у
0,15(200 – у) + 0,65у = 0,3 * 200
30 – 0,15у + 0,65у = 60
0,5у = 30
у = 60
х = 140
3. Возвращаемся к условиям задачи. Необходимо было найти массу первого и второго сплава. Масса первого сплава — 140 г, масса второго сплава -60 г.
Ответ: 140 г и 60 г.
Задача 3
В первом сплаве содержание меди составляет 70%, а во втором – 40%. В каком отношении надо взять эти сплавы, чтобы получить из них новый сплав, который содержит 50% меди?
Решение:
1. Составим таблицу. Обозначим массу первого сплава – х, массу второго сплава – у. Тогда:
2. По условиям задачи содержание меди в третьем сплаве равно 50%. Таким образом, масса чистого вещества равна 0,5 (х + у). Приравняем полученное уравнение к массе чистого вещества в составе третьего сплава из таблицы, получим:
0,7х + 0,4у = 0,5 (х + у)
0,7х + 0,4у = 0,5х + 0,5у
0,2х = 0,1у
х/у = ½
3. Возвращаемся к условию задачи. Необходимо было определить отношение первого и второго сплавов в третьем сплаве. Отношение сплавов равно ½.
Ответ: ½
Итак, решение задач на сплавы и смеси можно свести к трем действиям: составление таблицы, составление уравнения (или системы уравнений), возвращение к условиям задачи, чтобы дать ответ на поставленный вопрос. Задание 11 ЕГЭ по математике профильного уровня является одной из самых сложных задач, так как может содержать текстовую задачу любого типа. Это может быть как задача на сплавы и смеси, так и задача на движение, работу, проценты. Как решать все эти задачи вы можете узнать на нашем сайте или
Табличный способ решения задач на смеси и сплавы.
Автор: Тавадян М.М., учитель математики МАОУ СОШ №71, г. Краснодар
Задачи на смеси, сплавы и растворы встречаются в вариантах и ОГЭ и ЕГЭ.
В этих задачах речь идет, чаще всего, о сплавлении каких–либо металлов,
растворении друг в друге различных веществ или переливании жидкостей,
состоящих из нескольких компонентов.
Практика показывает, что многие учащиеся даже не начинают решать эти
задачи, считая их сложными, хотя задачи такого типа не только не сложнее, а
иногда бывают даже проще других текстовых задач, к которым учащиеся
больше привыкли и считают их более знакомыми и простыми.
Причина заключается в том, что задачи на смеси, сплавы, растворы редко
встречаются в учебниках практически всех авторов. Никаких приемов решения
таких задач в учебниках не описывается.
Для решения задач на смеси и сплавы нужно знать, что:
1. Процентным содержанием (концентрацией) вещества в смеси называется
отношение массы чистого вещества к общей массе всей смеси:
К =
𝒎
𝑴
∗ 𝟏𝟎𝟎%
где K – процентное содержание чистого вещества в сплаве или растворе
m – масса чистого вещества
M – масса сплава или раствора;
2. масса раствора (смеси, сплава) равна сумме масс всех составляющих;
3. при смешивании нескольких растворов (смесей, сплавов) масса нового
раствора равна сумме масс всех смешанных растворов;
4. масса чистого вещества при смешивании двух растворов суммируется;
5. чтобы найти % от числа, нужно перевести % в дробь и умножить на это
число.
(Найти 3% от 250. 3%=0,03; 0,03*250=7,5).
Табличный способ решения задач на смеси и сплавы значительно облегчает
решение любой задачи. Для этого нужно всего лишь данные условия задачи
занести в таблицу, разложив все, буквально «по полочкам». Последний
столбец таблицы заполняется по предыдущим двум, согласно п.5. Уравнение
составляется согласно п.4.
Рассмотрим примеры решения задач.
Работа на тему: «Решение задач на концентрацию, смеси
и сплавы».
Задачи на
концентрацию, смеси, сплавы.
Задачи на
концентрацию традиционно являются слабым звеном в подготовке школьников и
абитуриентов, кажутся многим из них довольно сложными. Обучение решению этих
задач начинается с 6 класса и продолжается на продолжении всей основной школы.
Однако, в 11 классе эти задачи у большинства вызывают затруднения. При
повторении можно начинать с решения самых простых задач, взятых из учебника
математики для 6 класса. В таких задачах речь обычно идет о растворах
некоторого вещества в другом веществе и об изменении концентрации этого
вещества после каких-либо манипуляций. При этом водные растворы, смеси, сплавы
играют сходные роли и позволяют лишь несколько разнообразить сюжеты задач без
изменения математического содержания. Ключевой при решении таких задач является
идея отслеживания изменений, происходящих с «чистым» веществом.
В качестве модельной задачи рассмотрим следующую.
Смешали х литров п- процентного водного раствора некоторого вещества
с у литрами к- процентного водного раствора этого же вещества. Требуется найти
концентрацию получившейся смеси.
Воспользуемся ключевой идеей: проследим за изменениями, происходящими
с чистым веществом. В первом растворе его было 0,01хп литров, во втором
растворе 0,01ук литров. Значит количество чистого вещества в полученной смеси
будет равно 0,01хп + 0,01ук литров, а всего смеси получится х + у литров.
Теперь найти искомую концентрацию легко.
( 0,01хп + 0,01ук):
(х + у) ×100= (хп + ук):(х + у). Заметим, что растворы в этой задаче можно было
бы заменить двумя сплавами разной массы и с разным содержанием чистого
вещества. Решение при этом практически не изменится, поменяются лишь единицы
измерения и названия веществ.
Тема : Задачи на проценты и концентрацию.
Цель: формировать умение решать задачи на концентрацию, смеси и сплавы.
1.Устная работа.
Найдите:
а) 50% от
80; б) 10% от 300 в) 1% от 30 г) 20% от 25 д)25%
от 400
е) 5% от 200;
ж) 50% от 17 з) 40% от 10 и) 70% от 30 к) 9% от 500.
2.Формирование
умений и навыков.
Задача. Имеются 3 раствора морской соли в воде: первый раствор содержит 10%
соли, второй содержит 15 % соли и третий – 20% соли. Смешали 130 мл первого
раствора, 200 мл второго раствора и 170 мл третьего раствора.
Определите, сколько
процентов составляет морская соль в полученном растворе
Решение:
1)
В 130 мл первого раствора содержится 130 × 0,1 = 13
(г) морской соли. В 200 мл второго раствора содержится 200 × 0,15 = 30 (г)
морской соли. В 170 мл третьего раствора содержится 170 × 0,2 = 34 (г) морской
соли.
2)
После того, как эти растворы смешали, получили 130
+ 200 + 170 = 500 (мл) нового раствора, который содержит 13 + 30 + 34 = 77 (г)
морской соли.
3)
Найдем, сколько процентов составляют 77 (г) морской
соли от 500 мл раствор
.
Задача. Сколько граммов воды надо добавить к 50
г раствора, содержащего 8 % соли, чтобы получить 5 % – ный раствор?
Заметим, что задачи на концентрацию вызывают наибольшие
затруднения у учащихся. Поэтому следует подробнее остановиться на решении
данной задачи, начав не с составления уравнения, а с вопросов, которые помогут
учащимся уяснить условие и осознанно подойти к её решению.
Вопросы учащимся:
1) Сколько граммов соли содержится в имеющемся растворе?
(50×0,08 = 4 г).
2) Если к имеющемуся раствору добавить воды, изменится ли
массовая составляющая соли? (Нет.)
3) При добавлении воды изменится ли процентное содержание
соли в растворе? (Да.)
4) Если к имеющемуся раствору добавить х г воды,
какова станет масса всего раствора? (50 + х). Сколько граммов соли в нем
будет? (4г).
5) Каково процентное содержание соли в новом растворе?
(5%.)
6) Какую пропорцию, согласно полученным результатам, можно
составить?
4 г соли – 5%
(50 + х) г раствора – 100%.
Имеем уравнение:
5(50 + х) = 400, откуда х = 30.
Ответ: 30г.
Алгоритм.
Поскольку при добавлении к раствору какого-либо вещества
масса другого вещества не изменяется, а меняется его процентное содержание, то
сначала необходимо найти массу изменяющегося вещества.
Затем за х обозначить массу добавляемого вещества и
составить пропорцию, в которой масса неизмененного вещества будет составлять
новое количество процентов, а масса всего раствора 100%.
Задание учащимся.
Решите следующие две задачи по составленному выше
алгоритму.
Задача №1.
Сколько граммов воды надо добавить к 180
г сиропа, содержащего 25% сахара, чтобы получить 20%-ый сироп?
Решение.
Веществом, которое не меняет своей массы в новом растворе,
является сахар. Поэтому найдем его массу.
180×0,25 = 45 г.
После добавления воды 45
г сахара в новом растворе будут составлять 20 % от всей массы. Пусть х
г воды надо добавить, тогда масса нового раствора составляет (180 + х)
г.
Имеем пропорцию:
45 г сахара – 20%;
(180 + х) г сиропа – 100%.
Из пропорции составим уравнение:
20(180 + х)= 4500, откуда х = 45.
Ответ: 45г.
Задача №2.
Сколько граммов воды надо выпарить из 80
г 6%-ого раствора соли, чтобы получить 10%-й раствор?
Решение.
Масса соли в имеющемся растворе равна 80 × 0,06 = 4,8
г. В новом растворе соль будет составлять 10%.
Пусть х граммов воды нужно выпарить, тогда масса
нового раствора будет равна (80 – х) г.
Составим пропорцию:
4,8 г соли – 10%;
(80 – х) г раствора – 100%.
Получаем уравнение:
10(80 – х) = 4,8×100, откуда х = 32.
Ответ: 32 г.
Задача №3.
Имеются два сплава. Первый сплав содержит 10% никеля,
второй 30% никеля. Из этих двух сплавов получили третий сплав массой 200
кг, содержащий 25 % никеля. Насколько кг масса первого сплава меньше массы
второго?
Решение.
Пусть масса первого сплава х кг, а масса второго у
кг. Масса третьего сплава х + у и по условию задачи х + у = 200. Первый сплав
содержит 0,1х кг чистого вещества, а второй 0,3у кг. Третий сплав содержит 0,25×200=50
кг. Значит, 0,1х + 0,3у =50. Получили систему из двух линейных уравнений.
Решением системы является пара чисел х=50 и у=150. Итак, масса первого сплава
на 150 – 50 =100 кг меньше.
Ответ: 100.
Задача №4.
Первый сплав содержит 10% меди, второй – 40 % меди. Масса
второго сплава больше массы первого на 3
кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите
массу третьего сплава. Ответ дайте в килограммах.
Решение.
Пусть масса первого сплава х кг, тогда масса второго сплава
( х + 3 )кг. Масса третьего сплава х + х + 3 = 2х +3
кг. Масса чистого вещества в первом сплаве 0,1х кг, во втором – 0,4×( х+3),
значит всего чистого вещества 0,1х + 0,4(х+3). Так как третий сплав содержит
30% меди, т.е. 0,3( 2х +3), то имеем уравнение 0,3( 2х +3)= 0,1 + 0,4( х+3),
откуда х = 3. Масса третьего сплава равна 2×3 +3 = 9
кг.
Ответ: 9.
Задача №5.
Виноград содержит 91% влаги, а изюм – 7%. Сколько
килограммов винограда требуется для получения 21 килограмма изюма?
Решение.
Используем ключевую идею: будем следить за массой
«чистого», т.е. в данном случае «сухого» вещества в винограде и изюме. Виноград
содержит чистого вещества 100% – 91% = 9%, а изюм содержит чистого вещества
100% – 7% = 93%. Пусть для получения 21 килограмма изюма требуется х кг
винограда. Из условия следует, что масса «сухого» вещества в х кг
винограда равна 0,09х кг. Поскольку эта масса равна массе «сухого»вещества в 21
килограмме изюма, то по условию задачи можно составить уравнение
0,09х=0,93×21,
откуда
9х = 93×21,
т.е. х = 217
кг.
Ответ: 217 кг.
Задача для самостоятельного решения.
Виноград содержит 90% влаги, а изюм – 5%. Сколько
килограммов винограда требуется для получения 20 килограмма изюма?
Ответ:190кг.
Задача №6.
В сосуд, содержащий 5
литров 12-процентного водного раствора некоторого вещества, добавили 7
литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение.
В 5 литрах раствора содержится 0,12×5 = 0,6
л чистого вещества. Масса нового раствора 12
литров, а чистого вещества в нем по прежнему 0,6
л. Значит концентрация нового раствора равна 0,6 : 12×100% =5%.
Ответ: 5.
Задача №7.
Смешали некоторое количество 15-процентного раствора
некоторого вещества с таким же количеством 19- процентного раствора этого же
вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение.
Пусть масса первого раствора х г, он содержит 0,15х г
чистого вещества. Масса второго раствора тоже х г, он содержит 0,19х г чистого
вещества. Масса нового раствора равна х + х = 2х г и он содержит 0,15х + 0,19х
= 0,34х г чистого вещества. Тогда концентрация нового раствора равна ( 0,34х) :
(2х)×100% = 17%.
Ответ: 17.
Задача для самостоятельного решения.
Смешали 4 литра 15-процентного раствора некоторого вещества
с 6 литрами 25-процентного водного раствора этого же вещества. Сколько
процентов составляет концентрация получившегося раствора?
Ответ: 21.
Итоги урока.
Вопросы учащимся:
– Как найти процент от величины?
– Как найти величину по ее проценту?
– Как найти, сколько процентов одна величина составляет от
другой величины?
– Каков алгоритм решения задач на концентрацию, в которых к
имеющемуся раствору добавляют одно из составляющих его веществ?
– По какому плану решаются задачи на смешивание нескольких
растворов?
ЛИТЕРАТУРА
1.Математика. 6 класс: поурочные планы по учебнику
Г.В.Дорофеева, С.Б.Суворовой, И.Ф.Шарыгина. Часть 1/авт.-сост. Т.Ю.Дюмина. –
Волгоград: Учитель,2007.
2.Алгебра. 7 класс: поурочные планы по учебнику под
редакцией Г.В.Дорофеева / авт.-сост. М.Ф. Калинина. – Волгоград: Учитель,2008.
3.Алгебра. 8 класс: поурочные планы по учебнику под
редакцией Г. .В. Дорофеева / авт. – сост. Т. Ю. Дюмина. – Волгоград:
Учитель,2008.
4.Шестаков С.А., Гущин Д.Д. ЕГЭ 2011. Математика. Задача
В12. Задачи на составление уравнений. Рабочая тетрадь / Под ред. А.Л.Семенова и
И.В.Ященко. – М.: МЦНМО, 2011.
