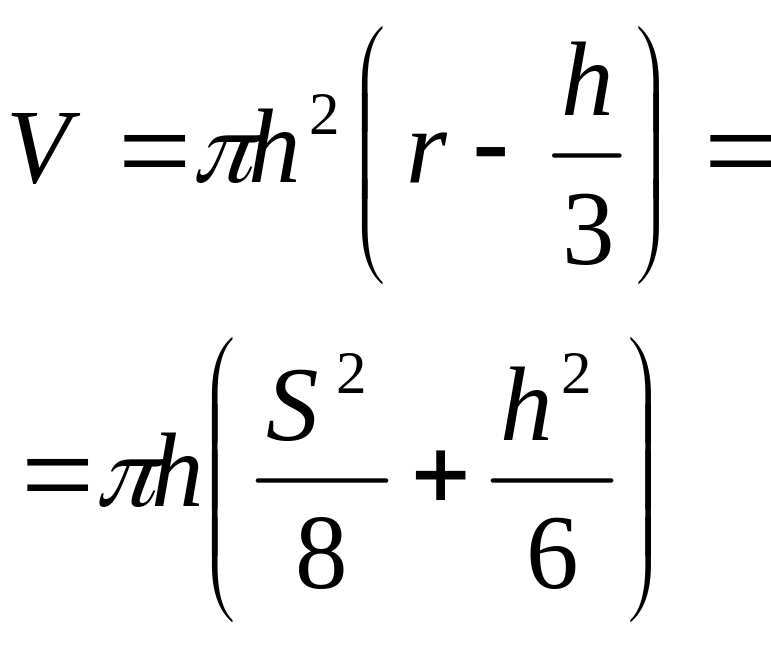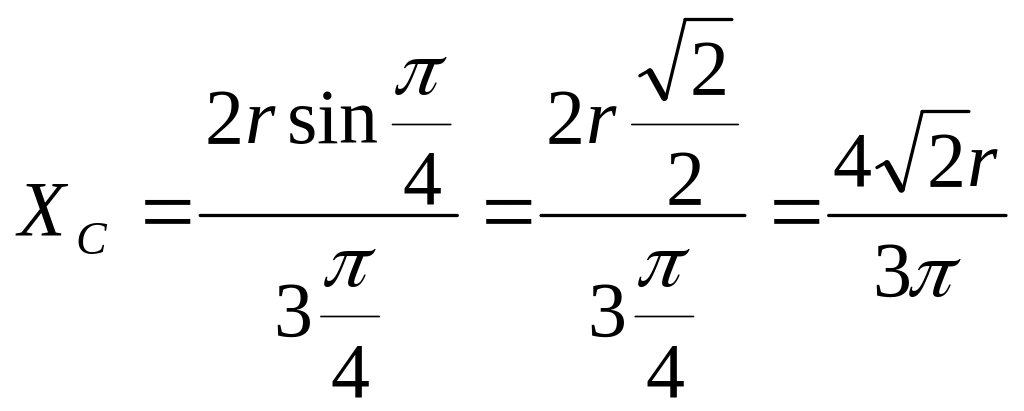Масса сплошной детали
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем 

Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой 
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
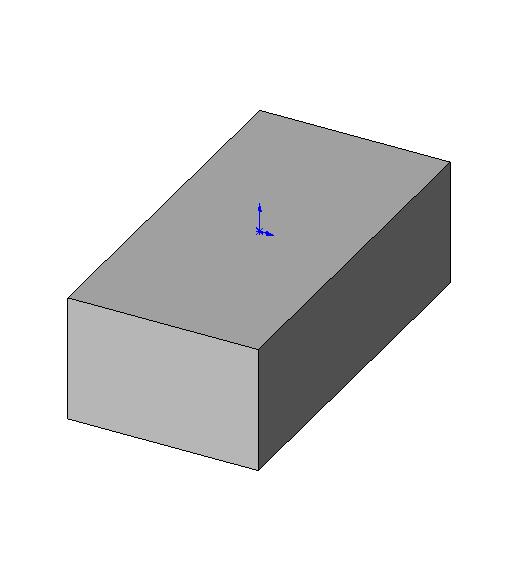
1. Масса параллелепипеда (бруска)





Тогда масса:
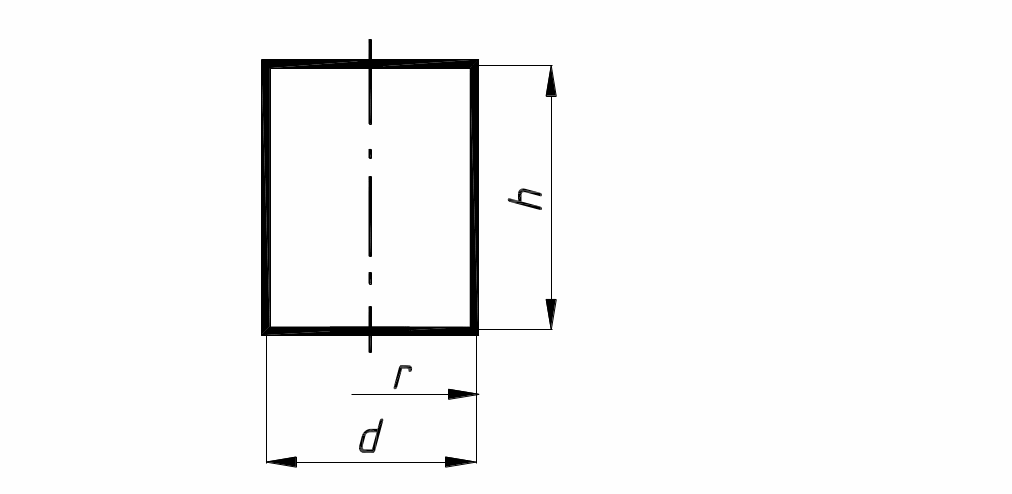
2. Масса цилиндра




Тогда масса:
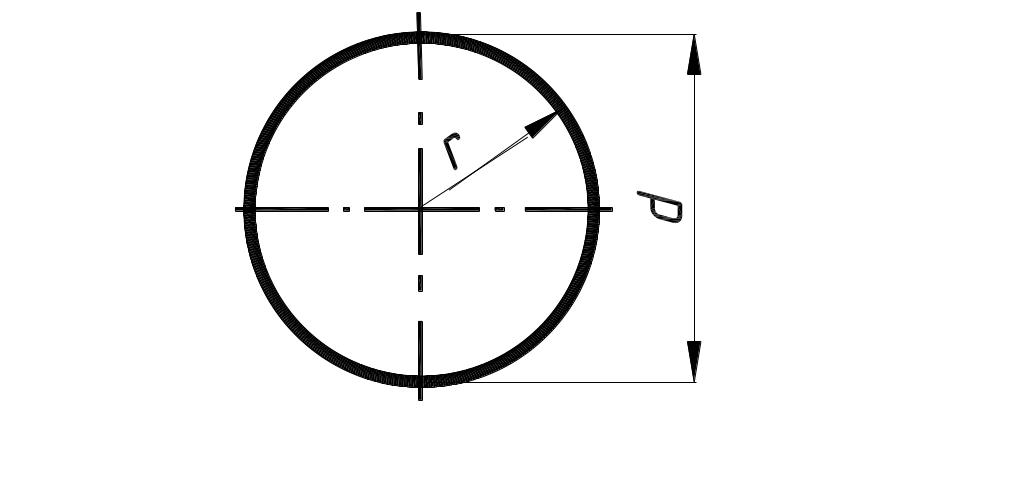
3. Масса шара



Тогда масса:
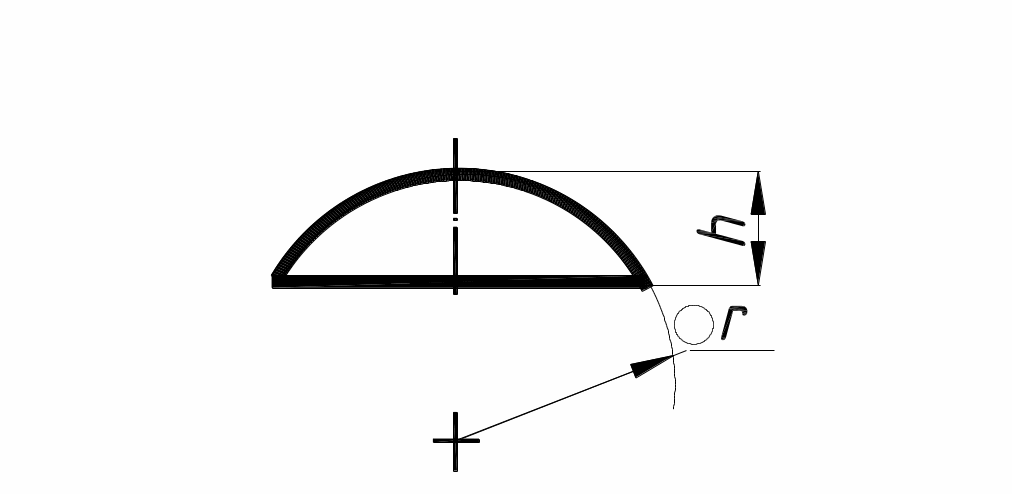
4. Масса сегмента шара




Тогда масса:
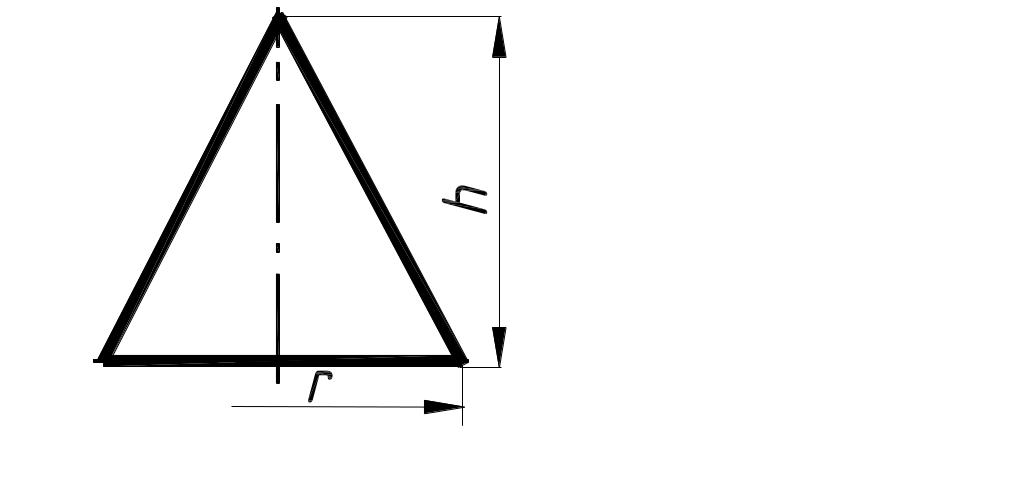
5. Масса конуса




Для круглого конуса: 


Масса круглого конуса:
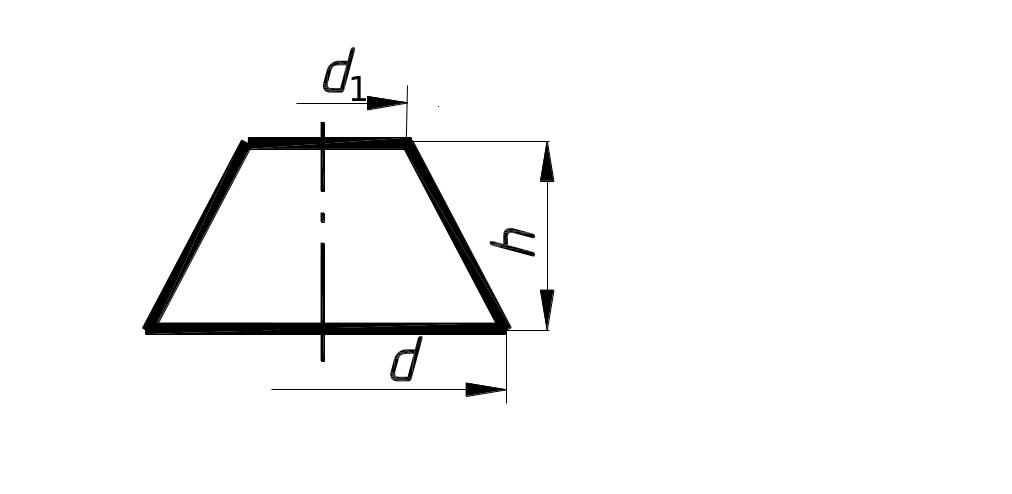
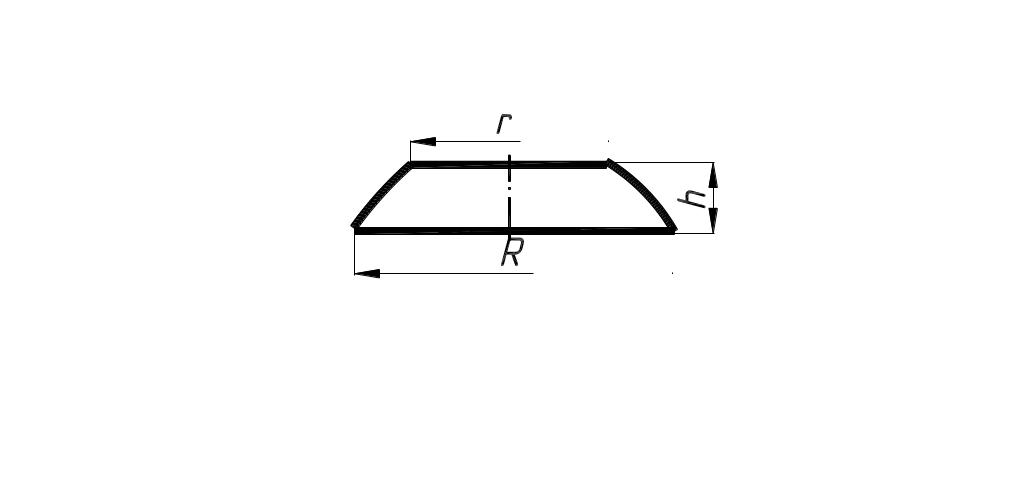
6. Масса усеченного конуса










Отсюда масса:
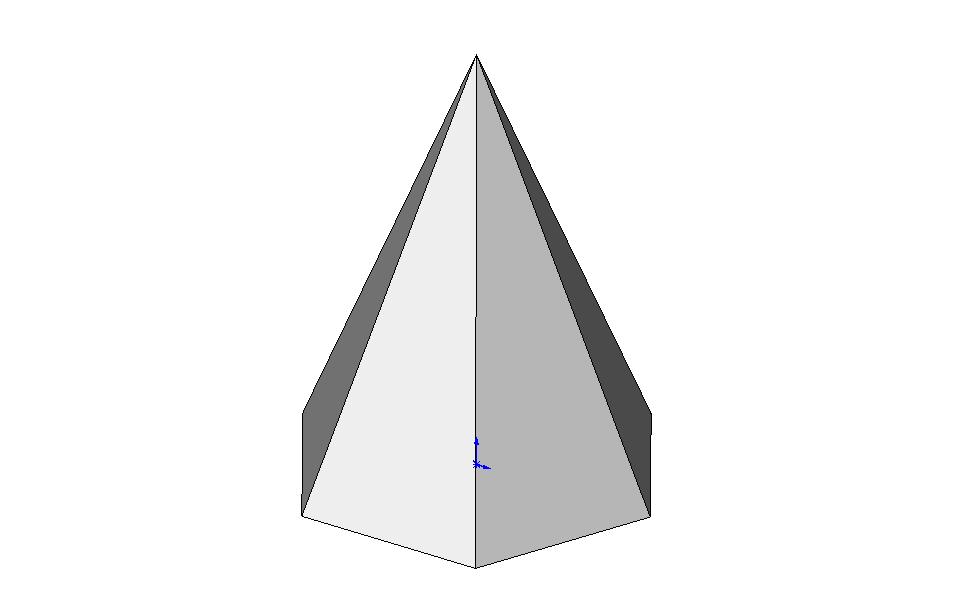
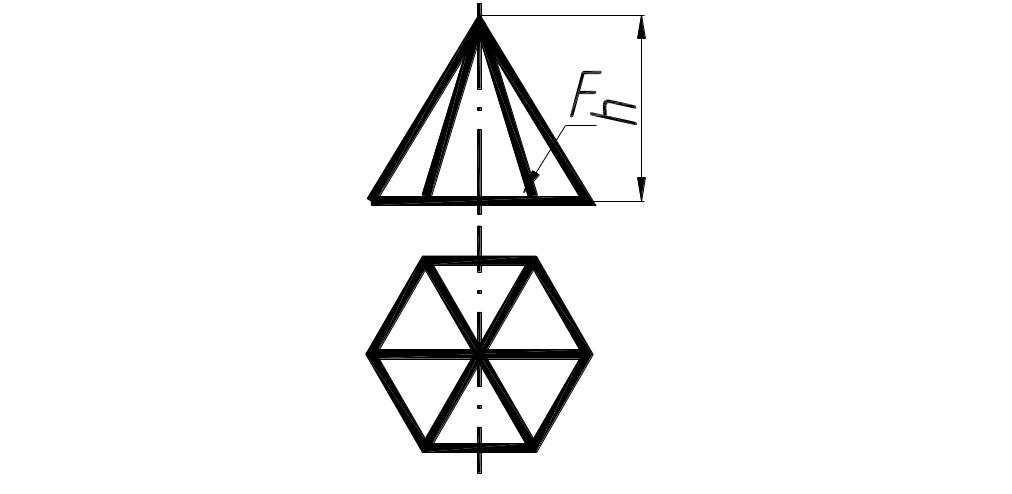
7. Масса пирамиды




Для пирамиды с прямоугольным основанием: 



Тогда масса пирамиды:
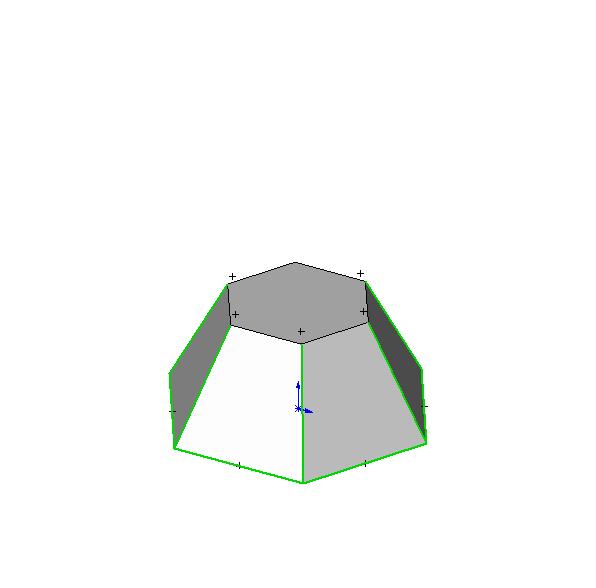
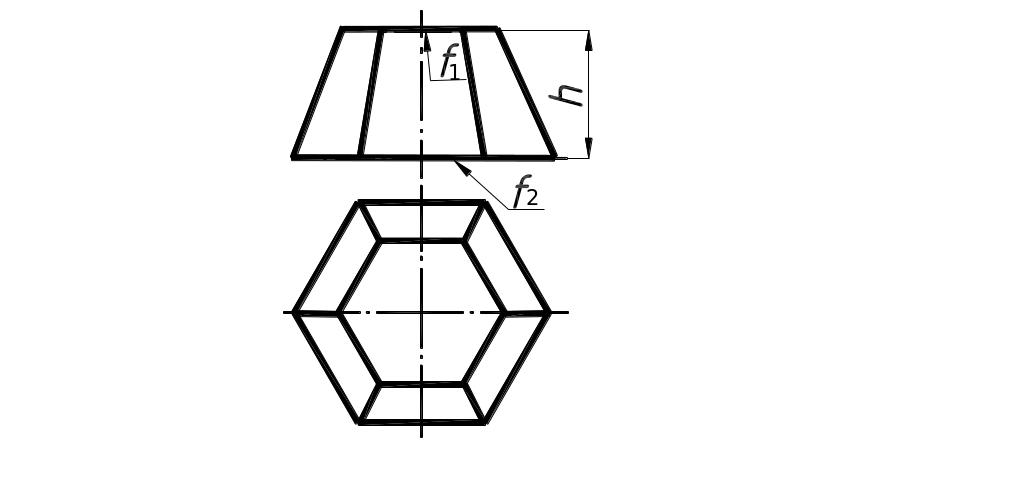
8. Масса усеченной пирамиды






Исчеркав половину тетрадного листа, получаем: 





И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: 
Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (

-
Определение массы детали по ее чертежу
Масса детали
определяется
G
= V,
где V
– объем детали,
‑ плотность материала из которого
изготовлена данная деталь.
Таким образом,
для определения массы детали необходимо
определить объем детали. Для этого
разбиваем деталь на фигуры, для которых
можно определить объем детали по
известным формулам (табл. 2.1)
Таблица 2.1
|
Наим. |
Наглядное изображение |
Эскиз |
Объем |
|
1 |
2 |
3 |
4 |
|
Цилиндр |
|
|
|
|
Призма |
|
|
V = аbc |
|
Пирамида |
|
|
|
Продолжение табл.
2.1
|
1 |
2 |
3 |
4 |
|
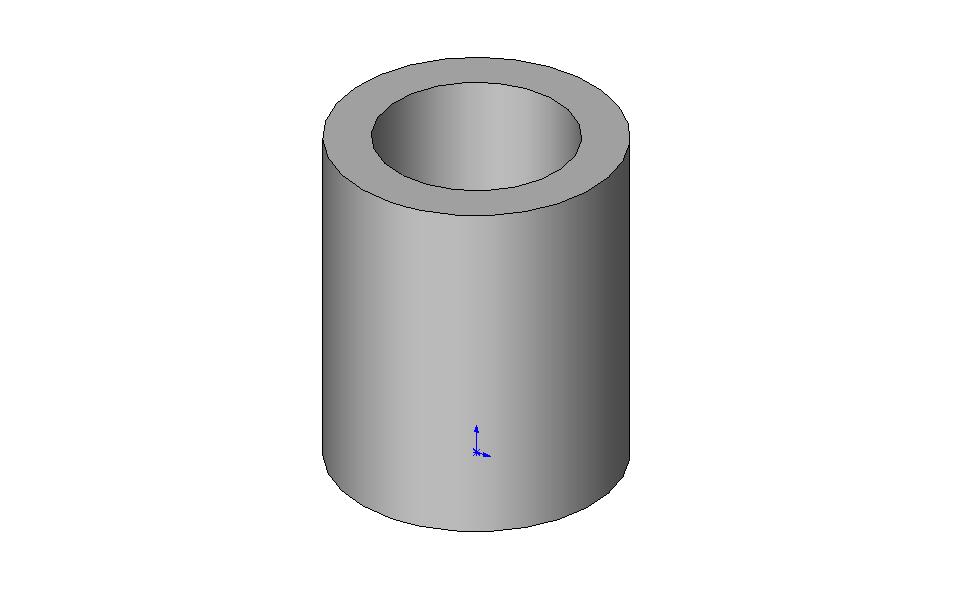
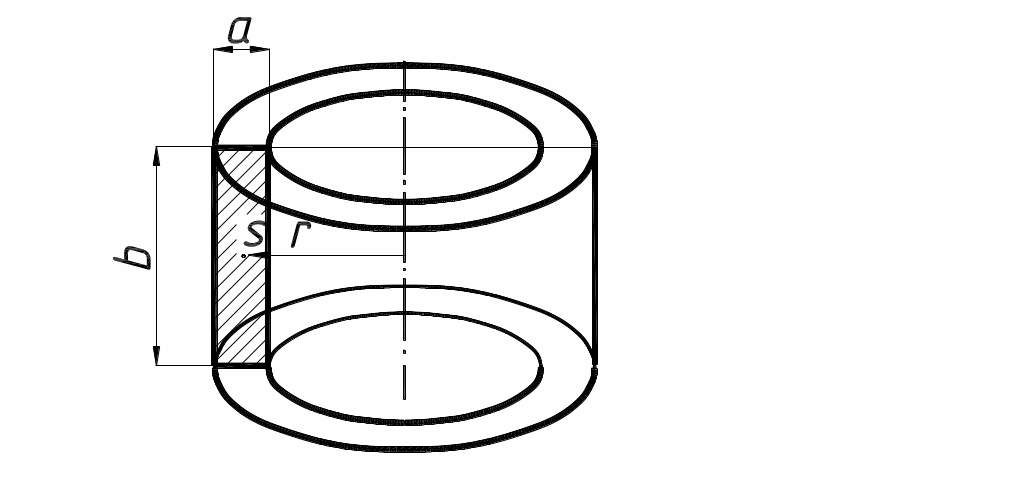
Полый цилиндр |
|
|
|
|
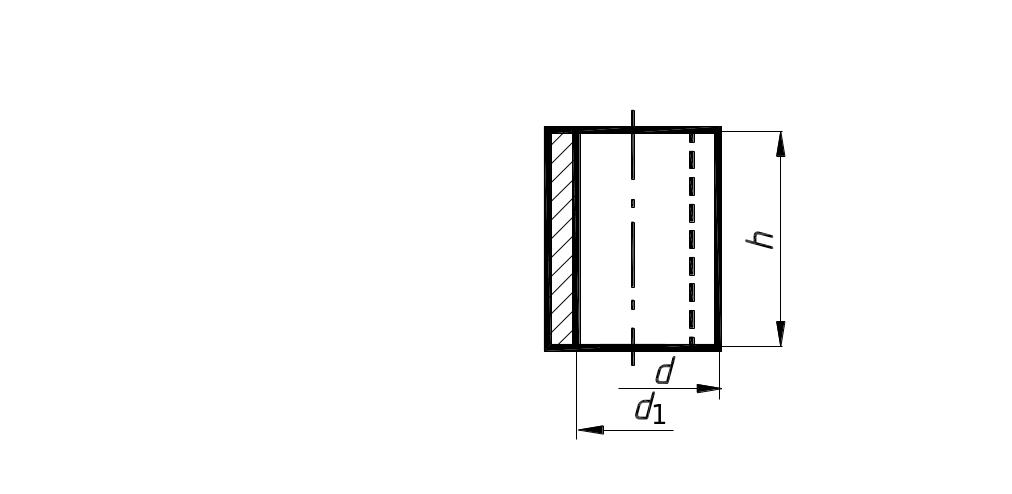
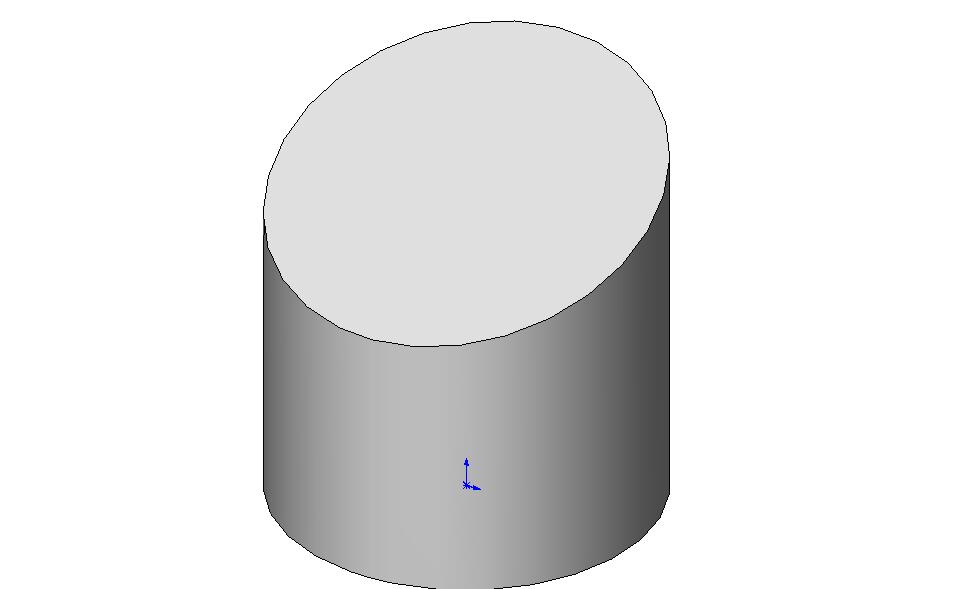
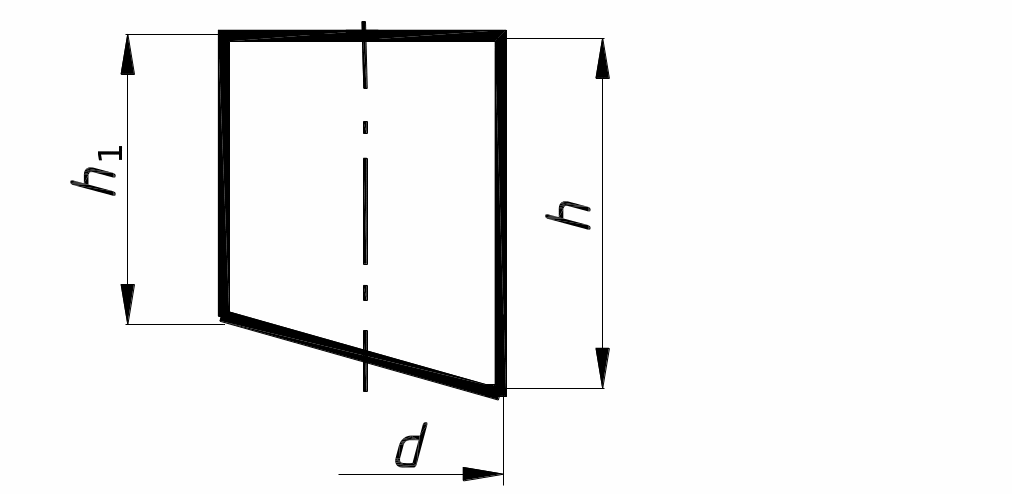
Косо срезанный цилиндр |
|
|
|
|
Шар |
|
|
|
|
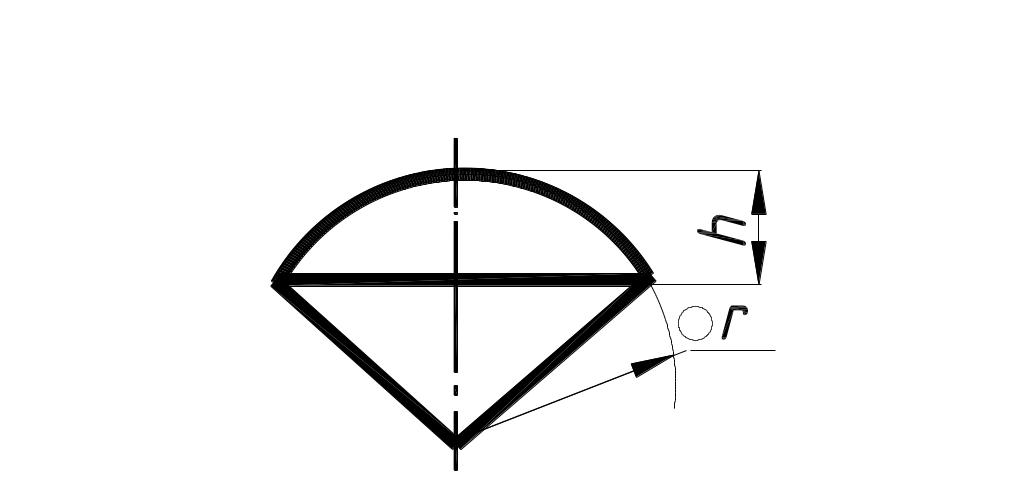
Шаровой сектор |
|
|
|
|
Шаровой сегмент |
|
|
|
Продолжение табл.
2.1
|
1 |
2 |
3 |
4 |
|
Конус |
|
|
|
|
Усеченная пирамида |
|
|
где f1 |
|
Усеченный конус |
|
|
|
|
Бочка |
|
|
|
|
Тело вращения |
|
Объем V тела вращения, V=2rF=2rab |
В качестве примера
рассмотрим определение объема вала,
изображенного на рис. 2.1. Разобьем вал
на простые (с точки зрения вычисления
объема) тела (рис. 2.2) и вычислим их объем.
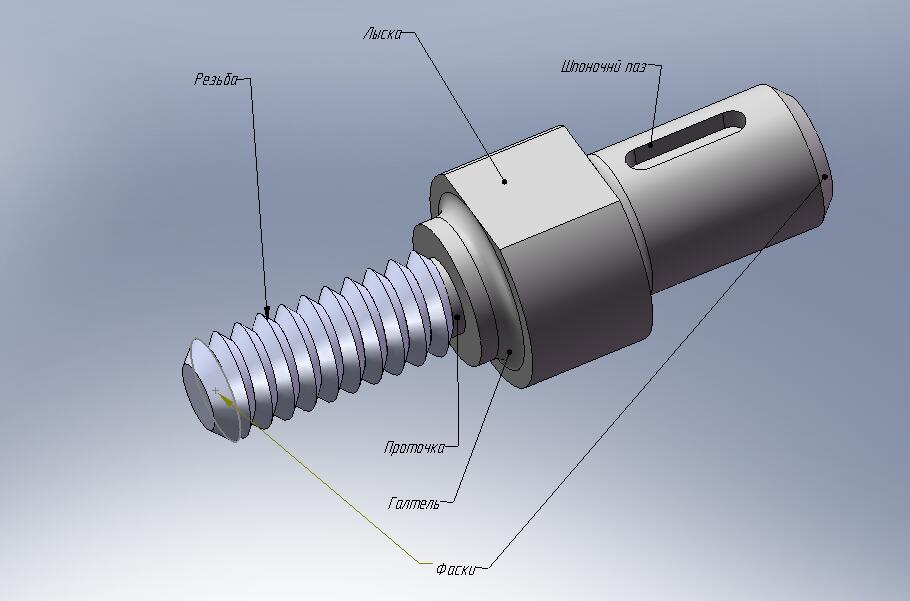
Рис.2.1
1. Объем фаски (1) –
усеченный конус (рис. 2.2)
,
где h
= 2 мм; r
= d/2=6
мм; r1
= r
– 2 = 4 мм.
Тогда
.
-
Объем цилиндра
(2)
.

Рис. 2.2
3. Объем паза (3) с
поперечным сечением S
(рис. 2.3, а)
и длиной 10 мм для призматической части
паза
а б
Рис. 2.3
,
где S
= Sсег.
+
Sпр,
Sсег.
– площадь сегмента с радиусом R,
Sпр
– площадь прямоугольника b
ĥ
h,
б.
Sсег.
=
Sсек.
– Sтр.
Sсек.
– площадь
сектора круга, Sтр
– площадь треугольника – рис. 2.3
Sсег.
=
Sсек.
– Sтр=

здесь
Sпр
= b
ĥ
h
= 5∙10 = 50 мм2,
S
= Sсег.
+
Sпр
= 16,16 + 50 =66,16 мм2
.
Учтем объем цилиндра
от боковых полуцилиндров паза. Примем
r
=b/2
= 2,5 мм
– радиус цилиндра,
h/
= h
+ 0,5(R
–
)
= 3 + 0,5(6 –
‑ высота
цилиндра равная
глубине паза и верхнюю часть цилиндра
паза.
Тогда объем
цилиндрической части шпоночного паза,
получим:
Vц
≈
πr2h/=π6,25∙3,27
= 64,2 мм3
Окончательно объем
шпоночного паза будет
V3
= Vпр
+ Vц
= 661,6+64,2 = 725,8 мм3
4. Объем галтели 4
с радиусом r
= 1 мм
(рис. 2.4).
Площадь галтели
определится как разность площадей
квадрата Sк
= r2
и четверти
круга (сектора) Sc
= r2/4
(рис. 2.4)
Sг
= r2
– r2/4
= r2(4-
)/4=
12(4-π)/4
= 0,22 мм2
Р
ис.
2.4
Центр тяжести
вдоль оси Х
квадрата xК
=
,
а четверти круга – сектора круга с углом
90º
,
Центр тяжести
галтели вдоль оси X:
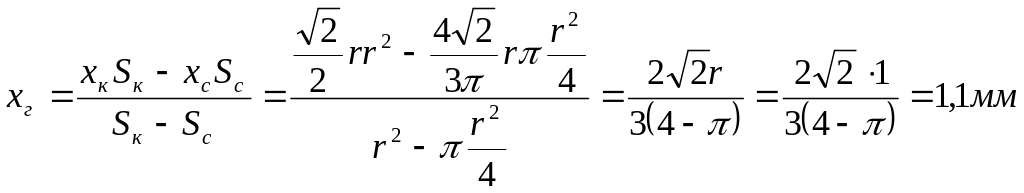
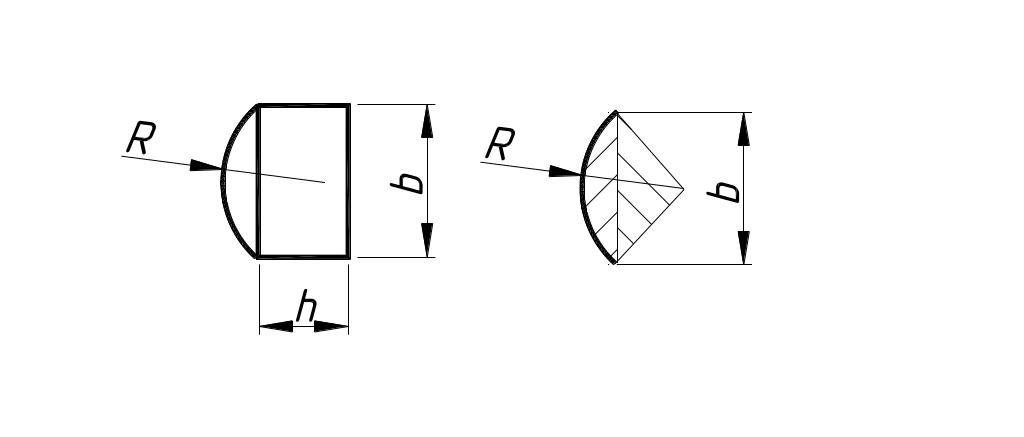
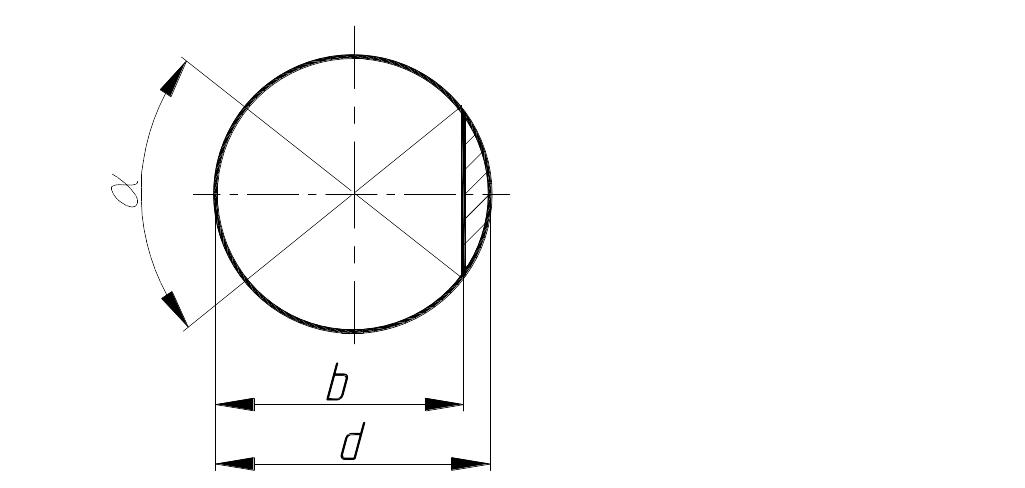
5. Объем лыски (рис.
2.5) 5:
V5
= Sсег.h
Площадь сегмента
Sсег.
определится
как разность площади сектора с углом α
и площади треугольника
Sсег.=
Sсек.
– Sтр=
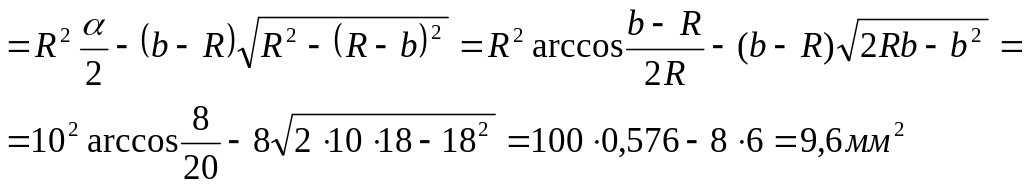
Находим численное
значение объема лыски
V5
= Sсег.h
= 9,6∙15 = 144
мм3
Рис. 2.5
6. Объем цилиндра
(6)
.
7. Объем цилиндра
(7,8)
,
где р=
1,5 мм
– шаг резьбы.
8. Объем резьбы
V9
= SLn,
где S=p2tg60o/4,
L
= 2πr
– длина
витка резьбы, n
= l/p
– количество витков, l
‑ длина резьбы.
Тогда
V9
= 2πr
p2tg60o
l/4p
= πr
ptg60o
l/2
= π5∙1,5∙1,732∙12/2
= 245 мм3
9. Фаска 10:
.
Окончательно,
складываем все объемы, вычитая объем
лыски и шпоночного паза, получим
V1 + V2
– V3 +V4
– V5 + V6
+ V7,8 + V9
+ V10
= 160 + 2035,75 – 725,8 + 16,76 -144 + 4712,4 + 3329 + 245 + 63,87
= 9693,8 мм3.
Массу тела получим,
используя ранее приведенную формулу m
= V.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Калькулятор массы
Для различных изделий сложной формы и профиля, с наличием прорезей и отверстий очень трудно рассчитать вес, а это очень важный момент – для транспортировки, для расчета монтажных параметров, для конструкторской документации и других целей. Процесс взвешивания также представляет собой сложности, особенно, когда изделия крупногабаритные – например, трубы, валы, турбины, металлические или деревянные конструкции, изделия из бетона и железобетона и т.д., или же вес небольшой детали, но сложной конфигурации.
Но, узнать точную массу таких изделий можно гораздо проще на нашем сайте
Мы предлагаем Вашему вниманию универсальный интерактивный калькулятор массы для самостоятельного расчета массы изделий самой разной формы из материалов цилиндрической или листовой формы. Его особенность в том, что он позволяет узнать вес детали или изделия не только из металлопроката и сплавов, но и любых других материалов: дерева и МДФ, пластиков и полимеров, бумаги, картона, резины, бетона, кирпича. Сделать это можно просто внеся габаритные показатели детали с вычетом размеров отверстий и прорезей, а также, величину коэффициента плотности материала, из которого деталь изготовлена. Точные данные можно найти в представленной рядом таблице.
Масса цилиндрической детали рассчитывается следующим образом:
• В соответствующие поля калькулятора массы внести размерные показатели: диаметр, длину и справочную плотность материала – калькулятор рассчитает общую массу изделия.
• Второй шаг – если на изделии есть выступы, ступени – надо добавить их габариты.
• И третий шаг – вычесть размеры отверстий, выемок, прорезей.
• Результат – точная расчетная масса цилиндрической детали.
Масса детали из листа рассчитывается следующим образом:
• В соответствующие поля калькулятора массы внести размерные показатели: ширину, длину, толщину и справочную плотность материала – калькулятор рассчитает общую массу изделия.
• Второй шаг – если на изделии есть выступы – надо добавить их габариты.
• И третий шаг – вычесть размеры прямоугольных или круглых отверстий.
• Результат – точная расчетная масса детали из листа.
Наш калькулятор массы изделий будет полезен как конструктору, так и для заказчиков, ведь он позволяет очень быстро и почти со 100%-точностью получить необходимые данные относительно веса изделия без сложных математических расчетов и процедуры взвешивания.
Обратите внимание, что по умолчанию в калькуляторе стоит масса марки стали 40 ГОСТ 1050-88.
| Плотность материалов | |
| Наименование | Плотность ρ, кг/м3 |
| Черные металлы | |
| Сталь 10 ГОСТ 1050-88 | 7856 |
| Сталь 20 ГОСТ 1050-88 | 7859 |
| Сталь 40 ГОСТ 1050-88 | 7850 |
| Сталь 60 ГОСТ 1050-88 | 7800 |
| С235-С375 ГОСТ 27772-88 | 7850 |
| Ст3пс ГОСТ 380-2005 | 7850 |
| Чугун ковкий КЧ 70-2 ГОСТ 1215-79 | 7000 |
| Чугун высокопрочный ВЧ35 ГОСТ 7293-85 | 7200 |
| Чугун серый СЧ10 ГОСТ 1412-85 | 6800 |
| Чугун серый СЧ20 ГОСТ 1412-85 | 7100 |
| Чугун серый СЧ30 ГОСТ 1412-85 | 7300 |
| Алюминий и сплавы алюминиевые | |
| Силумин АК12ж ГОСТ 1583-93 | 2700 |
| Сплав АК12 ГОСТ 1583-93 | 2710 |
| Сплав АК5М ГОСТ 1583-93 | 2640 |
| Сплав АК7 ГОСТ 1583-93 | 2700 |
| Сплав АО9-1 ГОСТ 14113-78 | 2700 |
| Магний и сплавы магниевые | |
| Сплав ВМЛ9 | 1850 |
| Сплав ВМЛ5 | 1890 |
| Сплав МЛ10…МЛ19 ГОСТ 2856-79 | 1810 |
| Баббиты оловянные и свинцовые | |
| Б83 ГОСТ 1320-74 | 7380 |
| Б87 ГОСТ 1320-74 | 7300 |
| БН ГОСТ 1320-74 | 9550 |
| Медь и медные сплавы | |
| Бронза оловянная БрО10C10 | 8800 |
| Бронза оловянная БрО19 | 8600 |
| Бронза оловянная БрОC10-10 | 9100 |
| Бронза оловянная БрОA10-1 | 8750 |
| Бронза БрА10Ж3Мч2 ГОСТ 493-79 | 8200 |
| Бронза БрА9Ж3Л ГОСТ 493-79 | 8200 |
| Бронза БрМц5 ГОСТ 18175-78 | 8600 |
| Латунь Л60 ГОСТ 15527-2004 | 8800 |
| Латунь ЛА ГОСТ 1020-97 | 8500 |
| Медь М0, М1, М2, М3 ГОСТ 859-2001 | 8940 |
| Медь МСр1 ГОСТ 16130-90 | 8900 |
| Титан и титановые сплавы | |
| ВТ1-0 ГОСТ 19807-91 | 4500 |
| ВТ14 ГОСТ 19807-91 | 4500 |
| ВТ20Л ГОСТ 19807-91 | 4470 |
| Фторопласты | |
| Ф-4 ГОСТ 10007-80 Е | 2100 |
| Фторопласт – 1 ГОСТ 13744-87 | 1400 |
| Фторопласт – 2 ГОСТ 13744-87 | 1700 |
| Фторопласт – 3 ГОСТ 13744-87 | 2710 |
| Фторопласт – 4Д ГОСТ 14906-77 | 2150 |
| Термопласты | |
| Дакрил-2М ТУ 2216-265-057 57 593-2000 | 1190 |
| Полиметилметакрилат ЛПТ ТУ 6-05-952-74 | 1180 |
| Полиметилметакрилат суспензионный ЛСОМ ОСТ 6-01-67-72 | 1190 |
| Винипласт УВ-10 ТУ 6-01-737-72 | 1450 |
| Поливинилхлоридный пластикат ГОСТ 5960-72 | 1400 |
| Полиамид ПА6 блочный Б ТУ 6-05-988-87 | 1150 |
| Полиамид ПА66 литьевой ОСТ 6-06-369-74 | 1140 |
| Капролон В ТУ 6-05-988 | 1150 |
| Капролон ТУ 6-06-309-70 | 1130 |
| Поликарбонат | 1200 |
| Полипропилен ГОСТ 26996-86 | 900 |
| Полиэтилен СД | 960 |
| Лавсан литьевой ТУ 6-05-830-76 | 1320 |
| Лавсан ЛС-1 ТУ 6-05-830-76 | 1530 |
| Стиролпласт АБС 0809Т ТУ 2214-019-002 03521-96 | 1050 |
| Полистирол блочный ГОСТ 20282-86 | 1050 |
| Сополимер стирола МСН ГОСТ 12271-76 | 1060 |
| Полистирол ударопрочный УПС-0505 ГОСТ 28250-89 | 1060 |
| Стеклопластик ВПС-8 | 1900 |
| Стеклотекстолит конструкционный КАСТ-В ГОСТ 10292-74 | 1850 |
| Винилискожа-НТ ГОСТ 10438-78 | 1440 |
| Резина 6Ж ТУ 38-005-1166-98 | 1050 |
| Резина ВР-10 ТР 18-962 | 1800 |
| Стекло листовое ГОСТ 111-2001 | 2500 |
| Стекло органическое техническое ТОСН ГОСТ 17622-72 | 1180 |
| Прочие металлы | |
| Вольфрам ВА ГОСТ 18903-73 | 19300 |
| Вольфрам ВТ-7 ГОСТ 18903-73 | 19300 |
| Золото Зл 99,9 ГОСТ 6835-2002 | 19300 |
| Индий ИНО ГОСТ 10297-94 | 7300 |
| Кадмий КдО ГОСТ 1467-93 | 8640 |
| Олово О1пч ГОСТ 860-75 | 7300 |
| Паладий Пд 99,8 ГОСТ 13462-79 | 12160 |
| Платина Пд 99,8 ГОСТ 13498-79 | 21450 |
| Свинец С0 ГОСТ 3778-98 | 11400 |
| Серебро 99,9 ГОСТ 6836-2002 | 11500 |
| Цинк Ц1 ГОСТ 3640-94 | 7130 |
| Прочие материалы | |
| Древесина, пробка | 480 |
| Древесина, лиственница | 660 |
| Древесина, липа | 530 |
| Древесина, ель | 450 |
| Древесина, сосна | 520 |
| Древесина, береза | 650 |
| Древесина, бук | 690 |
| Бумага | 700-1200 |
| Резина | 900-2000 |
| Кирпич | 1400-2100 |
| Фарфор | 2300 |
| Бетон | 2000-2200 |
| Цемент | 2800-3000 |
Припуски на механическую обработку
Припуски на механическую обработку наносят на чертеж там, где стоят знаки механической обработки ().
Припуски назначаются на посадочные внутренние цилиндрические поверхности, а также на торцевые поверхности. На чертеже 2.2 припуски указаны сплошными тонкими линиями.
Величина припусков зависит от габаритных размеров обрабатываемой поверхности, и от положения ее при заливке. Величину припуска на отверстия определяем по таблице 4. Припуски на нижние и боковые поверхности — 1 мм, на верхние — 1,5 мм. Припуски на верхние поверхности увеличены из-за неметаллических включений, пузырьков газа, всплывающих на поверхность жидкого металла.
Правильное определение величины припусков (zi) очень важно, так как от этого зависят многие технико-экономические показатели технологического процесса (расход металла, точность и качество обработанных поверхностей, время обработки, расходы на режущий инструмент, электроэнергию, амортизацию станка и др.).
В современной технологии машиностроения, особенно при значительном объеме выпуска деталей, необходимо, чтобы припуск на каждых технологический переход был минимальным, но достаточным для осуществления предполагаемой обработки.
В практике технологов-машиностроителей используют два метода выполнения работы по установлению величины операционных припусков: табличный и расчетно-аналитический, причем каждый из них находит применение в определенных производственных условиях. В данной работе использован табличный метод определения припусков на обработку.
Рассчитаем припуск на внутреннее отверстие диаметром (0,017).
Источник: vuzlit.ru
Калькулятор массы
Для различных изделий сложной формы и профиля, с наличием прорезей и отверстий очень трудно рассчитать вес, а это очень важный момент – для транспортировки, для расчета монтажных параметров, для конструкторской документации и других целей. Процесс взвешивания также представляет собой сложности, особенно, когда изделия крупногабаритные – например, трубы, валы, турбины, металлические или деревянные конструкции, изделия из бетона и железобетона и т.д., или же вес небольшой детали, но сложной конфигурации.
Но, узнать точную массу таких изделий можно гораздо проще на нашем сайте
Мы предлагаем Вашему вниманию универсальный интерактивный калькулятор массы для самостоятельного расчета массы изделий самой разной формы из материалов цилиндрической или листовой формы. Его особенность в том, что он позволяет узнать вес детали или изделия не только из металлопроката и сплавов, но и любых других материалов: дерева и МДФ, пластиков и полимеров, бумаги, картона, резины, бетона, кирпича. Сделать это можно просто внеся габаритные показатели детали с вычетом размеров отверстий и прорезей, а также, величину коэффициента плотности материала, из которого деталь изготовлена. Точные данные можно найти в представленной рядом таблице.
| Диаметр | Длина | Плотность |
| мм | мм | кг/мм 3 |
| Масса общая | ||
| кг |
| Длина | Ширина | Толщина | Плотность |
| мм | мм | мм | кг/мм 3 |
| Масса общая | |||
| кг |
| Длина | Ширина | Количество |
| мм | мм | шт |
Масса цилиндрической детали рассчитывается следующим образом:
• В соответствующие поля калькулятора массы внести размерные показатели: диаметр, длину и справочную плотность материала – калькулятор рассчитает общую массу изделия. • Второй шаг – если на изделии есть выступы, ступени – надо добавить их габариты. • И третий шаг – вычесть размеры отверстий, выемок, прорезей. • Результат – точная расчетная масса цилиндрической детали.
Масса детали из листа рассчитывается следующим образом:
• В соответствующие поля калькулятора массы внести размерные показатели: ширину, длину, толщину и справочную плотность материала – калькулятор рассчитает общую массу изделия. • Второй шаг – если на изделии есть выступы – надо добавить их габариты. • И третий шаг – вычесть размеры прямоугольных или круглых отверстий. • Результат – точная расчетная масса детали из листа.
Наш калькулятор массы изделий будет полезен как конструктору, так и для заказчиков, ведь он позволяет очень быстро и почти со 100%-точностью получить необходимые данные относительно веса изделия без сложных математических расчетов и процедуры взвешивания.
Обратите внимание, что по умолчанию в калькуляторе стоит масса марки стали 40 ГОСТ 1050-88.
Источник: azmen.a-idea.ru
Масса сплошной детали
Главная > Вычисление масс > Масса сплошной детали
9.05.2013 // Владимир Трунов
Это странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей): Объем сплошной детали — это… ее объем и больше ничего.
Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр. Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота. Тогда масса:
Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра. Тогда масса:
Масса шара
Объем шара: , где — диаметр шара. Тогда масса:
Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента. Тогда масса:
Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса. Для круглого конуса: , где — диаметр основания, — высота конуса. Масса круглого конуса:
Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем: , где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса. Отсюда масса:
Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды. Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды. Тогда масса пирамиды:
Масса усеченной пирамиды
Рассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , . Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды. И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: . Тогда масса усеченной прямоугольной пирамиды:
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
вычисление массы
-
Масса кольца, звена
-
Масса полой детали
-
Масса проволоки, прутка, проката
Похожие записи
Считаем вес листового проката
Определение! Во всех наших расчётах базовой величиной является усреднённая плотность стали – 7 850 кг/м3 по системе СИ.
Проведём для начала несложное действие – узнаем массу квадратного метра стального листа толщиной 1 мм. Выглядит это так – 1 м х 1 м х 0,001 м х 7850 кг/м3. То есть, мы перемножили длину, ширину и толщину листа (все величины взяли в метрах), и получили объём изделия. Произведение объёма и плотности даёт массу – 7,85 кг. Таким образом, мы выяснили, что метр квадратный стального листа толщиной 1 мм весит 7,85 кг.
А далее все вычисления производят умножением величины 7,85 кг на площадь и толщину реального листа. Например, вам надо купить лист толщиной 4 мм и площадью 2 м2. Массу такого изделия определяют по формуле 7,85х4х2= 62,8 кг. Лист такого же размера, но толщиной 2 мм весит 7,85х2х2=31,4 кг.
Если вас устраивает приблизительный расчёт – округлите значение 7,85 кг до 8 кг. Тогда вычисления можно проводить даже в уме без калькулятора, а погрешность составит менее 2%.
Приведём веса стальных листов наиболее популярных размеров.
| Толщина листа, мм | Размеры листа, м | Вес листа, кг | Вес 1 м 2 , кг |
| 0,35 | 1,0х2,0 | 5,5 | 2,75 |
| 0,35 | 1,25х2,5 | 8,59 | |
| 0,5 | 1,0х2,0 | 7,85 | 3,93 |
| 0,5 | 1,25х2,5 | 12,27 | |
| 0,8 | 1,0х2,0 | 12,56 | 6,28 |
| 0,8 | 1,25х2,5 | 19,63 | |
| 1,0 | 1,0х2,0 | 15,7 | 7,85 |
| 1,0 | 1,25х2,5 | 24,53 | |
| 1,5 | 1,0х2,0 | 23,55 | 11,78 |
| 1,5 | 1,25х2,5 | 36,8 | |
| 2,0 | 1,0х2,0 | 31,4 | 15,7 |
| 2,0 | 1,25х2,5 | 49,06 | |
| 2,5 | 1,0х2,0 | 39,25 | 19,63 |
| 2,5 | 1,25х2,5 | 61,33 | |
| 3,0 | 1,0х2,0 | 47,1 | 23,55 |
| 3,0 | 1,25х2,5 | 73,59 | |
| 3,5 | 1,25х2,5 | 85,86 | 27,48 |
| 4,0 | 1,5х6,0 | 282,6 | 31,4 |
| 5,0 | 1,5х6,0 | 353,25 | 39,25 |
Расчет веса по математическим формулам
Вес любого изделия находится так: M = ρV (ρ – плотность, V – объем изделия) или по формуле массы через площадь сечения: M = ρSL (S — площадь сечения, L — длина). Для углеродистой стали принято использовать усредненное значение ρ, равное 7850 кг/м3 или 0,00785 г/мм3, либо 7,85 г/см3 (в зависимости от выбранных единиц измерений). Самое простое вычисление – это масса стального куба со стороной 1 м. Она равна 7850 кг, или 7,85 т.
Различают практические и теоретические формулы массы. Первые адаптированы к определенным условиям, чтобы облегчить и ускорить расчеты.
Листовой прокат
Для расчета веса листового металла нужно перемножить 3 измерения – длину, ширину и толщину изделия, полученный результат умножить на плотность металла. Например: длина проката 1 м, ширина – 2 м, толщина – 2мм, тогда M = 1×2×0,002×7850 = 31,4 (кг).
При определении массы нескольких одинаковых листов железа, достаточно рассчитать вес 1 листа и умножить на количество.
Пруток, проволока и арматура
Для определения массы прутка или любого изделия круглого сечения, используется такая теоретическая формула: M= πR2Lρ, где L – длина, R – радиус заготовки, π = 3,14, ρ – плотность металла. Другая, практическая, формула: M = (0,02466R2)L. Ее можно использовать и для рифленой арматуры.
Из объема найти массу прямоугольного прутка совсем просто. Нужно перемножить длину, ширину и толщину (это объём V), затем найти в справочнике соответствующую плотность и умножить ее на V: M = ABLρ, где A, B – ширина и толщина.
Круг
Чтобы найти вес металлического круга, нужно подставить числовые значения в формулу: M = πR2dρ (R– радиус, d – толщина).
Шестигранный пруток
Лучше всего обратиться за помощью к готовым таблицам, но в их отсутствии расчеты можно произвести самостоятельно:
M = (3√3/2)а2Lρ,
где а – длина стороны шестигранника (мм), L – длина прутка (мм), ρ = 0,00785 г/мм3.
Прямоугольный профиль
Узнать массу прямоугольной профильной трубы можно так:
M = 2(a+b)sLρ,
где a и b – ширина и высота сечения (мм), s – толщина стенки (мм), L – длина трубы (мм), ρ = 0,00785 г/мм3 . Если стенки разной толщины, проводится несколько измерений и находится среднее значение.
Масса круглой трубы
Рассчитывают вес трубы по следующим формулам:
M = π(R2 – r2)Lρ, M = 2πRsLρ, M = (D-s)s×0,2466
где М – масса, R2 – внешний радиус, r2 – внутренний радиус, L – длина трубы, ρ. – плотность стали, s – толщина стенки, 0,2466 – константа, соответствующая плотности углеродистой стали ρ = 7,85 г/см3.
Трубу с закрытым концом можно рассматривать как бочку и применить для нахождения ее веса представленные выше формулы для трубы и круга.
Вес фигурных изделий
Посчитать массу, зная объем и плотность, можно для изделий любой конфигурации. Нужно только правильно вычислить объем и подставить значение в известную формулу M = Vρ.
Объем пирамиды рассчитывается по формуле: V = 1/3 SH, где S – площадь основания, H – высота пирамиды.
Для усеченной пирамиды V = 1/3 h(F + f + √Ff), где F и f – площади большего и меньшего основания.
Объем цилиндра: V = πR2H.
Объем конуса: V = 1/3 πR2H, объем усеченного конуса: V = 1/3 πH(R2 + Rr + r2), где H – высота, R и r – радиусы большего и меньшего основания.
Объем шара: V = πD3/6 (D – диаметр).
Для уголка: V = s(h1 + h2)L, где L – длина уголка, s – толщина металла, h1 и h2 – ширина полок.
Объем изделия витиеватой формы и небольших габаритов находят по количеству вытесненной жидкости, поместив его в емкость с водой.
Если конструкция изготовлена из разных металлов и сплавов, тогда можно найти ее массу через вес отдельных деталей.
Теоретический вес рассчитывается по формулам, практический (фактический) определяется взвешиванием. Естественно, что всегда между этими величинами будет несоответствие. Расчет массы заготовки, произведенный самостоятельно по математическим формулам, также может отличаться от табличных или же выданных калькулятором.
Для получения более точных результатов целесообразно пользоваться данными справочников или электронных вычислительных устройств.
Что такое переводной коэффициент
Усложним задачу. Предположим, вам надо купить лист из цветного металла. Воспользуемся переводным коэффициентом, который представляет собой отношение плотности конкретного металла или сплава к усреднённому значению плотности стали. Путём умножения веса стального изделия определённого сортамента и размера на коэффициент нужного металла или сплава получаем вес детали.
| Наименование металла или сплава | Коэффициент |
| Алюминий | 0,34 |
| Медь | 1,14 |
| Латунь ЛС59 | 1,08 |
| Бронза ОЦС 5-5-5 | 1,12 |
| Чугун серый | 0,9 |
Пример – рассчитаем массу бронзового листа толщиной 2 мм и площадью 2 м2.
7,85х2х2х1,12 = 35,2 кг
Внимание! Этот же простой алгоритм можно применять и для неметаллических листовых материалов, для которых также существуют переводные коэффициенты. Например, для резины – 0,17-0,23, органического стекла – 0,15, капролона – 0,15, текстолита – 0,18, резины – 0,17-0,23.
Как узнать массу трубы
Для определения массы труб оптимально воспользоваться таблицами.
| Условный проход, дюйм/мм | Толщина стенки, мм | Вес, кг | Условный проход, дюйм/мм | Толщина стенки, мм | Вес, кг |
| 1/4 (8) | 2,35 | 0,65 | 1 1/4 (32) | 3,25 | 3,14 |
| 1/2 (15) | 2,65 | 1,22 | 1 1/2 (40) | 3,25 | 3,61 |
| 3/4 (20) | 2,65 | 1,58 | 2 (50) | 3,65 | 5,1 |
| 1 (25) | 3,25 | 2,44 | 2 1/2 (65) | 3,65 | 6,51 |
Если же доступа к справочным материалам нет, а несложные геометрические формулы не являются для вас препятствием, вычислите вес самостоятельно. Для этого находим разницу площади круга по внешнему радиусу и площади по внутреннему радиусу. Полученную разность умножаем на длину трубы и плотность стали – 7 850 кг/м3.
Для труб из цветных металлов применяют переводные коэффициенты, о которых мы говорили выше.
Теоретическая выкладка
Ещё в Древней Греции учёные знали формулу определения объема вещей в зависимости от массы и плотности. Так Архимед открыл закон, названный его именем. Почему же ведро с водой поднять заметно легче, чем с песком? Всё объясняется различной плотностью веществ. В единице объёма песка больше вещества, чем в воде, значит, он плотнее жидкой субстанции.
Структура практически всех окружающих субстанций неравномерна, а значит, и концентрация массы в единице веществ отличается, но незначительно. В задачах этой разницей пренебрегают.
Плотностью называется величина, получаемая вследствие разделения массы объекта на занимаемое им пространство. В физике имеет вид:
ρ = m/V, ρ – читается как «ро».
В системе СИ измеряется в кг/м³, на практике применяются кратные и дольные единицы измерения, например, см/кг3.
В физике существует несколько трактовок или типов плотностей:
- объёмная – рассматриваемая величина;
- поверхностная – отношение веса к площади;
- линейная – указывает на обратную пропорциональность массы к длине, применяется в двухмерных вычислениях;
- плотность электрического заряда.
Относительно к газам формула видоизменяется:
ρ = M / Vm, здесь, M и Vm – молярные масса с объёмом соответственно.
Как рассчитать массу равнополочного уголка, швеллера, двутавра
Масса метра погонного углового металлопроката зависит от ширины и толщины полок.
Внимание! Рассчитанный по геометрической формуле или определённый по таблице вес уголка может сильно отличаться от фактического. Это связано с тем, что некоторые производители в целях удешевления продукции снижают толщину полки уголка в местах, где не предусматриваются проверочные замеры. Такая разница может значительно превышать допуски, предусмотренные ГОСТом.
Вес погонного метра наиболее распространённого сортамента равнополочного уголка
| Ширина полки, мм | Толщина полки, мм | Вес 1 м уголка, кг | Ширина полки, мм | Толщина полки, мм | Вес 1 м уголка, кг |
| 20 | 3 | 0,89 | 40 | 3 | 1,85 |
| 20 | 4 | 1,15 | 40 | 4 | 2,42 |
| 25 | 3 | 1,12 | 45 | 3 | 2,08 |
| 25 | 4 | 1,46 | 45 | 4 | 2,73 |
| 32 | 3 | 1,46 | 50 | 3 | 2,32 |
| 32 | 4 | 1,91 | 50 | 4 | 3,05 |
| 36 | 3 | 1,65 | 63 | 4 | 3,9 |
| 36 | 4 | 2,16 | 63 | 5 | 4,81 |
Самостоятельно просчитать массу швеллера и двутавра затруднительно из-за сложной формы сечения. В данном случае пользуются таблицами.
Таблица весов швеллера
| Номер профиля | Вес 1 м, кг | Номер профиля | Вес 1 м, кг | Номер профиля | Вес 1 м, кг |
| 5 | 4,84 | 12 | 10,4 | 20 | 18,4 |
| 6,5 | 5,9 | 14 | 12,3 | 22 | 21,0 |
| 8 | 7,05 | 16 | 14,2 | 24 | 24 ,0 |
| 10 | 8,59 | 18 | 16,3 | 27 | 27,7 |
Таблица весов двутавра
| Номер профиля | Вес 1 м, кг | Номер профиля | Вес 1 м, кг | Номер профиля | Вес 1 м, кг |
| 10 | 9,46 | 18 | 18,4 | 27 | 31,5 |
| 12 | 11,5 | 20 | 21,0 | 30 | 36,5 |
| 14 | 13,7 | 22 | 24,0 | 33 | 42,2 |
| 16 | 15,9 | 24 | 27,3 | 36 | 48,6 |
Определение расчетной массы состава
Масса состава один из важнейших показателей, влияющих на
эффективность работы железной дороги. Масса состава определяет
провозную способность линий, себестоимость и экономичность перевозок, а
также удельный расход топлива или электроэнергии (для ЭПС) на тягу поездов.
Масса состава определяется для каждого участка пути или перегона из
условия наиболее полного использования мощности локомотива и движения
со скоростью обеспечивающей длительный режим работы.
Масса состава определяется по расчетному подъему по формуле, т:
Q= = ≈ 5000т (2.2) где
Fкр – расчетная сила тяги данного локомотива, Н. ;
Р – расчетная масса , т;
– основное удельное сопротивление движению локомотива в режиме тяги, Н/кН;
– основное удельное сопротивление движению состава (груженых вагонов), Н/кН;
– крутизна расчетного подъема, ‰;
g – ускорение свободного падения (g= 9,81 м/с2).
Величины рассчитываются с точностью до двух знаков после запятой.
=1.9+0.348+0.47=2.7
=0.7+
=1.3
=0.7+
=1.3
Основное удельное сопротивление движению состава определяется по
формуле:
= 1.3*0.1+1.3*0.9 = 1.3 (2.3) где
и – основное удельное сопротивление движению вагонов соответственно 4-осных и 8-осных, Н/кН;
и – весовые доли в составе соответствующих вагонов (задаются в процентах в задании к курсовой работе, которые надо перевести в доли).
Осевая нагрузка вагонов рассчитывается по формуле:
(2.4) где
– средняя масса брутто соответствующих вагонов (см. бланк задания), т;
– осность соответствующих типов вагонов.
=17,5
=17,5
Подставляя полученные значения сопротивления движению вагонов в выражение (2.3), найдем основное удельное сопротивление движению состава.
После этого по формуле (2.2) определяется масса расчетная состава.
Полученное значение округляем кратно 50 т в большую или меньшую сторону.
Проверка расчетной массы.
Проверка расчетной массы на преодоление кинетического
Подъема.
После определения массы состава при следовании по расчетному подъему с равномерной скоростью ее проверяют на возможность прохождения более крутого кинетического (скоростного или инерционного) iк подъема с учетом использования кинетической энергии при движении с замедляющейся скоростью аналитическим способом.
Аналитический способ проверки заключается в том, что определяют длину пути, который поезд должен преодолеть в режиме тяги с использованием кинетической энергии при снижении скорости от наибольшей в начале скоростного подъема Vн до расчетной в конце его (Vн = Vр) и сравнивают её с длиной этого подъема ( Sк ).
Для повышения точности расчета интервал изменения скорости следует брать равным 10 км/ч.
Путь, проходимый поездом за время изменения скорости от Vн до Vк определяют по формуле:
,
где где 4,17 – коэффициент, учитывающий ускорение поезда, км/ч2; Vкj,V н.j – скорость поезда в конце и начале задаваемого интервала скорости на проверяемом кинетическом подъеме, км/ч; средняя удельная равнодействующая сила, приложенная к поезду в пределах выбранного интервала скорости, Н/кН.
Скорость в начале кинетического подъема определяется известными в тяговых расчетах методами в зависимости от крутизны элементов, расположенных перед этим подъемом и в курсовой работе скорость в начале кинетического подъема принимается исходя из анализа профиля пути в пределах 60…80 км/ч.
Удельная сила тяги определяется выражением:
(2.6)
где Fk – сила тяги, определяемая по тяговым характеристикам локомотивов для средней скорости интервала Vсрj, Н.
Средняя скорость для выбранного интервала движения определяется по формуле:
(2.7)
Удельная замедляющая сила скоростей находится по формуле:
, (2.8)
где , – основные удельные сопротивлению движению локомотива и состава, определяемые для средней скорости интервалов по формулам, приведенным выше, Н/кН; iк – кинетический подъем, ‰.
Отрезки пути, полученные за время снижения скорости в каждом интервале, суммируют и сравнивают с длиной кинетического подъема, т.е.:
(2.9)
1050м ≤ 1895м
Если условие (2.9) выполняется , то можно сделать вывод:
«Поезд с локомотивом серии ВЛ 80Р и массой состава Q = 5000 т преодолевает кинетический подъем крутизной iк = -10 ‰ и длиной Sk = 1050 км при изменении скорости от vн = 80 до vк = 70 км/ч и массу состава следует считать определившейся для данного участка работы локомотивов».
Калькуляторы расчёта веса металла
Если у вас есть доступ к интернету – расчёты массы металлопроката не составляют никакого труда. Калькулятором металла можно пользоваться в режиме он-лайн или скачать его на компьютер.
Как выполняется расчёт:
- В списке выбирают тип металлопроката.
- Заполняют данные в размерности, указанной в программе.
- Нажимают кнопку расчёта.
- В калькуляторах также обычно указывают массу погонного метра конкретного сортамента и количество метров в тонне.
Внимание! Все данные, предоставляемые металлокалькуляторами, основаны на ГОСТ. При отсутствии табличных величин масса рассчитывается по геометрическим формулам с поправкой на особенности изготовления данных изделий. При стандартных подсчётах плотность стали принимается равной 7 850 кг/м3.
Реальная масса металлопроката практически всегда отличается от теоретической.
Чем усложняется расчёт веса металла?
Серьёзным различием в полученных данных по расчёту массы стального изделия является технология его производства. Разница между холоднокатаным прокатом металла и горячекатаным может быть достаточно существенная. Речь идет о точности геометрических характеристик при сохранении плотности по всей протяжённости изделия.
Применение непрерывного нагрева и последующего охлаждения приводит к таким негативным явлениям как окисление, рекристаллизация. Неравномерность этих процессов вызывает изменение такого параметра как толщина.
Вес металла
Точность расчетов холоднокатаных и горячекатаных металлических профилей будет отличаться. Погрешность, вызванная нестабильностью толщины, требует получения некоторого усредненного значения.
Как пользоваться справочниками
Удобным справочным материалом является сборник авторов Поливанова П.М. и Поливановой Е.П. «Таблицы для подсчёта массы деталей и материалов». В справочнике представлены таблицы, позволяющие легко и быстро определить массу проката круглого, прямоугольного, шестиугольного сечений, листа и полосы, равнополочной и неравнополочной угловой стали, двутавра, швеллера, круглых и профильных труб.
В сборнике даны формулы, по которым можно рассчитать площади и объёмы геометрических фигур. Подробная таблица переводных коэффициентов позволяет точно подсчитать массу цветного металла или его сплава.
Приближёнными методиками расчётов можно воспользоваться только для предварительного определения массы материалов, изделий и конструкций. Для составления проектной документации применяют только точные данные, полностью соответствующие ГОСТ.
Источник: www.navigator-beton.ru
Как найти массу детали (вес) ? по формуле, точно ее не помню
Руслан Подгаецкий
Мастер
(1241),
закрыт
9 лет назад
Лучший ответ
Andrey Ermilov
Мудрец
(17624)
9 лет назад
надо энать объем и плотность материала
Руслан ПодгаецкийМастер (1241)
9 лет назад
знаю. дальше что?
Умножить плотность на объём
Остальные ответы
Алексей Скипетров
Ученик
(234)
9 лет назад
плотность умноженная на обьем -масса тела а вес масса умноженная на ускорение свободного подения.
1.p*V
2m*q
Похожие вопросы