Ефросиныч
28 января, 23:54
-

Коняша
29 января, 00:42
0
Попробуй составить пропорцию:
5 кг – 0,3 м
хкг – 0,5 м
Но я не уверенна
- Комментировать
- Жалоба
- Ссылка
-

Анджела
29 января, 01:49
0
М=F*L
1) М=mg*L
M=50*30=1500
2) 1500 = 500*m
m = 3
Ответ: 3 кг
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Какова масса второго груза на рычаге если первый 5 кг. первое плечо 30 см второе 50 см. …» по предмету 📙 Физика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » Физика » Какова масса второго груза на рычаге если первый 5 кг. первое плечо 30 см второе 50 см.
Пружинный маятник .
Пружинный маятник представляет из себя груз на пружине.
(T=2 pi sqrt{dfrac{m}{k}} )
(k) – жесткость пружины маятника
(m) – масса груза
Задача 1.
Вычислить период (T) пружинного маятника, если жесткость его пружины (k=8 Н/м ), а масса его груза
(m=0,5 кг ) ,
(pi=3,14 )
Показать ответ
Показать решение
Видеорешение
Задача 2.
Вычислить период (T) пружинного маятника, если жесткость его пружины (k=81 Н/м ), а масса его груза
(m=1 кг ) ,
(pi=3,14 )
Ответ округлить до десятых
Показать ответ
Показать решение
Видеорешение
Задача 3.
Вычислить период (T) пружинного маятника, если жесткость его пружины (k=400 Н/м ), а масса его груза
(m=0,25 кг ) ,
(pi=3,14 )
Ответ округлить до сотых
Показать ответ
Показать решение
Видеорешение
Задача 4.
Найти массу груза пружинного маятника, если его период ( T=1 с )
, а коэффициент жесткости пружины ( k=400 Н/м ; )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 5.
Найти массу груза пружинного маятника, если его период ( T=0,3 с )
, а коэффициент жесткости пружины ( k=350 Н/м ; )
(pi=3,14 ).
Ответ округлить до десятых.
Показать ответ
Показать решение
Видеорешение
Задача 6.
Найти массу груза пружинного маятника, если его период ( T=0,07 с )
, а коэффициент жесткости пружины ( k=150 Н/м ; )
(pi=3,14 ).
Ответ округлить до сотых.
Показать ответ
Показать решение
Видеорешение
Задача 7.
Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,07 с )
, а масса груза ( m=0,0186 кг )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 8.
Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,32 с )
, а масса груза ( m=0,8 кг )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 9.
Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,6 с )
, а масса груза ( m=4 кг )
(pi=3,14 ).
Ответ округлить до целых.
Показать ответ
Показать решение
Видеорешение
Задача 10.
Найти частоту колебаний ( nu ) пружинного маятника, если жесткость его пружины (k=400 Н/м ), а масса его груза
(m=0,25 кг ) ,
(pi=3,14 )
Ответ округлить до сотых
Показать ответ
Показать решение
Видеорешение
Задача 15.
Массу груза пружинного маятника увеличили в 4 раза. Во сколько раз увеличился период колебаний этого
пружинного маятника?
Показать ответ
Показать решение
Видеорешение
Задача 16.
Массу груза пружинного маятника увеличили в 25 раза. Во сколько раз увеличился период колебаний этого
пружинного маятника?
Показать ответ
Показать решение
Видеорешение
Задача 25.
Пружинный маятник совершает гармонические колебания с периодом (T_1=0,4 с. ;; )
Масса его груза (m_1=1 кг ).
В какой-то момент
к грузу пружинного маятника жестко прикрепили дополнительный груз массой (m_2=3 кг. ; )
Вычислить период колебаний пружинного маятника после присоединения дополнительного груза.
Показать ответ
Показать решение
Видеорешение
Задача 30.
Пружинный маятник совершает гармонические колебания с периодом (T_1=0,15 с. ;; )
Масса его груза (m_1= 0,6 кг ).
В какой-то момент
к грузу пружинного маятника жестко прикрепили дополнительный груз , после чего
его период стал равен (T_2=0,45 с )
Найти массу (m_2 ) дополнительного груза.
Показать ответ
Показать решение
Видеорешение
Решение задачи по физике на нахождения массы дополнительного груза в условиях невесомого блока.
ork oki
Знаток
(391),
закрыт
1 год назад
Через блок с неподвижной осью перекинута нить, к концам которой прикреплены грузы одинаковой массы равной 0,24 кг, система приходит в движение после того, как на один из грузов положили перегрузок с ускорением 0, 2. Найти массу перегруза, при условии, что нить не растяжима и не весома.
С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.
Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.
На данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.
Устройство рычага
Что представляет собой рычаг?
Рычаг — это любое твердое тело, которое может вращаться вокруг неподвижной опоры.
Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.
На камень действует сила — вес $P$. Для того чтобы поднять камень, необходимо преодолеть его вес, направленный вертикально вниз. В первом случае (рисунок 2, а) Образавр давит на конец палки с силой $F$, а во втором (рисунок 2, б) — поднимает конец палки.
В обоих случаях у этого рычага есть неподвижная точка опоры — точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.
Сила, с которой Образавр действует на палку (рычаг), меньше веса камня, но тем не менее у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.
Виды рычагов
Таким образом, рычаги бывают двух видов (рисунок 3):
- Рычаг 1-го рода — силы приложены по разные стороны от точки опоры O (рисунок 3, а);
- Рычаг 2-го рода — силы приложены по одну сторону от точки опоры O (рисунок 3, б).
Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.
Плечо силы рычага
На рисунке 4 изображен рычаг. Его точки A и B — это точки приложения сил $F_1$ и $F_2$ соответственно. Точка опоры O расположена между точками A и B — значит, перед нами рычаг 1-го рода.
А теперь взгляните на схему этого рычага (рисунок 4). Силы $F_1$ и $F_2$ направлены в одну сторону.
Длина отрезка OA обозначена как $l_1$, а длина отрезка OB — $l_2$. Эти величины называются плечом силы.
Что называют плечом силы?
Плечо силы — это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Как найти плечо силы?
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.
Тогда, OA или $l_1$ — это плечо силы $F_1$, а OB или $l_2$ — плечо силы $F_2$.
Условие равновесия рычага
Чтобы получить условие равновесия рычага, нужно провести опыты. К рычагу по обе стороны от точки опоры подвешиваются разные груза так, чтобы каждый раз рычаг оставался в равновесии. В каждом случае измеряются модули сил и их плечи. В нашем случае (рисунок 4) видно, что сила $2 space Н$ уравновешивает силу $4 space Н$. А плечо меньшей силы в 2 раза больше плеча большей силы.
С помощью таких опытов было установлено правило равновесия рычага.
В чем состоит правило равновесия рычага?
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил:
$frac{F_1}{F_2} = frac{l_2}{l_1}$,
где $F_1$ и $F_2$ — силы, которые действуют на рычаг, $l_1$ и $l_2$ — плечи этих сил.
Кто установил правило равновесия рычага?
Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют — правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: «Дайте мне точку опору, и я переверну Землю!».
Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.
Например, возьмем рычаг, у которого одно плечо будет в 2 раза больше другого (как на рисунке 4). Приложим к точке A силу в $100 space Н$. Тогда в точке B мы сможем уравновесить силу в $200 space Н$ (в 2 раза большую). Если нам нужно поднять более тяжелый груз, то можно увеличить плечо рычага $l_1$, к которому мы прикладываем силу.
Примеры задач
Задача №1
Рабочий поднимает груз массой $300 space кг$ c помощью рычага 1-го рода. Большее плечо силы рано $3 space м$, а меньшее — $0.6 space м$. Какую силу рабочий прикладывает к большему плечу рычага?
Дано:
$m = 300 space кг$
$l_1 = 3 space м$
$l_2 = 0.6 space м$
$g = 9.8 frac{Н}{кг}$
$F_1 — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем правило равновесия рычага:
$frac{F_1}{F_2} = frac{l_2}{l_1}$.
Выразим отсюда силу $F_1$, которую прикладывает к рычагу рабочий:
$F_1 = F_2 cdot frac{l_2}{l_1}$.
Сила $F_2$ — это вес груза $P$, который мы можем рассчитать формуле: $P = gm$. Подставим в нашу формулу и рассчитаем силу $F_1$:
$F_1 = F_2 cdot frac{l_2}{l_1} = gm cdot frac{l_2}{l_1} = 9.8 frac{Н}{кг} cdot 300 space кг cdot frac{0.6 space м}{3 space м} = 2940 space Н cdot 0.2 = 588 space Н$.
Ответ: $F_1 = 588 space Н$.
Задача №2
На рисунке 7 схематически изображен рычаг. Точка опоры находится в точке O. Одно деление на шкале рычага равно $10 space см$. Какую массу должен иметь груз, подвешенный в точке A, чтобы рычаг находился в равновесии?
Дано:
$m_1 = 100 space г$
$m_2 = 200 space г$
$l_1 = 40 space см$
$l_2 = 20 space см$
$g = 9.8 frac{Н}{кг}$
СИ:
$m_1 = 0.1 space кг$
$m_2 = 0.2 space кг$
$l_1 = 0.4 space м$
$l_2 = 0.2 space м$
$m_3 — ?$
Показать решение и ответ
Скрыть
Решение:
Найдем силу, которая будет действовать на рычаг в точке B. Эта сила будет равна весу $P_2$, с которым груза массой $m_1$ и $m_2$ действуют на подвес. Обозначим эту силу $F_2$.
$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 frac{Н}{кг} cdot (0.1 space кг + 0.2 space кг) = 9.8 frac{Н}{кг} cdot 0.3 space кг approx 3 space Н$.
Запишем правило равновесия рычага:
$frac{F_1}{F_2} = frac{l_2}{l_1}$.
Выразим отсюда и рассчитаем силу $F_1$, с которой будет действовать на рычаг груз неизвестной массы:
$F_1 = frac{F_2 cdot l_2}{l_1} = frac{3 space Н cdot 0.2 space м}{0.4 space м} = 1.5 space Н$.
Сила $F_1$ будет равна весу $P_1$, с которым груз массой $m_3$ действуют на подвес:
$F_1 = P_1 = gm_3$.
Найдем массу груза:
$m_3 = frac{F_1}{g} = frac{1.5 space Н}{9.8 frac{Н}{кг}} approx 0.15 space кг = 150 space г$.
Ответ: $m_3 = 150 space г$.
Из того, что было сказано в предыдущем параграфе, становится ясно, почему тело при условиях, показанных на рисунке 163, б, находится в равновесии.
Поступательно тело не может двигаться, потому что ось закреплена. Поворачиваться же оно не может потому, что моменты сил и равны друг другу по абсолютному значению, но одна сила может повернуть тело по часовой стрелке, а другая – против. И если приписать моментам сил, вращающим это тело в противоположных направлениях, разные знаки, то алгебраическая сумма этих двух моментов окажется равной нулю.
Два условия, необходимые для неподвижного тела твердого тела, заключаются в следующем. Результирующая внешняя сила, действующая на тело, должна оставаться нулевой. Проектируйте и производьте весь или часть технического объекта в команде, чтобы перевести технологическое решение на необходимость.
Материя, движение, энергия, информация: Наблюдайте и описывайте различные типы движений. Цикл 4: Физико-химическое движение и взаимодействия: характеристика движения.
. Технология Моделирование и моделирование объектов и технических систем: анализ работы и структуры объекта.
Тело, способное вращаться вокруг закрепленной оси, находится в равновесии, если сумма моментов сил относительно закрепленной оси, вращающих тело по часовой стрелке, равна сумме моментов сил относительно той же оси, вращающих его против часовой стрелки.
Это и есть правило моментов – условие равновесия тела, имеющего закрепленную ось вращения.
Некоторые студенты думают о себе, но это не всегда так. Поэтому вы можете предложить своим ученикам после окончания катапульты найти способ сделать это мобильным. Эта работа позволяет заинтересоваться передачей движения. Таким образом, добавление колес к модели не так просто. Большинство учеников просто приклеивают колпачки для бутылок прямо к раме своей катапульты и в этот момент осознают, что колеса не вращаются! После отражения группа может найти простое решение, которое должно наклеить солому на раму и передать деревянную палочку, которая будет служить осью вращения для колес.
Момент силы зависит от двух величин: от значения самой силы и длины плеча. Один и тот же момент силы может быть создан малой силой, плечо которой велико, и большой силой с малым плечом. Если, например, пытаться закрыть дверь, толкая ее
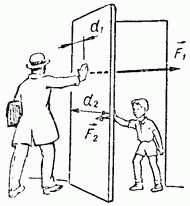
поблизости от петель, то этому с успехом сможет противодействовать ребенок, который догадается толкать ее в другую сторону, приложив силу поближе к краю, и дверь останется в покое (рис. 164).
Говорят, что объект находится в равновесии, если он не может развиваться в одиночку. Если физика пугает вас, имейте в виду, что.
. Рычаг – это объект, который может поворачивать точку поворота. В этой последовательности вы изучили рычаги, поставив на каждом конце два объекта 1 и 2, и вы сделали следующие выводы.
Если обе массы равны, то ось вращения должна находиться в середине рычага. Если массы разные, то ось вращения должна быть ближе к более тяжелому объекту.

В случае проводов для мобильного устройства стержень является точкой крепления провода к штангу. Мы также можем ввести понятие момента силы, которое дает: для равновесия момент силы, которая делает один оборот в направлении, должен быть равен моменту силы, которая делает поворот вращения. другой смысл.
В справедливости правила моментов можно убедиться на опытах, которые проводятся с прибором, изображенным на рисунке 165. Он представляет собой диск А, укрепленный на оси, проходящей через его центр. На диске нанесены окружности, радиусы которых последовательно увеличиваются на 1 см, так что радиус первой, ближайшей к центру окружности равен 1 см, Второй – 2 см и т. д. На окружностях по нескольким диаметрам диска вбиты гвоздики, к которым можно привязывать нити с гирями. Нити переброшены через блоки В и С. Привязывая нити к гвоздикам на разных окружностях и подвешивая к ним различные грузы, создают различные моменты сил, действие которых можно уравновесить моментом силы тяжести третьего груза, подвешенного непосредственно к диску. При этом легко убедиться, что диск находится в равновесии, т. е. не поворачивается, когда алгебраическая сумма моментов всех трех сил равна нулю.
Создание мобильного телефона – Отчет для цикла 2 округа Пертуи. С поверхностью, обработанной плазменным электролитическим окислением, алюминиевый сердечник меняет свое ядро. Процесс «Плазменного электролитического окисления» дает поверхности очень особые характеристики с точки зрения твердости и износостойкости благодаря созданию очень тонкого и компактного массива альфа и микрокристаллического оксида алюминия и аморфного оксида алюминия. Благодаря высокой твердости слоя это новое колесо обладает отличной износостойкостью.
Для этой новой модели предусматривается использование специальных синих тормозных колодок. Это означает большую эффективность передачи мощности на колесо. Благодаря безошибочному характеру, который всем хорошо известно, абсолютная способность передавать свою энергию на асфальте, его экстремальная точность вождения.
Величина момента силы, с которым действует каждый из грузов, определяется произведением силы тяжести груза на длину перпендикуляра, опущенного из центра диска на нить. Длина же этого перпендикуляра, выраженная в сантиметрах, равна номеру окружности, которой касается нить в точке, куда опущен перпендикуляр.

Непревзойденная в середине группы: необыкновенная производительность и сильная эстетическая характеристика делают это колесо ориентиром для велосипедистов. Большая реактивность при каждом изменении темпа педалирования и большей эффективности при передаче мощности на колесо.
Хотя толщины материалов были сведены к минимуму, долговечность и прочность гарантируют полное преимущество веса. Поскольку нет внутренней трубки, фактически, трения из-за трения с крышкой устраняются, и идеальное сцепление шины с ободом предотвращает потери энергии. Тогда нет риска защемления, потому что нет трубки, чтобы сломаться. Закрытие с эксцентриковой системой позволяет модулировать усилие, необходимое для управления рычагом, и иметь большую чувствительность для правильной фиксации замка. Преимущество в круге: отсутствие отверстия и, следовательно, ленты без обода, в пользу жесткости и веса.


Нетрудно понять, что из правила моментов следует знаменитое правило рычага: рычаг находится в равновесии, когда действующие на него силы обратно пропорциональны плечам. Но это не что иное, как другое выражение правила моментов! Не следует думать, что к рычагу должны быть приложены обязательно параллельные силы. На рисунке 166 показан пример рычага, к которому приложены взаимно перпендикулярные силы
Рекомендованная розничная цена: € 507. Этот процесс позволяет уменьшить периферийный вес обода и сделать колесо чрезвычайно реактивным. Позволяют максимально проникать в воздух. Он позволяет держать спицы всегда в положении максимального проникновения воздуха.
Позволяет обеспечить высокий уровень боковой жесткости и снизить вес до минимума. Позволяет снизить трение, поддерживать производительность с течением времени. Увеличение крутильной жесткости на 9%. Новый замок полностью переработан и освещен. Стальная вилка и эксцентрик, рычаг с отверстием для облегчения и алюминиевая гайка. Простота использования, материал устойчив к износу, коррозии и стресса. Универсальный и агрессивный, это колесо, предназначенное для тех, кто каждый день бегает и развлекается всегда на разных путях.
Теперь мы можем сформулировать общее условие равновесия тела:
Для того, чтобы тело находилось в равновесии, необходимо, чтобы были равны нулю геометрическая сумма приложенных к телу сил и сумма моментов этих сил относительно оси вращения.
Задача. Однородный стержень массой 2 кг прикреплен своим нижним концом к шарниру (рис. 167). К другому его концу подвешен груз массой 2 кг. Стержень удерживается в равновесии горизонтальной оттяжкой, прикрепленной к неподвижной вертикальной стойке. Пользуясь числами, указанными на рисунке, найдите силу натяжения оттяжки.
Рекомендованная розничная цена: € 361. Разработан для достижения наилучшего баланса между аэродинамикой, маневренностью и легкостью. Профиль 35 мм. увеличивает крутильную и боковую жесткость по сравнению с традиционным профилем, что обеспечивает большую стабильность на высоких скоростях.
Преувеличенные спицы с аэродинамическим стальным профилем позволяют максимально проникать в воздух. Алюминиевые ниппели уменьшают периферийную массу колеса до минимума, что повышает реактивность. Крупногабаритный алюминиевый корпус ступицы обеспечивает высокую боковую жесткость и минимизирует вес.
Решение. На стержень действуют четыре силы: сила тяжести, приложенная к его середине, сила тяжести груза сила упругости оттяжки и сила упругости в шарнире. Осью вращения служит шарнир у нижнего конца стержня. Из перечисленных сил только первые три создают вращающие моменты относительно этой оси. Линия действия силы реакции в шарнире проходит через ось шарнира, и ее момент равен нулю. Из трех указанных сил только одна сила упругости оттяжки поворачивает стержень против часовой стрелки. Две другие вращают его по часовой стрелке. По правилу моментов
Быстрая и простая регистрация. Алюминиевый штифт уменьшает вес колеса. Большая сторона фланца коробки увеличивает крутильную жесткость, повышая ее реактивность при каждом изменении темпа велосипедиста. Исключительная 5-осевая система обработки ступиц позволяет создать спицевое сиденье идеально в соответствии с натяжной линией. Это решение позволяет иметь одинаковые значения напряжения в каждой точке радиуса; уменьшает напряжение обода и спиц и держит колесо сбалансированным.
Стальная вилка и эксцентриковая, рычажная и алюминиевая гайка. Новый асимметричный профиль задних колес и новый дизайн с 20 спицами обеспечивают значительные преимущества в производительности как с точки зрения повышенной боковой и крутильной жесткости, так и большей реактивности.
Решая это уравнение, получаем:


Упражнение 41
1. На рисунке 168 изображен однородный стержень, ось вращения которого находится в точке О. На нем в точках А и В подвешены грузы массой
0,2 кг и 0,4 кг соответственно. Какой массы груз должен быть подвешен в точке С, чтобы стержень находился в равновесии?
2. К однородному стержню, который может вращаться вокруг оси О, прикреплен в точке А груз массой 0,8 кг (рис. 169). Какой массы груз нужно прикрепить в точке В, чтобы стержень был в равновесии, если масса стержня 400 г?
3. Приведите примеры практического использования рычага.
4. Покажите, что правило рычага следует из правила моментов.
5. При каком условии рычаг, показанный на рисунке 166, находится в равновесии?
Основы технической механики.
Контрольные задания. Высшая школа 1981
Основы технической механики.
Контрольные задания с программой на 120-140 учебных часов и методическими указаниями для учащихся технологических немашиностроительных специальностей. Таблица с вариантами

Основы технической механики.
Контрольные задания. Номера заданий выбираются по последним двум цифрам шифра (табл. 1) из промежутков 1-10; 21-30; 41-50; 61-70; 101-110; 141-150
![]()
Задача 1.
Определить силу Р, при которой цилиндр весом 800 Н начнет вкатываться на наклонную плоскость, а также реакцию наклонной плоскости. Трением пренебречь. Указание: в момент начала вкатывания цилиндр отрывается от горизонтальной опорной плоскости. Задача 3.
Груз P=10 кН равномерно поднимается с помощью троса, перекинутого через блок В и наматываемого на барабан D лебедки. Определить силы в стержнях АВ и СВ кронштейна. Радиусом блока, весом частей конструкции и трением на блоке пренебречь

Задача 2 (рис. 32).
Кулачковый механизм состоит из кулачка треугольной формы, движущегося равномерно и горизонтально под действием силы Р=50 Н и получающего вертикальное перемещение толкателя с роликом на конце. В данном положении мехизма ролик касается гипотенузы в ее середине. Определить реакцию горизонтальной опорной поверхности и силу давления кулачка на ролик. Весом частей механизма, а также трением пренебречь
Задача 4 (рис. 32).
Под действием расположенной параллельно наклонной плоскости сжатой пружины, сила упругости которой равна 2 Н, шарик перекрывает проходное отверстие пневматического клапана. Определить силу Р давления сжатого воздуха, при которой проходное отверстие откроется, а также реакцию наклонной опорной поверхности. Весом частей механизма, a также трением пренебречь. Указание: в момент начала отжатия шарик отрывается от стенок проходного отверстия
Задача 5 (рис. 32).
Груз весом G=5 кН с помощью наматываемого на барабан троса равномерно перемещается вверх по наклонной плоскости. Приняв силу сопротивления движению (силу трения) F=0,1 G, определить силу в тяговом тросе, а также нормальную реакцию опорной плоскости. Задача 6 (рис. 32).
Определить силы в стержнях АВ и СВ кронштейна, удерживающего груз Р=15 кН. Весом частей конструкции пренебречь
Задача 7 (рис. 32).
Из-за разной длины стропильных тросов АВ и СВ равномерный подъем трубы АС весом 7 кН происходит с перекосом, причем трос СВ оказался расположенным горизонтально. Определить силы в стропильных тросах. Указание: центр тяжести трубы лежит на вертикали, проходящей через точку В. Задача 5 (рис. 32).
С помощью опорного троса АВ и двух блоков удерживаются в равновесии три груза. Определить вес груза Р и силу в опорном тросе, если Q=4 кН и F=8 кН. Трением на блоках пренебречь
Задача 9.
Тело весом G=6 Н под действием горизонтальной силы Р равномерно перемещается вверх по наклонной плоскости. Приняв силу сопротивления движению (силу трения) F=0,18 G, определить значение силы Р, а также нормальную реакцию опорной плоскости. Задача 10.
Четыре стержня, приваренные к косынке, образуют узел фермы строительной конструкции. Стержень 2 расположен вертикально. Силы в стержнях 1 и 2 известны и равны соответственно P 1 =10 кН и Р 2 =15 кН. Определить силы
Задача 11.
Груз Р=15 кН, поднятый с помощью троса, намотанного на барабан диаметром d 0 =0,2 м, удерживается в покое храповым механизмом, состоящим из зубчатого колеса с расчетным диаметром d=0,3 м и упорного рычага. Определить силу в упорном рычаге. Задача 12.
К концу рукоятки ручного рычажного пресса приложена сила человека Р=150 Н. Приняв АС=300 мм и АВ=45 мм, определить силу давления поршня на прессуемый материал. Крепление в точках А и В шарнирное

Задача 13 (рис. 33).
В лентопротяжном механизме прибора лента держится в натянутом состоянии с помощью двуплечего рычага АВС. На одном конце рычага расположен нажимной ролик, другой конец оттянут пружиной с силой упругости 6 Н. Определить силу давления ролика на ленту, считая, что общая нормаль в точке их касания расположена вертикально. Принять АВ=40 мм и ВС=15 мм. Весом частей механизма, а также трением пренебречь

Задача 14.
Груз весом 850 Н равномерно поднимается с помощью ворота, состоящего из барабана диаметром 0,18 м и рукоятки с плечом 0,45 м. Для данного положения механизма определить силу рабочего Р, считая ее приложенной вертикально. Задача 15.
Для перевода однородной колонны АВ из горизонтального положении в вертикальное один ее конец зацепили тросом подъемного крапа, а к другому концу приставили упор. Определить силу в тяговом тросе в момент начала подъема колонны, если ее вес 5 кН и длина 6 м

Задача 16.
Под действием передаваемого зубчатым колесом вращающего момента М=4 Нм вал с насаженным на него кулачком равномерно вращается. Кулачок, надавливая на тарельчатый конец подпружиненного толкателя, сообщает ему вертикалыюе перемещение. Для данного положения кулачкового механизма определить силу упругости сжатой пружины, если плечо кулачка ОА=30 мм. Весом частей механизма, а также трением пренебречь
Задача 17 (рис. 33).
В измерительном приборе рычаг АС, несущий груз весом 1,5 Н, удерживается в горизонтальном положении с помощью растянутой пружины. Определить силу упругости пружины, приняв АВ=25 мм и ВС=75 мм. Весом частей механизма пренебречь
Задача 18 (рис. 33).
Поплавковый регулятор уровня, состоящий из двуплечего рычага АВС с поплавком D и запирающего трубопровод клапана Е, служит для перекрытия трубопровода в момент заполнения бака водой. В этот момент плечо АВ рычага располагается горизонтально. Приняв АВ=250 мм, ВС=20 мм и силу давления воды на клапан Р=80 Н, определить величину действующей на поплавок подъемной силы F. Весом частей механизма пренебречь
Задача 19.
Кулачковый механизм состоит из кулачка, равномерно вращающегося под действием момента М=0,5 Н×м, и горизонтально перемещающегося подпружиненного толкателя. Для данного положения механизма определить силу давления кулачка на толкатель, если плечо кулачка ОА=45 мм. Весом частей механизма, а также трением пренебречь
Задача 20.
Для данного положения заводной рукоятки автомобиля определить силу давления человека на рукоятку Р, считая ее приложенной вертикально. Принять плечо рукоятки l=0,2 м, плечо крестовины а=30 мм и силу сопротивления на крестовине F=1,4 кН. Вращение рукоятки считать равномерным. Весом рукоятки, а также трением пренебречь
Задача 21.
Однородная лестница АВ весом 120 Н опирается на пол и стены приямка. В точке С на лестнице стоит человек весом 700 Н. Приняв АВ=3 м и АС=2 м, определить опорные реакции в точках А и В. Трением пренебречь. Задача 22.
Однородная стрела АВ платформенного подъемного крана весом 7 кН, несущая на своем конце груз весом 30 кН, удерживается в равновесии с помощью троса CD барабанной лебедки D. Приняв АВ=6 м и ВС=2 м, определить реакции опорного шарнира А и силу в тросе CD
Задача 23.
Поворотный однородный рычаг АВ с помощью растянутой пружины силой упругости 4 Н прижат к вращающейся кулачковой шайбе в точке С. Приняв AD=70 мм и DC=80 мм, определить реакции опорного шарнира А и силу давления рычага на кулачок. Весом частей механизма. Задача 24.
Однородную плиту АВ весом 5 кН равномерно вытягивают из приямка с помощью барабанной лебедки D. Приняв АВ=2 м и СВ=2 м, определить для данного положения плиты опорные реакции в точках А и С и силу в тяговом тросе BD
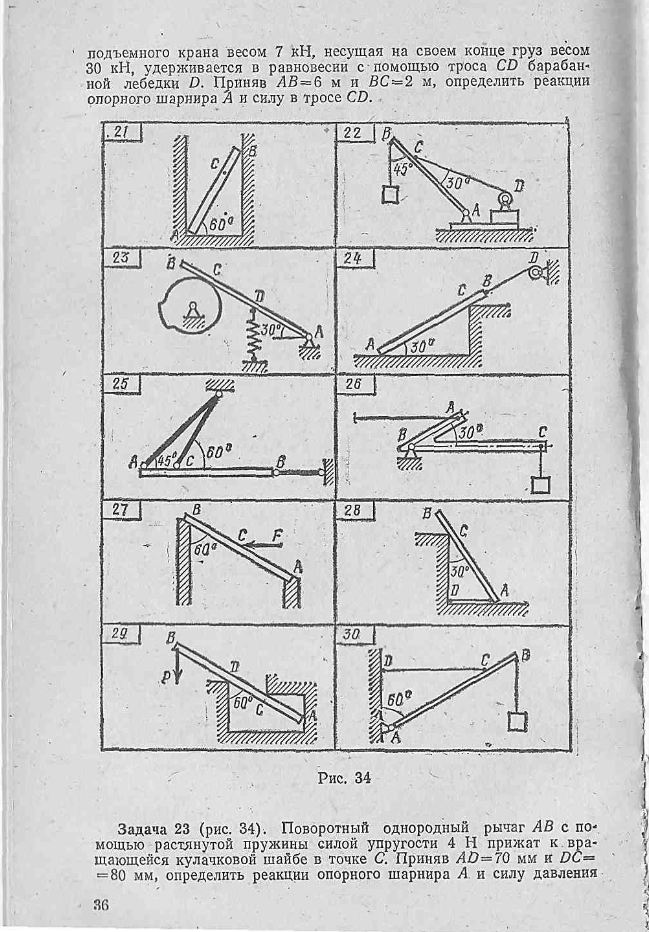
Задача 25.
Однородная плита АВ весом 2 кН удерживается в равновесии в горизонтальном положении с помощью трех стержней. Приняв АВ=6 м и АС=1,5 м, определить силы в стержнях. Задача 26.
Натяжное устройство представляет собой двуплечий рычаг АВС, одно плечо которого несет груз весом 800 Н, а другое плечо служит для натяжения троса. Приняв АВ=0,1 м и ВС=0,3 м, определить реакции опорного шарнира В и силу в натягиваемом тросе. Весом рычага пренебречь 
Задача 27.
Однородная плита АВ односкатной крыши весом 20 кН испытывает ветровую нагрузку, равнодействующая которой F=8 кН приложена в точке С горизонтально. Приняв АВ=8 м и АС=СВ, определить опорные реакции в точках А и В. Задача 28.
Стоящий наклонно однородный щит АВ весом 300 Н удерживается в равновесии веревкой AD Пренебрегая трением и приняв АВ=8 м и АС=7 м, определить опорные реакции в точках А и С и силу в веревке

Задача 29.
Неподвижно зажатый, как показано на рисунке, опорный столб А В нагружен силой Р=3 кН. Приняв АВ=8 и AC=CD=2 м, определить опорные реакции в точках А, С и D. Весом столба, а также трением пренебречь. Задача 30.
Однородная стрела АВ настенного крана весом 2 кН, несущая, груз весом 10 кН, удерживается в равновесии тросом CD, Приняв АВ=3 м и СВ=1 м, определить реакции опорного шарнира А и силу в тросе CD

Задачи 31-40.
Для заданной консольной балки определить опорные реакции заделки. Задачи 41-50.
Для заданной тонкой однородной пластины определить положение центра тяжести. Размеры на чертеже даны в сантиметрах.
Задачи 51-60.
Для заданного сечения, составленного из прокатных профилей, определить главные центральные моменты инерции
Title=”Задачи 31-40. Для заданной консольной балки определить опорные реакции заделки. Задачи 41-50.
Для заданной тонкой однородной пластины определить положение центра тяжести. Размеры на чертеже даны в сантиметрах. Задачи 51-60. Для заданного сечения, составленного из прокатных профилей, определить главные центральные моменты инерции”>
Задачи 61, 66, 68, 70.
Для заданного бруса построить эпюру продольных сил и определить размеры поперечного сечения на обоих участках. Для материала бруса (сталь СтЗ) принять [σ Р ]=160 МПа, [σ С ]=120 МПа.
Задачи 62, 64, 69.
Для заданного бруса определить допускаемые значения нагрузок Р1 и Р2 и построить эпюру продольных сил. Для материала бруса (сталь СтЗ) принять [σ Р ]=160 МПа, [σ С ]=120 МПа. При решении задачи считать, что на обоих участках бруса вид нагружения одинаков

Задачи 63, 65, 67.
Для заданного бруса построить эпюру продольных сил и проверить прочность на обоих участках. Для материала бруса (сталь СтЗ) принять [σ Р ]=160 МПа, [σ С ]=120 МПа.
Задачи 71-74.
Для стержней кронштейна, выполненных из прокатного профиля (равнополочного уголка), подобрать размеры поперечного сечения. Определить также удлинение (укорочение) стержня ВС. Для материала стержней (сталь СтЗ) принять [σ Р ]=160 МПа, [σ С ]=120 МПа и модуль продольной упругости Е=2×10 5

Задачи 75, 76 (рис. 64, табл. 7).
Для стержней, удерживающих жесткую балку и выполненных из прокатного профиля (сдвоенных равнополочных уголков, швеллера или двутавра), подобрать размеры поперечного сечения. Определить также удлинение (укорочение) стержня ВС. Для материала стержней (сталь 03) принять [σ Р ]=160 МПа, [σ С ]=120 МПа и модуль продольной упругости Е=2×10 5 МПа

Задачи 77-80 (рис. 64, табл. 7).
Для стержня ВС, удерживающего жесткую балку и выполненного из прокатного профиля (сдвоенных равнополочных уголков, швеллера или двутавра), подобрать размеры поперечного сечения и определить удлинение (укорочение) стержня. Для материала стержня (сталь СтЗ) принять [σ Р ]=160 МПа, [σ С ]=120 МПа и модуль продольной упругости Е=2×10 5 МПа

Задачи 81-90.
Для заданного бруса круглого поперечного сечения построить эпюру крутящих моментов и определить диаметр на каждом из трех участков. Для материала бруса (сталь СтЗ) принять [τ]=70 МПа

Задачи 91-100.
Для заданной консольной балки построить эпюры поперечных сил и изгибающих моментов и подобрать размеры поперечного сечения в двух вариантах: а) двутавр или сдвоенный швеллер; б) прямоугольник с заданным отношением h/b высоты и ширины. Сравнить массу балки по обоим расчетным вариантам. Для материала балки (сталь СтЗ) принять [σ]=160 МПа
Задачи 101-110 (рис. 67, табл. 10).
Для заданной двухопорной балки построить эпюры поперечных сил и изгибающих моментов и подобрать размеры поперечного сечения (круг или квадрат). Для материала балки (сталь СтЗ) с учетом повышенных требований к ее жесткости принять [σ]=130 МПа

Задачи 111-120.
На валу, вращающемся в подшипниках с постоянной угловой скоростью ω и передающем мощность N, жестко закреплены два зубчатых колеса, расчетные диаметры которых соответственно d 1 и d 2 . Требуется: а) определить действующие на зубья колес окружные (касательные) силы Р 1 и Р 2 ; б) построить эпюры крутящих и изгибающих моментов; в) определить требуемый диаметр вала. Диаметр вала считать постоянным по всей длине. Для материала вала (сталь 45) с учетом предотвращения [σ]=80

Задачи 121-130.
Тело массой m с помощью троса, наматываемого на барабан диаметром d, перемещается вверх или вниз по наклонной плоскости с углом наклона α. Уравнение движения тела s=f(t), уравнение вращения барабана φ=f(t), где а – в метрах; φ – в радианах; t – в секундах. N и ω – соответственно мощность и угловая скорость на валу барабана в момент конца разгона или начала торможения

Задачи 121-130.
Время t 1 – время разгона (из состояния покоя до заданной скорости) или торможения (от заданной скорости до остановки). Коэффициент трения скольжения между телом и плоскостью – f. Потерями на трение на барабане, а также массой барабана пренебречь. При решении задачи принять g=10 м/с2; sin45°=0,7; sin 60°=0,9. Величины, подлежащие в задаче определению, указаны в таблице
Шарнирное соединение стержней 1 и 4 осуществлено с помощью пальца 3 через промежуточную накладку 2, приваренную к стержню 1 фланговыми швами. Стержень 1 выполнен из стального проката – швеллера (1 или 2 шт.), уголка (2 или 4 шт.) или квадрата; стержень 4 и накладка 2 – из полосовой стали одинаковой толщины s, ширина которой не задана и определению не подлежит
Задачи 131-140 (рис. 90, табл. 15).
Требуется определить: а) длину нахлеста l сварного соединения; б) диаметр d пальца шарнирного соединения, Для материала деталей 1, 2 и 4 (сталь СтЗ) принять [σ Р ]=160 МПа и [σ СМ ]=250 МПа; для материала пальца (сталь 45) – [τ СР ]=90 МПа; для материала сварного шва – [τ СР ]=100 МПа

Привод состоит из электродвигателя мощностью N ДВ с угловой скоростью вала ω ДВ и многоступенчатой передачи, характеристики звеньев которой указаны на кинематической схеме. Угловая скорость выходного (рабочего) вала привода ω Р. Требуется определить: а) общие КПД и передаточное отношение привода; б) мощности, прпщшощие моменты и угловые скорости для всех валов. Кроме того, следует дать характеристику привода и его отдельных передач

Задачи 141-150 (рис. 91, табл. 16).
При расчете принять следующие значения КПД передач (с учетом потерь и подшипника) а) червячных – 0,77 (задачи 143 и 148), 0,82 (задача 146) и 0,87 (задача 149); б) зубчатых, цепных и ременных – в соответствии с рекомендациями, данными н методических указаниях к выполнению контрольной работы. Упругим скольжением в ременных передачах пренебречь

Задачи 151-160 (табл. 17).
Выполнить геометрический расчет одной из ступеней передачи привода по данным предыдущей (141-150) задачи. Номер рассчитываемой ступени передачи, а также ее межосевое расстояние а даны в таблице. При расчете принять: а) для червячных передач коэффициент диаметра червяка q=10; б) для зубчатых передач относительная ширина колеса ψ ba =0,25 (прямозубые) и ψ ba =0,4 (косозубые)

