|
|
Макеты страниц
Удельный заряд электрона (т. е. отношение 
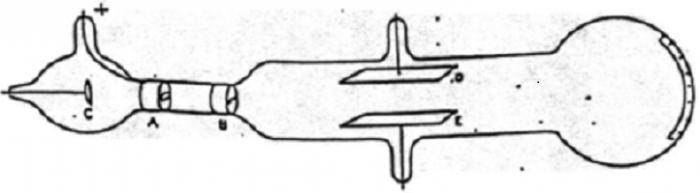
Подавая напряжение на пластины конденсатора, можно было воздействовать на пучок практически однородным электрическим полем. Трубка помещалась между полюсами электромагнита, с помощью которого можно было создавать на том же участке пути электронов перпендикулярное к электрическому однородное магнитное поле (область этого поля обведена на рис. 74.1 пунктирной окружностью). При выключенных полях пучок попадал на экран в точке О. Каждое из полей в отдельности вызывало смещение пучка в вертикальном направлении. Величины смещений определяются полученными в предыдущем параграфе формулами (73.3) и (73.4).
Включив магнитное поле и измерив вызванное им смещение следа пучка

Томсон включал также электрическое поле и подбирал его значение так, чтобы пучок снова попадал в точку О. В этом случае электрическое и магнитное поля действовали на электроны пучка одновременно с одинаковыми по величине, но противоположно направленными силами. При этом выполнялось условие

Решая совместно уравнения (74.1) и (74.2), Томсон вычислял 
Буш применил для определения удельного заряда электронов метод магнитной фокусировки. Суть этого метода заключается в следующем. Допустим, что в однородном магнитном поле вылетает из некоторой точки слегка расходящийся симметричный относительно направления поля пучок электронов, имеющих одинаковую по величине скорость v. Направления, по которым вылетают электроны, образуют с направлением В небольшие углы а. В § 72 было выяснено, что электроны движутся в этом случае по спиральным траекториям, совершая за одинаковое время

полный оборот и смещаясь вдоль направления поля на расстояние 


Рис. 74.1.
Вследствие малости угла а расстояния (74.3) для разных электронов оказываются практически одинаковыми и равными 


В опыте Буша электроны, испущенные раскаленным катодом К (рис. 74.2), ускоряются, проходя разность потенциалов U, приложенную между катодом К и анодом А. В результате они приобретают скорость и, значение которой может быть найдено из соотношения

Вылетев затем из отверстия в аноде, электроны образуют узкий пучок, направленный вдоль оси эвакуированной трубки, вставленной внутрь соленоида. На входе в соленоид помещается конденсатор, на который подается переменное напряжение. Поле, создаваемое конденсатором, отклоняет электроны пучка от оси прибора на небольшие изменяющиеся со временем углы а. Это приводит к «завихрению» пучка — электроны начинают двигаться по различным спиральным траекториям. На выходе из соленоида ставится флуоресцирующий экран. Если подобрать магнитную индукцию В так, чтобы расстояние Г от конденсатора до экрана удовлетворяло условию

(l — шаг спирали, 

Наиболее точное значение удельного заряда электрона, установленное с учетом результатов, полученных разными методами, равно

Величина (74.7) дает отношение заряда электрона к его массе покоя 


Рис. 74.2
В опытах Томсона скорость электронов составляла примерно 0,1 с. При такой скорости релятивистская масса превышает массу покоя на 0,5%. В последующих опытах скорость электронов достигала очень больших значений. Во всех случаях было обнаружено уменьшение измеряемых значений 
Заряд электрона был определен с большой точностью Милликеном в 1909 г. В закрытое пространство между горизонтально расположенными пластинами конденсатора (рис. 74.3) Милликен вводил мельчайшие капельки масла. При разбрызгивании капельки электризовались, и их можно было устанавливать неподвижно, подбирая величину и знак напряжения на конденсаторе.
Равновесие наступало при условии

здесь 

(









Движение капельки наблюдалось с помощью микроскопа. Для измерения 
Точно зафиксировать равновесие капельки очень трудно. Поэтому вместо поля, отвечающего условию (74.9), включалось такое поле, под действием которого капелька начинала двигаться с небольшой скоростью вверх. Установившаяся скорость подъема 



Исключив из уравнения (74.10), (74.11) и (74.12) Р и 


(в эту формулу Милликен вносил поправку, учитывающую, что размеры капелек были сравнимы с длиной свободного пробега молекул воздуха).

Рис. 74.3.
Итак, измерив скорость свободного падения капельки 





Измеренные Милликеном изменения заряда капельки 


Значение элементарного заряда, установленное с учетом измерений Милликена и данных, полученных другими методами, равно

Такую же величину имеет заряд электрона.
Из (74.7) и (74.13) получается для массы покоя электрона значение

приблизительно в 1840 раз меньшее массы самого легкого из атомов — атома водорода.
В обнаружении дискретной природы электричества сыграли большую роль законы электролиза, установленные экспериментально Фарадеем в 1836 г. Согласно этим законам масса 


Здесь М — масса моля выделяющегося вещества, 

Разделив обе части равенства (74.15) на массу иона, получим




Следовательно, заряд иона оказывается целым кратным величины

«угорая представляет собой элементарный заряд.
Таким образом, из анализа законов электролиза вытекает дискретность зарядов, которыми могут обладать ионы в электролитах.
Подстановка в (74.17) значения (74.16) для F и найденного из зпытов Перрена (см. § 


Поскольку точность, с которой определяется постоянная Фарадея F, и точность значения 


Оглавление
- ПРЕДИСЛОВИЕ
- МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
- ЧАСТЬ 1. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
- § 1. Электрический заряд
- § 2. Закон Кулона
- § 3. Системы единиц
- § 4. Рационализованная запись формул
- § 5. Электрическое поле. Напряженность поля
- § 6. Потенциал
- § 7. Энергия взаимодействия системы зарядов
- § 8. Связь между напряженностью электрического поля и потенциалом
- § 9. Диполь
- § 10. Поле системы зарядов на больших расстояниях
- § 11. Описание свойств векторных полей
- Дивергенция.
- Циркуляция.
- Теорема Стокса.
- § 12. Циркуляция и ротор электростатического поля
- § 13. Теорема Гаусса
- § 14. Вычисление полей с помощью теоремы Гаусса
- Поле двух разноименно заряженных плоскостей.
- Поле заряженной сферической поверхности.
- Поле объемно-заряженного шара.
- ГЛАВА II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ДИЭЛЕКТРИКАХ
- § 15. Полярные и неполярные молекулы
- § 16. Поляризация диэлектриков
- § 17. Поле внутри диэлектрика
- § 18. Объемные и поверхностные связанные заряды
- § 19. Вектор электрического смешения
- § 20. Примеры на вычисление поля в диэлектриках
- § 21. Условия на границе двух диэлектриков
- § 22. Силы, действующие на заряд в диэлектрике
- § 23. Сегнетоэлектрики
- ГЛАВА III. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 24. Равновесие зарядов на проводнике
- § 25. Проводник во внешнем электрическом поле
- § 26. Электроемкость
- § 27. Конденсаторы
- ГЛАВА IV. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
- § 28. Энергия заряженного проводника
- § 29. Энергия заряженного конденсатора
- § 30. Энергия электрического поля
- ГЛАВА V. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
- § 31. Электрический ток
- § 32. Уравнение непрерывности
- § 33. Электродвижущая сила
- § 34. Закон Ома. Сопротивление проводников
- § 35. Закон Ома для неоднородного участка цепи
- § 36. Разветвленные цепи. Правила Кирхгофа
- § 37. Мощность тока
- § 38. Закон Джоуля — Ленца
- ГЛАВА VI. МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ
- § 39. Взаимодействие токов
- § 40. Магнитное поле
- § 41. Поле движущегося заряда
- § 42. Закон Био — Савара
- § 43. Сила Лоренца
- § 44. Закон Ампера
- § 45. Магнитное взаимодействие как релятивистский эффект
- § 46. Контур с током в магнитном поле
- § 47. Магнитное поле контура с током
- § 48. Работа, совершаемая при перемещении тока в магнитном
- § 49. Дивергенция и ротор магнитного поля
- § 50. Поле соленоида и тороида
- ГЛАВА VII. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
- § 51. Намагничение магнетика
- § 52. Напряженность магнитного поля
- § 53. Вычисление поля в магнетиках
- § 54. Условия на границе двух магнетиков
- § 55. Виды магнетиков
- § 56. Магнитомеханические явления
- § 57. Диамагнетизм
- § 58. Парамагнетизм
- § 59. Ферромагнетизм
- ГЛАВА VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 60. Явление электромагнитной индукции
- § 61. Электродвижущая сила индукции
- § 62. Методы измерения магнитной индукции
- § 63. Токи Фуко
- § 64. Явление самоиндукции
- § 65. Ток при замыкании и размыкании цепи
- § 66. Взаимная индукция
- § 67. Энергия магнитного поля
- § 68. Работа перемагничивания ферромагнетика
- ГЛАВА IX. УРАВНЕНИЯ МАКСВЕЛЛА
- § 69. Вихревое электрическое поле
- § 70. Ток смещения
- § 71. Уравнения Максвелла
- ГЛАВА X. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЯХ
- § 72. Движение заряженной частицы в однородном магнитном поле
- § 73. Отклонение движущихся заряженных частиц электрическим и магнитным полями
- § 74. Определение заряда и массы электрона
- § 75. Определение удельного заряда ионов. Масс-спектрографы
- § 76. Ускорители заряженных частиц
- ГЛАВА XI. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ
- § 77. Природа носителей тока в металлах
- § 78. Элементарная классическая теория металлов
- § 79. Эффект Холла
- ГЛАВА XII. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
- § 80. Несамостоятельная и самостоятельная проводимость
- § 81. Несамостоятельный газовый разряд
- § 82. Ионизационные камеры и счетчики
- § 83. Процессы, приводящие к появлению носителей тока при самостоятельном разряде
- § 84. Газоразрядная плазма
- § 85. Тлеющий разряд
- § 86. Дуговой разряд
- § 87. Искровой и коронный разряды
- ГЛАВА XIII. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ
- § 88. Квазистационарные токи
- § 89. Свободные колебания в контуре без активного сопротивления
- § 90. Свободные затухающие колебания
- § 91. Вынужденные электрические колебания
- § 92. Переменный ток
- ЧАСТЬ 2. ВОЛНЫ
- § 93. Распространение волн в упругой среде
- § 94. Уравнения плоской и сферической волн
- § 95. Уравнение плоской волны, распространяющейся в произвольном направлении
- § 96. Волновое уравнение
- § 97. Скорость упругих волн в твердой среде
- § 98. Энергия упругой волны
- § 99. Стоячие волны
- § 100. Колебания струны
- § 101. Звук
- § 102. Скорость звука в газах
- § 103. Эффект Доплера для звуковых волн
- ГЛАВА XV. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 104. Волновое уравнение для электромагнитного поля
- § 105. Плоская электромагнитная волна
- § 106. Экспериментальное исследование электромагнитных волн
- § 107. Энергия электромагнитных волн
- § 108. Импульс электромагнитного поля
- § 109. Излучение диполя
- ЧАСТЬ 3. ОПТИКА
- § 110. Световая волна
- § 111. Представление гармонических функций с помощью экспонент
- § 112. Отражение и преломление плоской волны на границе двух диэлектриков
- § 113. Световой поток
- § 114. Фотометрические величины и единицы
- § 115. Геометрическая оптика
- § 116. Центрированная оптическая система
- § 117. Тонкая линза
- § 118. Принцип Гюйгенса
- ГЛАВА XVII. ИНТЕРФЕРЕНЦИЯ СВЕТА
- § 119. Интерференция световых волн
- § 120. Когерентность
- § 121. Способы наблюдения интерференции света
- § 122. Интерференция света при отражении от тонких пластинок
- § 123. Интерферометр Майкельсона
- § 124. Многолучевая интерференция
- ГЛАВА XVIII. ДИФРАКЦИЯ СВЕТА
- § 126. Принцип Гюйгенса—Френеля
- § 127. Зоны Френеля
- § 128. Дифракция Френеля от простейших преград
- § 129. Дифракция Фраунгофера от щели
- § 130. Дифракционная решетка
- § 131. Дифракция рентгеновских лучей
- § 132. Разрешающая сила объектива
- § 133. Голография
- ГЛАВА XIX. ПОЛЯРИЗАЦИЯ СВЕТА
- § 134. Естественный и поляризованный свет
- § 135. Поляризация при отражении и преломлении
- § 136. Поляризация при двойном лучепреломлении
- § 137. Интерференция поляризованных лучей
- § 138. Прохождение плоскополяризованного света через кристаллическую пластинку
- § 139. Кристаллическая пластинка между двумя поляризаторами
- § 140. Искусственное двойное лучепреломление
- § 141. Вращение плоскости поляризации
- ГЛАВА XX. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ
- § 142. Дисперсия света
- § 143. Групповая скорость
- § 144. Элементарная теория дисперсии
- § 145. Поглощение света
- § 146. Рассеяние света
- § 147. Эффект Вавилова — Черенкова
- ГЛАВА XXI. ОПТИКА ДВИЖУЩИХСЯ СРЕД
- § 148. Скорость света
- § 149. Опыт Физо
- § 150. Опыт Майкельсона
- § 151. Эффект Доплера
- ПРИЛОЖЕНИЯ
- I. Единицы электрических и магнитных величин в СИ и в гауссовой системе
- Приложение II. Основные формулы электромагнетизма в СИ и в гауссовой системе
- Приложение III. Векторный потенциал
From Wikipedia, the free encyclopedia
| Constant | Values | Units |
|---|---|---|
| me | 9.1093837015(28)×10−31[1] | kg |
| 5.48579909065(16)×10−4[2] | Da | |
| 0.51099895000(15) | MeV/c2 | |
| mec2 | 8.1871057769(25)×10−14 | J |
| 0.51099895000(15)[3] | MeV |
In particle physics, the electron mass (symbol: me) is the mass of a stationary electron, also known as the invariant mass of the electron. It is one of the fundamental constants of physics. It has a value of about 9.109×10−31 kilograms or about 5.486×10−4 daltons, which has an energy-equivalent of about 8.187×10−14 joules or about 0.511 MeV.[3]
Terminology[edit]
The term “rest mass” is sometimes used because in special relativity the mass of an object can be said to increase in a frame of reference that is moving relative to that object (or if the object is moving in a given frame of reference). Most practical measurements are carried out on moving electrons. If the electron is moving at a relativistic velocity, any measurement must use the correct expression for mass. Such correction becomes substantial for electrons accelerated by voltages of over 100 kV.
For example, the relativistic expression for the total energy, E, of an electron moving at speed v is
where
- c is the speed of light;
- γ is the Lorentz factor,
- me is the “rest mass”, or more simply just the “mass” of the electron.
This quantity me is frame invariant and velocity independent. However, some texts[which?] group the Lorentz factor with the mass factor to define a new quantity called the relativistic mass, mrelativistic = γme.[citation needed]
Determination[edit]
Since the electron mass determines a number of observed effects in atomic physics, there are potentially many ways to determine its mass from an experiment, if the values of other physical constants are already considered known.
Historically, the mass of the electron was determined directly from combining two measurements. The mass-to-charge ratio of the electron was first estimated by Arthur Schuster in 1890 by measuring the deflection of “cathode rays” due to a known magnetic field in a cathode ray tube. Seven years later J. J. Thomson showed that cathode rays consist of streams of particles, to be called electrons, and made more precise measurements of their mass-to-charge ratio again using a cathode ray tube.
The second measurement was of the charge of the electron. This was determined with a precision of better than 1% by Robert A. Millikan in his oil drop experiment in 1909. Together with the mass-to-charge ratio, the electron mass was determined with reasonable precision. The value of mass that was found for the electron was initially met with surprise by physicists, since it was so small (less than 0.1%) compared to the known mass of a hydrogen atom.
The electron rest mass can be calculated from the Rydberg constant R∞ and the fine-structure constant α obtained through spectroscopic measurements. Using the definition of the Rydberg constant:
thus
where c is the speed of light and h is the Planck constant.[4] The relative uncertainty, 5×10−8 in the 2006 CODATA recommended value,[5] is due entirely to the uncertainty in the value of the Planck constant. With the re-definition of kilogram in 2019, there is no uncertainty by definition left in Planck constant anymore.
The electron relative atomic mass can be measured directly in a Penning trap. It can also be inferred from the spectra of antiprotonic helium atoms (helium atoms where one of the electrons has been replaced by an antiproton) or from measurements of the electron g-factor in the hydrogenic ions 12C5+ or 16O7+.
The electron relative atomic mass is an adjusted parameter in the CODATA set of fundamental physical constants, while the electron rest mass in kilograms is calculated from the values of the Planck constant, the fine-structure constant and the Rydberg constant, as detailed above.[4][5]
Relationship to other physical constants[edit]
The electron mass is used to calculate[citation needed] the Avogadro constant NA:
Hence it is also related to the atomic mass constant mu:
where
- Mu is the molar mass constant (defined in SI);
- Ar(e) is a directly measured quantity, the relative atomic mass of the electron.
Note that mu is defined in terms of Ar(e), and not the other way round, and so the name “electron mass in atomic mass units” for Ar(e) involves a circular definition (at least in terms of practical measurements).
The electron relative atomic mass also enters into the calculation of all other relative atomic masses. By convention, relative atomic masses are quoted for neutral atoms, but the actual measurements are made on positive ions, either in a mass spectrometer or a Penning trap. Hence the mass of the electrons must be added back on to the measured values before tabulation. A correction must also be made for the mass equivalent of the binding energy Eb. Taking the simplest case of complete ionization of all electrons, for a nuclide X of atomic number Z,[4]
As relative atomic masses are measured as ratios of masses, the corrections must be applied to both ions: the uncertainties in the corrections are negligible, as illustrated below for hydrogen 1 and oxygen 16.
| Physical parameter | 1H | 16O |
|---|---|---|
| relative atomic mass of the XZ+ ion | 1.00727646677(10) | 15.99052817445(18) |
| relative atomic mass of the Z electrons | 0.00054857990943(23) | 0.0043886392754(18) |
| correction for the binding energy | −0.0000000145985 | −0.0000021941559 |
| relative atomic mass of the neutral atom | 1.00782503207(10) | 15.99491461957(18) |
The principle can be shown by the determination of the electron relative atomic mass by Farnham et al. at the University of Washington (1995).[6] It involves the measurement of the frequencies of the cyclotron radiation emitted by electrons and by 12C6+ ions in a Penning trap. The ratio of the two frequencies is equal to six times the inverse ratio of the masses of the two particles (the heavier the particle, the lower the frequency of the cyclotron radiation; the higher the charge on the particle, the higher the frequency):
As the relative atomic mass of 12C6+ ions is very nearly 12, the ratio of frequencies can be used to calculate a first approximation to Ar(e), 5.4863037178×10−4. This approximate value is then used to calculate a first approximation to Ar(12C6+), knowing that 
References[edit]
- ^ “2018 CODATA Value: electron mass”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-05-20.
- ^ “2018 CODATA Value: electron mass in u”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2020-06-21.
- ^ a b “2018 CODATA Value: electron mass energy equivalent in MeV”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2022-07-11.
- ^ a b c “CODATA Value: electron mass”. The NIST Reference on Constants, Units and Uncertainty. May 20, 2019. Retrieved May 20, 2019.
- ^ a b The NIST reference on Constants, Units, and Uncertainty, National Institute of Standards and Technology, 10 June 2009
- ^ Farnham, D. L.; Van Dyck Jr., R. S.; Schwinberg, P. B. (1995), “Determination of the Electron’s Atomic Mass and the Proton/Electron Mass Ratio via Penning Trap Mass Spectroscopy”, Phys. Rev. Lett., 75 (20): 3598–3601, Bibcode:1995PhRvL..75.3598F, doi:10.1103/PhysRevLett.75.3598, PMID 10059680
Как получили вес электрона?
Просветленный
(36696),
закрыт
8 лет назад
Алексей Баскаков
Мудрец
(16962)
8 лет назад
Измеряя частоту “вибраций” электрона в магнитном поле и скорость его вращения при помощи особого прибора, ловушки Пеннинга.
NetEgoУченик (154)
8 лет назад
В описании работы прибора, присутствуют:
Ио́н (др. -греч. ἰόν — идущее) — электрически заряженная частица (атом, молекула, свободный радикал), имеющая положительный или отрицательный заряд электричества, кратный заряду электрона.
—
а) Это как? Ион отрицательный или положительный?
б) Кратный заряду электрона, а какой у него заряд?
с) Так атом, молекула или радикал?
Электрозаряд не может быть отрицательным или положительным, но может быть недостаточным, избыточным или равным.
NetEgoУченик (154)
8 лет назад
2) Циклотронная частота зависит только от отношения электрического заряда к массе
Ма́сса (от др. -греч. μάζα, кусок теста) как он оказался в физике и стал главным непонятно.
Масса, как мера веса, не существует. Но есть электрическая плотность. То есть действует лишь закон плотностей, менее плотное выталкивается, более плотное стремится к ещё более плотному пока не достигнет равенства.
Илья
Высший разум
(360537)
8 лет назад
ВЕС электрона не удается измерить никакими приборами. Вес – это сила, с которой тело действует на опору, а для электрона значение этой силы настолько мало, что измерить ее пока даже не пытаются. Измерить можно МАССУ электрона.
Пролетая в магнитном поле перпендикулярно силовым линиям, заряженная частица испытывает действие силы Лоренца, которая действует строго перпендикулярно скорости. Так частица начнет описывать окружность. Если различные частицы, несущие одинаковый заряд, влетают в одно и то же поле с одинаковой скоростью, то чем больше масса частицы, тем больший радиус будет иметь окружность, которую она описывает. Измеряя радиус – можно пересчитать его в массу. Так вычислили массу электрона, точнее, отношение заряда к массе, но так как заряд электрона был уже известен, то таким образом вычислили массу.
Известно, что электроны имеют отрицательный заряд. Но каким образом можно убедиться в том, что масса электрона и его заряд постоянны для всех этих частиц? Проверить это можно, только поймав его на лету. Остановившись, он затеряется среди молекул и атомов, из которых состоит лабораторное оборудование. Процесс познания микромира и его частиц проделал долгий путь: от первых примитивных экспериментов до новейших разработок в области экспериментальной атомной физики.
Первые сведения об электронах
Сто пятьдесят лет назад электроны известны не были. Первым звоночком, указывающим на существование «кирпичиков» электричества, были опыты по электролизу. Во всех случаях каждая заряженная частичка вещества несла стандартный электрический заряд, имевший одну и ту же величину. В некоторых случаях количество заряда удваивалось или утраивалась, но всегда оставалось кратным одной минимальной величине заряда.
Эксперименты Дж. Томпсона
В лаборатории Кавендиша Дж. Томсон провел эксперимент, реально доказывающий существование частиц электричества. Для этого ученый исследовал излучение, исходящее из катодных трубок. В эксперименте лучи отталкивались от отрицательно заряженной пластины и притягивались к положительно заряженной. Гипотеза о постоянном присутствии в электрическом поле неких электрических частиц подтвердилась. Скорость движения их была сопоставима со скоростью света. Электрический заряд в пересчете на массу частицы оказался неимоверно большим. Из своих наблюдений Томпсон вывел несколько заключений, которые впоследствии были подтверждены другими исследованиями.
Выводы Томпсона
- Атомы могут быть разбиты при бомбардировке более быстрыми частицами. При этом из середины атомов вырываются отрицательно заряженные корпускулы.
- Все заряженные частицы имеют одинаковую массу и заряд вне зависимости от вещества, из которого они были получены.
- Масса этих частиц гораздо меньше массы самого легкого атома.
- Каждая частица вещества несет в себе наименьшую возможную долю электрического заряда, меньше которого в природе не существует. Любое заряженное тело несет в себе целое количество электронов.
Подробные опыты дали возможность произвести расчеты параметров таинственных микрочастиц. В результате было выяснено, что открытые заряженные корпускулы являются неделимыми атомами электричества. Впоследствии им было дано название электронов. Оно пришло еще из Древней Греции и оказалось уместным для описания новооткрытой частицы.
Прямое измерение скорости электрона
Поскольку нет никаких возможностей увидеть электрон, опыты, необходимые для измерения базовых величин этой элементарной частицы, производятся с помощью полей – электромагнитного и гравитационного. Если первое воздействует только на заряд электрона, то с помощью тонких опытов, учитывая гравитационное воздействие, можно было приблизительно рассчитать массу электрона.
Электронная пушка
Самые первые измерения масс и зарядов электронов были проведены с помощью электронной пушки. Глубокий вакуум в теле пушки позволяет электронам нестись узким пучком от одного катода к другому.
Электроны заставляют дважды проходить через узкие отверстия с постоянной скоростью v. Происходит процесс, подобный тому, как струя из садового шланга попадает в дырку в заборе. Порции электронов летят вдоль трубки с постоянной скоростью. Экспериментально доказано, что если напряжение, приложенное к электронной пушке, составляет 100 В, то скорость электрона будет рассчитана как 6 млн м/с.
Экспериментальные выводы
Прямое измерение скорости электрона показывает, что вне зависимости от того, из каких материалов сделана пушка и какова разность потенциалов, выполняется соотношение e/m = const.
Этот вывод был сделан уже в начале XX столетия. Однородные пучки заряженных частиц тогда еще создавать не умели, для опытов использовались другие приборы, но результат оставался тем же. Эксперимент позволил сделать несколько выводов. Отношение заряда электрона к его массе имеет одну и ту же величину для электронов. Это дает возможность сделать заключение об универсальности электрона как составной части любой материи в нашем мире. При очень больших скоростях величина e/m оказывается меньше ожидаемой. Этот парадокс вполне объясним тем фактом, что при высоких скоростях, сопоставимых со скоростью света, масса частицы увеличивается. Граничные условия преобразований Лоренца говорят о том, что при скорости тела, равной скорости света, масса этого тела становится бесконечной. Заметное увеличение массы электрона происходит в полном согласии с теорией относительности.
Электрон и его масса покоя
Парадоксальное заключение о том, что масса электрона непостоянна, влечет за собой несколько интересных выводов. В обычном состоянии масса покоя электрона не меняется. Ее можно измерить на основании различных экспериментов. В настоящее время масса электрона неоднократно измерена и составляет 9,10938291(40)·10⁻³¹ кг. Электроны с такой массой вступают в химические реакции, формируют движение электрического тока, улавливаются точнейшими приборами, регистрирующими ядерные реакции. Заметное увеличение этого значения возможно только при скоростях, близких к скорости света.
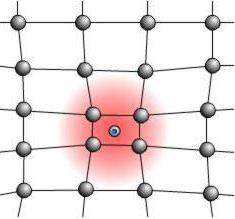
Электроны в кристаллах
Физика твердого тела – это наука, ведущая наблюдения за поведением заряженных частиц в кристаллах. Итогом многочисленных экспериментов стало создание особой величины, характеризующей поведение электрона в силовых полях кристаллических веществ. Это так называемая эффективная масса электрона. Ее величина вычисляется исходя из того, что движение электрона в кристалле подчиняется дополнительным силам, источником которых является сама кристаллическая решетка. Такое движение можно описать как стандартное для свободного электрона, но при расчете импульса и энергии такой частицы следует принимать во внимание не массу покоя электрона, а эффективную, значение которой будет другим.
Импульс электрона в кристалле
Состояние любой свободной частицы может быть охарактеризовано величиной ее импульса. Поскольку значение импульса уже определено, то, согласно принципу неопределенности, координаты частицы словно размыты по всему кристаллу. Вероятность встретить электрон в любой точке кристаллической решетки практически одинакова. Импульс электрона характеризует его состояние в любой координате энергетического поля. Расчеты показывают, что зависимость энергии электрона от его импульса такая же, как и свободной частицы, но при этом масса электрона может принимать значение, отличающееся от обычного. В целом энергия электрона, выраженная через импульс, будет иметь вид E(p)=p2/2m*. В данном случае m* – эффективная масса электрона. Практическое применение эффективной массы электрона чрезвычайно важно при разработке и изучении новых полупроводниковых материалов, применяемых в электронике и микротехнике.
Масса электрона, как и любой другой квазичастицы, не может быть охарактеризована стандартными характеристиками, пригодными в нашей Вселенной. Любая характеристика микрочастицы способна удивлять и подвергать сомнению все наши представления об окружающем мире.
МИР АТОМА
ЭЛЕКТРОН
Мы упоминали уже о частицах атомов, движущихся по проводам, внутри радиоламп, рентгеновских трубок и многих других приборов. Эти частицы, получившие название электронов, являются мельчайшими частичками отрицательного электричества.
В отличие от атомов химических элементов электрон является элементарной частичкой; мы никогда не наблю
Дали её частей; при современных возможностях мы не можем разбить её на части. Электрон — это наименьший отрицательный электрический заряд.
Все электроны совершенно одинаковы, независимо от того, какому атому они принадлежали или принадлежат.
Масса электрона в 1838 раз меньше массы легчайшего (водородного) атома и равна
О, ООО ООО ООО ООО ООО ООО ООО ООО ООО 910 660 грамма.
Электрический заряд одного электрона также чрезвычайно мал. Через нить горящей двадцативаттной лампочки (при юродском напряжении в сети) каждую секунду проходит миллиард миллиардов электронов; все они весят менее одной миллиардной доли грамма!
Невольно напрашивается вопрос, как были определены с такой точностью заряд и масса электрона?
Чтобы измерить заряд и массу электрона, нужно прежде всего получить свободные, не связанные с веществом электроны. Для этого существует множество способов. Электроны вырываются как из твёрдого вещества, так и из молекул и атомов газа при сильном нагревании, в некоторых случаях при освещении светом, в особенности невидимыми ультрафиолетовыми лучами и ещё лучше — рентгеновыми лучами. Особенно легко можно вырывать электроны из металлов, в которых они очень свободно перемещаются (в этом отличие металлов от непроводников-изоляторов, в которых электроны «крепко связаны»).
Итак, мы имеем свободные электроны. Можно ли непосредственно, на весах, взвесить один электрон? Очевидно, это невозможно, он слишком мал. Но оказалось возможным определить заряд электрона, а затем косвенным путём найти и его массу.
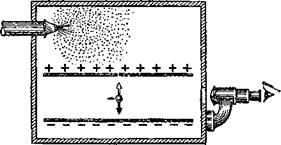
Представьте себе крошечную капельку масла, медленно падающую между двумя металлическими пластинками под действием силы тяжести (рис. 8). Создадим на капельке электрический заряд. Тогда падение капельки можно будет приостановить, зарядив пластинки, между которыми движется капелька, так, чтобы верхняя пластинка притягивала заряд капельки, а нижняя отталкивала его. Капелька остановится, если электрическая сила, тянущая вверх заряд капельки, окажется в точности равной силе тяжести, которая тянет капельку вниз.
Таким образом, мы сможем определить действующую на капельку электрическую силу, а значит, и её заряд; необходимо только точно знать силу тяжести, действующую на капельку, а для этого нужно знать и её массу. Массу капельки удалось определить, определив скорость её свободного падения (без действия электрических сил), — чем тяжелее капелька, тем быстрее падает она, преодолевая сопротивление воздуха.
Этим способом был определён заряд электрона.
Опыт проводился так. Пульверизатор, расположенный над пластинками, распылял немного масла. Нужно было
Рис. 8. Схематическое изображение прибора (изображён в разрезе) для определения заряда электрона. Размер капельки между пластинками сильно увеличен. Белая стрелка — электрическая сила, тянущая заряд капельки вверх, чёрная стрелка — сила тяжести.
Подождать, пока какая-либо из капелек масла не попадала между пластинками, проникая туда через крошечное, специально для этого сделанное отверстие в верхней пластинке. С помощью специального микроскопа очень точно определялась скорость падения капельки. После этого на короткое время зажигалась рентгеновская лампа. Рентгеновы лучи, проходя между пластинками, вырывали из молекул воздуха множество электронов. Очень скоро один или несколько электронов или положительно заряженных молекул оседало на капельку; капелька приобретала необходимый заряд. Затем пластинкам сообщался заряд такой величины, чтобы капелька повисла неподвижно.
Определив наименьший из зарядов, который могла нести капелька, нашли заряд одного электрона. Все другие получавшиеся заряды были больше найденного
наименьшего в два, в три, в четыре и в большее целое число раз, что соответствовало двум, трём, четырём и более электронам, осевшим на капельку.
Теперь нужно определить его массу, не взвешивая его. Как это сделать?
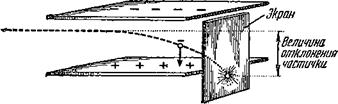
Представьте себе поток невидимых заряженных частичек, проносящихся между заряженными пластинками (или полюсами магнита). Под действием электрических (или магнитных) сил они отклоняются вниз (рис. 9). Цель, в которую попадают частички, мы видим благодаря экрану, покрытому сернистым цинком, или обычной фотопластинке. Сернистый цинк светится от ударов заряженных частичек, а на фотопластинку эти заряженные
Рис. 9. Отклонение летящего электрона под действием электрических сил позволяет определить массу электрона, если известны его скорость и действующая на него сила.
Частицы действуют так же, как и лучи света. Мы видим по маленькой светящейся точке на экране (или чёрной точке на фотопластинке), как отклонились частички. Мы можем судить о массе частичек, если знаем их скорость и силу, которая вызвала отклонение. А силу эту мы знаем, зная заряд частичек.
На самом деле прибор, конечно, оказывается гораздо более сложным, чем изображённый на рисунке, так как нужно ещё получить частички с одинаковой скоростью.
Определив массу электрона, мы убеждаемся в том, что эти мельчайшие отрицательно заряженные частички обладают массой, во много раз меньшей массы любого атома.
Рыло время, когда говорили, что физика — это техника ” завтрашнего дня. Теперь это неверно. Физика — это не только наука, изучающая мир, — это основа техники сегодняшнего дня. Раскрывая …
Обстреливая ядра нейтронами, быстрыми протонами, дейтронами, гелиевыми ядрами, можно осуществить множество ядерных превращений. При этом получаются не только атомы известных устойчивых изотопов, но и новые, неустойчивые, то-есть радиоактивные атомы. На …
Советский учёный Д. В. Скобельцын изучал с помощью камеры Вильсона приходящие на З’емлю из глубин мирового пространства «космические лучи». Камера была помещена между полюсами больших магнитов. Пролетавшие сквозь неё сверху …